Прямолинейное равноускоренное движение как найти время - Сайт, где вы сможете решить свои вопросы

Равноускоренное движение

Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению (в случае равнозамедленного движения модуль скорости равномерно меняется). Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение, в отличие от неравномерного, – частный случай ускоренного в равной степени движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под углом к горизонту) более подробно с вычислением. Такое движение можно рассчитать и представить в виде суммы движений относительно вертикальной и горизонтальной осей.

Как найти ускорение в физике? Нахождение ускорения в физике происходит с учетом того, что в любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.

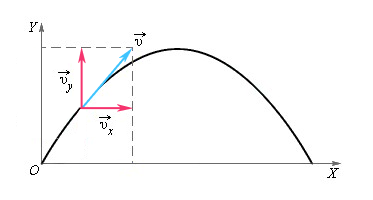
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – движение равноускоренное и прямолинейное. Будем рассматривать определенные проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости (формула ускорения) при равноускоренном движении:

v=v0+at.

Здесь v0 – начальная скорость тела, a=const – ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Вот небольшой тест.

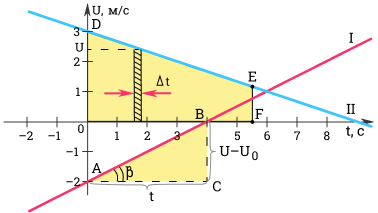
Как найти ускорение? Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC. Вот как выглядит формула ускорения в физике.

a=v-v0t=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v0=-2 мс; a=0,5 мс2.

Для второго графика: v0=3 мс; a=-13 мс2.

По данному графику физик может также вычислить (произвести определение) перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.

Мы знаем, что v-v0=at, поэтому окончательная формула или расчет для перемещения тела примет вид:

s=v0t+at22

Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.

Закон равноускоренного движения

y=y0+v0t+at22.

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – находить координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s=v2-v022a.

По известным начальной скорости, ускорению и перемещению может находиться конечная скорость тела:

v=v02+2as.

При v0=0 s=v22a и v=2as

Важно!

Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. Они могут принимать как положительные, так и отрицательные значения – это будет зависеть от характера движения и направления координатных осей в условиях конкретной задачи.

Источник

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

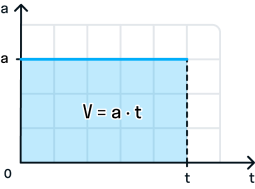
Взаимосвязь скорости, времени и расстояния:
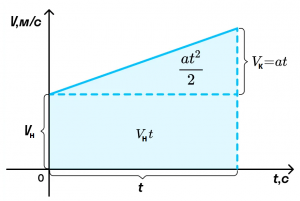
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

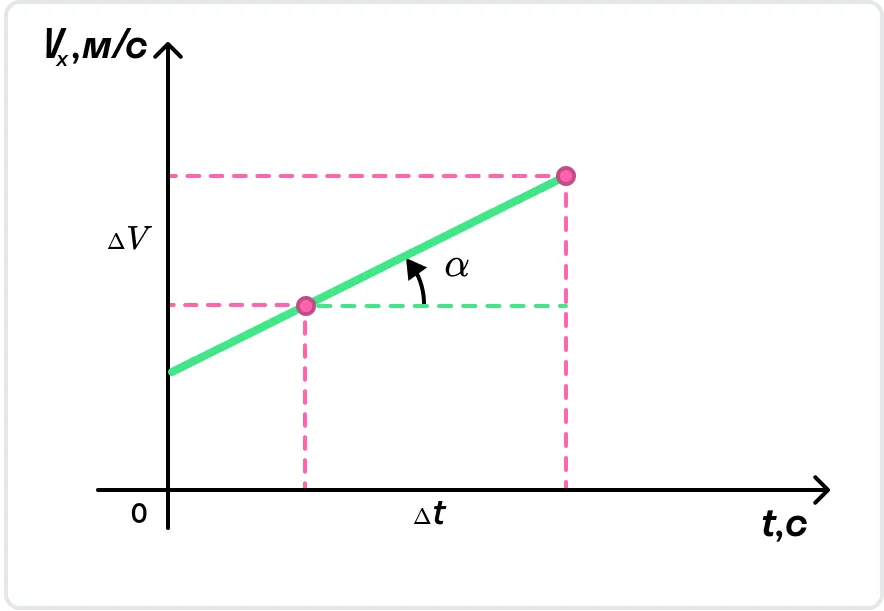
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

Конвертер единиц измерения расстояния (длины)
Конвертер единиц измерения скорости
Конвертер единиц измерения времени

Источник

«Формула времени. Решение задач»

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.

Время обозначается как t. Единица измерения времени – с (секунды).

Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v₀) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v₀).

Решение задач через формулу времени

Задача № 1.

Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Ответ: 200 с.

Задача № 2.

Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

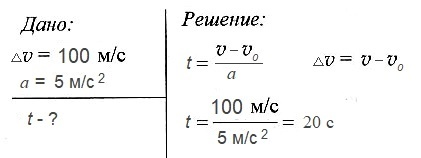Ответ: 20 с.

Задача № 3.

Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t₁ = 3 ч, а плот то же расстояние – за время t₀ =12 ч. Какое время t₂ затратит моторная лодка на обратный путь?

Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через v_л , а скорость течения через v_т. Тогда t₀ = L / v_т , t₁ = L / (v_л + v_т) , t₂ = L / (v_л — v_т) . Исключая из записанной системы уравнений L, v_л и v_т
находим

Ответ: 6 ч.

Конспект урока «Формула времени. Решение задач».

Следующая тема: «».

Источник

Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения

Равноуско́ренное движе́ние — движение тела, при котором его ускорение постоянно по модулю и направлению^[1].

Скорость при этом определяется формулой

${displaystyle {vec {v}}(t)={vec {v}}_{0}+{vec {a}}t}$

где ${displaystyle {vec {v}}_{0}}$ — начальная скорость тела, — время. Траектория имеет вид участка параболы или прямой.

Примером такого движения является полёт камня, брошенного под углом alpha к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением , направленным вертикально вниз.

Частным случаем равноускоренного движения является равнозамедленное, когда векторы vec{v} и противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для ${displaystyle alpha =90^{0}}$ при подъёме).

Характер равноускоренного движения[править | править код]

Равноускоренное движение происходит в плоскости, содержащей векторы ускорения и начальной скорости ${displaystyle {vec {v}}_{0}}$ . С учётом того, что (здесь — радиус-вектор), траектория описывается выражением

${displaystyle {vec {r}}(t)={vec {r}}_{0}+{vec {v}}_{0}t+{frac {{vec {a}}t^{2}}{2}}}$

На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со или противо- направленности) векторов и ${displaystyle {vec {v}}_{0}}$ превращается в отрезок прямой.

Для каждой из координат, скажем , могут быть записаны аналогичные по структуре выражения:

${displaystyle y(t)=y_{0}+v_{0y}t+{frac {a_{y}t^{2}}{2}}}$

где ${displaystyle a_{y}}$ — составляющая ускорения вдоль оси , а ${displaystyle {vec {r}}_{0}=x_{0}{vec {i}}+y_{0}{vec {j}}+z_{0}{vec {k}}}$ — радиус-вектор материальной точки в момент ( vec{i} , vec{j} , vec{k} — орты).

В примере с камнем ${displaystyle x_{0}=y_{0}=z_{0}=0}$ , компоненты ускорения ${displaystyle a_{x}=a_{z}=0}$ , ${displaystyle a_{y}=-g}$ , начальной скорости ${displaystyle v_{x0}=v_{0}cos alpha }$ , ${displaystyle v_{y0}=v_{0}sin alpha }$ , ${displaystyle v_{z0}=0}$ , при этом ${displaystyle x(t)=v_{0x}t}$ , а значит, ${displaystyle y=operatorname {tg} alpha cdot x-g/2v_{0}^{2}cos ^{2}alpha cdot x^{2}}$ .

Перемещение и скорость[править | править код]

В случае равноускоренного движения любая из компонент скорости, например ${displaystyle v_{x}}$ , зависит от времени линейно:

${displaystyle v_{x}=v_{0x}+a_{x}t}$

При этом имеет место следующая связь между перемещением ( ${displaystyle Delta x=x-x_{0}}$ ) вдоль координаты и скоростью вдоль той же координаты:

$Delta x={frac {v_{x}^{2}-v_{{0x}}^{2}}{2a_{x}}}$

Отсюда можно получить выражение для -составляющей конечной скорости тела при известных -составляющих начальной скорости и ускорения:

$v_{x}=pm {sqrt {v_{{0x}}^{2}+2a_{x}Delta x}}$

Если ${displaystyle a_{x}=0}$ , то ${displaystyle v_{x}=v_{ox}}$ , а ${displaystyle Delta x=v_{0x}t}$ .

Выражения для смещений Delta y , Delta z и компонент скорости вдоль координат и принимают точно такой же вид, как для Delta x и $v_{x}$ , но символ всюду заменяется на или .

Суммарно, по теореме Пифагора, перемещение составит

${displaystyle |Delta {vec {r}}|={sqrt {(Delta x)^{2}+(Delta y)^{2}+(Delta z)^{2}}}}$

а модуль конечной скорости находится как

$|{vec v}|={sqrt {v_{{x}}^{2}+v_{{y}}^{2}+v_{{z}}^{2}}}$

Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени , модуль скорости тела превысит величину скорости света в вакууме , что исключается теорией относительности.

Условие осуществления[править | править код]

Равноускоренное движение реализуется при действии на тело (материальную точку) постоянной силы vec{F} , обычно в однородном гравитационном или электростатическом поле, если величина скорости тела значительно меньше, чем скорость света . Тогда, по второму закону Ньютона, ускорение составит

${vec {a}}={frac {{vec {F}}}{m}},$

где через обозначена масса тела. В примере с камнем роль vec{F} играет сила тяжести.

Если же скорость тела сопоставима со скоростью света, то закон Ньютона в выписанном виде неприменим. При этом, в случае действия постоянной силы, происходит так называемое релятивистски равноускоренное движение, при котором постоянно только собственное ускорение, а ускорение в фиксированной ИСО приближается к нулю со временем по мере приближения величины скорости к её пределу .

Теорема о кинетической энергии точки[править | править код]

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

$ma_{x}Delta x={frac {mv_{x}^{2}}{2}}-{frac {mv_{{0x}}^{2}}{2}}$

Записав аналогичные соотношения для координат и и просуммировав все три равенства, получим соотношение:

${displaystyle {vec {F}}cdot Delta {vec {r}}={frac {mv^{2}}{2}}-{frac {mv_{0}^{2}}{2}}}$

Слева стоит работа постоянной равнодействующей силы vec F , а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения^[2].

Равнопеременное движение[править | править код]

Равнопеременным называется движение, при котором тангенциальная (параллельная скорости) составляющая ускорения постоянна^[3]. Такое движение не является равноускоренным, кроме ситуации, когда оно происходит по прямой, но в математическом плане может быть рассмотрено аналогично.

В этом случае вводится обобщённая координата , часто называемая путём, соответствущая длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

$Delta S={frac {v^{2}-v_{{0}}^{2}}{2a_{tau }}}$

где $a_{tau }$ — тангенциальное ускорение, «отвечающее» за изменение модуля скорости тела. Для скорости получаем:

$v=pm {sqrt {v_{{0}}^{2}+2a_{tau }Delta S}}$

При ${displaystyle a_{tau }=0}$ имеем движение с постоянной по модулю скоростью.

Иногда прилагательное равнопеременное заменяют на криволинейное равноускоренное, что вносит путаницу, так как, скажем, равноускоренное движение камня по кривой (параболе) в поле тяжести не равнопеременное.

См. также[править | править код]

Релятивистски равноускоренное движение

Примечания[править | править код]

↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 37. — 560 с. — ISBN 5-9221-0225-7.
↑ Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М.: «Высшая школа», 1995. — С. 214. — 416 с. — ISBN 5-06-003117-9.
↑ См. Физический энциклопедический словарь — М.: Советская энциклопедия, под. ред. А. М. Прохорова (1983), статья «Равнопеременное движение», стр. 602.

Источник

Равноускоренное движение

Формулы для равноускоренного движения

Закон равноускоренного движения

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

Vк=Vн+at

Формула для ускорения при равноускоренном движении:

a=(Vк-Vн)/t

Задача 1

Формула расстояния при равноускоренном движении

S = t*(Vн+ Vк)/2

S = Vнt + at2/2 = t*(Vн + at/2)

2аS = Vк2−Vн2

Задача 2

Перемещение при равноускоренном движении

Равноускоренное движение: графически

Задача 3

«Формула времени. Решение задач»

Решение задач через формулу времени

Задача № 1.

Задача № 2.

Задача № 3.

Характер равноускоренного движения[править | править код]

Перемещение и скорость[править | править код]

Условие осуществления[править | править код]

Теорема о кинетической энергии точки[править | править код]

Равнопеременное движение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Вам также может понравиться

Как составить требования в прокуратуру

Как найти местоположение телефона по почте

Как найти все буквы на клавиатуре андроид

Добавить комментарий Отменить ответ

V_к=V_н+at

a=(V_к-V_н)/t

S = t*(V_н+ V_к)/2

S = V_нt + at²/2 **= t*(V_н + at/2)**

2аS = V_к²−V_н²