XXV СТАВРОПОЛЬСКАЯ КРАЕВАЯ ОТКРЫТАЯ НАУЧНАЯ КОНФЕРЕНЦИЯ ШКОЛЬНИКОВ
Секция: математика
Название работы:
«Кратчайшие расстояния на прямоугольном параллелепипеде»
Автор работы:
Беглов Никита Владимирович
Место выполнения работы:
с. Тугулук, МКОУ СОШ 8,
5 класс
Научный руководитель:
Шеховцова Елена Сергеевна,
учитель математики и информатики
МКОУ СОШ 8 с. Тугулук
г. Ставрополь, 2014
Оглавление
- Введение……………………………………………………………1
- Развертка многогранника…………….……………………….…..2
- Развертка помогает решать задачи…………………………….….3
4.1. Кратчайшие на кубе……………………………………………..3
4.2. Головоломка Генри Эрнеста Дьюдени…………………………4
4.3. Задача о пауке и мухе……………………………………………5
- Заключение…………………………………………………….……8
- Используемая литература…………………………………………..9
I. Введение
Нахождение кратчайших расстояний на поверхности между двумя точками находит широкое применение в геодезических практических задачах. Самыми простыми поверхностями являются куб и прямоугольный параллелепипед, которые и рассматриваются в данном исследовании.
Расстоянием между двумя точками называют отрезок, соединяющий эти точки. Однако в жизни довольно часто трудно добраться от одного пункта до другого по прямой. Тем не менее, из всех возможных вариантов стараются выбрать самую короткую дорогу.
В пространстве это несколько сложнее, чем на плоскости.
Цели исследования: научиться выполнять построения кратчайших расстояний на поверхностях куба и прямоугольного параллелепипеда, выяснить, сколько существует разверток у куба.
Задачи исследования: научиться строить развертки для куба и прямоугольного параллелепипеда; изучить задачу «о пауке и мухе», определить кратчайшие расстояния на кубе и прямоугольном параллелепипеде для различных расположений «мухи» и «паука».
Гипотеза: определение кратчайшего расстояния на поверхности прямоугольного параллелепипеда зависит от правильно выбранного вида развертки.
Методы исследования: изучение математической литературы, анализ собранного материала, математические методы, графические методы.
Предмет исследования: поиск кратчайших линий между двумя точками на поверхностях.
Объект исследования: развертки прямоугольного параллелепипеда и куба.
II. Развертка многогранника
Понятие развертки включает в себя больше, чем просто кусок картона. Представим себе многогранник не как тело, а как поверхность, составленную по некоторым правилам из многоугольников. Поэтому, многогранник как поверхность – это конечный набор плоских многоугольников, расположенных в пространстве так, что 1) каждая сторона любого из них одновременно служит стороной ровно другого, 2) любые два из них соединяются «дорожкой» из многоугольников набора, причем в «дорожке» последовательные многоугольники граничат по стороне, 3) если два многоугольника имеют общую вершину, то соединяющую их «дорожку» можно выстроить из многоугольников с той же вершиной. Условие 1 обеспечивает замкнутость поверхности – у нее нет края, условие 2 говорит о том, что поверхность связная – состоит из одного куска, условие 3 – исключает из числа многогранников, например, фигуру из двух кубов с общей вершиной, которые не имеют других общих точек. Куб является прямоугольным параллелепипедом, у которого все грани – квадраты.
Куб очень симметричная фигура и на подсознательном уровне нам кажется, что и число развёрток куба должно быть каким-то «красивым», похожим на другие характеристики куба (напомним, что куб имеет 12 рёбер, 8 вершин, 6 граней и 4 диагонали). Как оказалось, куб имеет 11 развёрток(рис.1).
Рис.1. Развертки куба
IV. Развертка помогает решать задачи
4.1. Кратчайшие на кубе
Задача1.
Рис. 2
На поверхности прозрачного куба сидит паук и видит сидящую на другой грани куба муху(рис. 2). Чтобы поймать муху пауку нужно как можно скорее до нее добраться, ведь муха может улететь. Другими словами, пауку необходимо двигаться к мухе кратчайшим маршрутом. Изобразите путь, по которому должен двигаться паук.
Решение. Мысленно отогнем грань куба на которой сидит паук, расположив верхнюю и боковую грани в одной плоскости. Посмотрим на эти грани сверху. Кратчайший путь от паука до мухи теперь найти очень просто. Достаточно соединить отрезком точки в которых они сидят(рис.3).
Рис. 3
Задача 2.
На ребре куба сидит муха. Она хочет проползти по каждой его грани вернутся в исходную точку. Укажите кратчайший путь мухи.
Решение. Воспользуемся разверткой куба №10(рис.1). Точки А и В представляют одну и ту же точку на ребре куба. Кратчайшим путем, их соединяющим, является отрезок АВ(рис. 4).
Рис. 4
4.2. Головоломка Генри Эрнеста Дьюдени
Наиболее известная головоломка Дьюдени – задача о пауке и мухе – представляет собой элементарную, но весьма изящную задачу из геометрии геодезических. Впервые она была опубликована в 1903 году в одной английской газете, но внимание широкой публики привлекла лишь два года спустя, после того как ее перепечатала лондонская газета «Дейли мейл».
Комната имеет форму прямоугольного параллелепипеда, размеры которого указаны на рисунке 5. Посредине боковой стены на расстоянии одного фута от потолка сидит паук. Посредине противоположной стены на расстоянии одного фута от пола сидит муха. От страха у нее отнялись ноги, и она не может двинуться с места. Спрашивается, каково кратчайшее расстояние, которое должен преодолеть паук для того, чтобы схватить муху?
Рис. 5
Для решения задачи нужно построить развертку граней прямоугольного параллелепипеда и провести на ней прямую от местонахождения паука к точке, в которой сидит муха. Поскольку построить развертку можно многими способами, найти кратчайшее расстояние не так легко, как кажется на первый взгляд. Кратчайший путь определяется только с такой разверткой (рис. 6)
Рис. 6
4.3. Задача о пауке и мухе
На потолке в углу С комнаты сидит паук, а на полу в противоположном углу К спит муха(рис.7). Какой путь должен избрать паук, чтобы добраться до мухи по кратчайшему расстоянию?
Рис. 7
Развернем параллелепипед, изображающий комнату, на плоскость (рисунок 8). Паук сидит в точке С, а муха – в точке К. Соединим СК отрезком. Этот путь будет кратчайшим среди всех путей, пересекающих ребро EG. Аналогично, путь KC2 будет кратчайшим среди всех путей, пересекающих ребро FD(точка С2 также отвечает вершине С нашего параллелепипеда). Для того, чтобы представить себе кратчайший среди путей, пересекающих ребро GF, развернем комнату, как показано на рисунке 9. Мы видим, что КС3 – кратчайший из путей, пересекающих ребро GF. Остается решить вопрос: какой же из этих трех путей (КС, КС2, КС3) будет самым коротким. Оказывается, что это зависит от относительных размеров комнаты в длину, ширину и высоту.
Рис. 8
Рис. 9
Если а>b, a>c, то кратчайшим путем будет путь КС.
Если с>a, c>b, то кратчайший путь КС2.
Если b>a, b>c, то кратчайший путь КС3.
Можно заметить, что кратчайший путь паука должен пересекать самое длинное из ребер EG, GF, FD.
Задача о пауке и мухе оказалась сложнее, чем можно было думать с первого взгляда.
V. Заключение
В работе были рассмотрены задачи на кратчайшее расстояние на поверхности прямоугольного параллелепипеда и куба, как частного вида прямоугольного параллелепипеда.
При нахождении кратчайших расстояний на изучаемых поверхностях использовались их развертки. Работая с источниками, выяснилось, что у куба существует 11 различных разверток, составленных из граней.
Решая задачу «о пауке и мухе» стало очевидно, для того чтобы изобразить кратчайший путь на поверхности прямоугольного параллелепипеда, необходимо знать его относительные размеры, так как от этого зависит выбор развертки, что влияет на получение искомого результата.
VI. Используемая литература
- Депман И.Я. За страницами учебника математики. М.. Просвещение.1989.
- Еленский Щ. По следам Пифагора. М., Детгиз. 1961.
- Смирнова И. Смирнов В. Экстремальные задачи по геометрии. Математика. № 2. 2007.
- Франц Герман. О развертках куба.KIW-Gesellschaft e. V., Dresden, BRD.
- Е. И. Игнатьев. Математическая смекалка. Занимательные задачи, игры, фокусы, парадоксы. Москва, «Омега», 1994.
Среди огромного количества стереометрических
задач в учебниках геометрии, в различных
сборниках задач, пособиях по подготовке в ВУЗы
крайне редко встречаются задачи на нахождение
расстояния между скрещивающимися прямыми.
Возможно, это обусловлено как узостью их
практического применения (относительно школьной
программы, в отличие от “выигрышных” задач на
вычисление площадей и объемов), так и сложностью
данной темы.
Практика проведения ЕГЭ показывает, что многие
учащиеся вообще не приступают к выполнению
заданий по геометрии, входящих в экзаменационную
работу. Для обеспечения успешного выполнения
геометрических заданий повышенного уровня
сложности необходимо развивать гибкость
мышления, способность анализировать
предполагаемую конфигурацию и вычленять в ней
части, рассмотрение которых позволяет найти путь
решения задачи.
Школьный курс предполагает изучение четырех
способов решения задач на нахождение расстояния
между скрещивающимися прямыми. Выбор способа
обусловлен, в первую очередь, особенностями
конкретной задачи, предоставленными ею
возможностями для выбора, и, во вторую очередь,
способностями и особенностями
“пространственного мышления” конкретного
учащегося. Каждый из этих способов позволяет
решить самую главную часть задачи – построение
отрезка, перпендикулярного обеим скрещивающимся
прямым (для вычислительной же части задач
деление на способы не требуется).
Основные способы решения задач на нахождение
расстояния между скрещивающимися прямыми
Нахождение длины общего перпендикуляра двух
скрещивающихся прямых, т.е. отрезка с концами на
этих прямых и перпендикулярного каждой из этих
прямых.
Нахождение расстояния от одной из
скрещивающихся прямых до параллельной ей
плоскости, проходящей через другую прямую.
Нахождение расстояния между двумя
параллельными плоскостями, проходящими через
заданные скрещивающиеся прямые.
Нахождение расстояния от точки, являющейся
проекцией одной из скрещивающихся прямых, на
перпендикулярную ей плоскость (так называемый
“экран”) до проекции другой прямой на ту же
самую плоскость.
Проведем демонстрацию всех четырех способов на
следующей простейшей задаче: “В кубе с
ребром а найти расстояние между любым ребром
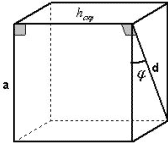
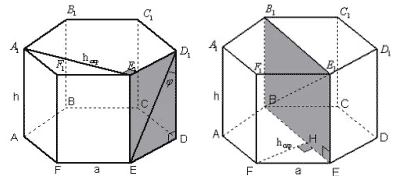
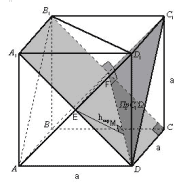
и диагональю не пересекающей его грани”. Ответ: .
1 способ.
Рисунок 1
hскр перпендикулярна плоскости боковой
грани, содержащей диагональ d и
перпендикулярна ребру, следовательно, hскр
и является расстоянием между ребром а и
диагональю d.
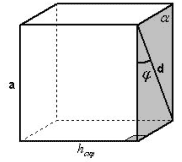
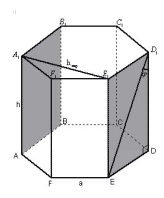
2 способ.
Рисунок 2
Плоскость A параллельна ребру и проходит через
данную диагональ, следовательно, данная hскр
является не только расстоянием от ребра до
плоскости A, но и расстоянием от ребра до данной
диагонали.
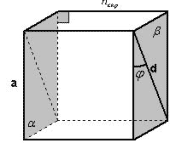
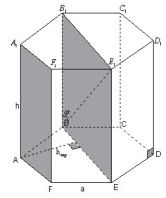
3 способ.
Рисунок 3
Плоскости A и B параллельны и проходят через две
данные скрещивающиеся прямые, следовательно,
расстояние между этими плоскостями равно
расстоянию между двумя скрещивающимися прямыми.
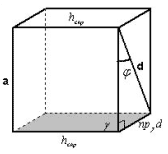
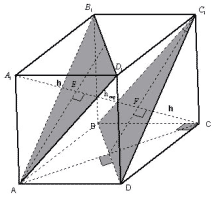
4 способ.
Рисунок 4
Плоскость A перпендикулярна ребру куба. При
проекции на A диагонали d данная диагональ
обращается в одну из сторон основания куба.
Данная hскр является расстоянием между
прямой, содержащей ребро, и проекцией диагонали
на плоскость C, а значит и между прямой,
содержащей ребро, и диагональю.
Остановимся подробнее на применении каждого
способа для изучаемых в школе многогранников.
СПОСОБ I.
Применение первого способа достаточно
ограничено: он хорошо применяется лишь в
некоторых задачах, так как достаточно сложно
определить и обосновать в простейших задачах
точное, а в сложных – ориентировочное
местоположение общего перпендикуляра двух
скрещивающихся прямых. Кроме того, при
нахождении длины этого перпендикуляра в сложных
задачах можно столкнуться с непреодолимыми
трудностями.
Примеры
Задача 1. В прямоугольном параллелепипеде с
размерами a, b, h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю основания.
Рисунок 5
Пусть AHBD.
Так как А1А перпендикулярна плоскости АВСD ,
то А1А
AH.
AH перпендикулярна обеим из двух скрещивающихся
прямых, следовательно AH?- расстояние между
прямыми А1А и BD. В прямоугольном
треугольнике ABD, зная длины катетов AB и AD, находим
высоту AH, используя формулы для вычисления
площади прямоугольного треугольника. Ответ:
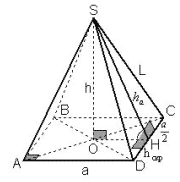
Задача 2. В правильной 4-угольной пирамиде с
боковым ребром L и стороной основания a
найти расстояние между апофемой и стороной
основания, пересекающей боковую грань,
содержащую эту апофему.
Рисунок 6
SHCD как
апофема, ADCD,
так как ABCD – квадрат. Следовательно, DH –
расстояние между прямыми SH и AD. DH равно половине
стороны CD. Ответ:
СПОСОБ II
Применение этого способа также ограничено в
связи с тем, что если можно быстро построить (или
найти уже готовую) проходящую через одну из
скрещивающихся прямых плоскость, параллельную
другой прямой, то затем построение
перпендикуляра из любой точки второй прямой к
этой плоскости (внутри многогранника) вызывает
трудности. Однако в несложных задачах, где
построение (или отыскивание) указанного
перпендикуляра трудностей не вызывает, данный
способ является самым быстрым и легким, и поэтому
доступен.
Примеры
Задача 2. Решение уже указанной выше задачи
данным способом особых трудностей не вызывает.
Рисунок 7
Плоскость EFM параллельна прямой AD, т. к AD || EF.
Прямая MF лежит в этой плоскости, следовательно,
расстояние между прямой AD и плоскостью EFM равно
расстоянию между прямой AD и прямой MF. Проведем OHAD. OH
EF, OH
MO,
следовательно, OH(EFM),
следовательно, OH – расстояние между прямой AD и
плоскостью EFM, а значит, и расстояние между прямой
AD и прямой MF. Находим OH из треугольника AOD.
Ответ:
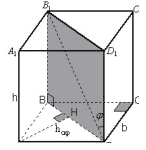
Задача 3. В прямоугольном параллелепипеде с
размерами a,b и h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю параллелепипеда.
Рисунок 8
Прямая AA1 параллельна плоскости BB1D1D,
B1D принадлежит этой плоскости,
следовательно расстояние от AA1 до
плоскости BB1D1D равно расстоянию между
прямыми AA1 и B1D. Проведем AHBD. Также, AH
B1B,
следовательно AH(BB1D1D), следовательно AH
B1D, т. е. AH –
искомое расстояние. Находим AH из прямоугольного
треугольника ABD.
Ответ:
Задача 4. В правильной шестиугольной призме
A:F1 c высотой h и стороной основания a
найти расстояние между прямыми:
Рисунок 9 Рисунок 10
а) AA1 и ED1.
Рассмотрим плоскость E1EDD1. A1E1EE1, A1E1
E1D1,
следовательно
A1E1 (E1EDD1). Также A1E1
AA1.
Следовательно, A1E1 является
расстоянием от прямой AA1 до плоскости E1EDD1.
ED1(E1EDD1).,
следовательно AE1 – расстояние от прямой AA1
до прямой ED1. Находим A1E1 из
треугольника F1A1E1 по теореме
косинусов. Ответ:
б) AF и диагональю BE1.
Проведем из точки F прямую FH перпендикулярно BE.
EE1FH, FH
BE, следовательно
FH(BEE1B1),
следовательно FH является расстоянием между
прямой AF и (BEE1B1), а значит и
расстоянием между прямой AF и диагональю BE1.
Ответ:
СПОСОБ III
Применение этого способа крайне ограничено,
так как плоскость, параллельную одной из прямых
(способ II) строить легче, чем две параллельные
плоскости, однако способ III можно использовать в
призмах, если скрещивающиеся прямые принадлежат
параллельным граням, а также в тех случаях, когда
в многограннике несложно построить параллельные
сечения, содержащие заданные прямые.
Примеры
Задача 4.
Рисунок 11
а) Плоскости BAA1B1 и DEE1D1
параллельны, так как AB || ED и AA1 || EE1. ED1DEE1D1,
AA1(BAA1B1),
следовательно, расстояние между прямыми AA1
и ED1 равно расстоянию между плоскостями BAA1B1
и DEE1D1. A1E1AA1, A1E1
A1B1, следовательно, A1E1
BAA1B1.
Аналогично доказываем, что A1E1(DEE1D1). Т.о., A1E1
является расстоянием между плоскостями BAA1B1
и DEE1D1, а значит, и между прямыми AA1
и ED1. Находим A1E1 из треугольника
A1F1E1, который является
равнобедренным с углом A1F1E1,
равным .
Ответ:
Рисунок 12
б) Расстояние между AF и диагональю BE1
находится аналогично.
Ответ:.
Задача 5. В кубе с ребром а найти
расстояние между двумя непересекающимися
диагоналями двух смежных граней.
Данная задача рассматривается как
классическая в некоторых пособиях, но, как
правило, ее решение дается способом IV, однако
является вполне доступной для решения с помощью
способа III.
Рисунок 13
Некоторую трудность в данной задаче вызывает
доказательство перпендикулярности диагонали A1C
обеим параллельным плоскостям (AB1D1 ||
BC1D). B1CBC1 и BC1
A1B1, следовательно,
прямая BC1 перпендикулярна плоскости A1B1C,
и следовательно, BC1A1C. Также, A1C
BD.
Следовательно, прямая A1C перпендикулярна
плоскости BC1D. Вычислительная же часть
задачи особых трудностей не вызывает, так как hскр
= EF находится как разность между диагональю куба
и высотами двух одинаковых правильных пирамид A1AB1D1
и CC1BD.
Ответ:
СПОСОБ IV.
Данный способ имеет достаточно широкое
применение. Для задач средней и повышенной
трудности его можно считать основным. Нет
необходимости применять его только тогда, когда
один из трех предыдущих способов работает проще
и быстрее, так как в таких случаях способ IV может
только усложнить решение задачи, или сделать его
труднодоступным. Данный способ очень выгодно
использовать в случае перпендикулярности
скрещивающихся прямых, так как нет необходимости
построения проекции одной из прямых на “экран”
Примеры.
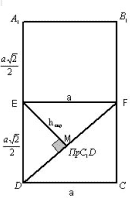
Задача 5. Все та же “классическая” задача
(с непересекающимися диагоналями двух смежных
граней куба) перестает казаться сложной, как
только находится “экран” – диагональное
сечение куба.
Рисунок 14
Экран:
Рисунок 15
Рассмотрим плоскость A1B1CD. C1F (A1B1CD),
т. к. C1FB1C
и C1FA1B1.
Тогда проекцией C1D на “экран” будет
являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием
между двумя непересекающимися диагоналями двух
смежных граней. Находим EM из прямоугольного
треугольника EDF. Ответ:.
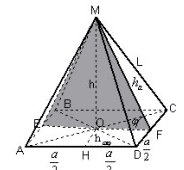
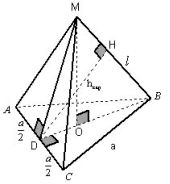
Задача 6. В правильной треугольной пирамиде
найти расстояние и угол между скрещивающимися
прямыми: боковым ребром l и стороной
основания a.
Рисунок 16
В данной и аналогичных ей задачах способ IV
быстрее других способов приводит к решению, так
как построив сечение, играющее роль “экрана”,
перпендикулярно AC (треугольник BDM), видно, что
далее нет необходимости строить проекцию другой
прямой (BM) на этот экран. DH – искомое расстояние. DH
находим из треугольника MDB, используя формулы
площади. Ответ: .
1
2
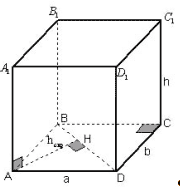
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
3
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
4
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
5
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
6
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
7
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
8
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
9
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
10
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
11
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
12
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
13
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
14
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
15
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
16
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
17
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
18
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
19
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
20
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
21
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
22
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
23
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
24
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
25
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
26
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
27
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
28
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
29
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
30
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
31
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
32
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
33
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
34
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
35
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
36
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
37
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
38
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
39
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
40
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
41
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
42
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
43
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
44
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
45
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
46
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
47
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
48
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
49
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
50
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
51
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
52
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
53
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
54
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
55
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
56
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
57
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
58
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
59
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
60
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
61
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
62
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
63
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
64
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
65
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
66
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
67
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
68
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
69
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
70
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
71
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
72
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
73
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
74
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
75
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
76
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
77
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
78
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
79
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
80
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
81
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
82
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
83
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
84
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
85
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
86
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
87
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
88
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
89
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
90
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
91
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
92
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
93
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
94
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
95
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
96
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
97
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
98
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
99
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
100
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
101
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
102
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
103
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
104
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
105
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
106
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
107
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
108
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
109
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
110
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
111
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
112
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
113
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
114
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
115
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
116
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
117
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
118
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
119
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
120
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
121
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
122
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
123
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
124
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
125
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
126
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
127
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
128
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
129
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
130
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
131
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
132
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
133
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
134
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
135
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
136
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
137
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
138
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
139
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
140
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
141
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
142
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
143
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
144
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
145
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
146
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
147
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
148
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
149
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
150
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
151
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
152
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
153
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
154
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
155
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
156
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
157
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
158
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
159
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
160
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
161
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
162
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
163
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
164
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
165
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
166
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
167
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
168
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
169
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
170
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
171
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
172
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
173
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
174
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
175
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
176
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
177
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
178
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
179
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
180
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
181
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
182
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
183
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
184
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
185
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
186
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
187
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
188
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
189
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
190
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
191
Найдите расстояние между вершинами A и C прямоугольного параллелепипеда, для которого
192
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
193
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
194
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
195
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
196
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
197
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
198
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
199
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
200
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
201
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
202
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
203
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
204
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
205
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
206
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
207
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
208
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
209
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
210
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
211
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
212
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
213
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
214
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
215
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
216
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
217
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
218
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
219
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
220
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
221
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
222
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
223
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
224
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
225
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
226
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
227
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
228
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
229
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
230
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
231
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
232
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
233
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
234
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
235
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
236
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
237
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
238
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
239
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
240
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
241
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
242
Найдите расстояние между вершинами A и прямоугольного параллелепипеда, для которого
243
Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого
244
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
245
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
246
Найдите расстояние между вершинами и
прямоугольного параллелепипеда, для которого
247
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
248
Найдите расстояние между вершинами C и прямоугольного параллелепипеда, для которого
249
Найдите расстояние между вершинами B и прямоугольного параллелепипеда, для которого
250
Найдите расстояние между вершинами D и прямоугольного параллелепипеда, для которого
Объяснение длинное, зато решение очень короткое.
Проведем плоскость через диагональ параллелепипеда и ребра, с которыми она пересекается.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
Ребра параллелепипеда параллельны между собой. Следовательно, раз данное ребро параллельно прямой на плоскости, содержащей диагональ параллелепипеда, оно параллельно и самой этой плоскости.
Рассмотрим рисунок.
Ребро и диагональ не параллельны между собой.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых, в данном случае ребром параллелепипеда, и плоскостью, проходящей через другую прямую – диагональ параллелепипеда – параллельно этому ребру.
Для того, чтобы найти расстояние между двумя данными в задаче скрещивающимися прямыми, нужно:
из любой точки ребра опустить перпендикуляр на плоскость, содержащую диагональ параллелпепипеда, и найти длину этого перпендикуляра. . На данном рисунке – это расстояние mn=m1n1
Но расстояние m1n1- это половина диагонали прямоугольника, лежащего в основании параллелепипеда.
Половину диагонали параллелепипеда найдем по тепореме Пифагора:
m1n1=1/2 √(а²+b²)
Ответ: расстояние равно 1/2 √(а²+b²)
Ниже приведены основные формулы, которые могут пригодиться при решении задач с прямоугольным параллелепипедом на ЕГЭ.
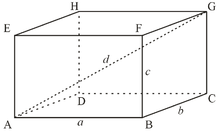
Прямоугольный параллелепипед. Формулы:
| Чертеж: | Обозначения: | Формулы: |
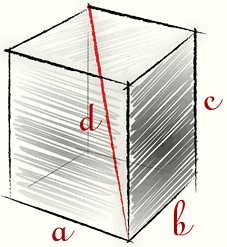 |
V — Объем. Sполн — площадь d — диагональ. a,b,c — ребра. |
V = a * b * c Sполн = 2(ab + bc + ac) d2 = a2 + b2 + c2 |
Рейтинг: 2.5 из 5.0
Проголосовало: 16
Комментарии
Всего комментариев: 0
Прямоугольный параллелепипед
Прямоуго́льный параллелепи́пед (кубоид) — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником.
Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине, взаимно перпендикулярны.
Примерами тел, имеющих форму прямоугольного параллелепипеда, служат классная комната, кирпич, спичечный коробок или системный блок компьютера.
Длины трёх рёбер прямоугольного параллелепипеда, принадлежащих одной вершине, иногда называют измерениями. Например, распространённый спичечный коробок имеет измерения 15, 35, 50 мм.
Правильным или квадратным параллелепипедом называют параллелепипед, у которого два измерения равны, у такого параллелепипеда две (из шести) противолежащие грани представляют собой квадраты.
Объём прямоугольного параллелепипеда можно найти по формуле:
где — его измерения.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
соответственно, длина диагонали равна:
Площадь поверхности прямоугольного параллелепипеда равна
Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты.
См. также[править | править код]
- Совершенный кубоид
Ссылки[править | править код]
- uztest.ru Прямоугольный параллелепипед
- Прямоугольный параллелепипед, учебный фильм
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
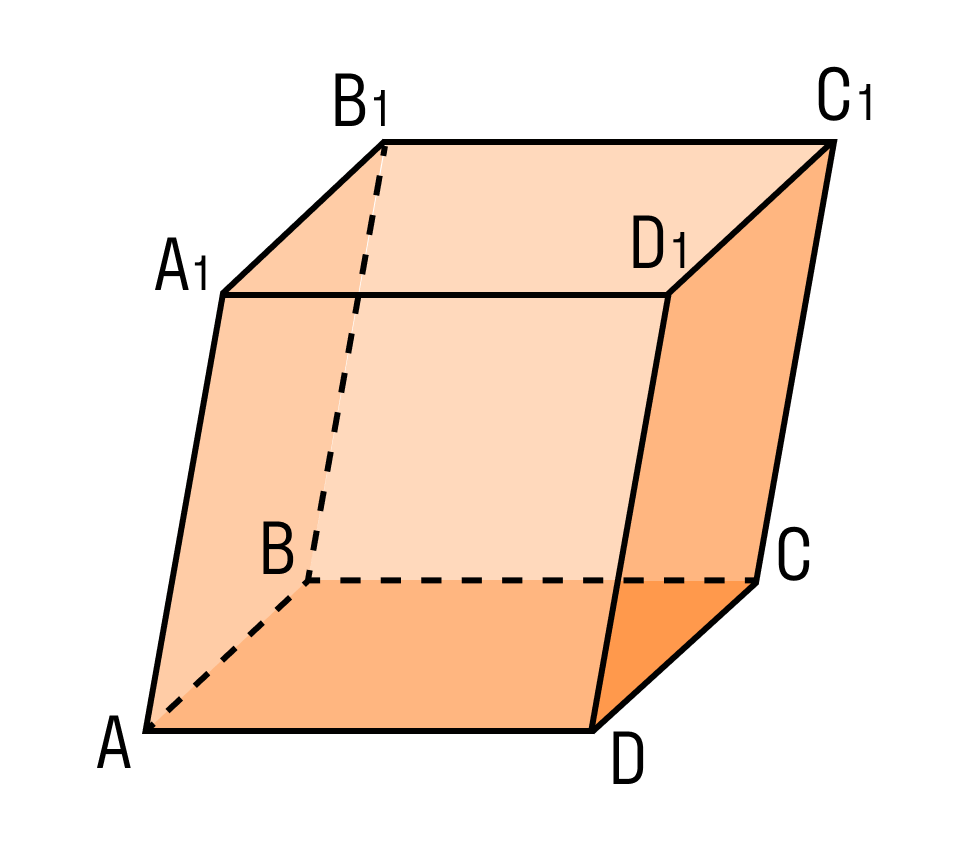
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
- основание;
- грани;
- ребра;
- диагонали;
- диагонали граней;
- высота.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
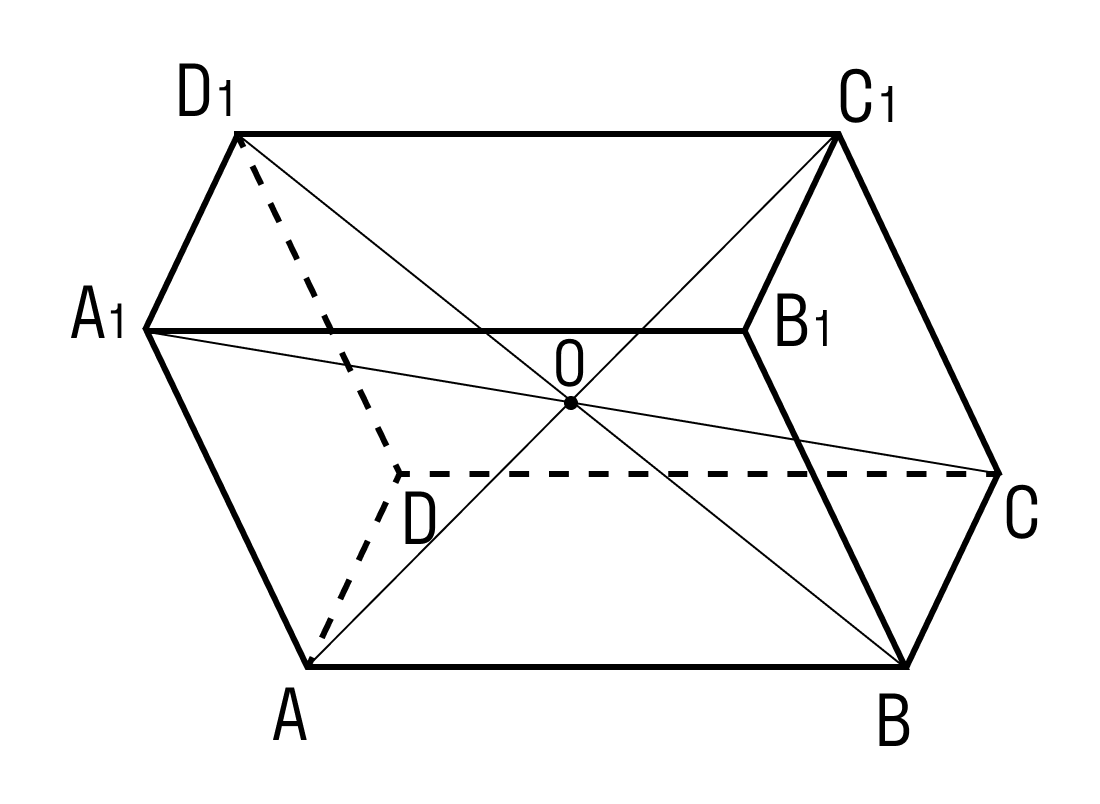
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
На рисунке: ребро АА1 перпендикулярно основанию ABCD. АА1 перпендикулярна прямым АB и АD, которые лежат в плоскости основания
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
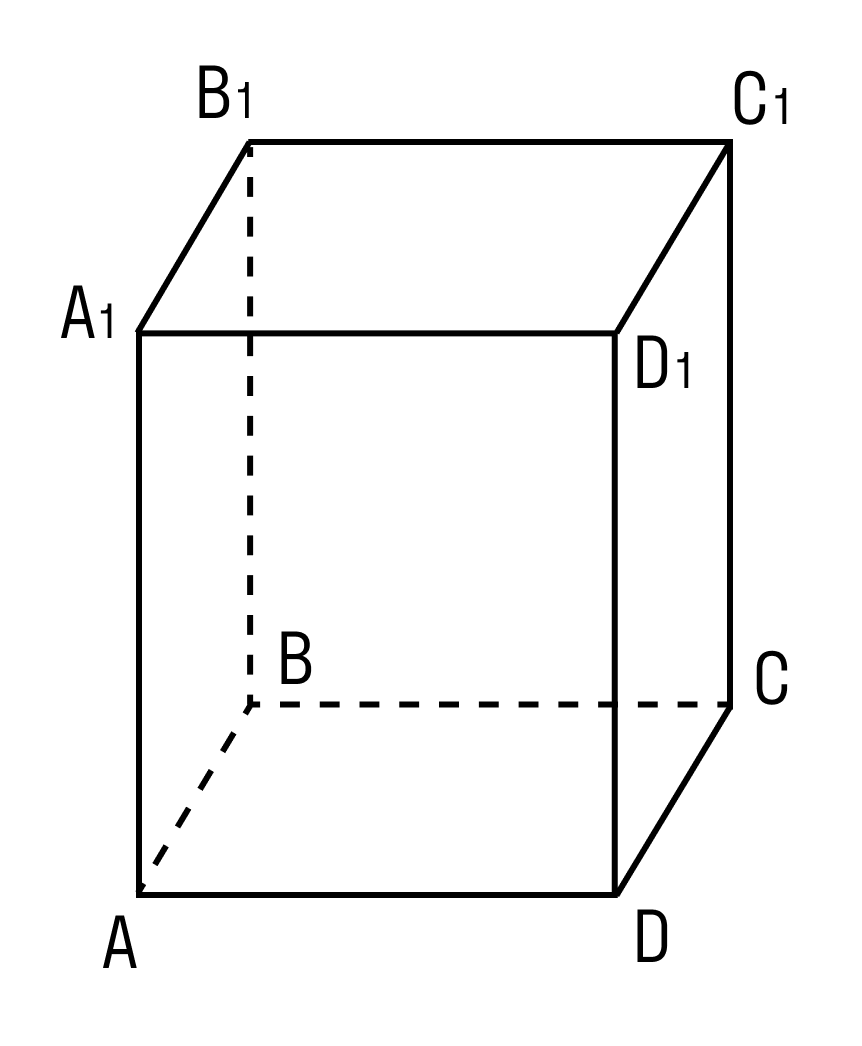
На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
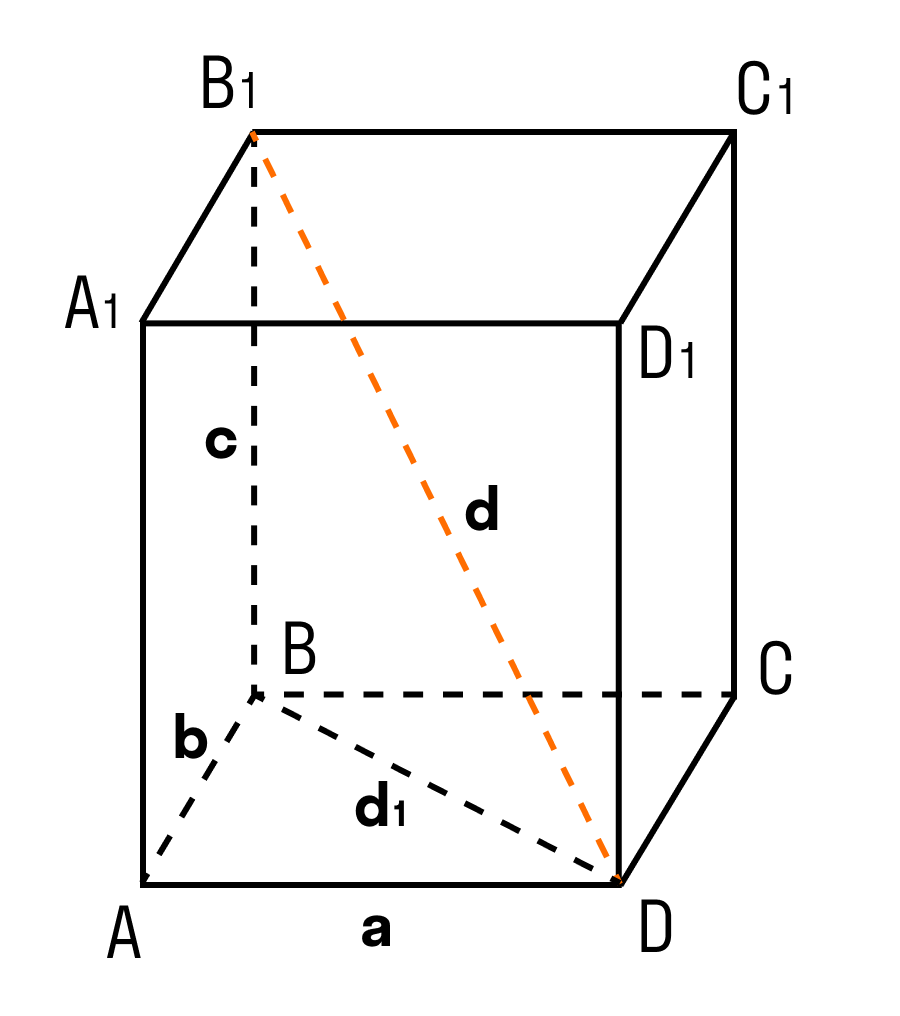
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Применяем формулу:
d² = a² + b² + c²
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
d₁² = a² + b²
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
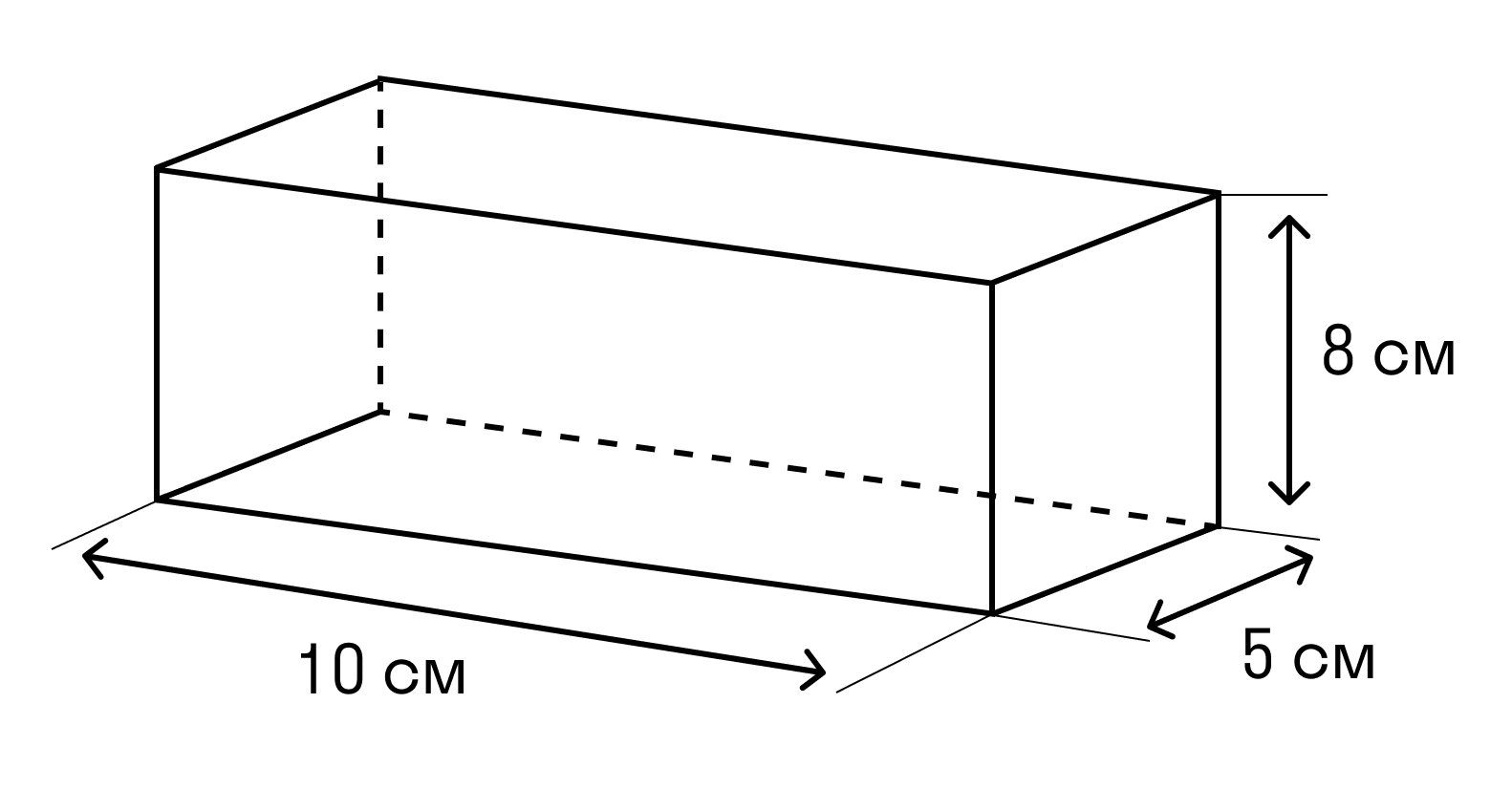
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
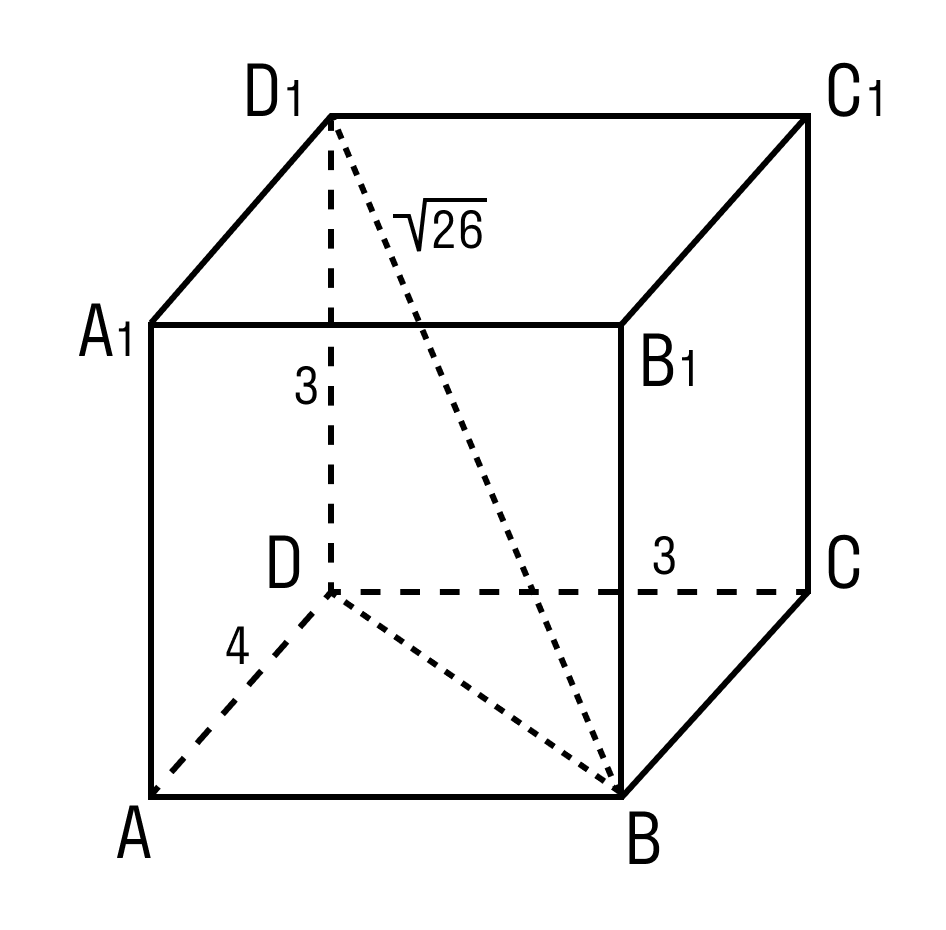
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
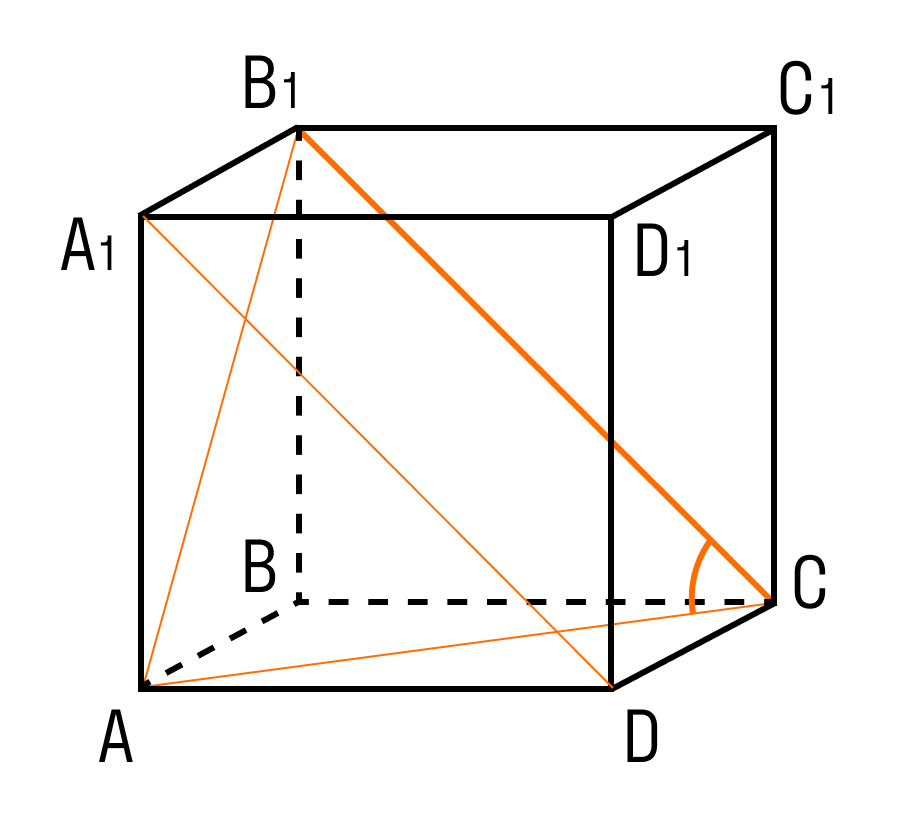
D1B = √26
BB1 = 3
A1D1 = 4
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°.
По теореме Пифагора:
BD12 = DD12 + BD2
BD2 = BD12 – DD12
BD2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD2 = AD2 + AB2
AB2 = BD2 — AD2 = (√17)2 — 42 = 1
A1B1 = AB = 1.
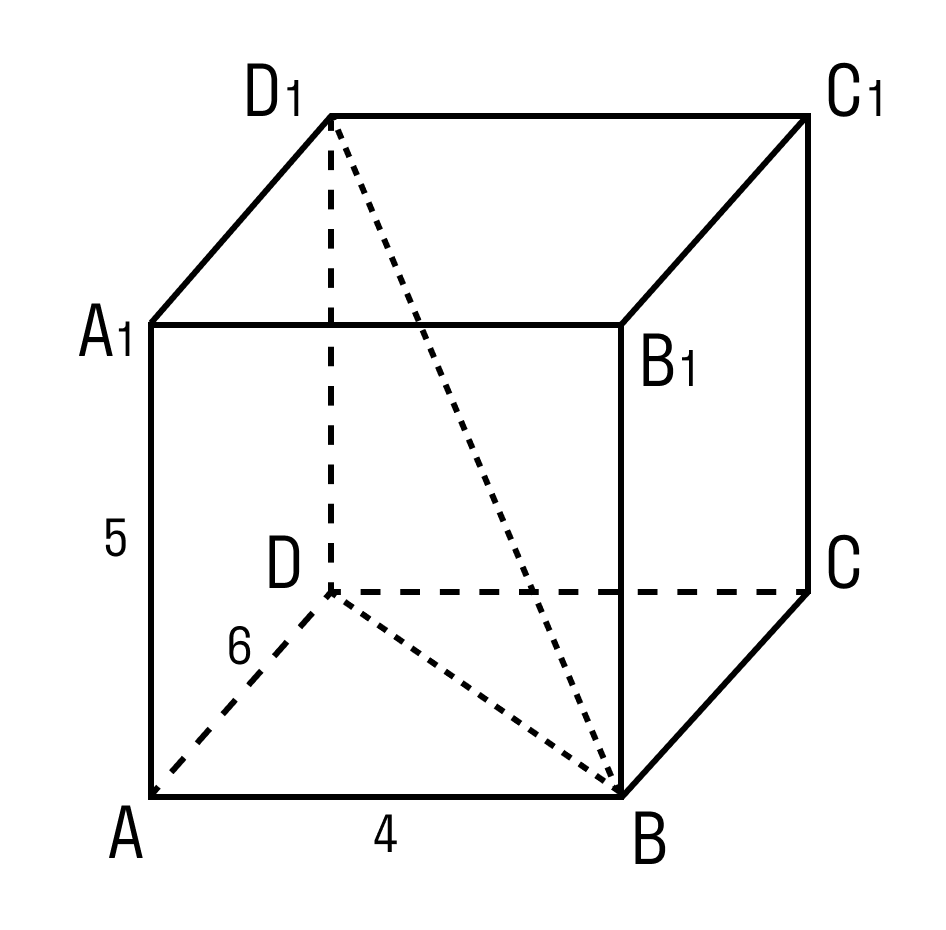
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD2 = AB2+AD2
BD2 = 42 + 62 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD12 = 52 + 25 = 77
BD1 = √77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AC1= 15
C1D1 = 3
B1C1= 12
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
- прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
- параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
- основание прямоугольного параллелепипеда — прямоугольник;
- три измерения прямоугольного параллелепипеда: длина, ширина, высота;
- диагональ параллелепипеда равна сумме квадратов его измерений.
Решение задачи
В видео уроке представлено решение геометрической задачи из ЕГЭ (В13) про прямоугольный параллелепипед. При решении задачи вспоминается формула нахождения длины диагонали: квадрат диагонали равен сумме квадратов трёх её измерений (измерения параллелепипеда — это рёбра выходящие из одной вершины). Задача сводится к нахождению неизвестного ребра параллелепипеда. Отмечается, что в прямоугольнике противоположные стороны равны. При вычислении искомой величины используется арифметическая операция возведение в степень.
Видео урок предназначен для учащихся 10 класса при изучении темы : «Параллельность прямых и плоскостей» (Прямоугольный параллелепипед). Решение данной задачи будет полезным учащимся 11 класса при подготовке к ЕГЭ.
Отзывы учеников
-
Светлана ИвановаК ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
Влад ДолгорукийБольшое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
Александр ШпикHello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.