Инфоурок
›
Математика
›Другие методич. материалы›Математический тренажер по теме “Вычисление диагонали прямоугольного параллелепипеда”
Математический тренажер по теме “Вычисление диагонали прямоугольного параллелепипеда”
Скачать материал
Скачать материал


- Сейчас обучается 612 человек из 77 регионов


- Сейчас обучается 25 человек из 17 регионов


- Сейчас обучается 48 человек из 26 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 259 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 21.11.2022
- 145
- 12
Контрольная работа “Таблицы и диаграммы”
- Учебник: «Математика», Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. / Под ред. Дорофеева Г.В., Шарыгина И.Ф.
- Тема: Глава 11. Таблицы и диаграммы
- 21.11.2022
- 191
- 3

- 21.11.2022
- 64
- 1
- 21.11.2022
- 49
- 1
- 21.11.2022
- 82
- 0

Урок по математике 3 класс.
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Часть 1
- 21.11.2022
- 105
- 0

- 21.11.2022
- 345
- 15

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Настоящий материал опубликован пользователем Плотникова Валентина Сергеевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 5 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 3013
-
Всего материалов:
13
Каталог заданий.
3. Вычисление диагонали прямоугольного параллелепипеда
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 15 № 558 

Найдите диагональ прямоугольного параллелепипеда
если
O — точка пересечения диагоналей параллелепипеда.
Аналоги к заданию № 558: 559 Все
Решение
·
Помощь
2
Тип 15 № 559 

Найдите диагональ прямоугольного параллелепипеда
если
O — точка пересечения диагоналей параллелепипеда.
Аналоги к заданию № 558: 559 Все
Решение
·
Помощь
3
Тип 15 № 560 

Найдите диагональ прямоугольного параллелепипеда
если
Аналоги к заданию № 560: 561 Все
Решение
·
Помощь
4
Тип 15 № 561 

Найдите диагональ прямоугольного параллелепипеда
если
Аналоги к заданию № 560: 561 Все
Решение
·
Помощь
5
Тип 15 № 562 

Найдите диагональ прямоугольного параллелепипеда
если
Аналоги к заданию № 562: 563 Все
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Прямоугольный параллелепипед»
(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).
Тогда:
1) противоположные грани равны между собой;
2) боковые ребра перпендикулярны основаниям, то есть являются высотами;
3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.
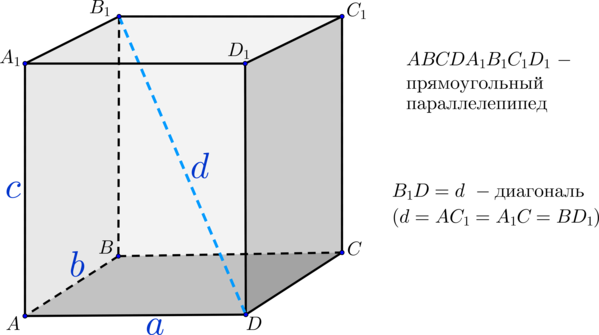
(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.
1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;
2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).
Задание
1
#2863
Уровень задания: Легче ЕГЭ
Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.
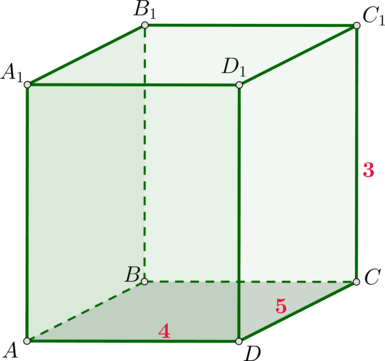
Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).
Ответ: 20
Задание
2
#2864
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
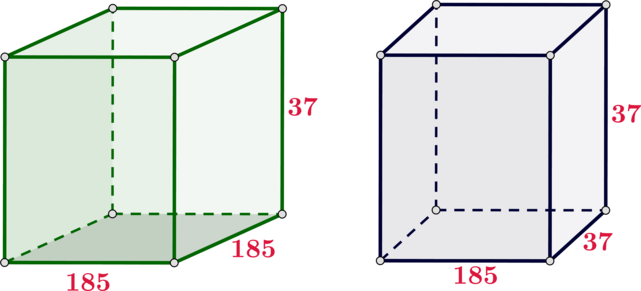
Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]
Ответ: 5
Задание
3
#2865
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).
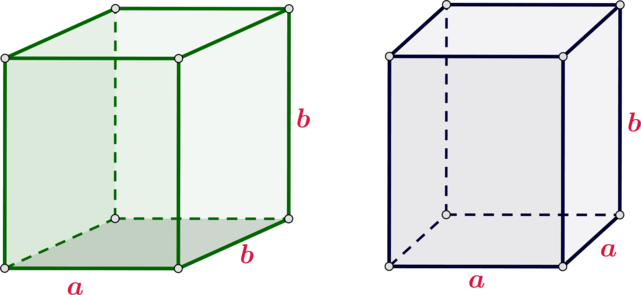
Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]
Ответ: 4002
Задание
4
#3974
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?
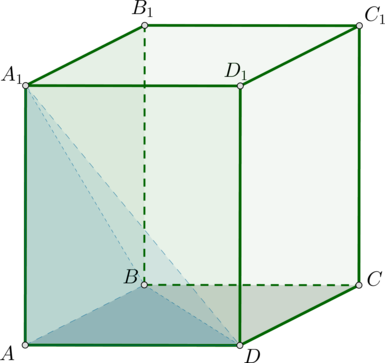
Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.
Ответ:
6
Задание
5
#2867
Уровень задания: Равен ЕГЭ
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.
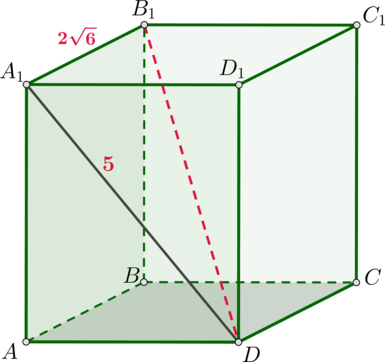
Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]
Ответ: 7
Задание
6
#2641
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.
Пусть (AB=2, AD=3 , AA_1=6).
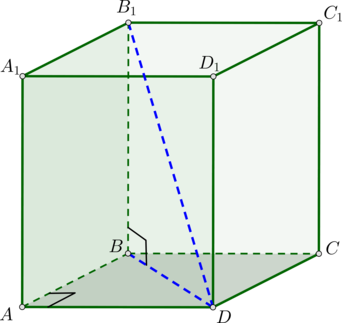
По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).
Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).
Подставляя (BD^2) из первого равенства во второе, получим:
[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]
Ответ: 7
Задание
7
#2689
Уровень задания: Равен ЕГЭ
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
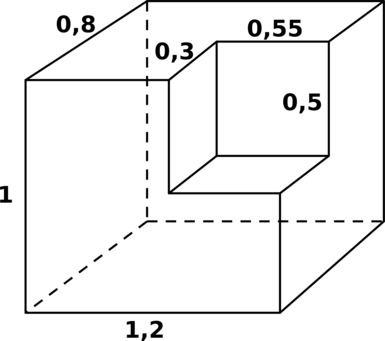
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).
Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 – 0,3cdot 0,5cdot 0,55 = 0,8775,.]
Ответ: 0,8775
Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.
При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Готовьтесь к ЕГЭ вместе со «Школково»!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.
Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.
Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

УСТАЛ? Просто отдохни
|
Как найти длину диагонали прямоугольного параллелепипеда ? По какой формуле найти диагональ параллелепипеда ?
Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий его противоположные вершины . Итак, у нас есть прямоугольный параллелепипед с диагональю d и со сторонами a, b, c . Одно из свойств параллелепипеда гласит, что квадрат длины диагонали d равен сумме квадратов трёх его измерений a, b, c. Отсюда вывод, что длина диагонали может быть легко рассчитана по следующей формуле :
Также :Как найти высоту параллелепипеда?модератор выбрал этот ответ лучшим
Nonsense 7 лет назад Прямоугольным параллелепипедом (ПП) является ни что иное, как призма, основанием у которой прямоугольник. У ПП все диагонали равны, значит любая его диагональ рассчитывается по формуле:
где
Можно дать и другое определение, рассматривая декартову прямоугольную систему координат: Диагональ ПП это радиус-вектор любой точки пространства, заданной координатами x, y и z в декартовой системе координат. Этот радиус вектор к точке проводится из начала координат. А координатами точки будут проекции радиус-вектора (диагонали ПП) на координатные оси. Проекции совпадают с вершинами данного параллелепипеда.
Zolotynka 8 лет назад Если у прямоугольного параллелепипеда известны длина, высота и ширина (a,b,c) то формула для расчета диагонали будет выглядеть таким образом:
Обычно учителя не предлагают своим ученикам “голую” формулу, а прилагают усилия, чтобы те могли самостоятельно ее вывести, задавая наводящие вопросы:
Обычно после ответа на поставленные вопросы, ученики без труда самостоятельно выводят данную формулу.
Лолочка611 8 лет назад Прямоугольный параллелепипед это один из так званных многогранников, который состоит из 6 граней, каждая из которых является прямоугольником. А диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Если длину, ширину и высоту прямоугольного параллелепипеда принять за a, b, c соответственно, то формула его диагонали ( D ) будет выглядеть следующим образом: D^2=a^2+b^2+c^2.
дольфаника 8 лет назад Нашлась в интернете неплохая схема-таблица с полным перечислением всего, что есть в параллепипеде. Есть формула, чтобы найти диагональ, которая обозначается d. Есть изображение грани, вершины и других важных для параллепипеде вещей.
Багира999 8 лет назад Прямоугольный параллелепипед – это разновидность многогранника, состоящая из 6 граней, в основании которого — прямоугольник. Диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Формула нахождения длины диагонали – квадрат диагонали равен сумме квадратов трех измерений параллелограмма.
Koluchiy 8 лет назад Диагонали прямоугольного параллелепипеда равны. Также как и диагонали его противоположных граней. Длину диагонали можно вычислить, зная длину рёбер параллелограмма, исходящих из одной вершины. Эта длина равна корню квадратному из суммы квадратов длин его рёбер.
ДРЕССИРОВЩИК 9 лет назад Квадрат диагонали, квадратного параллилепипеда (смотрите свойства квадратного параллепипеда) равна сумме квадратов трёх его разных сторон (ширине, высоте, толщине), а соответственно диагонали квадратного параллепипеда равна корню из этой суммы.
haleron 8 лет назад Насколько мне известно еще со школьной программы, класс 9 если не ошибаюсь, и если не изменяет память , то диагональ прямоугольного параллелепипеда ровна корню квадратному суммы квадратов его всех трех сторон. [пользователь заблокирован] 8 лет назад квадрат диагонали равен, сумме квадратов ширины , высоты и длинны , исходя с этой формулы получаем ответ , диагональ равно корню квадратному с суммы его трех разных измерений , буквами они позначаюnсz abc
Космос111 7 лет назад Вспоминаю школьную программу по геометрии, можно сказать так: диагональ параллелепипеда равняется корню квадратному полученному из суммы его всех трех сторон (обозначаются они маленькими буквами a, b, c). Николай Л 10 лет назад Длина диагонали прямоугольного параллепипеда равна корню квадратному из суммы квадратов его сторон. Знаете ответ? |
Прямоугольный параллелепипед — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.
Объём прямоугольного параллелепипеда можно найти по формуле:
$$ V = abc, $$
где (a), (b) и (c) — измерения.
Квадрат длины диагонали (d) прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
$$ d^2 = a^2+b^2+c^2, $$
соответственно, длина диагонали равна:
$$ d = sqrt{a^2+b^2+c^2}. $$
Площадь полной поверхности прямоугольного параллелепипеда вычисляется по формуле:
$$ S = 2(ab+ac+bc). $$
Задача 1. Измерения прямоугольного параллелепипеда равны соответственно 3, 4 и 12. Найдите объем, площадь и длину диагонали.
Решение задачи:
Инструкция. Для вашего примера введите ваши данные в математическом блокноте ниже. Если данные будут введены не верно, то появится сообщение об ошибке. Чтобы восстановить исходный пример просто перезагрузите страницу (клавиша F5). После ввода данных в строку следует нажать клавишу «Enter» для выполнения вычислений.
Задача 2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 5. Объем этого параллелепипеда равен 60. Найдите третье ребро, выходящее из той же вершины.
Решение задачи:
2016-05-22 • Просмотров [ 2451 ]










