Прямоугольный треугольник как найти гипотенузу онлайн - Сайт, где вы сможете решить свои вопросы

Расчет гипотенузы

Заполните размеры в мм:

Ширина: Y

Длина: X

Инструкция к онлайн расчету гипотенузы прямоугольного треугольника

Укажите известные размеры в миллиметрах:

Y – длина стороны прилегающей к прямому углу слева.

X – размер стороны справа от угла 90°.

Отметив пункт «Черно-белый чертеж» Вы получите приближенный к требованиям ГОСТ чертеж и сможете его распечатать, не расходуя зря цветную краску или тонер.

Нажмите «Рассчитать».

Результаты расчета:

Иногда возникает необходимость (например, при строительстве, производстве мебели, планировании участка) найти гипотенузу, зная две стороны и имея прямой угол между ними. Не вдаваясь в подробности школьного курса геометрии это легко решить с помощью данного калькулятора. Возможности программы позволяют рассчитать длину диагонали (гипотенузы) прямоугольного треугольника и проверить, таким образом, действительно ли угол равен 90°. Необходимо только ввести известные данные и сравнить натурный размер диагонали с расчетным значением.

Источник

Как найти стороны прямоугольного треугольника

Главная
/
Математика
/
Геометрия
/
Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для гипотенузы (с):

длины катетов a и b
длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)

для катета:

длину гипотенузы (с) и длину одного из катетов
длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Катет a =
Катет b =
Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

c = ^a/_cos(β) = ^b/_cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

c = ^a/_sin(α) = ^b/_sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Гипотенуза c =
Катет _{(известный)} =
Катет _{(искомый)} =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

a = √c² – b²

b = √c² – a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² – 4² = √25 – 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Гипотенуза c =
Угол (прилежащий катету) = °
Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Гипотенуза c =
Угол (противолежащий катету) = °
Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см

См. также

Источник

Теорема пифагора

Определение теоремы пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обозначив гипотенузу буквой – c, катеты буквами a и b получим следующее равенство

c²=a²+b²

Расчёт катета по теореме пифагора

Введите гипотенузу

c =

Введите катет

b =

Формула пифагора для катета

Где a, b – катеты прямоугольного треугольника,
с – гипотенуза прямоугольного треугольника

Расчёт гипотенузы по теореме пифагора

Введите первый катет

a =

Введите второй катет

b =

Формула пифагора для гипотенузы

Где a, b – катеты прямоугольного треугольника,
с – гипотенуза прямоугольного треугольника

Доказательство теоремы пифагора

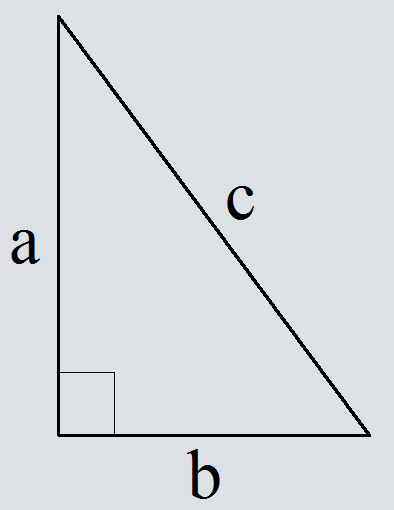
Дано

Прямоугольный треугольник с катетами a, b и гипотенузой c.

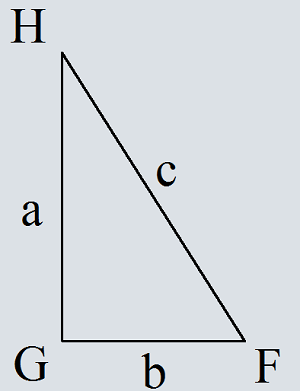
Доказать

c²=a²+b²

Доказательство

Достроим треугольник HFG до квадрата со стороной a+b.

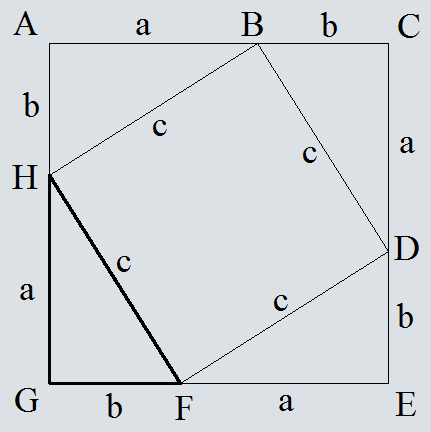
Запишем площадь получевшегося квадрата двумя способами

S=(a+b)²

S=4*0.5*a*b +c²

Приравняем площади

(a+b)²=4*0.5*a*b +c²

a²+2*a*b +b²=2*a*b +c²

a²+b²=c²

Теорема доказана

Источник

Недавно поступил запрос пользователя – длинна гипотенузы.
Я подумал, что в самом деле — калькуляторов про треугольники на сайте уже довольно много, а вот про прямоугольный треугольник еще нет. Отчасти видимо потому, что там все просто — теорема Пифагора. Но раз надо кому-то лень считать, то можно и сделать.

Калькулятор ниже — вводим длины двух сторон и выбираем их тип.
Если это два катета, то длина гипотенузы
$c=sqrt{a^2+b^2}$
Если это катет и гипотенуза, то длина оставшегося катета
$a=sqrt{c^2-b^2}$

Длина стороны прямоугольного треугольника

Точность вычисления

Знаков после запятой: 2

На закуску — в (Википедии можно прочитать, что существует 367 доказательств теоремы Пифагора.

Источник

Гипотенуза прямоугольного треугольника в см по катетам (сторонам)

Как найти гипотенузу прямоугольного треугольника, если известны его катеты?

Гипотенуза — это сторона противоположная прямому углу (90 градусов) прямоугольного треугольника, является самой длинной стороной.

Катеты — это стороны прилегающие к прямому углу (90 градусов) прямоугольного треугольника.

Гипотенузу прямоугольного треугольника можно найти по теореме Пифагора: длина гипотенузы в квадрате равна сумме длин катетов в квадрате.

Формула теоремы Пифагора для поиска длины гипотенузы прямоугольного треугольника:

c² = a² + b²⇒

c = √(a² + b²)

a — известная длина первого катета прямоугольного треугольника в см (сантиметрах);

b — известная длина второго катета прямоугольного треугольника в см (сантиметрах);

c — длина гипотенузы прямоугольного треугольника в см (сантиметрах).

Например:

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 5 см и 12 см.

Краткое решение: c = √(a² + b²) = √(5² + 12²) = 13 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 3 см и 4 см.

Краткое решение: c = √(a² + b²) = √(3² + 4²) = 5 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 6 см и 8 см.

Краткое решение: c = √(a² + b²) = √(6² + 8²) = 10 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 9 см и 12 см.

Краткое решение: c = √(a² + b²) = √(9² + 12²) = 15 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 25 см и 60 см.

Краткое решение: c = √(a² + b²) = √(25² + 60²) = 65 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 12 см и 16 см.

Краткое решение: c = √(a² + b²) = √(12² + 16²) = 20 см

Источник

Расчет гипотенузы

Инструкция к онлайн расчету гипотенузы прямоугольного треугольника

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Формула

Пример

Найти гипотенузу по катету и прилежащему к нему острому углу

Формула

Пример

Найти гипотенузу по катету и противолежащему к нему острому углу

Формула

Пример

Найти гипотенузу по двум углам

Найти катет

Найти катет по гипотенузе и катету

Формула

Пример

Найти катет по гипотенузе и прилежащему к нему острому углу

Формула

Пример

Найти катет по гипотенузе и противолежащему к нему острому углу

Формула

Пример

Найти катет по второму катету и прилежащему к нему острому углу

Формула

Пример

Найти катет по второму катету и противолежащему к нему острому углу

Формула

Пример

См. также

Теорема пифагора

Определение теоремы пифагора

Расчёт катета по теореме пифагора

Формула пифагора для катета

Расчёт гипотенузы по теореме пифагора

Формула пифагора для гипотенузы

Доказательство теоремы пифагора

Длина стороны прямоугольного треугольника

Гипотенуза прямоугольного треугольника в см по катетам (сторонам)

Как найти гипотенузу прямоугольного треугольника, если известны его катеты?

Вам также может понравиться

Как найти площадь трапеции зная все стороны

Как найти свою половинку по знаку зодиака

Как исправить руку ребенку

Добавить комментарий Отменить ответ