Псевдообратная матрица как найти – Сайт, где вы сможете решить свои вопросы

Псевдообратная матрица

Для любой матрицы A, A⁺ является псевдообратной матрицей тогда и только тогда, когда выполнены следующие условия:

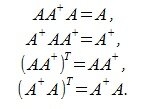(0)

Построение псевдообратной матрицы.

Пусть C r×n матрица, r<n и rank(C)=r. Тогда

C⁺=C^T(CC^T)^-1.

Пусть B m×r матрица, m>r и rank(B)=r. Тогда

B⁺=(B^TB)^-1B^T.

Для произвольной матрицы A порядка m×n и ранга r, псевдообратная матрица A⁺ можно получить следующим образом:

1. Производиться скелетное разложение матрицы A:

A=BC,

где B m×r матрица, rank(B)=r, C rxn матрица, rank(C)=r.

2. Строятся матрицы С⁺ и B⁺:

C⁺=C^T(CC^T)^-1,

B⁺=(B^TB)^-1B^T.

3. Матрица A⁺ вычисляется из следующего выражения:

A⁺=(BC)⁺=C⁺B⁺.

Заметим, что если A n×n матрица и rank(A)=n, то

A⁺=A^-1.

Пример вычисления псевдообратной матрицы

Рассмотрим пример из раздела скелетное разложение матрицы:

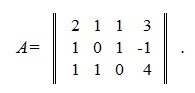
Для построения псевдообратной матрицы сделаем скелетное разложение:

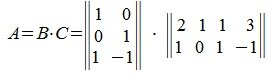
Тогда

Подставляя A и A⁺ в уравнения (0), можно убедиться, что A⁺ является псевдообратной к A матрицей.

Решение системы линейных уравнений с помощью псевдообратной матрицы

Пусть задана система линейных уравнений

где A – m×n – матрица, x∈Rⁿ, b∈R^m.

Найдем решение системы (1), если оно существует.

Перепишем систему (1) в следующем виде:

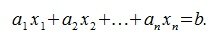(2)

где 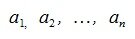– векторы столбцы матрицы A, 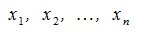– координаты вектора x.

Из системы (2) следует, что для того, чтобы система (1) имела решение вектор b должен быть линейной комбинацией векторов столбцов матрицы A c коэффициентами 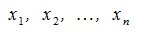. Таким образом, можно записать, что для совместности системы (1) должно выполняться условие

где R(A) – пространство столбцов матрицы A.

Построим псевдообратную к A матрицу A⁺. Рассмотрим вектор

Подставим (4) в систему (1):

Если система совместна, т.е. если выполнено условие (3), то R(AA⁺)≡R(A) и, следовательно, справедливо равенство (5) и x’ является решением (1).

Онлайн нахождение псевдообратной матрицы

Для нахождения псевдообратной матрицы пользуйтесь матричным онлайн калькулятором .

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июля 2021 года; проверки требуют 3 правки.

Псевдообра́тная ма́трица — обобщение понятия обратной матрицы в линейной алгебре. Псевдообратная матрица к матрице $A$ обозначается $A^+$ .

Впервые концепцию псевдообратных интегрирующих операторов в 1903 году представил Фредгольм. Наиболее известно псевдообращение Мура — Пенроуза, которое было независимо описано Элиакимом Муром^[1] в 1920 году и Роджером Пенроузом^[2] в 1955 году; утверждение о существовании и единственности для любой матрицы над действительными и комплексными числами псевдообратной матрицы носит название теоремы Мура — Пенроуза.

Обобщённое обращение (англ. generalized inverse) — псевдообращение, удовлетворяющее более строгим условиям. Псевдообращение можно понимать как решение задачи наилучшей аппроксимации (по методу наименьших квадратов с предельным вариантом регуляризации) для соответствующей системы линейных уравнений^[⇨]. Псевдообратная матрица может быть вычислена с помощью сингулярного разложения матрицы.

Определение[править | править код]

$A^+$ называется псевдообратной матрицей для матрицы $A$ , если она удовлетворяет следующим критериям:

$A A^+A = A$ ;
$A^+A A^+ = A^+$ ( $A^+$ является слабым обращением в мультипликативной полугруппе);
$(AA^+)^* = AA^+$ (это означает, что $AA^+$ — эрмитова матрица);
$(A^+A)^* = A^+A$ ( $A^+A$ — тоже эрмитова матрица).

Здесь $M^*$ — эрмитово сопряжённая матрица M (для матриц над полем действительных чисел $M^* = M^T$ ).

Существует эквивалентный способ задания псевдообратной матрицы через предел обратных (регуляризация Тихонова):

$A^+ = lim_{delta to +0} (A^* A + delta I)^{-1} A^* = lim_{delta to +0} A^* (A A^* + delta I)^{-1}$ ,

где $I$ — единичная матрица. Этот предел существует, даже если $(A A^*)^{-1}$ и $(A^* A)^{-1}$ не определены.

Свойства[править | править код]

Особые случаи[править | править код]

Если столбцы матрицы $A$ линейно независимы, тогда матрица $A^* A$ обратима. В таком случае псевдообратная матрица задаётся формулой:

$A^+ = (A^* A)^{-1} A^*$ .

Это эквивалентно тому, что в первой части определения через предел убирается слагаемое с $delta$ .
Отсюда следует что в этом случае $A^+$ — левая обратная матрица для $A$ : $A^+ A = I$ .

Если строки матрицы $A$ линейно независимы, тогда матрица $A A^*$ обратима. В таком случае псевдообратная матрица задаётся формулой:

$A^+ = A^*(A A^*)^{-1}$ .

Это эквивалентно тому, что во второй части определения через предел полагаем $delta=0$ .
Отсюда следует, что в этом случае $A^+$ — правая обратная матрица для A: $A A^+ = I$ .

Если и столбцы, и строки линейно независимы (что верно для квадратных невырожденных матриц), то псевдообращение совпадает с обращением:

$A^+ = A^{-1}$ .

Если $A$ и $B$ таковы, что произведение $AB$ определено и:

тогда

$(AB)^+ = B^+ A^+$ .

Псевдообращение можно применять и к скалярам, и к векторам. Это подразумевает, что они рассматриваются как матрицы соответствующей размерности. Псевдообратный к скаляру $x$ — ноль, если $x$ — ноль, и обратный к $x$ в противном случае:

$x^+ = left{begin{matrix} 0, & x=0; \ x^{-1}, & x ne 0. end{matrix}right.$

Псевдообратный для нулевого вектора — транспонированый нулевой вектор. Псевдообратный для ненулевого вектора — сопряжённый транспонированный вектор, делённый на квадрат своей длины:

$x^+ = left{begin{matrix} 0^T, & x = 0; \ {x^* over x^* x}, & x ne 0. end{matrix}right.$

Для доказательства достаточно проверить, что эти величины удовлетворяют определению псевдообратных.

Происхождение[править | править код]

Если $(A^* A)^{-1}$ существует, то из равенства:

$Ax = b,$

следует

$A^* A x = A^* b,$

$(A^* A)^{-1}(A^* A) x = (A^* A)^{-1}A^* b,$

$x = (A^* A)^{-1}A^* b,$

что порождает понятие псевдообращения

$A^+ = (A^* A)^{-1}A^*$ .

Вычисление[править | править код]

Пусть $k$ — ранг матрицы $A$ размера $mtimes n$ . Тогда $A$ может быть представлена как $A = BC$ , где B — матрица размера $m times k$ с линейно независимыми столбцами и $C$ — матрица размера $k times n$ с линейно независимыми строками. Тогда:

$A^+ = C^*(CC^*)^{-1}(B^*B)^{-1}B^*$ .

Если $A$ имеет полнострочный ранг, то есть $k = m$ , тогда в качестве $B$ может быть выбрана единичная матрица и формула сокращается до $A^+ = A^*(AA^*)^{-1}$ . Аналогично, если $A$ имеет полностолбцовый ранг, то есть, $k = n$ , то $A^+ = (A^*A)^{-1}A^*$ .

Простейший вычислительный путь получения псевдообратной матрицы — использовать сингулярное разложение.

Если $A = USigma V^*$ — сингулярное разложение $A$ , тогда $A^+ = VSigma^+ U^*$ . Для диагональной матрицы, такой как $Sigma$ , псевдообратная получается из неё заменой каждого ненулевого элемента на диагонали на обратный к нему.

Существуют оптимизированые подходы вычисления псевдообратной для блочных матриц.

Иногда объём расчётов по нахождению псевдообратной матрицы можно сократить, если известна псевдообратная для некоторой аналогичной матрицы. В частности, если аналогичная матрица отличается от начальной на один изменённый, добавленный или удалённый столбец или строку — существуют накопительные алгоритмы, которые могут использовать взаимосвязь между матрицами.

Применение[править | править код]

Псевдообращение тесно связано с методом наименьших квадратов (МНК) для системы линейных уравнений^[3].

В этом методе задача решения данной системы $A x = b$ заменяется задачей минимизации квадрата евклидовой нормы невязки $|A x - b|^2$ . На практике МНК обычно используют когда исходная система $A x = b$ несовместна, однако ниже мы рассмотрим случай когда эта система совместна.

Общее решение неоднородной системы $A x = b$ представимо как сумма частного решения неоднородной системы и общего решения соответствующей однородной системы $A x = 0$ .

Лемма: Если $(A A^*)^{-1}$ существует, тогда общее решение $x$ всегда представимо как сумма псевдообратного решения неоднородной системы и решения однородной системы:

${displaystyle x=A^{*}(AA^{*})^{-1}b+(I-A^{*}(AA^{*})^{-1}A)y.}$

Доказательство:

$Ax$	$=$	$A A^(A A^)^{-1}$	$b$	$+$	$A y - A A^(A A^)^{-1} A y$
$Ax$	$=$		$b$	$+$	$A y - A y$
$Ax$	$=$		$b$	.

Здесь вектор $y$ произвольный (с точностью до размерности). В двух других членах есть псевдообратная матрица $A^*(A A^*)^{-1}$ . Переписав её в форме $A^+$ , приведём выражение к форме:

${displaystyle x=A^{+}b+(I-A^{+}A)y.}$

Первый член — псевдообратное решение. В терминах метода наименьших квадратов — это $x$ , дающее минимальную евклидову норму для невязки. Следующий член даёт решение однородной системы $A x = 0$ , потому что ${displaystyle A^{+}A=A^{*}(AA^{*})^{-1}A}$ — оператор проектирования на образ оператора $A^{*}$ и, соответственно, ${displaystyle (I-A^{+}A)}$ — оператор проектирования на ядро оператора $A$ .

Литература[править | править код]

↑ Э. Х. Мур (E. H. Moore): On the reciprocal of the general algebraic matrix. Bulletin of the American Mathematical Society 26, 394—395 (1920) http://www.ams.org/bull/1920-26-09/S0002-9904-1920-03322-7/S0002-9904-1920-03322-7.pdf
↑ Роджер Пенроуз: A generalized inverse for matrices. Proceedings of the Cambridge Philosophical Society 51, 406—413 (1955)
↑ Роджер Пенроуз: On best approximate solution of linear matrix equations. Proceedings of the Cambridge Philosophical Society 52, 17-19 (1956)
↑ Алберт А.: Регрессия, псевдоинверсия и рекуррентное оценивание. перев. с англ. Москва, «Наука», 224 с.(1977)
↑ Беклемишев Д. В.: Дополнительные главы линейной алгебры. Москва, Наука. (1983)

Источник

Псевдообратная матрица

Обратная матрица в отличие от полуобратной имеет в силу определения очевидные свойства:

$begin{pmatrix}Acdot A^{-1}end{pmatrix}^{ast}=Acdot A^{-1},qquad begin{pmatrix}A^{-1}cdot Aend{pmatrix}^{ast}=A^{-1}cdot A,$

так как единичная матрица $E=AA^{-1}=A^{-1}A$ , разумеется, эрмитова. В определении полуобратной матрицы имеется некоторый произвол (см. п.3 замечаний 4.6), которым можно воспользоваться так, чтобы полуобратная матрица обладала аналогичными свойствами.

Пусть — произвольная матрица размеров mtimes n . Полуобратная матрица $A^{sim1}$ размеров ntimes m называется псевдообратной для матрицы , если матрицы $AA^{sim1}$ и $A^{sim1}A$ эрмитовы, т.е. псевдообратная матрица $A^{sim1}$ определяется четырьмя условиями

$AA^{sim1}A=A;qquad A^{sim1}AA^{sim1}=A^{sim1};$

(4.17)

$begin{pmatrix}AA^{sim1}end{pmatrix}^{ast}=AA^{ast};qquad begin{pmatrix}A^{sim1}Aend{pmatrix}^{ast}=A^{sim1}A.$

(4.18)

Покажем, что псевдообратная матрица $A^{sim1}$ существует для любой матрицы . Действительно, если A=O — нулевая матрица размеров mtimes n , то $A^{sim1}=O^T$ — нулевая размеров ntimes m , что следует из равенств (4.17).

Пусть матрица — ненулевая. Тогда матрица $A^{sim1}$ , удовлетворяющая равенствам (4.17), имеет вид (4.14):

$A^{sim1}=Tcdot! begin{pmatrix}dfrac{E_r}{U}end{pmatrix}!cdot! begin{pmatrix}E_rmid Vend{pmatrix}!cdot S.$

(4.19)

Покажем, что выбором матриц и в формуле (4.19) можно получить матрицу, удовлетворяющую условиям (4.18). В самом деле, запишем скелетное разложение (4.10) матрицы

$A=S^{-1}Lambda T^{-1}= S^{-1}! begin{pmatrix}E_r!!&vline!!&O\hline O!!&vline!!&Oend{pmatrix}!T^{-1}= S^{-1}cdot! begin{pmatrix}dfrac{E_r}{O} end{pmatrix}!cdot! begin{pmatrix}E_rmid Oend{pmatrix}!cdot T^{-1}.$

Найдем произведение

$begin{gathered}AA^{-1}= S^{-1}cdot!begin{pmatrix} dfrac{E_r}{O} end{pmatrix}!cdot! begin{pmatrix}E_rmid Oend{pmatrix}!cdotunderbrace{T^{-1}cdot T}_{E_n}cdot! begin{pmatrix}dfrac{E_r}{U} end{pmatrix}!cdot! begin{pmatrix}E_rmid Uend{pmatrix}!cdot S=\[2pt] =S^{-1}cdot! begin{pmatrix}dfrac{E_r}{O}end{pmatrix}!cdot underbrace{begin{pmatrix}E_rmid Oend{pmatrix}!cdot begin{pmatrix}dfrac{E_r}{U} end{pmatrix}}_{E_r}cdot! begin{pmatrix} E_rmid Vend{pmatrix}!cdot S=S^{-1}cdot! begin{pmatrix}dfrac{E_r}{O} end{pmatrix}!cdot! begin{pmatrix}E_rmid Vend{pmatrix}!cdot S= S^{-1}cdot! begin{pmatrix} E_r!!&vline!!&V\ hline O!!&vline!!& Oend{pmatrix}!cdot S.end{gathered}$

Подставим его в первое из равенств (4.18):

$left[S^{-1}cdot! begin{pmatrix}E_r!!&vline!!&V\ hline O!!&vline!!& Oend{pmatrix}!cdot Sright]^{ast}= S^{-1}cdot! begin{pmatrix}E_r!!&vline!!&V\ hline O!!&vline!!& Oend{pmatrix}!cdot S.$

Используя свойства операции сопряжения, а также п. 1 замечаний 4.2, получаем

$S^{ast}cdot! begin{pmatrix} E_r!!&vline!!&O\ hline V^{ast}!!&vline!!& O end{pmatrix}!cdot! begin{pmatrix}S^{-1}end{pmatrix}^{ast}= S^{-1}cdot! begin{pmatrix} E_r!!&vline!!&V\ hline O!!&vline!!& O end{pmatrix}!cdot S.$

Умножая обе части равенства на матрицу слева и на матрицу $S^{ast}$ справа, приходим к равенству

$begin{pmatrix}SS^{ast}end{pmatrix}!cdot! begin{pmatrix} E_r!!&vline!!&O\ hline V^{ast}!!&vline!!& O end{pmatrix}= begin{pmatrix} E_r!!&vline!!&V\ hline O!!&vline!!& O end{pmatrix}!cdot! begin{pmatrix}SS^{ast}end{pmatrix}!.$

Подставим в это равенство матрицу $SS^{ast}$ , предварительно разбив ее на блоки $SS^{ast}=begin{pmatrix} S_1!!&vline!!&S_2\ hline S_3!!&vline!!& S_4 end{pmatrix}$ квадратными матрицами S_1 и S_4 порядков и (m-r) и прямоугольными матрицами S_2 и S_2 размеров rtimes(m-r) и (m-r)times r соответственно. Выполняя умножение блочных матриц, получаем

$begin{gathered} begin{pmatrix} S_1!!&vline!!&S_2\ hline S_3!!&vline!!& S_4end{pmatrix}!cdot! begin{pmatrix} E_r!!&vline!!&O\ hline V^{ast}!!&vline!!& Oend{pmatrix}= begin{pmatrix} S_1+S_2V^{ast}!!&vline!!&O\ hline S_3+S_4V^{ast}!!&vline!!& Oend{pmatrix}!,\[2pt] begin{pmatrix} E_r!!&vline!!&V\ hline O!!&vline!!& Oend{pmatrix}!cdot! begin{pmatrix} S_1!!&vline!!&S_2\ hline S_3!!&vline!!& S_4end{pmatrix}= begin{pmatrix} S_1+VS_3!!&vline!!&S_2+VS_4\ hline O!!&vline!!& Oend{pmatrix}!.end{gathered}$

Равенство полученных блочных матриц обеспечивается условием

$V=-S_2S_{4}^{-1}$ , поскольку $S_3=S_2^{ast},~S_1=S_1^{ast},~ S_4=S_4^{ast}$

в силу эрмитовости матрицы $SS^{ast}$ , а $begin{pmatrix}S_4^{-1}end{pmatrix}^{ast}= begin{pmatrix}S_4^{ast}end{pmatrix}^{-1}$ .

Аналогичным образом можно показать, что второе из равенств (4.18) выполняется, если положить

$U=-T_4^{-1}T_3,$

где T_3,T_4 — блоки размеров (n-r)times r и (n-r)times(n-r) матрицы $T^{ast}T=begin{pmatrix} T_1!!&vline!!&T_2\ hline T_3!!&vline!!& T_4end{pmatrix}$ .

Таким образом, для любой матрицы существует псевдообратная матрица и притом только одна.

Замечания 4.7

1. Если матрица обратимая, то обратная матрица $A^{-1}$ , как следует из п. 1 замечаний 4.6, совпадает с псевдообратной, т.е. $A^{-1}=A^{sim1}$ .

2. Из невырожденности матриц и следует, что при любом раз биении эрмитовых матриц

$SS^{ast}=begin{pmatrix} S_1!!&vline!!&S_2\ hline S_3!!&vline!!& S_4end{pmatrix}!.,qquad T^{ast}T=begin{pmatrix} T_1!!&vline!!&T_2\ hline T_3!!&vline!!& T_4end{pmatrix}!.$

на квадратные блоки S_1,,S_4,,T_1,,T_4 , существуют обратные матрицы $S_1^{-1},,S_4^{-1},,T_1^{-1},,T_4^{-1}$ .

3. Имеются другие определения псевдообратной матрицы, равносильные приведенному выше. Например,

$A^{sim1}= lim_{varepsilonto0}Bigl(A^{ast}A+varepsilon^2cdot EBigr)^{-1}A^{ast}= lim_{varepsilonto0}A^{ast}Bigl(A^{ast}A+varepsilon^2cdot EBigr)^{-1}.$

4. В общем случае произведение псевдообратных матриц некоммутативно $(AB)^{sim1}ne B^{sim1}cdot A^{sim1}$ .

Свойства псевдообратной матрицы

Операция псевдообращения матриц обладает следующими свойствами:

$begin{aligned} bold{1.}&~~ (A^{sim1})^{sim1}=A;\[2pt] bold{2.}&~~ (A^{ast})^{sim1}=(A^{sim1})^{ast};\[2pt] bold{3.}&~~ A^{sim1}=(A^{ast}A)^{sim1}A^{ast}=A^{ast}(AA^{ast})^{sim1};\[2pt] bold{4.}&~~ (AA^{sim1})^2=AA^{sim1};\[2pt] bold{5.}&~~ (A^{sim1}A)^2=A^{sim1}A. end{aligned}$

Эти свойства доказываются по определению (4.17), (4.18). Докажем, например, свойство 3 (первое равенство). По определению псевдообратной матрицы имеем:

$Bigl[(A^{ast}A)^{sim1}A^{ast}Bigr]cdot AcdotBigl[(A^{ast}A)^{sim1}A^{ast}Bigr]= (A^{ast}A)^{sim1}cdot(A^{ast}A)cdot(A^{ast}A)^{sim1}A^{ast}= (A^{ast}A)^{sim1}A^{ast}.$

Следовательно, $A=bigl[(A^{ast}A)^{sim1}A^{ast}bigr]^{sim1}$ . Тогда по свойству 1: $A^{sim1}=(A^{ast}A)^{sim1}A^{ast}$ .

Способы нахождения псевдообратной матрицы

Пусть дана ненулевая матрица размеров mtimes n . Требуется найти псевдообратную матрицу $A^{sim1}$ .

Первый способ. Для нахождения псевдообратной матрицы (4.19) нужно выполнить следующие действия.

1. Составить блочную матрицу $begin{pmatrix}A!!&vline!!&E_m\hline E_n!!&vline!!&{} end{pmatrix}$ , приписывая к матрице слева и снизу единичные матрицы соответствующих размеров. Правый нижний блок этой матрицы может быть произвольным, так как не участвует в дальнейших преобразованиях.

2. Элементарными преобразованиями над первыми строками и первыми столбцами привести блочную матрицу к виду $begin{pmatrix}Lambda!!& vline!!&S\hline T!!&vline!!&{}end{pmatrix}$ , где Lambda — матрица размеров mtimes n простейшего вида (4.8), т.е. $Lambda=begin{pmatrix} E_r!!&vline!!&O\hline O!!&vline!!&Oend{pmatrix}$ , в которой E_r — единичная матрица r-го порядка (1leqslant rleqslantmin{m;n}) , — нулевые матрицы соответствующих размеров.

3. Найти произведения $SS^{ast},,T^{ast}T$ и представить их в виде блочных матриц

$SS^{ast}=begin{pmatrix}S_1!!&vline!!&S_2\hline S_3!!&vline!!&S_4end{pmatrix}!,quad T^{ast}T=begin{pmatrix}T_1!!&vline!!&T_2\hline T_3!!&vline!!&T_4end{pmatrix}!,$

(4.20)

выделяя блоки S_2,,S_4,,T_3,,T_4 размеров rtimes(m-r),,(m-r)times(m-r),,(n-r)times r,,(n-r)times(n-r) соответственно.

4. Вычислить матрицы $U=-T_4^{-1}T_3,~V=-S_2S_4^{-1}.$ .

5. Получить псевдообратную матрицу

$A^{sim1}=Tcdot! begin{pmatrix}dfrac{E_r}{U}end{pmatrix}!cdot! begin{pmatrix}E_rmid Vend{pmatrix}!cdot S.$

(4.21)

Замечание 4.8. Если r=m или r=n в (4.20) будут отсутствовать блоки S_2,,S_4 или T_3,,T_4 , так как в формуле (4.21) будут отсутствовать блоки или соответственно (см. п.5 замечаний 4.6). В частных случаях, когда строки матрицы линейно независимы (r=m) или столбцы матрицы линейно независимы (r=n) , псевдообратную матрицу $A^{sim1}$ можно найти проще, чем описанным выше способом (см. далее частные случаи нахождения псевдообратной матрицы).

Второй способ. Для нахождения псевдообратной матрицы используем скелетное разложение (4.10).

1, 2. Выполнить два первых пункта, указанных в первом способе. Получим матрицы S,,T и Lambda , удовлетворяющие условию

Lambda=Scdot Acdot T,

где S,,T — элементарные преобразующие матрицы порядков тип соответственно; $Lambda=begin{pmatrix}E_r!!&vline!!&O\hline O!!&vline!!&Oend{pmatrix}$ — матрица простейшего вида; E_r — единичная r-го порядка (1leqslant rleqslant min{m;n}) , — нулевые матрицы соответствующих размеров.

3. Найти обратные матрицы $S^{-1}$ и $T^{-1}$ .

4. Записать матрицы $B=S^{-1}cdot! begin{pmatrix}dfrac{E_r}{O}end{pmatrix}$ и $C=begin{pmatrix}E_rmid Oend{pmatrix}!cdot T^{-1}$ . Матрица В составлена из первых столбцов матрицы $S^{-1}$ , а матрица — из первых строк матрицы $T^{-1}$ .

5. Получить псевдообратную матрицу по формуле

$A^{sim1}=C^{ast}cdot(CC^{ast})^{-1}cdot(B^{ast}B)^{-1}cdot B^{ast}.$

(4.22)

Докажем, что второй способ дает ту же псевдообратную матрицу, что и первый. В самом деле, имея в виду скелетное разложение матицы

$A=BC;quad B=S^{-1}cdot! begin{pmatrix}dfrac{E_r}{O}end{pmatrix}!,quad C=begin{pmatrix}E_emid Oend{pmatrix}!cdot T^{-1},$

найдем произведение

$begin{gathered}begin{pmatrix}B^{ast}Bend{pmatrix}^{-1}cdot B^{ast}cdot S^{-1}= left[begin{pmatrix}E_r&mid Oend{pmatrix}!cdot(S^{-1})^{ast}cdot S^{-1}cdot! begin{pmatrix} dfrac{E_r}{O}end{pmatrix}right]^{-1}cdot! begin{pmatrix}E_rmid Oend{pmatrix} !cdot (S^{-1})^{ast}cdot S^{-1}=\[2pt] =left[begin{pmatrix}E_rmid Oend{pmatrix}!cdot! begin{pmatrix} SS^{ast}end{pmatrix}^{-1}!cdot! begin{pmatrix} dfrac{E_r}{O}end{pmatrix} right]^{-1}cdot! begin{pmatrix}E_rmid Oend{pmatrix}!cdot! begin{pmatrix} SS^{ast}end{pmatrix}^{-1} end{gathered}$

Обращая блочную матрицу $SS^{ast}=begin{pmatrix}S_1!!&vline!!&S_2\hline S_3!!&vline!!&S_4end{pmatrix}$ по формуле Фробениуса (4.4), имеем

$begin{pmatrix} S_1!!&vline!!&S_2\hline S_3!!&vline!!&S_4end{pmatrix}^{-1}= begin{pmatrix} M!!&vline!!&-MS_2S_4^{-1}\hline -S_4^{-1}S_3M!!& vline!!&N end{pmatrix}!,$

где $M=begin{pmatrix}S_1-S_2S_4^{-1}S_3end{pmatrix}^{-1},~ N=begin{pmatrix}S_4-S_3S_1^{-1}S_2end{pmatrix}^{-1}$ . Подставляя $(SS^{ast})^{-1}$ и няя умножение блочных матриц в квадратных скобках, имеем

$begin{gathered}begin{pmatrix} B^{ast}Bend{pmatrix}^{-1}cdot B^{ast}cdot S^{-1}=M^{-1}cdot! begin{pmatrix}E_rmid Oend{pmatrix}!cdot! begin{pmatrix} M!!&vline!!&-MS_2S_4^{-1}\hline -S_4^{-1}S_3M!!&vline!!&Nend{pmatrix}=\[2pt] M^{-1}cdot! begin{pmatrix}Mmid -MS_2S_4^{-1}end{pmatrix}= begin{pmatrix}E_rmid -S_2S_4^{-1}end{pmatrix}= begin{pmatrix}E_rmid Vend{pmatrix}!.end{gathered}$

Таким образом, $begin{pmatrix}E_rmid Vend{pmatrix}!S$ , где $V=-S_2S_4^{-1}$ .

Аналогично показывается, что $Tcdot! begin{pmatrix}dfrac{E_r}{U}end{pmatrix}= C^{ast}(CC^{ast})^{-1}$ для $U=-T_4^{-1}T_3$ . Поэтому формулы (4.22) и (4.21) дают одну и ту же псевдообратную матрицу.

Пример 4.11. Для матрицы $A=begin{pmatrix}1&-1&2&0\-1&2&-3&1\ 0&1&-1&1 end{pmatrix}$ найти псевдообратную.

Решение. Первый способ. 1, 2. Первые два пункта алгоритма выполнены при решении примера 1.38, где получены матрицы

$Lambda=begin{pmatrix}1&0!!&vline!!&0&0\ 0&1!!&vline!!&0&0\hline 0&0!!&vline!!&0&0end{pmatrix}!,quad S=begin{pmatrix}1&0&0\1&1&0\-1&-1&1 end{pmatrix}!,quad T=begin{pmatrix}1&1&-1&-1\ 0&1&1&-1\ 0&0&1&0\ 0&0&0&1 end{pmatrix}!,$

удовлетворяющие равенству Lambda=SAT . Следовательно, r=operatorname{rg}A= operatorname{rg}Lambda=2 .

3. Найдем произведения

$begin{gathered}SS^{ast}= begin{pmatrix}1&0&0\1&1&0\-1&-1&1end{pmatrix} !cdot! begin{pmatrix}1&1&-1\0&1&-1\ 0&0&1 end{pmatrix}= begin{pmatrix}1&1!!&vline!!&-1\ 1&2!!&vline!!&-2\hline -1&-2!!&vline!!&3end{pmatrix}!;\[5pt] TT^{ast}= begin{pmatrix}1&0&0&0\1&1&0&0\-1&1&1&0\-1&-1&0&1end{pmatrix}!cdot! begin{pmatrix}1&1&-1&-1\ 0&1&1&-1\ 0&0&1&0\ 0&0&0&1end{pmatrix}= begin{pmatrix} 1&1!!&vline!!&-1&-1\ 1&2!!&vline!!&0&-2\hline -1&0!!&vline!!&3&0\ -1&-2!!&vline!!&0&3 end{pmatrix}end{gathered}$

Следовательно, $S_2=begin{pmatrix}-1\-2end{pmatrix}!,~S_4=(3),~T_3=begin{pmatrix}-1&0\ -1&-2end{pmatrix}!,~T_4=begin{pmatrix}3&0\0&3end{pmatrix}$

4. Находим произведения

$begin{gathered}U=-T_4^{-1}T_3= -frac{1}{9}! begin{pmatrix} 3&0\0&3end{pmatrix}!cdot! begin{pmatrix}-1&0\ -1&-2end{pmatrix}= begin{pmatrix} 1/3&0\1/3&2/3end{pmatrix}!,\[5pt] V=-S_2S_4^{-1}=-begin{pmatrix}-1\-2end{pmatrix}!cdot! begin{pmatrix}dfrac{1}{3}end{pmatrix}= begin{pmatrix}1/3\2/3end{pmatrix}!. end{gathered}$

5. По формуле (4.21) получим псевдообратную матрицу

$begin{aligned}A^{-1}&= Tcdot! begin{pmatrix}dfrac{E_r}{U}end{pmatrix}!cdot! begin{pmatrix}E_rmid Vend{pmatrix}!cdot S= begin{pmatrix}1&1&-1&-1\ 0&1&1&-1\ 0&0&1&0\ 0&0&0&1end{pmatrix}!cdot! begin{pmatrix}1&0\0&1\hline 1/3&0\1/3& 2/3 end{pmatrix}!cdot! begin{pmatrix}1&0!!&vline!!&1/3\ 0&1!!&vline!!&2/3 end{pmatrix} !cdot! begin{pmatrix} 1&0&0\1&1&0\ -1&-1&1end{pmatrix}=\[2pt] &=begin{pmatrix} 1/3&1/3\ 0&1/3\1/3&0\1/3&2/3end{pmatrix}!cdot! begin{pmatrix}2/3&-1/3&1/3\ 1/3&1/3&2/3 end{pmatrix}= begin{pmatrix}1/3&0&1/3\ 1/9&1/9&2/9\1/9&1/9&2/9\2/9&-1/9&1/9\ 4/9&1/9&5/9 end{pmatrix}!.end{aligned}$

Псевдообратная матрица найдена.

Второй способ. 1, 2. Первые два пункта алгоритма выполнены при решении примера 1.38.

3. Найдем обратные матрицы

$S^{-1}=begin{pmatrix}1&0&0\1&1&0\-1&-1&0\-1&-1&1end{pmatrix}^{-1}= begin{pmatrix}1&0&0\-1&1&0\0&1&1end{pmatrix}!;quad T^{-1}=begin{pmatrix}1&1&-1&-1\0&1&1&-1\0&0&1&0\0&0&0&1end{pmatrix}^{-1}= begin{pmatrix}1&-1&2&0\ 0&1&-1&1\ 0&0&1&0\ 0&0&0&1end{pmatrix}!.$

4. Запишем матрицы

$begin{gathered}B=S^{-1}cdot! begin{pmatrix}dfrac{E_r}{O}end{pmatrix}= begin{pmatrix}1&0&0\-1&1&0\ 0&1&1end{pmatrix}!cdot! begin{pmatrix}1&0\0&1\hline 0&0end{pmatrix}= begin{pmatrix}1&0\-1&1\0&1end{pmatrix}!,\[2pt] C=begin{pmatrix}E_rmid Oend{pmatrix}!cdot T^{-1}= begin{pmatrix}1&0!!&vline!!&0&0\ 0&1!!&vline!!&0&0 end{pmatrix}!cdot! begin{pmatrix}1&-1&2&0\0&1&-1&1\ 0&0&1&0\ 0&0&0&1end{pmatrix}= begin{pmatrix}1&-1&2&0\0&1&-1&1end{pmatrix}!.end{gathered}$

5. Псевдообратную матрицу получим по формуле (4.22). Для этого сначала найдем произведения и обратные матрицы

$begin{aligned}B^{ast}B&= begin{pmatrix}1&-1&0\0&1&1end{pmatrix}!cdot! begin{pmatrix}1&0\-1&1\0&1end{pmatrix}= begin{pmatrix}2&-1\-1&2end{pmatrix}!,quad begin{pmatrix}B^{ast}Bend{pmatrix}^{-1}= frac{1}{3}! begin{pmatrix}2&1\1&2end{pmatrix}= begin{pmatrix}2/3&1/3\1/3&2/3end{pmatrix}!;\[5pt] CC^{ast}&= begin{pmatrix}1&-1&2&0\0&1&-1&1end{pmatrix}!cdot! begin{pmatrix}1&0\-1&1\2&-1\0&1end{pmatrix}= begin{pmatrix}6&-3\-3&3end{pmatrix}!,quad begin{pmatrix}CC^{ast}end{pmatrix}^{-1}= frac{1}{9}! begin{pmatrix} 3&3\3&6end{pmatrix}= begin{pmatrix}1/3&1/3\1/3&2/3end{pmatrix}!, end{aligned}$

а затем псевдообратную матрицу

$begin{gathered}A^{-1}= C^{ast}begin{pmatrix}CC^{ast}end{pmatrix}^{-1}!begin{pmatrix}B^{ast}Bend{pmatrix}^{-1}B^{ast}= begin{pmatrix}1&0\-1&1\2&-1\0&1end{pmatrix}!! begin{pmatrix}1/3&1/3\1/3&2/3end{pmatrix}!cdot! begin{pmatrix} 2/3&1/3\1/3&2/3 end{pmatrix}!! begin{pmatrix}1&-1&0\0&1&1end{pmatrix}=\[2pt] = begin{pmatrix}1/3&1/3\0&1/3\1/3&0\1/3&2/3end{pmatrix}!cdot! begin{pmatrix}2/3&-1/3&1/3\ 1/3&1/3&2/3end{pmatrix}= begin{pmatrix}1/3&0&1/3\ 1/9&1/9&2/9\ 2/9&-1/9&1/9\ 4/9&1/9& 5/9end{pmatrix}!,end{gathered}$

что совпадает с полученным ранее результатом.

Третий способ. Для последовательного нахождения строк псевдообратной матрицы используется метод Гревилля.

Пусть a_k — k-й столбец матрицы A,(1leqslant kleqslant n) ; A_k — матрица, образованная первыми к столбцами матрицы (A_1=a_1,~A_n=A) ; $A_k^{-1}$ — соответствующие псевдообратные матрицы (k=1,2,ldots,n) ; b_k — последняя строка в матрице $A_k^{-1}$ ( k=1,2,ldots,n) ; — как и ранее, нулевой столбец.

1. Положить k=1 . Если a_1ne o , найти $A_1^{-1}=a_1^{-1}=frac{1}{a_1^{ast}a_1}cdot a_1^{ast}$ . Если a_1=o , то $A_1^{-1}=o^T$ .

2. Положить k=k+1 . Найти:

а) $d_k=A_{k-1}^{-1}cdot a_k$ ;

б) $c_k= a_k-A_{k-1}d_k$ ;

в) если c_kne o ,то $b_k=c_k^{-1}=(c_k^{ast}c_k)^{-1}c_k^{ast}$ ; если c_k=o ,то $b_k=(1+d_k^{ast}d_k)^{-1}d_k^{ast}A_{k-1}^{-1}$ ;

г) $B_k=A_{k-1}^{-1}-d_kb_k$ ;

д) $A_k^{-1}=begin{pmatrix}dfrac{B_k}{b_k}end{pmatrix}$ .

3. Если k=n , процесс завершить: $A^{-1}=A_k^{-1}$ . Иначе перейти к п.2.

Пример 4.12. Для матрицы $A=begin{pmatrix}1&-1&0\-1&2&1\ 2&-3&-1\0&-1&1 end{pmatrix}$ найти псевдообратную методом Гревилля.

Решение. Так как данная матрица действительная, операция сопряжения совпадает с операцией транспонирования.

1. Положим k=1 . Так как первый столбец $a_1=begin{pmatrix}1&-1&2&0 end{pmatrix}^T$ ненулевой, то

$A_1^{-1}= frac{1}{a_1^Ta_1}cdot a_1^T= frac{1}{6}cdot begin{pmatrix}1&-1&2&0 end{pmatrix}= begin{pmatrix}dfrac{1}{6}&-dfrac{1}{6}&dfrac{1}{3}&0 end{pmatrix}!.$

2. Положим k=k+1=2 .

a) $d_2=A_1^{-1}cdot a_2= begin{pmatrix}dfrac{1}{6}&-dfrac{1}{6}&dfrac{1}{3}&0 end{pmatrix}!cdot! begin{pmatrix}-1\2\-3\1end{pmatrix}= -frac{3}{2}.$ ;

б) $c_2=a_2-A_1d_2= begin{pmatrix}-1\2\-3\1end{pmatrix}- begin{pmatrix}1\-1\ 2\0 end{pmatrix}!cdot! begin{pmatrix}-dfrac{3}{2}end{pmatrix}= begin{pmatrix}1/2\1/2\0\1 end{pmatrix}$ ;

в) так как c_2ne o , то

$b_2=c_2^{-1}= begin{pmatrix} c_2^Tc_2end{pmatrix}^{-1}c_2^{T}= left[begin{pmatrix}dfrac{1}{2}&dfrac{1}{2}&0&1end{pmatrix}!! begin{pmatrix}1/2\1/2\0\1 end{pmatrix}right]^{-1}!begin{pmatrix}dfrac{1}{2}&dfrac{1}{2}& 0&1 end{pmatrix}= dfrac{2}{3}! begin{pmatrix} dfrac{1}{2}&dfrac{1}{2}&0&1end{pmatrix}= begin{pmatrix} dfrac{1}{3}&dfrac{1}{3}&0&dfrac{2}{3}end{pmatrix}!;$

г) $B_2=A_1^{-1}-d_2b_2= begin{pmatrix}dfrac{1}{6}&-dfrac{1}{6}& dfrac{1}{3}& 0end{pmatrix}- begin{pmatrix}-dfrac{3}{2}end{pmatrix}!! begin{pmatrix}dfrac{1}{3}& dfrac{1}{3}&0&dfrac{2}{3}end{pmatrix}= begin{pmatrix}dfrac{2}{3}&dfrac{1}{3}& dfrac{1}{3}&1end{pmatrix}$ .

д) $A_2^{-1}= begin{pmatrix}dfrac{B_2}{b_2}end{pmatrix}= begin{pmatrix}2/3&1/3&1/3&1\ 1/3&1/3&0&2/3end{pmatrix}$ .

3. Так как k=2ne n=3 , то перейдем к п.2.

2. Положим k=k+1=3 .

а) $d_3=A_2^{-1}cdot a_3= begin{pmatrix}2/3&1/3&1/3&1\ 1/3&1/3&0&2/3 end{pmatrix} !cdot! begin{pmatrix}0\1\-1\1end{pmatrix}= begin{pmatrix}1\1end{pmatrix}$ ;

б) $c_3=a_3-A_2d_3= begin{pmatrix}0\1\-1\1end{pmatrix}- begin{pmatrix}1&-1\ -1&2\ 2&-3\ 0&1end{pmatrix}!cdot! begin{pmatrix}1\1end{pmatrix}= begin{pmatrix}0\1\-1\1end{pmatrix}- begin{pmatrix}0\1\-1\1end{pmatrix}= begin{pmatrix}0\0\0\0end{pmatrix}!;$

в) так как c_3=o , то

$begin{gathered}b_3=begin{pmatrix}1+d_3^Td_3end{pmatrix}^{-1}d_3^TA_2^{-1}= begin{bmatrix}1+ begin{pmatrix}1&1 end{pmatrix}!cdot! begin{pmatrix}1\1 end{pmatrix} end{bmatrix}^{-1}!cdot!begin{pmatrix}1&1end{pmatrix}!cdot! begin{pmatrix} 2/3&1/3&1/3&1\ 1/3&1/3&0&2/3end{pmatrix}=\[2pt] =begin{pmatrix} dfrac{1}{3}&dfrac{1}{3}end{pmatrix}!cdot! begin{pmatrix} 2/3&1/3&1/3&1\ 1/3&1/3&0&2/3end{pmatrix}= begin{pmatrix}dfrac{1}{3}&dfrac{2}{9}&dfrac{1}{9}&dfrac{5}{9} end{pmatrix}!; end{gathered}$

г) $B_3=A_2^{-1}-d_3b_3= begin{pmatrix}2/3&1/3&1/3&1\ 1/3&1/3&0&2/3end{pmatrix}- begin{pmatrix} 1\1end{pmatrix}!cdot! begin{pmatrix}dfrac{1}{3}&dfrac{2}{9}&dfrac{1}{9}& dfrac{5}{9}end{pmatrix}= begin{pmatrix}1/3&1/9&2/9&4/9\ 0&1/9&-1/9&1/9end{pmatrix}!;$

д) $A_3^{sim1}= begin{pmatrix}dfrac{B_3}{b_3}end{pmatrix}= begin{pmatrix} 1/3&1/9&2/9&4/9\ 0&1/9&-1/9&1/9\ 1/3&2/9&1/9&5/9end{pmatrix}!.$

3(2). Так как k=3=n , то процесс завершен и $A^{sim1}=A_3^{sim1}$ .

Частные случаи нахождения псевдообратной матрицы

1. Если матрица $A=(a_{11})$ — число, то

$A^{sim1}= begin{cases}dfrac{1}{a_{11}},&a_{11}ne0,\[4pt] 0,&a_{11}=0. end{cases}$

2. Если матрица диагональная $A=operatorname{diag}!begin{pmatrix}a_{11},a_{22},ldots,a_{nn}end{pmatrix}$ , то псевдообратная матрицы также диагональная

$A^{sim1}=operatorname{diag}begin{pmatrix}a_{11}^{-1}, a_{22}^{-1},ldots, a_{nn}^{-1}end{pmatrix},~~text{where}~~a_{ii}^{-1}=begin{cases}dfrac{1}{a_{ii}},&a_{ii}ne0,\0,&a_{ii}=0,end{cases}i=1,2,ldots,n.$

(4.23)

3. Если столбцы матрицы линейно независимы, то

$A^{sim1}=begin{pmatrix}A^{ast}cdot Aend{pmatrix}^{-1}cdot A^{ast}.$

(4.24)

4. Если строки матрицы линейно независимы, то

$A^{sim1}=A^{ast}cdot! begin{pmatrix}AA^{ast}end{pmatrix}^{-1}.$

(4.25)

Пример 4.13. Для матриц найти псевдообратные

$A=begin{pmatrix}1&0&0\0&2&0\0&0&0end{pmatrix}!,quad B=begin{pmatrix}1&2&3end{pmatrix}!,quad C=begin{pmatrix}1&0\1&1\1&1 end{pmatrix}!.$

Решение. Матрица — диагональная. По формуле (4.23) находим

$A^{sim1}=begin{pmatrix}1&0&0\0&1/2&0\0&0&0end{pmatrix}!.$

Для матрицы-строки по формуле (4.25) получаем

$B^{sim1}=begin{pmatrix}1\2\3end{pmatrix}!cdot begin{bmatrix}begin{pmatrix} 1&2&3end{pmatrix}!cdot! begin{pmatrix}1\2\3end{pmatrix}end{bmatrix}^{-1}= begin{pmatrix} 1\2\3end{pmatrix}!cdot(14)^{-1}= begin{pmatrix}1/14\2/14\ 3/14 end{pmatrix}!.$

Столбцы матрицы линейно независимы. По формуле (4.24) имеем

$begin{aligned}C^{sim1}&= begin{bmatrix} begin{pmatrix}1&1&1\ 0&1&2 end{pmatrix}!cdot! begin{pmatrix} 1&0\1&1\1&1end{pmatrix}end{bmatrix}^{-1}cdot! begin{pmatrix}1&1&1\0&1&1end{pmatrix}= begin{pmatrix}3&2\2&2end{pmatrix}^{-1}cdot! begin{pmatrix}1&1&1\0&1&1end{pmatrix}=\[2pt] &=frac{1}{2}! begin{pmatrix}2&-2\ -2&3 end{pmatrix}!cdot! begin{pmatrix}1&1&1\0&1&1end{pmatrix}= begin{pmatrix}1&0&0\ -1&1/2&1/2end{pmatrix}!.end{aligned}$

Найдем матрицу $C^{sim1}$ первым способом

1. Составляем блочную матрицу

2. Приводим блок к простейшему виду

$begin{pmatrix} C!!&vline!!&E_3\ E_2!!&vline!!&{}end{pmatrix}= begin{pmatrix}1&0!!&vline!!&1&0&0\ 1&1!!&vline!!&0&1&0\ 1&1!!&vline!!& 0&0&1\hline 1&0!!&vline!!&{}&{}&{}\ 0&1!!&vline!!&{}&{}&{}end{pmatrix}sim begin{pmatrix}1&0!!&vline!!&1&0&0\ 0&1!!&vline!!&-1&1&0\ 0&1!!&vline!!& -1&0&1\hline 1&0!!&vline!!&{}&{}&{}\ 0&1!!&vline!!&{}&{}&{}end{pmatrix}sim begin{pmatrix}1&0!!&vline!!&1&0&0\ 0&1!!&vline!!&-1&1&0\ 0&0!!&vline!!& 0&-1&1\hline 1&0!!&vline!!&{}&{}&{}\ 0&1!!&vline!!&{}&{}&{}end{pmatrix}$

Получили матрицы $T=E_2,~ S=begin{pmatrix}1&0&0\-1&1&0\ 0&-1&1end{pmatrix}$ . Ранг матрицы равен количеству ненулевых строк, т.е. r=operatorname{rg}C=2=n, E_r=E_2 .

3. Находим произведения

$SS^{ast}= begin{pmatrix}1&0&0\-1&1&0\ 0&-1&1end{pmatrix}!cdot! begin{pmatrix}1&-1&0\0&1&-1\ 0&0&1end{pmatrix}= begin{pmatrix}1&-1!!&vline!!&0\ -1&2!!&vline!!&-1\hline 0&-1!!&vline!!&2end{pmatrix}=begin{pmatrix}S_1!!&vline!!&S_2\hline S_3!!&vline!!&S_4end{pmatrix}!;quad T^{ast}T=begin{pmatrix}1&0\0&1 end{pmatrix}=(T_1).$

В матрице $T^{ast}T$ блоки T_2,T_3,T_4 отсутствуют (см. замечание 4.8).

4. Из-за отсутствия блоков T_3,T_4 вычислять матрицу не нужно. Находим только матрицу

$V=-S_2S_4^{-1}= -begin{pmatrix}0\-1end{pmatrix}!cdot(2)^{-1}= begin{pmatrix} 0\1/2end{pmatrix}!.$

5. Находим псевдообратную матрицу по формуле (4.21), учитывая отсутствие матрицы (см. п.5 замечаний 4.6):

$begin{aligned}C^{sim1}&= Tcdot E_2cdot! begin{pmatrix}E_2mid Vend{pmatrix}!cdot S= begin{pmatrix}1&0\0&1end{pmatrix}!cdot! begin{pmatrix}1&0\0&1 end{pmatrix}!cdot! begin{pmatrix}1&0!!&vline!!&0\ 0&1!!&vline!! &1/2 end{pmatrix}!cdot! begin{pmatrix}1&0&0\-1&1&0\ 0&-1&1end{pmatrix}=\[2pt] &= begin{pmatrix}1&0!!&vline!!&0\ 0&1!!&vline!! &1/2end{pmatrix}!cdot! begin{pmatrix}1&0&0\-1&1&0\ 0&-1&1end{pmatrix}= begin{pmatrix}1&0&0\-1&1/2&1/2 end{pmatrix}!.end{aligned}$

Результаты обоих способов нахождения матрицы $C^{sim1}$ совпадают.

Псевдообращение блочных матриц

Пусть дана блочная матрица $M=begin{pmatrix}A!!&vline!!&B\hline C!!&vline!!&D end{pmatrix}!$ , где — квадратная невырожденная матрица r-го порядка и r=operatorname{rg}A= operatorname{rg}M .

Тогда псевдообратная матрица $M^{sim1}$ — является блочной матрицей и находится по формуле

$M^{sim1}= begin{pmatrix}dfrac{A^{ast}}{B^{ast}}end{pmatrix}!cdot! begin{pmatrix}AA^{ast}+BB^{ast}end{pmatrix}^{-1}cdot Acdot! begin{pmatrix}A^{ast}A+ C^{ast}Cend{pmatrix}^{-1}cdot! begin{pmatrix}A^{ast}mid C^{ast} end{pmatrix}!.$

(4.26)

Пример 4.14. Для блочной матрицы $M=begin{pmatrix}1&-1!!&vline!!&2&0\ -1&2!!&vline!!&-3&1\hline 0&1!!&vline!!&-1&1end{pmatrix}= begin{pmatrix} A!!&vline!!&B\hline C!!&vline!!&D end{pmatrix}$ найти псевдообратную.

Решение. Заметим, что operatorname{rg}A=2=operatorname{rg}M . Последовательно вычисляем

$begin{aligned}begin{pmatrix}AA^{ast}+BB^{ast}end{pmatrix}^{-1}&= begin{bmatrix}begin{pmatrix}1&-1\-1&2end{pmatrix}!cdot! begin{pmatrix}1&-1\-1&2 end{pmatrix}+ begin{pmatrix}2&0\-3&1end{pmatrix}!cdot! begin{pmatrix}2&-3\ 0&1end{pmatrix}end{bmatrix}^{-1}=\[2pt] &=begin{bmatrix}begin{pmatrix}2&-3\-3&5end{pmatrix}+ begin{pmatrix}4&-6\-6&10end{pmatrix} end{bmatrix}^{-1}= begin{pmatrix}6&-9\ -9&15end{pmatrix}^{-1}= frac{1}{3}! begin{pmatrix}5&3\3&2end{pmatrix}!;\[5pt] begin{pmatrix}A^{ast}A+C^{ast}Cend{pmatrix}^{-1}&= begin{bmatrix}begin{pmatrix}1&-1\-1&2end{pmatrix}!cdot! begin{pmatrix}1&-1\-1&2 end{pmatrix}+ begin{pmatrix}0\1 end{pmatrix}!cdot! begin{pmatrix}0&1end{pmatrix}end{bmatrix}^{-1}=\[2pt] &=begin{bmatrix}begin{pmatrix}2&-3\-3&5end{pmatrix}+ begin{pmatrix}0&0\0&1end{pmatrix} end{bmatrix}^{-1}= begin{pmatrix}2&-3\ -3&6end{pmatrix}^{-1}= frac{1}{3}! begin{pmatrix}6&3\3&2end{pmatrix}!;end{aligned}$

$begin{pmatrix} AA^{ast}+ BB^{ast}end{pmatrix}^{-1}cdot Acdot! begin{pmatrix} A^{ast}A+ C^{ast}Cend{pmatrix}^{-1}= frac{1}{3}! begin{pmatrix}5&3\ 3&2 end{pmatrix}!cdot! begin{pmatrix}1&-1\-1&2end{pmatrix}!cdot frac{1}{3}! begin{pmatrix}6&3\3&2end{pmatrix}= frac{1}{9}! begin{pmatrix}2&1\1&1end{pmatrix}!cdot! begin{pmatrix} 6&3\3&2end{pmatrix}= frac{1}{9}! begin{pmatrix} 15&8\9&5 end{pmatrix}!.$

По формуле (4.26) имеем

$begin{aligned}M^{sim1}&= begin{pmatrix}1&-1\-1&2\hline 2&-3\0&1end{pmatrix}!cdotfrac{1}{9}! begin{pmatrix}15&8\9&5end{pmatrix}!cdot! begin{pmatrix}1&-1!!&vline!!&0\ -1&2!!&vline!!&1end{pmatrix}= frac{1}{9}! begin{pmatrix}1&-1\-1&2\hline 2&-3\0&1end{pmatrix}!cdot! begin{pmatrix} 7&1!!&vline!!&8\ 4&1!!&vline!!&5end{pmatrix}=\[2pt] &=frac{1}{9}! begin{pmatrix}3&0!!&vline!!&3\ 1&1!!&vline!!&2\hline 2&-1!!&vline!!&1\ 4&1!!&vline!!&5end{pmatrix}= begin{pmatrix}1/3&0&1/3\ 1/9&1/9&2/9\ 2/9&-1/9&1/9\ 4/9&1/9&5/9end{pmatrix}!,end{aligned}$

что совпадает с результатами примера 4.11.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Псевдообратные матрицы — обобощение обратных матриц в линейной алгебре.
Псевдообратная матрица к матрице $A$ обозначается $A^+$ .
Псевдообращение можно понимать как наилучшую апроксимацию (по методу наименьших квадратов) решения соответствующей системы линейных уравнений. Псевдообращение определено для любых матриц над действительными и комплексными числами.
Псевдообратная матрица может быть вычислена с помощью собственного представления матрицы.

Содержание

1 Определение
2 Происхождение
3 Свойства
4 Особые случаи
5 Вычисление
6 См. также

Определение

$A^+$ называется псевдообратной матрицей для матрицы $A$ , если она удовлетворяет следующим критериям:

$A A^+A = A;$
$A^+A A^+ = A^+$ ( $A^+$ является слабым обращением в мультипликативной полугруппе);
$(AA^+)^* = AA^+$ (это означает, что $AA^+$ — эрмитова матрица);
$(A^+A)^* = A^+A$ ( $A^+A$ – тоже эрмитова матрица).

Здесь $M^*$ – эрмитова сопряжённая матрица M. Для матриц над полем действительных чисел $M^* = M^T$ .

Происхождение

По методу наименьших квадратов для решения несовместной СЛАУ $Amathbf{x}=mathbf{b}$ ,
состоящей из $M$ уравнений с $N$ неизвестными, необходимо решить уравнение

$A^TAmathbf{x}=A^Tmathbf{b},$

называемое нормальным уравнением.
Пусть столбцы матрицы $A$ линейно независимы, тогда она обратима и система имеет единственное решение

$mathbf{x}=(A^TA)^{-1}A^Tmathbf{b}.$

Таким образом мы приходим к понятию псевдообращения действительных матриц:

$A^+=(A^TA)^{-1}A^T.$

Свойства

Особые случаи

$A^+ = (A^* A)^{-1} A^*.$

Отсюда следует что $A^+$ – левая обратная матрица для A: $A^+ A = I$ .

$A^+ = A^*(A A^*)^{-1}.$

Отсюда следует, что $A^+$ — правая обратная матрица для A: $A A^+ = I$ .

Если и столбцы и строки линейно независимы (что верно для квадратных невырожденных матриц), псевдообращение равно обращению:

$A^+ = A^{-1} .$

Если A и B таковы, что произведение $AB$ определено, и

$x^+ = left{begin{matrix} 0, & x=0; \ x^{-1}, & x ne 0. end{matrix}right.$

Псевдообратный для нулевого вектора – транспонированый нулевой вектор. Псевдообратный для иного вектора – сопряжённый транспонированный вектор, делённый на квадрат своей длины:

$x^+ = left{begin{matrix} 0^T, & x = 0;\ {x^* over x^* x}, & x ne 0. end{matrix}right.$

Для доказательства достаточно проверить, что эти величины удовлетворяют определению псевдообратных.

Вычисление

Простейший вычислительный путь получения псевдообратной матрицы — использование собственного представления матрицы (СПМ).

Если $A = USigma V^*$ — собственное представление A, тогда $A^+ = VSigma^+ U^*.$ Для диагональной матрицы, такой как $Sigma$ , псевдообратная вычисляется обращением каждого ненулевого элемента на диагонали.

Существуют оптимизированые подходы для вычисления псевдоинверсии блочных матриц.

Если псевдоинверсия известна для некой матрицы и нужно найти псевдоинверсию для аналогичной матрицы, иногда она может быть вычислена с помощью специальных алгоритмов, требующих меньшего количества расчётов. В частности, если аналогичная матрица отличается от начальной на один изменённый, добавленный или удалённый столбец или строку — существуют накопительные алгоритмы, которые могут использовать взаимосвязь между матрицами.

См. также

Практикум ММП ВМК, 4й курс, осень 2008
Метод наименьших квадратов
Решение переопределённой СЛАУ

Источник

Если — квадратная и
неособенная матрица, то для нее существует обратная матрица
. Если же
— не квадратная,
а прямоугольная -матрица
() или
квадратная, но особенная, то матрица не имеет
обратной и символ не имеет смысла. Однако, как
будет показано далее, для произвольной прямоугольной матрицы
существует
«псевдообратная» матрица , которая
обладает некоторыми свойствами обратной матрицы и имеет важные применения при
решении системы линейных уравнений. В случае, когда — квадратная неособенная матрица,
псевдообратная матрица совпадает с обратной .

1. Скелетное разложение матрицы. В дальнейшем мы
будем пользоваться представлением произвольной прямоугольной -матрицы
ранга в виде произведения
двух матриц и , имеющих соответственно размеры и :

. (36)

Здесь ранги сомножителей и обязательно равны
рангу произведения ,. Действительно (см. стр. 22), Но ранги и не могут
превосходить ,
так как —
один из размеров матриц и . Поэтому .

Для того чтобы получить
разложение (36), достаточно в качестве столбцов матрицы взять любые линейно независимых
столбцов матрицы ,
либо любые линейно
независимых столбцов, через которые линейно выражаются столбцы матрицы . Тогда произвольный
-й столбец
матрицы будет
линейной комбинацией столбцов матрицы с коэффициентами ; эти коэффициенты и образуют
-й столбец
матрицы (, см. стр. 19).

Поскольку
матрицы и
имеют
максимально возможный ранг , то квадратные матрицы и являются
неособенными:

, .
(37)

Действительно, пусть столбец — произвольное
решение уравнения

.
(38)

Помножим это уравнение слева на строку . Тогда . Отсюда следует и (поскольку — линейная
комбинация линейно независимых столбцов матрицы ; ср. с формулой (13″)) . Из того, что
уравнение (38) имеет только нулевое решение , вытекает, что. Аналогично устанавливается
второе неравенство (37).

Разложение (36) будем называть скелетным разложением
матрицы .

2. Существование и единственность псевдообратной
матрицы. Рассмотрим матричное уравнение

.
(39)

Если — квадратная неособенная матрица, то
это уравнение имеет единственное решение . Если же — произвольная прямоугольная -матрица, то искомое
решение имеет
размеры но
не определяется однозначно. В общем случае уравнение (39) имеет бесчисленное
множество решений. Ниже будет показано, что среди этих решений имеется только
одно, обладающее тем свойством, что его строки и столбцы являются линейными
комбинациями соответственно строк и столбцов сопряженной матрицы . Именно это решение
мы будем называть псевдообратной матрицей для и обозначать через .

Определение 5. Матрица размеров называется псевдообратной для -матрицы , если выполняются
равенства

, (40)

, (41)

где и — некоторые матрицы

Докажем сначала, что для данной матрицы не может существовать
двух различных псевдообратных матриц и . Действительно, из равенств

, , ,

Полагая , , , найдем:

, .

Отсюда

и, следовательно (см. конец § 3),

Но тогда , т.е. .

Для того чтобы установить существование матрицы , мы воспользуемся
скелетным разложением (36) и будем искать сначала псевдообратные матрицы и . Так как по
определению должны иметь место равенства

, (42)

где — некоторая матрица, то

Умножая слева на и замечая, что — неособенная квадратная
матрица, найдем:

Но тогда второе из равенств (42) дает искомое
выражение для :

. (43)

Совершенно аналогично найдем:

. (44)

Покажем теперь, что матрица

(45)

удовлетворяет условиям (40), (41)
и, следовательно, является псевдообратной матрицей для .

В самом деле,

С другой стороны, из равенств (43),
(44) и (45) с учетом равенства , полагая, находим

где

, .

Таким образом доказано, что для
произвольной прямоугольной матрицы существует одна и только одна псевдообратная матрица , которая определяется формулой (45), где и — сомножители в скелетном разложении матрицы .
Из самого определения псевдообратной матрицы непосредственно следует, что в
случае квадратной неособенной матрицы псевдообратная матрица совпадает с обратной .

Пример. Пусть

Здесь . в качестве
столбцов матрицы первые два
столбца матрицы . Тогда

, .

Поэтому,
согласно формуле (45)

3. Свойства
псевдообратной матрицы. Отметим
следующие свойства псевдообратной матрицы:

1 ;

2 ;

3 , ;

4 , .

Первое свойство означает, что
операции перехода к сопряженной и к псевдообратной матрице перестановочны между
собой. Равенство 2° выражает собой взаимность понятия псевдообратной матрицы,
тан как согласно 2° псевдообратной матрицей для является
исходная матрица . Согласно равенствам 3° и 4°
матрицы и являются
эрмитовыми и инволютивными (квадрат каждой из этих
матриц равен самой матрице).

Для вывода равенства 1°
воспользуемся скелетным разложением (36): . Тогда
равенство дает скелетное
разложение матрицы . Поэтому, заменяя в формуле
(45) матрицу на , а матрицу
на ,
получим:

Равенства , , являются скелетными
разложениями. Следовательно,

Используя свойство 1°, а также
выражения для и
, найдем:

Справедливость равенств 3° и 4°
проверяется непосредственно путем подстановки в эти равенства вместо соответствующего
выражения из формулы (45).

Заметим, что в общем случае, когда
разложение не
является скелетным, не всегда имеет место равенство . Так,
например

Здесь

, ,

Поэтому

4. Наилучшее
приближенное решение (по методу
наименьших квадратов). Рассмотрим произвольную систему линейных уравнений

(46)

или в
матричной записи

. (46′)

Здесь
–
заданные
числа, а –
искомые.

В
общем случае система (46) может быть и несовместной.

Столбец

(47)

называется наилучшим приближенным решением системы (46), если при значениях «квадратичное
отклонение»

(48)

достигает своего наименьшего
значения и среди всех столбцов , для которых это отклонение имеет минимальное
значение, столбец имеет наименьшую «длину», т. е. для этого столбца
величина

(49)

имеет наименьшее значение.

Покажем, что система (46) всегда
имеет одно и только одно наилучшее приближенное решение и это приближенное
решение определяется по формуле

, (50)

где — псевдообратная матрица для матрицы .

Для этого рассмотрим произвольный
столбец и
положим

где

, . (51)

Тогда

. (52)

Но

. (53)

Исходя из разложения (36) и формулы
(45), найдем:

Поэтому из равенства
(53) следует

,
(54)

но тогда и

.
(54′)

Поэтому
из равенства (52) находим

,
(55)

и,
следовательно, для любого столбца

.
(56)

Пусть
теперь

;

тогда,
согласно равенству (55)

,
(57)

где

С другой
стороны,

.
(58)

Вспоминая,
что (см.определение
5), получим в силу (57):

. (59)

Но
тогда и

Поэтому
из равенства (58) находим

и,
следовательно

,
(60)

причем
знак = имеет место только при , т.е. при , где .

Пример.
Найти наилучшее приближенное решение (по методу наименьших квадратов) системы
линейных уравнений:

Здесь

Но
тогда (см. пример на стр. 35)

и
поэтому

Следовательно,

, , , .

Определим
норму – матрицы как
неотрицательное число, задаваемое формулой

.
(61)

При
этом очевидно, что

.
(61′)

Рассмотрим
матричное уравнение

,
(62)

где
и – заданные и -матрицы, а – искомая
-матрица.

Определим
наилучшее приближенное решение уравнения (62) из условия

причем
в случае, когда

требуется,
чтобы

Из
соотношений

,
(63)

(64)

следует,
что -й
столбец искомой матрицы должен быть наилучшим приближенным
решением системы линейных уравнений

Поэтому

Поскольку
это равенство справедливо при любом то

.
(65)

Таким
образом, уравнение (62) всегда имеет одно и только одно наилучшее приближенное
решение, определяемое формулой (65).

В
частном случае, когда — единичная матрица -го порядка, имеем . Следовательно,
псевдообратная матрица является наилучшим приближенным
решением (по методу наименьших квадратов) матричного уравнения

Это
свойство псевдообратной матрицы может быть принято в
качестве ее определения.

5.
Метод Гревилля последовательного нахождения псевдообратной матрицы состоит в
следующем. Пусть –
-й столбец в -матрице , — матрица, образованная
первыми столбцами
матрицы . —
последняя строка в матрице (, , ). Тогда

(66)

и
для имеют
место рекуррентные формулы

, , ;
(67)

при
этом, если ,
то

;
(68)

если
же , т.е. , то

.
(69)

Предлагаем читателю проверить, что
матрица является
псевдообратной для матрицы , если матрица и строка определяются формулами (61)-(64). Этот метод не
требует вычисления детерминантов и может быть использован для вычисления
обратной матрицы. Пример. Пусть