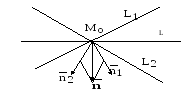Пучок прямых как найти центр

В статье рассматриваются определения пучка прямых с центром в заданной точке плоскости. Разбирается подробное решение с применением определения, рассматриваются задачи на составление уравнения пучка прямых, нахождение координат.

Пучок прямых – это определение

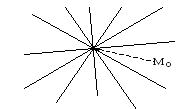
Пучок прямых определяется на плоскости, но не в трехмерном пространстве. Аксиома геометрии говорит о том, что если имеются две несовпадающие точки, расположенные на плоскости, то через них можно провести только одну прямую. Если на плоскости γ задается точка М0 и M1, то через них можем провести прямую. Когда имеется еще одна точка М2, которая не лежит на прямой М0М1, тогда можно провести прямую М0М2. Если отметим точку М3, не принадлежащую ни одной из проведенных прямых, через нее также може провести прямую, проходящую через М0.

Отсюда следует, что в плоскости γ можно провести множество прямых через заданную точку. Это и привело к определению пучка прямых.

Заданная плоскость γ с множеством всех прямых, которые лежат в плоскости γ и проходящие через точку М0 называют пучком прямых с центром в точке М0.

Исходя из определения, имеем, что любые две прямые из этого пучка пересекутся в центре данного пучка прямых. Пучок определяется при условии, если указан центр данного пучка.

Уравнение пучка прямых – решение задач

Для решения задач применяется уравнение пучка прямых, то есть сам пучок рассматривается относительно систему координат Оху на плоскости.

Когда имеем на плоскости прямоугольную систему координат Оху с указанными пересекающимися прямыми а1 и а2_, пучок задает эти прямые. За систему координат Оху отвечает общее уравнение прямой, которое имеет вид A1x+B1y+C1=0 или A2x+B2y+C2=0.

Введем обозначение пересечения прямых как точка М0  с координатами х0 и y0. Отсюда следует, что точка М имеет координаты M0(x0, y0).

Чтобы определить вид используемого уравнения в пучках, рассмотрим на теореме.

При заданных двух пересекающихся прямых а1 и а2 имеются прямые, которые входят в пучок прямых, образованных в системе координат Оху. Их уравнения имеют вид A1x+B1y+C1=0 и A2x+B2y+C2=0 тогда  и только тогда, когда уравнение прямой α·(A1x+B1y+C1=0)+β·(A2x+B2y+C2)=0 соответствует ей,a α и βявляются действительными числами, неравными нулю. Данное условие записывается так: α2+β2≠0.

Что и требовалось доказать.

Можем сделать вывод, что уравнение, которое имеет вид α·A1x+B1y+C1+β·A2x+B2y+C2=0 и есть уравнение пучка.

Значения α и β необходимы для того, чтобы определять прямые, находящиеся в данном пучке, с уравнениями A1x+B1y+C1=0 и  A2x+B2y+C2=0.

Необходимо, чтобы как минимум один из параметров был не равен нулю, тогда можно упростить выражение. При условии, что α≠0 получаем выражение вида A1x+B1y+C1+λ·A2x+B2y+C2=0 с λ=αβ. 

При β≠0 выражение принимает вид μ·A1x+B1y+C1+A2x+B2y+C2=0 с μ=αβ.

Они не являются эквивалентными уравнению пучка прямых, относящихся к виду α·A1x+B1y+C1+β·A2x+B2y+C2=0. Уравнение A1x+B1y+C1+λ·A2x+B2y+C2=0 при любых значениях λ не даст возможности  получить уравнение вида A2x+B2y+C2=0.

Уравнение μ·A1x+B1y+C1+A2x+B2y+C2=0 при любых значениях μ не даст в результате A1x+B1y+C1=0.

Подробно рассмотрим на решении примеров.

353 Найти центр пучка прямых,
данного уравнением . 354 Найти уравнение
прямой, принадлежащей пучку прямых и 354.1 Проходящей через
точку А(3; -1); 354.2 Проходящей через
начало координат; 354.3 Параллельной оси Ox; 354.4 Параллельной оси Oy; 354.5 Параллельной
прямой ; 354.6 Перпендикулярной к
прямой . 355 Составить
уравнение прямой, проходящей через точку
пересечения прямых , и отсекающий на оси ординат отрезок
b=-3. Решить задачу, не определяя координат точки
пересечения данных прямых. 356 Составить
уравнение прямой, которая проходит через точку
пересечения прямых , и делит пополам отрезок,
ограниченный точками M₁(5; -6), M₂(-1;
-4). Решить задачу, не вычисляя
координат точки пересечения данных прямых. 357 Дано уравнение
пучка прямых . Написать уравнение
прямой этого пучка, проходящей через центр масс
однородной треугольной пластинки, вершины
которой суть точки A(-1; 2), B(4; -4), C(6; -1). 358 Дано уравнение
пучка прямых . Найти прямую этого пука,
проходящую через середину отрезка прямой , заключенного
между прямыми ,
. 359 Даны уравнения
сторон треугольника , , . Не определяя координат его вершин,
составить уравнения высот этого трегоульника. 360 Составить
уравнение прямой, проходящей через точку
пересечения прямых , под углом 45⁰ к прямой . Решить задачу, не
вычисляя координат точки пересечения данных
прямых. 361 В треугольнике АВС
даны уравнения высоты AN: , высоты
BN: и стороны АВ: . Не определяя
координат вершин и точки пересечения высот
треугольника, составить уравнение двух других
сторон и третьей высоты. 362 Составить
уравнения сторон треугольника АВС, зная одну его
вершину А(2; -1), а также уравнения высоты и биссектрисы , проведенных из
одной вершины. Решить задачу, не вычисляя
координат вершин В и С. 363 Дано уравнение
пучка прямых . Найти прямые этого пучка,
отрезки которых, заключенные между прямыми , , равны . 364 Дано уравнение
пучка прямых . Доказать, что прямая принадлежит
этому пучку. 365 Дано уравнение
пучка прямых . Доказать, что прямая не
принадлежит этому пучку. 366 Дано уравнение
пучка прямых . Найти, при каком значении
С прямая будет принадлежать этому пучку. 367 Дано уравнение
пучка прямых . Найти, при каких
значениях a прямая не будет принадлежать
этому пучку. 368 Центр пучка прямых является вершиной квадрата,
диагональ которого лежит на прямой . Составить
уравнения сторон и второй диагонали этого
квадрата. 369 Дано уравнение
пучка прямых . Найти прямую этого пучка,
отсекающую на координатных осях отличные от нуля
отрезки равной величины (считая от начала
координат). 370 Дано уравнение
пучка прямых . Найти прямые этого пучка,
отсекающие на координатных осях отрезки равной
длины (считая от начала координат). 371 Дано уравнение
пучка прямых . Найти прямые этого пучка,
отсекающие от координатных углов треугольники с
площадью, равной 9. 372 Дано уравнение
пучка прямых . Доказать, что среди
прямых этого пучка существует только одна
прямая, отстоящая от точки Р(2; -3) на расстояние . Написать
уравнение этой прямой. 373 Дано уравнение
пучка прямых . Доказать, что среди
прямых этого пучка нет прямой, отстоящей от точки
Р(3; -1) на расстояние d=3. 374 Составить
уравнение прямой, проходящей через точку
пересечения прямых , и отстоящей от точки С(-1; 2) на
расстояние d=5. Решить задачу, не вычисляя точки
пересечения даных прямых. 375 Дано уравнение
пучка прямых . Написать уравнения
прямых этого пучка, которые вместе с прямыми , образуют
равнобедренные треугольники. 376 Составить
уравнение прямой, которая проходит через точку
пересечения прямых , на одинаковых расстояниях от точек
А(3; -2) и В(-1; 6). Решить задачу, не вычисляя
координат точки пересечения данных прямых. 377 Даны уравнения двух
пучков прямых , . Не определяя их центров, составить
уравнение прямой, принадлежащей обоим пучкам. 378 Стороны АВ, ВС, CD, DA
четырехугольника ABCD заданы соответственно
уравнениями , , , . Не определяя
координат вершин этого четырехугольника,
составить уравнения его диагоналей AC и BD. 379 Центр пучка прямых является одной из вершин
треугольника, две высоты которого даны
уравнениями , . Составить
уравнения сторон этого треугольника.

Пучок прямых. Уравнение пучка прямых

В данной статье мы рассмотрим понятие пучка прямых. Представим уравнение пучка прямых. Приведем примеры нахождения уравнения пучка прямых, проходящих через данную точку.

Пучком прямых называется множество прямых, проходящих через данную точку P. P называется центром пучка прямых. Две разные прямые в пучке прямых определяют центр пучка прямых.

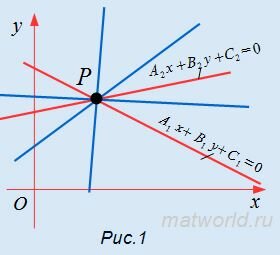
Найдем уравнение пучка прямых, центром которого служит точка пересечения двух прямых (Рис.1):

и

Докажем следующую теорему.

Теорема 1. Пусть (1) и (2) уравнения двух прямых, пересекающихся в точке P, а λ₁ и λ₂ некоторые числа, которые одновременно не равны нулю. Тогда

является уравнением прямой, проходящей через точку P. Обратно, любая прямая, проходящая через точку P определяется уравнением (3), при некотороых числах λ₁ и λ₂.

Доказательство. Во первых покажем, что уравнение (3) является линейным уравнением (уравнением первого порядка), т.е. уравнением, при котором коэффициент при x или y не равен нулю.

Группируем коэффициенты при x и y:

Пусть

Тогда, например при λ₁≠0 (по условию теоремы хотя бы один из чисел λ₁ и λ₂ не равен нулю), получим:

т.е.

Полученное равенство является условием параллельности прямых, определяемых уравнениями (1) и (2), что противоречит условию теоремы (эти прямые пересекаются и не совпадают). Таким образом хотя бы один из равенств (5) не выполняется, т.е. хотя бы один коэффициент при x и y в уравнении (4) не равен нулю. Отсюда следует, что уравнение (4) является линейным уравнением (уравнением первой степени) и является уравнением некоторой прямой. По условию теоремы, эта прямая проходит через точку P(x₀, y₀), которая является пересечением прямых (1) и (2), т.е. выполняются равенства:

Из уравнениий (8) следует, что при любых λ₁ и λ₂:

т.е. уравнение (3) проходит через точку P.

Докажем вторую часть теоремы. Покажем, что любая прямая, проходящая через точку P определяется уравнением (3) при некоторых значениях λ₁ и λ₂.

Возьмем некоторую прямую проходящую через точки P и M’(x’, y’). Покажем, что данная прямая определяется уравнением (3) при некоторых значениях λ₁ и λ₂, не равных одновременно нулю.

В первой части доказательства теоремы мы показали, что прямая, проходящая через точку P определяется уравнением (3). Теперь, если эта прямая проходит через еще одну точку M’(x’, y’), то координаты этой точки должны удовлетворять уравнению (3):

Заметим, что выражения в скобках не могут быть равным нулю одновременно, т.к. это означало бы, что оба уравнения проходят через точки P и M’(x’, y’) и, следовательно, совпадают. Пусть, например, λ₁(A₁x’₀+B₁y’₀+C₁)≠0. Тогда задав λ₂ произвольное число, отличное от нуля, решим (9) относительно λ₁:

Таким образом, при указанных коэффициентов λ₁ и λ₂, прямая (3) проходит через точки P и M’(x’, y’). Если же λ₁(A₂x’₀+B₂y’₀+C₂)≠0, то аналогичным образом вычисляются коэффициенты λ₁ и λ₂.

Теорема доказана.

Пример 1. Пучок прямых задан уравнениями:

и

Найти уравнение прямой из пучка прямых, проходящий через точку M(−3, 1).

Решение. Уравнение пучка прямых, заданных прямыми (10) и (11) имеет следующий вид:

Подставим координаты точки M в уравннение (12):

Упростим (13):

Задав, например, λ₂=4, получим λ₁=−5.

Положим значения λ₁ и λ₂ в (12):

Упростив уравнение (14), получим уравнение из пучка прямых проходящих через точку M(−3, 1):

Ответ:

Пример 2. Построить уравнение пучка прямых с центром M(4,1):

Решение. Возьмем две различные точки, не совпадающие с точкой M: M₁(2,1), M₂(−1,3). Построим уравнение, проходящие через точки M и M₁. Нормальный вектор n₁ этой прямой должен быть ортогональным вектору , равному разностьям координат точек M и M₁: ={2−4, 1−1}={−2,0}. Т.е. можно взять n₁={0,1}. Тогда уравнение прямой с нормальным вектором n₁, проходяще через точку M имеет следующий вид:

или

Построим уравнение проходящее через точки M и M₂. 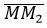={−1−4, 3−1}={−5,2}. Возмем в качестве нормального вектора второго уравнения n₂={2, 5}. Тогда второе уравнение имеет слеждующий вид:

или

Из уравнений (15) и (16) можно записать уравнение пучка прямых с центром M(4,1):

Ответ:

Заметим, что взяв другие точки M₁ и M₂, мы получим уравнение того же пучка прямых, но с другими двумя прямыми.

Лекции
по алгебре и геометрии. Семестр 1.

Лекция
14. Уравнения пучка прямых на плоскости,
пучка плоскостей и связки плоскостей.

Краткое содержание: пучок прямых на
координатной плоскости и его уравнение,
уравнение прямой, проходящей через
заданную точку, пучок плоскостей и его
уравнение, связка плоскостей и его
уравнение, основные типы задач на прямые
и плоскости.

Глава
14. Уравнения пучка прямых на плоскости,
пучка плоскостей и связки плоскостей.

п.1.
Уравнение пучка прямых на плоскости.

Определение.
Пучком прямых на плоскости называется
множество всех прямых данной плоскости,
имеющих одну общую точку, которая
называется центром пучка.

рис.1.

На
рис.1 точка

– центр пучка.

Теорема.
Пусть

и

– две
прямые в координатной плоскости Оху,
пересекающиеся в точке
.
Тогда уравнение

,
(1)

где

– произвольные действительные числа
одновременно не равные нулю, есть
уравнение пучка прямых с центром пучка
в точке
.

Доказательство.

рис.2.

Пусть L
– призвольная прямая этого пучка с
центром пучка в точке

и

– ее нормальный вектор. Тогда векторное
уравнение прямой L имеет
вид:

,
(2)

где

– радиус-вектор точки
,

– текущий радиус-вектор, т.е. радиус-вектор
текущей точки
.

Так
как прямые

и

по условию теоремы пересекаются, то их
нормальные векторы не коллинеарные и,
следовательно, образуют базис.

Тогда вектор

может быть разложен по этому базису:

,

где

– кэффициенты этого разложения
одновременно не равные нулю, т.к. по
определению нормальный вектор
.
Подставляя в (2) получаем

или

.
(3)

Но

и

– векторные уравнения прямых

и
,
т.е.
,

.

Подставляя
в (3), получаем равенство (1).

Таким образом, мы
доказали, что уравнение любой прямой
из данного пучка имеет вид (1).

Обратно, докажем,
что при любых
,
одновременно не равных нулю, уравнение
(1) есть уравнение некоторой прямой из
данного пучка.

Действительно, с
одной стороны, при любых
,
одновременно не равных нулю, уравнение
(1) есть общее уравнение прямой

.

С
другой стороны, пусть в уравнении (1)

– произвольные действительные числа,
одновременно не равные нулю, и пусть

– координаты центра пучка. Так как

и
,
то координаты центра пучка удовлетворяют
уравнениям прямых

и
:

и
.

Тогда,
подставляя координаты точки

в уравнение (1), получаем

,
т.е. уравнение (1) есть уравнение прямой,
проходящей через точку
,
а значит прямая принадлежит данному
пучку, ч.т.д.

Теорема
доказана.

Замечание.
Если в (1)
,
то уравнение (1) есть уравнение прямой
.
Если
,
то уравнение (1) есть уравнение прямой
.
Поэтому, если уравнение (1) рахделить на
,
то получим уравнение любой прямой из
данного пучка, кроме прямой
:

.
(4)

Пример.
Написать уравнение произвольной прямой,
проходящей через заданную точку
.

Решение.
Искомая прямая есть прямая пучка прямых
с центром пучка в точке
.
Очевидно, следующие две прямые принадлежат
этому пучку:

и

Или
,
.
Тогда уравнение любой прямой этого
пучка имеет вид

.

Если
заменить в этом уравнении греческие
буквы на латинские, получаем

(5)

–
уравнение прямой,
проходящей через заданную точку
.
В частности, при
,
получаем уравнение пучка прямых с
центром пучка в начале координат:
.

Разделив уравнение
(5) на
,
получаем уравнение прямой с угловым
коэффициентом, проходящей через заданную
точку
:

,
(6)

а
при
,
получаем уравнение прямой с угловым
коэффициентом, проходящей через начало
координат:

.

Другими словами,
уравнение
,
где
,
есть уравнение пучка прямых с центром
пучка в начале координат.

п.2.
Уравнение связки плоскостей.

Определение.
Связкой плоскостей называется множество
всех плоскостей, имеющих одну общую
точку, которая называется центром
связки.

Теорема.
Пусть
,
,

– три
плоскости в ПДСК Охуz,
имеющие единственную общую точку
.
Тогда уравнение
,
(7)

где

– произвольные действительные числа
одновременно не равные нулю, есть
уравнение связки плоскостей с центром
связки в точке
.

Доказательство
практически один к одному повторяет
доказательство предыдущей теоремы об
уравнении пучка прямых.

Пример.
Найти уравнение связки плоскостей с
центром связки в точке
.

Решение.
Очевидно, что следующие три плоскости
пересекаются в единственной точке
:

,
,
.

Тогда
уравнение

,
(8)

где

и одновременно не равны нулю, есть
искомое уравнение.

В
частности, если
,
то уравнение

(9)

есть
уравнение связки плоскостей с центром
связки в начале координат.

п.3.
Уравнение пучка плоскостей.

Определение.
Пучком плоскостей называется множество
всех плоскостей пересекающихся по одной
и той же прямой, называемой осью пучка.

рис.3.

Теорема.
Пусть

и

– две
плоскости, пересекающиеся по прямой L.
Тогда уравнение

,
(10)

где

– произвольные действительные числа
одновременно не равные нулю, есть
уравнение пучка плоскостей с осью пучка
L.

Доказательство
аналогично доказательству теоремы об
уравнении пучка прямых и предоставляется
читателю.

Пример.
Найти уравнение пучка плоскостей, осью
которого является ось абсцисс.

Решение.
Очевидно, что координатные плоскости

и

пересекаются по оси Ох.

рис.4.

Тогда
уравнение (10) в данном случае принимает
вид

.
Заменив греческие буквы на латинские,
получаем

,
(11)

где

– произвольные действительные числа,
одновременно не равные нулю. Уравнение
(11) есть искомое уравнение пучка плоскостей
с осью пучка Ох.

Аналогично,
уравнение

,
(12)

есть
уравнение пучка плоскостей с осью пучка
Оу, а уравнение

(13)

есть
уравнение пучка плоскостей с осью пучка
Оz.

п.4.
Основные задачи на прямые и плоскости.

Задача
1. Найти уравнение прямой, проходящей
через две заданные точки

и
.

Эта
задача нами уже решена, см. лекцию 11,
параграф 4, задача 1:

.

Задача
2. Найти угол между двумя прямыми

и
.

Эта
задача была решена в лекции 11, параграф
4:

Искомый
угол равен либо углу между их направляющими
векторами

,

или
.

Задача
3. Найти общее уравнение плоскости, если
известны координаты ее нормального
вектора

и координаты точки
,
лежащей на данной плоскости.

Решение.
Одно решение этой задачи приведено в
параграфе 2, формула (8).

,
(8)

Это
же уравнение можно получить и по другому.
Общее уравнение плоскости имеет вид

,

где

– координаты ее нормального вектора.
Осталось найти коэффициент D.
С этой целью подставим в уравнение
координаты точки
:
,
откуда
.

Подставляя
в уравнение получаем:

или

–
искомое уравнение
плоскости.

Задача
4. Найти уравнение плоскости, проходящей
через три заданные точки
,

и
.

Решение.

рис.11.

Как
мы видели в задаче 3, для составления
общего уравнения плоскости достаточно
знать координаты ее нормального вектора

и координаты любой точки, лежащей на
данной плоскости.

В
качестве нормального вектора плоскости
можно взять векторное произведение
вектора

на вектор
,
а в качестве точки, лежащей на плоскости
можно взять точку
.
Получаем

,

где
.

Искомое уравнение
плоскости можно получить и в другом
виде. Уравнение плоскости в векторной
форме имеет вид

,

откуда

или

.

Задача
5. Найти угол между двумя плоскостями.

Решение.
Из геометрии нам известно, что двугранный
угол между двумя плоскостями измеряется
линейным углом

(см. рис.12).

рис.12.

Нетрудно видеть,
что линейный угол
,
измеряющий двугранный угол между двумя
плоскостями равен углу

между нормальными векторами этих
плоскостей или равен
.
Здесь используется признак равенства
углов со взаимно перпендикулярными
сторонами.

Итак,

или
.

Таким образом,
задача вычисления угла между плоскостями
сводится к задаче вычисления угла между
векторами.

Задача
6. Найти расстояние от заданной точки

до заданной плоскости

.

Решение. Выберем
произвольную точку
,
лежащую на данной плоскости. Заметим,
что если
,
то начало координат лежит на плоскости
и его можно взять в качестве точки
.
Если же
,
то в качестве такой точки можно взять
точку пересечения плоскости с одной из
координатных осей. Так как плоскость
не может быть параллельной всем трем
координатным осям, то хотя бы одна
координатная ось пересекает данную
плоскость.

Пусть, например,

– точка пересечения плоскости с
координатной осью Ох. Здесь
,
если
.

рис.13.

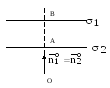
Итак, пусть точка

тем или иным способом выбрана, тогда
расстояние

от заданной точки

до заданной плоскости

равно модулю проекции вектора

на нормальный вектор плоскости
:

.

Так
как
,
то эту формулу можно записать в виде

.
(14)

Определение.
Пусть дано произвольное общее уравнение
плоскости

и произвольная точка пространства
.
Число

называется
невязкой точки

относительно плоскости
.

С
помощью введенного понятия невязки,
формула расстояния от точки до плоскости
иожет быть записана в виде:

.

Определение.
Величина

(15)

называется
отклонением точки

от плоскости
.

Из
последнего определения следует, что
расстояние от точки

до плоскости

равно модулю отклонения точки

от плоскости
:

.
(16)

Из
формулы (21) видно, что отклонение и
невязка имеют одинаковый знак.

Замечание.
Формулы (14) – (16) можно записать в другом
виде. Приведем данное уравнение плоскости
к нормальному виду:

,

где
,

,
причем знак плюс берется в случае, когда

и минус, в противном случае.

Теперь, формула
(14) расстояния от точки до плоскости
принимает вид:

,
(17)

где

(18)

–
отклонение точки

от плоскости
.

Задача
7. Найти расстояние от данной точки

до данной прямой
.

Решение. Задача
решается аналогично предыдущей.

рис.14.

.
Так как
,
то

.

Аналогично вводятся
понятия невязки точки относительно
прямой и отклонения точки от прямой.

Определение.
Пусть дано произвольное общее уравнение
прямой

и произвольная точка плоскости
.
Число

называется
невязкой точки

относительно прямой L.

Определение.
Величина

называется
отклонением точки

от плоскости
.

Если
привести уравнение прямой к нормальному
виду:

,

где

,

,
причем знак плюс берется в случае, когда

и минус, в противном случае, то формула
расстояния от точки до прямой принимает
вид:

,

где

–
отклонение точки

от прямой L.

Задача
8. Найти расстояние между двумя
параллельными плоскостями.

Решение. 1-й способ.
Найти на одной плоскости произвольную
точку и найти расстояние от нее до второй
плоскости, т.е. свести эту задачу к задаче
6.

2-й
способ. Приведем оба уравнения параллельных
плоскостей к нормальному виду:

,

где

и

– нормальные векторы плоскостей

и

соответственно,
,

– расстояния от начала координат до
плоскостей

и

соответственно.

Так
как нормальные векторы

и

направлены от начала координат к
плоскости, то возможны 2 случая:

а)
.
На следующем рисунке схематически
изображены две параллельнве плоскости

и

и их единичные нормальные векторы,
отложенные от начала координат О.

рис.15.

Здесь,
,

– расстояния от начала координат до
соответствующих плоскостей. Так как
неизвестно, какая плоскость ближе к
началу координат, то расстояние между
плоскостями

.

б)
.
Так как нормальные векторы

и

направлены от начала координат к
плоскостям и противоположны,то начало
координат находится между плоскостями,
см. следующий рисунок.

рис.16.

Здесь,
как и в предыдущем случае,
,

– расстояния от начала координат до
соответствующих плоскостей. Отсюда
следует, что расстояние между плоскостями

.

Задача
9. Найти расстояние между двумя
параллельными прямыми.

Пучок прямых. Уравнение пучка прямых

В данной статье мы рассмотрим понятие пучка прямых. Представим уравнение пучка прямых. Приведем примеры нахождения уравнения пучка прямых, проходящих через данную точку.

Пучком прямых называется множество прямых, проходящих через данную точку P. P называется центром пучка прямых . Две разные прямые в пучке прямых определяют центр пучка прямых.

Найдем уравнение пучка прямых, центром которого служит точка пересечения двух прямых (Рис.1):

Докажем следующую теорему.

Теорема 1. Пусть (1) и (2) уравнения двух прямых, пересекающихся в точке P, а λ₁ и λ₂ некоторые числа, которые одновременно не равны нулю. Тогда

λ1(A1x+B1y+C1) +λ2(A2x+B2y+C2)=0.

(3)

является уравнением прямой, проходящей через точку P. Обратно, любая прямая, проходящая через точку P определяется уравнением (3), при некотороых числах λ₁ и λ₂.

Доказательство. Во первых покажем, что уравнение (3) является линейным уравнением (уравнением первого порядка), т.е. уравнением, при котором коэффициент при x или y не равен нулю.

Группируем коэффициенты при x и y:

(λ1A1+λ2A2)x+(λ1B1+λ2B2)y+(λ1C1+λ2C2)=0

(4)

λ1A1+λ2A2=0, λ1B1+λ2B2=0.

(5)

Тогда, например при λ₁≠0 (по условию теоремы хотя бы один из чисел λ₁ и λ₂ не равен нулю), получим:

(6)

.

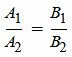(7)

Полученное равенство является условием параллельности прямых, определяемых уравнениями (1) и (2), что противоречит условию теоремы (эти прямые пересекаются и не совпадают). Таким образом хотя бы один из равенств (5) не выполняется, т.е. хотя бы один коэффициент при x и y в уравнении (4) не равен нулю. Отсюда следует, что уравнение (4) является линейным уравнением (уравнением первой степени) и является уравнением некоторой прямой. По условию теоремы, эта прямая проходит через точку P(x₀, y₀), которая является пересечением прямых (1) и (2), т.е. выполняются равенства:

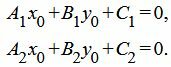(8)

Из уравнениий (8) следует, что при любых λ₁ и λ₂:

λ₁(A₁x₀+B₁y₀+C₁)+λ₂(A₂x₀+B₂y₀+C₂)=0,

т.е. уравнение (3) проходит через точку P.

Докажем вторую часть теоремы. Покажем, что любая прямая, проходящая через точку P определяется уравнением (3) при некоторых значениях λ₁ и λ₂.

Возьмем некоторую прямую проходящую через точки P и M’(x’, y’). Покажем, что данная прямая определяется уравнением (3) при некоторых значениях λ₁ и λ₂, не равных одновременно нулю.

В первой части доказательства теоремы мы показали, что прямая, проходящая через точку P определяется уравнением (3). Теперь, если эта прямая проходит через еще одну точку M’(x’, y’), то координаты этой точки должны удовлетворять уравнению (3):

λ1(A1x’0+B1y’0+C1)+λ2(A2x’0+B2y’0+C2)=0,

(9)

Заметим, что выражения в скобках не могут быть равным нулю одновременно, т.к. это означало бы, что оба уравнения проходят через точки P и M’(x’, y’) и, следовательно, совпадают. Пусть, например, λ₁(A₁x’₀+B₁y’₀+C₁)≠0. Тогда задав λ₂ произвольное число, отличное от нуля, решим (9) относительно λ₁:

Пример 1. Пучок прямых задан уравнениями:

Найти уравнение прямой из пучка прямых, проходящий через точку M(−3, 1).

Решение. Уравнение пучка прямых, заданных прямыми (10) и (11) имеет следующий вид:

λ1(2x+3y−1)+λ2(x−4y+2)=0.

(12)

Подставим координаты точки M в уравннение (12):

λ1(2·(−3)+3·1−1)+λ2(−3−4·1+2)=0.

(13)

−5(2x+3y−1)+4(x−4y+2)=0.

(14)

Упростив уравнение (14), получим уравнение из пучка прямых проходящих через точку M(−3, 1):

Пример 2. Построить уравнение пучка прямых с центром M(4,1):

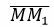
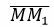
Решение. Возьмем две различные точки, не совпадающие с точкой M: M₁(2,1), M₂(−1,3). Построим уравнение, проходящие через точки M и M₁. Нормальный вектор n₁ этой прямой должен быть ортогональным вектору , равному разностьям координат точек M и M₁: =<2−4, 1−1>=<−2,0>. Т.е. можно взять n₁=<0,1>. Тогда уравнение прямой с нормальным вектором n₁, проходяще через точку M имеет следующий вид:

Построим уравнение проходящее через точки M и M₂. 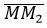=<−1−4, 3−1>=<−5,2>. Возмем в качестве нормального вектора второго уравнения n₂=<2, 5>. Тогда второе уравнение имеет слеждующий вид:

Из уравнений (15) и (16) можно записать уравнение пучка прямых с центром M(4,1):

Заметим, что взяв другие точки M₁ и M₂, мы получим уравнение того же пучка прямых, но с другими двумя прямыми.

Пучок прямых, уравнение пучка прямых

В статье рассматриваются определения пучка прямых с центром в заданной точке плоскости. Разбирается подробное решение с применением определения, рассматриваются задачи на составление уравнения пучка прямых, нахождение координат.

Пучок прямых – это определение

Пучок прямых определяется на плоскости, но не в трехмерном пространстве. Аксиома геометрии говорит о том, что если имеются две несовпадающие точки, расположенные на плоскости, то через них можно провести только одну прямую. Если на плоскости γ задается точка М 0 и M 1 , то через них можем провести прямую. Когда имеется еще одна точка М 2 , которая не лежит на прямой М 0 М 1 , тогда можно провести прямую М 0 М 2 . Если отметим точку М 3 , не принадлежащую ни одной из проведенных прямых, через нее также може провести прямую, проходящую через М 0 .

Отсюда следует, что в плоскости γ можно провести множество прямых через заданную точку. Это и привело к определению пучка прямых.

Заданная плоскость γ с множеством всех прямых, которые лежат в плоскости γ и проходящие через точку М 0 называют пучком прямых с центром в точке М 0 .

Исходя из определения, имеем, что любые две прямые из этого пучка пересекутся в центре данного пучка прямых. Пучок определяется при условии, если указан центр данного пучка.

Уравнение пучка прямых – решение задач

Для решения задач применяется уравнение пучка прямых, то есть сам пучок рассматривается относительно систему координат О х у на плоскости.

Когда имеем на плоскости прямоугольную систему координат О х у с указанными пересекающимися прямыми а 1 и а 2 _, пучок задает эти прямые. За систему координат О х у отвечает общее уравнение прямой, которое имеет вид A 1 x + B 1 y + C 1 = 0 или A 2 x + B 2 y + C 2 = 0 .

Введем обозначение пересечения прямых как точка М 0 с координатами х 0 и y 0 . Отсюда следует, что точка М имеет координаты M 0 ( x 0 , y 0 ) .

Чтобы определить вид используемого уравнения в пучках, рассмотрим на теореме.

При заданных двух пересекающихся прямых а 1 и а 2 имеются прямые, которые входят в пучок прямых, образованных в системе координат О х у . Их уравнения имеют вид A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 тогда и только тогда, когда уравнение прямой α · ( A 1 x + B 1 y + C 1 = 0 ) + β · ( A 2 x + B 2 y + C 2 ) = 0 соответствует ей,a α и β являются действительными числами, неравными нулю. Данное условие записывается так: α 2 + β 2 ≠ 0 .

Начнем рассмотрение доказательства с рассмотрения прямой a с указанного пучка, после чего докажем, что ее можно задавать при помощи уравнения α · ( A 1 x + B 1 y + C 1 ) + β · ( A 2 x + B 2 y + C 2 ) = 0 .

Центр пучка возьмем за точку с координатами M 0 = ( x 0 , y 0 ) .

Отсюда получаем, что n → = ( A 1 , B 1 ) является нормальным вектором прямой A 1 x + B 1 y + C 1 = 0 , тогда n 2 → = ( A 2 , B 2 ) – нормальный вектор для прямой A 2 x + B 2 y + C 2 = 0 . Получаем, что n → 1 и n 2 → – это неколлинеарные векторы, потому что у прямой а 1 и а 2 нет общих точек пересечения. Значит, необходимо разложить нормальный вектор n → по двум неколлинеарным n 1 → и n 2 → . Разложение необходимо выполнять по формуле n → = α · n 1 → + β · n 2 → . В итоге получаем, что n → = ( α · A 1 + β · A 2 , α · B 1 + β · B 2 ) .

После вычислений получаем координаты нормального вектора прямой a , равные n → = α · A 1 + β · A 2 , α · B 1 + β · B 2 . Координаты точки, пересекающиеся с прямой a в точке M 0 ( x 0 , y 0 ) , записываются при помощи общего уравнения прямой a . Тогда получаем выражение вида:

α · A 1 + β · A 2 · x – x 0 + α · B 1 + β · B 2 · y – y 0 = 0 ⇔ ⇔ α · ( A 1 x + B 1 y – A 1 x 0 + B 1 y 0 ) + β · A 2 x + B 2 y – A 2 x 0 – B 2 y 0 = 0

По – A 1 x 0 – B 1 y 0 = C 1 и – A 2 x 0 – B 2 y 0 = C 2 получим общее уравнение прямой a , имеющее вид α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 . Вышесказанная необходимость доказана.

Осталось найти доказательства достаточности.

Значит, нужно произвести доказательство выражения α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 , где имеем α и β некоторыми действительными числами неравными нулю, существует уравнение из пучка прямых с точкой пересечения M 0 ( x 0 , y 0 ) . Такое уравнение определено при помощи двух пересекающихся прямых A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Запишем уравнение α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 в виде α · A 1 + β · A 2 · x + α · B 1 + β · B 2 · y + α · C 1 + β · C 2 = 0 .

Уравнение будет считаться общим, если выполняется условие, когда α · A 1 + β · A 2 и α · B 1 + β · B 2 отличны от нуля. Иначе мы получили выражение вида α · A 1 + β · A 2 = 0 ⇔ A 1 = – β α · A 2 и α · B 1 + β · B 2 = 0 ⇔ B 1 = – β α · B 2 или α · A 1 + β · A 2 = 0 ⇔ A 2 = – α β · A 1 и α · B 1 + β · B 2 = 0 ⇔ B 2 = – α β · B 1 . Это значило бы, что векторы не коллинеарны.

Это невозможно в данном случае, так как n 1 → и n 2 → – это нормальные векторы прямых а 1 и а 2 , которые пересекаются.

Имеем, что уравнение α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 является общим уравнением прямой. Далее необходимо произвести доказательство удовлетворения координат точки при их пересечении, то есть координаты точки M 0 ( x 0 , y 0 ) . Докажем, справедливо ли равенство α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 .

M 0 ( x 0 , y 0 ) является точкой пересечения прямых, значит, ее координаты должны удовлетворять уравнениям обеих пересекающихся прямых.

Когда A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 справедливы, отсюда следует, что α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = α · 0 + β · 0 = 0 .

Что и требовалось доказать.

Можем сделать вывод, что уравнение, которое имеет вид α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = 0 и есть уравнение пучка.

Значения α и β необходимы для того, чтобы определять прямые, находящиеся в данном пучке, с уравнениями A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Необходимо, чтобы как минимум один из параметров был не равен нулю, тогда можно упростить выражение. При условии, что α ≠ 0 получаем выражение вида A 1 x + B 1 y + C 1 + λ · A 2 x + B 2 y + C 2 = 0 с λ = α β .

При β ≠ 0 выражение принимает вид μ · A 1 x + B 1 y + C 1 + A 2 x + B 2 y + C 2 = 0 с μ = α β .

Они не являются эквивалентными уравнению пучка прямых, относящихся к виду α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = 0 . Уравнение A 1 x + B 1 y + C 1 + λ · A 2 x + B 2 y + C 2 = 0 при любых значениях λ не даст возможности получить уравнение вида A 2 x + B 2 y + C 2 = 0 .

Уравнение μ · A 1 x + B 1 y + C 1 + A 2 x + B 2 y + C 2 = 0 при любых значениях μ не даст в результате A 1 x + B 1 y + C 1 = 0 .

Подробно рассмотрим на решении примеров.

Написать уравнение прямой пучка с заданным центром в точке M 0 ( – 1 , 4 ) , k = 3 .

Необходимо составить уравнение прямой, которая будет проходить через заданную точку с координатами M 0 ( – 1 , 4 ) с угловым коэффициентом равным 3 . Тогда запишем уравнение прямой с угловым коэффициентом и получим y – 4 = 3 · ( x – ( – 1 ) ) ⇔ y = 3 x + 7 .

Ответ: y = 3 x + 7 .

Найти координаты центра пучка прямых в О х у , если известны два уравнения пересекающихся прямых x – 4 2 = y + 3 0 и x 2 3 + y – 1 = 1 .

Чтобы найти координаты центра пучка, необходимо найти точки пересечения x – 4 2 = y + 3 0 и x 2 3 + y – 1 = 1 .

Получим, что каноническое уравнение прямой на плоскости x – 4 2 = y + 3 0 эквивалентно x 2 3 + y – 1 = 1 , а уравнение в отрезках x 2 3 + y – 1 = 1 общему уравнению прямой 3 2 x – y – 1 = 0 .

Теперь составляем систему уравнений, включающую в себя уравнения прямых.

y + 3 = 0 3 2 x – y – 1 = 0 ⇔ y = – 3 3 2 x – ( – 3 ) – 1 = 0 ⇔ y = – 3 x = – 4 3

Получим, что – 4 3 , – 3 – это координаты центральной точки, где пересекаются все прямые.

Произвести составление уравнения пучка прямых в О х у , которое задано при помощи прямых 3 x – 2 y + 1 = 0 и x = – 2 + 2 · λ y = 5 · λ , имеющих общую точку пересечения.

Для начала необходимо получить общее уравнение прямой. Оно определено параметрическим уравнением x = – 2 + 2 · λ y = 5 · λ .

Отсюда следует, что

x = – 2 + 2 · λ y = 5 · λ ⇔ λ = x + 2 2 λ = y 5 ⇔ x + 2 2 = y 5 ⇔ ⇔ 5 · ( x + 2 ) = 2 · y ⇔ 5 x – 2 y + 10 = 0

Произведем запись уравнения пучка прямых и получим α · ( 3 x – 2 y + 1 ) + β · ( 5 x – 2 y + 10 ) = 0 , а α и β являются действительными числами, где обязательным условием считается α 2 + β 2 ≠ 0 .

Ответ: α · ( 3 x – 2 y + 1 ) + β · ( 5 x – 2 y + 10 ) = 0 .

Написать уравнение прямой, проходящей через точку M 1 ( 2 , – 1 ) и принадлежащей пучку прямых с уравнением α · ( 5 x + y – 19 ) + β · ( 2 x – 3 y + 6 ) = 0 .

Задача решается двумя способами.

Первый способ начинается с определения М 0 , являющейся центром пересечения. Тогда нужно найти точки пересечения уравнений 5 x + y – 19 = 0 и 2 x – 3 y + 6 = 0 , а их результат и будет являться координатами для M 0 .

Определяем координаты, решив получившуюся систему:

5 x + y – 19 = 0 2 x – 3 y + 6 = 0 ⇔ y = 19 – 5 x 2 x – 3 · ( 19 – 5 x ) + 6 = 0 ⇔ y = 19 – 5 x x = 3 ⇔ ⇔ y = 19 – 5 · 3 x = 3 ⇔ y = 4 x = 3

Значит точка М 0 имеет координаты ( 3 , 4 ) . Это записывается как M 0 ( 3 , 4 ) . Чтобы получить искомое уравнение , которое проходит через точки с координатами M 0 ( 3 , 4 ) и M 1 ( 2 , – 1 ) . В итоге получаем:

x – 3 2 – 3 = y – 4 – 1 – 4 ⇔ x – 3 – 1 = y – 4 – 5 ⇔ x – 3 1 = y – 4 5

Второй способ начинается с того, что необходимо определить параметры α и β , чтобы уравнение α · ( 5 x + y – 19 ) + β · 2 x – 3 y + 6 = 0 было уравнением прямой, которая проходит через M 1 ( 2 , – 1 ) . Для этого найдем координаты М 1 и получим, что

α · 5 · 2 + ( – 1 ) – 19 + β · 2 · 2 – 3 · ( – 1 ) + 6 = 0 ⇔ ⇔ – 10 · α + 13 · β = 0 ⇔ α = 13 · β 10

Принимаем значение β = 10 , при желании можно выбирать любое другое такое значение β , которое дает несложное вычисление α . Получаем α = 13 · β 10 = 13 · 10 10 = 13 .

При подстановке значений α = 13 и β = 10 в заданное уравнение пучка, преобразуем:

13 · ( 5 x + y – 19 ) + 10 · ( 2 x – 3 y + 6 ) = 0 ⇔ 85 x – 17 y – 187 = 0 ⇔ 5 x – y – 11 = 0

Необходимо проверить эквивалентность получившихся уравнений.

x – 3 1 = y – 4 5 ⇔ 5 · x – 3 = 1 · y – 4 ⇔ 5 x – y – 11 = 0

Отсюда следует, что все решено верно.

Ответ: 5 x – y – 11 = 0 .

Определить принадлежность прямой 3 x – y + 5 = 0 пучку прямых α · ( x – 2 y + 4 ) + β · ( x – y + 4 ) = 0 .

Решение производится двумя способами.

Первый способ решения начинается с нахождения центров координаты заданного уравнения пучка и их проверки:

x – 2 y + 4 = 0 x – y + 4 = 0 ⇔ x = 2 y – 4 x – y + 4 = 0 ⇔ x = 2 y – 4 2 y – 4 – y + 4 = 0 ⇔ ⇔ x = 2 y – 4 y = 0 ⇔ x = 2 · 0 – 4 y = 0 ⇔ x = – 4 y = 0 3 · ( – 4 ) – 0 + 5 = 0 ⇔ – 7 = 0

Получим, что подстановка координат центра в уравнение прямой 3 x – y + 5 = 0 дает неверное равенство. Делаем вывод, что прямая не пересекает центр пучков, значит, и не принадлежит ему.

Второй способ начинается с раскрытия скобок и приведения подобных слагаемых α · ( x – 2 y + 4 ) + β · x – y + 4 = 0 ⇔ 2 α + β · y + 4 α + 4 β = 0 .

Когда прямая 3 x – y + 5 = 0 принадлежит пучку прямых, тогда имеются такие значения α и β , что два уравнения α + β · x – 2 α + β · y + 4 α + 4 β = 0 и 3 x – y + 5 = 0 являются эквивалентными.

Тогда получаем систему, состоящую из трех равнений α + β = 3 2 α + β = 1 4 α + 4 β = 5 .

Для ее преобразования необходимо приравнять коэффициенты перед переменными x и y и свободные членов имеющихся уравнений α + β · x – 2 α + β · y + 4 α + 4 β = 0 и 3 x – y + 5 = 0 , чтобы получать результат решения.

Для проверки необходимо применить теорему Кронекера-Капелли.

Для этого необходимо записать основную и расширенную матрицы для составленной системы уравнений. Получим, что A = 1 1 2 1 4 4 и T = 1 1 3 2 1 1 4 4 5 .

Требуется посчитать ранг матрицы A . Он равен 2 , потому что 1 1 2 1 = – 1 ≠ 0 .

Результат нахождения ранга расширенной матрицы равняется 3 , потому как 1 1 3 2 1 1 4 4 5 = 7 ≠ 0 .

Отсюда имеем, что система уравнений α + β = 3 2 α + β = 1 4 α + 4 β = 5 не определена, то есть имеет решений. Так как решения отсутствуют, прямая не проходит через центр прямой имеющихся пучков прямых.

Ответ: нет, прямая 3 x – y + 5 = 0 не принадлежит заданному пучку прямых, записанных уравнением вида α · ( x – 2 y + 4 ) + β · ( x – y + 4 ) = 0 .

Решение уравнений с параметром методом применения понятия пучка прямых на плоскости

Разделы: Математика

Образовательная цель: Совершенствовать навыки решения уравнений с параметром с помощью понятия «пучок прямых на плоскости».

Развивающая цель: Развить исследовательскую и познавательную деятельность учащихся.

Оборудование: Проектор, экран.

Ход урока

I. Оргмомент

Приветствие, объявление темы урока и его целей

II. Подготовка к основному этапу урока

Мотивация: Тема «Задачи с параметрами» занимает особое место в подготовке к вступительным экзаменам в вузы по математике. Решение таких задач развивает исследовательские умения и навыки, что позволяет абитуриентам выдержать конкурсные испытания в престижные вузы. Задачи с параметром каждый год предлагаются в наиболее трудной части С единого государственного экзамена. Поэтому для того, чтобы с ними справиться, нужна специальная подготовка по решению различных типов таких задач.

Актуализация опорных знаний:

1. Ответы учащихся на вопросы учителя по слайду 2

1. Каким одним уравнением можно задать эти прямые?
2. Какие значения принимает параметр а?
3. Приведите примеры.

Обобщение учителя: Уравнение у = ах есть уравнение данного пучка прямых.

Число а – параметр пучка, характеризующий направление

прямой. Точка (О;О) — центр пучка.

2. Выполнение задания по слайду 3

Задание учителя: Выполним последовательно параллельный перенос пучка прямых у = ах на 3 единицы вверх по оси Оу и затем параллельный перенос на 2 единицы вправо вдоль оси Ох.

Назовите центр пучка. Выведите уравнение нового пучка прямых.

Замечание учителя: Перепишем полученное уравнение: у – 3 = а (х -2). В таком виде легко сразу назвать центр пучка.

3. Выполнение упражнения: Среди данных уравнений найти уравнение пучка прямых и назвать его центр:

1. у=аx 2 +4х-7;
2. у=ах+1;
3. у=аx 3 -3;
4. у=а +2;
5. у=ах-3а-2.

4. Вывод учащихся: Уравнение пучка прямых, проx₀дящих через точку (x₀;уо), имеет вид:

у – уо = а (х- x₀); (x₀;уо) — центр пучка; параметр а угловой коэффициент конкретной прямой.

III. Усвоение новых знаний и способов действий

Слово учителя: Мы сегодня будем решать задачи с параметром, в которых надо найти значения параметра, при которых уравнение имеет заданное число корней. При этом применим понятие пучка прямых.

Задача 1 Найдите значения параметра а, при котором уравнение | x 2 – 5х +6| = ах имеет ровно три корня.

Построим графики данных функций на одной координатной плоскости.

Уравнение у = ах – уравнение пучка прямых с центром в точке (0;0).

Работа по слайду 4: Ищем значения параметра а, при которых прямая из пучка у = ах пересекает график функции у =|x 2 -5х+6| в 3-х точках. В динамике видно, что такой прямой будет прямая пучка, касающаяся графика в точке, абсцисса которой принадлежит промежутку [2 ; 3].

Выведем ее уравнение:

Так как эта прямая принадлежит пучку прямых у = ах, имеем x₀ 2 – 6 = 0.

Отсюда, x₀ = ±, є [2;3]. Тогда а = 5- 2.

Уравнение прямой имеет вид: у = (5 – 2) х.

Ответ: а = 5-2.

Задача 2 Найдите значения параметра а, при которых уравнение |3х +3| = ах +5 имеет единственное решение.

Решим графически систему уравнении

y = |3х +3|	y = |3х +3|
у=ах+5	у-5=а(х-0)

Построим графики данных функций на одной координатной плоскости.

Работа по слайдам 5 и 6

Что представляет собой 2-е уравнение системы?

В чем состоит графический способ решения данной системы?

Из множества прямых пучка у – 5 = а (х – 0) выбрать те прямые, которые пересекают

график функции у =|3х +3 | в единственной точке и определить, при каких значениях параметра это происxодит.

Проследим за динамикой прямых пучка по слайду 6.

Определим границы: у = – 3х+5, у = 3х +5. Кроме этих прямых условию задачи удовлетворяют и прямые пучка «внутри» угла.

Ответ: а є (- ∞; – 3]U [3; +∞).

IV. Первичная проверка знания

Самостоятельная работа учащихся с последующей проверкой.

Задача 3 Определите значения параметра а, при которых уравнение |x 2 – 2х -3| = ах+1- а имеет три решения.

Проверка по образцу:

Показ слайдов 7 и 8.

V. Закрепление знаний и способов действий

Работа у доски учащегося

Задача 4. Исследовать количество решений уравнения |х| -3 =а (х-9) в зависимости от а.

• имеет 1 корень, если а є (- ∞; – 1] U (1;+ ∞) и а = ⅓
• имеет два корня, если а є (-1; ⅓ );
• не имеет корней, если а є (⅓; 1].

VI. Обобщение и систематизация знаний

Работа по задачам 1. 2, 3

Задание: Исследовать количество решений в зависимости от параметра а.

VII. Контроль и самопроверка знаний

Самостоятельная работа учащихся по вариантам

1. Найти все значения параметра а, при каждом из которых уравнение х – а = 2| 2 |х| – а 2 | имеет три различных корня.
2. Найти все значения параметра а, при каждом из которых уравнение |2х – а| + 1 = |х + 3| имеет единственное решение.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/puchok-prjamyh-uravnenie-puchka-prjamyh/

http://urok.1sept.ru/articles/610663

[/spoiler]