Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 февраля 2023 года; проверки требует 1 правка.

Математический маятник. Чёрный пунктир — положение равновесия, 
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
Характер движения маятника[править | править код]
Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).
При колебаниях в одной плоскости маятник движется по дуге окружности радиуса 
Уравнение колебаний маятника[править | править код]

Маятник (схема с обозначениями)
Если в записи второго закона Ньютона 

,
так как 

,
где неизвестная функция 




.
Для решения ДУ второго порядка, то есть для определения закона движения маятника, необходимо задать два начальных условия — угол 


Решения уравнения движения[править | править код]
Возможные типы решений[править | править код]
В общем случае решение ДУ с начальными условиями для маятника может быть получено численно. Варианты движения (в случае, если маятник — это материальная точка на лёгком стержне), качественно, представлены на анимации. В каждом окне вверху показана зависимость угловой скорости 

-

Маятник висит
-

Малые колебания (размах 45°)
-

Колебания с размахом 90°
-

Колебания с размахом 135°
-

Колебания с размахом 170°
-

Фиксация в верхнем положении
-

Движение близкое к сепаратрисе
-

Вращение маятника
Гармонические колебания[править | править код]
Уравнение малых колебаний маятника около нижнего положения равновесия, когда уместна замена 
,
где 


.
Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону[2]:
,
где 

Если пользоваться переменной 







Случай нелинейных колебаний[править | править код]
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 


Параметр 
.
Период колебаний нелинейного маятника составляет
,
где K — эллиптический интеграл первого рода.
Для вычислений практически удобно разлагать эллиптический интеграл в ряд:
где 

При углах до 1 радиана (≈ 60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:
.
Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года[3]:
,
где 

Движение по сепаратрисе[править | править код]
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.
Факты[править | править код]
Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.
- Если амплитуда колебания маятника близка к
, то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения[4].
- Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
- В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).
См. также[править | править код]
- Физический маятник
- Маятник Фуко
- Маятник Дубошинского
Примечания[править | править код]
- ↑ 1 2 Главный редактор А. М. Прохоров. Маятник // Физический энциклопедический словарь. — М.: Советская энциклопедия. — 1983. — Статья в Физическом энциклопедическом словаре
- ↑ Скорость и ускорение маятника при гармонических колебаниях также изменяются во времени по синусоидальному закону.
- ↑ Adlaj S. An Eloquent Formula for the Perimeter of an Ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 59, no. 8. — P. 1096—1097. — ISSN 1088-9477.
- ↑ В. В. Вечеславов. Хаотический слой маятника при низких и средних частотах возмущений // Журнал технической физики. — 2004. — Т. 74, № 5. — С. 1—5. Архивировано 14 февраля 2017 года.
Ссылки[править | править код]
- Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
- Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
- Учебный фильм «Математический и физический маятник», производство СССР
Механические колебания и волны

1. Механические колебания — точно или приблизительно повторяющееся движение, при котором тело смещается относительно положения равновесия, отклоняясь от него то в одну, то в другую сторону.
Для того чтобы возникли и совершались механические колебания необходима колебательная система. В механике изучаются две колебательные систем: математический и пружинный маятники.
2. Колебательная система — математический маятник — представляет собой тело, подвешенное на нити, размеры которого много меньше длины нити. Кроме того, нить математического маятника нерастяжима и не имеет массы, вся масса такого маятника сосредоточена в подвешенном к нити грузе.
В положении равновесия (рис. 59) на маятник действуют противоположно направленные сила тяжести ( vec{F}_т ) и сила упругости ( vec{F}_у ). Их равнодействующая равна нулю.
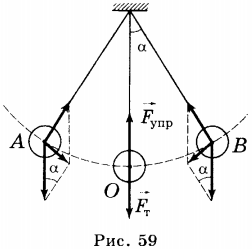
При отклонении маятника от положения равновесия вправо эти две силы направлены
под углом друг к другу, и их равнодействующая ( vec{F} ) уже не равна нулю. Под действием равнодействующей силы ( vec{F} ) маятник начнёт двигаться к положению равновесия. Поскольку груз обладает инертностью, то он пройдет положение равновесия и отклонится от него в другую сторону. Дойдя до крайнего левого положения, маятник под действием равнодействующей сил тяжести и упругости начнёт двигаться к положению равновесия. Пройдя его, он опять отклонится вправо. Процесс будет повторяться. Таким образом, в процессе колебаний изменяются смещение, скорость, действующая на него сила, ускорение маятника. При этом ускорение маятника прямо пропорционально его смещению и направлено в противоположную сторону. Для математического маятника это равенство имеет вид: ( vec{a}=-frac{vec{g}}{l} ), где ( l ) — длина нити маятника.
3. Колебательная система — пружинный маятник — это груз, прикреплённый к пружине (рис. 60). Считают, что масса пружины маятника мала по сравнению с массой груза, деформацией тела пренебрегают по сравнению с деформацией пружины. Кроме того, полагают, что деформация пружины подчиняется закону Гука ( (F=-kx) ).
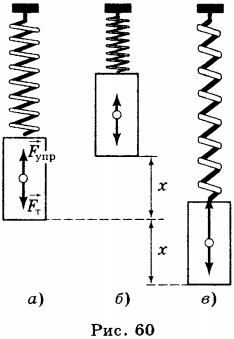
В состоянии равновесия пружина не деформирована (рис. 60), и на груз в горизонтальном направлении силы не действуют.
При выведении груза из состояния равновесия, на него будет действовать сила упругости
пружины ( vec{F}_у ), прямо пропорциональная её удлинению и направленная к положению равновесия. Под действием этой силы груз начнёт двигаться к положению равновесия.
Благодаря инертности груз пройдёт положение равновесия. Пружина сожмется, и в ней опять возникнет сила упругости. Дойдя до крайнего левого положения, груз остановится, а затем под действием силы упругости начнёт возвращаться в положение равновесия. Пройдя его, он отклонится вправо, и процесс повторится. Пружинный маятник будет совершать свободные колебания относительно положения равновесия.
Колебания, которые маятник совершает за счет однократно переданной ему энергии, называются свободными.
В соответствии со вторым законом Ньютона ( F=ma ). С другой стороны, ( F=-kx ). Откуда ( ma=-kx ), ( a=-frac{kx}{m} ). Таким образом, ускорение колебаний пружинного маятника, так же как и математического, прямо пропорционально его смещению с обратным знаком. Такие колебания называются гармоническими.
4. Отклонение маятника от положения равновесия называется смещением ( (x) ), а максимальное отклонение — амплитудой колебаний ( (A, или ,x_0) ).
Движение маятника от т. А до т. В и обратно до т. А называется полным колебанием. Время, за которое маятник совершает одно полное колебание, называется периодом колебаний (см. рис. 59). Период обозначают буквой ( T ) и измеряют в секундах.
Если маятник совершил за 4 секунды 8 полных колебаний, то его период равен 0,5 с.
Величину, обратную периоду, называют частотой колебаний. Частоту обозначают буквой ( nu ). По определению ( nu=1/T ). Единица частоты 1 герц (Гц).
Один герц — это частота таких колебаний, при которых за 1 секунду совершается одно полное колебание: 1 Гц = 1 с-1.
Если частота колебаний 5 Гц, то это означает, что за 1 секунду совершается 5 полных колебаний. Период таких колебаний равен: ( T ) = 0,2 с.
Период колебаний математического и пружинного маятников зависит от характеристик этих систем.
Формула периода колебаний математического маятника: ( T=2pisqrt{frac{l}{g}} ), где ( l ) — длина нити маятника, ( g ) — ускорение свободного падения.
Формула периода колебаний пружинного маятника имеет вид: ( T=2pisqrt{frac{m}{k}} ), где ( m ) — масса груза, ( k ) — коэффициент жёсткости пружины.
5. Основной задачей механики является определение положения тела, т.е. его координаты, в любой момент времени. Эта задача может быть решена, если известно уравнение, выражающее зависимость координаты тела от времени. Для гармонического колебания это уравнение имеет вид: ( x=x_0!cos!omega t ) или ( x=x_0!sin!omega t ), в зависимости от того, какой была координата (смещение) маятника в начальный момент времени. В том случае, если маятник в начальный момент времени был отклонен от положения равновесия (начальная координата не равна нулю), изменение координаты происходит по закону косинуса; если он начал двигаться из положения равновесия ( (x_0=0) ), то изменение координаты (смещения) подчиняется закону синуса. В записанном уравнении координаты ( omega ) — циклическая частота колебаний. Циклическая частота колебаний равна числу колебаний за ( 2pi ) секунд: ( omega=2pisqrt{frac{2pi}{T}} ). Циклическая частота, так же как и период колебаний маятника, зависит от параметров колебательной системы: ( omega=2pisqrt{frac{g}{l}} ) и ( omega=2pisqrt{frac{k}{m}} ).
6. При выведении маятника из положения равновесия ему сообщают потенциальную энергию. За счет этой энергии происходит движение маятника к положению равновесия. В процессе движения потенциальная энергия переходит в кинетическую. В положении равновесия потенциальная энергия маятника равна нулю, а его кинетическая энергия максимальна. При движении маятника влево кинетическая энергия переходит в потенциальную; в крайнем левом положении кинетическая энергия равна нулю, а потенциальная — максимальна. В отсутствие трения полная механическая энергия маятника сохраняется.
7. При наличии сопротивления воздуха сообщенная маятнику энергия расходуется на совершение работы против силы трения, энергия маятника постоянно уменьшается, и колебания со временем прекращаются. Говорят, что они затухают.
Таким образом, реальные свободные колебания маятника всегда затухающие.
Для получения незатухающих колебаний необходимо компенсировать потери энергии. Это можно сделать, действуя на маятник с некоторой периодической силой. В этом случае колебания происходят под действием внешней силы и становятся вынужденными. Работа этой силы и восполняет потери энергии, вызванные трением. Эти колебания будут вынужденными.
Вынужденные колебания — это колебания, происходящие под действием внешней, периодически изменяющейся силы. Частота вынужденных колебаний равна частоте изменения действующей на тело силы. Частота вынужденных колебаний равна частоте изменения внешней силы.
8. Если подвесить к верёвке, прикреплённой к стойке, несколько маятников разной длины и привести в колебания один из них, то и другие маятники начнут колебаться. Частота их колебаний будет равна частоте колебаний маятника, возбудившего колебании. При этом с наибольшей амплитудой будет колебаться маятник, длина которого равна длине этого маятника. Следовательно, наибольшую амплитуду колебаний имеет маятник, собственная частота колебаний которого совпадает с частотой вынуждающей силы. Явление, которое наблюдается в этом случае, называется резонансом.
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний тела, наступающего при равенстве частоты изменения внешней силы и частоты собственных колебаний тела.
Явление резонанса необходимо учитывать в практике. Известны случаи, когда вследствие резонанса разваливался на части самолёт в воздухе, ломались гребные винты у судов, рушились железнодорожные рельсы. Во всех этих случаях с резонансом приходится бороться, изменяя либо собственную частоту системы, либо частоту силы, вызывающей колебания.
9. Механической волной называется процесс распространения механических колебаний в среде.
Если закрепить конец шнура, слегка натянуть его и сместить свободный конец вверх, а затем вниз, т.е. привести его в колебания, то но шнуру «побежит» волна. Каждая точка
шнура будет совершать вынужденные колебания с частотой внешней силы, но с некоторым опозданием. При распространении колебаний по шнуру волна «бежит» в горизонтальном направлении, а колебания частицы совершают в вертикальном направлении.
Волны, направление распространения которых перпендикулярно направлению колебаний частиц среды, называются поперечными.
Поперечные волны представляют собой чередование горбов и впадин (рис. 61).
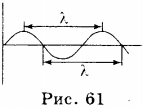
Расстояние между двумя ближайшими горбами или впадинами называется длиной волны.
Длина волны обозначается букой ( lambda ) и измеряется в метрах.
На расстояние, равное длине волны, волна распространяется за время, равное периоду колебаний.
10. Если закрепить один конец длинной пружины, а по другому ударить, то возникшее на конце пружины сгущение витков «побежит» по ней (рис. 62). В этом случае волна представляет собой распространение сгущений и разрежений. Частицы среды при этом совершают колебания вдоль направления распространения волны. Такие волны называют продольными.
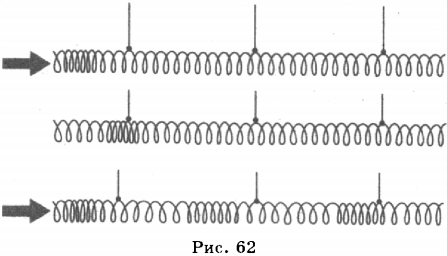
Продольные волны — это такие, направление распространения которых совпадает с направлением колебаний частиц среды.
11. Волновое движение имеет следующие особенности:
- механические волны образуются благодаря инертности частиц среды и взаимодействию между ними, проявляющемуся в существовании сил упругости;
- каждая частица среды совершает вынужденные колебания такие же, что и первая частица, приведенная в колебания, частота которых равна частоте внешней силы. Период колебаний всех частиц одинаков;
- колебание каждой частицы происходит с запаздыванием, которое обусловлено её инертностью. Это запаздывание тем больше, чем дальше находится частица от источника колебаний;
- вместе с волной не переносится вещество, переносится энергия.
12. Распространение продольных волн связано с изменением объёма тела. Они могут распространяться как в твёрдых, так и в жидких и газообразных телах, поскольку во всех этих телах при изменении объёма возникают силы упругости.
Распространение поперечных волн связано главным образом с изменением формы тела. В газах и жидкостях при изменении формы силы упругости не возникают, поэтому поперечные волны в них распространяться не могут. Поперечные волны распространяются только в твёрдых телах.
Примером волнового движения в твёрдом теле является распространение колебаний во время землетрясений. От центра землетрясения распространяются как продольные, так и поперечные волны. Сейсмическая станция принимает сначала продольные волны, а затем поперечные, т.к. скорость последних меньше. Если известны скорости поперечной и продольной волн и измерен промежуток времени между их приходом, то можно определить расстояние от центра землетрясения до станции.
13. Скоростью волны считается скорость перемещения гребня или впадины в поперечной волне, сгущения или разрежения в продольной волне.
За время, равное периоду колебаний ( (T) ), гребень или впадина перемещаются на расстояние, равное длине волны ( (lambda) ). Следовательно, скорость волны ( (v) ) равна: ( v=frac{lambda}{T} ).
Поскольку ( T=frac{1}{v} ), то формулу для скорости можно записать иначе: ( v=lambda nu ).
Скорость волны равна произведению длины волны и частоты колебаний.
14. Колебания, происходящие с частотой от 16 Гц до 20 000 Гц, являются звуковыми колебаниями. Для распространения звуковых колебаний, так же как и любых механических колебаний, необходима упругая среда.
Скорость звука можно определить, если известны расстояние от источника звука ( S ) и время распространения звука ( t ): ( v=frac{S}{t} ). Скорость звука неодинакова в разных средах и зависит от температуры среды.
Физиологическим характеристикам звука (громкости, высоте тона) соответствуют физические характеристики. Громкость звука определяется амплитудой колебаний. Чем она больше, тем громче звук. Звук тем выше, чем больше частота колебаний.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Какой путь пройдёт груз математического маятника за 10 полных колебаний, если амплитуда колебаний равна 3 см?
1) 30 см
2) 60 см
3) 90 см
4) 120 см
2. Маятник совершает 20 полных колебаний за 10 с. Чему равна частота колебаний маятника?
1) 20 Гц
2) 2 Гц
3) 1 Гц
4) 0,5 Гц
3. Во сколько раз надо изменить массу груза пружинного маятника, чтобы период колебаний увеличился в 9 раз?
1) увеличить в 3 раза
2) уменьшить в 9 раз
3) уменьшить в 81 раз
4) увеличить в 81 раз
4. Массу груза математического маятника, совершающего гармонические колебания, увеличили в 9 раз. При этом период колебаний
1) увеличился в 3 раза
2) увеличился в 9 раз
3) уменьшился в 3 раза
4) не изменился
5. Если перенести математический маятник с Земли на Марс, то
1) частота колебаний не изменится
2) частота колебаний увеличится
3) частота колебаний уменьшится
4) маятник не будет колебаться
6. На рисунке представлен график колебаний математического маятника. Период колебаний маятника равен
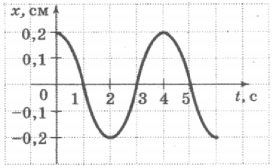
1) 1 с
2) 2 с
3) 3 с
4) 4 с
7. Период колебаний частиц в волне можно вычислить по формуле
1) ( T=frac{nu}{lambda} )
2) ( T=frac{lambda}{nu} )
3) ( T=lambdanu )
4) ( T=vnu )
8. На рисунке показан график волны, бегущей вдоль упругого шнура, в некоторый момент времени. Длина волны равна расстоянию
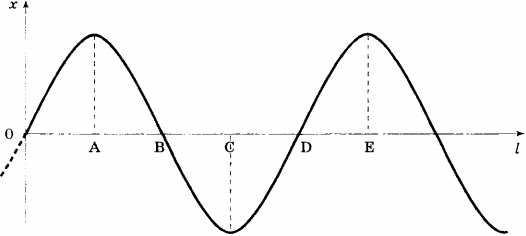
1) ВС
2) BD
3) BE
4) OD
9. Сравните громкость звука и высоту тона двух звуковых колебаний, если для первого колебания: амплитуда ( A_1 ) = 2 мм, частота ( nu_1 ) = 500 Гц, для второго колебания: ( A_2 ) = 4 мм, частота ( nu_w ) = 300 Гц.
1) громкость первого звука больше, чем второго, а высота тона меньше
2) и громкость, и высота тона первого звука больше, чем второго
3) и громкость и высота тона первого звука, меньше, чем второго
4) громкость первого звука меньше, чем второго, а высота тона больше
10. Волна частотой 3 Гц распространяется в среде со скоростью 6 м/с. Длина волны равна
1) 18 м
2) 2 м
3) 1 м
4) 0,5 м
11. Математический маятник отвели в сторону и отпустили. Как будут изменяться значения величин, характеризующих колебания маятника при его движении к положению равновесия. Для каждой величины из первого столбца подберите соответствующее характеру её изменения слово из второго столбца. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры могут повторяться.
ВЕЛИЧИНЫ
A) смещение
Б) скорость
B) потенциальная энергия
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется
12. Среди приведённых ниже положений укажите два правильных и запишите их номера в таблице.
1) Звук распространяется только в воздухе.
2) Колебания, частота которых больше 20 000 Гц, называются ультразвуком.
3) Инфразвук — колебания, частота которых больше 16 Гц.
4) Эхо — явление многократного отражения звуковых волн от преград.
5) Звуковые волны — поперечные.
Часть 2
13. Мимо рыбака, сидящего на пристани, прошло 5 гребней волны за 10 с. Каков период колебаний поплавка на волнах?
Ответы
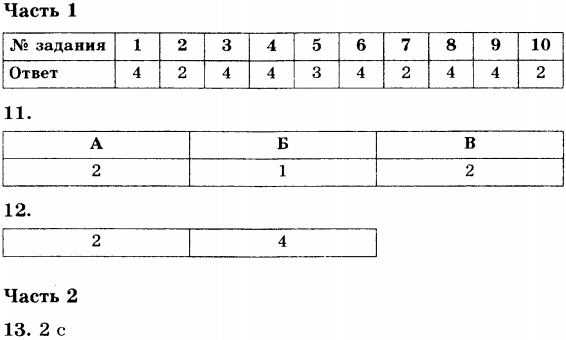
Механические колебания и волны
3.3 (65.64%) 39 votes
Содержание:
Пружинные и математические маятники:
Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.
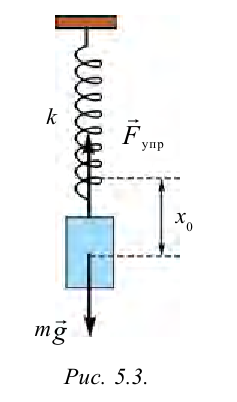
Система, состоящая из груза массой 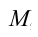

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:
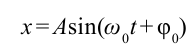
Если учесть, что ускорение тела, совершающего гармонические колебания 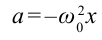 , то уравнение (5.10) примет вид:
, то уравнение (5.10) примет вид:
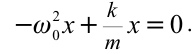
Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника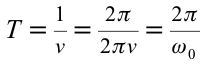 .
.
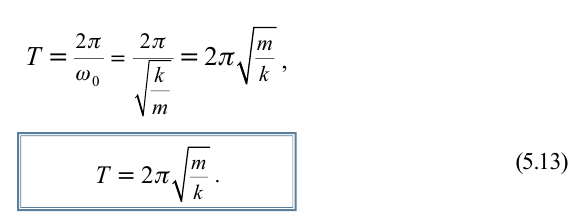
Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, 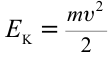 . В предыдущих темах было показано, что скорость можно выразить формулой
. В предыдущих темах было показано, что скорость можно выразить формулой 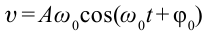 . В таком случае кинетическая энергия маятника равна
. В таком случае кинетическая энергия маятника равна
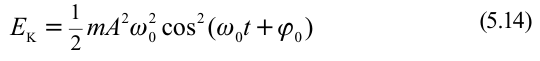
Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:
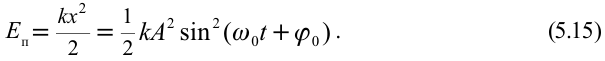
В большинстве случаев важно знать полную энергию системы:
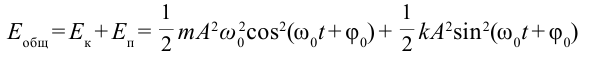
Если учесть, что 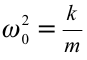 ,
,
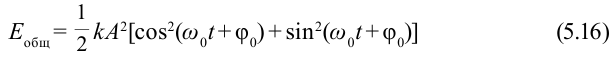

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки 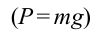 уравновешивает силу натяжения
уравновешивает силу натяжения  (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол
(рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол 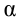 , силы
, силы 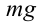 и
и  не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.
не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.
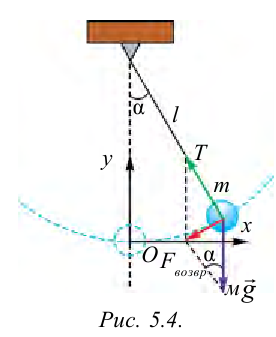
Из рис. 5.4. видим, что:
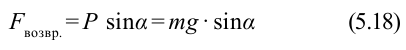
Согласно второму закону Ньютона, сила 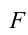 придает материальной точке ускорение
придает материальной точке ускорение 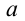 , поэтому
, поэтому
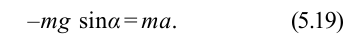
Из-за того, что угол наклона очень маленький 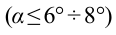 , а сила
, а сила 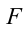 направлена противоположно смещению, формулу (5.19) можно записать в виде
направлена противоположно смещению, формулу (5.19) можно записать в виде

Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой 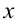 и учитывать соотношение
и учитывать соотношение 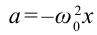 , получим
, получим 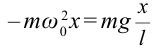
Следовательно 
Исходя из смысла периода колебания и учитывая, что 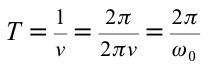 получаем
получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:
- при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
- период колебания математического маятника также не зависит от массы подвешенного на него груза;
- период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.
Отсюда колебание математического маятника записывается следующим выражением:
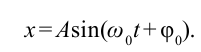
Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 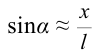 и для решения уравнения движения не применяется закон синусов или косинусов.
и для решения уравнения движения не применяется закон синусов или косинусов.
Пример:
Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.
Дано:
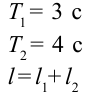
Найти:
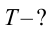
Формула:
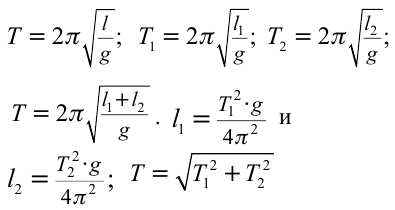
Решение:
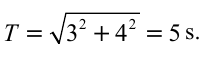
Ответ: 5 cек.
Пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
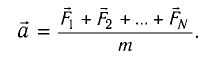
Закон Гука: модуль силы упругости 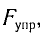 , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию)
, возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) 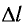 :
:
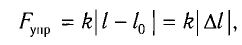
где k — жесткость тела, 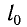 — длина недеформированного тела, l — длина деформированного тела.
— длина недеформированного тела, l — длина деформированного тела.
Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).
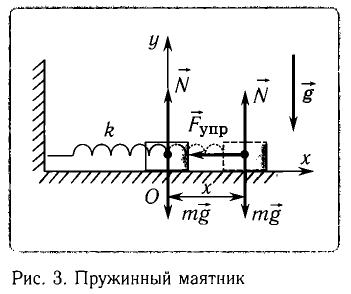
Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 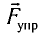 направленная влево.
направленная влево.
Запишем второй закон Ньютона для движения груза:
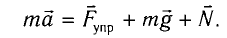
В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем
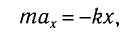 или
или 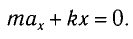
Следовательно,
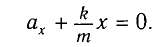
Это уравнение аналогично уравнению гармонических колебаний
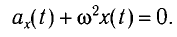
Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:
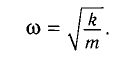
Тогда период колебаний пружинного маятника можно найти по формуле
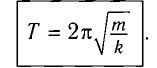
Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов 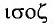 , — равный и
, — равный и 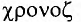 — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.
— время). Таким образом, колебания пружинного маятника обладают свойством изохронности.
Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).
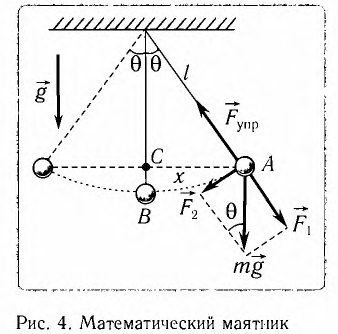
Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.
Галилео Галилей экспериментально определил, что период малых колебаний (9 < 10°) математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения  ). Он установил также, что период этих колебаний прямо пропорционален
). Он установил также, что период этих колебаний прямо пропорционален 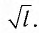 .
.
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
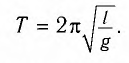
При углах отклонения математического маятника 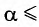 20° погрешность расчета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
20° погрешность расчета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
Отклонение маятника от положения равновесия будем характеризовать углом  (см. рис. 4), который нить образует с вертикалью.
(см. рис. 4), который нить образует с вертикалью.
Согласно второму закону Ньютона для движения шарика можем записать:
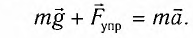
Смещение маятника вдоль дуги х = l , где угол
, где угол  выражен в радианах. Возвращающей силой в данном случае является проекция
выражен в радианах. Возвращающей силой в данном случае является проекция 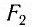 силы тяжести на касательную к дуге (см. рис. 4), которая определяется по формуле:
силы тяжести на касательную к дуге (см. рис. 4), которая определяется по формуле:
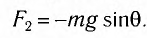
Заметим, что при малых углах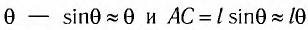 и длина дуги
и длина дуги
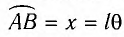 очень мало отличается от длины хорды
очень мало отличается от длины хорды 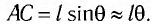 Для небольших углов (до 10°) значения
Для небольших углов (до 10°) значения  и sin
и sin различаются меньше чем на I %. Поэтому для таких углов равенство
различаются меньше чем на I %. Поэтому для таких углов равенство
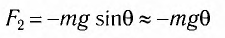 (1)
(1)
является очень хорошим приближением.
Подставляя в выражение (1) значение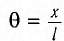 , получим
, получим
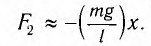
Таким образом, уравнение движения маятника запишется в виде
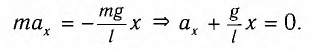
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 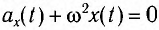 , то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
, то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
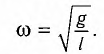
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 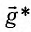 , характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
, характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
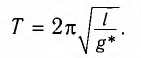
Пример:
Определите амплитуду А, циклическую частоту 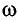 , период Т и начальную фазу
, период Т и начальную фазу 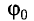 колебаний тела массой m = 0,50 кг, подвешенного к вертикальной пружине (рис. 5). Известно, что в состоянии покоя тело растягивает пружину на
колебаний тела массой m = 0,50 кг, подвешенного к вертикальной пружине (рис. 5). Известно, что в состоянии покоя тело растягивает пружину на 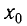 = 10 мм и для возбуждения колебаний его смещают вниз на x = 30 мм и отпускают.
= 10 мм и для возбуждения колебаний его смещают вниз на x = 30 мм и отпускают.
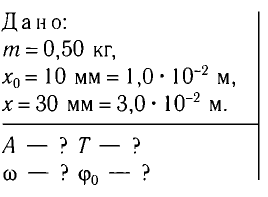
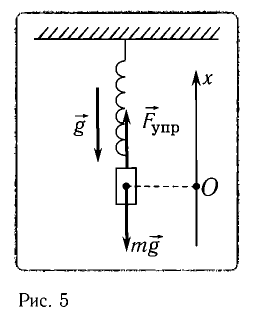
Решение
Циклическая частота колебаний «вертикального» пружинного маятника также определяется по формуле
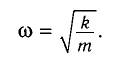
Найдем жесткость k пружины. Из условия равновесия тела следует
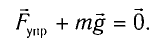
По закону Гука
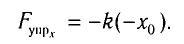
В проекции на ось Ох условие равновесия запишется в виде:
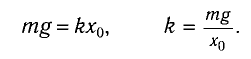
Отсюда для циклической частоты 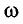 получаем
получаем
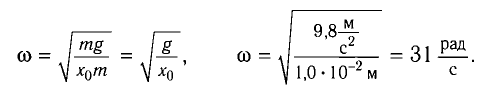
Так как по условию задачи тело сместили на расстояние х = 30 мм от положения равновесия, то амплитуда его колебаний
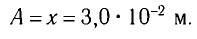
Период колебаний находим из соотношения
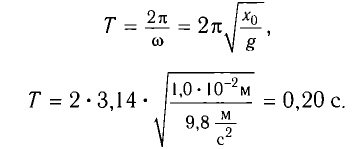
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний 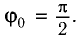
Ответ: 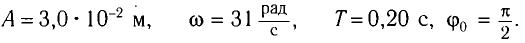
Пример:
Металлический шарик, подвешенный на длинной легкой нерастяжимой нити, поднимают по вертикали до точки подвеса и отпускают. Затем нить маятника отклоняют на небольшой угол от вертикали и также отпускают. В каком из этих случаев шарик быстрее возвратится в начальное положение?
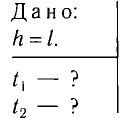
Решение
В первом случае шарик свободно падает без начальной скорости с высоты h = l, следовательно,
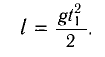
Отсюда находим промежуток времени 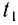 , необходимый для возвращения шарика в начальное положение:
, необходимый для возвращения шарика в начальное положение:
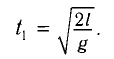
Во втором случае промежуток времени 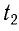 , необходимый шарику для возвращения из отклоненного положения в положение равновесия, найдем из уравнения гармонических колебаний
, необходимый шарику для возвращения из отклоненного положения в положение равновесия, найдем из уравнения гармонических колебаний
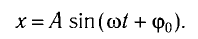
Поскольку в начальный момент времени t = 0 маятник имеет максимальное
отклонение от положения равновесия, то начальная фаза колебаний 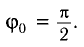 Так как в положении равновесия x = 0, то
Так как в положении равновесия x = 0, то
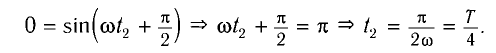
Используя формулу для периода колебаний математического маятника
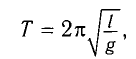 находим
находим 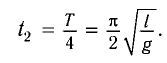
Разделив почленно уравнения для промежутков времени 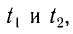 получим
получим
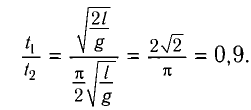
Ответ: шарик быстрее возвратится в начальное положение в случае, когда он движется вертикально вниз.
Пример:
Найдите периоды колебаний математического маятника длиной l= 1,0 м при перемещении его точки подвеса с ускорением, модуль которого а = 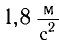 , направленным: а) вертикально вверх; б) вертикально вниз.
, направленным: а) вертикально вверх; б) вертикально вниз.
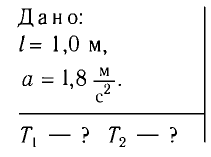
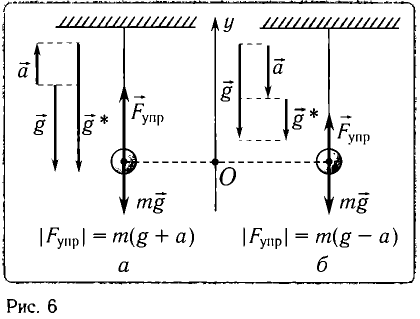
Решение
Период колебаний математического маятника в поле силы тяжести Земли
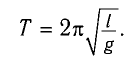
а) При движении маятника с ускорением 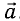 , направленным вверх (рис. 6, а), уравнение движения вдоль оси Оу
, направленным вверх (рис. 6, а), уравнение движения вдоль оси Оу
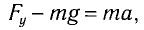
где Fy — проекция силы упругости нити.
Откуда находим
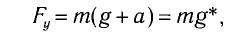
где g* = g + а — «эффективное ускорение».
Период колебаний определяется по формуле
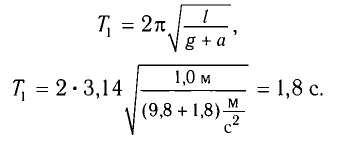
б) При движении точки подвеса маятника с ускорением 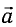 , направленным вниз (рис. 6, б), уравнение движения вдоль оси Оу
, направленным вниз (рис. 6, б), уравнение движения вдоль оси Оу
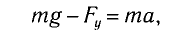
где Fy — проекция силы упругости нити. Откуда находим
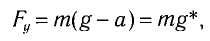
где g*=g-a — «эффективное ускорение». Период колебаний
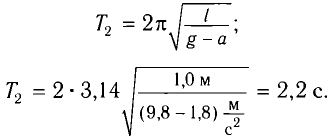
Ответ: 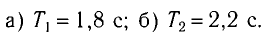
Что такое пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение тела прямо пропорционально результирующей силе и обратно пропорционально массе тела:
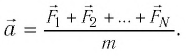
Закон Гука: при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
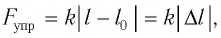
где 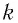 — жесткость тела,
— жесткость тела, 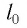 — длина недеформированного тела,
— длина недеформированного тела, 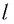 -длина деформированного тела.
-длина деформированного тела.
Колебательная система, состоящая из тела с прикрепленной к нему пружиной, называется пружинным маятником. Пружина может располагаться как вертикально (вертикальный пружинный маятник), так и горизонтально (горизонтальный пружинный маятник).
Рассмотрим колебания горизонтального пружинного маятника. Пусть груз массой 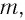 лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу легкой (невесомой) пружины жесткостью
лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу легкой (невесомой) пружины жесткостью 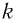 (рис. 6). Второй конец пружины неподвижен относительно данной инерциальной системы отсчета (ИСО).
(рис. 6). Второй конец пружины неподвижен относительно данной инерциальной системы отсчета (ИСО).
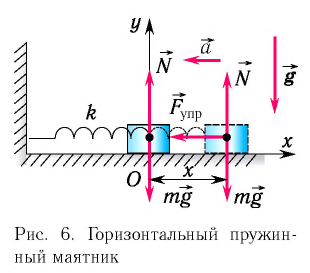
Выведем груз из положения равновесия, сместив его на расстояние 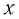 вправо (см. рис. 6). Тогда в пружине возникнет сила упругости
вправо (см. рис. 6). Тогда в пружине возникнет сила упругости 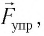 действующая на груз и направленная влево.
действующая на груз и направленная влево.
Согласно второму закону Ньютона для движения груза
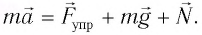
В проекции на ось 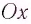 действующих на груз сил (см. рис. 6) с учетом закона Гука получаем:
действующих на груз сил (см. рис. 6) с учетом закона Гука получаем:
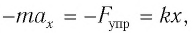
или
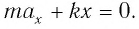
Перепишем полученное соотношение в виде:
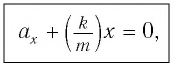
которое является уравнением гармонических колебаний пружинного маятника.
Сравнивая (1) с уравнением гармонических колебаний 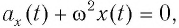 находим циклическую частоту колебаний горизонтального пружинного маятника
находим циклическую частоту колебаний горизонтального пружинного маятника
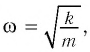
которая определяется массой 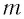 груза и жесткостью
груза и жесткостью 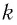 пружины.
пружины.
Для нахождения периода колебаний пружинного маятника воспользуемся формулой 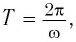 подставив в нее выражение (2):
подставив в нее выражение (2):
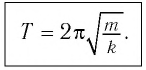
Как следует из формул (2) и (3), период и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греч. 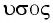 (изос) — равный и
(изос) — равный и 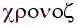 (хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности.
(хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности.
Изохронность колебаний маятника была открыта Гали-лео Галилеем в 1583 г. при изучении движения груза, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Колебательная система, состоящая из находящегося в поле силы тяжести тела, подвешенного на легкой нерастяжимой нити, размеры которого малы по сравнению с длиной нити, а его масса значительно больше массы нити, называется математическим маятником. При таких условиях тело можно считать материальной точкой, а нить — легкой нерастяжимой (рис. 7).
Рассмотрим колебания математического маятника.
Отклонение маятника от положения равновесия будем характеризовать углом 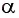 (см. рис. 7), который нить образует с вертикалью.
(см. рис. 7), который нить образует с вертикалью.
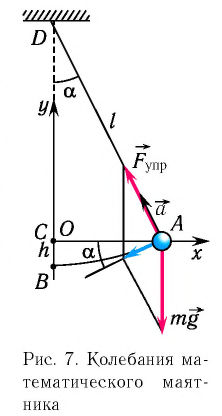
После отклонения маятника на него действуют две силы: направленная вертикально вниз сила тяжести 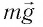 и направленная вдоль нити сила упругости
и направленная вдоль нити сила упругости 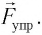 Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия.
Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия.
Согласно второму закону Ньютона для движения маятника можем записать:
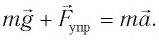
В проекциях на выбранные оси координат 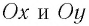 (см. рис. 7) получаем:
(см. рис. 7) получаем:
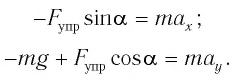
Для углов отклонения 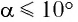 значения
значения 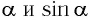 различаются меньше чем на 1 %. Поэтому при малых углах отклонения
различаются меньше чем на 1 %. Поэтому при малых углах отклонения 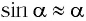 и длина дуги
и длина дуги 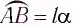 очень мало отличается от длины хорды
очень мало отличается от длины хорды 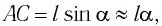 где угол
где угол 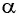 выражен в радианах. Тогда смещение маятника вдоль дуги
выражен в радианах. Тогда смещение маятника вдоль дуги 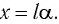 Но практически маятник движется вдоль оси
Но практически маятник движется вдоль оси 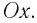 Из
Из 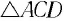 находим
находим 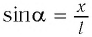 и, подставив это выражение в (5), получим:
и, подставив это выражение в (5), получим:
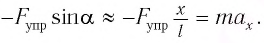
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия, является сила упругости его нити.
При малых углах отклонения маятника проекция вектора ускорения 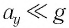 и ею можно пренебречь, а
и ею можно пренебречь, а 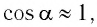 тогда из уравнения (6) следует, что
тогда из уравнения (6) следует, что 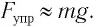
Следовательно, уравнение движения маятника вдоль оси 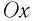 запишется в виде:
запишется в виде:
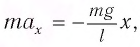
где 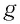 — ускорение, сообщаемое грузу маятника силой упругости нити.
— ускорение, сообщаемое грузу маятника силой упругости нити.
Отсюда получаем уравнение гармонических колебаний математического маятника:
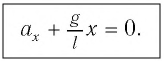
При сравнении уравнения (8) с уравнением гармонических колебаний 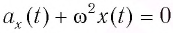 можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой
можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой
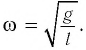
Тогда период малых колебаний математического маятника в поле тяжести Земли определяется по формуле Гюйгенса:
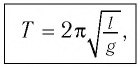
которую впервые получил ученик И. Ньютона Христиан Гюйгенс.
При углах отклонения математического маятника 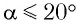 погрешность рас-чета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
погрешность рас-чета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
Как видно из формул (9) и (10), циклическая частота и период математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной 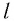 и модулем ускорения свободного падения
и модулем ускорения свободного падения 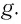
Галилео Галилей первый экспериментально определил, что период малых колебаний 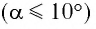 математического маятника длиной
математического маятника длиной 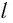 в поле силы тяжести не зависит от его массы
в поле силы тяжести не зависит от его массы 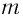 и амплитуды колебаний (угла начального отклонения
и амплитуды колебаний (угла начального отклонения 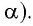 Он установил также, что период этих колебаний прямо пропорционален
Он установил также, что период этих колебаний прямо пропорционален 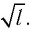
Если маятник приобретает дополнительное ускорение 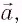 обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле:
обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле:
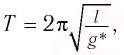
где 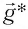 — «эффективное ускорение», равное векторной разности
— «эффективное ускорение», равное векторной разности 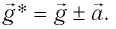
- Заказать решение задач по физике
Пример:
Выведите формулу для периода колебаний вертикального пружинного маятника, если масса груза 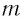 и жесткость пружины
и жесткость пружины 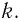
Решение
Рассмотрим вертикальное движение груза, происходящее под действием силы упругости пружины и силы тяжести груза после толчка. Начало координат поместим в точку, соответствующую равновесному положению тела (рис. 8). В этом положении пружина растянута на величину 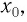 определяемую соотношением:
определяемую соотношением:
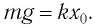
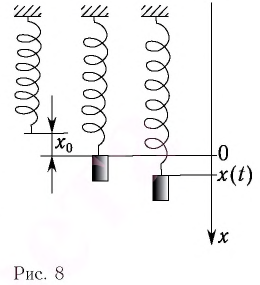
При смещении груза на величину 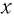 из положения равновесия сила, действующая со стороны пружины на груз, равна
из положения равновесия сила, действующая со стороны пружины на груз, равна 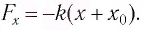
Тогда по второму закону Ньютона
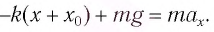
С учетом соотношения (1) это уравнение перепишем в виде:
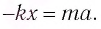
Если ввести обозначение 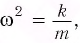 то уравнение движения груза запишется в виде:
то уравнение движения груза запишется в виде:
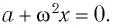
Оно описывает гармонические колебания вертикального пружинного маятника с частотой такой же, как у горизонтального пружинного маятника. Следовательно, период колебаний вертикального пружинного маятника такой же, как и горизонтального:
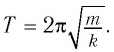
Ответ: 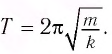
Таким образом, действующая в колебательной системе постоянная сила только смещает положения равновесия, но не изменяет частоту колебаний.
Пример:
Определите амплитуду 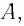 циклическую частоту
циклическую частоту 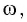 период
период 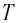 и начальную фазу
и начальную фазу 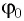 колебаний тела массой
колебаний тела массой 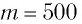 г подвешенного к вертикальной пружине (рис. 9). Известно, что в состоянии покоя тело растягивает пружину на расстояние
г подвешенного к вертикальной пружине (рис. 9). Известно, что в состоянии покоя тело растягивает пружину на расстояние 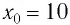 мм и для возбуждения колебаний его смещают вниз на расстояние
мм и для возбуждения колебаний его смещают вниз на расстояние 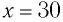 мм от положения равновесия и отпускают.
мм от положения равновесия и отпускают.
Дано:
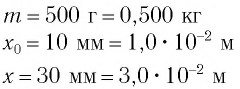
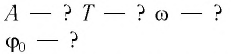
Решение
Циклическая частота колебаний вертикального пружинного маятника так же, как и горизонтального, определяется по формуле (см. пример 1):
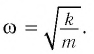
Для нахождения жесткости к пружины запишем условие равновесия тела:
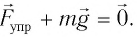
По закону Гука
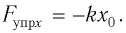
В проекции на ось 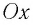 условие равновесия запишется:
условие равновесия запишется:
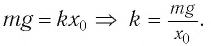
Отсюда для циклической частоты 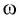 получаем:
получаем:
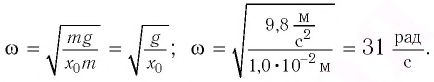
Амплитуда колебаний маятника определяется начальным смешением:
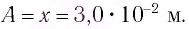
Период колебаний находим из соотношения:
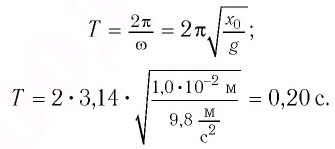
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний 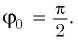
Ответ: 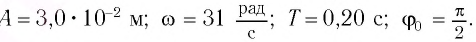
Подробное объяснение пружинного и математического маятника
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
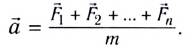
Закон Гука: модуль силы упругости 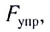 возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию)
возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) 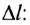
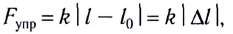
где k — жесткость тела, 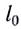 — длина недеформированного тела, l — длина деформированного тела.
— длина недеформированного тела, l — длина деформированного тела.
Простейшая колебательная система может быть получена с использованием груза и пружины.
Прикрепим груз массой m, лежащий на гладкой горизонтальной поверхности, к невесомой упругой пружине жесткостью k, второй конец которой зафиксирован (рис. 181). Такая система называется пружинным маятником.
Запишем второй закон Ньютона для этой системы
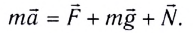
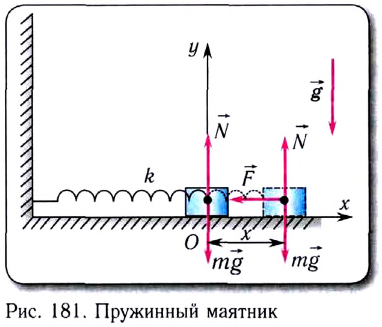
В проекции на ось Ох с учетом закона Гука получаем
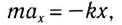 или
или
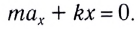
Запишем это уравнение в форме, аналогичной уравнению движения гармонического осциллятора:
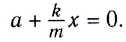
Сравнивая полученное выражение с уравнением гармонических колебаний
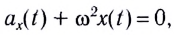
находим циклическую частоту колебаний пружинного маятника
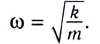
Тогда период колебаний пружинного маятника можно найти по формуле
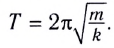
Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов 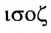 — равный и
— равный и 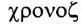 — время).
— время).
Как видим, пружинный маятник обладает свойством изохронности, поскольку период его колебаний не зависит от амплитуды.
Одной из наиболее распространенных колебательных систем является математический маятник.
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 182).
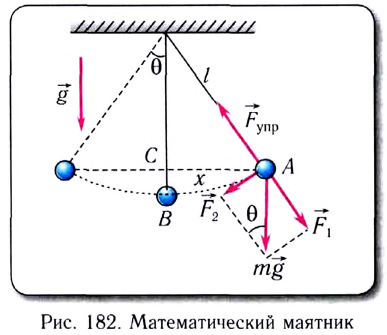
Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален 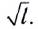
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
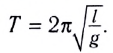
При углах отклонения математического маятника 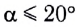 погрешность формулы Гюйгенса не превышает 1 %.
погрешность формулы Гюйгенса не превышает 1 %.
Отклонение маятника от положения равновесия будем характеризовать углом 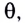 который нить образует с вертикалью.
который нить образует с вертикалью.
Из второго закона Ньютона следует (см. рис. 182):
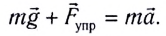
Смещение маятника вдоль дуги 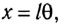 где угол
где угол 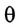 выражен в радианах.
выражен в радианах.
Возвращающей силой в данном случае является проекция на касательную к дуге силы тяжести 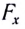 (см. рис. 182), которая определяется по формуле
(см. рис. 182), которая определяется по формуле
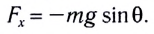
Заметим, что при малых углах 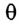 длина дуги АВ = х =
длина дуги АВ = х = 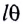 очень мало отличается от длины хорды
очень мало отличается от длины хорды 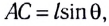 так как при малых
так как при малых 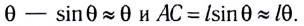
Для небольших углов (до 10°) значения 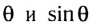 различаются меньше чем на 1 %. Поэтому для таких углов равенство
различаются меньше чем на 1 %. Поэтому для таких углов равенство
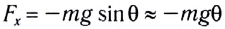 является очень хорошим приближением.
является очень хорошим приближением.
Используя полученное соотношение между координатой х и углом 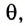 находим
находим 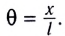 Подставляем его в выражение для проекции силы:
Подставляем его в выражение для проекции силы:
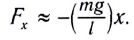
Таким образом, уравнение движения маятника запишется в виде 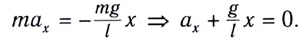
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 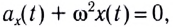 то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
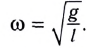
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 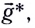 характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
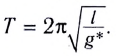
Математический и пружинный маятники и энергия колебаний
Колебательные движения очень разнообразны. При этом существует «классика» колебательных движений — они описаны сотни лет назад, их изучением занимались Галилео Галилей (1564– 1642) и Христиан Гюйгенс (1629–1695). Это колебания пружинного и математического маятников.
Колебания пружинного маятника
Пружинный маятник — это колебательная система, представляющая собой закрепленное на пружине тело.
Рассмотрим колебания горизонтального пружинного маятника — тележки массой m, закрепленной на пружине жесткостью k. Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот.
Колебания пружинного маятника:


Обратите внимание! В течение всего времени колебания сила упругости направлена в сторону, противоположную смещению тележки, — сила упругости все время «толкает» тележку к положению равновесия.
Итак, причины свободных колебаний пружинного маятника: 1) действующая на тело сила всегда направлена к положению равновесия; 2) колеблющееся тело инертно, поэтому оно не останавливается в положении равновесия (когда равнодействующая сил становится равной нулю), а продолжает движение в том же направлении.
Как вычислить период колебаний пружинного маятника
Рассмотрим колебания тележки, закрепленной на горизонтальной пружине, с точки зрения второго закона Ньютона (рис. 20.1). Запишем уравнение второго закона Ньютона в векторном виде: 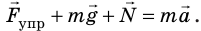
Сила тяжести и сила нормальной реакции опоры уравновешивают друг друга, поэтому 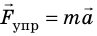 . Спроецировав это уравнение на ось ОХ
. Спроецировав это уравнение на ось ОХ 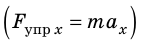 и воспользовавшись законом Гука
и воспользовавшись законом Гука 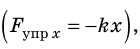 получим:
получим: 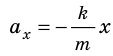 .
.
Последнее уравнение можно записать в виде 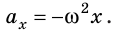 Таким образом, колебания тележки на пружине являются гармоническими колебаниями, а циклическая частота этих колебаний равна:
Таким образом, колебания тележки на пружине являются гармоническими колебаниями, а циклическая частота этих колебаний равна: 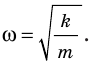
Приняв во внимание, что 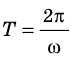 , получим формулу для вычисления периода колебаний пружинного маятника:
, получим формулу для вычисления периода колебаний пружинного маятника:
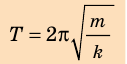
Обратите внимание! Период колебаний пружинного маятника не зависит ни от амплитуды колебаний, ни от места расположения маятника (на поверхности Земли или Луны, в космическом корабле и т. д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость k пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
Что называют математическим маятником
Любое твердое тело, которое совершает или может совершать колебания относительно оси, проходящей через точку подвеса, называют физическим маятником. Примером может быть игрушка, подвешенная на нити в салоне автомобиля. Если игрушку вывести из положения равновесия, она начнет колебаться. Однако изучать такие колебания сложно: их характер определяется размерами и формой игрушки, свойствами нити и другими факторами.
Чтобы размеры тела не влияли на характер его колебаний, следует взять нить, длина которой намного больше размеров тела, а масса незначительна по сравнению с его массой. В таком случае тело можно считать материальной точкой. А чтобы во время колебаний тело все время находилось на одинаковом расстоянии от точки подвеса, нить должна быть нерастяжимой. Таким образом будет получена физическая модель — математический маятник.
Математический маятник — это физическая модель колебательной системы, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити, и гравитационного поля.
Колебания математического маятника
Возьмем небольшой, но достаточно тяжелый шарик и подвесим его на длинной нерастяжимой нити — такой маятник можно считать математическим. Если отклонить шарик от положения равновесия и отпустить, то в результате действия гравитационного поля Земли (силы тяжести) и силы натяжения нити шарик начнет колебаться около положения равновесия. Поскольку сопротивление воздуха пренебрежимо мало, а силы, действующие в системе, являются консервативными, полная механическая энергия шарика будет сохраняться: потенциальная энергия шарика будет превращаться в его кинетическую энергию, и наоборот.
Рассмотрите колебательное движение шарика (рис. 20.2). Объясните причины его движения. Какие происходят превращения энергии?
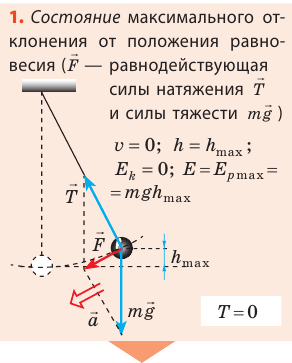
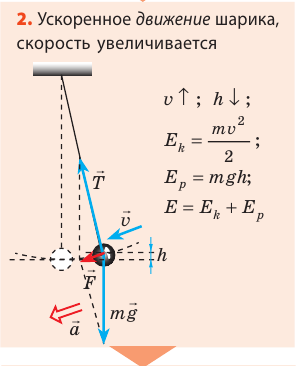
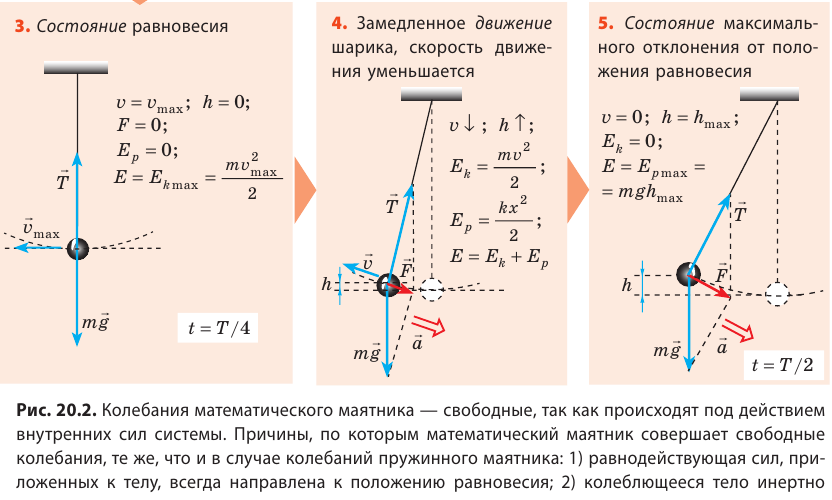
Как вычислить период колебаний математического маятника
Математический маятник, отклоненный от положения равновесия на небольшой угол (3–5°), будет совершать гармонические колебания, то есть ускорение его движения все время будет прямо пропорционально смещению и направлено в сторону, противоположную смещению: 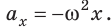
Для математического маятника: 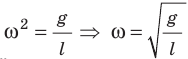 . Поскольку
. Поскольку 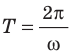 , имеем формулу для периода колебаний математического маятника:
, имеем формулу для периода колебаний математического маятника:
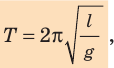
где l — длина маятника; g — ускорение свободного падения.
Данную формулу впервые получил в XVII в. голландский ученый Христиан Гюйгенс, поэтому ее называют формулой Гюйгенса.
Период колебаний математического маятника не зависит от массы маятника, а определяется только длиной нити и ускорением свободного падения в том месте, где расположен маятник. Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности.
Пример:
Уравнение колебаний груза массой 1 кг на пружине имеет вид: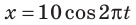 (cм). Найдите полную механическую энергию колебаний; наибольшую скорость груза; кинетическую и потенциальную энергии системы через
(cм). Найдите полную механическую энергию колебаний; наибольшую скорость груза; кинетическую и потенциальную энергии системы через 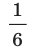 с после начала отсчета времени. Трением пренебречь.
с после начала отсчета времени. Трением пренебречь.
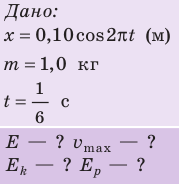
Решение:
Трение отсутствует, поэтому полная механическая энергия сохраняется:
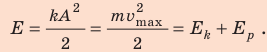
Сравним уравнение колебаний в общем виде с уравнением, приведенным в задаче:
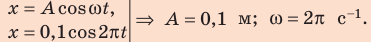
Поскольку
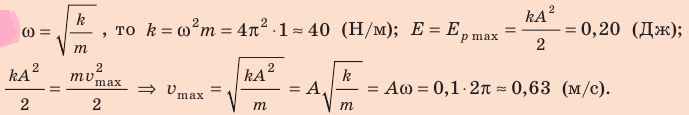
Определив удлинение пружины через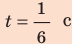 , вычислим потенциальную и кинетическую энергии пружины:
, вычислим потенциальную и кинетическую энергии пружины: 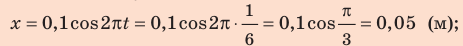
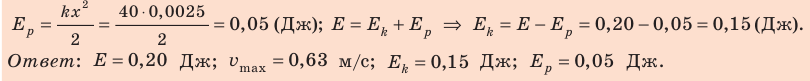
Выводы:
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
Простая гравитация
Так называемый простой маятник — это всего лишь идеализированная математическая модель. Это груз на конце безмассового шнура, подвешенного на оси без трения. Если его толкнуть, он будет раскачиваться с постоянной амплитудой, но с некоторыми условиями:
- Стержень или нить, на котором качается отвес, не имеет массы и не может растягиваться.
- Груз — это точечная масса.
- Движение происходит только в двух измерениях, то есть отвес не может очертить эллипс, а только дугу.
- Энергия движения не расходуется на трение или сопротивление воздуха.
- Гравитационное поле однородно.
- Поддержка всей конструкции не двигается.
Дифференциальное уравнение, которое представляет движение простого маятника, выглядит следующим образом (где g – ускорение силы тяжести, ℓ – длина маятника, θ – угловое смещение): d² / dt² + g / ℓ sin θ = 0.
На графике 1 показаны силы, действующие на отвес. Стоит обратить внимание, что груз описывает дугу. Угол θ измеряется в радианах, и это имеет решающее значение для этой формулы. Синяя стрелка — гравитационная сила, которая действует на маятник, а фиолетовые векторы — это та же самая сила, только разложенная на компоненты, параллельные и перпендикулярные мгновенному движению груза.
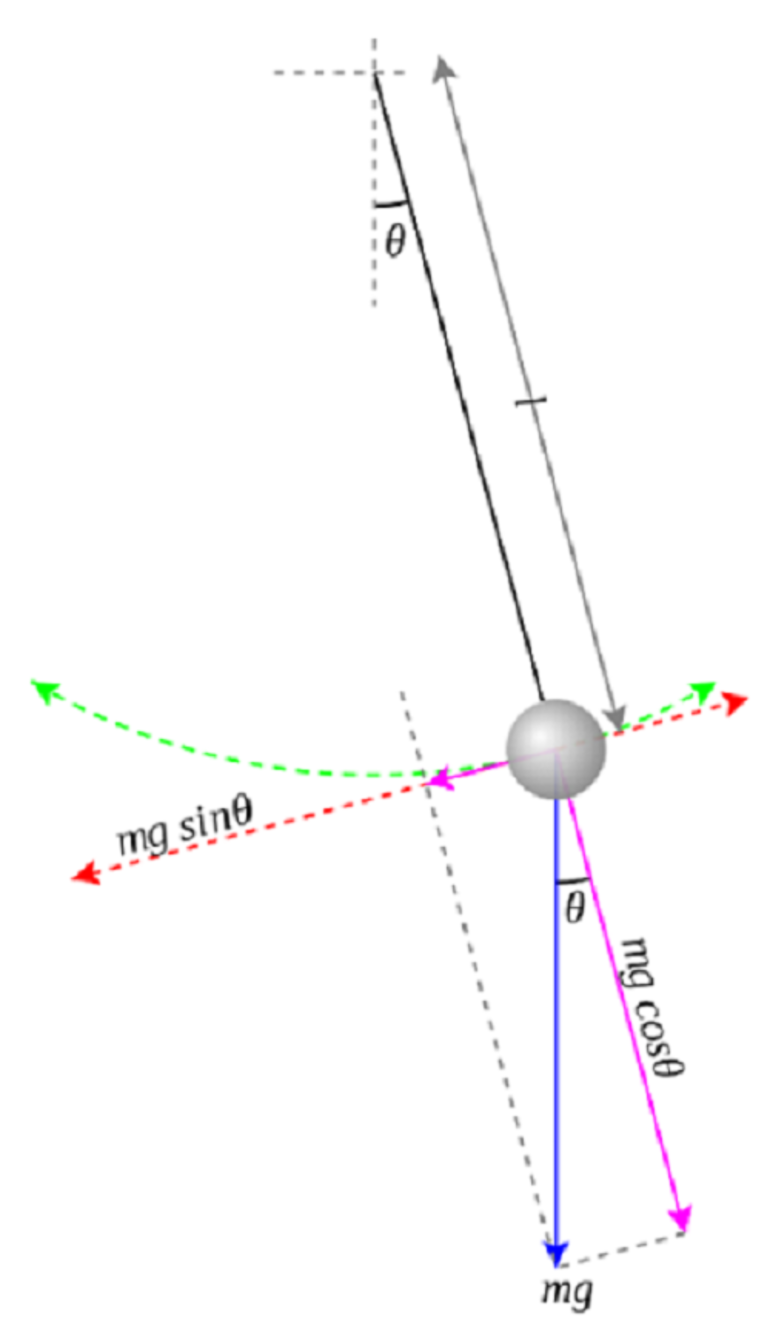
График 1.
Направление мгновенной скорости всегда указывается вдоль красной оси, которая считается тангенциальной, поскольку её направление всегда касается окружности. И прежде чем вывести уравнение силы деривации, стоит вспомнить второй закон Ньютона: F = ma. За F принимают сумму сил, действующих на объект, m – масса, a — ускорение.
Поскольку интерес составляет только измерение скорости, а груз вынужден оставаться на круговой траектории, уравнение Ньютона применяется только к тангенциальной оси. Короткая фиолетовая стрелка представляет компонент гравитационной силы, используя тригонометрию можно определить её величину. Таким образом, получается (g – ускорение силы тяжести вблизи поверхности земли): F = – mg sin θ = ma; a = – g sin θ.
Отрицательный знак на правой стороне означает, что θ и отвес всегда указываются в противоположных направлениях. Это вполне логично, поскольку когда маятник качается сильнее влево, ожидается, что он ускорится при движении назад — вправо. Это линейное ускорение, a вдоль красной оси может быть связано с изменением угла θ по формулам длины дуги (s): s = ℓθ; v = ds / dt = ℓdθ / dt; a = d²s / dt² = ℓd²θ / dt². Из этого следует: ℓd²θ/dt² = – gsin θ, d²θ / dt² + d / ℓ sin θ = 0.
Крутящий момент
Для начала нужно определить этот показатель на маятниковом шарнире, используя силу, вызванную гравитацией (Fg): T = ℓ x Fg, где ℓ – векторы длины маятника.
Здесь самое время рассмотреть величину крутящего момента на маятнике: |T| = – mgℓ sinθ, где m – масса, g – ускорение силы тяжести, ℓ – длина, а θ – угол между вектором длины и гравитацией. Далее, самое время переписать момент импульса: L = r x p = mr x (ꞷ x r).
Просто величина углового момента и его производная по времени: |L| = mr² w = mℓ² d²θ / dt². Формула крутящего момента после всех вычислений будет выглядеть следующим образом: T = r x F = dL / dt.
Сохранение механической энергии
Такое уравнение можно получить с помощью одноимённого принципа. Формулируется он так: любой объект, падающий на вертикальное расстояние h, получит кинетическую энергию, равную той, которую потерял при падении. Изменение потенциальной энергии выражается: Δ U = mgh, тогда как кинетическая (отвес начал движение с покоя) представлена формулой: Δ K = 1/2 mu².
Поскольку, как известно, никакая энергия не теряется, выигрыш в одном должен быть равен потере в другом: 1/2 mu² = mgh.
Колебательные движения
Период колебаний математического маятника (простого гравитационного) зависит от его длины, локальной силы тяжести и в небольшой степени от максимального угла, от которого отвес отклоняется от вертикали θ 0, называемого амплитудой.

Он не зависит от массы груза. Если амплитуда ограничена малыми колебаниями, то на период T, время, необходимое для полного цикла является: T≈ 2 π √ L/g. При этом L – длина маятника, а g – местное ускорение гравитации.
Нужно сказать, что для небольших колебаний период не зависит от амплитуды. Такое свойство называется изохронизмом, именно оно стало причиной того, что маятники используются для хронометража. Последовательные колебания маятника, даже если они меняются по амплитуде, занимают одинаковое количество времени. Для большого размаха свойственно увеличение периода с каждым раскачиванием, поэтому он длиннее, чем задано уравнением, отражающим частоту колебаний математического маятника.
Период возрастает до бесконечности как только θ 0 приближается к 180°, так как это значение является нестабильной точкой равновесия для маятника. Истинный период может быть записан в нескольких различных формах, например, бесконечный ряд: T = 2 π √ L/g )1+ 1/16 θ²/º + 11/3072 θ ⁴/º + …). Разница между истинным и периодом небольших колебаний называется круговой ошибкой. В случае с типичными напольными часами, у которых маятник имеет размах 6° и, следовательно, амплитуду 3° (0,05 радиана), разница составит около 15 секунд в день.
Формула математического маятника, при малых колебаниях, когда он приближается к гармоническому осциллятору, и его движение, как функция времени t, находит выражение следующим образом: θ(t) = θₒ cos (2 π / T * t + ⱷ). Где фи (ⱷ) — постоянная величина, зависящая от начальных условий. Для маятников этот период незначительно меняется в зависимости от некоторых факторов, например:
- плавучесть и вязкостное сопротивление воздуха;
- масса нити или стержня;
- размер и форма отвеса и способы его прикрепления к шнуру;
- гибкость и растяжение нити.
Если необходимы точные расчёты, конечно, все эти поправки должны учитываться.
Составной маятник
Другое название — физический, представляет собой любое качающееся твёрдое тело, свободно вращающееся вокруг фиксированной горизонтальной оси. Соответствующая эквивалентная длина – L, а для расчёта времени используется расстояние от оси до центра колебаний. Эта точка расположена над центром массы на расстоянии от оси, традиционно называемым радиусом колебаний, который зависит от распределения веса груза.

Христиан Гюйгенс в 1673 году доказал, что точка вращения и центр колебаний взаимозаменяемы. Это означает, если какой-либо маятник перевёрнут и ротирован от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, и новый центр будет находиться в старой точке вращения.
В 1817 году Генри Кэтер использовал эту идею для создания обратимого маятника, теперь известного под именем создателя, для улучшения измерений ускорения под действием силы тяжести.
Историческая хроника
Одним из самых ранних известных применений маятника было устройство сейсмометра (I века) китайского учёного династии Хань Чжан Хэна. Его функция состояла в том, чтобы раскачивать и активировать один из серии рычагов после того, как он был нарушен тремором землетрясения, которое происходило далеко от места измерения. Освобождённый рычагом, маленький шарик выпадал из устройства в форме урны в одну из восьми горловин металлической жабы внизу, в восьми точках компаса, что указывало направление землетрясения.
Многие источники утверждают, что египетский астроном X века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году с британским историком Эдвардом Бернардом.
В эпоху Возрождения большие маятники с ручной накачкой использовались в качестве источников энергии для ручных поршневых машин, таких как пилы, сильфоны и насосы. Леонардо Давинчи сделал много рисунков движения маятников, хотя и не осознавал его значения для хронометража.
Исследования Галилея
Итальянский учёный Галилео Галилей был первым, кто начал изучать свойства маятников, начиная примерно с 1602 года. Самый ранний существующий отчёт о его исследованиях содержится в письме Гвидо Убальдо дель Монте из Падуи от 29 ноября 1602 года. Его биограф и ученик, Винченцо Вивиани, утверждал, что его интерес был вызван около 1582 года, когда физик раскачивал люстры в соборе Пизы.
Галилей обнаружил важнейшее свойство, которое делает маятники полезными в качестве хронометриста, называемое изохронизмом; период маятника приблизительно не зависит от амплитуды или ширины качания. Он также обнаружил, что период не зависит от массы отвеса и пропорционален квадратному корню из длины всей конструкции. Сначала он использовал маятники свободного вращения в простых приложениях синхронизации.
Его друг — врач Санторио Санторий, используя наработки Галилея, изобрёл прибор, который измерял пульс пациента. В 1641 году Галилео задумал и продиктовал своему сыну Винченцо конструкцию маятниковых часов. Тот начал строительство, но не завершил его, поскольку умер в 1649 году. Так, появился первый гармонический осциллятор, использованный человеком.
Маятниковые часы
Первый образец построил в 1656 году голландский учёный Христиан Гюйгенс. Это было значительное улучшение по сравнению с существующими механическими часами. Их точность была улучшена с отклонений от 15 минут до 15 секунд в день. Маятники распространились по Европе, так как все существующие часы стали модифицироваться.
Английский учёный Роберт Гук изучил конический маятник (около 1666), который мог свободно колебаться в двух измерениях, а груз вращаться по кругу или эллипсу. Он использовал движение этого устройства в качестве модели для анализа орбитального движения планет. Гук предложил Исааку Ньютону в 1679 году свои наработки.

Он утверждал, что составляющие орбитального движения состояли из инерционного движения по касательному направлению и привлекательного движения в радиальном направлении. Это сыграло свою роль в формулировке Ньютоном закона всемирного тяготения. Роберт Гук также был ответственным за то, что ещё в 1666 году предположил, что маятник можно использовать для измерения силы тяжести.
Во время своей экспедиции в Кайенна (Французская Гвиана) в 1671, Жан Рише обнаружил, что там часы с маятником шли на 2,5 минуты медленнее, чем в Париже. Из этого он сделал вывод, что сила гравитации была ниже в Кайенне. В 1687 году Исаак Ньютон в Principia Mathematica показал, что это произошло потому, что Земля была не настоящей сферой, а слегка сплюснутой (сплющенной на полюсах) от действия центробежной силы из-за её вращения, это и вызывает увеличение силы гравитации.

Портативные маятники стали совершать рейсы в дальние страны, в качестве прецизионных гравиметров для измерения ускорения свободного падения в разных точках Земли, что в итоге привело к определению точной модели формы планеты. Затем последовало превращение исследований и выводов учёных в новые классы приборов, с дополнительными параметрами. Например:
- 1721 г. — маятник с температурной компенсацией;
- 1851 г. — маятник Фуко.
В 1930 году решение задачи по точному хронометражу было найдено, в 1921 был изобретён кварцевый генератор.


![{displaystyle T=T_{0}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {theta _{0}}{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {theta _{0}}{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {theta _{0}}{2}}right)+dots right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5346cf06ad62d5c061cf5527d53a86e61cf89478)
