Pv urt как найти t

Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

,

где

Уравнение состояния идеального газа можно записать в виде:

,

где  — масса,  — молярная масса, (так как количество вещества ):

или в виде

,

где  — концентрация частиц (атомов или молекул) – количество частиц,  — постоянная Больцмана.

Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.

Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную значение которой необходимо было измерять для каждого газа:

Менделеев обнаружил, что прямо пропорциональна , коэффициент пропорциональности он назвал универсальной газовой постоянной.^{[источник не указан 1457 дней]}

Связь с другими законами состояния идеального газа[править | править код]

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта — Изотермический процесс.

 — Закон Гей-Люссака — Изобарный процесс.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс

В форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.

С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:

.

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

.

Закон Бойля — Мариотта

Закон Бойля — Мариотта

назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

где  — показатель адиабаты,  — внутренняя энергия единицы массы вещества.

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.

С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.

С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение увеличивается.

См. также[править | править код]

• Совершенный газ
• Реальный газ
• Уравнение состояния реального газа

Примечания[править | править код]

Литература[править | править код]

• Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.

ВикиЧтение

Теплотехника
Бурханова Наталья

Термодинамический
процесс
(тепловой процесс) – изменение
макроскопического состояния
термодинамической системы. Если разница
между начальным и конечным состояниями
системы бесконечно мала, то такой процесс
называют элементарным (инфинитезимальным).

Система,
в которой идёт тепловой процесс,
называется рабочим телом.

Тепловые
процессы можно разделить на равновесные
и неравновесные. Равновесным называется
процесс, при котором все состояния,
через которые проходит система, являются
равновесными состояниями. Такой процесс
приближённо реализуется в тех случаях,
когда изменения происходят достаточно
медленно, т. е. процесс является
квазистатическим.

Тепловые
процессы можно разделить на обратимые
и необратимые. Обратимым называется
процесс, который можно провести в
противоположном направлении через все
те же самые промежуточные состояния.

Виды
тепловых процессов:

Адиабатный
процесс — без теплообмена с окр. средой;

Изохорный
процесс — происходящий при постоянном
объёме;

Изобарный
процесс — происходящий при постоянном
давлении;

Изотермический
процесс — происходящий при постоянной
температуре;

Изоэнтропийный
процесс — происходящий при постоянной
энтропии;

Изоэнтальпийный
процесс — происходящий при постоянной
энтальпии;

Политропный
процесс — происходящий при постоянной
теплоёмкости.

Уравнение
Менделеева-Клайперона (уравнение
состояния идеального газа):

PV
= nRT,
где n
– число молей газа, P
– давление газа, V
– объем газа, T
– температура газа, R
– универсальная газовая постоянная

Изопроцессы
идеального газа. Их изображение в P–V
диаграммах.

1)
Изобарный процесс p
= const,
V/T
= const

2)
Изохорный процесс V
= const,
p/T
= const

3)
Изотермический процесс T
= const,
pV
= const

Термодинамические
процессы. Уравнение Менделеева-Клапейрона.
Изопроцессы идеального газа. Их
изображение на Р-V
диаграммах.

Термодинамические
процессы. Совокупность изменяющихся
состояний рабочего тела называется
термодинамическим процессом.

Идеальный
газ — изучаемый в термодинамике
воображаемый газ, у которого отсутствуют
силы межмолекулярного притяжения н
отталкивания, а сами молекулы представляют
собой материальные точки, не имеющие
объема. Многие реальные газы по своим
физическим свойствам весьма близки к
идеальному газу.

Основными
процессами в термодинамике являются:

• изохорный,
  протекающий при постоянном объеме;

• изобарный,
  протекающий при постоянном давлении;

• изотермический,
  происходящий при постоянной температуре;

• адиабатный,
  при котором теплообмен с окружающей
  средой отсутствует;

Изохорный
процесс

При
изохорном процессе выполняется условие
v= const.

Из
уравнения состояния идеального газа
(pv=RT) следует:

 p/T=R/v= const,

т.
е. давление газа прямо пропорционально
его абсолютной температуре:

 p₂/p₁=T₂/T₁.

Работа
расширения в изохорном процессе равна
нулю (l= 0), так как объем рабочего
тела не меняется (Δv= const).

Количество
теплоты, подведенной к рабочему телу в
процессе 1-2 при c_v= const
определяется по формуле:

q=c_v(T₂
—  T₁). 

Т.
к.l= 0, то на основании первого закона
термодинамики Δu=q, а значит
изменение внутренней энергии можно
определить по формуле:

Δu=c_v(T₂
— T₁).

Изменение
энтропии в изохорном процессе определяется
по формуле:

s₂
– s₁=
Δs =
c_vln(p₂/p₁)
= c_vln(T₂/T₁).

Изобарный
процесс

Изобарным
называется процесс, протекающий при
постоянном давлении p= const. Из
уравнения состояния идеального газа
слуедует:

v/T=R/p=const

или

 v₂/v₁=T₂/T₁,

т.
е. в изобарном процессе объем газа
пропорционален его абсолютной температуре.

Работа
будет равна:

l=p(v₂ – v₁).

Т.
к. pv₁=RT₁иpv₂=RT₂,
то

l=R(T₂ – T₁).

Количество
теплоты при c_p= const
определяется по формуле:

q=c_p(T₂
– T₁).

Изменение
энтропии будет равно: 

s₂
– s₁=
Δs =
c_pln(T₂/T₁).

Изотермический
процесс

При
изотермическом процессе температура
рабочего тела остается постоянной T= const, следовательно:

pv
= RT =
const

или

p₂/p₁=v₁/v₂,

т.
е. давление и объем обратно пропорциональны
друг другу, так что при изотермическом
сжатии давление газа возрастает, а при
расширении – снижается.

Работа
процесса будет равна:

l=RTln (v₂ – v₁)
=RTln (p₁ – p₂).

Так
как температура остается неизменной,
то и внутренняя энергия идеального газа
в изотермическом процессе остается
постоянной (Δu= 0) и вся подводимая
к рабочему телу теплота полностью
превращается в работу расширения:

q=l.

При
изотермическом сжатии от рабочего тела
отводится теплота в количестве, равном
затраченной на сжатие работе.

Изменение
энтропии равно:

s₂
– s₁= Δs=Rln(p₁/p₂)
=Rln(v₂/v₁).

Адиабатный
процесс

Адиабатным
называется процесс изменения состояния
газа, который происзодит без теплообмена
с окружающей средой. Так как dq= 0,
то уравнение первого закона термодинамики
для адиабатного процесса будет иметь
вид:

du+pdv= 0

или

Δu+l= 0,

следовательно

Δu=
—l. 

В
адиабатном процессе работа расширения
совершается только за счет расходования
внутренней энергии газа, а при сжатии,
происходящем за счет действия внешних
сил, вся совершаемая ими работа идет на
увеличение внутренней энергии газа.

Обозначим
теплоемкость в адиабатном процессе
через c_ад, и условие dq=
0 выразим следующим образом:

dq=c_адdT= 0.

Это
условие говорит о том, что теплоемкость
в адиабатном процессе равна нулю (c_ад= 0).

Известно,
что

с_p/c_v
=k

и
уравнение кривой адиабатного процесса
(адиабаты) в p, v-диаграмме имеет
вид:

pv^k= const.

В
этом выражении kносит названиепоказателя адиабаты(так же
ее называют коэффициентом Пуассона).

Значения
показателя адиабаты k для некоторых
газов:

k_{воздуха}= 1,4

k_{перегретого
пара}= 1,3

k_{выхлопных
газов ДВС}= 1,33

k_{насыщенного
влажного пара}= 1,135

Из
предыдущих формул следует:

l=
— Δu
= c_v(T₁
– T₂);

i₁
– i₂=
c_p(T₁
– T₂).

Техническая
работа адиабатного процесса (l_техн)
равна разности энтальпий начала и конца
процесса (i₁ – i₂).

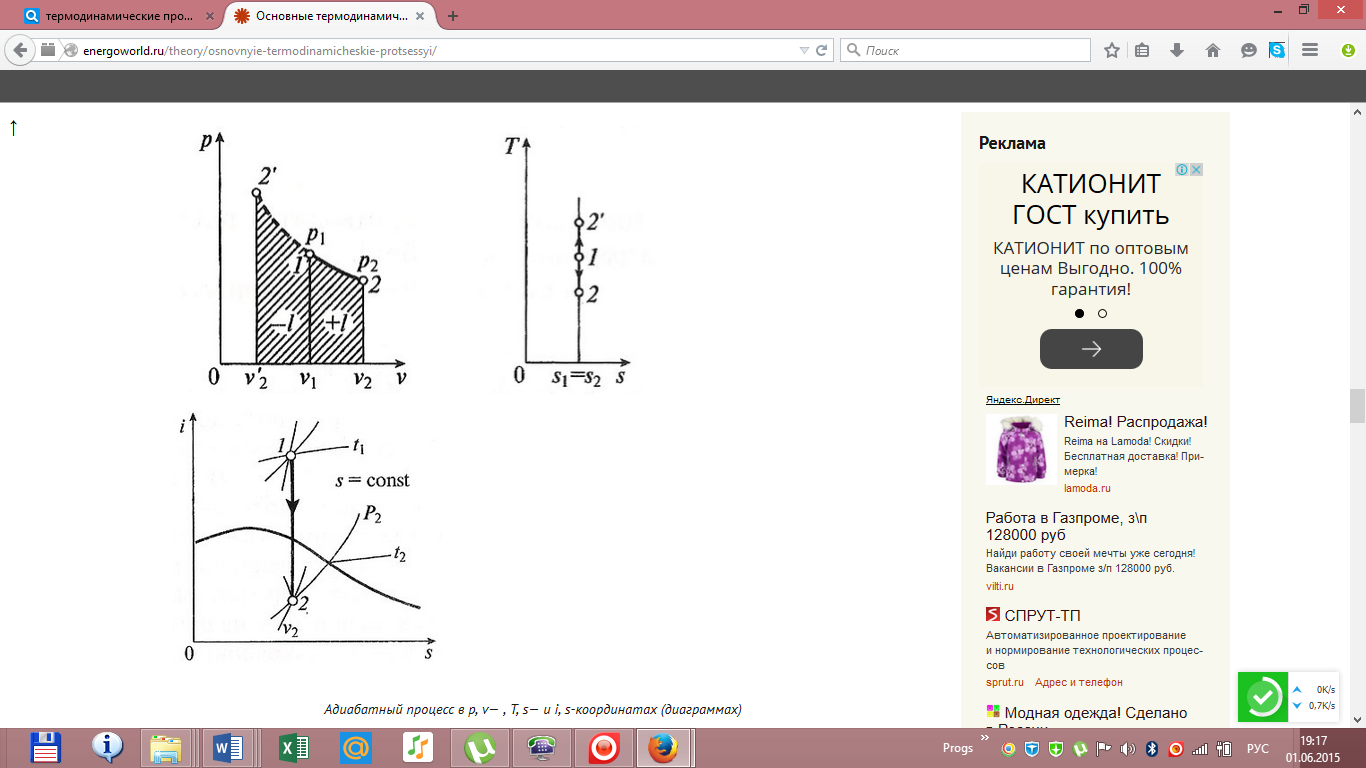
Адиабатный
процесс, происходящий без внутреннего 
трения в рабочем теле, называется
изоэнтропийным. ВT, s-диаграмме
он изображается вертикальной линией.

Обычно
реальные адиабатные процессы протекают
при наличии внутреннего трения в рабочем
теле, в результате чего всегда выделяется
теплота, которая сообщается самому
рабочему телу. В таком случае ds>
0, и процесс называетсяреальным
адиабатным процессом.

Уравнение
Менделеева-Клапейрона

Газы
нередко бывают реагентами и продуктами
в химических реакциях. Не всегда удается
заставить их реагировать между собой
при нормальных условиях. Поэтому нужно
научиться определять число молей газов
в условиях, отличных от нормальных.

Для
этого используют уравнение состояния
идеального газа(его также называют
уравнением Клапейрона-Менделеева):

PV
= nRT

где
n– число молей газа;

P
– давление газа (например, в атм;

V
– объем газа (в литрах);

T
– температура газа (в кельвинах);

R
– газовая постоянная (0,0821 л·атм/моль·K).

Например,
в колбе объемом 2,6 л находится кислород
при давлении 2,3 атм и температуре
26^оС. Вопрос: сколько молей O₂содержится в колбе?

Из
газового закона найдем искомое число
молей n:

Не
следует забывать преобразовывать
температуру из градусов Цельсия в
кельвины: (273 ^оС + 26^оС) = 299 K.
Вообще говоря, чтобы не ошибиться в
подобных вычислениях, нужно внимательно
следить за размерностью величин,
подставляемых в уравнение
Клапейрона-Менделеева. Если давление
дается в мм ртутного столба, то нужно
перевести его в атмосферы, исходя из
соотношения: 1атм = 760 мм рт. ст.
Давление, заданное в паскалях (Па), также
можно перевести в атмосферы, исходя из
того, что 101325 Па = 1атм.

Билет
16

Вывод
основного уравнения молекулярно-кинетической
теории. Число степеней свободы молекулы.
Закон распределения энергии по степеням
свободы.

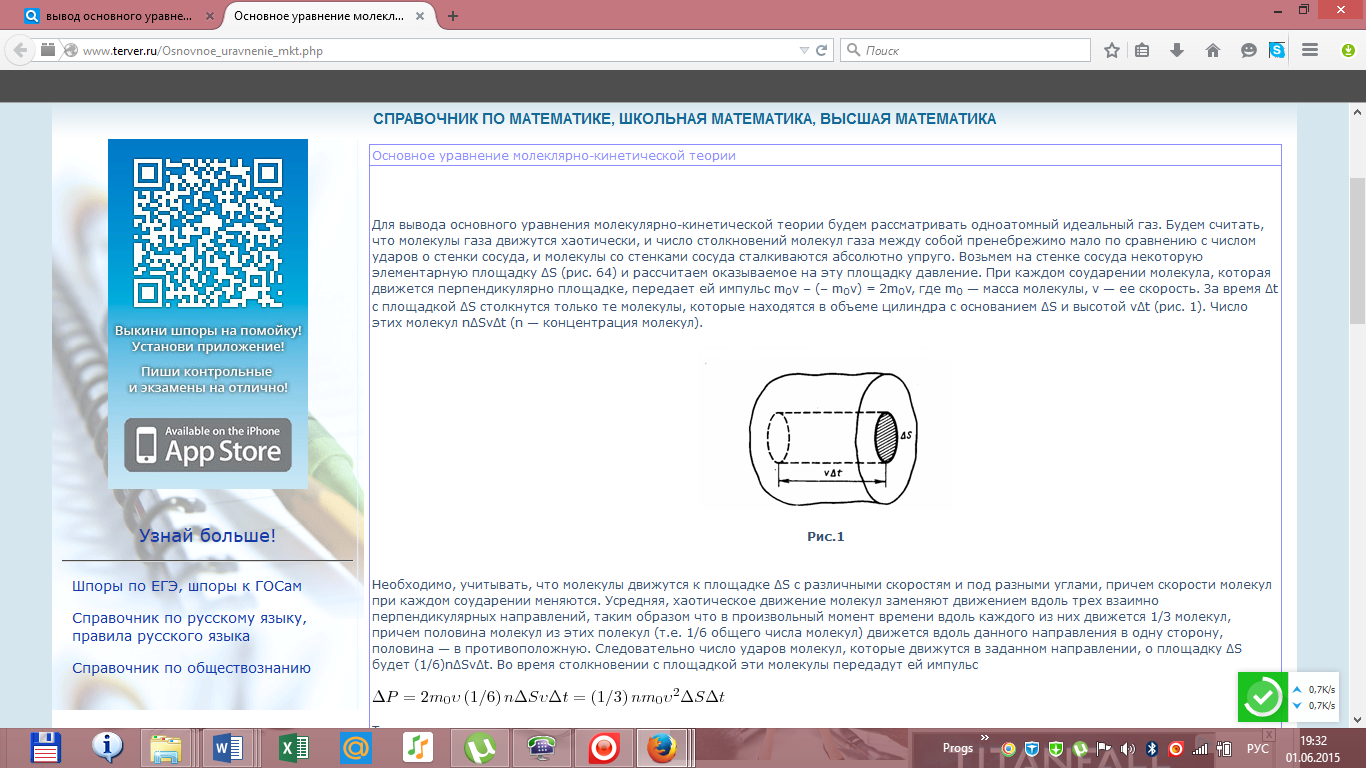
Вывод
основного уравнения МКТ.

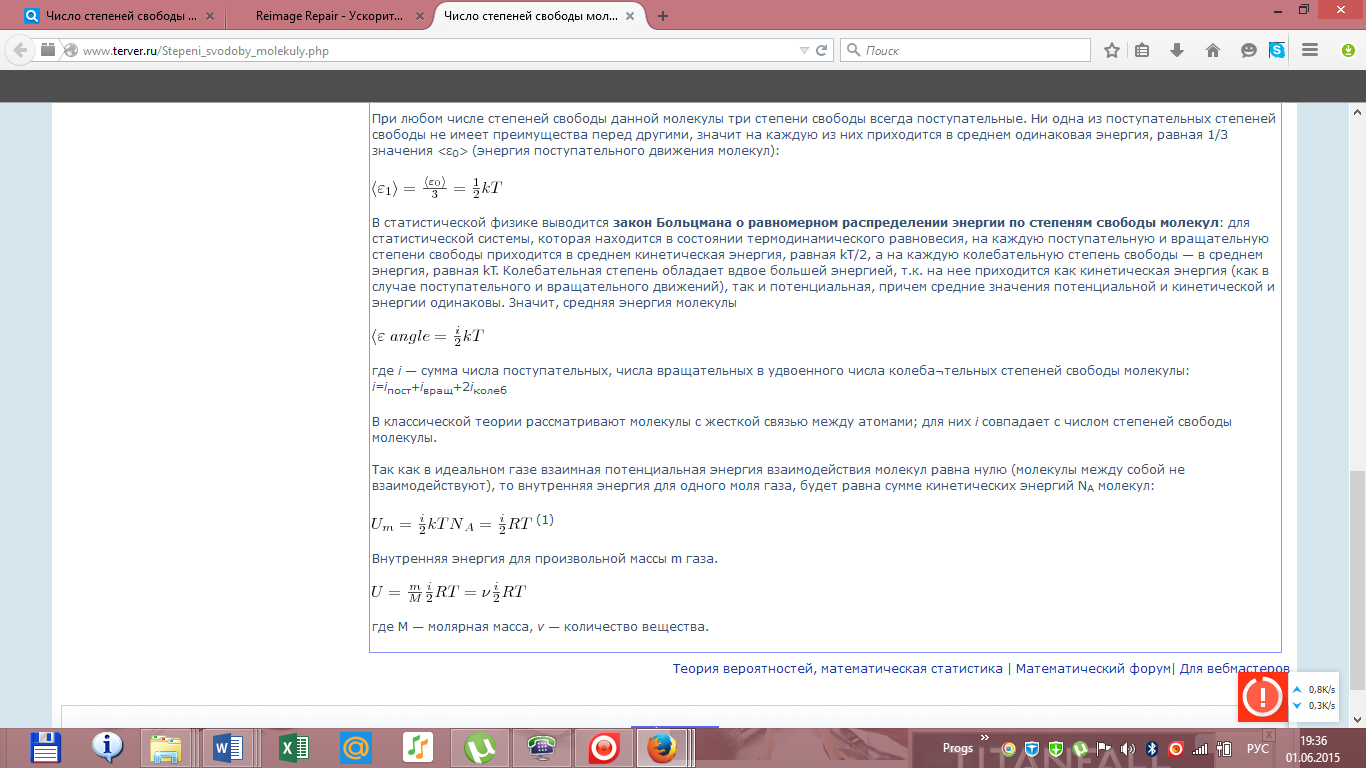
Число
степеней свободы молекулы. Закон
распределения энергии по степеням
свободы.

Билет
17.

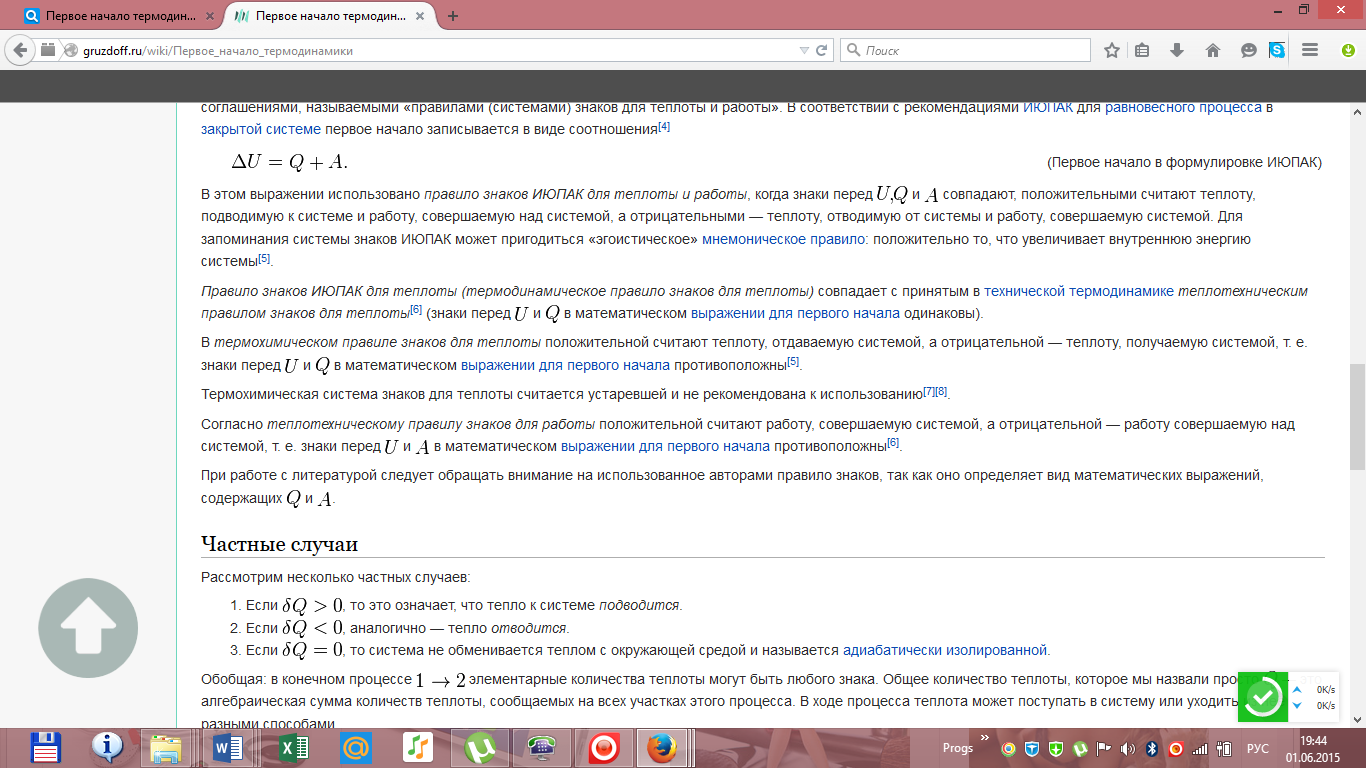
Первое
начало термодинамики. Работа газа при
изменении объема. Вычислить работу
изотермического расширения газа.

Количество
теплоты,
полученное системой, идёт на изменение
её внутренней энергии и совершение
работы против внешних сил

Изменение
внутренней энергии системы при переходе
её из одного состояния в другое равно
сумме работы внешних сил и количества
теплоты, переданного системе, то есть,
оно зависит только от начального и
конечного состояния системы и не зависит
от способа, которым осуществляется этот
переход. В циклическом процессе внутренняя
энергия не изменяется.

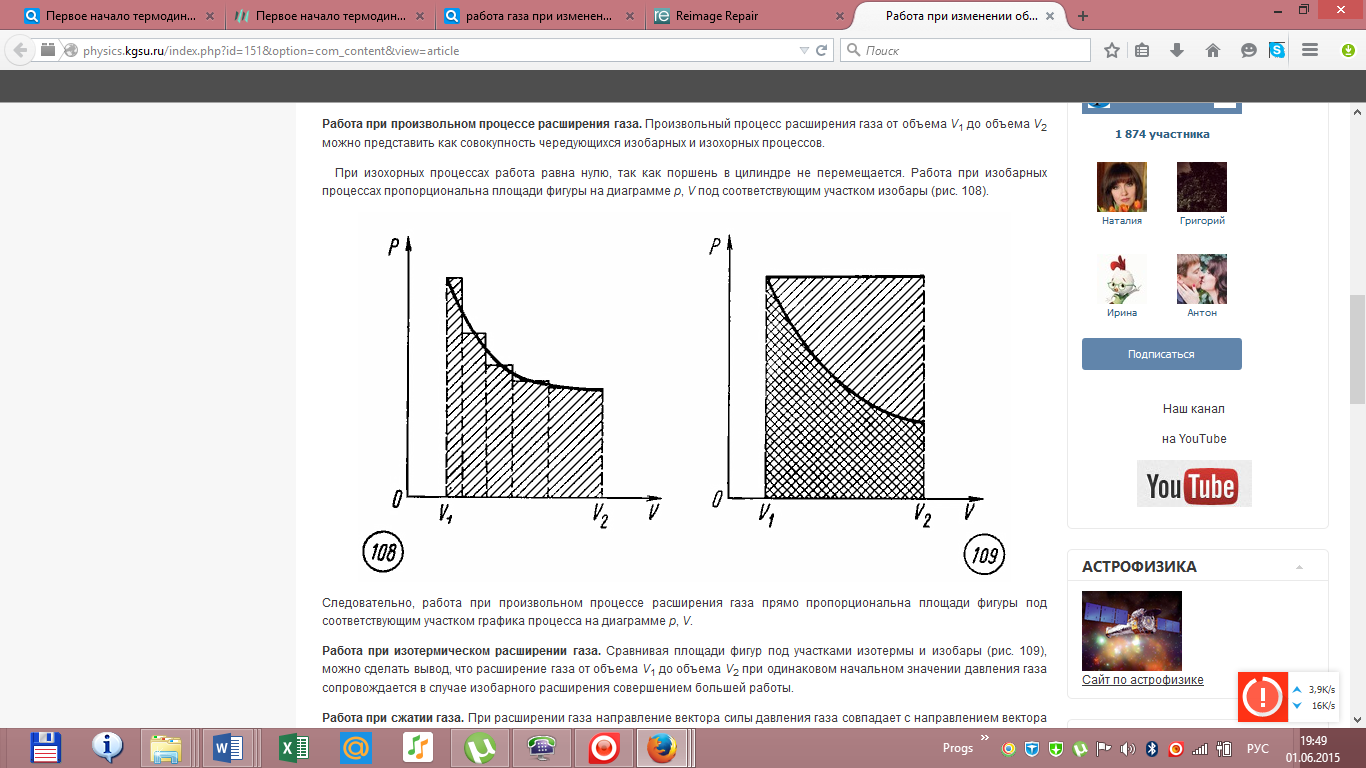
Работа
при изотермическом расширении газа
вычисляется как площадь фигуры под
графиком процесса.

Билет
18.

Теплоемкость
идеального газа.

Если
в результате теплообмена телу передается
некоторое количество теплоты, то
внутренняя энергия тела и его температура
изменяются. Количество теплоты Q,
необходимое для нагревания 1 кг
вещества на 1 К называют удельной
теплоемкостью вещества c. c = Q / (mΔT).

Во многих случаях удобно использовать
молярную теплоемкость C:

где
M – молярная масса вещества.

Определенная
таким образом теплоемкость не является
однозначной характеристикой вещества.
Согласно первому закону термодинамики
изменение внутренней энергии тела
зависит не только от полученного
количества теплоты, но и от работы,
совершенной телом. В зависимости от
условий, при которых осуществлялся
процесс теплопередачи, тело могло
совершать различную работу. Поэтому
одинаковое количество теплоты, переданное
телу, могло вызвать различные изменения
его внутренней энергии и, следовательно,
температуры.

Такая
неоднозначность определения теплоемкости
характерна только для газообразного
вещества. При нагревании жидких и твердых
тел их объем практически не изменяется,
и работа расширения оказывается равной
нулю. Поэтому все количество теплоты,
полученное телом, идет на изменение его
внутренней энергии. В отличие от жидкостей
и твердых тел, газ в процессе теплопередачи
может сильно изменять свой объем и
совершать работу. Поэтому теплоемкость
газообразного вещества зависит от
характера термодинамического процесса.
Обычно рассматриваются два значения
теплоемкости газов: C_V
– молярная теплоемкость в изохорном
процессе (V = const) и C_p
– молярная теплоемкость в изобарном
процессе (p = const).

В
процессе при постоянном объеме газ
работы не совершает: A = 0. Из первого
закона термодинамики для 1 моля газа
следует

C_VΔT = ΔU.

Изменение
ΔU внутренней энергии газа прямо
пропорционально изменению ΔT его
температуры.

Для
процесса при постоянном давлении первый
закон термодинамики дает:

p (V₂– V₁) = C_VΔT + pΔV,

где
ΔV – изменение объема 1 моля идеального
газа при изменении его температуры на
ΔT. Отсюда следует:

Отношение
ΔV / ΔT может быть найдено из уравнения
состояния идеального газа, записанного
для 1 моля:

pV = RT,

где
R – универсальная газовая постоянная.
При p = const

или

Таким
образом, соотношение, выражающее связь
между молярными теплоемкостями C_p
и C_V,
имеет вид (формула Майера):

Cp = CV + R.

Молярная
теплоемкость C_p
газа в процессе с постоянным давлением
всегда больше молярной теплоемкости
C_V
в процессе с постоянным объемом

Отношение
теплоемкостей в процессах с постоянным
давлением и постоянным объемом играет
важную роль в термодинамике. Оно
обозначается греческой буквой γ.

Билет
19.

Цикл
Карно. Тепловая и холодильная машины.
КПД цикла Карно.

В
термодинамике цикл
Карно́ или процесс
Карно — это обратимый
круговой процесс, состоящий из двух
адиабатических и двух изотермических
процессов. В процессе Карно термодинамическая
система выполняет механическую работу
и обменивается теплотой с двумя тепловыми
резервуарами, имеющими постоянные, но
различающиеся температуры. Резервуар
с более высокой температурой называется
нагревателем, а с более низкой
температурой — холодильником.

Цикл
Карно назван в честь французского
учёного и инженера Сади Карно, который
впервые его описал в своём сочинении
«О движущей силе огня и о машинах,
способных развивать эту силу» в 1824 году.

Поскольку
обратимые процессы могут осуществляться
лишь с бесконечно малой скоростью,
мощность тепловой машины в цикле Карно
равна нулю. Мощность реальных тепловых
машин не может быть равна нулю, поэтому
реальные процессы могут приближаться
к идеальному обратимому процессу Карно
только с большей или меньшей степенью
точности. В цикле Карно тепловая машина
преобразует теплоту в работу с максимально
возможным коэффициентом полезного
действия из всех тепловых машин, у
которых максимальная и минимальная
температуры в рабочем цикле совпадают
соответственно с температурами
нагревателя и холодильника в цикле
Карно

.
Пусть тепловая машина
состоит из нагревателя
с температурой Тн, холодильника с
температурой Тх и рабочего
тела.

Цикл
Карно состоит из четырёх обратимых
стадий, две из которых осуществляются
при постоянной температуре (изотермически),
а две — при постоянной энтропии
(адиабатически). Поэтому цикл Карно
удобно представить в координатах T
(температура)
и S
(энтропия).

1.
Изотермическое
расширение
(на рис. 1 — процесс A→Б). В начале
процесса рабочее тело имеет температуру
Тн, то есть температуру нагревателя.
Затем тело приводится в контакт с
нагревателем, который изотермически
(при постоянной температуре) передаёт
ему количество
теплоты
Q.
При этом объём рабочего тела увеличивается,
оно совершает механическую работу, а
его энтропия возрастает.

2.
Адиабатическое
расширение
(на рис. 1 — процесс Б→В). Рабочее тело
отсоединяется от нагревателя и продолжает
расширяться без теплообмена с окружающей
средой. При этом температура тела
уменьшается до температуры холодильника
Тх, тело совершает механическую работу,
а энтропия остаётся постоянной.

3.
Изотермическое
сжатие
(на рис. 1 — процесс В→Г). Рабочее
тело, имеющее температуру Тн, приводится
в контакт с холодильником и начинает
изотермически сжиматься под действием
внешней силы, отдавая холодильнику
количество теплоты Q.
Над телом совершается работа, его
энтропия уменьшается.

4.
Адиабатическое
сжатие
(на рис. 1 — процесс Г→А). Рабочее тело
отсоединяется от холодильника и сжимается
под действием внешней силы без теплообмена
с окружающей средой. При этом его
температура увеличивается до температуры
нагревателя, над телом совершается
работа, его энтропия остаётся постоянной.

Обратный
цикл Карно

В
термодинамике
холодильных установок и тепловых насосов
рассматривают
обратный
цикл Карно,
состоящий из следующих стадии:
адиабатического сжатия за счёт совершения
работы (на рис. 1 — процесс В→Б);
изотермического сжатия с передачей
теплоты более нагретому тепловому
резервуару (на рис. 1 — процесс Б→А);
адиабатического расширения (на рис. 1 —
процесс
А→Г); изотермического расширения с
отводом теплоты от более холодного
теплового резервуара (на рис. 1 —
процесс Г→В).

Билет
20.

Второе
начало термодинамики. Энтропия. Третье
начало термодинамики.

Второе
начало термодинамики —
физический принцип, накладывающий
ограничение на направление процессов,
которые могут происходить в термодинамических
системах.

Второе
начало термодинамики запрещает так
называемые вечные
двигатели второго рода,
показывая, что коэффициент
полезного действия
не может равняться единице, поскольку
для кругового процесса температура
холодильника не может равняться
абсолютному нулю (невозможно построить
замкнутый цикл, проходящий через точку
с нулевой температурой).

Второе
начало термодинамики является постулатом,
не доказываемым в рамках классической
термодинамики.
Оно было создано на основе обобщения
опытных фактов и получило многочисленные
экспериментальные подтверждения.

Постулат
Клаузиуса:
«Невозможен
круговой процесс, единственным результатом
которого является передача теплоты от
менее нагретого тела к более нагретому»
(такой
процесс называется процессом
Клаузиуса).

Постулат
Томсона
(Кельвина):
«Невозможен
круговой процесс, единственным результатом
которого было бы производство работы
за счет охлаждения теплового резервуара»
(такой процесс называется процессом
Томсона).

Энтропия
изолированной системы не может
уменьшаться» (закон
неубывания энтропии).

Такая
формулировка основывается на представлении
об энтропии как о функции
состояния
системы, что также должно быть
постулировано.

В
состоянии с максимальной энтропией
макроскопические необратимые процессы
(а процесс передачи тепла всегда является
необратимым из-за постулата Клаузиуса)
невозможны.

Третье
начало термодинамики
(теорема
Нернста) —
физический принцип, определяющий
поведение энтропии
при приближении температуры
к абсолютному
нулю.
Является одним из постулатов
термодинамики,
принимаемым на основе обобщения
значительного количества экспериментальных
данных.

Третье
начало термодинамики может быть
сформулировано так:

«Приращение
энтропии при абсолютном нуле температуры
стремится к конечному пределу, не
зависящему от того, в каком равновесном
состоянии находится система».

Третье
начало термодинамики относится только
к равновесным состояниям.

Поскольку
на основе второго начала термодинамики
энтропию можно определить только с
точностью до произвольной аддитивной
постоянной (то есть, определяется не
сама энтропия, а только её изменение).
Третье начало термодинамики может быть
использовано для точного определения
энтропии. При этом энтропию равновесной
системы при абсолютном нуле температуры
считают равной нулю.

Третье
начало термодинамики позволяет находить
абсолютное значение энтропии, что нельзя
сделать в рамках классической термодинамики
(на основе первого и второго начал
термодинамики).

Термодинамическая
энтропия
S,
часто просто именуемая энтропия,
— физическая
величина,
используемая для описания термодинамической
системы,
одна из основных термодинамических
величин.
Энтропия является функцией
состояния
и широко используется в термодинамике,
в том числе химической.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #