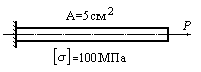Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
skEp |
Заголовок сообщения: Определить работу деформации шаров после удара
|
||
|
два шара массами 2кг и 3 кг, движутся по одной прямой навстречу друг другу со скоростями 8 м/с и 4 м/с, соответственно, неупруго сталкиваются и движутся после удара совместно. Определить работу деформации шаров после удара.
|
||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Определить зарплату, начисленную работнику, если он после в
в форуме Экономика и Финансы |
Alina95B |
1 |
437 |
02 апр 2014, 23:03 |
|
Определить координаты всех вершин куба после его поворота
в форуме Геометрия |
Rejuvka |
2 |
477 |
10 дек 2014, 16:22 |
|
Определить работу
в форуме Электричество и Магнетизм |
Orion |
0 |
338 |
13 дек 2014, 14:58 |
|
Определить путь, работу силы
в форуме Механика |
Caxapok |
1 |
645 |
27 окт 2013, 20:56 |
|
Определить работу для увеличения диаметра мыльного пузыря
в форуме Молекулярная физика и Термодинамика |
Kikki |
0 |
762 |
07 июн 2013, 10:43 |
|
Изменение характеристик фигуры при её деформации
в форуме Геометрия |
Vovsla |
6 |
130 |
26 авг 2022, 01:15 |
|
Деформации стержня вследствие ускоренного движения
в форуме Механика |
Corundum |
0 |
312 |
04 янв 2017, 15:24 |
|
Центр удара
в форуме Интересные задачи участников форума MHP |
wrobel |
0 |
271 |
14 сен 2020, 13:10 |
|
Уравнения определения точки удара
в форуме Аналитическая геометрия и Векторная алгебра |
DDONN |
0 |
213 |
26 янв 2015, 14:22 |
|
В урне 15 шаров
в форуме Теория вероятностей |
contor |
8 |
592 |
06 фев 2015, 13:17 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
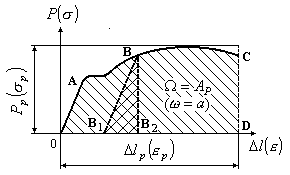
В
предыдущем разделе было показано, что
работа внешней силы
при растяжении стержня в пределах
упругой деформации равна площади
диаграммы растяжения в этих же пределах.
Очевидно, что полная работа внешней
силы,
затраченная на разрыв образца, может
измеряться площадью диаграммы растяжения
(Рис.3.16).
Рис.3.16
Площадь
диаграммы растяжения определяется по
формуле:
,
(3.23)
где
площадь прямоугольника
(Рис.3.16);коэффициент
заполнения диаграммы.
Работу,
затрачиваемую на деформацию образца,
можно разделить на две части: работу,
затраченную на упругие деформации, и
работу, которая идет на пластические
деформации. Первая является обратимой,
за счет нее в образце накапливается
потенциальная энергия. Работа,
затрачиваемая на остаточные деформации,
является необратимой.
Чтобы
определить потенциальную энергию,
накапливаемую в образце на какой-либо
стадии растяжения (Рис.3.16), необходимо
из соответствующей точки В провести
линию
,
параллельную прямой ОА и вертикальную
линию.
Площадь треугольника
численно равна потенциальной
энергии, остальная площадь диаграммы,
взятая от начала координат до линии,
равна необратимой части работы.
Отнесем
полную работу внешних сил к первоначальному
объему образца. Получим так называемую
удельную работу(Рис.3.16). Удельная работа, затраченная
на разрушение образца, будет численно
равна площади диаграммы растяжения в
осях(условной диаграммы напряжений):
.
(3.24)
Как
следует из выражения (3.24), удельная
работа, затрачиваемая на разрыв, зависит
от предела прочности материала,
наибольшего относительного удлинения
образца и формы условной диаграммы
напряжений.
3.11. Допускаемые напряжения. Условия прочности и жесткости при осевом растяжении и сжатии
Анализируя
условную диаграмму напряжений (Рис.3.6),
можно сделать вывод, что опасными для
образца являются следующие напряжения:
предел текучести
,
так как по достижении предела текучести
в образце возникают большиенеобратимые
деформации
в виде остаточного удлинения
,
и предел прочности,
так как при достижении предела прочности
в образце начинаются процессыразрушения
с образованием шейки. Обозначим опасные
напряжения буквой
и найдем допускаемые напряжения
,
разделив опасные напряжения на коэффициент
запаса прочности:
.
(3.25)
Коэффициент
запаса
является нормативной величиной и
устанавливается нормами проектирования.
Выбор величины коэффициента запаса
прочности зависит от состояния материала
(хрупкое или пластичное), характера
приложения нагрузки (статическая,
динамическая или повторно-переменная),
от неоднородности материала, неточности
задания величин внешних нагрузок,
неточности принятых методов расчета
.
Величина
коэффициента запаса прочности зависит
от того, какое напряженипе считать
опасным. Для пластичных материалов
опасным напряжением следует считать
предел текучести
,
а.
На основании длительной практики
конструирования, расчета и эксплуатации
машин и сооружений, величина запаса
прочностидля стали при статической нагрузке
принимается равной 1,41,6.
Чем более однороден метал, чем лучше
изучены его свойства, полнее учтены
нагрузки, точнее метод расчета, тем
меньшим принимается величина коэффициента
запаса прочности.
Для
хрупких матералов при статических
нагрузках опасным напряжением является
предел прочности
,
а.
В этом случае величина коэффициента
запаса прочности принимается равной.
Допускаемое
напряжение, определяемое по формуле
(3.25) называется основным
допускаемым напряжением.
Допускаемые напряжения устанавливаются
государственными нормирующими органами
и публикуются в технических условиях
и нормах проектирования, которые имеют
силу закона и обязательны для всех
инженерно-технических работников.
Имея
величину основного допускаемого
напряжения для данного материала
,
запишем условие прочности по нормальным
напряжениям в общем виде:
.
(3.26)
При осевом растяжении
и сжатии условие прочности принимает
вид:
.
(3.27)
Это условие решает
три задачи:
-
Задача
проверочного расчета. -
Задача
определения допускаемой величины для
внешней нагрузки. -
Задача
проектировочного расчета.
Задача
проверочного
расчета
предполагает, что нагрузка и геометрические
параметры конструкции известны.
Вычисляются напряжения в конструкции
и максимальные из них сравниваются с
допускаемыми. Максимальные нормальные
напряжения в конструкции не
должны превышать допускаемых напряжений.
Вторая
задача
предполагает, что геометрические
параметры конструкции известны, известна
также величина допускаемого напряжения.
Требуется найти величину допускаемых
нагрузок, которые не привели бы к потере
конструкцией прочности.
Третья
задача
определяет допускаемые размеры поперечных
сечений элементов конструкции при
известной их форме, нагрузке и допускаемом
напряжении.
Условие,
ограничивающее величину деформаций,
называется условием жесткости при
осевом растяжении и сжатии:
.
(3.28)
Условие
жесткости (3.28) носит не основной, а
вспомогательный характер. Если при
решении задачи выполняется условие
прочности (3.15), то проверяют выполнение
условия жесткости. При невыполении
условия жесткости, размеры поперечного
сечения элемента конструкции рассчитывают
следующим образом:
(3.29)
Рассмотрим
несколько примеров использования
условия прочности (3.27) и условия жесткости
(3.28) при расчете стержней при осевом
растяжении и сжатии.
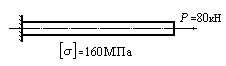
Пример
3.4. Определить
величину внешней силы, приложенной к
стержню, изображенному на рис. 3.17.
Рис.3.17
Решение:
1.
Выразим усилие в стержне через силу
:
.
2.
Определяем величину допускаемой внешней
силы
из условия прочности
50кН.
Пример
3.5.
Найти площадь поперечного сечения
стержня, изображенного на рис 3.18.
Рис.3.18
Решение:
1.
Выразим усилие в стержне через величину
внешней силы
:
80кН.
2.
Определяем площадь поперечного сечения
:
5см2.
Пример
3.6.
Определить площадь поперечного сечения
для приведенного на рис.3.19 стержня из
условия жесткости.
Рис.3.19
Решение:
-
Выразим
усилие в стержне через внешнюю силу
:
20кН.
-
Найдем
площадь поперечного сечения
м2
=
10 см2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Работа деформации
- Трансформационная работа Чем выше прочность материала, тем больше внутренняя сила взаимодействия частиц. Таким образом, сопротивление разрыву, которое называют единицей объема материала, может служить характеристикой его прочности. В этом смысле прочность на растяжение не является радикальной
характеристикой прочностных свойств материала. При разрыве связи на всю площадь поперечного сечения, а разрывные изменения при любой постоянной деформации-только локальная корреляция.
На их уничтожение тратится специфическая задача внутренних сил
Людмила Фирмаль
взаимодействия.: Рис 1.8. КОМНАТА. Два. Но Здесь коэффициент ’ > ’ 2 является результатом статического действия увеличения нагрузки/0+P В момент его приложения от 0 до Р (среднее -)•в момент разрыва упругая составляющая деформации мгновенно исчезает. При упругой деформации работа силы определяется площадью
треугольника OAV (см. рисунок). 1.4). Полная работа, затраченная на деформацию образца и его разрушение, ^^м а КС’(1-б) Где t] — коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой OA и прямой OA, L4L», и квадратов прямоугольников со сторонами 0 max и D. В этом случае необходимо вычесть работу, которая определяется площадью работы,
- затраченной на деформацию и разрушение объекта.— 12разца является одним из важнейших свойств материала, определяющим степень его хрупкости. Деформация сжатия протекает подобно растяжению: сначала наблюдается упругая деформация, а затем пластическая деформация выходит за пределы упругого предела. Показана природа деформации и разрушения при сжатии Q5 Поперек волокон Рис 1.8: а-для пластических материалов; Б-для хрупких; в-для древесины вдоль волокон; В-для древесины поперек волокон. Испытания на сжатие не очень удобны для установления
механических свойств пластических материалов из-за сложности фиксации момента разрушения. Согласно ГОСТ 25503-80 2000 испытания на сжатие определяют только механические свойства хрупких материалов. В этом случае определяется только прочность на растяжение. Для риса. А-чугун, Б-дерево: 1.9 показана диаграмма напряжений сжатия. Во время испытания на сжатие форма образца и его размеры могут отличаться(табл. 1.7). Когда материал подвергается постоянной нагрузке при постоянном напряжении, упругая деформация, возникающая почти одновременно с увеличением нагрузки, со временем удаляется
дополнительная упругая деформация, а когда деформация упругой деформации
Людмила Фирмаль
становится равной нулю, Т А Б Л Е1.7 увеличивается одновременно. Стандартные размеры образцов для испытаний на сжатие Образец, см размер материала Чугун: куб цилиндр Camia: натуральный (куб) цемент бетонный кирпич (распиленный пополам) 2×2 x 2 или 3×3 X 3d=h=2 7×7 x 7 7×7 x 7 20×20×20 или 30×30 12×12×6 При увеличении нагрузки потеря напряжения исчезает одновременно, дополнительная-замедляется. Дополнительная упругая деформация из-за постоянного напряжения, которое не исчезает сразу после разгрузки, называется упругим последствием (см. Главу 12).
Смотрите также:
- Учебник по сопротивлению материалов: сопромату
Работа затрачиваемая на деформацию, формула
Работа, затрачиваемая на деформацию упругих тел, также накапливается в этих телах в виде потенциальной энергии.
Если
| Wп | потенциальная энергия, работа, затраченная на упругую деформацию, | Джоуль |
|---|---|---|
| D | Жесткость тела или пружины, | Ньютон / метр |
| s | величина деформации, | метр |
то
[
W_{п} = frac{Ds^2}{2}
]
Работа затрачиваемая на деформацию |
стр. 466 |
|---|