В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.
Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.
Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.
Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).
Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).
Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)
Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.
И далее мы с вами выведем работы в этих основных процессах.
1. Изохорный процесс
Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
2. Изотермический процесс
Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.
3. Изобарный процесс
Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.
4. Адиабатный процесс
Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.
5. Политропный процесс (p∙Vⁿ = const )
Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.
n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const
Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).
Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
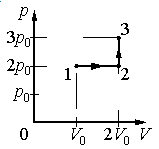
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.9k
Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ “изыскивает внутренние резервы”. Кроме того, работа численно равна площади под кривой процесса, а работа за цикл – площади внутри цикла.
Задача 1.
На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и
– адиабаты. Вычислите КПД
данной тепловой машины и максимально возможный КПД
.
К задаче 1
КПД тепловой машины можно вычислить как
Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:
Работа численно равна площади, ограниченной циклом. Поэтому
Участк и
по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» – то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и
,
и
, это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать
. Но, так как
, а
,то изменение внутренней энергии будет равно
Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке
:
Ответ: ,
.
Задача 2.
Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу
кДж. Найдите КПД данной тепловой машины.
К задаче 2
Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.
Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД
Ответ: .
Задача 3.
КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе
кДж. Найдите разность
максимальной и минимальной температур газа в цикле.
К задаче 3
Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна
, а под кривой 3-1 –
. В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.
Ответ: 500 K.
Закон Бойля – Мариотта – один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Закон является частным случаем уравнения состояния идеального газа.
Закон Бойля – Мариотта гласит: при постоянной температуре и массе идеального газа произведение его давления и объема постоянно. В математической форме это утверждение записывается следующим образом:
(pV = const),
где (p) – давление газа; (V) – объем газа.
Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молекулярная масса газа, тем больше это отличие.
Закон Бойля – Мариотта, закон Шарля и закон Гей-Люссака, дополненные законом Авогадро, образуют уравнение состояния идеального газа.
Закон Шарля – объем газа при постоянном давлении прямо пропорционален его абсолютной температуре. Эта зависимость была впервые выведена Жаком Шарлем в 1787 г. Его иногда называют законом Гей-Люссака, поскольку Жозеф Гей-Люссак заново вывел его и уточнил в 1802 г.
Закон Гей-Люссака – закон пропорциональной зависимости объема газа от абсолютной температуры при постоянном давлении, названный в честь французского физика и химика Жозефа Луи Гей-Люссака, впервые опубликовавшего его в 1802 году (в англоязычной литературе закон Гей-Люссака обычно называют законом Шарля и наоборот). Кроме того, законом Гей-Люссака называют также химический закон объемных отношений.
Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах t этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t он изображается прямой, называемой изохорой. Процесс, протекающий при постоянной температуре, называется изотермическим. На диаграмме р, V этот процесс изображается прямой, называемой изотермой.
Работа – это один из способов изменения внутренней энергии, легко рассчитать работу газа в изобарном процессе. На данном этапе необходимо подчеркнуть, что сила давления газа на всем пути не меняется и, по третьему закону Ньютона, (|F_2| = |F_1|), знак работы находим из формулы (A = Fs cosα.) Если (α = 0^{circ}), то (A > 0), если (α = 180^{circ}), то (A < 0). На графике зависимости (р(V)) работа численно равна площади под графиком.
Пусть газ расширяется или сжимается изотермически. Например, газ сжимается под поршнем, давление изменяется, и в любой момент времени (p=frac vVRT.)
При бесконечно малом перемещении поршня на (dl) мы получим бесконечно малое изменение объема (dV), а давление р можно считать постоянным. По аналогии с нахождением механической работы переменной силы, составим простейшее дифференциальное соотношение (dA = pdV), тогда (A=intlimits_{V_1}^{V_2}pdV,) и, зная зависимость (p (V)), запишем (A=intlimits_{V_1}^{V_2}vRTfrac {dV}V.) Это табличный интеграл типа (intlimits_{x_1}^{x_2}frac{dx}x). Работа газа в этом случае отрицательна, т. к. (alpha = 180^circ):
(A=vRTlnfrac{V_2}{V_1}<0,)
т. к. (V_2 < V_1). Полученную формулу можно переписать, используя соотношение
(frac {V_2}{V_1}=frac{p_1}{p_2}.)
-
Чем можно пренебречь в случае идеального газа?
-
В цилиндре под поршнем изобарически охлаждают (10) л газа от (127^{circ}C) до (7^{circ}C). Объем охлажденного газа равен
-
Изобарно увеличили температуру (2) молей идеального газа с (20) до (120^{circ}C). Количество теплоты, которое было при этом сообщено, равно ((R = 8,31) Дж/(моль · К)
-
Чтобы изобарно увеличить объем двух молей идеального одноатомного газа в (5) раз, ему необходимо передать количество теплоты, равное
-
При постоянном давлении (10^5) Па объем воздуха, находящегося в помещении, увеличился на (200) дм(^3). При этом газ совершил работу, равную
-
В закрытом сосуде при температуре (150) К находится (6) моль одноатомного идеального газа. Если средняя квадратичная скорость его молекул возросла в (1,5) раза, то газу передано количество теплоты, равное ((R=8,31)Дж/(моль · К))
-
Работа идеального газа равна нулю в процессе
-
Изобарному процессу соответствуют участки
-
На графиках представлены процессы
-
Если в теплоизолированном сосуде газ сжимается, то температура газа
-
Чтобы при постоянном давлении объем газа увеличился в (2) раза, его температуру нужно
-
В закрытом сосуде при температуре (27^{circ}C) находится (3) моль одноатомного идеального газа. Если средняя квадратичная скорость его молекул возросла в (1,5) раза, то газу передано количество теплоты, равное
-
Газ в количестве 1 кмоль при давлении 1 МПа и температуре 127°C занимает объем ( R = 8,31 Дж/(моль · К)
-
Газ совершает работу при переходе из состояния (1) в состояние (3). Если (p_1=0,1) МПа, (V_1=1) л, (T_2 =2T_1), (T_3 =2T_2), то работа газа равна
-
При постоянном давлении (2cdot10^5) Па объем воздуха, находящегося в помещении, увеличился на (2) м(^3). При этом газ совершил работу, равную
-
Если концентрация газа увеличится в (3) раза, а скорость уменьшится в (3) раза, то его давление
-
Идеальный газ сначала нагревался при постоянном объеме, потом его объем увеличивался при постоянном давлении, затем при постоянной температуре давление газа уменьшалось до первоначального. Эти изменения представлены
-
На увеличение внутренней энергии газа пошло (10%) подведенного к нему тепла. Если его внутренняя энергия возросла на (4) кДж, то газ совершил работу, равную
-
Газ при температуре (273^{circ}C) занимает объем в (4) м(^3). Какой объем занимает этот газ при температуре (546^{circ}C) и при прежнем давлении?
-
Что приводит к изменению внутренней энергии идеального газа при данной массе?
-
На каком из ниже представленных рисунков изображена изобара идеального газа?
-
Определите работу по ниже представленному рисунку, если газ перешел из состояния (1) в состояние (3) в процессе (1-2-3.)
-
На увеличение внутренней энергии газа пошло (30%) подведенного к нему тепла. Какую работу совершил газ, если его внутренняя энергия возросла на (3) кДж?
-
За счет какого процесса совершается работа при адиабатном расширении идеального газа?
-
Определите количество теплоты, необходимое для изобарного увеличения объема пяти молей идеального одноатомного газа в (4) раза.
-
Если при температуре (27^{circ}C) давление газа в закрытом сосуде равнялось (90) кПа, то какое давление будет у газа при температуре (t=-23^{circ}C)?
-
Идеальный газ имеет температуру (T_0 = 150) К и давление (P_0= 0,!8) кПа. Не меняя массу и объем газа, температуру уменьшили на (25%). Как при этом изменилось давление газа?
-
Физическую величину, определяемую выражением (frac{mRT}{MV}), можно измерить в таких единицах измерения, как
-
Во сколько раз увеличится давление газа в баллоне, если его нагреть от (-330^{circ}C) до (+330^{circ}C)?
-
Когда объем газа уменьшили на (50) мл, его давление возросло в (3) раза. Каков был его первоначальный объем?
-
Газ занимает объем в (2) м(^3) при нормальных условиях. Его изотермически сжали до давления в (9,8) МПа. Какой объем теперь занимает газ?
-
На графике представлена зависимость давления от температуры идеального одноатомного газа. Выберите правильные утверждения.
-
(5) молей идеального одноатомного газа, который находился при температуре (+27^{circ}C), не меняя давление, нагрели. Абсолютная температура газа при этом увеличилась в (4) раза. Какое количество теплоты было сообщено этому газу? (Универсальная газовая постоянная – (8,!31 frac{Дж}{мольcdot К})).
-
Не меняя температуры, объем газа уменьшили в (6) раз. Давление газа (P_2) при этом по отношению к первоначальному давлению (P_1)
-
Уравнение Менделеева – Клапейрона может быть записано в виде
-
Найдите начальную температуру газа, если при уменьшении его объема на (20%) его давление возросло на (40%), а температура увеличилась на (36) К.
-
В закрытом баллоне находится газ под давлением (10) кПа. Если температура газа повысится в (2) раза, чему станет равным давление газа?
-
Как изменится температура газа, если, не меняя давления, его объем увеличить в полтора раза?
Как найти работу газа
Работа газа осуществляется при изменении его объема. Именно при изменении объема газа приходят в движение узлы тепловых двигателей, будь то двигатель внутреннего сгорания или пуля в стволе ружья. При различных процессах работа газа вычисляется по-разному.

Вам понадобится
- – манометр;
- – термометр.
Инструкция
Если работа газа осуществляется при изобарном процессе (при постоянном давлении), то для того чтобы найти работу газа с помощью манометра, измерьте давление газа. После этого замерьте его объем перед выполнением работы и после. Найдите изменение объема газа, отняв от конечного значения начальное. После этого найдите произведение давления газа на изменение его объема. Это и будет работа газа при постоянном давлении A=p•ΔV.
Для идеального газа вычислить работу при постоянном давлении можно, применив уравнение Клапейрона-Менделеева. Найдите работу газа, умножив его массу на число 8,31 (универсальную газовую постоянную) и изменение температуры при выполнении работы. Результат поделите на молярную массу газа A=m•R•ΔT/M. При расчетах учитывайте то, что если работа выполняется газом (он расширяется), то она положительна. Если же работа выполняется над газом (его сжимают сторонние силы), то работа отрицательна.
Если работа выполняет при изотермическом расширении (когда температура постоянна), узнайте изменение объема газа и значение его температуры. Для того чтобы найти работу газа, умножьте его массу на число 8,31 (универсальную газовую постоянную) и температуру при выполнении работы. Результат поделите на молярную массу газа. Получившееся число умножьте на логарифм натуральный из отношения конечного и начального объемов газа A=m•R•T•ln(V2/V1)/M.
В общем случае, чтобы найти работу газа возьмите интеграл из функции давления по объему. Границы интеграла – от начального до конечного объема ∫pdV. Если есть график газового процесса в координатах (V,p), как правило, он представляет собой прямую линию, найдите площадь трапеции ограниченной по бокам линиями перпендикулярными оси Vв точках V1 и V2, снизу осью V, а сверху графиком функции. В более сложных случаях ищется площадь криволинейной трапеции.
Полезный совет
Если объем газа не изменяется, работа им не выполняется.
Источники:
- как изменяется объем газа
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

















