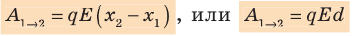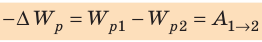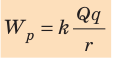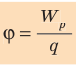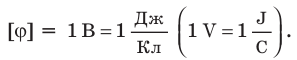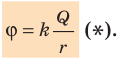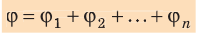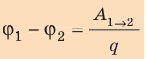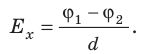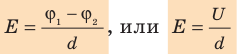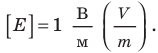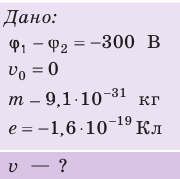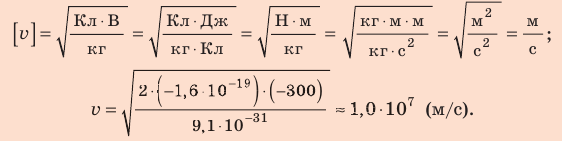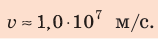Содержание:
Работа по перемещению заряда в электростатическом поле:
В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.
Работа по перемещению заряда в однородном электростатическом поле
Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.
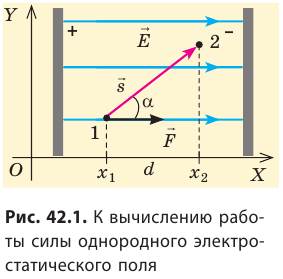
Пусть в однородном электростатическом поле напряженностью
Вычислим работу А, которую совершает сила 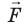
Поле однородное, поэтому сила 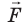
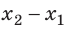
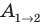
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.
Обратите внимание! Формула 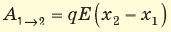
Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.
Потенциальная энергия заряженного тела в поле, созданном точечным зарядом
Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом 
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна (


Что называют потенциалом электростатического поля
Потенциал 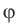

Единица потенциала в Си — вольт:
Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:
Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.
Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 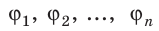
Как определяют разность потенциалов
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: 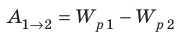
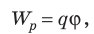
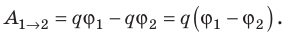
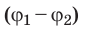
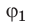
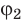
Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:
Единица разности потенциалов в Си — вольт: 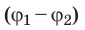
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 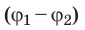
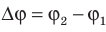
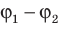
Как связаны напряженность однородного электростатического поля и разность потенциалов
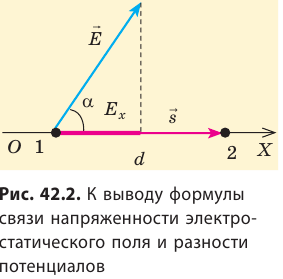
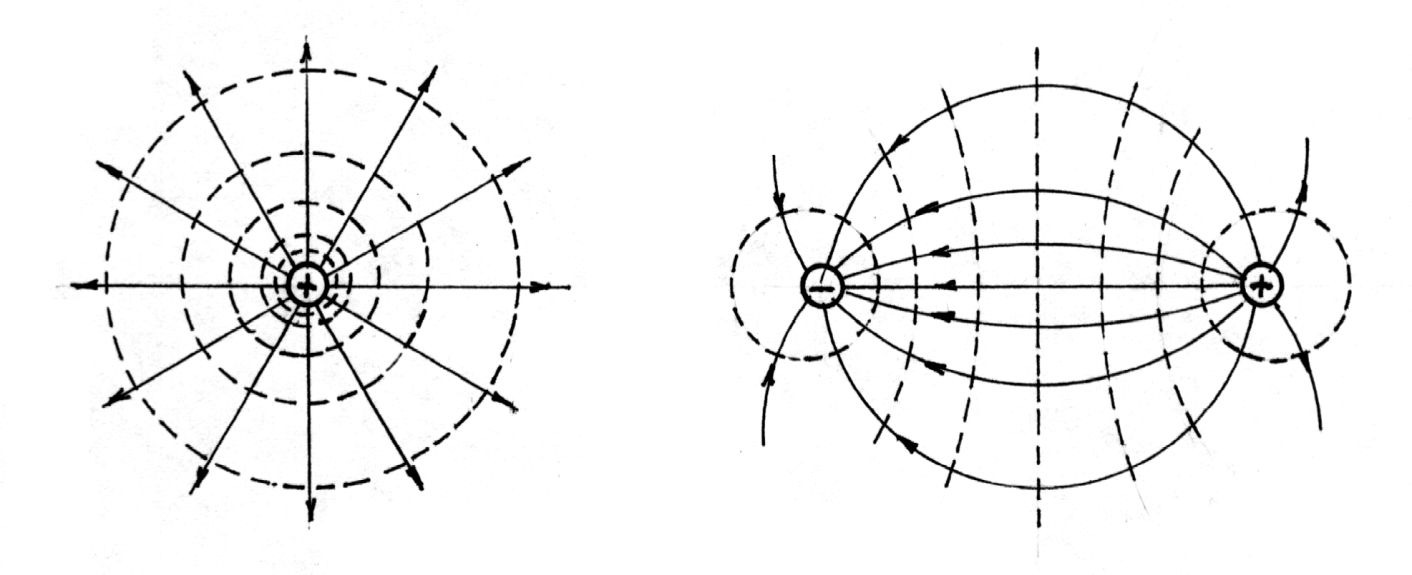
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: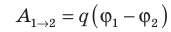
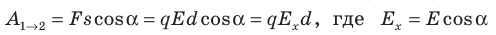
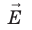
Приравняв оба выражения для работы, получим: 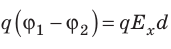
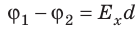
Если заряд перемещается в направлении напряженности электрического поля (
Из последней формулы следует единица напряженности в Си — вольт на метр:
Какие поверхности называют эквипотенциальными
Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.
Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.
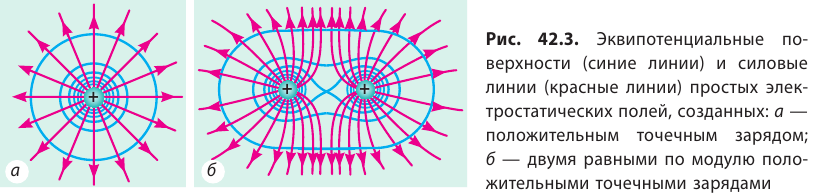
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 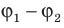
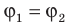
Работу электростатического поля также можно представить через силу 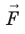
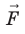
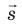
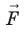
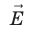
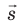
Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.
- Заказать решение задач по физике
Пример решения задачи
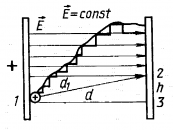
Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 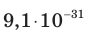
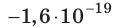
Заряд электрона — отрицательный, его начальная скорость 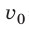
Решение:
Поиск математической модели, решение Согласно теореме о кинетической энергии:
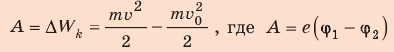
Таким образом, 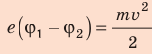
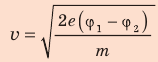
Проверим единицу, найдем значение искомой величины:
Ответ:
Выводы:
- Закон Ома для однородного участка электрической цепи
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
- Сила и закон Ампера
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
Чем на самом деле является напряжение? Это способ описания и измерения напряженности электрического поля. Само по себе напряжение не может существовать без электронного поля вокруг положительных и отрицательных зарядов. Так же, как магнитное поле окружает Северный и Южный полюса.
По современным понятиям, электроны не оказывают взаимного влияния. Электрическое поле – это нечто, что исходит от одного заряда и его присутствие может ощущаться другим.
О понятии напряженности можно сказать то же самое! Просто это помогает нам представить, как электрическое поле может выглядеть. Честно говоря, оно не обладает ни формой, ни размером, ничем подобным. Но поле функционирует с определённой силой на электроны.
Силы и их действие на заряженную частицу
На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.
Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.
Свойства силовых линий:
- путешествуют с севера на юг;
- не имеют взаимных пересечений.
Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.
Силовые линии демонстрируют:
- направления электрических полей;
- напряженность. Чем ближе линии, тем больше сила поля и наоборот.
Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.
Что такое потенциал?
Потенциалом называется энергия, которая затрачивается на передвижение заряженной частицы из первой точки, имеющей нулевой потенциал во вторую точку.
Разность потенциалов меж пунктами А и Б – это работа, производимая силами для передвижения некоего положительного электрона по произвольной траектории из А в Б.
Чем больший потенциал у электрона, чем больше плотность потока на единицу площади. Такое явление подобно гравитации. Чем больше масса, тем больше потенциал, тем интенсивнее и плотнее гравитационное поле на единицу площади.
Небольшой заряд с низким потенциалом, с прореженной плотностью потока показан на следующем рисунке.
А ниже показан заряд с большим потенциалом и плотностью потока.
Например: во время грозы электроны истощаются в одной точке и собираются в другой, образуя электрическое поле. Когда сила станет достаточной, чтобы сломать диэлектрическую проницаемость, получается удар молнии (состоящий из электронов). При выравнивании разности потенциалов электрическое поле разрушается.
Электростатическое поле
Это разновидность электрического поля, неизменного повремени, образуемого зарядами, которые не двигаются. Работа передвижения электрона определяется соотношениями,
где r1 и r2 – расстояния заряда q до начальной и конечной точки траектории движения. По полученной формуле видно, что работа при перемещении заряда из точки в точку не зависит от траектории, а зависит лишь от начала и конца перемещения.
На всякий электрон действует сила, и поэтому при перемещении электрона в поле выполняется определенная работа.
В электростатическом поле работа зависит лишь от конечных пунктов следования, а не от траектории. Поэтому, когда движение происходит по замкнутому контуру, заряд приходит в исходное положение, и величина работы становится равной нулю. Это происходит потому, что падение потенциала нулевое (поскольку электрон возвращается в ту же самую точку). Так как разность потенциалов нулевая, чистая работа будет также нулевой, ведь потенциал падения равен работе, деленной на значение заряда, выраженное в кулонах.
Об однородном электрическом поле
Однородным называется электрическое поле меж двух противоположно заряженных плоских металлических пластин, где линии напряженности параллельны между собой.
Почему сила действия на заряд в таком поле всегда одинаковая? Благодаря симметрии. Когда система симметрична и есть только одна вариация измерения, всякая зависимость исчезает. Есть много других фундаментальных причин для ответа, но фактор симметрии – самый простой.
Работа по передвижению положительного заряда
Электрическое поле – это поток электронов от «+» до «-», приводящий к высокой напряженности области.
Поток – это количество линий электрического поля, проходящих через него. В каком направлении будут положительные электроны двигаться? Ответ: по направлению электрического поля от положительного (высокого потенциала) к отрицательному (низкому потенциалу). Поэтому положительно заряженная частица будет двигаться именно в этом направлении.
Интенсивность поля во всякой точке определяется как сила, воздействующая на положительный заряд, помещенный в эту точку.
Работа заключается в переносе электронных частиц по проводнику. По закону Ома, можно определить работу разными вариациями формул, чтобы провести расчет.
Из закона сохранения энергии следует, что работа – это изменение энергии на отдельном отрезке цепи. Перемещение положительного заряда против электрического поля требует совершения работы и в результате получается выигрыш в потенциальной энергии.
Заключение
Из школьной программы мы помним, что электрическое поле образуется вокруг заряженных частиц. На любой заряд в электрическом поле воздействует сила, и вследствие этого при движении заряда выполняется некоторая работа. Большим зарядом создается больший потенциал, который производит более интенсивное или сильное электрическое поле. Это означает, что возникает больший поток и плотность на единицу площади.
Важный момент заключается в том, что должна быть выполнена определенной силой работа по перемещению заряда от высокого потенциала к низкому. Тем самым уменьшается разница заряда между полюсами. Перемещение электронов от токи до точки требует энергии.
Загляните на карту сайта Электронщик, буду рад если вы найдете на моем сайте еще что-нибудь полезное. Делитесь информацией в соцсетях, ставьте лайки, если вам понравилось – это поможет развитию канала
Рассмотрим однородное электрическое поле. Оно образуется между заряженными плоскостями, если они параллельны и бесконечно большие. Практически можно считать однородным электрическое поле между конечными параллельными заряженными плоскостями, если размеры их значительно больше, чем расстояние между ними.
При перемещении пробного заряда в таком электростатическом поле электрические силы осуществляют работу.
Определение работы по перемещению заряда
Произвольное электрическое поле напряженностью ЕЕ действует на пробный заряд q0q_0 с силой
F=q0E.F = q_0E.
Смещение этого заряда вдоль определенной траектории сопровождается выполнением работы, элемент которой
dA=F→d=Fdlcosα=q0Edlcosα,dA=overrightarrow{F}d=Fdlcos alpha ={{q}_{0}}Edlcos alpha,
где dldl –вектор элементарного перемещения заряда q0q_0, αα – угол между векторами dldl и dFdF.
Пусть заряд q0q_0 перемещается из точки 1 в точку 2 в поле, созданном заданным точечным зарядом qq (рис. 1).
Рис. 1.
Определим работу такого перемещения А12А_{12}, подставив в формулу для элементарной работы выражение напряженности поля точечного заряда Также учтем, что dlcosα=drdlcosα = dr (рис. 1). Тогда А12А_{12} выразим так:
A12=qq04πε0∫r1r2drr2=qq04πε0[1r1−1r2]{{A}_{12}}=frac{q{{q}_{0}}}{4pi {{varepsilon }_{0}}}intlimits_{{{r}_{1}}}^{{{r}_{2}}}{frac{dr}{{{r}^{2}}}}=frac{q{{q}_{0}}}{4pi {{varepsilon }_{0}}}left[ frac{1}{{{r}_{1}}}-frac{1}{{{r}_{2}}} right]
Проанализируем это выражение по знаку А12А_{12}. Если знаки зарядов qq и q0q_0 одинаковые, то работа А12А_{12} положительная при условии удаления зарядов (r2>r1r_2 > r_1) и отрицательная при их приближении.
Если qq и q0q_0 отличаются знаками, то работа А12А_{12}, наоборот, положительная при приближении зарядов и отрицательная при их удаления, то есть, положительной считают работу, выполненную самым полем.
Определение свойств электростатического поля
По выражению работы $А_{12} видно, что работа не зависит от формы пути перемещения заряда между точками 1-2, а определяется лишь размещением начальной и конечной точек. Такие силовые поля называют потенциальными (консервативными).
Итак, электростатическое поле точечного заряда является потенциальным. Если перемещение происходит вдоль замкнутого контура, то работа равна нулю.
Математическое условие потенциальности поля получают, проинтегрировав вдоль замкнутого контура выражение dA:
A=∮Lq0Edlcosα=q0∮LE→dl→=0A=ointlimits_{L}{{{q}_{0}}Edlcos alpha }={{q}_{0}}ointlimits_{L}{overrightarrow{E}doverrightarrow{l}}=0
Поскольку q0q_0 не равно 00, то циркуляция вектора EE
∮LE→dl→=0ointlimits_{L}{overrightarrow{E}doverrightarrow{l}}=0
Данное уравнение отражает то, что силовые линии электростатического поля незамкнуты. В условиях перемещения пробного точечного заряда вдоль замкнутого контура в таких полях на определенных участках пути работа будет положительной, на других – отрицательной, а полная работа равна нулю.
Тест по теме «Работа перемещения заряда»
Работа по перемещению заряда в электрическом поле. Потенциал
Теперь
известно, что на заряд, помещенный в
электрическое поле, действует сила.
Следовательно, перемещение заряда в
электрическом поле будет сопровождаться
работой
dA
= Fdl
dA
> 0 в случае, если работа совершается
силами поля;
dA
< 0 в случае, если работа совершается
внешними силами против сил поля.
Рассмотрим
перемещение пробного заряда Q0
из точки 1 в точку 2 в поле сил, создаваемых
зарядом Q.
Поле
сил – центральное (рис. 73). Работа на
пути dl
будет равна
Отсюда
работа по перемещению заряда из точки
1 в точку 2
Если
работа совершается внешними силами, то
Электростатическое
поле является потенциальным. Это значит,
что работа по перемещению заряда не
зависит от пути, по которому перемещается
заряд, а зависит только от начального
и конечного положения заряда.
Тело,
находящееся в потенциальном поле сил,
обладает потенциальной энергией, за
счет которой совершается работа силами
поля. Следовательно, полученное выражение
для работы можно представить как разность
потенциальных энергий заряда Q0
в поле сил, созданном зарядом Q
Таким
образом, потенциальная энергия в каждой
точке поля зависит от величины пробного
заряда Q0.
Но если взять отношение W/Q0,
то оно будет зависеть только от точки
поля, и не будет зависеть от величины
помещенного в эту точку заряда.
Отношение
= φ называют потенциалом поля.
Потенциалом
электрического поля
называется физическая величина, равная
отношению потенциальной энергии, которую
приобретает положительный заряд Q0,
если его переместить из
в данную точку поля, к величине этого
заряда
.
Из
равенства А12
= -А21
следует другое определение.
Потенциалом
поля называется
физическая величина, численно равная
работе, которую совершают силы поля над
единичным положительным зарядом, при
удалении его из данной точки поля в
бесконечность.
Потенциал
– величина скалярная. При суперпозиции
(наложении) электрических полей
потенциал суммарного электрического
поля определяется как алгебраическая
сумма потенциалов налагаемых полей
Выражение
для работы по перемещению заряда из
точки с потенциалом φ1в
точку с потенциалом φ2
имеет вид
A12
= Q
(φ2
– φ1).
Работа
измеряется в Дж или эВ. 1эВ = 1,6 ∙10-19
Дж.
Для
наглядного изображения поля вместо
линий напряженности (силовых линий)
можно воспользоваться поверхностями
равного потенциала или эквипотенциальными
поверхностями. Эквипотенциальная
поверхность
– это такая поверхность, все точки
которой имеют одинаковый потенциал.
Если потенциал задан как функция
координат x,
y,
z,
то уравнение эквипотенциальной
поверхности имеет вид:
φ
(x,y,z)
= const.
Эквипотенциальные
линии – линии, образующиеся от пересечения
эквипотенциальной поверхности плоскостью
проводятся так, что направление нормали
к ним совпадает с направлением вектора
в той же точке (рис.74).
Эквипотенциальную
поверхность можно провести через любую
точку поля. Следовательно, таких
поверхностей может быть бесконечное
множество.
Рис.
74
Условились, однако,
проводить их таким образом, чтобы
разность потенциалов для двух соседних
эквипотенциальных поверхностей была
всюду одна и та же. Тогда по их густоте
можно судить о величине напряженности
поля.
Соседние файлы в папке физика
- #
- #
- #
- #
- #
- #
- #
- #
Основные ссылки
CSS adjustments for Marinelli theme

Вы здесь
Главная » Работа электростатического поля по перемещению…
Работа электростатического поля по перемещению заряда
|
Работа электростатического поля по перемещению заряда. |
|
|
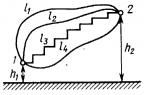
а) Однородное электростатическое поле:
|
W=qEr |
|
Т.к. если вектор перемещения перпендикулярен вектору силы (напряженности поля), работа поля равна нулю, то работа электростатического поля по перемещению заряда по любой траектории определяется разностью координат этих точек. |
|
|
Если обозначить координаты заряда в начальной и последующей точках r1 и r2, то: Т.е. работа равна разности двух эквивалентных величин, зависящих от характера взаимодействия и взаимного расположения. Но мы знаем, что работа – мера изменения энергии. Можно предположить: W=qEr – потенциальная энергия заряда в данной точке электростатического поля. Зависит от выбора начальной точки отсчета потенциальной энергии. |
|
|
Тогда: |
|
|
Т. е. работа при перемещении заряда между двумя точками в электростатическом поле – не зависит от формы траектории, а зависит от положения этих точек. – равна убыли потенциальной энергии заряда в этом поле; – работа по замкнутой траектории равна нулю. |
|
|
Электростатическое поле, как и гравитационное, потенциальное: А = – mg(h2— h1) = –ΔW |
|
|
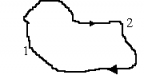
б) Произвольное электростатическое поле. При перемещении заряда в произвольном поле из точки 1 в точку 2 работа должна быть равна по величине и противоположна по знаку работе в направлении от точки 2 к точке 1. В противном случае нарушается закон сохранения энергии: Пусть А12 < A21. Тогда внешняя сила может перемещать заряд по пути 12, а силы поля – по пути 21. Мы будем получать выигрыш в работе, т.е. получим вечный двигатель, что невозможно. |
|