Работа постоянной силы как найти - Сайт, где вы сможете решить свои вопросы

Рис.
2

Механическая
работа совершается, если тело (м.т.) под
действием силы перемещается. Величина
работы постоянной силы ()
равна произведению ее составляющей F_
на направление перемещения и величины
этого перемещения (рис. 3.18):

А=
F_

=S
, (1)

где
F_
= F cos a,.

В
векторном виде работа равна скалярному
произведению вектора силы и вектора
перемещения

,
(2)

где

Согласно
(2) перемещение необязательно вызывается
действием силы, входящей в эту формулу.
Особенно это проявляется при нахождении
работы сил сопротивления и трения,
которые никак не способствуют перемещению
тела в заданном направлении при

0, F_сопр

0, F_тр

0.

Следовательно,
работа силы совершается независимо от
того, под действием каких причин тело
совершает перемещение. Работа, как
показывает практика, может быть
положительной, отрицательной и равной
нулю. Для выяснения этого воспользуемся
формулой работы А = F Ds
cosa.

1.
Работа силы положительна (А >
0), если угол 
между векторами силы и перемещения
острый: cos a
>
0 (рис. 3, а).

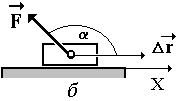
Рис. 3

2.
Работа силы отрицательна (А < 0), если
угол 
тупой:
cos 
0 (рис. 3, б). 3. Работа силы равна нулю (А
= 0).

При
этом возможны 3 случая: а) F = 0, если на
тело не действуют силы, но оно движется
равномерно и прямолинейно, б) Dr
= 0, тело не перемещается, несмотря на
действие силы (F ¹
0). Пусть на тело действуют какие-то
другие силы; в) сила действует
перпендикулярно к перемещению: cos a
= 0, т. е. a
= p/2
(рис. 3, в). Например, сила Кориолиса,
сила Лоренца
всегда перпендикулярны направлению
перемещения.

В СИ
работа измеряется в джоулях
(Дж).

1.3. Работа переменой силы

Рис. 4

Для нахождения
полной работы на конечном участке пути,
когда на движущее тело действует
переменная сила, необходимо весь путь
разбить на малые участки пути (перемещения)
и найти на каждом из них элементарную
работу.

Любые
элементарные перемещения (малые
участки пути s_i)
можно считать прямолинейными, в пределах
их действующая сила остается постоянной,
т. е.

F_i=
const.
На элементарном участке пути Ds_iсовершается
элементарная работа: А_i=
F s_icos
_i.

Работа на конечном
участке пути

Для
нахождения полной работы на всём участке
пути перейдем к пределу, когда
.
Тогда

(3)

или
при бесконечно малом перемещении
м. т. под действием силы совершает
бесконечно малую работу (рис. 4,ds=dl):

.
(4)

Поскольку
работа не является функцией состояния
системы, то она не может быть представлена
в виде полного дифференциала, поэтому,
вместo dA, будем использовать символ
dА.
Полная работа на участке 1 – 2

.
(5)

Если
на тело одновременно действуют несколько
сил:
,
то полная работа равна алгебраической
сумме работ, совершаемых каждой силой
в отдельности:

Рис.
5

A
= A₁+ A₂+…+ A_n
=.
(6)

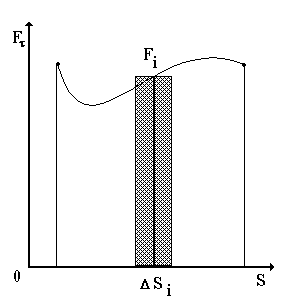
Работу
можно найти графически (рис. 5), где она
может быть представлена площадью
криволинейной трапеции. В случае
прямолинейного движения тела (в
прямоугольных декартовых координатах),
учитывая, что

где
– единичные векторы осей Х, У,Z
соответственно, формулу (6) можно
представить в виде

=
Fdxcos
+ Fdycos
+ Fdzcos
= F_xdx
+ F_ydy
+ F_zdz,

где
,
,

– углы, которые вектор силы составляет
с векторами
;

F_x=
Fcos;
F_y
= Fcos;
F_z
= F
cos
– проекции

на оси координат.

Источник

Работа, формула

Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу.

Работа W есть произведение силы F на перемещение s.

[
W = F cdot s
]

Работа — величина скалярная.

Единица СИ работы

[ [W] = [F][s] = text{Ньютон} cdot text{метр} ]
[ [W] = text{Джоуль (дж)} = Вт cdot с = кг cdot frac{метр^2}{сек^2} ]

Работа постоянной силы, формула

Если сила F постоянна во времени и ее направление совпадает с направлением перемещения тела,
то работа W находится по формуле.

[
W = F cdot s
]

Здесь:
W — совершенная работа (Джоуль),
F — постоянная сила, совпадающая по направлению с перемещением (Ньютон),
s — перемещение тела (метр)

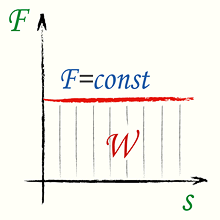Вычислить, найти работу постоянной силы по формуле (4)

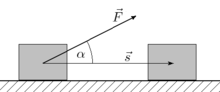
Работа постоянной силы, направленной под углом к перемещению, формула

Если сила и перемещение составляют между собой угол α < 90º, то перемещение следует умножать на составляющую силы в направлении перемещения (или силу умножать на составляющую перемещения в направлении действия силы).

В векторной форме

[
W = vector{F} times vector{s}
]

[
W = Fscos(α)
]

Здесь:
α — угол между вектором силы и вектором перемещения, º

Работа постоянной силы, направленной под углом к перемещению, формула

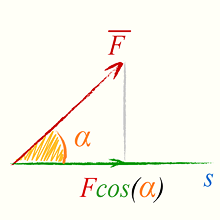Вычислить, найти работу постоянной силы направленной под углом к перемещению по формуле (4)

Работа переменной силы, направленной под углом к перемещению, формула

Если сила не постоянна по величине и является функцией перемещения F = F(s), и направлена под углом α к перемещению, то работа есть интеграл от силы по перемещению.

[ W = int_{s_1}^{s_2} vector{F} dvector{s} ]

Работа переменной силы, направленной под углом к перемещению, формула

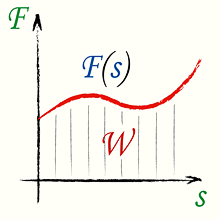Площадь под кривой на графике зависимости F от s равна работе, произведенной данной силой

Работа	стр. 462

Источник

У этого термина существуют и другие значения, см. Работа.

Работа

Размерность	L²MT⁻²
Единицы измерения
СИ	Дж
СГС	эрг
Примечания
скалярная величина

Механическая работа
Ключевые статьи
Работа в физике Механическая работа Закон сохранения энергии Термодинамическая работа Первое начало термодинамики
Размерность Джоуль Эрг
См. также: Портал:Физика

Механи́ческая рабо́та — физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)^[1].

При постоянной силе и прямолинейном движении материальной точки, работа рассчитывается как произведение величины силы на перемещение и на косинус угла между векторами перемещения и силы: . В более сложных случаях (непостоянная сила, криволинейное движение) это соотношение применимо к малому промежутку времени, а для вычисления полной работы необходимо суммирование по всем таким промежуткам.

В механике совершение работы над телом является единственной причиной изменения его энергии; в других областях физики энергия изменяется и за счёт иных факторов (например, в термодинамике — теплообмена).

Определение работы[править | править код]

По определению, «элементарная» (совершаемая за бесконечно малое время) работа — скалярное произведение действующей на материальную точку силы vec{F} на перемещение , то есть

{displaystyle delta A={vec {F}}cdot d{vec {s}}}

Использование символа δ (а не ) обусловлено тем, что дифференциал работы не обязательно полный.
Работа за конечный промежуток времени — интеграл элементарной работы:

Если имеется система материальных точек, выполняется суммирование по всем точкам. При наличии нескольких сил их работа определяется как работа равнодействующей (векторной суммы) этих сил.

Обозначения, размерность[править | править код]

Работа обычно обозначается заглавной буквой (от нем. Arbeit — работа, труд) или заглавной буквой (от англ. work — работа, труд).

Единицей измерения (размерностью) работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг. При этом

1 Дж = 1 кг·м²/с² = 1 Н·м;

1 эрг = 1 г·см²/с² = 1 дин·см;

1 эрг = 10⁻⁷ Дж.

Вычисление работы[править | править код]

Случай одной материальной точки[править | править код]

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

$A=F_{s}s=Fs {mathrm {cos}}(F,s)={vec F}cdot {vec s}$

Здесь «» обозначает скалярное произведение, {vec s} — вектор перемещения.

Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа этой силы равна нулю.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки^[2]:

{displaystyle A=int {vec {F}}cdot d{vec {s}}}

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из перемещений , если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[3], интеграл определяется^[4] следующим образом:

${displaystyle A=int limits _{{vec {r}}_{0}}^{{vec {r}}_{1}}{vec {F}}left({vec {r}}right)cdot d{vec {r}}}$

где ${vec r}_{0}$ и ${vec r}_{1}$ — радиус-векторы начального и конечного положения тела. Например, если движение происходит в плоскости , а ${displaystyle {vec {F}}=F_{x}{vec {e}}_{x}+F_{y}{vec {e}}_{y}}$ и ${displaystyle d{vec {r}}=dx{vec {e}}_{x}+dy{vec {e}}_{y}}$ ( $vec{e}_x$ , $vec{e}_y$ — орты), то последний интеграл обретёт вид ${displaystyle A=int (F_{x}+F_{y}|dy/dx|)dx}$ , где производная берётся для кривой y(x) , по которой движется точка.

Если сила vec{F} является консервативной (потенциальной), результат вычисления работы будет зависеть только от начального и финального положения точки, но не от траектории, по которой она перемещалась.

Случай системы точек или тела[править | править код]

Работа сил по перемещению системы из материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой):

${displaystyle A=sum A_{n},quad n=1,2,..,N}$

Если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл:

${displaystyle A=int delta A({vec {r}}')=iint {frac {d{vec {F}}({vec {r}}')}{dV'}}cdot d{vec {r}}({vec {r}}')dV'}$

где — работа по перемещению бесконечно малого фрагмента объёма тела , локализованного около координаты (в системе отсчёта тела), от начального до финального положения, (Н/м³) — плотность действующей силы, а интегрирование проводится по всему объёму тела.

Эти формулы могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Работа и кинетическая энергия[править | править код]

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

С использованием второго закона Ньютона, позволяющего выразить силу через ускорение как (где — масса материальной точки), а также соотношений и ${displaystyle d(v^{2})/dt=d({vec {v}}cdot {vec {v}})/dt=2{vec {a}}cdot {vec {v}}}$ , элементарная работа может быть переписана как

${displaystyle delta A=m{vec {a}}cdot {vec {v}}dt={frac {d}{dt}}left({frac {mv^{2}}{2}}right)dt}$

При интегрировании от начального до финального момента получится

${displaystyle A=Delta left({frac {mv^{2}}{2}}right)=Delta E_{k}}$

где E_k — кинетическая энергия. Для материальной точки она определяется как половина произведения массы этой точки на квадрат её скорости и выражается^[5] как ${displaystyle E_{k}=mv^{2}/2}$ . Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Работа и потенциальная энергия[править | править код]

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая $E_{p}$ , такая, что

${displaystyle {vec {F}}=-nabla E_{p}}$

Здесь nabla — оператор набла. Если все силы, действующие на частицу, консервативны, и $E_{p}$ является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, то

${displaystyle {vec {F}}cdot d{vec {s}}=-nabla E_{p}cdot d{vec {s}}=-dE_{p}Rightarrow -dE_{p}=dE_{k}Rightarrow d(E_{k}+E_{p})=0}$

Данный результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия

${displaystyle E=E_{k}+E_{p}}$

в замкнутой системе, в которой действуют консервативные силы, является постоянной во времени. Этот закон широко используется при решении задач классической механики.

Работа силы в теоретической механике[править | править код]

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, , и на неё действует сила F(s) , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F(s) проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).

Величина $F(xi _{i})triangle s_{i},triangle s_{i}=s_{i}-s_{{i-1}},i=1,2,...,i_{{tau }}$ , называется элементарной работой силы на участке $G_{i}$ и принимается за приближённое значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую $G_{i}$ . Сумма всех элементарных работ $sum _{{i=1}}^{{i_{{tau }}}}F(xi _{i})triangle s_{i}$ является интегральной суммой Римана функции F(s) .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма $sum _{{i=1}}^{{i_{{tau }}}}F(xi _{i})triangle s_{i}$ всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

${displaystyle A=lim _{|tau |rightarrow 0}sum _{i=1}^{i_{tau }}F(xi _{i})triangle s_{i}=int limits _{0}^{s}F(s)ds}$

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути s=s(t) , является непрерывно дифференцируемой функцией, то из последней формулы получится

${displaystyle A=int limits _{a}^{b}F[s(t)]s'(t)dt}$

Работа в термодинамике[править | править код]

В термодинамике работа, совершённая газом при расширении^[6], рассчитывается как интеграл давления по объёму:

${displaystyle A_{1rightarrow 2}=int limits _{V_{1}}^{V_{2}}PdV}$

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости ), в частности, к циклическим процессам.
В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула непосредственно связана с механической работой, хотя, казалось бы, относится к другому разделу физики. Сила давления газа направлена ортогонально к каждой элементарной площадке и равна произведению давления на площадь площадки.
При расширении сосуда, работа, совершаемая газом для смещения одной такой элементарной площадки, составит

Это и есть произведение давления на приращение объёма вблизи элементарной площадки. После суммирования по всем , получится результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

См. также[править | править код]

Закон сохранения энергии
Теорема о кинетической энергии системы
Механические приложения криволинейных интегралов

Примечания[править | править код]

↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введённым выше. Затем работы на всех этих перемещениях суммируется, что и даёт в результате интеграл.
↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд.
↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объёму (что часто выполняется в термодинамике, поскольку речь там часто идёт о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведёт к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература[править | править код]

История механики с древнейших времён до конца XVIII в. В 2 т. М.: Наука, 1972.
Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
Льоцци М. История физики. М.: Мир, 1970.
Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.

Источник

Консервативными силами являются силы гравитационного взаимодействия, силы упругости, электростатические силы. Силы, не удовлетворяющие условию (1), называются неконсервативными. К неконсервативным силам относят силы трения и сопротивления. Поле, в котором действуют консервативные силы, называется потенциальным.

§3. Мощность

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность: P=A/t, где t – время, в течение которого произведена работа A. В общем случае мощность рассчитывается: P=FV

Следовательно, мощность равна произведению силы на скорость движения.

Единицей измерения мощности в системе СИ является Ватт (1 вт=1 дж/сек). В технике за единицу мощности часто принимается 1 лошадиная сила, равная 736 Вт.

Работу, произведенную машиной, можно измерять произведением ее мощности на время работы: A=P·t

Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 кВт-ч = 3,6∙10⁶ Дж).

Из равенства P=FV видно, что у двигателя, имеющего данную мощность P сила F тяги будет тем больше, чем меньше скорость движения V. Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низшие передачи, позволяющие при полной мощности двигаться с меньшей скоростью и развивать большую силу тяги.

§4. Коэффициент полезного действия

Создавая механизм, важно не только обеспечить движение рабочих органов машины, удовлетворяющих заданному технологическому процессу, но необходимо чтобы машина обладала высоким коэффициентом полезного действия (КПД).

При наличии сил трения и сопротивления воздуха не вся затраченная работа А_зиспользуется в машинах. Полезная работа Ап всегда меньше затраченной, т.е. А_п<Аз, это соотношение определяет важнейшую технико-экономическую характеристику – КПД.

ή= (А_п/Аз) 100%

КПД не может быть больше 1, следовательно не может быть больше 100%.

Вопросы для самопроверки:

– Каковы две меры механического движения и соответствующие им измерители действия силы?

– Какие силы называют движущими?

– Какие силы называют силами сопротивления?

– Запишите формулы для определения работы при поступательном и вращательном движениях?

– Как определяется работа постоянной по модулю и направлению силы на прямолинейном перемещении?

– Чему равна работа силы трения скольжения, если эта сила постоянна по модулю и направлению?

– Как вычисляются работа силы тяжести и работа силы упругости?

– На каких перемещениях работа силы тяжести: а) положительна, б) отрицательна, в) равна нулю.

– В каком случае работа силы упругости положительна и в каком – отрицательна?

– Какая сила называется: а) консервативной; б) неконсервативной; в) диссипативной?

– Запишите формулы для расчета работы при поступательном движении?

– Вагон массой 1000 кг перемещают по горизонтальному пути на 5 м, коэффициент трения 0,15. Определите работу силы тяжести?

– Запишите формулы для расчета мощности при поступательном и вращательном движениях?

– Определите мощность, необходимую для подъема груза весом 0,5 кН на высоту 10 м за 1 мин?

– Чему равна работа силы, приложенной к прямолинейно движущемуся телу массой 100 кг, если скорость тела увеличилась с 5 до 25 м/с?

Источник

Содержание:

Работа и мощность силы
Работа силы
Элементарная работа
Аналитическое выражение элементарной работы силы. Работа силы на конечном перемещении
Работы сил тяжести и упругости
Работа силы, приложенная к вращающемуся телу
Мощность силы
Порядок решения задач на определение работы и мощности силы
Примеры решения задач на тему: работа и мощность силы

Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними. Мощность – отношение работы к интервалу времени, за который эта работа совершена.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Работа и мощность силы

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность N=A/t, где t – время, в течение которого произведена работа.

Работа силы

Работа силы на любом перемещении является одной из основных характеристик, которая оценивает действие силы на этом перемещении.

Работа постоянной силы (рис.9.1) на некотором прямолинейном перемещении точки приложения силы определяется по выражению:

Если угол острый, то работа – положительная, .

При работа равна:

Если угол – тупой, то работа отрицательная, .

При работа равна:

Если угол , то есть сила направлена перпендикулярно перемещению, то работа равна нулю: .

Знак работы имеет такой смысл: работа – положительная, когда сила ускоряет движение; работа – отрицательная, когда сила тормозит движение.

Выражение для вычисления работы можно представить как скалярное произведение векторов:

Работа постоянной по модулю и направлению силы при прямолинейном перемещении определяется скалярным произведением вектора силы на вектор перемещения точки ее приложения.

Элементарная работа

В общем случае, когда материальная точка движется по криволинейной траектории под действием переменной силы вводится понятие элементарной работы.

Элементарная работа силы на элементарном перемещении (рис.9.2) определяется следующим образом:

где – проекция силы на тангенциальную ось, которая направлена в сторону перемещения точки; – бесконечно малое перемещение точки.

Поскольку

то

Аналитическое выражение элементарной работы силы. Работа силы на конечном перемещении

Элементарную работу силы можно представить в виде скалярного произведения векторов и (рис.9.3):

где – вектор элементарного перемещения точки .

Выражение элементарной работы переменной силы через проекции силы на оси декартовых координат имеет вид:

где – проекции силы на координатные оси, а – проекции вектора элементарного перемещения на координатные оси.

Работа силы на любом конечном перемещении определяется интегралом:

или

Работы сил тяжести и упругости

Работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения

где – сила тяжести;

– вертикальное перемещение точки приложения силы.

Из этой формулы вытекает, что работа силы тяжести не зависит от формы траектории между начальной и конечной точками движения, а зависит только от расстояния между горизонтальными плоскостями, которые проходят через исходное и конечное положение точки.

Если начальная точка расположена выше конечной, то работа силы тяжести положительная, в противном случае – отрицательная.

Работа силы упругости равна половине произведения коэффициента жесткости пружины на разность квадратов начального и конечного удлинений (или сжатий) пружины

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, то есть когда . Это соответствует перемещению конца пружины от положения равновесия. Если , работа будет положительная. В этом случае конец пружины перемещается к положению равновесия.

Работа силы, приложенная к вращающемуся телу

Элементарная работа силы, приложенной к любой точке тела, которое вращается вокруг неподвижной оси, например , равна произведению момента силы относительно оси вращения на дифференциал угла поворота:

Для того, чтобы определить работу силы, которая действует на тело при его повороте на угол от к , необходимо проинтегрировать уравнение в этих пределах, выразив момент силы как функцию угла поворота:

В отдельном случае, когда момент силы является постоянным, то есть , работа равна произведению момента силы на угол поворота тела:

Единицей измерения работы в системе СИ является Джоуль (1), а в системе

Мощность силы

Мощностью называется величина, определяющая работу, которую выполняет сила за единицу времени:

Это выражение справедливо, если работа выполняется равномерно.

В общем случае

Поскольку , то:

Таким образом, мощность равна произведению величины касательной составляющей силы на скорость движения.

При вращательном движении тела:

Тогда

Мощность выражается произведением вращательного момента на угловую скорость.

Единицей измерения мощности в системе СИ является Ватт в системе

Порядок решения задач на определение работы и мощности силы

При определении работы необходимо различать следующие случаи:

Прямолинейное движение под действием постоянной силы; в этом случае применяются формулы (9.2) и (9.3).

Прямолинейное движение под действием силы, которая является функцией расстояния; в этом случае используют формулу (9.5), которая, если направить ось по траектории точки, принимает вид:

Криволинейное движение под действием постоянной по модулю и направлению силы; в этом случае можно использовать формулу (9.4) или (9.5).

Криволинейное движение под действием силы, что определяется функцией координат точки приложения силы; в этом случае определение работы сводится к вычислению криволинейного интеграла по формуле (9.5).

Вращательное движение твердого тела под действием постоянного момента или момента, который является функцией угла поворота тела; в этом случае для вычисления работы используются формулы (9.8) или (9.9).

Для вычисления мощности в зависимости от характера движения пользуются формулой (9.11), если имеет место прямолинейное или криволинейное движение точки приложения силы, или формуле (9.12) – в случае вращательного движения твердого тела.

Во всех этих случаях перед вычислением работы или мощности необходимо изобразить все внешние силы, которые приложены к телу или рассматриваемой механической системе.

Примеры решения задач на тему: работа и мощность силы

Задача № 1

Определить наименьшую работу , которую необходимо выполнить, чтобы поднять на высоту груз передвигая его по наклонной плоскости, которая составляет с горизонтом угол ; коэффициент трения

Решение: Изобразим груз в произвольном положении на наклонной плоскости и покажем все действующие на него силы (рис.9.4): силу тяжести , силу трения и нормальную реакцию .

Работа, расходуемая на подъем груза на высоту , равна сумме работ силы трения вдоль длины и силы тяжести на перемещении точки ее приложения. Нормальная реакция работы не выполняет, поскольку она перпендикулярна перемещению.

Вычислим работу силы трения:

Поскольку и то

Работа силы тяжести в нашем случае отрицательная, поскольку груз движется вверх, и равна:

Полная работа, затраченная на подъем груза, равна

Ответ:

Задача № 2

Тело (рис.9.5) удерживается в равновесии на гладкой наклонной поверхности, расположенной под углом к горизонту, с помощью пружины. Вследствие полученного толчка тело переместилось вниз по наклонной поверхности на расстояние .

Определить сумму работ всех сил, приложенных к телу на этом перемещении, если сила тяжести тела угол жесткость пружины

Решение. К телу приложены следующие силы: сила тяжести , нормальная реакция поверхности и сила упругости растянутой пружины (рис.9.5).

Ось направим параллельно наклонной поверхности, а начало отсчета совместим с концом недеформированной пружины.

Тогда тело под действием толчка начнет двигаться из положения , которое характеризуется координатой , что равно:

где – статическое отклонение пружины.

Вычислим сумму работ сил , , на перемещении

где – работа силы тяжести на перепаде высот между точками и ,

– работа силы упругости пружины,

– работа нормальной реакции.

Работа силы тяжести равна:

Работа силы упругости пружины определяется по формуле:

где

Итак.

Окончательно

Вычислим – статическое отклонение пружины, которое имеет место в положении равновесия тела (точка ), когда пружина растянута постоянной силой тяжести. Для этого положения запишем в проекции на ось уравнение равновесия для сил тяжести и силы упругости пружины , которые действуют на тело:

Поскольку

Тогда

Окончательно,

Работа нормальной реакции равна нулю, так как эта сила перпендикулярна перемещению тела, то есть

Итак,

Ответ:

Задача № 3

Материальная точка массой движется прямолинейно по горизонтальной плоскости по закону под действием силы (рис.9.6).

Определить работу этой силы при перемещении точки ее приложения из исходного положения ( ) в положение, где

Решение Сила, действующая на материальную точку , меняется с течением времени. Следовательно, для определения работы этой силы необходимо воспользоваться уравнением (9.4):

где – проекция силы на элементарное перемещение точки приложения силы.

В нашем случае заданная сила совпадает по направлению с перемещением точки , а работу необходимо высчитывать на перемещении от к .

Таким образом, уравнение (1) примет вид:

Найдем зависимость между силой и перемещением , исключив параметр , который входит в выражения для значения силы и перемещения:

Подставив новое выражение для силы в уравнение (2), получим:

Вычислим этот интеграл:

Ответ:

Задача № 4

Шлифовальный камень радиусом делает об/мин. Потребляемая мощность равна коэффициент трения шлифовального камня равен

Определить, с какой силой прижимает камень деталь, которая шлифуется?

Решение. Деталь (рис.9.7) прижимается к шлифовальному камню с силой . Возникающая при этом сила трения развивает мощность , равную потребленной мощности 1,5 , то есть

где – скорость точки на ободе камня, к которому приложена сила .

Сила трения между камнем и деталью будет составлять:

угловая скорость камня будет:

а скорость точки на ободе камня равна:

Тогда

Откуда:

Ответ:

Задача № 5

Для измерения мощности двигателя на его шкив надета лента с деревянными колодками (рис.9.8).

Правая часть ленты удерживается упругими весами силой , а левая ее часть натягивается грузом .

Определить мощность двигателя , если его вал при равномерном вращении делает об/мин, при этом пружинные весы показывают натяжение ленты вес груза диаметр шкива

Примечание: разность натяжений частей и ленты равна силе, которая тормозит шкив.

Решение. Поскольку шкив вращается равномерно, то сила трения, которая возникает между шкивом и деревянными колодками, вместе с силой уравновешивают силу (рис.9.8), следовательно

Мощность силы трения равна мощности двигателя при условии, что шкив вращается равномерно:

– скорость точки обода шкива, на который действует сила трения и которая равна:

Ответ:

Задача № 6

Груз весом , который опускается по наклонной плоскости, приводит к вращению барабана весом , на который намотана нить (рис.9.9). Принять за механическую систему совокупность тел и , которые соединены между собой невесомой нитью, которая не растягивается.

Определить сумму работ всех сил, приложенных к этой системе за один оборот барабана , если – радиус барабана, – коэффициент трения скольжения груза по наклонной плоскости, которая составляет угол с горизонтом.

Решение. Данная механическая система является неизменной. На нее наложены следующие связи: наклонная плоскость и шарнирная опора барабана у точке .

Реакция наклонной плоскости состоит из нормальной реакции и силы трения , которая направлена в сторону, противоположную перемещению груза .

Реакция () шарнира лежит в плоскости, перпендикулярной оси шарнира, проходит через ось шарнира и может занимать в этой плоскости любое положение.

Поскольку данная система является неизменной, то работа всех сил, которые приложены к ней, определяется только работой внешних сил: силы тяжести груза ; нормальной реакции наклонной плоскости; силы трения груза по наклонной плоскости; силы тяжести барабана ; реакции шарнира .

Вычислим элементарную работу внешних сил системы

где – элементарные работы внешних сил, приложенных, соответственно, к телам и .

Тело движется поступательно. Элементарная работа внешних сил, приложенных к этому телу, равна

где – элементарные работы силы тяжести , нормальной реакции и силы трения .

Элементарная работа реакции равна нулю, поскольку перпендикулярна перемещению тела.

Элементарная работа силы тяжести равна

Элементарная работа силы трения определяется из выражения:

Поскольку

то

Итак,

Тело вращается вокруг неподвижной оси, которая проходит через точку перпендикулярно плоскости рисунка. Элементарная работа внешних сил, приложенных к телу , определится из выражения:

где – главный момент внешних сил ( и ) относительно оси вращения;

– элементарное угловое перемещение тела относительно оси вращения.

Поскольку линии действия сил и пересекают ось вращения, то и

Подставляя (2) и (3) в (1), получим

Перемещение груза связано с углом поворота барабана равенством , тогда последнее уравнение дает выражение элементарной работе всех сил, приложенных к данной механической системе, на элементарном перемещении барабана :

Для определения работы сил за один оборот барабана возьмем определенный интеграл в пределах от к :

Ответ:

Задача № 7

Колесо радиусом катится без скольжения по прямолинейной горизонтальной рейке (рис.9.10) под действием устойчивой силы , которая приложена в центре тяжести колеса и параллельна рельсу, и постоянного вращательного момента .

Определить сумму работ всех внешних сил, если ось колеса переместилась на расстояние . Трением качения пренебречь.

Решение. К колесу приложены внешние силы и момент: – сила тяжести колеса, – движущая сила, – вращательный момент, – нормальная реакция рейки, – сила трения.

Работы реакции и силы трения равны нулю, поскольку эти силы приложены в мгновенном центре вращения колеса , элементарное перемещение которого равно нулю. Работа силы тяжести колеса тоже равна нулю, в связи с тем, что элементарное перемещение точки перпендикулярно линии действия силы тяжести .

Следовательно необходимо вычислить только работу движущей силы и момента :

где

Согласно условию задачи, колесо катится без скольжения, поэтому

Соответственно, уравнение (1) запишется следующим образом:

Для определения суммы работ всех сил на перемещении оси колеса на расстояние проинтегрируем последнее уравнение в пределах от к :

Ответ:

Услуги по теоретической механике:

Заказать теоретическую механику
Помощь по теоретической механике
Заказать контрольную работу по теоретической механике

Учебные лекции:

Статика
Система сходящихся сил
Момент силы
Пара сил
Произвольная система сил
Плоская произвольная система сил
Трение
Расчет ферм
Расчет усилий в стержнях фермы
Пространственная система сил
Произвольная пространственная система сил
Плоская система сходящихся сил
Пространственная система сходящихся сил
Равновесие тела под действием пространственной системы сил
Естественный способ задания движения точки
Центр параллельных сил
Параллельные силы
Система произвольно расположенных сил
Сосредоточенные силы и распределенные нагрузки
Кинематика
Кинематика твердого тела
Движения твердого тела
Динамика материальной точки
Динамика механической системы
Динамика плоского движения твердого тела
Динамика относительного движения материальной точки
Динамика твердого тела
Кинематика простейших движений твердого тела
Общее уравнение динамики
Обратная задача динамики
Поступательное и вращательное движение твердого тела
Плоскопараллельное (плоское) движение твёрдого тела
Сферическое движение твёрдого тела
Движение свободного твердого тела
Сложное движение твердого тела
Сложное движение точки
Плоское движение тела
Статика твердого тела
Равновесие составной конструкции
Равновесие с учетом сил трения
Центр масс
Колебания материальной точки
Относительное движение материальной точки
Статические инварианты
Дифференциальные уравнения движения точки под действием центральной силы и их анализ
Динамика системы материальных точек
Общие теоремы динамики
Теорема об изменении кинетической энергии
Теорема о конечном перемещении плоской фигуры
Потенциальное силовое поле
Метод кинетостатики
Вращения твердого тела вокруг неподвижной точки

Источник

1.3. Работа переменой силы

Работа, формула

Работа постоянной силы, формула

Вычислить, найти работу постоянной силы по формуле (4)

Работа постоянной силы, направленной под углом к перемещению, формула

Вычислить, найти работу постоянной силы направленной под углом к перемещению по формуле (4)

Работа переменной силы, направленной под углом к перемещению, формула

Работа

Определение работы[править | править код]

Обозначения, размерность[править | править код]

Вычисление работы[править | править код]

Случай одной материальной точки[править | править код]

Случай системы точек или тела[править | править код]

Работа и кинетическая энергия[править | править код]

Работа и потенциальная энергия[править | править код]

Работа силы в теоретической механике[править | править код]

Работа в термодинамике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Работа и мощность силы

Работа силы

Элементарная работа

Аналитическое выражение элементарной работы силы. Работа силы на конечном перемещении

Работы сил тяжести и упругости

Работа силы, приложенная к вращающемуся телу

Мощность силы

Порядок решения задач на определение работы и мощности силы

Примеры решения задач на тему: работа и мощность силы

Вам также может понравиться

Как найти imei телефона на коробке

Как найти индекс изменения цен

Smite crash dialog как исправить

Добавить комментарий Отменить ответ