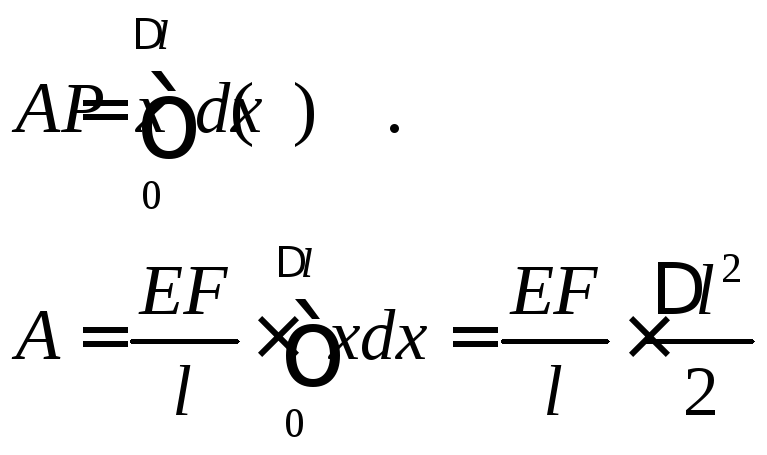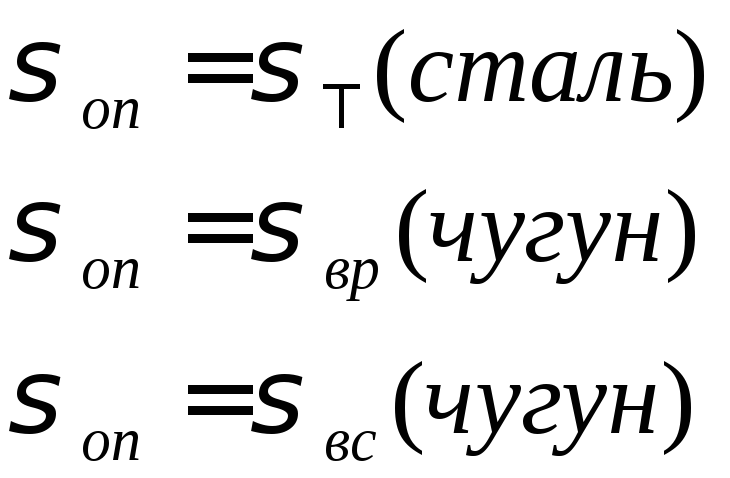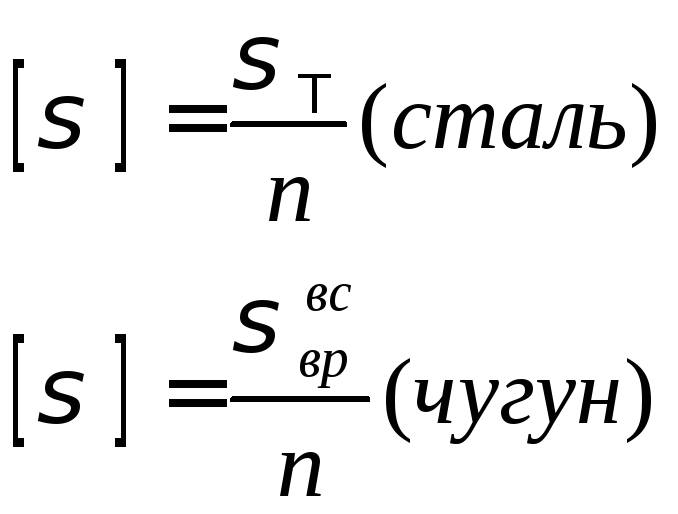Сила упругости, как и
сила тяжести, является консервативной. Напомним, что консервативная сила —
это такая сила, работа которой при движении тела по замкнутому контуру, равна
нулю. В одном из уроков мы уже убедились, что работу силы упругости нельзя
вычислить, пользуясь общей формулой для работы силы. Дело в том, что сила
упругости изменяется с изменением растяжения или сжатия пружины. Поэтому нам
необходимо будет воспользоваться графиком зависимости силы упругости от
удлинения.
Поскольку сила упругости
линейно зависит от удлинения, нам не составит труда найти площадь под графиком
функции силы упругости. Эта площадь и будет являться работой. На графике
зависимости силы упругости от удлинения обозначим два произвольных значения
силы: F1
и F2.
Этим значениям будут соответствовать значения удлинения х1 и х2.
Как видно из графика, чтобы найти работу, нам нужно вычислить площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований и высоты. Очевидно, что
основания — это F1
и F2,
а высота равна х1 − х2. Тогда,
используя формулу для силы упругости, мы можем вывести окончательное выражение
для работы силы упругости:
Напомним, что изучая
работу силы, мы пришли к выводу, что работа равна изменению кинетической
энергии. В данном случае мы видим, что работа силы упругости равна изменению
потенциальной энергии пружины. Но о потенциальной энергии мы поговорим
немного позже.
Итак, мы выяснили, что работа
силы упругости, так же, как и работа силы тяжести, не зависит от траектории
движения.
Пример решения задачи.
Задача.
Когда пружину, изначально находящуюся в расслабленном состоянии, растянули на 2
см, сила упругости составила 5 Н. Найдите работу силы упругости при растяжении этой
пружины на 8 см.
Возьмем диаграмму растяжения в координатах
РиΔlи
посмотрим, что выражает собой вся площадь
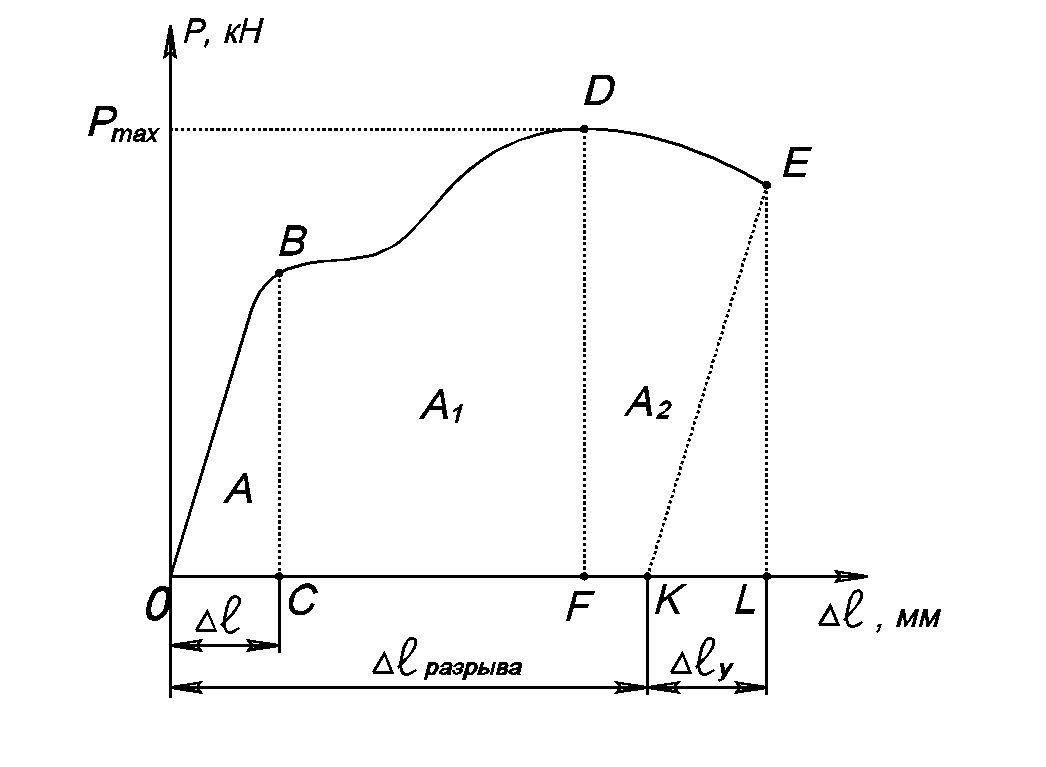
диаграммы ОАВDЕ (рис.8).
Рис.8.
Диаграмма растяжения (в абсолютных
единицах).
По оси абсцисс отложены полные удлинения
образца, иначе, пути, пройденные точкой
приложения растягивающих сил, а на оси
ординат – величины этих сил. Площадь
всей диаграммы очевидно выражает собой
работу внешних растягивающих сил,
затраченную на разрыв образца.
Вся работа деформации может быть
разделена на три части.
Площадь диаграммы ОВС представляет
собой работу упругой деформации, которая
накапливается в материале в виде
потенциальной энергии и может быть
полностью возвращена материалом, если
снять нагрузку, и равна площади ΔОВС.
По этой формуле можно вычислять работу
деформации для любой точки диаграммы
до предела упругости.
Вторая часть диаграммы – от предела
упругости до предела прочности – площадь
СВDF– представляет собой
работу А1, затрачиваемую
преимущественно на образование остаточной
деформации.
А1= площади СВDF–
работа, затрачиваемая на образование
остаточной деформации.
Третья часть диаграммы – от предела
прочности до напряжения, при котором
происходит разрыв образца, т.е. площадь
FDЕК. Представляет собой
работу А2, затрачиваемую на разрыв
образца после образования в нем шейки.
А2= площадиFDЕК –
работа, затрачиваемая на разрыв образца
после образования шейки.
Аразр= А+А1+А2– вся
работа деформации до полного разрушения.
1.4. Работа силы при удлинении наΔl.
Определим работу, которую выполняет
сила Р при удлинении стержня на Δl.
В процессе растяжения стержня сила
меняется линейно от нуля до максимального
значения.
Элементарная работа силы равна
Работа силы равна
,
следовательно
1.5. Испытание на сжатие (сталь, чугун, дерево, цемент).
Как показал опыт, результаты, получающиеся
при испытании стали на растяжение и
сжатие равноценны.
Характерные точки диаграммы растяжения
(А, В, С, D,) будут повторяться
(см. рис.5). После точки D кривая пойдет
вверх. Пластичные материалы при испытании
на сжатие не разрушаются, но изменяют
первоначальную форму и размеры (от
цилиндрической к бочкообразной).
Результаты испытаний чугуна на растяжение
и сжатие неравноценны. Опыт показал,
что хрупкие материалы гораздо лучше
работают на сжатие, чем на растяжение.
Разрушение происходит под углом 45°,
т.к. чугун разрушается от максимальных
касательных напряжений.
,
так как
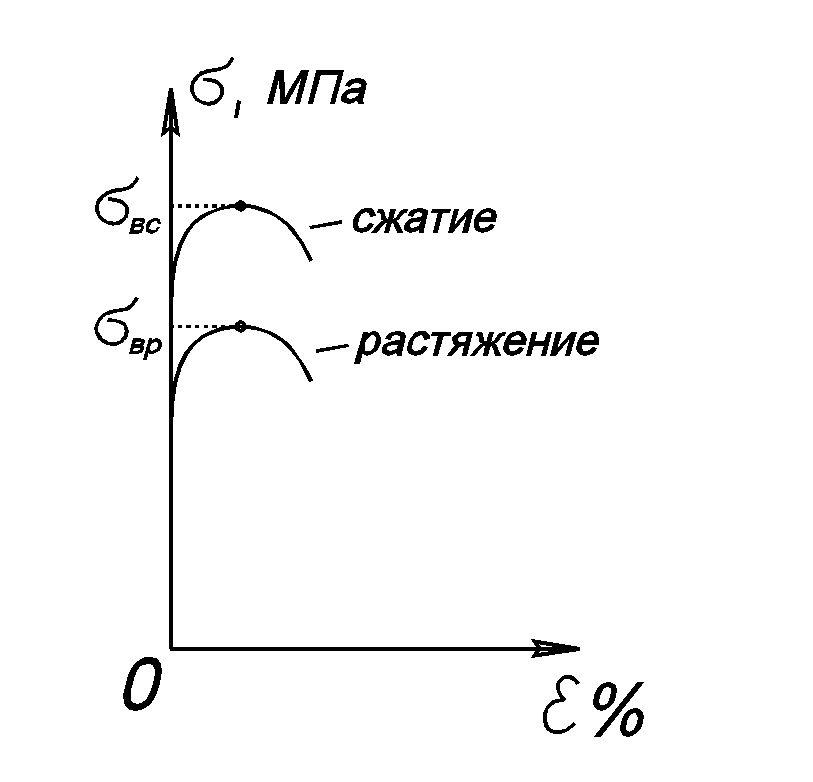
Рис.9.
Диаграмма сжатия и растяжения для
чугуна.
– верхнее значение напряжения при
растяжении,
– верхнее значение напряжения при сжатии.
Образцы для испытания на сжатие дерева
и цемента имеют кубическую форму. Дерево
– материал анизотропный, т.к. его
физико-механические свойства различны
по направлениям. Дерево сжимают вдоль
волокон и поперек волокон. Вдоль волокон
дерево выдерживает большие нагрузки и
лучше работает на сжатие, чем поперек
волокон. Форма, которую приобретает
образец после испытаний зависит от
материала, от отношения его высоты к
размерам поперечного сечения и, главным
образом, от трения, возникающего в
полостях соприкосновения оснований
образцов с плитами пресса. Большое
трение по торцам образца ведет к
неравномерному распределению напряжений
в плоскостях поперечных сечений, что
нежелательно, поэтому это трение
необходимо уменьшать (шлифовка, смазка
оснований парафином).
Лекция № 5
Напряжения максимальные, опасные,
допустимые.
Правила построения эпюр на
растяжение-сжатие.
Напряжения бывают:
Максимаьные
-наибольшие
напряжения возникающие в конструкции
Опасные-минимальные
напряжения при которых появляются
значительные остаточные деформации.
Для стали предел текучести, для чугуна
верхнее значение при растяжении и
верхнее значение при сжатии.
Допустимые
Где
–
коэффициент запаса прочности зависит
от материала и от степени ответственности
детали в конструкции.
Условие прочности первый тип расчёта
на прочность – проверочный:
1.
-максимальные
напряжения меньше или равны допустимым
– проверочный расчёт на прочность. Если
данное условие не выполняется необходимо
пересчитать площадь сечения, это второй
тип расчёта – проектный:
2.
Правила построения эпюр на
растяжение-сжатие.
1. На рисунке проводиться ось ОХ,
совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две
базовые нулевые линии, параллельно
продольной оси стержня. Одна для эпюры
продольной силы Nz
Вторая базовая нулевая линия для эпюры
нормальных напряжений(Мпа).
3. Стержень разбивается на участки. Для
границ участков проводятся вертикальные
линии в точках приложения нагрузки и
изменения площади поперечного сечения
вниз до пересечения с базовыми нулевыми
линиями. Нумерация участков начинается
со свободной стороны стержня для задачи
статически определимой. Если задача
статически неопределимая, то нумерация
выполняется слева направо.
4. Для определения значения продольной
силы используется метод сечений. В
середине участка проводится сечение.
Указывается направление продольной
силы. Положительным считается направление
продольной силы, направленной от сечения
(растягивает). Значение продольной силы
Nzопределяется из условия равновесия
отсечённой части (сумма проекций на ось
ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных
напряжений.
6. Положительные значения продольной
силы и нормального напряжения откладываем
вверх от базовой нулевой линии,
отрицательные вниз.
7. Проверяем правильность решения задачи
по эпюре продольной силы. В точках, где
приложена сосредоточенная сила, на
эпюре должен быть скачок равный значению
продольной силы.
8. Условие прочности
проверяем по эпюре нормальных напряжений.
Максимальные напряжения, возникающие
в конструкции, не должны превышать
допускаемых.
Пример №1: Построить эпюры продольной
силы Nи
нормального напряженияσ,проверить на прочность стальной стержень,
закрепленный с одной стороны (статически
определимая задача). Р1
=10кН Р2
=15кН
Р3 =15кН
=100
Мпа; А1 =F;
А2 =2F; F
=100мм2
Решение:
Параллельно продольной оси стержня
проводим две базовые нулевые линии для
продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная
со свободной стороны. Проводим вниз
вертикальные линии в точках приложения
сил и изменения площади поперечного
сечения до пересечения с нулевыми
линиями. Нумерация участков начинается
со свободной стороны стержня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Работа силы упругости

4.4
Средняя оценка: 4.4
Всего получено оценок: 465.
4.4
Средняя оценка: 4.4
Всего получено оценок: 465.
В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.
Механическая работа
Работа – это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:
A=FS
Где:
- F – модуль вектора силы, которая совершает работу;
- S – модуль вектора перемещения.
Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.
Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:
A=FScosα
Где:
α – угол между векторами силы и перемещения.
Значит, механическая работа – это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.
Знак механической работы
В зависимости от направления силы относительно перемещения тела работа A может быть:
- положительной (0°≤ α<90°);
- отрицательной (90°<α≤180°);
- равной нулю (α=90°).
Если A>0, то скорость тела увеличивается. Пример – падение яблока с дерева на землю. При A<0 сила препятствует ускорению тела. Например, действие силы трения скольжения.
Единица измерения работы в СИ (Международной системе единиц) – Джоуль (1Н*1м=Дж). Джоуль – это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.
Работа силы упругости
Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком Fs(x).
Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.
Она равна:
A=kx2/2
Где:
- k – жесткость;
- x – абсолютное удлинение.
Что мы узнали?
Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Саша Волков
5/5
-
Николай Топченский
5/5
-
Катя Пу
5/5
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 465.
А какая ваша оценка?
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа растяжения пружины A>kxm2 , где k – жесткость пружины, xm – максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
Показано, что работа растяжения пружины A>kxm2 , где k – жесткость пружины, xm – максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
It is shown, that work of a stretching of a spring A>kxm2 , where k – rigidity of a spring, xm – the maximal stretching. At calculation of work it is necessary to use values x and dx, the equations of movement received from the decision.
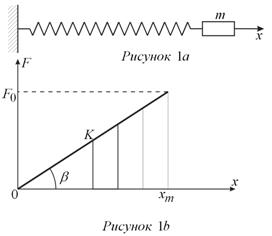
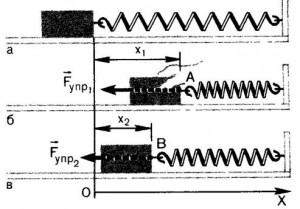
Рассмотрим спиральную пружину, один конец которой закреплен (рис. 1а), а к другому прикреплен груз массой m. Если пружину растянуть или сжать, то возникает сила F, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях x справедлив закон Гука – сила пропорциональна растяжению пружины: F = -kx. Постоянная k называется коэффициентом упругости, или жесткостью пружины. Знак минус означает, что сила F направлена в сторону, противоположную смещению x, т.е. к положению равновесия x = 0. Геометрически (рис. 1b) , k = tgβ, xm – максимальное (амплитудное) растяжение пружины.
В курсах физики утверждается, что работа при растяжении от x = 0 до xm будет равна
(1)
и эта работа равна потенциальной энергии пружины, растянутой (или сжатой) на величину xm и обладающей жесткостью k. Однако это одно из заблуждений классической механики. Растягивающей силой, равной F = kx, нельзя растянуть пружину даже на долю микрона. Чтобы растянуть пружину, надо приложить растягивающую силу в виде (F1 + k1x ), где F1 >0 (рис. 2а). Уравнение движения (II закон Ньютона) запишем в следующем виде:
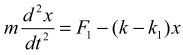
Решение при нулевых начальных условиях (при t = 0, x =0 и V =0) имеет вид
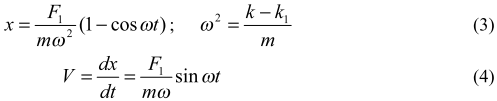
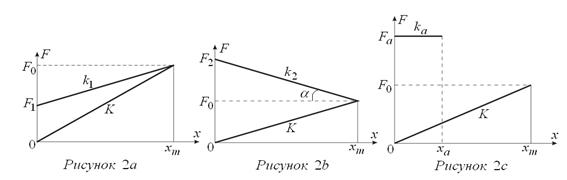
Из решения следует, что если F1 =0, то растяжения пружины не происходит. Амплитудные значения (при x = xm):
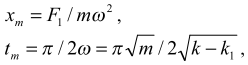
Работу вычисляем по формуле , где F = F1 – (k – k1)x, а x и dx определяются из выражений (3) и (4). Работа, совершаемая растягивающей силой
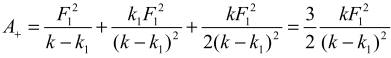
Работа, совершаемая силой упругости пружины
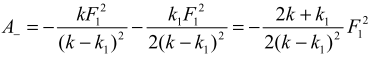
Из соотношения (5) следует, что работа, совершаемая растягивающей силой, не зависит от величин F1 и k1 и равна работе
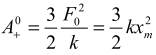
совершаемой постоянной силой F0, при этом работа, совершаемая силой упругости пружины A–0 = -kxm2 разность работ ΔA0 = kxm2 / 2 , конечная скорость при x = xm На рис. 3 даны графики зависимостей Vm / V0 и ΔA = kxm2 от величины отношения K1 / K. ΔA – кинетическая энергия груза.
Рассмотрим случай растягивающей силы FP > F0 (рис.2b) FP = F2 + k2x = F2 – b2x , где b2 = -k2 = tgα. Дифференциальное уравнение движения имеет вид:
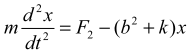
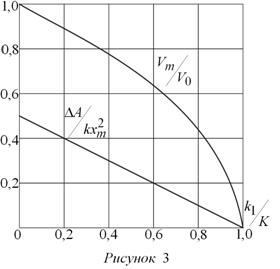
Его решение при нулевых начальных условиях имеет вид:
;
(8)
(9)
Амплитудные значения (при x = xm): xm = F2 / mω2; ;
.
Работа, совершаемая растягивающей силой
(10)
Работа, совершаемая силой упругости пружины
(11)
Кинетическая энергия груза при x = xm
(12)
На рис. 4 даны графики изменения безразмерных комплексов ΔA / kxm2 и Vm / V0 в зависимости от величины отношения k2 / k.
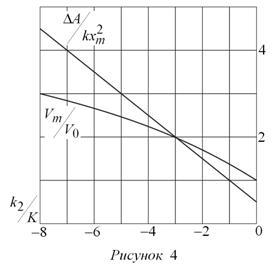
Рассмотрим третий способ растяжения пружины с грузом (рис. 2с). Прикладываем растягивающую силу Fa >>F0 для растяжения пружины на некоторое расстояние xa, затем сила Fa отключается, а оставшийся отрезок пути, равный xm – xa, груз проходит по инерции, используя запас кинетической энергии Ka, приобретенный в точке xa. Для первого участка пути дифференциальное уравнение имеет вид
(13)
Его решение при нулевых начальных условиях:
;
(14)
(15)
Время движения до x = xa
(16)
Работу вычисляем по формуле , где F(x) = Fa – kx, а x и dx определяются выражениями (14) и (15). Работа растяжения на участке до x = x0
(17)
Работа, совершаемая силой упругости пружины на этом же участке
(18)
Кинетическая энергия, приобретенная грузом:
(19)
Для второго участка уравнение движения имеет вид
(20)
Начальные условия для этого уравнения примем в виде: при t = 0 координата x = xa, скорость Va определяется выражением (15) при t = ta. Решение будет иметь вид:
(21)
(21a)
Работа силы упругости пружины на участке от x = xa до xm определится интегралом , где x и dx определяются выражениями (21) и (21а):
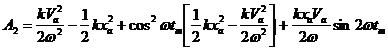
где tm ─ время движения груза от x=xa до x = xm. Условием достижения этой точки является равенство начальной кинетической энергии Ka работе силы упругости пружины A2. Это равенство сводится к трансцендентному уравнению
(23)
где a = kxa2 / 2; b = Ka – a; c = kxaVa / 2ω; φ = ωtm.
Приведем численный пример. Груз массой m = 1 кг, прикрепленный к пружине с жесткостью k = 400 Н/м, растягивается силой F0 = 80 Н на расстояние xm = 0,2. Работа силы растяжения Дж, работа силы упругости пружины
Дж, время t = 0,0785 с.
Проведем растяжение силой Fa по схеме, показанной на рис. 2с. Расчет сведем в таблицу 1.
Таблица 1.
|
Fa [H] |
Ka [Дж] |
ta [c] |
xa [м] |
A+ [Дж] |
A– [Дж] |
tm [c] |
|
8000 |
8 |
0,0005 |
0,001 |
16 |
-8 |
0,078 |
|
800 |
7 |
0,00468 |
0,00876 |
14,015 |
-7,015 |
0,0762 |
|
200 |
6 |
0,0176 |
0,0309 |
12,19 |
-6,19 |
0,0696 |
|
80 |
3,75 |
0,0377 |
0,054 |
8,088 |
-4,338 |
0,0597 |
Таким образом, только в случае растяжения пружины с грузом по схеме, показанной на рис.2с, можно затратить работу на растяжение A+, близкую к потенциальной энергии растянутой пружины П = kxm2 / 2.
Библиографическая ссылка
Иванов Е.М. РАБОТА ДЕФОРМАЦИИ ПРУЖИННОГО МАЯТНИКА // Современные наукоемкие технологии. – 2007. – № 3.
– С. 15-19;
URL: https://top-technologies.ru/ru/article/view?id=24676 (дата обращения: 19.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2
Коэффициент жесткости пружины k называется жесткостью тела, он зависит от материала, из которого тело изготовлено, а также от его геометрических размеров и формы. Жесткость выражается в ньютонах на метр (Н/м).
Сила упругости зависит только от изменения расстояний между взаимодействующими частями данного упругого тела. Работа силы упругости не зависит от формы траектории и при перемещении по замкнутой траектории равна нулю. Поэтому силы упругости являются потенциальными силами.
Обозначения:
A — Работа силы упругости
k — Коэффициент упругости пружины
x — Деформация пружины