Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
Формула работа выхода электронов
В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.
Потенциальная энергия электрона внутри металла постоянна и равна:
Wp = -eφ , где j – потенциал электрического поля внутри металла.
При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.
В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.
Aвых = eφ
Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.
Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.
Aвых = eφ’ – EF
где φ’ – среднее значение потенциала электрического поля внутри металла.
Таблица работа выхода электронов из простых веществ
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
|
Вещество |
Формула вещества |
Работа выхода электронов (W, эВ) |
|
серебро |
Ag |
4,7 |
|
алюминий |
Al |
4,2 |
|
мышьяк |
As |
4,79 – 5,11 |
|
золото |
Au |
4,8 |
|
бор |
B |
(4,60) |
|
барий |
Ba |
2,52 |
|
бериллий |
Be |
3,92 |
|
висмут |
Bi |
4,34 |
|
углерод (графит) |
C |
4,45 – 4,81 |
|
кальций |
Ca |
2,76 – 3,20 |
|
кадмий |
Cd |
4,04 |
|
церий |
Ce |
2,6 – 2,88 |
|
кобальт |
Co |
4,40 |
|
хром |
Cr |
4,60 |
|
цезий |
Cs |
1,94 |
|
медь |
Cu |
4,36 |
|
железо |
Fe |
4,40 – 4,71 |
|
галлий |
Ga |
3,96 – 4,16 |
|
германий |
Ge |
4,66 |
|
гафний |
Hf |
(3,53) |
|
ртуть |
Hg |
4,52 |
|
индий |
In |
(3,60 – 4,09) |
|
иридий |
Ir |
(4,57) |
|
калий |
K |
2,25 |
|
лантан |
La |
(3,3) |
|
литий |
Li |
2,49 |
|
магний |
Mg |
3,67 |
|
марганец |
Mn |
3,76 – 3,95 |
|
молибден |
Mo |
4,20 |
|
натрий |
Na |
2,28 |
|
ниобий |
Nb |
3,99 |
|
неодим |
Nd |
(3,3) |
|
никель |
Ni |
4,91 – 5,01 |
|
осмий |
Os |
(4,55) |
|
свинец |
Pb |
4,05 |
|
палладий |
Pd |
(4,98) |
|
празеодим |
Pr |
(2,7) |
|
платина |
Pt |
5,30 – 5,55 |
|
рубидий |
Rb |
2,13 |
|
рений |
Re |
4,98 |
|
родий |
Rh |
4,75 |
|
рутений |
Ru |
(4,52) |
|
сурьма |
Sb |
4,08 – 4,56 |
|
скандий |
Sc |
(3,2 – 3,33) |
|
селен |
Se |
4,86 |
|
кремний |
Si |
3,59 – 4,67 |
|
самарий |
Sm |
(3,2) |
|
олово (γ-форма) |
Sn |
4,38 |
|
олово (β-форма) |
Sn |
4,50 |
|
стронций |
Sr |
2,74 |
|
тантал |
Ta |
4,13 |
|
теллур |
Te |
4,73 |
|
торий |
Th |
3,35 – 3,47 |
|
титан |
Ti |
4,14 – 4,50 |
|
таллий |
Tl |
3,68 – 4,05 |
|
уран |
U |
3,27 – 4,32 |
|
ванадий |
V |
3,77 – 4,44 |
|
вольфрам |
W |
4,54 |
|
цинк |
Zn |
4,22 – 4,27 |
|
цирконий |
Zr |
3,96 – 4,16 |
Таблица работа выхода электронов из неорганических соединений
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
|
Вещество |
Формула вещества |
Работа выхода электронов (W, эВ) |
|
бромистое серебро |
AgBr |
~3,9 |
|
хлористое серебро |
AgCl |
~4,6 |
|
иодистое серебро |
AgI |
~4,0 |
|
сульфид серебра |
Ag2S |
~3,8 |
|
триоксид бора |
B2O3 |
4,7 |
|
оксид бария |
BaO |
1,0 – 1,6 |
|
барий вольфрамовокислый |
BaWO4 |
2,27 |
|
окись бериллия |
BeO |
3,8 – 4,7 |
|
окись кальция |
CaO |
1,8 – 2,4 |
|
ортовольфрамат кальция |
Ca3WO6 |
2,13 |
|
борид хрома |
CrB2 |
3,36 |
|
окись цезия |
Cs2O |
1,0 – 1,17 |
|
окись меди |
CuO |
4,35 – 5,34 |
|
закись меди |
Cu2O |
5,15 |
|
окись железа |
FeO |
3,85 |
|
вода |
H2O |
6,1 |
|
карбид гафния |
HfC |
2,04 |
|
оксид магния |
MgO |
3,1 – 4,4 |
|
диборид марганца |
MnB2 |
4,14 |
|
диборид молибдена |
MoB2 |
3,38 |
|
триоксид молибдена |
MoO3 |
4,25 |
|
силицид молибдена |
MoSi2 |
5,0 – 6,0 |
|
хлористый натрий |
NaCl |
4,2 |
|
борид ниобия |
NbB2 |
3,65 |
|
карбид ниобия |
NbC |
2,24 |
|
окись никеля |
NiO |
5,55 |
|
борид скандия |
ScB2 |
2,3 – 2,9 |
|
кремнезём |
SiO2 |
5,0 |
|
окись стронция |
SrO |
2,0 – 2,6 |
|
карбид тантала |
TaC |
3,05 – 3,14 |
|
пентаоксид тантала |
Ta2O5 |
4,65 |
|
дикарбид тория |
ThC2 |
3,5 |
|
оксид тория |
ThO2 |
2,54 – 2,67 |
|
сульфид титана |
TiS |
3,4 |
|
диборид титана |
TiB2 |
3,88 – 3,95 |
|
карбид титана |
TiC |
2,35 – 3,35 |
|
нитрид титана |
TiN |
2,92 |
|
окись титана |
TiO |
2,96 – 3,1 |
|
двуокись титана |
TiO2 |
4,7 |
|
карбид урана |
UC |
2,9 – 4,6 |
|
диборид ванадия |
VB2 |
3,88 – 3,95 |
|
диборид вольфрама |
WB2 |
2,62 |
|
диоксид вольфрама |
WO2 |
4,96 |
|
дисилицид вольфрама |
WSi2 |
5,0 – 6,0 |
|
борид циркония |
ZrB |
4,48 |
|
диборид циркония |
ZrB2 |
3,70 |
|
карбид циркония |
ZrC |
2,2 – 3,8 |
|
нитрид циркония |
ZrN |
2,92 |
_______________
Источник информации:
1. Landolt-Borstein’s Zahlenwerte und Funktionen aus Phsik, Chemie, Astrunumie, Geophysik, Thechnik, 6-е издание., Берлин, т. I, ч.4, 1955; т. II, ч.6, разд. 1, 1959.
2. В.С. Фоменко. Эмиссионные свойства элементов и химических соединений. Изд. АН УСССР, Киев, 1961.
Работа выхода в металлах
В металлах, согласно электронной теории проводимости, свободные электроны находятся в состоянии постоянного хаотичного теплового движения. Однако при нормальных температурах они не покидают металл. У поверхности металла существует задерживающее электрическое поле. Чтобы вылететь из металла электрон должен совершить работу по преодолению задерживающих сил. Эта работа называется работой выхода.
Работа выхода – работа, которую должен совершить электрон, чтобы выйти из металла.
Формула для работы выхода:
A=eU,
где e – заряд электрона, U – разность потенциалов между точками в металле и за пределами задерживающего слоя.
Работа выхода измеряется в электронвольтах.
Электронвольт – внесистемная единица измерения, равная энергии, которую приобретает электрон при движении между двумя точками с разностью потенциалов в 1 Вольт.
Как у поверхности металла образуется задерживающее поле?
- Вследствие теплового движения электроны с поверхности металла могут отрываться и образуют над поверхностью электронное облако.
- На местах покинувших металл электронов образуются положительные ионы. По закону Кулона, они стремяться вернуть покинувшие металл электроны обратно.
В результате у поверхности металла образуется двойной электрический слой.

В вакууме за пределами задерживающего слоя поле отсутствует, поэтому формула для работы выхода запишется в виде:
A=eφ,
где φ – потенциал выхода, равный потенциалу поля внутри металла.
Контактная разность потенциалов
Явление контактной разности потенциалов в 1797 году открыл Алессандро Вольта (1745 -1827).
Контактная разность потенциалов – разность потенциалов, которая возникает при контакте поверхностей двух разных металлов.
- Разность потенциалов, возникающая при контакте двух разных металлов, зависит от их химического состава и температуры.
- Если цепь составлена из нескольких разных проводников при одинаковой температуре, контактная разность потенциалов определяется только контактной разностью между крайними проводниками.
Причины возникновения контактной разности потенциалов:
- Разная работа выхода для разных металлов.
- Разная концентрация свободных электронов в разных металлах.
Схематически рассмотрим контакт двух металлов. Пусть у металла 1 работа выхода больше, чем у металла 2, и в металле 1 концентрация свободных электронов больше.
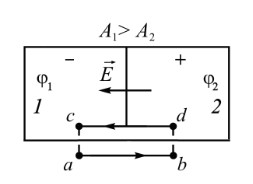
Между точками a и b, лежащими рядом с поверхностью, но не принадлежащими проводнику, возникает внешняя контактная разность потенциалов.
Электроны диффундируют из одного металла в другой, при этом из металла 1 в металл 2 уходит больше электронов, так как n1>n2. В результате металл 1 приобретает положительный, а металл 2 – отрицательный заряд. Возникшая разность потенциалов называется внутренней контактной разностью потенциалов.
Цель работы:
Изучение
явления термоэлектронной эмиссии и
определение работы выхода электрона
из металла.
Приборы и
принадлежности:
Панель с собранной электрической схемой,
набор цифровых вольтметров, амперметров
и миллиамперметров для измерения
анодного напряжения накала и тока
накала.
Теоретическое
введение.
В металле при
нормальной температуре имеется некоторое
количество электронов, энергия которых
достаточна для того, чтобы преодолеть
потенциальный барьер, имеющийся на
границе металла, и покинуть его
поверхность. При повышении температуры
металла число таких электронов резко
возрастает и делается вполне заметным.
Выход электронов из металла вследствие
нагревания последнего называется
термоэлектронной эмиссией. Величина
же энергии, которую необходимо сообщить
электрону для того, чтобы он покинул
поверхность металла, от состояния
поверхности, в частности, от ее чистоты
(подобрать надлежащим образом покрытые
поверхности, можно сильно снизить работу
выхода, например оксидированием чистого
металла).
В данной работе,
используя метод прямых Ричардсона,
предлагается определить работу выхода
электрона из чистого металла и по ее
величине указать название метала,
используя справочник.
Исходя из квантовых
представлений, Дешман в 1923 г. получил
для тока насыщения следующую формулу:
![]()
(1)
Где Т
– абсолютная температура катода; К
– постоянная Больцмана; А
– константа, не зависящая от рода
металла.
Формулу (1) можно
записать в виде
![]() ,
,
так как
![]() ,
,
где S
– площадь катода.
Прологарифмируем
это выражение:
![]()
или
![]() ,
,
где
![]()
(2)
Работа выхода
электрона из металла практически не
зависит от температуры, ее можно считать
величиной постоянной, и, следовательно,
![]()
является функцией от 1/Т
. График
зависимости
![]()
представляет прямую линию, угловой
коэффициент которой равен
![]() .
.
Построив график зависимости
![]()
от 1/Т
и определив коэффициент этой прямой,
можно найти работу выхода:
![]()
(3), где![]()
(4)
Рассмотренный
метод называется методом прямых
Ричардсона.
Таблица №1 –
измерение анодного тока Ja
до получения тока насыщения.
|
I1 |
I2 |
I3 |
I4 |
||||
|
JH=1,15 UH=3,0 |
JH=1,2 UH=3,2 |
JH=1,25 UH=3,4 |
JH=1,3 UH=3,7 |
||||
|
Ua, |
Ja, |
Ua, |
Ja, |
Ua, |
Ja, |
Ua, |
Ja, |
|
0 5 10 15 20 25 30 35 40 45 |
0,005 0,282 0,298 0,305 0,310 0,314 0,317 0,320 0,322 0,325 |
0 5 10 15 20 25 30 35 40 45 |
0,008 0,491 0,547 0,560 0,568 0,574 0,579 0,584 0,588 0,592 |
0 5 10 15 20 25 30 35 40 45 |
0,012 0,762 1,025 1,048 1,064 1,076 1,086 1,095 1,102 1,110 |
0 5 10 15 20 25 30 35 40 45 |
0,017 1,118 2,049 2,123 2,159 2,184 2,206 2,223 2,239 2,254 |
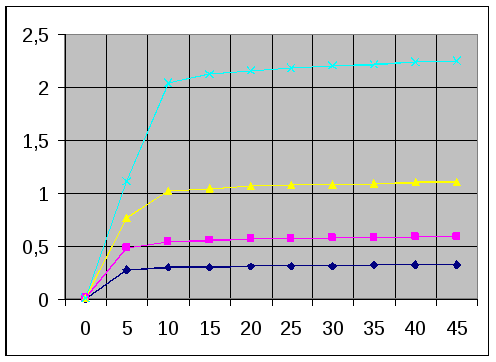
Провели измерения
анодного тока Ja
до получения тока насыщения и записали
полученные значения в таблицу №1.
Повторили измерения для нескольких
значений тока накала. Построили на одной
из координатных сетке вольт – амперные
характеристики лампы, используя данные
таблицы №1 для различных токов накала.
Вольт – амперные
характеристики лампы.
Ua,
B
Ja,
mA
Вычислили по
величине тока и напряжения накала
мощность Р
(Р
= JН
· UН),
потребляемую катодом, разделить ее
величину на площадь катода S=0,05
cм2
и по табличным данным определили
температуру накала, соответствующую
каждому из четырех токов накала. Значение
Р/S,
Т
и токи насыщения записали в таблицу №2.
Таблица №2 –
Значение Р/S,
Т
и токи насыщения.
|
№ |
Р/S·104, |
Т, |
1/Т·10-4, |
1/Т2·10-7, |
Jнас, |
Jнас/Т2·10-7, |
ln(Jнас/Т2) |
|
1 |
82,8 |
2050 |
4,9 |
2,38 |
0,325 |
0,77 |
-16,4 |
|
2 |
93,6 |
2120 |
4,72 |
2,22 |
0,595 |
1,32 |
-15,8 |
|
3 |
102,5 |
2170 |
4,61 |
2,12 |
1,110 |
2,36 |
-15,3 |
|
4 |
117,0 |
2190 |
4,57 |
2,09 |
2,255 |
0,47 |
-16,9 |
Используя данные
таблицы №2, построили два графика: график
зависимости тока насыщения от температуры
накала
![]() ;
;
график зависимости
![]()
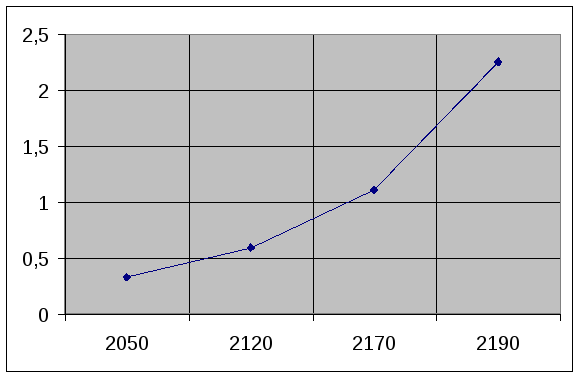
График зависимости
тока насыщения от температуры накала
![]()
T,
K
Jнас,
мА
График зависимости
![]()
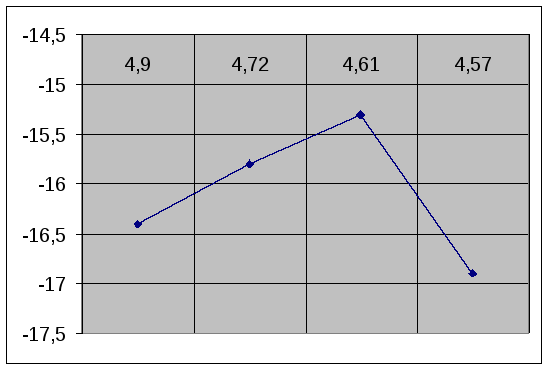
T-1-10-4(K-1)
По графику можно
найти тангенс угла α:
![]()
Теперь можно найти
работу выхода по формуле:
![]()
![]()
По табличными
данными мы получили металл – титан(его
работа выхода, по табличным данным,
равна 3,92).
Вывод:
Изучили
явления термоэлектронной эмиссии и
смогли определить работу выхода электрона
из металла.
Работа выхода
электрона из металла практически не
зависит от температуры, ее можно считать
величиной постоянной, и, следовательно,
![]()
является функцией от 1/Т . График
зависимости
![]()
представляет ломаную, угловой коэффициент
которой равен
![]() .
.
Построив график зависимости
![]()
от 1/Т и определив коэффициент этой
прямой, смогли найти работу выхода(метод
прямых Ричардсона).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Одним из интереснейших квантовых эффектов, рассматриваемых в курсе школьной физики, является фотоэлектрический эффект или фотоэффект. Фотоэффект — явление взаимодействия света с веществом, в результате которого энергия фотонов передаётся электронам вещества.

Рис. 1. Фотоэффект
Облучаем поверхность вещества. Энергия каждого фотона равна . Фотон, попадающий внутрь вещества, поглощается электроном, который, в свою очередь, приобретает дополнительную энергию. Вырываясь из поверхности вещества, электрон теряет часть энергии (взаимодействуя с ионами вещества) и, становясь свободным (когда электрон перестаёт взаимодействовать с веществом), улетает в пространство.
С точки зрения зрения закона сохранения энергии, можно получить уравнение Эйнштейна:
(1)
- где
Работа выхода электрона () — минимальная энергия, которую необходимо передать электрону, чтобы он «выбрался» на поверхность. Если энергия фотона равна точно энергии выхода, то электрон, «выйдя» на поверхность, там и останавливается, т.е. после выхода электрона, его кинетическая энергия численно равна нулю. Тогда уравнение Эйнштейна примет вид:
(2)
- где
Красная граница фотоэффекта () — частота излучения (фотона), ниже которой фотоэффект не происходит.
Аналогично можно ввести:
(3)
Вывод: задачи на фотоэффект вводятся именно этим словом. Единственное, что мы можем использовать при этом, — уравнение Эйнштейна (1).
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.

Александр Столетов
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
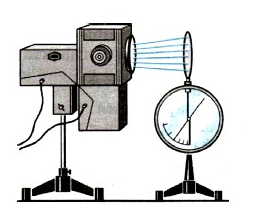
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
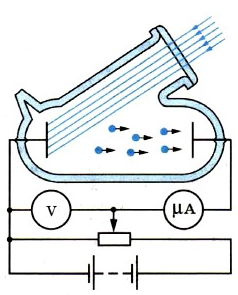
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
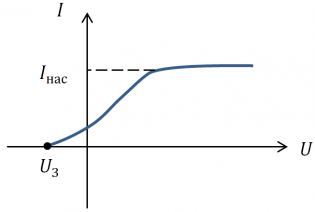
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как Iн. Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
Iн=qt
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
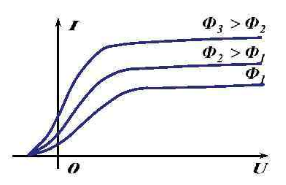
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное Uз, сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное Uз, называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
mv22=eUз
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
E=hν
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10–34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10–7 м.
Энергия фотона равна:
E=hν
Выразим частоту фотона через скорость света:
ν=cλ
Следовательно:
![]()
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
hν=A+mv22
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
hν>A
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
νmin=Ah
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
λmax=hcA
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10-7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10–19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
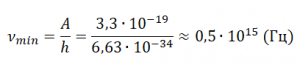
Задание EF15717
При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅1015 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Переписать формулу закона сохранения энергии применительно к опытам 1 и 2.
4.Используя формула, связывающую задерживающее напряжение и кинетическую энергию фотона, определить работу выхода.
5.Записать формулу для красной границы фотоэффекта.
6.Выполнить решение в общем виде.
7.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Частота света в опыте 1: ν1 = ν = 0,75∙1015 Гц.
• Частота света в опыте 2: ν2 = 2ν1 = 2ν Гц.
• Задерживающее напряжение в опыте 1: U1 = U В.
• Задерживающее напряжение в опыте 2: U2 = 3U1 = 3U В.
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
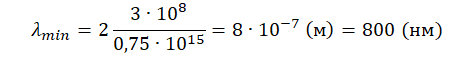
Ответ: 800
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17645
При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался красный светофильтр, а во второй – жёлтый. В каждом опыте измеряли напряжение запирания.
Как изменяются длина световой волны, напряжение запирания и кинетическая энергия фотоэлектронов? Для каждой величины определите соответствующий характер её изменения:
| 1) | увеличится |
| 2) | уменьшится |
| 3) | не изменится |
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Алгоритм решения
1.Определить, от чего зависит и как меняется длина световой волны.
2.Записать закон сохранения энергии, формулу зависимости кинетической энергии от напряжения запирания.
3.Используя формулы, становить, как меняется напряжение запирания и кинетическая энергия.
Решение
Длина световой волны определяется ее цветом. Красный свет имеет большую длину волны. Следовательно, во втором опыте длина световой волны уменьшится.
Закон сохранения энергии для фотоэффекта:
hν=A+mv22
Формула зависимости кинетической энергии от напряжения запирания:
mv22=eUз
Следовательно:
hν=A+eUз
Работы выхода — величина постоянная для данного вещества. Следовательно, напряжение запирания зависит только от частоты световой волны. Частота — величина обратная длине волны. Так как длина волны уменьшилась, частота увеличилась. Следовательно, увеличилось и напряжение запирания.
Поскольку напряжение запирания прямо пропорционально кинетической энергии фотонов, то эта энергия также увеличивается.
Ответ: 211
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17973
На металлическую пластинку падает монохроматическая электромагнитная волна, выбивающая электроны из пластинки. Максимальная кинетическая энергия фотоэлектронов, вылетевших из пластинки в результате фотоэффекта, составляет 3 эВ, а работа выхода из металла в 2 раза больше этой энергии. Чему равна энергия фотонов в падающей волне?
Ответ:
а) 9 эВ
б) 2 эВ
в) 3 эВ
г) 6 эВ
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Максимальная кинетическая энергия выбитых электронов: Emax = 3 эВ.
• Работа выхода из металла: A = 2 Emax.
Закона сохранения энергии для фотоэффекта:
hν=A+mv22
Или:
E=A+Emax=2Emax+Emax=3Emax=3·3=9 (эВ)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.3k
