ЦЕЛЬ
РАБОТЫ
Изучение
геометрических характеристик линзы и
ознакомление с одним из методов
определения радиуса кривизны и показателя
преломления линзы.
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ РАБОТЫ
Линзой
называется прозрачное тело, ограниченное
сферическими поверхностями (одна из
поверхностей может быть плоской).
Линзы
бывают двояковыпуклые, двояковогнутые,
плоско-выпуклые, плоско-вогнутые,
выпукло-вогнутые, вогнуто-выпуклые.
Выпукло-вогнутые
и вогнуто-выпуклые линзы называют
менисковыми. Их используют, в частности,
в очках.
Линзы
изготавливают из различных материалов
стекла и пластика для видимого излучения,
кварца
для ультрафиолетового, каменной соли
(или сильвинии)
для инфракрасного.
Формула
линзы связывает фокусное расстояние F
с расстоянием от оптического центра
линзы до предмета d
и до изображения f:
.
(1)
Фокусное
расстояние F
подставляется в эту формулу со знаком
“+”, если линза собирающая, и со
знаком “”,
если линза рассеивающая.
Расстояние
до изображения f
подставляется со знаком “+”, если
изображение действительное, и со знаком
“”,
если оно мнимое.
Величина
называется оптической силой и измеряется
в диоптриях (дптр).
=
дптр.
Оптическая
сила линзы связана с ее геометрическими
характеристиками формулой:
,
(2)
где
nл
и nо
показатели преломления линзы и окружающей
среды;
R1
и R2
радиусы кривизны поверхностей линзы,
которые подставляются со знаком “+”
в случае выпуклой поверхности и со
знаком
“”
в случае вогнутой поверхности.
Если
в формуле (2) получается Ф
0, то линза собирающая,
Ф
0
рассеивающая. Это связано со знаками
обеих скобок в правой части. Например,
при R1
0, R2
0 (двояковыпуклая линза) получим собирающую
линзу, если nл
nо
(например, стеклянная линза в воздухе)
и рассеивающую, если nл
nо
(например, воздушная линза в стекле). В
другом случае может быть nл
nо
(воздушная линза в стекле), но R1
0, R2
0, то есть поверхности линзы вогнутые.
Тогда каждая скобка будет иметь знак
“”
, а их произведение даст “+”, и линза
будет собирающей.
Поперечное
увеличение линзы
, (3)
где
y1
и y2
расстояния соответственно светящейся
точки и ее изображения до главной
оптической оси линзы.
Собирающая
линза может использоваться в качестве
лупы. В этом случае ее увеличение равно
,
где
D
это расстояние наилучшего зрения; для
нормального глаза
D
= 25 см
один из стандартов для создания оптических
приборов, вооружающих глаз; F
фокусное расстояние лупы.
К
важнейшим оптическим приборам,
изготовленным из линз, относятся
микроскоп и телескоп.
Увеличение
микроскопа
,
(4)
где
расстояние между фокусами объектива и
окуляра, называемое длиной тубуса
микроскопа; D
расстояние наилучшего зрения; Fоб
и Fок
фокусные расстояния объектива и окуляра,
причем в микроскопе Fоб
Fок.
Увеличение
телескопа
, (5)
где
Fоб
и Fок
– фокусные расстояния объектива и
окуляра, причем в телескопе Fоб
Fок.
ОПИСАНИЕ
ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
В
данной работе на установке с линзой 3
(рис. 1) определяют расстояние f
от линзы до
действительного изображения нити
лампочки и по формуле (1) определяют
фокусное расстояние плоско-выпуклой
линзы.
;
, (6)
г
де
d
= 691 мм для данной установки. Расстояние
f
измеряют по шкале 6, передвигая экран 7
и добиваясь на нем резкого изображения
нити лампочки 1.
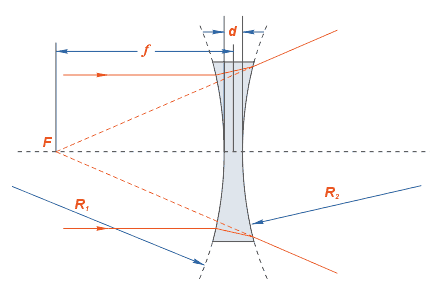
Из формулы (2)
получаем для плоско-выпуклой линзы
,
(7)
где
n
= nл
– показатель преломления линзы;
nо
= nвозд
1 – показатель
преломления воздуха;
R1
= R
– радиус выпуклой поверхности линзы;
R2
=
– радиус плоской поверхности линзы.
Из формулы (7)
получаем показатель преломления:
;
;
. (8)
Радиус
кривизны R
линзы можно измерить с помощью индикатора
2 (рис.1). Если представить сечение линзы
в виде сегмента круга (рис.2), то по теореме
Пифагора получим:
,
где
а
хорда, h
стрела сегмента.
После
преобразований получаем значение
радиуса:
.
(9)
П
ередвигая
индикатор в горизонтальном направлении,
измеряют по шкале 4 длину хорды а,
записывая соответствующую стрелу
сегмента h
по показаниям индикатора. Вычислив по
формуле (9) радиус кривизны R,
а по формуле (6) фокусное расстояние
линзы, можно определить показатель
преломления линзы по формуле (8).
Схема
установки приведена на рис.1. Передвигая
руками стойку с индикатором 2, можно
записать показания по шкале 4 (половина
хорды а/2)
и соответствующие показания индикатора
– стрелу сегмента h.
Целое число миллиметров на индикаторе
показывает маленькая стрелка, а десятые
и сотые доли – большая.
ПОРЯДОК
ВЫПОЛНЕНИЯ РАБОТЫ
ПРЕДУПРЕЖДЕНИЕ.
Следите за тем, чтобы оптические
поверхности линзы оставались чистыми
– нельзя касаться их пальцами или
предметами. Индикатор – точный прибор
и все манипуляции с ним необходимо
выполнять плавно, без рывков. Наконечник
сделан из фторопласта для уменьшения
трения. При всех передвижениях руками
стойки с индикатором нужно учесть, что
стойка должна быть всегда прижата к
основанию. В противном случае показания
индикатора будут неточными.
1.
Установка нуля. Получите индикатор и
установите его на место. Для этого
необходимо передвинуть руками стойку
индикатора и установить указатель шкалы
4 на ноль при вертикальном положении
ножки. Вставьте ножку индикатора в паз,
слегка прижмите ее стопорным винтом и
передвижением вверх и вниз самого
индикатора добейтесь нулевого показания
малой и большой стрелок. При этом большая
стрелка должна быть близка к вертикальному
положению. Закрепив индикатор в таком
положении, необходимо найти наивысшую
точку линзы. Для этого передвигайте
стойку на 1 – 2 см влево и вправо и по
стрелке индикатора найдите вершину
сферической поверхности линзы. При этом
нужно учесть, что вблизи вершины есть
мертвая зона протяженностью около 2-х
мм, в пределах которой стрелка неподвижна
– стойку нужно установить посередине
этой зоны. Установив стойку, подведите
шкалу 4 кремальерой 5 точно на ноль и в
дальнейшем кремальеру 5 не трогайте.
Если при этом большая стрелка индикатора
отклонилась от вертикали, вновь установите
индикатор должным образом и закрепите
его. Далее вращением внешнего кольца
индикатора совместите ноль круговой
шкалы с положением большой стрелки.
Учитывая то, что точность установки
нуля определяет точность дальнейших
измерений, еще раз или два повторите
манипуляции пункта 1 с тем, чтобы ноль
шкалы 4 совпадал с нулем индикатора и
это соответствовало вершине сферической
поверхности линзы.
Таблица
1
|
Показания шкалы |
Показания |
Хорда а (мм) |
Стрела сегмента (мм) |
Радиус кривизны |
|
|
При движении |
При движении |
||||
|
20 |
40 |
||||
|
25 |
50 |
||||
|
30 |
60 |
||||
|
35 |
70 |
||||
|
40 |
80 |
||||
|
Среднее значение |
R |
2.
Передвигая стойку вправо, устанавливайте
указатель шкалы 4 на значениях 20, 25, 30,
35, 40 мм (значения, равные половине
соответствующих хорд) и записывайте
показания индикатора h1
(стрела сегмента) в таблицу 1. При этом
целое число миллиметров снимайте по
показаниям маленькой стрелки, а десятые
и сотые доли – по показаниям большой
стрелки.
3.
Передвигая стойку влево от нуля, снимайте
показания индикатора h2
при тех же значениях половины хорды.
4. Передвиньте
стойку с индикатором вправо до упора.
5.
Подключите лампочку к напряжению
12 В.
6.
Слегка вращая “столб” с лампочкой,
добейтесь того, чтобы изображение
лампочки на экране 7 находилось в центре
перекрестия. При этом одновременно
нужно слегка поднять экран рукой и
сфокусировать изображение нити лампочки.
Добившись резкого изображения, запишите
по шкале 6 значение f
в миллиметрах. Повторите измерения f
еще четыре раза.
7. Выключите лампочку
и приступите к расчетам. Все расчеты в
данной работе удобнее проводить с
миллиметрах.
8.
Найдите среднее арифметическое f
результатов наблюдений и определите
полуширину доверительного интервала
f.
Запишите результат измерения f
в виде: f
f.
9.
По формуле 6 вычислите фокусное расстояние
линзы F
в миллиметрах. Для нашей установки d
= 691 мм.
10.
Пренебрегая погрешностью измерения d,
определите полуширину доверительного
интервала F
фокусного расстояния линзы по формуле:
.
11.
Заполните таблицу 1 и по формуле 9
определите радиус R
кривизны линзы в миллиметрах. Найдите
среднее арифметическое значение R
и полуширину доверительного интервала
R.
12.
По формуле 8 найдите показатель преломления
линзы, а по формуле
определите полуширину n
доверительного интервала. Запишите
результат измерения показателя
преломления n
в виде: n
n.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Сформулируйте
цель лабораторной работы. -
Что
такое линза? -
Из
каких материалов изготавливают линзы
для ультрафиолетового и инфракрасного
излучений? -
Укажите
формулу линзы. -
Какая
величина называется оптической силой
линзы? -
В
каких единицах измеряется оптическая
сила линзы? -
Укажите
знак фокусного расстояния F
линзы для собирающей и рассеивающей
линз. -
Укажите
знак расстояния f
действительного и мнимого изображений
до линзы. -
Как
оптическая сила линзы зависит от
радиусов поверхностей, ограничивающих
линзу? -
На
стеклянную двояковогнутую линзу в
воздухе падают параллельные лучи света.
Как направлены эти лучи после прохождения
линзы? -
На
воздушную двояковыпуклую линзу в стекле
падают параллельные лучи света. Как
направлены эти лучи после прохождения
линзы? -
Какая
величина называется поперечным
увеличением линзы? -
Напишите
формулу увеличения лупы. -
Линза
для очков изготовлена из стекла крон
с показателем преломления n
= 1,5. Радиус кривизны выпуклой и вогнутой
поверхностей линзы равны соответственно
50 см и 25 см. Определите оптическую силу
линзы. -
Решите
предыдущую задачу для плоско-выпуклой
линзы, если радиус кривизны выпуклой
поверхности равен R
= 50 см. -
Укажите,
какие изображения будут получены в
собирающей линзе при d
= 2F, d
= 3F, F
d
2F. -
Постройте
увеличенное и уменьшенное изображения,
даваемые собирающей линзой. -
Постройте мнимое
изображение, даваемое собирающей
линзой. -
Постройте
изображение, даваемое рассеивающей
линзой. -
Нарисуйте
эскиз экспериментальной установки. -
Укажите
расчетную формулу для определения
фокусного расстояния F
линзы. -
По
какой формуле нужно вычислять полуширину
F
доверительного интервала фокусного
расстояния F линзы? -
Выведите
формулу для определения показателя
преломления n плоско-выпуклой
линзы в данной работе. -
По
какой формуле нужно вычислять полуширину
n
доверительного
интервала показателя преломления n
линзы в данной работе? -
Выведите
формулу для расчета радиуса кривизны
R плоско-выпуклой
линзы в данной работе. -
Определите
показатель преломления плоско-выпуклой
линзы, у которой фокусное расстояние
вдвое больше радиуса кривизны выпуклой
поверхности. -
Найдите
фокусное расстояние линзы F,
если действительное изображение
предмета находится от линзы на расстоянии
вдвое большем расстояния предмета до
линзы, а расстояние между предметом и
его изображением равно 30 см. -
Как
изменится фокусное расстояние собирающей
стеклянной линзы(nЛ
= 1,5), если ее из воздуха (n01
1) поместить в воду
(n02 = 1,33)? -
Меняется
ли расстояние d предмета
до линзы в данной работе? -
Укажите
порядок выполнения данной лабораторной
работы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Страницы работы
Содержание работы
Министерство образования и науки
Российской Федерации
Федеральное агентство по образованию
Государственное
образовательное учреждение высшего профессионального образования
« ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА»СФУ
Кафедра физики
Лабораторная работа № 6
Определение радиуса кривизны линзы
с помощью колец Ньютона
Выполнил: Проверил:
Красноярск 2010 г.
Цель работы: Определение радиуса
кривизны линзы R, входящей в устройство колец Ньютона, а также оценка
доверительного интервала и относительной погрешности в определении величины R.
Оборудование:
Оптическая скамья, осветитель, диафрагма, прибор Ньютона, линза-объектив,
экран, светофильтр.
Теоретическое введение.
Кольца Ньютона наблюдаются в
случае соприкосновении выпуклой поверхности плоско-выпуклой линзы малой
кривизны с плоско-параллельной поверхностью. Воздушная прослойка между
плоскостью и линзой имеет переменную толщину, разность хода интерферирующих их
лучей зависит от толщины этой прослойки. Чем больше толщина воздушной
прослойки, тем больше число наблюдаемых колец.
Кольца Ньютона могут
наблюдаться в отраженном и проходящем свете.
В отраженном свете оптическая
разность хода для колец Ньютона определяют, учитывая λ/2,условием:
,
В отраженном свете по условию
образовании максимума:
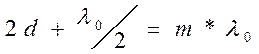
Для минимумов в отраженном
свете:
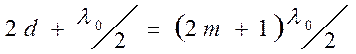
Так как на экране получаются
увеличенные интерференционные кольца, то вначале надо рассчитать радиусы
действительных колец:
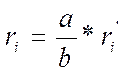
Радиусы действительных колец
рассчитывают для опыта с проходящим и отраженным светом. В первом случае берут
радиусы колец определенного цвета, во втором – радиусы темных колец при
условии, что в опыте с отраженным светом использовали фильтр того же цвета.
Радиус кривизны линзы, входящей
в устройство колец Ньютона, определяется теоретически по формуле:
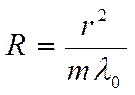
Так как практически трудно добиться
идеального контакта сферической поверхности линзы и плоской пластинки в одной
точке вследствие упругой деформации стекла и падения в место соприкосновения
пылинки, то формулу использовать непосредственно нельзя: кольцу с номером m в действительности может
соответствовать номер (m+p), где p – неизвестное целое число, одинаковое для всех колец. Для
исключения числа p вычисление
радиуса кривизны надо делать по разности квадратов радиуса двух колец:
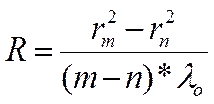
Ход работы:
Измеряем радиусы полученных колец:
;
;
.
Вычисляем радиусы действительных колец по формуле:
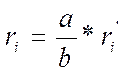
где =155
мм=0,155 м; =445мм=0,445м.
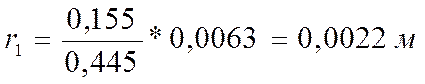
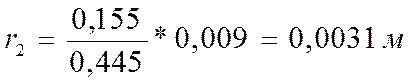
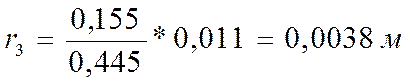
После того как мы вычислили действительные радиусы колец, вычисляем
радиус кривизны линзы по формуле:
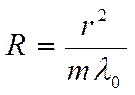
Где =435
Нм=м,
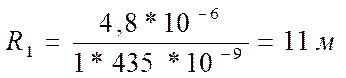
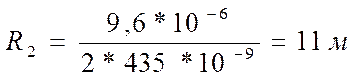
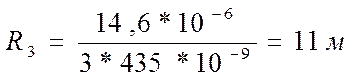
Найдем среднее значение:
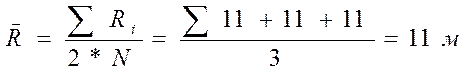
Найдем средне квадратичную
погрешность:
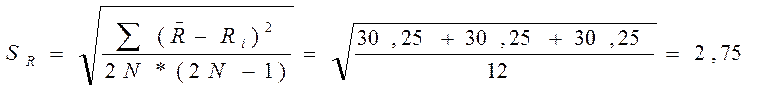
Доверительный интервал найдем
по формуле:
;
;
Найдем относительную
погрешность:
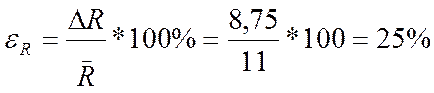
Вывод: Мы определили радиусы
кривизны линзы R, входящей в устройство колец Ньютона, а также
оценили доверительный интервал и относительную погрешность в определении
величины R.
Похожие материалы
- Изучение гармонических колебаний пружинного маятника
- Изучение законов кинематики и динамики поступательного движения на машине Атвуда
- Изучение основных законов внешнего фотоэлектрического эффекта
Информация о работе
Тип:
Отчеты по лабораторным работам
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
У этого термина существуют и другие значения, см. Линза (значения).
Ли́нза (нем. Linse, от лат. lens — чечевица) — деталь из прозрачного однородного материала , имеющая две преломляющие полированные поверхности, например, обе сферические или же одну плоскую, а другую — сферическую. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, кристаллы, оптически прозрачные пластмассы и другие материалы[1].
Термин «линза» используют также применительно к другим приборам и явлениям, действие которых на излучение подобно действию линзы, например:
- плоские «линзы», изготовленные из материала с переменным показателем преломления, изменяющимся в зависимости от расстояния от центра;
- линзы Френеля;
- зонная пластинка Френеля, использующая явление дифракции;
- «линзы» воздуха в атмосфере — неоднородность свойств, в частности показателя преломления (проявляется в виде мерцания изображения звёзд в ночном небе);
- гравитационная линза — наблюдаемый на межгалактических расстояниях эффект отклонения электромагнитных волн массивными объектами;
- магнитная линза — устройство, использующее постоянное магнитное поле для фокусирования пучка заряженных частиц (ионов или электронов) и применяющееся в электронных и ионных микроскопах;
- изображение линзы, сформированное оптической системой или частью оптической системы. Используется при расчёте сложных оптических систем.
История[править | править код]
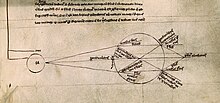
Свет преломляется сферическим стеклянным сосудом, наполненным водой. Роджер Бэкон, XIII век
Объектив для LSST, планируемого телескопа для обзора неба
Слово линза происходит от lēns, латинского названия чечевицы, потому что двояковыпуклая линза имеет форму чечевицы. Линзой также называется геометрическая фигура[2].
Некоторые учёные утверждают, что археологические свидетельства указывают на широкое использование линз в древности на протяжении нескольких тысячелетий[3]. Так называемая линза Нимруда — артефакт из горного хрусталя, датируемый VIII веком (750—710 гг.) до нашей эры, который, возможно, использовался в качестве увеличительного или зажигательного стекла либо предназначался для других целей[4][5][6]. Другие предположили, что некоторые египетские иероглифы изображают «простые стеклянные менисковые линзы»[7].
Самый древний литературный источник, в котором упоминается об использовании линз, а именно зажигательного стекла, — пьеса Аристофана «Облака» (424 г. до н. э.)[8]. Плиний Старший (I век н. э.) подтверждает, что зажигательные стёкла были известны в античности, а именно в римский период[9]. В работах Плиния содержится также самая ранняя из известных ссылок на использование корректирующих линз: он упоминает, что Нерон, как говорят, смотрел гладиаторские игры, используя изумруд (предположительно вогнутый, чтобы исправить близорукость, хотя отсылка не точна)[10]. И Плиний, и Сенека Младший (3 г. до н. э. — 65 г. н. э.) описали увеличивающий эффект стеклянного шара, наполненного водой.
Птолемей (II век) написал книгу по оптике, которая, однако, сохранилась только в латинском переводе с неполного и очень плохого арабского перевода. Однако книга была принята средневековыми учёными в исламском мире и прокомментирована Ибн Салом (X век), чей вклад, в свою очередь, был улучшен Альхазеном (Книга об оптике, XI век). Арабский перевод Оптики Птолемея стал доступен в латинском переводе в XII веке (Евгений Палермский, 1154 г.). Между XI и XIII веками были изобретены «камни для чтения». Это были примитивные плоско-выпуклые линзы, изначально сделанные путем разрезания стеклянной сферы пополам. Средневековые (XI или XII век) линзы Висбю из горного хрусталя могли быть предназначены для использования в качестве зажигательных стёкол, однако возможно, что их изготовили для каких -то иных целей[11].
Очки были изобретены как усовершенствование «камней для чтения» периода Высокого Средневековья в Северной Италии во второй половине XIII века[12]. Это стало началом развития оптической индустрии шлифовки и полировки линз для очков — сначала в Венеции и Флоренции в конце XIII века[13], а затем в центрах производства очков в Нидерландах и Германии[14]. Создатели очков сделали улучшенные типы линз для коррекции зрения, основанные больше на эмпирических знаниях, полученных при наблюдении за эффектами линз (вероятно, без знания элементарной оптической теории того времени)[15][16]. Практические разработки и эксперименты с линзами привели к изобретению составного оптического микроскопа около 1595 года и телескопа-рефрактора в 1608 году — и тот и другой появились в центрах изготовления очков в Нидерландах[17][18].
С изобретением телескопа в XVII веке и микроскопа в начале XVIII было проведено множество экспериментов с формами линз в стремлении исправить наблюдаемые в последних хроматические ошибки. Оптики пытались конструировать линзы различной формы кривизны, ошибочно полагая, что ошибки возникли из-за дефектов сферической формы их поверхностей[19]. Оптическая теория преломления и эксперименты показали, что ни один одноэлементный объектив не может сфокусировать все цвета. Это привело к изобретению составной ахроматической линзы Честером Муром Холлом в Англии в 1733 году, изобретение также было заявлено англичанином Джоном Доллондом в патенте 1758 года.
Растение, видимое через двояковыпуклую линзу
Характеристики простых линз[править | править код]
В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирающих линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.
Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), и фокусным расстоянием.
Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, показатель преломления, коэффициент дисперсии, показатель поглощения и показатель рассеяния материала в выбранном оптическом диапазоне.
Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким показателем преломления (см. иммерсионный микроскоп, иммерсионные жидкости).
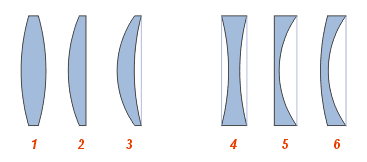
Виды линз: собирающие: 1 — двояковыпуклая; 2 — плоско-выпуклая; 3 — вогнуто-выпуклая (положительный (выпуклый) мениск); рассеивающие: 4 — двояковогнутая; 5 — плоско-вогнутая; 6 — выпукло-вогнутая (отрицательный (вогнутый) мениск)
Использование линзы для изменения формы волнового фронта. Здесь плоский волновой фронт становится сферическим при прохождении через линзу
Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски.
Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равна нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна).
Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.
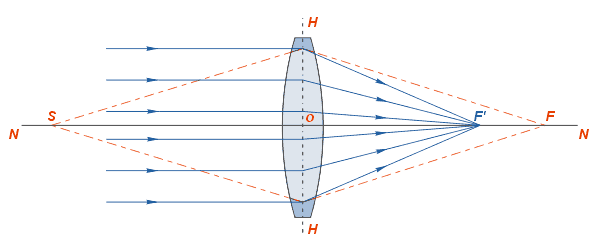
Основные элементы линзы: NN — оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре)[20].
Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или просто фокуса.
Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то на выходе из неё лучи преломляются под бо́льшим углом, и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется фокусом F’, а расстояние от центра линзы до фокуса — фокусным расстоянием.
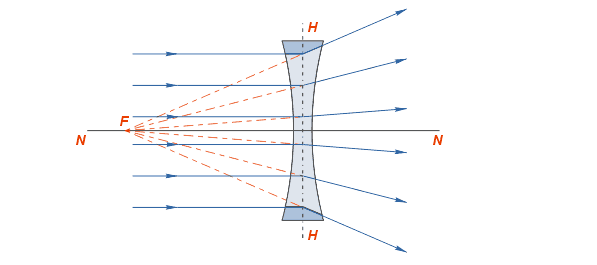
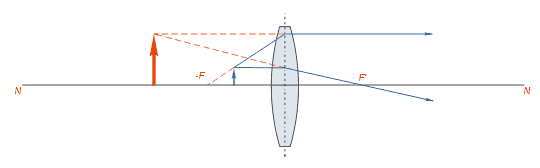
Лучи, падающие на рассеивающую линзу, на выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.
Мнимый фокус рассеивающей линзы
Сходящиеся лучи слева от линзы являются лучами, отраженными от поверхности линзы, и не связаны с положением мнимого фокуса
Сказанное о фокусе на оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на наклонной линии, проходящей через центр линзы под углом к оптической оси. Плоскость, перпендикулярная оптической оси, расположенная в фокусе линзы, называется фокальной плоскостью.
Собирающие линзы могут быть направлены к предмету любой стороной, вследствие чего лучи при прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от главных точек линзы.
Часто в технике применяется понятие увеличение линзы (лупы) и обозначается как 2×, 3× и т. д. В данном случае увеличение определяется по формуле 


Ход лучей в тонкой линзе[править | править код]
Линза, для которой толщина принята равной нулю, в оптике называется «тонкой». Для такой линзы показывают не две главных плоскости, а одну, в которой как бы сливаются вместе передняя и задняя.
Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы:
- луч, прошедший через оптический центр линзы, не меняет своего направления;
- параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости.
Рассмотрим луч SA произвольного направления, падающий на линзу в точке A. Построим линию его распространения после преломления в линзе. Для этого построим луч OB, параллельный SA и проходящий через оптический центр O линзы. По первому свойству линзы луч OB не изменит своего направления и пересечёт фокальную плоскость в точке B. По второму свойству линзы параллельный ему луч SA после преломления должен пересечь фокальную плоскость в той же точке. Таким образом, после прохождения через линзу луч SA пойдёт по пути AB.
Аналогичным образом можно построить другие лучи, например луч SPQ.
Обозначим расстояние SO от линзы до источника света через u, расстояние OD от линзы до точки фокусировки лучей через v, фокусное расстояние OF через f. Выведем формулу, связывающую эти величины.
Рассмотрим две пары подобных треугольников: 



Разделив первую пропорцию на вторую, получим
После деления обеих частей выражения на v и перегруппировки членов, приходим к окончательной формуле
где 
Ход лучей в системе линз[править | править код]
Ход лучей в системе линз строится теми же методами, что и для одиночной линзы.
Рассмотрим систему из двух линз, одна из которых имеет фокусное расстояние OF, а вторая O2F2. Строим путь SAB для первой линзы и продолжаем отрезок AB до вхождения во вторую линзу в точке C.
Из точки O2 строим луч O2E, параллельный AB. При пересечении с фокальной плоскостью второй линзы этот луч даст точку E. Согласно второму свойству тонкой линзы луч AB после прохождения через вторую линзу пойдёт по пути CE. Пересечение этой линии с оптической осью второй линзы даст точку D, где сфокусируются все лучи, вышедшие из источника S и прошедшие через обе линзы.
Построение изображения тонкой собирающей линзой[править | править код]
При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус. Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а передний позади.
Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние. От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображён ход только трёх лучей.
Три луча, исходящие из точки A, пройдут через линзу и пересекутся в соответствующих точках схода на A1B1, образуя изображение. Полученное изображение является действительным и перевёрнутым.
В данном случае изображение получено в сопряжённом фокусе в некоторой фокальной плоскости FF, несколько удалённой от главной фокальной плоскости F’F’, проходящей параллельно ей через главный фокус.
Далее приведены различные случаи построения изображений предмета, помещённого на различных расстояниях от линзы.
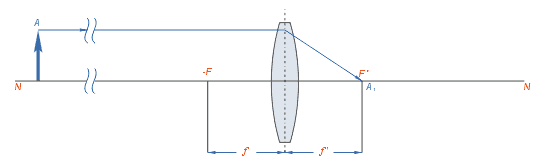
Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки.
Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием.
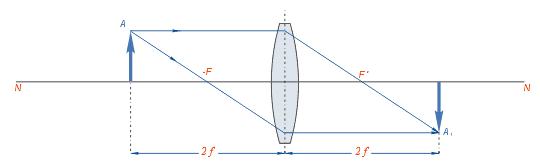
Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету.
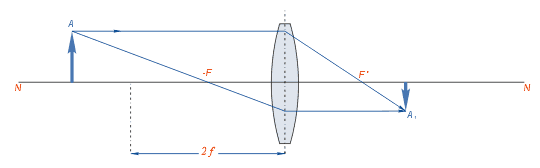
Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным.
Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности.
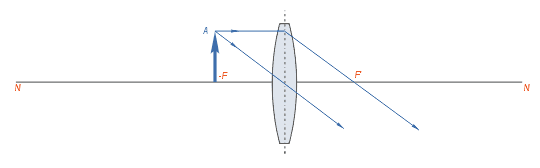
Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, то есть в данном случае линза работает как лупа.
Нетрудно заметить, что при приближении предмета из бесконечности к переднему фокусу линзы изображение удаляется от заднего фокуса и по достижении предметом плоскости переднего фокуса оказывается в бесконечности от него.
Эта закономерность имеет большое значение в практике различных видов фотографических работ, поэтому для определения зависимости между расстоянием от предмета до линзы и от линзы до плоскости изображения необходимо знать основную формулу линзы.
Формула тонкой линзы[править | править код]
Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями.
Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы (впервые полученной Исааком Барроу):
где 


Для нахождения той или иной неизвестной величины при двух известных пользуются следующими уравнениями:
Следует отметить, что знаки величин 


Изображения чёрных букв через тонкую выпуклую линзу с фокусным расстоянием f (красным цветом). Показаны лучи для букв E, I и K (синим, зелёным и оранжевым соответственно). Изображение буквы E (находящейся на расстоянии 2f) действительное и перевернутое, такого же размера. Изображение I (на f) — в бесконечности. Изображение К (на f/2) мнимое, прямое, увеличенное в 2 раза
Линейное увеличение[править | править код]
Линейным увеличением 



Здесь 
В практике вычислений гораздо удобнее это соотношение выражать в значениях 



Расчёт фокусного расстояния и оптической силы линзы[править | править код]
Значение фокусного расстояния для линзы может быть рассчитано по следующей формуле:
, где





Для 


Эту формулу также называют формулой тонкой линзы. Величина фокусного расстояния положительна для собирающих линз, и отрицательна для рассеивающих. Величина 

Указанные формулы могут быть получены аккуратным рассмотрением процесса построения изображения в линзе с использованием закона Снелла, если перейти от общих тригонометрических формул к параксиальному приближению. Кроме того, для вывода формулы тонкой линзы удобно заменить её треугольной призмой и затем использовать формулу угла отклонения этой призмы[23].
Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям, величина которых зависит от того, какой стороной линза повёрнута к свету.
Комбинация нескольких линз (центрированная система)[править | править код]
Линзы могут комбинироваться друг с другом для построения сложных оптических систем. Оптическая сила системы из двух линз может быть найдена как простая сумма оптических сил каждой линзы (при условии, что обе линзы можно считать тонкими и они расположены вплотную друг к другу на одной оси):
.
Если линзы расположены на некотором расстоянии друг от друга и их оси совпадают (система из произвольного числа линз, обладающих таким свойством, называется центрированной системой), то их общую оптическую силу с достаточной степенью точности можно найти из следующего выражения:
,
где 
Недостатки простой линзы[править | править код]
В современных оптических приборах к качеству изображения предъявляются высокие требования.
Изображение, даваемое простой линзой, в силу целого ряда недостатков не удовлетворяет этим требованиям. Устранение большинства недостатков достигается соответствующим подбором ряда линз в центрированную оптическую систему — объектив. Недостатки оптических систем называются аберрациями, которые делятся на следующие виды:
- геометрические аберрации:
- сферическая аберрация;
- кома;
- астигматизм;
- дисторсия;
- кривизна поля изображения;
- хроматическая аберрация;
- дифракционная аберрация (эта аберрация вызывается другими элементами оптической системы, и к самой линзе отношения не имеет).
Линзы со специальными свойствами[править | править код]
Линзы из органических полимеров[править | править код]
Полимеры дают возможность создавать недорогие асферические линзы с помощью литья.
В области офтальмологии созданы мягкие контактные линзы. Первыми производителями линз такого вида стала компания Bausch+Lomb[24]. Производство мягких линз основано на применении материалов, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля. Работа в течение более 20 лет привела к созданию в конце 1990-х годов силикон-гидрогелевых линз, которые благодаря сочетанию гидрофильных свойств и высокой кислородопроницаемости могут непрерывно использоваться в течение 30 дней круглосуточно.[25]
Линзы из кварцевого стекла[править | править код]
Кварцевое стекло — однокомпонентное стекло, состоящее из диоксида кремния, с незначительным (около 0,01 % и меньше) содержанием примесей Al2О3, СаО и MgO. Оно отличается высокой термостойкостью и инертностью ко многим химическим реактивам за исключением плавиковой кислоты.
Прозрачное кварцевое стекло хорошо пропускает ультрафиолетовые и видимые лучи света.
Линзы из кремния[править | править код]
Кремний хорошо пропускает инфракрасное излучение с длинами волн от 1 до 9 мкм, имеет большой показатель преломления (n = 3,42 при 
Кроме того, свойства кремния и современные технологии его обработки позволяют создать линзы для рентгеновского диапазона электромагнитных волн[27].
Просветлённые линзы[править | править код]
Путём нанесения на поверхность линзы многослойных диэлектрических покрытий можно добиться значительного уменьшения отражения света и, вследствие этого, увеличения коэффициента пропускания.Такие линзы легко узнать по фиолетовым бликам: они не отражают зелёный цвет, отражая красный и синий, что в сумме даёт фиолетовый. Подавляющее большинство линз для фототехники производства СССР, в том числе для бытовых объективов, изготавливалось просветлёнными.
Применение линз[править | править код]
Линзы являются широко распространённым оптическим элементом большинства оптических систем.
Традиционное применение линз — бинокли, телескопы, оптические прицелы, теодолиты, микроскопы, фото- и видеотехника. Одиночные собирающие линзы используются как увеличительные стёкла.
Другая важная сфера применения линз — офтальмология, где без них невозможно исправление недостатков зрения — близорукости, дальнозоркости, неправильной аккомодации, астигматизма и других заболеваний. Линзы используют в таких приспособлениях, как очки и контактные линзы. Также существует подвид линз, ночные линзы. Они имеют более жесткую основу и используются исключительно во время сна, для временной коррекции зрения в дневное время.
В радиоастрономии и радарах часто используются диэлектрические линзы, собирающие поток радиоволн в приёмную антенну, либо фокусирующие их на цели.
В конструкции плутониевых ядерных бомб для преобразования сферической расходящейся ударной волны от точечного источника (детонатора) в сферическую сходящуюся, применялись линзовые системы, изготовленные из взрывчатки с разной скоростью детонации (то есть с разным показателем преломления).
См. также[править | править код]
- Лентикулярный растр
- Линза Френеля
- Линза Люнеберга
- Билинза Бийе
- Цейс, Карл
- Контактные линзы
- Лупа
- Магнитная линза
- Фокус (физика)
- Оптические системы
- Оптические приборы
- Оптические материалы
- Аберрации оптических систем
Примечания[править | править код]
- ↑ Ананьев Ю. А. Линза // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 591—592. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ The variant spelling lense is sometimes seen. While it is listed as an alternative spelling in some dictionaries, most mainstream dictionaries do not list it as acceptable.
- ↑ Sines, George (1987). “Lenses in antiquity”. American Journal of Archaeology. 91 (2): 191—196. DOI:10.2307/505216.
- ↑ Whitehouse. World’s oldest telescope?, BBC News (1 July 1999). Архивировано 1 февраля 2009 года. Дата обращения: 10 мая 2008.
- ↑ The Nimrud lens/The Layard lens. Collection database. The British Museum. Дата обращения: 25 ноября 2012. Архивировано 19 октября 2012 года.
- ↑ D. Brewster. On an account of a rock-crystal lens and decomposed glass found in Niniveh // Die Fortschritte der Physik : [нем.]. — Deutsche Physikalische Gesellschaft, 1852. — P. 355.
- ↑ Kriss, Timothy C. (April 1998). “History of the Operating Microscope: From Magnifying Glass to Microneurosurgery”. Neurosurgery. 42 (4): 899—907. DOI:10.1097/00006123-199804000-00116. PMID 9574655.
- ↑ Aristophanes. The Clouds. — Project Gutenberg, 22 Jan 2013. — ISBN EBook #2562.
- ↑ Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 10 Архивная копия от 4 октября 2008 на Wayback Machine.
- ↑ Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 16 Архивная копия от 28 сентября 2008 на Wayback Machine
- ↑ Tilton, Buck. [[1] в «Книгах Google» The Complete Book of Fire: Building Campfires for Warmth, Light, Cooking, and Survival]. — Menasha Ridge Press, 2005. — P. 25. — ISBN 978-0-89732-633-9.
- ↑ Glick, Thomas F. [[2] в «Книгах Google» Medieval science, technology, and medicine: an encyclopedia]. — Routledge, 2005. — P. 167. — ISBN 978-0-415-96930-7.
- ↑ Al Van Helden. The Galileo Project > Science > The Telescope Архивная копия от 3 августа 2017 на Wayback Machine. Galileo.rice.edu. Retrieved on 6 June 2012.
- ↑ Henry C. King. [[3] в «Книгах Google» The History of the Telescope]. — Courier Dover Publications. — P. 27. — ISBN 978-0-486-43265-6.
- ↑ Paul S. Agutter. [[4] в «Книгах Google» Thinking about Life: The History and Philosophy of Biology and Other Sciences]. — Springer. — P. 17. — ISBN 978-1-4020-8865-0.
- ↑ Vincent Ilardi. [[5] в «Книгах Google» Renaissance Vision from Spectacles to Telescopes]. — American Philosophical Society, 2007. — P. 210. — ISBN 978-0-87169-259-7.
- ↑ Microscopes: Time Line Архивная копия от 9 января 2010 на Wayback Machine, Nobel Foundation. Retrieved 3 April 2009
- ↑ Fred Watson. [[6] в «Книгах Google» Stargazer: The Life and Times of the Telescope]. — Allen & Unwin. — P. 55. — ISBN 978-1-74175-383-7.
- ↑ This paragraph is adapted from the 1888 edition of the Encyclopædia Britannica.
- ↑ Ход лучей показан, как в идеализированной (тонкой) линзе, без указания на преломление на реальной границе раздела сред. Дополнительно показан несколько утрированный образ двояковыпуклой линзы.
- ↑ Хендель А. Основные законы физики. — М.: Физматгиз, 1959. — 284 с. Архивировано 21 января 2015 года.
- ↑ [psychology_pedagogy.academic.ru/14495/РАССТОЯНИЕ_НАИЛУЧШЕГО_ЗРЕНИЯ Расстояние наилучшего зрения на academic.ru]
- ↑ Ландсберг Г.С. §88. Преломление в линзе. Фокусы линзы // Элементарный учебник физики. — 13-е изд. — М.: Физматлит, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 236—242. — 656 с. — ISBN 5922103512.
- ↑ ИСТОРИЯ БРЕНДА Bausch & Lomb. Bausch & Lomb.
- ↑ Наука в Сибири. Дата обращения: 15 ноября 2007. Архивировано 20 января 2009 года.
- ↑ Физическая энциклопедия. В 5-ти томах. / А. М. Прохоров. — М.: Советская энциклопедия, 1988.
- ↑ Аристов В. В., Шабельников Л. Г. Современные достижения рентгеновской оптики преломления // УФН. — 2008. — Т. 178. — С. 61–83. — doi:10.3367/UFNr.0178.200801c.0061.
Литература[править | править код]
- Краткий фотографический справочник / Под общей редакцией д.т.н. В. В. Пуськова. — 2-е изд. — М.: Искусство, 1953.
- Ландсберг Г. С. Оптика. — 5-ое изд. — М.: Наука, 1976.
- Политехнический словарь / глав. ред. А. Ю. Ишлинский. — 3-е изд. — М.: Советская Энциклопедия, 1989.
- Линза // Фотокинотехника: Энциклопедия / Гл. ред. Е. А. Иофис. — М.: Советская энциклопедия, 1981. — 447 с.
Ссылки[править | править код]
- Как изготавливаются линзы для фотоаппаратов и видеокамер. Discovery (видео)
{{спам-ссылки|1=
- psychology_pedagogy.academic.ru
|2=1}