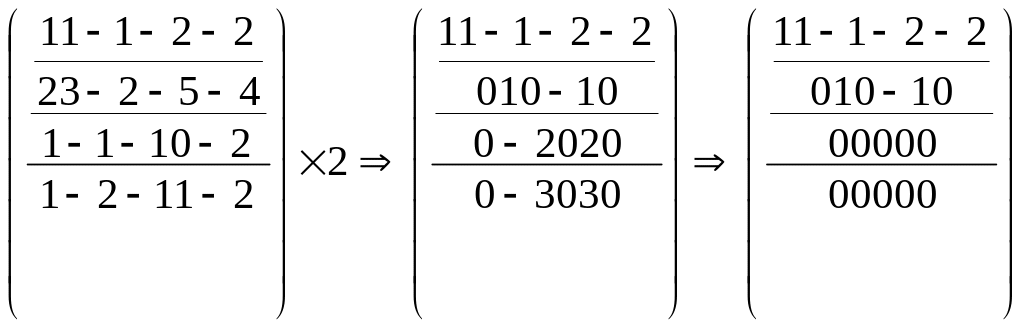Ранг матрицы как быстро найти

В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.

Минор матрицы

Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.

Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.

Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.

При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2

Другим минором 2-го порядка матрицы А является 0011=0

Предоставим иллюстрации построения миноров второго порядка матрицы А:

Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:

003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9

Иллюстрация, как получается минор 3-го порядка матрицы А:

Для данной матрицы миноров выше 3-го порядка не существует, потому что

k≤min(p, n)=min (3, 4)=3

Сколько существует миноров k-ого порядка для матрицы А порядка p×n?

Число миноров вычисляют по следующей формуле:

Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.

После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.

Ранг матрицы: методы нахождения

Ранг матрицы — наивысший порядок матрицы, отличный от нуля.

Rank (A), Rg (A), Rang (A).

Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.

Нахождение ранга матрицы по определению

Метод перебора миноров — метод, основанный на определении ранга матрицы.

Алгоритм действий способом перебора миноров:

Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).

Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.

Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.

Нахождение ранга матрицы методом окаймляющих миноров

Проще говоря, матрица, которая соответствует окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору Mok , вычеркиванием элементов одной строки и одного столбца.

Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.

Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.

Алгоритм действий:

Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.

Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.

Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.

Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)

Вспомним, что представляют собой элементарные преобразования.

Элементарные преобразования:

• путем перестановки строк (столбцов) матрицы;
• путем умножение всех элементов любой строки (столбца) матрицы на произвольное ненулевое число k;

путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.

Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).

Справедливость данного утверждения следует из определения матрицы:

• в случае перестановки строк или столбцов матрицы ее определитель меняет знак. Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю;
• в случае умножения всех элементов какой-либо строки (столбца) матрицы на произвольное число k, которое не равняется нулю, определитель полученной матрицы равен определителю исходной матрицы, которая умножена на k;

в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.

Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.

Для чего?

Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.

Проиллюстрируем этот процесс:

• для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов:

А~1b12b13⋯b1n-1b1n01b23⋯b2n-2b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01000⋯00⋮⋮⋮⋮⋮⋮000⋯00, Rank(A)=n

или

А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k

• для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов:

А~1b12b13⋯b1pb1p+1⋯b1n01b23⋯b2pb2p+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bpp+1⋯bpn, Rank(A)=p

или

А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0

• для квадратных матриц А порядка n на n:

А~1b12b13⋯b1n-1b1n01b23⋯b2n-1b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01, Rank(A)=n

или

A~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k, k<n

Если проводить элементарные преобразования, то не допускаются приближенные значения!

В примерах выше мы говорили об уникальности столбцов и строк. Ту же самую уникальность в математике обозначают еще одним термином — линейная независимость.

Сопоставим уже знакомый термин с новым понятием:

Другими словами, при линейной зависимости значения зависят друг от друга — из значений первой строки мы можем получить значения второй.

Все эти принципы будут работать, даже если мы представим матрицу как набор точек на графике.

Возьмем такой пример:

Опишем векторы так:

Здесь мы видим, что вектор

линейно зависит от

и

.

Также обратите внимание, что:

Используя только векторы

и

, мы можем достичь любого места на плоскости. Когда векторы линейно независимы и охватывают все пространство, их называют базисом этого пространства.

В нашем случае векторы

и

— это базис плоскости, потому что двумерное пространство часто называют плоскостью. Именно поэтому

и

так же полезны, как и оси

. То же самое можно сказать о любых двух линейно независимых векторах в двумерной плоскости.

Самая простая пара линейно независимых векторов — это

и

. Вместе они образуют матрицу

:

По сути, они образуют привычные оси

:

А теперь посмотрим на самые простые линейно независимые векторы в трехмерном пространстве. Матрица будет выглядеть так:

А так выглядит сам график:

Показать четырехмерное пространство на картинке не получится, но сама матрица выглядит так:

Максимальное число
линейно-зависимых строк матрицы A
наз. рангом
матрицы и обознач r(a).
Наибольшее из порядков миноров данной
матрицы отличных от 0 наз рангом
матрицы.

Свойства:

1)при транспонировании
rang=const.

2)если вычеркнуть
нулевой ряд, то rang=const;

3)rang=cost,
при элементарных преобразованиях.

3)для вычисл ранга
с помощью элементар преобраз матрица
A
преобраз в матриц B,
ранг которой легко находится.

4)ранг треуг
матрицы=числу ненулевых элем, располож
на глав. диагоналях.

Методы нахождения
ранга матрицы:

1. метод
   окаймляющих миноров

2. метод
   элементарных преобразований

метод
окаймляющих миноров:

метод
окаймляющих миноров позволяет
алгоритмизировать процесс нахождения
ранг-матрицы и позволяет свести к
минимуму количество вычисления миноров.

1. если
   в матрице все нулевые элементы, то ранг
   = 0

2. если
   есть хоть один ненулевой элемент =>
   r(a)>0

теперь
будем окаймлять минор М1, т.е. будем
строить всевозможные миноры 2-ого
порядка, ктр. содержат в себе i-тую
строку и j-тый
столбец, до тех пор, пока не найдем
ненулевой минор 2-ого порядка.

М2
(i,
i1,
j.j1)

Дальше
аналогично строим миноры 3-го порядка,
окаймляющие М2 (минор), до тех пор, пока
не получим минор, отличный от нуля.

Процесс
будет продолжаться до одного из
событий:

1. размер минора достигнет
числа к.

1. на
   каком-то этапе все окаймленные миноры
   окажутся = 0.

В
обоих случаях величина ранга-матрицы
будет равна порядку большего отличного
от нуля минора.

Метод
элементарных преобразований:

как
известно, понятие треугольной матрицы
определяется только для квадратных
матриц. Для прямоугольных матриц
аналогом является понятие трапецивидной
матрицы.

Например:

ранг
= 2.

7. Невырожденные системы слау. Способы решения.

СЛАУ
принято записывать в матричной форме,
когда сами неизвестные не указываются,
а указывается только матрица системы
А и столбец свободных членов В.

Решение
невырожденных СЛАУ методом Крамера:

Х=А^-1*В

А^-1=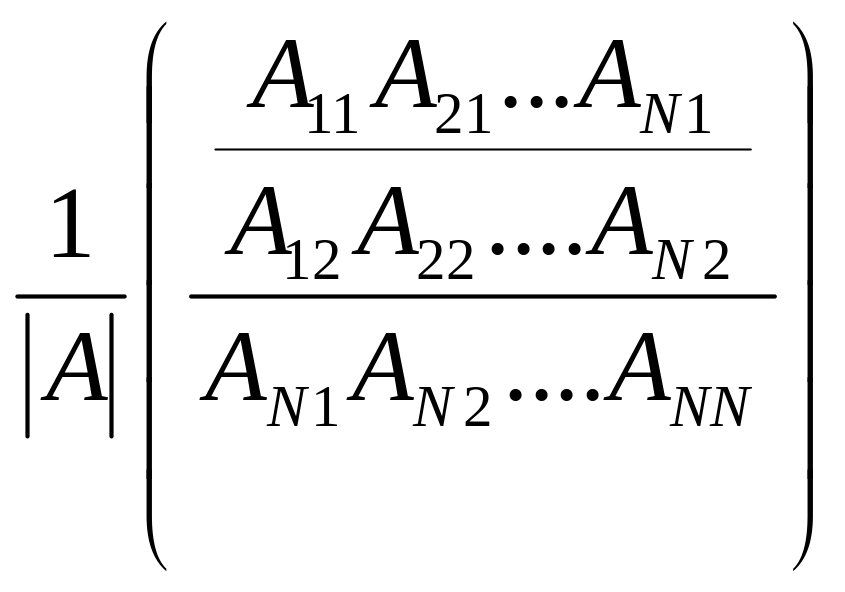

X1=
(A₁₁b₁
+ A₂₁b₂
+ …+A_n1b_n)

Теорема:
(Крамера):

решение
невырожденных уравнений АХ=В,

можно
записать так:

,
Ак получается из А путем замены к-го
столбца на столбец свободного члена
В.

8. Метод Гаусса. Произвольные слау. Теорема Кронекера-Капелли.

Система уравнений
(СУ), содерж m-уравнений
и n-неизвестных
наз. системой
вида
a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁
… a_M1x₁+a_M2x₂+…+a_Mnx_n=b_m,
где a_ij
– коэф системы и изменяется от 1 до n.
Расширенной
матрицей
наз матрица, сост из исходной матрицы
А и свободных .

Решением системы
наз n
значений неизвестных x₁=c₁
… x_n=c_n,
при подстановке которых все ур-ия
системы обращаются в верное равенство.

Система уравнений
наз. совместной,
если имеет хотя бы одно решение, иначе
она несовместна. Совместная система
наз. определённой,
если она имеет единственное решение.

Системы наз.
равносильными,
если они имеют одно и то же решение.

Замечание:
эквивалентные системы получаются при
элементарных преобразованиях при
условии, что преобраз вып только под
строками.

СЛАУ наз однородной,
если все свободные члены=0.

Теорема
Кронекера-Капелли:
система лин алг ур-ий совместна, когда
rangA=rang
(волнистая).
Теорема:
если rang
совместной системы= числу неизвестных,
то система имеет одно решение. Теорема:
если ранг совмест сист < числа
неизвестных, то система имеет бесконеч
решений.

Правило решения
СУ.

1)найти ранг основной
и расширенной матрицы (если rA
не =rA
с крыш, то система несовместна.

2) если rA=rA
с крыш и =r,
то система совместна и надо найти
базисный минор порядка r.

3)Берём r
ур-ий из коэф которых составлен базисн
минор. Остальные ур-ия отбрасываем.
Неизвестные, коэф которых входят в
минор наз главными. Из оставл слева, а
остальные (n-r)
– справа.

4)Найти выражения
главных неизв через свободные. Получено
общее решение системы

5)Придавая свободным
низвестным произвольное значение,
получим соотв значения главн неизв,
т.е. найдём частные решения.

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Ранг матрицы

Определение

Ранг матрицы $ A $ – это максимальное количество линейно-независимых строк (столбцов) этой матрицы. Обозначается $ rang A $ или $ r(A) $.

Формула ранга матрицы гласит, что он не должен превышать порядка этой же матрицы: 

$$ 0 leq rang A_{m times n} leq min (m,n) $$

Чтобы найти ранг матрицы существует два метода:

1. Метод окамляющих миноров
2. Метод элементарных преобразований

На практике применяется второй способ, так как он универсальный и позволяет вычислять ранг матриц любого порядка. Основан он на свойстве, заключаещегося в том, что $ rang A $ не меняется в случае проведения элементарных преобразований над матрицей. Путём приведения матрицы к ступенчатому виду мы узнаем количество линейно-независимых строк (столбцов), которое равно рангу матрицы.

Пример 1

Определить ранг матрицы $$ A = begin{pmatrix} 2&0&-2 \ -4&0&4 end{pmatrix} $$

Решение

Пример решаем с помощью элементарных преобразований. Приводим матрицу к ступенчатой форме.  Прибавляем удвоенную первую строку ко второй: $$ A = begin{pmatrix} 2&0&-2 \ -4&0&4 end{pmatrix} overset{c_2+2c_1}{thicksim} begin{pmatrix} 2&0&-2 \ 0&0&0 end{pmatrix} $$ В полученной матрице появилась нулевая строка, которую необходимо убрать из матрицы: $$ begin{pmatrix} 2&0&-2 \ 0&0&0 end{pmatrix} thicksim begin{pmatrix} 2&0&-2 end{pmatrix} $$ Теперь после преобразований количество строк $ m = 1 $, количество столбцов $ n=3 $. Наименьшее число $ m = 1 $, поэтому $ rang A = 1 $. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ rang A = 1 $$

Пример 2

Найти ранг матрицы: $$ A = begin{pmatrix} 4&2&3 \ 5&2&1 \ 9&4&4 end{pmatrix} $$

Решение

Выполняем элементарные преобразования над матрицей, чтобы узнать количество линейно-независимых строк. Вычитаем из второй строки, умноженной на четверку, первую строку, умноженную на пятерку: $$ A = begin{pmatrix} 4&2&3 \ 5&2&1 \ 9&4&4 end{pmatrix} overset{4c_2-5c_1}{thicksim} begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 9&4&4 end{pmatrix} $$ Вычитаем из третьей строки, умноженной на четыре, первую строку, умноженную на девять: $$ begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 9&4&4 end{pmatrix} overset{4c_3-9c_1}{thicksim}begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&-2&-11 end{pmatrix} $$ Вычитаем из третьей строки вторую строку: $$ begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&-2&-11 end{pmatrix} overset{4c_3-9c_1}{thicksim}begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&0&0 end{pmatrix} $$ Замечаем, что последняя строка матрицы нулевая, значит её можно вычеркнуть: $$ begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&-2&-11 end{pmatrix} thicksim begin{pmatrix} 4&2&3 \ 0&-2&-11 end{pmatrix} $$ После элементарных преобразований количество строк уменьшилось и стало $ m=2 $, а количество столбцов $ n = 3 $. По формуле ранга матрицы берем минимальные число из $ m $ и $ n $, то есть $ m=2 $. Получили, что $ rang A = 2 $

Ответ

$$ rang A = 2 $$

Найти ранг матрицы

На чтение 4 мин. Просмотров 1.5k. Опубликовано 02.04.2021

Ранг матрицы — это наибольшее число строк, которые линейно независимы и могут быть рассмотрены в качестве векторов. Более простым языком можно сказать, что рангом матрицы называется количество строк, в которых не все элементы равны нулю, после преобразования матрицы к ступенчатому виду. Ненулевыми строками называют те, в которых хотя бы один элемент имеет значение, отличное от нуля. В этой статье рассматриваются способы, с помощью которых можно найти ранг матрицы.

Содержание

1. Необходимые понятия
2. Способы для поиска ранга
3. Метод единиц и нулей
4. Сведение матрицы к ступенчатому виду
5. Метод окаймляющих миноров
6. Онлайн-калькуляторы для поиска ранга матрицы

Необходимые понятия

Элементарные преобразования – это преобразования, после которых полученная матрица является эквивалентной для исходной.

Элементарные преобразования означают следующие действия:

•  Умножить строку или столбец на число не равное 0;
•  Поменять местами любые 2 строки или 2 столбца;
•  Прибавить к строке другую строку (или к столбцу другой столбец) соответственно, помноженных на некоторое ненулевое число.

Матрица является ступенчатой, если она содержит хотя бы одну нулевую строку. Кроме этого если 1-й элемент некоторой строки не равный нулю расположен в i-м столбце, то этот элемент следующей строки должен находится в столбце с номером большим за i.

Минор k-го порядка – это определитель матрицы размера k на k, состоящей из k строк и такого же числа столбцов исходной матрицы. Порядок в этих строках и столбцах при этом остаётся прежним.

Способы для поиска ранга

Метод единиц и нулей

После применения элементарных преобразований, каждая матрица может быть приведена к такому виду, при котором все её столбцы будут состоять строго из нулей или иметь в своём составе максимум одну единицу. Посчитав количество единиц, мы сможем определить ранг.

Алгоритм, реализующий данный метод:

•  Выполняем элементарные преобразования до тех пор, пока матрица не будет состоять только из нулей и единиц
•  Считаем количество единиц
•  Количество единиц равно искомому рангу

Пример поиска ранга, используя метод нулей и единиц:

1.  Первоначально дана матрица такого вида:
2.  3-й столбец разделим на 2. 1-ую строку умножим на -2 и сложим с 4-й.
3.  Умножим 2-й столбец на -2 и сложим его с 4-м столбцом. После этого умножим 2-й столбец на -4 и сложим его с 1-м. Далее прибавим 2-й столбец к 5-му.
4.  3-ю строку умножим на -2. Прибавим её ко 2-ой.
5.  Сложим 5-й столбец с 1-м.
6.  3-й столбец умножим на 3 и сложим с 1-м.
7.  Умножим 3-й столбец на -1 и прибавим к нему 2-й и 4-й.
8.  Умножим 4-й столбец на -3 и сложим с 5-м. Наконец умножим 4-й столбец на -1. Итоговая матрица принимает следующий вид:

Количество единиц составляет 3, следовательно ранг имеет такое же значение.

Сведение матрицы к ступенчатому виду

Для данного способа также, как и для предыдущего, сперва нужно привести матрицу к определённому виду. Сведение её к ступенчатой позволяет найти ранг матрицы методом элементарных преобразований.

Алгоритм для данного метода:

•  Выполняем элементарные преобразования, пока матрица не станет ступенчатой
•  Считаем количество строк
•  Количество строк равно искомому рангу.

Метод окаймляющих миноров

Чтобы найти ранг матрицы методом окаймляющих миноров нужно рассмотреть большое количество миноров.

Алгоритм, реализующий данный метод:

•  Находим наименьшее число из величины матрицы по горизонтали и вертикали. Оно будет максимальным возможным значением ранга.
•  Далее начинаем поиск миноров от самых меньших.
• Если минор имеет значение 0, то рассматриваем другие миноры этого порядка. Если все они имеют значение 0, то ранг равняется предыдущему порядку.
•  Если существует хотя бы один минор не равный 0, то увеличиваем порядок на 1 и рассматриваем окаймляющие миноры. Возвращаемся на 3-й пункт.

Онлайн-калькуляторы для поиска ранга матрицы

Иногда у пользователя нет времени, чтобы самостоятельно изучить методы для поиска ранга. Из-за этого возникает вопрос: «Как найти ранг матрицы для чайников?».

В сети «Интернет» достаточно калькуляторов, которые помогают найти ранг матрицы онлайн с подробным решением. Однако почти все они производят поиск ранга, применяя при этом элементарные преобразования. Найти ранг матрицы методом окаймляющих миноров онлайн чаще всего не предоставляется возможным, так как этот способ не очень удобен и требует большого количества вычисления определителей.