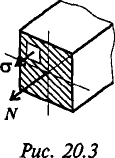
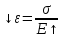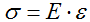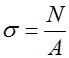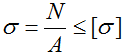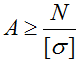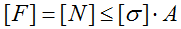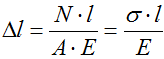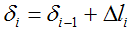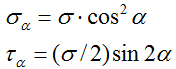Напряжения при растяжении и сжатии
При
растяжении и сжатии в сечении действует
только нормальное
напряжение.
Напряжения
в поперечных сечениях могут рассматриваться
как силы, приходящиеся на единицу
площади.
Таким
образом, направление
и знак напряжения в
сечении совпадают
с направлением и знаком силы в сечении
.
Исходя
из гипотезы плоских сечений, можно
предположить,
что напряжения при растяжении и сжатии
в пределах каждого сечения не меняются.
Поэтому
напряжение можно рассчитать по формуле
где
Nz
—
продольная сила в сечении;
А
—
площадь поперечного
сечения.
Величина
напряжения прямо пропорциональна
продольной силе и
обратно пропорциональна площади
поперечного сечения.
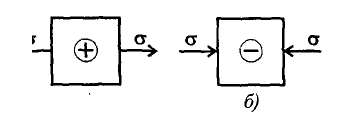
Нормальные
напряжения действуют при растяжении
от сечения,
а при сжатии к сечению.
Размерность
(единица измерения) напряжений — Н/м2
(Па), однако
это слишком малая единица, и практически
напряжения рассчитывают
в Н/мм2
(МПа): 1
МПа = 106Па
= 1 Н/мм2.
При
определении напряжений
брус разбивают на участки нагружений,
в пределах которых продольные
силы не изменяются,
и
учитывают
места изменений
площади
поперечных сечений.
Рассчитывают
напряжения по сечениям, и расчет оформляют
в виде эпюры нормальных напряжений.
Строится
и оформляется такая эпюра так же, как и
эпюра продольных
сил.
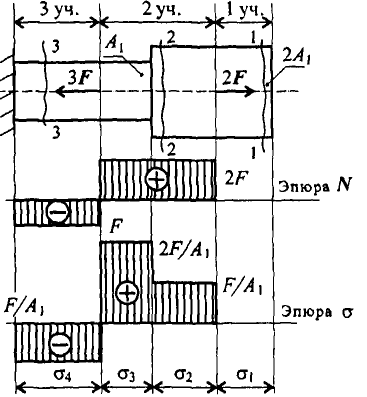
Рассмотрим
брус, нагруженный
внешними силами вдоль
оси .
Обнаруживаем
три участка
нагружения и определяем
величины продольных сил.
Участок
1:
Л/1 = 0. Внутренние
продольные силы равны
нулю.
Участок
2:
ЛГ2
= 2Р.
Продольная
сила на участке положительна.
Участок
3:
ЛГ3
= 2Р-—ЗР
= —Р. Продольная
сила на
участке отрицательна.
Брус
— ступенчатый.
С
учетом изменений величин
площади поперечного сечения
участков напряжений больше.
Строим
эпюры продольных сил и нормальных
напряжений. Масштабы
эпюр могут быть разными
и
выбираются исходя из удобства
построения.
Деформации при растяжении и сжатии
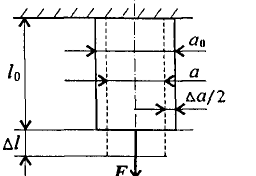
Рассмотрим
деформацию бруса под действием продольной
силы F.
Начальные
размеры бруса: lо
— начальная
длина, ао
— начальная ширина.
Брус
удлиняется на величину ∆l;
∆l
– абсолютное удлинение.
При
растяжении
поперечные размеры уменьшаются,
∆а
— абсолютное сужение;
∆l
>
0;
∆а
<0.
При
сжатии выполняется соотношение
∆l
<
0; ∆а
> 0.
В
сопротивлении материалов принято
рассчитывать деформации в относительных
единицах:
ε
= ∆l/
lо;
ε
—
относительное удлинение;
ε’
= ∆а/
ао;
ε’
—
относительное сужение.
Между
продольной и поперечной деформациями
существует зависимость
ε’
= με,
где
μ — коэффициент поперечной деформации,
или коэффициент Пуассона, характеристика
пластичности материала.
Закон Гука
В
пределах упругих деформаций деформации
прямо пропорциональны нагрузке:
F=k
∆l
где F
— действующая нагрузка; k
—
коэффициент.
В
современной форме: σ
=N/A;
ε
= ∆l/
lо;
Получим
зависимость σ=
Еε, где
Е
—
модуль упругости, характеризует
жесткость материала.
В
пределах упругости нормальные напряжения
пропорциональны относительному
удлинению.
Значение
Е
для
сталей в пределах (2…2,1) • 105
МПа.
При
прочих равных условиях, чем жестче
материал, тем меньше он деформируется:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
08.03.201514.37 Mб15Конспект лекций по ИУРЭ ДВОРСОН.doc
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Деформация агрегата
- Как рассчитывается растягивающее напряжение? (Примеры)
- Пример расчета
- Решенные упражнения
- – Упражнение 1
- Решение
- – Упражнение 2.
- Решение
- Ссылки
В Стресс-деформация Он определяется как сила, перпендикулярная площади на единицу площади, приложенная к объекту на его концах, чтобы оказывать на него тягу, благодаря которой он удлиняется. Его размеры – это сила / площадь, и в математической форме мы можем выразить это так:
τ = F / A
Единица усилия в Международной системе единиц такая же, как и для давления: паскаль, сокращенно Па, что эквивалентно 1 ньютону / м.2.
При растягивающем напряжении у вас есть две силы, действующие в одном и противоположных направлениях, которые растягивают тело. Если изначально длина объекта была Lили, при приложении растягивающего напряжения новая длина равна L, а растяжение ΔL рассчитывается по формуле:
ΔL = L – Lили
Твердые объекты обладают большей или меньшей эластичностью, а это означает, что когда растягивающее напряжение исчезает, они возвращаются к своим первоначальным размерам.
Это происходит до тех пор, пока напряжение не настолько велико, чтобы вызвать необратимую деформацию. Резина, резина или резиновые материалы хороши для создания эластичных предметов, а волосы и кожа, среди прочего, также обладают этим качеством.
Деформация агрегата
При изучении того, как тела деформируются под действием напряжения, очень удобно определять понятие напряжение, безразмерная величина. Деформация обозначается греческой буквой δ (строчная «дельта») и рассчитывается следующим образом:
δ = ΔL / Lили
Деформация используется для сравнительной оценки деформации объекта под напряжением. Давайте посмотрим на это так: растянуть штангу длиной 1 метр на 1 см – это не то же самое, что растянуть штангу длиной 10 м на 1 см. В первом случае деформация значительно больше, чем во втором.
Как рассчитывается растягивающее напряжение? (Примеры)
Английский физик и современник Ньютона по имени Роберт Гук (1635-1703) исследовал упругие свойства тел и установил закон, носящий его имя. При этом приложенное напряжение связано с деформацией, испытываемой при небольшом напряжении:
Напряжение ∝ Деформация (единица)
Логично ожидать, что чем выше растягивающее напряжение, тем больше произойдет удлинение. Используя определения, данные выше:
τ ∝ δ
Константа пропорциональности, необходимая для установления равенства, обозначается Y и известна как модуль Юнга или модуль упругости, характерный для материалов:
τ = Y⋅δ
Модуль Юнга имеет те же единицы растягивающего напряжения, поскольку деформация безразмерна.
Итак, один из способов рассчитать растягивающее напряжение в теле с упругими свойствами – это измерить деформацию и узнать ее модуль Юнга. Эта сумма была определена экспериментально для многих материалов и занесена в таблицу.
Пример расчета
Предположим, что проволока из закаленной стали диаметром 3 мм подвергается растягивающему напряжению, и на ней висит груз 250 Н. Какова будет величина этого напряжения?
Что ж, мы можем использовать определение растягивающего напряжения как частное между силой, перпендикулярной поверхности, и площадью этой поверхности. Давайте сначала рассчитаем площадь, считая провод круглого сечения:
А = π. (d / 2)2 = π. (d2 /4)
Диаметр провода 3 мм, и эти единицы необходимо перевести в метры:
г = 3 х 10-3 м.
А = π. (3 х 10-3 м)2 / 4 = 7,07 х 10-6 м2.
Растягивающее напряжение создается грузом, подвешенным к проволоке, который прикладывается перпендикулярно поперечному сечению проволоки, поэтому:
τ = 250 Н / 7,07 x 10-6 м2 = 3,5 х 10 7 Па
Паскаль – довольно маленькая единица, поэтому кратность не является чем-то необычным. Зная, что 1 мега-паскаль (МПа) равен 106 паскаль, растягивающее напряжение составляет:
τ = 35 МПа
Решенные упражнения
– Упражнение 1
Модуль упругости стержня 4 х 1011 Па. Какая деформация получается при приложении растягивающего усилия 420 МПа?
Решение
Используемое уравнение:
τ = Y⋅δ
С его помощью рассчитываем деформацию:
δ = τ / Y = 420 х 106 Па / 4 x 1011 Па = 0,00105
δ = ΔL / Lили
Следовательно, деформация ΔL равна:
ΔL = 0,00105 лили
Если, например, стержень изначально был длиной 1 метр, при этом растягивающем напряжении он растягивается всего на 0,00105 м = 1,05 мм.
– Упражнение 2.
Стальная проволока имеет длину 1,50 м и диаметр 0,400 мм. Один конец прикреплен к потолку, а к другому прикреплен заземляющий отражатель. м = 1,50 кг, которое выпущено. Рассчитать:
а) Растяжение проволоки.
б) Деформация и процент деформации. Может ли провод порваться под тяжестью отражателя?
Решение
Проволока будет растягиваться, так как при подвешивании отражателя он подвергается растягивающему напряжению. Сила, вызывающая это усилие, – это вес отражателя.
Вес объекта массы m равен произведению массы на значение ускорения свободного падения, поэтому:
F = 1,50 кг x 9,8 м / с2 = 14,7 Н
Площадь сечения провода нужна:
А = π. (d2 / 4) = π x (0,4 x 10-3 м) 2/4 = 1,26 x 10-7 м2.
На основе этих результатов рассчитывается усилие, прилагаемое грузом к проволоке:
τ = 14,7 Н / 1,26 x 10-7 м2 = 1,17 х 108 Па
Проволока имеет упругие свойства, поэтому можно предположить, что выполняется закон Гука:
τ = Y⋅δ
Из таблицы модулей упругости находим, что для стали Y = 207 x 109 Па. Кроме того, штамм бывает:
δ = ΔL / Lили
Подставляя в уравнение для усилия:
τ = Y⋅δ = Y⋅ (ΔL / Lили)
Следовательно, растяжка:
ΔL = Lили τ / Y =
= 1,50 м x 1,17 x 108 Па / 207 x 109 Па = 8,5 х 10-4 m = 0,849 мм.
Деформация проволоки составляет:
δ = ΔL / Lили = 8,5 х 10-4 м / 1,5 м = 5,652 х 10-4
Если выразить это в процентах, то деформация единицы в процентах составляет 0,0565%, менее 0,1%, поэтому ожидается, что провод будет выдерживать вес отражателя хорошо, не ломаясь, поскольку деформация, которую он испытывает, не слишком велика по сравнению до исходной длины.
Ссылки
- Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
- Бир, Ф. 2010. Механика материалов. Макгроу Хилл. 5-е. Издание.
- Джанколи, Д. 2006. Физика: принципы с приложениями. 6-е. Эд Прентис Холл.
- Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.
- Валера Негрете, Дж. 2005. Заметки по общей физике. UNAM.
Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Обозначения в формулах:
σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.
Закон Гука:
Формула для расчета напряжений в поперечном сечении стержня
Условие прочности (проверочный расчет) при растяжении-сжатии
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Формула для расчета абсолютных деформаций
Расчет перемещения сечений
Здесь: δi — перемещение рассматриваемого сечения,
δi-1 — перемещение предыдущего сечения,
Δli — деформация участка между указанными сечениями.
Напряжения в наклонных сечениях
Здесь α — угол отклонения сечения от поперечного.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений: