- Подробности
- Обновлено 20.01.2019 00:33
- Просмотров: 566
1. Что такое рычаг?
Самый простой и распространенный механизм — рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
2. Как используют рычаг?

Можно для поднятия груза использовать в качестве рычага лом.
Для этого надо с силой F нажимать на конец лома В или приподнимать конец В.
В любом случае при поднятии груза необходимо преодолеть вес груза Р — силу, направленную вертикально вниз.
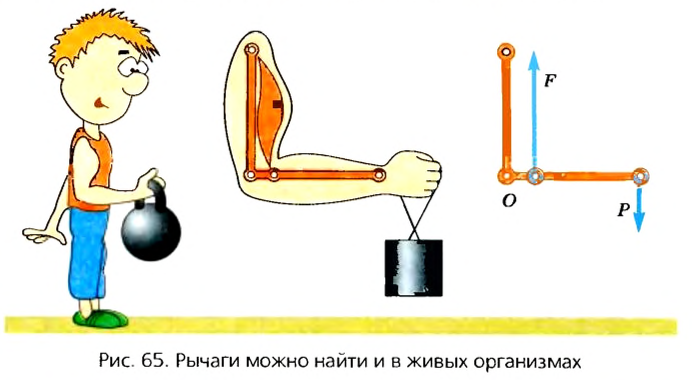
Для этого надо повернуть лом вокруг оси, проходящей через неподвижную точку лома — точку его опоры О.
Сила F, с которой человек действует на рычаг, меньше силы Р.
Используя рычаг, получаем выигрыш в силе.
2. Что называют плечом силы?
Например, есть рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В.
F1 и F2, действующие на рычаг, направлены в одну сторону.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
3. Как найти плечо силы? Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы.

OA — плечо силы F1,
OB — плечо силы F2.
4. Какое действие оказывают на рычаг силы?
Силы, действующие на рычаг, могут повернуть его вокруг оси или по ходу, или против хода часовой стрелки.
На рисунке выше:
С
ила F2 вращает рычаг по ходу часовой стрелки.
Сила F1 вращает рычаг против хода часовой стрелки.
Результат действия силы зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена.
5. В чем состоит правило (условие) равновесия рычага?
Правило равновесия рычага было установлено Архимедом (287—212 гг. до н. э.).
Правило (условие) равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

Например:
К рычагу по обе стороны от точки опоры подвешивают грузы так, чтобы рычаг оставался в равновесии.
Действующие на рычаг силы равны весам этих грузов.
Далее измеряют модули сил и их плечи.
Если сила F2 уравновешивает силу F1, то плечо меньшей силы в 2 раза больше плеча большей силы.

где
F1 и F2 — силы, действующие на рычаг,
l1 и l2 — плечи этих сил.
6. Как уравновесить меньшей силой большую?
При помощи рычага можно меньшей силой уравновесить большую силу.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.
Например:
Задача.
Человеку необходимо поднять с помощью рычага плиту массой 240 кг.
Большее плечо рычага равно 2,4 м.
Меньшее плечо рычага равно 0,6 м.
Какую силу надо приложить человеку к большему плечу рычага?

Человек преодолевает силу 2400 Н, прикладывая свою силу, равную 600 Н.
Здесь рычаг дает выигрыш в силе в 4 раза.
Однако плечо, на которое действует человек, в 4 раза длиннее того, на которое действует вес плиты:
2,4 м : 0,6 м = 4.
Следующая страница – смотреть
Назад в “Оглавление” – смотреть
С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.
Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.
На данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.
Устройство рычага
Что представляет собой рычаг?
Рычаг — это любое твердое тело, которое может вращаться вокруг неподвижной опоры.
Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.
На камень действует сила — вес $P$. Для того чтобы поднять камень, необходимо преодолеть его вес, направленный вертикально вниз. В первом случае (рисунок 2, а) Образавр давит на конец палки с силой $F$, а во втором (рисунок 2, б) — поднимает конец палки.
В обоих случаях у этого рычага есть неподвижная точка опоры — точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.
Сила, с которой Образавр действует на палку (рычаг), меньше веса камня, но тем не менее у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.
Виды рычагов
Таким образом, рычаги бывают двух видов (рисунок 3):
- Рычаг 1-го рода — силы приложены по разные стороны от точки опоры O (рисунок 3, а);
- Рычаг 2-го рода — силы приложены по одну сторону от точки опоры O (рисунок 3, б).
Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.
Плечо силы рычага
На рисунке 4 изображен рычаг. Его точки A и B — это точки приложения сил $F_1$ и $F_2$ соответственно. Точка опоры O расположена между точками A и B — значит, перед нами рычаг 1-го рода.
А теперь взгляните на схему этого рычага (рисунок 4). Силы $F_1$ и $F_2$ направлены в одну сторону.
Длина отрезка OA обозначена как $l_1$, а длина отрезка OB — $l_2$. Эти величины называются плечом силы.
Что называют плечом силы?
Плечо силы — это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Как найти плечо силы?
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.
Тогда, OA или $l_1$ — это плечо силы $F_1$, а OB или $l_2$ — плечо силы $F_2$.
Условие равновесия рычага
Чтобы получить условие равновесия рычага, нужно провести опыты. К рычагу по обе стороны от точки опоры подвешиваются разные груза так, чтобы каждый раз рычаг оставался в равновесии. В каждом случае измеряются модули сил и их плечи. В нашем случае (рисунок 4) видно, что сила $2 space Н$ уравновешивает силу $4 space Н$. А плечо меньшей силы в 2 раза больше плеча большей силы.
С помощью таких опытов было установлено правило равновесия рычага.
В чем состоит правило равновесия рычага?
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил:
$frac{F_1}{F_2} = frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, которые действуют на рычаг, $l_1$ и $l_2$ — плечи этих сил.
Кто установил правило равновесия рычага?
Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют — правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: «Дайте мне точку опору, и я переверну Землю!».
Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.
Например, возьмем рычаг, у которого одно плечо будет в 2 раза больше другого (как на рисунке 4). Приложим к точке A силу в $100 space Н$. Тогда в точке B мы сможем уравновесить силу в $200 space Н$ (в 2 раза большую). Если нам нужно поднять более тяжелый груз, то можно увеличить плечо рычага $l_1$, к которому мы прикладываем силу.
Примеры задач
Задача №1
Рабочий поднимает груз массой $300 space кг$ c помощью рычага 1-го рода. Большее плечо силы рано $3 space м$, а меньшее — $0.6 space м$. Какую силу рабочий прикладывает к большему плечу рычага?
Дано:
$m = 300 space кг$
$l_1 = 3 space м$
$l_2 = 0.6 space м$
$g = 9.8 frac{Н}{кг}$
$F_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда силу $F_1$, которую прикладывает к рычагу рабочий:
$F_1 = F_2 cdot frac{l_2}{l_1}$.
Сила $F_2$ — это вес груза $P$, который мы можем рассчитать формуле: $P = gm$. Подставим в нашу формулу и рассчитаем силу $F_1$:
$F_1 = F_2 cdot frac{l_2}{l_1} = gm cdot frac{l_2}{l_1} = 9.8 frac{Н}{кг} cdot 300 space кг cdot frac{0.6 space м}{3 space м} = 2940 space Н cdot 0.2 = 588 space Н$.
Ответ: $F_1 = 588 space Н$.
Задача №2
На рисунке 7 схематически изображен рычаг. Точка опоры находится в точке O. Одно деление на шкале рычага равно $10 space см$. Какую массу должен иметь груз, подвешенный в точке A, чтобы рычаг находился в равновесии?
Дано:
$m_1 = 100 space г$
$m_2 = 200 space г$
$l_1 = 50 space см$
$l_2 = 20 space см$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_1 = 0.1 space кг$
$m_2 = 0.2 space кг$
$l_1 = 0.5 space м$
$l_2 = 0.2 space м$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем силу, которая будет действовать на рычаг в точке B. Эта сила будет равна весу $P_2$, с которым груза массой $m_1$ и $m_2$ действуют на подвес. Обозначим эту силу $F_2$.
$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 frac{Н}{кг} cdot (0.1 space кг + 0.2 space кг) = 9.8 frac{Н}{кг} cdot 0.3 space кг approx 3 space Н$.
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда и рассчитаем силу $F_1$, с которой будет действовать на рычаг груз неизвестной массы:
$F_1 = frac{F_2 cdot l_2}{l_1} = frac{3 space Н cdot 0.2 space м}{0.5 space м} = 1.2 space Н$.
Сила $F_1$ будет равна весу $P_1$, с которым груз массой $m_3$ действуют на подвес:
$F_1 = P_1 = gm_3$.
Найдем массу груза:
$m_3 = frac{F_1}{g} = frac{1.2 space Н}{9.8 frac{Н}{кг}} approx 0.1 space кг = 100 space г$.
Ответ: $m_3 = 100 space г$.
К рычагу можно прикладывать две, или даже, несколько сил. В некоторых случаях рычаг остается неподвижным, то есть, находится в равновесии. Сформулируем условия, при которых рычаг, находящийся под действием нескольких сил, находится в равновесии.
Формула для условия равновесия рычага
Сумма вращательных моментов всех сил, приложенных к рычагу, должна равняться нулю.
На языке математики, это условие записывают так:
[large boxed { M_{1} + M_{2} + M_{3} + ldots + M_{n}= 0 } ]
Пояснение к формуле:
Для сил, вращающих рычаг в различные стороны, моменты будут иметь различные знаки. Поэтому, каждый вращательный момент в уравнение нужно подставлять со своим знаком!
Кратко условие знаков для моментов можно сформулировать так:
различные направления – разные знаки.
Например, если сила вращает рычаг по часовой стрелке, ее момент имеет знак «плюс», а если против часовой стрелки – то знак «минус».
Можно условиться наоборот: для сил, вращающих по часовой стрелке – знак «минус», а против часовой – знак «плюс». Главное, чтобы выполнялось условие: разные направления – разные знаки.
Советую освежить в памяти основные понятия о моменте силы. Для этого прочитайте такую статью (откроется в новой вкладке).
Для чего применяют рычаг
Рычаг позволяет поднимать или сдвигать тяжелые предметы с помощью малых сил.
То есть, рычаг помогает получить выигрыш в силе. Благодаря этому свойству мы часто пользуемся рычагами.
Однако, нужно помнить, что выигрыш в работе мы не получим, так как работу за нас рычаг не выполнит.
Поэтому, во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии.
Примечание:
Если совсем упростить, то работа – это сила, умноженная на расстояние.
Рычаги широко используют в технике. Нередко, в различных механических устройствах используются изогнутые рычаги, например, Г-образные.
Каким бы ни был рассматриваемый рычаг – прямым, или изогнутым, общий алгоритм для расчета его равновесия будет неизменным.
Алгоритм расчета для рычага, находящегося в равновесии
Решаем задачу, связанную с моментами двух сил, приложенных к рычагу.
1). Обращаем внимание на три точки:
- точку приложения первой силы,
- точку, к которой приложена вторая сила
- и, точку, через которую проходит ось вращения.
2). Ищем прямые углы между силами и расстояниями. Если какой-либо угол отличается от прямого, раскладываем либо силу, либо расстояние от точки приложения силы до оси вращения.
3). Составляем по одному уравнению для каждого вращательного момента.
Как рассчитать вращательный момент, написано здесь (откроется в новой вкладке)
4). Все моменты сил суммируем между собой. Напоминаю, что каждый момент силы записываем со своим знаком в левую часть уравнения для суммы моментов. Когда рычаг находится в равновесии, правая часть этого уравнения равна нулю.
Примечание:
Если к рычагу прикладывают больше двух сил, алгоритм расчетов аналогичен. С той лишь разницей, что нужно будет рассчитать большее количество вращательных моментов и записать их со своими знаками в общее уравнение для условия равновесия.
Примеры расчетов для рычага, находящегося в равновесии
Рассмотрим несколько случаев равновесия рычага, на который действуют две силы.
Во всех случаях условимся, что:
- силы прикладываются к различным точкам рычага;
- точки приложения сил не совпадают с точкой рычага, через которую проходит ось вращения.
Рычаг горизонтальный, силы перпендикулярны, ось вращения находится между точками приложения двух сил
Такое приложение сил применяют в рычажных весах, или башенном подъемном кране
Вокруг красной точки (рис. 1) рычаг может вращаться, так как через нее, в направлении «от нас», проходит ось вращения.
Пояснение к словам «через красную точку, в направлении «от нас», проходит ось вращения»: Если деревянный рычаг приложить к стене, то ось вращения – это гвоздь, забитый в красную точку.

Рис. 1. К горизонтальному рычагу перпендикулярно приложены две силы, ось вращения находится между точками приложения сил
Нас интересует два отрезка рычага:
- расстояние от силы (F_{1}) до оси вращения (красной точки). Это расстояние на рисунке обозначено (d_{1});
- и расстояние от силы (F_{2}) до красной точки. На рисунке оно обозначено (d_{2});
Каждая сила приложена перпендикулярно рычагу, расположенному горизонтально. Поэтому, расстояние (d_{1}) – это плечо силы (F_{1}) , а расстояние (d_{2}) являются плечом силы (F_{2}).
Запишем вращательные моменты этих сил.
(M_{1} = F_{1} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Запишем условие равновесия рычага:
(M_{1} + M_{2} = 0)
Сила (F_{2}) относительно красной точки вращает рычаг по часовой стрелке. Условимся моменты этой силы считать положительным.
А сила (F_{1}) будет вращать рычаг относительно красной точки против часовой стрелки, поэтому, ее момент будем считать отрицательным.
Теперь подставим знаки моментов в условие равновесия:
[-M_{1} + M_{2} = 0]
Это уравнение можно записать в развернутом виде
( — F_{1} cdot d_{1} + F_{2} cdot d_{2} = 0) – условие равновесия для рычага из рис. 1.
Рычаг горизонтальный, раскладываем силу, приложенную под непрямым углом
Не всегда силу прикладывают под прямым углом к рычагу. На рисунке 2 изображен горизонтальный рычаг, одна из сил приложена к нему под углом, не равным 90 градусам.

Рис. 2. К горизонтальному рычагу приложены две силы, ось вращения находится между точками приложения сил, одна из сил приложена перпендикулярно, другая – под тупым углом
Чтобы записать условие равновесия рычага, разложим (рис. 3) на проекции силу (F_{1}) и возьмем ту ее часть, которая будет располагаться перпендикулярно расстоянию (d_{1}).

Рис. 3. Одна из сил приложена под тупым углом к горизонтальному рычагу, разложив ее, возьмем часть, перпендикулярную рычагу
Для разложения силы (F_{1}) удобно заменить угол, обозначенный одной дугой, на угол, обозначенный на рисунке 3 двумя дугами. Будем обозначать угол, обозначенный двумя дугами символом (gamma).
Тогда
[ begin{cases} F_{1} cdot cos(gamma) = F_{1s} \ F_{1} cdot sin(gamma) = F_{1t} end{cases} ]
Примечание:
Просто и доступно о разложении вектора на проекции написано тут (откроется в новой вкладке).
Для записи момента ( M_{1} ) выберем перпендикулярную рычагу силу ( F_{1t}).
(M_{1} = F_{1t} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Вспомним о том, что противоположные направления вращения обозначают противоположными знаками
[-M_{1} + M_{2} = 0]
В развернутом виде условие равновесия для рисунка 3 выглядит так:
( — F_{1t} cdot d_{1} + F_{2} cdot d_{2} = 0)
Или так:
( F_{2} cdot d_{2} = F_{1t} cdot d_{1} )
Рычаг наклонный, раскладываем силу, приложенную под непрямым углом
В некоторых задачах рассматривают равновесие рычага, находящегося под наклоном к горизонтали (рис. 4).

Рис. 4. Одна из сил приложена под тупым углом к наклонному рычагу, разложим ее, и используем для вычисления вращательного момента часть, перпендикулярную рычагу
Здесь сила (F_{2}) приложена к рычагу под прямым углом, а угол между силой (F_{1}) и рычагом, отличается от прямого.
Разложим силу (F_{1}) на части и выберем для вычисления вращательного момента часть силы, расположенную перпендикулярно рычагу. Для разложения используем угол, обозначенный на рисунке 4 одной дугой и символом (alpha).
[ begin{cases} F_{1} cdot cos(alpha) = F_{1s} \ F_{1} cdot sin(alpha) = F_{1t} end{cases} ]
Вращательные моменты сил (F_{1t}) и (F_{2}):
(M_{1} = F_{1t} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Условие равновесия для рисунка 4 в развернутом виде:
( — F_{1} cdot sin(alpha) cdot d_{1} + F_{2} cdot d_{2} = 0)
Рычаг наклонный, раскладываем расстояние
В некоторых задачах (рис. 5) удобнее раскладывать не силу, а расстояние ( d ). На рисунке 5 для вычисления момента силы (M_{1}) разложим расстояние (d_{1}) между силой (F_{1}) и осью вращения (красной точкой).
Подробно о том, как раскладывать расстояние между точкой приложения силы и осью вращения, читайте тут (откроется в новой вкладке).

Рис. 5. Одна из сил приложена под тупым углом к наклонному рычагу, разложим расстояние d и, используем часть, перпендикулярную силе, для вычисления вращательного момента
Пользуясь рисунком 5, запишем моменты:
(M_{1} = F_{1} cdot d_{1t})
(M_{2} = F_{2} cdot d_{2})
Нам указали тупой угол (alpha) между силой и расстоянием от точки приложения силы до оси вращения. Но чтобы разложить (d_{1}) на части, удобнее использовать другой угол, смежный с углом (alpha).
Рассмотрим подробнее часть рисунка, на которой отмечены углы (рис. 6)

Рис. 6. Углы альфа и гамма образуют развернутый угол, угол гамма, обозначенный двумя дугами, используем для разложения расстояния d на перпендикулярную и, параллельную силе части
Из рисунка 6 видно, что углы (alpha) и (gamma) образуют развернутый угол. То есть, сумма углов (alpha) и (gamma) равна 180 градусам.
[ alpha + gamma = 180^{o} ]
Синусы таких углов равны.
[ sinleft(alpha right) = sinleft(gamma right)]
Разложим расстояние (d_{1}) на перпендикулярную и параллельную силе части, используя вместо угла (alpha ) угол (gamma).
[ begin{cases} d_{1} cdot cos(gamma) = d_{1s} \ d_{1} cdot sin(gamma) = d_{1t} end{cases} ]
Теперь можно записать условие равновесия для рычага, находящегося на рисунке 5.
(- M_{1} + M_{2} = 0)
( — F_{1} cdot d_{1t} + F_{2} cdot d_{2} = 0)
( — F_{1} cdot d_{1} cdot sin(gamma) + F_{2} cdot d_{2} = 0)
Или, используя угол (alpha ):
[ F_{2} cdot d_{2} = F_{1} cdot d_{1} cdot sin(alpha) ]
Точки приложения сил находятся по одну сторону от оси вращения
Так прикладывают силы, например, при устройстве шлагбаума.

Рис. 7. К горизонтальному рычагу приложены две силы, они направлены перпендикулярно рычагу и лежат по одну сторону от оси вращения
Из рисунка 7 видно, что силы перпендикулярны рычагу, значит моменты сил выражаются простыми соотношениями:
(M_{1} = F_{1} cdot d_{1})
(M_{2} = F_{2} cdot d_{2})
Сила (F_{2}) вращает рычаг по часовой стрелке относительно красной точки, поэтому, ее момент считаем положительным. Момент силы (F_{1}) отрицателен, так как она вращает рычаг относительно красной точки против часовой стрелки.
Равновесие рычага на рисунке 7 сохраняется, когда выполняется условие:
(- M_{1} + M_{2} = 0 )
(- F_{1} cdot d_{1} + F_{2} cdot d_{2} = 0)
Содержание:
Рычаг:
Взаимодействие может происходить через промежуточные тела.
Взаимодействие может происходить не только при непосредственном контакте, но и при наличии промежуточных тел. Таких примеров можно привести большое количество. Так, если мастер забивает гвоздь в углублении, он ставит на головку гвоздя металлический стержень и по нему ударяет молотком (рис. 58). Молоток действует на стержень, который, в свою очередь, уже действует на гвоздь.
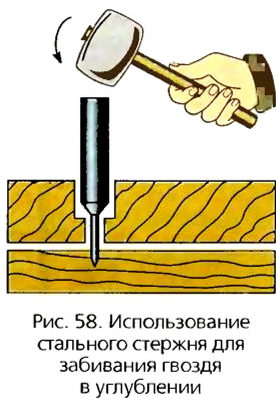
Можно ли изменять значения силы
Если взаимодействие между телами происходит через промежуточные тела, то можно изменять силы взаимодействия между ними. Оно может изменить как направление силы, так и ее значение. Одним из примеров такого использования промежуточных тел для взаимодействия между телами является рычаг. В быту и на производстве можно наблюдать много таких примеров.
Часто можно видеть, как тяжелый предмет поднимают или перемещают с помощью металлического стержня (рис. 59). В этом случае стержень называют рычагом.

Что такое рычаг
Рычагом называют жесткий стержень, имеющий ось вращения.
Ось вращения рычага может проходить через один из его концов или посередине рычага – между точками приложения сил.
Под действием нескольких сил рычаг может вращаться или быть неподвижным. В последнем случае говорят, что рычаг уравновешен.
Как уравновесить рычаг
Выясним, при каких условиях рычаг, на который действует несколько сил, будет уравновешен.
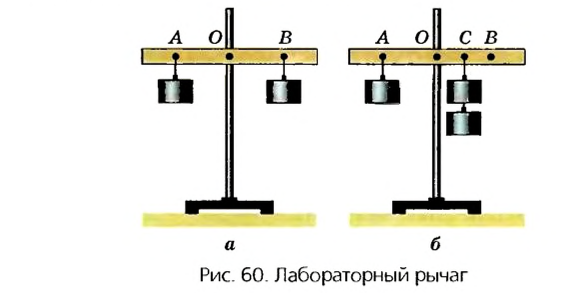
Для этого возьмем деревянную планку с отверстием посередине и поместим ее на оси, закрепленной в штативе (рис. 60). Это и будет рычаг. Слева от оси вращения повесим в точке А на расстоянии 10 см гирьку массой 102 г. В этом случае говорят, что точка А является точкой действия силы 1 Н. Под действием этой силы рычаг начнет вращаться против часовой стрелки. Для того чтобы он не вращался и оставался в горизонтальном положении, на другом конце рычага найдем такую точку В, при закреплении в которой гирьки массой 102 г рычаг перестанет вращаться. Измерив расстояние ОВ, увидим, что оно также равно 10 см. Таким образом, OA = ОВ, если Fl = F2. Если направление действия силы перпендикулярно к направлению оси вращения рычага, то расстояние от его оси вращения к направлению действия силы называют плечом силы.
Если силы, действующие на рычаг, находящийся в равновесии, равны, то равны и плечи этих сил.
Если левую гирьку оставить прикрепленной в точке А, а в точке В подвесить две такие гирьки массой по 102 г каждая, то равновесие рычага нарушится и он начнет вращаться. Достигнуть равновесия в этом случае можно, изменяя положение точки подвеса двух гирек. Так можно установить новое положение точки подвеса С. Измерив оба плеча, увидим, что правое плечо ОС в два раза меньше левого плеча OA.

В случае равновесия рычага плечо большей силы меньше, и наоборот, плечо меньшей силы больше.
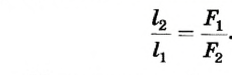
Используя свойства пропорции, получаем

В уравновешенном рычаге плечи сил обратно пропорциональны силам.
Что такое момент силы
Физическую величину, равную произведению силы на плечо, называют моментом силы. Единицей измерения момента силы является ньютон-метр (Н-м).
Сформулируем условие равновесия рычага в общем виде.
Рычаг пребывает в равновесии, если момент силы, вращающий рычаг по часовой стрелке, равен моменту силы, вращающему рычаг против часовой стрелки.
Конструктивно рычаг может быть таким, что силы будут действовать по одну сторону от оси вращения. Условие равновесия для него будет такое же, как и для рычага, рассмотренного выше.
Используя условие равновесия рычага, можно рассчитывать силы, действующие на него, или плечи этих сил.
Пример:
На одно из плеч рычага длиной 30 см действует сила 2 Н. Какая сила должна подействовать на другое плечо этого рычага длиной 15 см, чтобы он оставался неподвижным.
Дано:
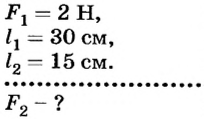
Решение
При условии равновесия рычага 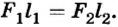 Отсюда
Отсюда
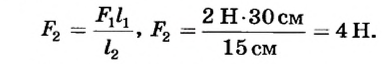
Ответ. На второе плечо рычага должна подействовать сила 4 Н.
Где используют рычаги
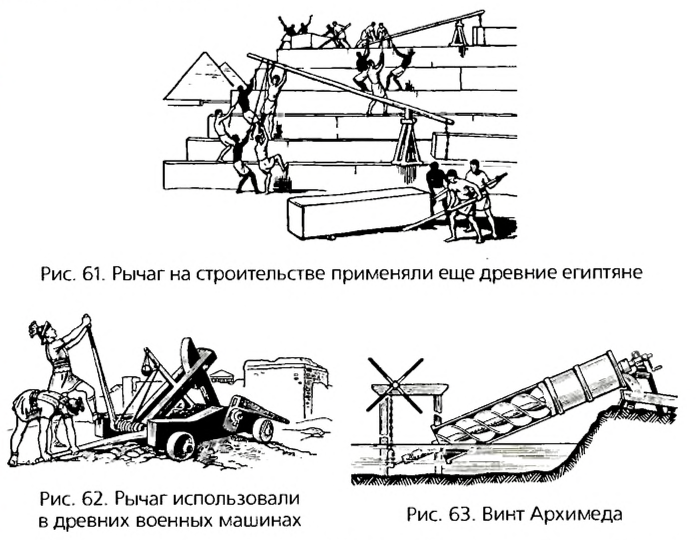
Рычаг известен человеку с того времени, когда человек взял палку, чтобы сбить плод с дерева. И вся следующая история человечества связана с использованием рычагов. Так, исследования историков показывают, что при строительстве пирамид древние египтяне использовали рычаги для поднятия тяжелых блоков на значительную высоту (рис. 61). Историкам науки известно, что древние римляне использовали рычаги для создания различных строительных и военных машин (рис. 62). Значительный вклад в теорию рычагов внес древнегреческий ученый и изобретатель Архимед. Сконструированные им машины помогали оборонять греческие города от захватчиков, подавать воду для орошения полей (рис. 63), перемещать значительные грузы на стройках, выполнять большое количество других подобных работ.
Рычаги широко используются и в современной технике, в самых разнообразных машинах.
Рычагом является стрела подъемного крана, используемого в строительстве. Она дает возможность получить выигрыш в силе или расстоянии. Момент силы, действующей на конце стрелы при подъеме груза, уравновешивается моментом противовеса, находящегося на противоположном конце стрелы.
Принцип рычага используется во многих устройствах и инструментах, которыми мы пользуемся ежедневно. На рисунке 64 изображены некоторые из них. На них легко найти части, исполняющие роль рычагов.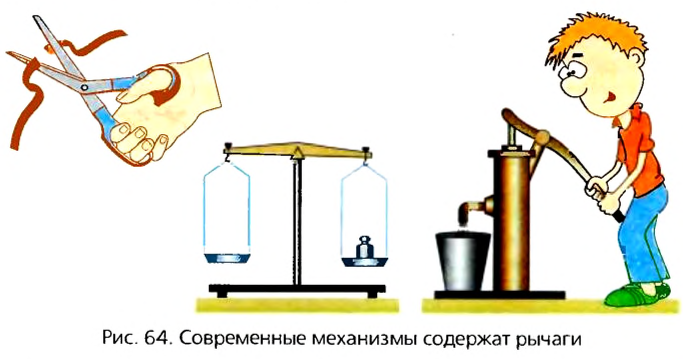
Рычаги можно найти и в живых организмах. По принципу рычага работают руки человека (рис. 65), ноги, голова.
 Архимед (около 287-212 гг. до н. э.) – известный древнегреческий ученый. Научные труды касаются математики, механики, физики и астрономии. Автор многих изобретений и открытий, в том числе машины для орошения полей, винта, рычагов, блоков, военных метательных машин и пр. В его труде «О плавающих телах» изложены основы гидростатики.
Архимед (около 287-212 гг. до н. э.) – известный древнегреческий ученый. Научные труды касаются математики, механики, физики и астрономии. Автор многих изобретений и открытий, в том числе машины для орошения полей, винта, рычагов, блоков, военных метательных машин и пр. В его труде «О плавающих телах» изложены основы гидростатики.
Условие равновесия рычага и момент силы
Как уже отмечалось, рычаг — твёрдое тело, которое может вращаться около неподвижной опоры. Его применяют для изменения направления и значения силы, например для уравновешивания большой силы малой. Рычаг имеет следующие характеристики
(рис. 202).
Точка приложения силы — это точка, в которой на рычаг действует другое тело.
Ось вращения — прямая, проходящая через неподвижную точку опоры рычага О, и вокруг которой он может свободно вращаться. Рассмотрим случай, когда ось вращения расположена между точками приложения сил  и
и 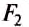 .
.
Линия действия силы — это прямая, вдоль которой направлена сила.
Плечо силы — кратчайшее расстояние от оси вращения тела О до линии действия силы. Плечо силы обозначается буквой d. Единицей плеча силы в СИ является один метр (1 м).
Опыт. Возьмём рычаг, подобный изображённому на рис. 203. На расстоянии 10 см от оси вращения подвесим к нему 6 грузиков, каждый массой по 100 г. Чтобы уравновесить рычаг двумя такими же грузиками, нам придётся их подвесить с другой стороны рычага, но на расстоянии 30 см.
Следовательно, для того чтобы рычаг находился в равновесии, нужно к длинному плечу приложить силу, во столько раз меньшую, во сколько раз его длина больше длины короткого плеча. Такое правило рычага описывают формулой обратно пропорциональной зависимости: 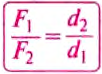 ,
,
где 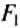 и
и 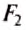 — силы, действующие на рычаг;
— силы, действующие на рычаг; 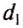 и
и 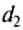 — плечи соответствующих сил. Поэтому правило (условие) равновесия рычага можно сформулировать так.
— плечи соответствующих сил. Поэтому правило (условие) равновесия рычага можно сформулировать так.
Рычаг находится в равновесии тогда, когда значения сил, действующих на него, обратно пропорциональны плечам этих сил.
С тех пор, когда Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский учёный П. Вариньон придал ему более общую форму, используя понятие момента силы.
Момент силы М– это физическая величина, значение которой опре-Г деляется произведением модуля силы F, вращающей тело, и ее плеча d : 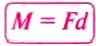 .
.
Единицей момента силы в СИ является один ньютон-метр (1 Н • м), равный моменту силы 1 Н, приложенной к плечу 1 м.
Докажем, что рычаг находится в равновесии под действием двух сил, если значение момента М1 силы, вращающей рычаг против часовой стрелки, равно значению момента М2 силы, вращающей его по часовой стрелке, т.е.: 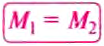
Из правша рычага 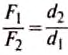 на основе свойства пропорции вытекает
на основе свойства пропорции вытекает
равенство: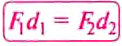 . Но
. Но 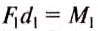 — момент силы, вращающей рычаг против часовой стрелки (рис. 202),
— момент силы, вращающей рычаг против часовой стрелки (рис. 202),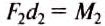 — момент силы, вращающей рычаг по часовой стрелке. Таким образом:
— момент силы, вращающей рычаг по часовой стрелке. Таким образом: 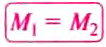 ,
,
что и требовалось доказать. Итак, правило (условие) равновесия рычага можно ещё сформулировать так.
Рычаг находится в равновесии под действием двух сил, если значение момента силы, вращающей рычаг против часовой стрелки, равно значению момента силы, вращающей его по часовой стрелке.
Момент силы — важная физическая величина, она характеризует действие силы, показывает, что оно зависит и от модуля силы, и от её плеча. Например, мы знаем, что действие силы на дверь зависит и от модуля силы, и оттого, где приложена сила: дверь тем легче повернуть, чем дальше от оси вращения приложена сила, действующая на неё; гайку легче открутить длинным гаечным ключом, чем коротким; ведро тем легче вытянуть из колодца, чем длиннее ручка ворота.
Основы статики и равновесие рычага
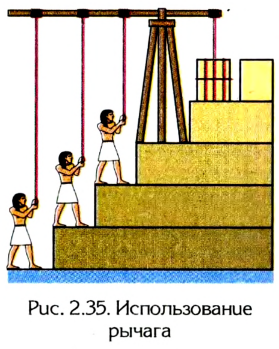
Еще в давние времена люди использовали обычную палку в качестве рычага, выигрывая этим в силе. На рисунке 2.35 показано, как с помощью рычага можно поднять по ступенькам большие каменные глыбы, например для строительства пирамид.
В древних книгах по механике, написанных учеными Греции и Египта, главным образом рассматривались вопросы статики. Важнейшие открытия в этой области принадлежали великому греческому философу Аристотелю, который и дал название «механика» науке, изучающей простейшие движения материальных тел, находящихся в природе или создающихся людьми в процессе их деятельности.
Ученые уже тогда понимали значение статики как одной из основных составляющих фундамента механики. Дальнейшее развитие науки и, особенно, техники подтвердило правильность их вывода: действие огромного количества £ механизмов и машин базируется на законах о равновесии сил.
Аристотель (384-322 до н. э.) – один из известнейших ученых Древней Греции. Изучал вопросы ста-тики, разработал классификацию механических движений, сформулировал закон прямолинейного распространения света, объяснил природу атмосферных явлений и др.
Основы науки о равновесии были заложены еще Архимедом. Именно он ввел в физику такое понятие, как центр тяжести и момент силы относительно точки и оси, определил положение центра тяжести для многих тел и фигур, математически обосновал законы рычага, сформулировал правила приложения параллельных сил.
- Заказать решение задач по физике
В своей работе «О равновесии плоских фигур» Архимед опирался на положения, которые считал само собой разумеющимися:
Архимед (287-212 до н. э.) – древнегреческий физик, математик, исследователь, инженер. Изучал условия равновесия тел, простые механизмы, плавание тел и др. Установил, что соотношение длины любой окружности к ее диаметру (число 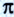 ) колеблется между
) колеблется между 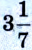 и
и 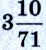 (3,142 – 3,140); на то время это были точные данные.
(3,142 – 3,140); на то время это были точные данные.
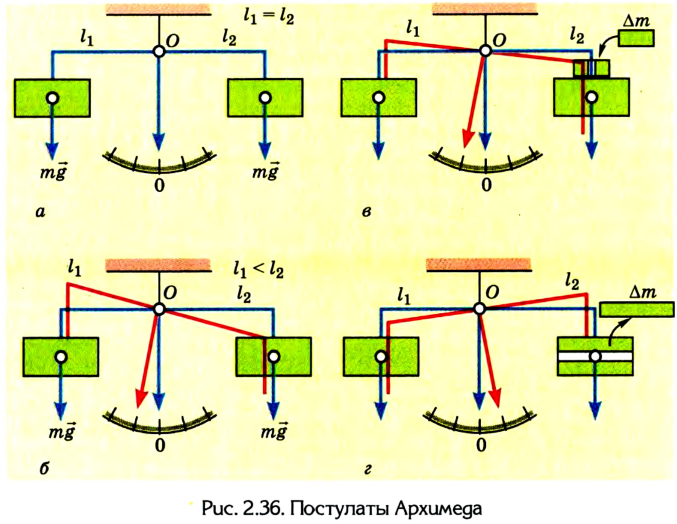
- одинаковые грузы, приложенные к одинаковым плечам рычага, уравновешиваются (рис. 2.36, а);
- одинаковые грузы, приложенные к неодинаковым плечам рычага, не находятся в равновесии; груз, приложенный к более длинному рычагу, падает (рис. 2.36, б);
- если грузы, подвешенные к неодинаковым плечам рычага, уравновешиваются и к одному из них что-либо прибавить, то равновесие нарушится и этот груз будет падать (рис. 2.36, в);
- если при тех же условиях, что в предыдущем случае, один груз уменьшить, то равновесие нарушится, и тогда другой груз будет падать (рис. 2.36, г).
Рычаг находится в равновесии, если плечи сил обратно пропорциональны значениям сил, действующих на него
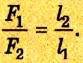
Из этих положений Архимед сделал вывод: грузы пребывают в равновесии, когда плечи рычага обратно пропорциональны грузам:
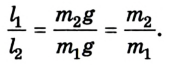
Условия равновесия тел. Устойчивое и неустойчивое равновесие
Равновесие – состояние тела, при котором в рассматриваемой системе отсчета отсутствуют перемещения каких-либо его точек под действием приложенных к нему сил.
Вспомним, что момент силы относительно какой-либо оси равен произведению модуля силы на ее плечо: М = Fl. Плечом силы l называется кратчайшее расстояние от оси вращения до линии действия данной силы. Момент силы считается положительным, если сила стремится повернуть тело по часовой стрелке, и отрицательным, если такое действие противоположно. Для равновесия тел необходимы два условия: 1) геометрическая сумма приложенных к телу сил равна нулю: 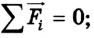
2) алгебраическая сумма моментов сил относительно любой неподвижной оси равна нулю: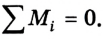
Момент силы: М = Fl.
Условия равновесия тел:
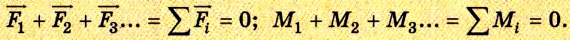
Равновесие устойчивое, если при незначительном смещении тело вновь возвращается в положение равновесия (рис. 2.37).
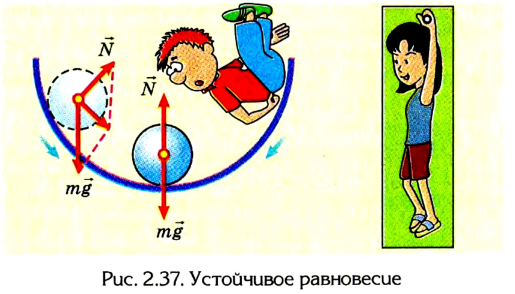
При неустойчивом равновесии незначительное смещение тела вызывает в дальнейшем значительное удаление его от исходного положения (рис. 2.38).
Равновесие тела может быть устойчивым, неустойчивым и безразличным.
Если любые смещения тела не нарушают его состояния равновесия, то можно говорить о безразличном равновесии (рис. 2.39).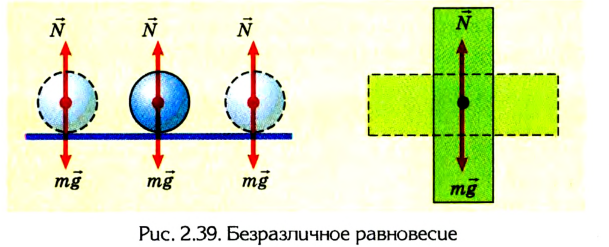
Примеры решения задач на равновесие рычага
Рассмотрим примеры решения задач статики.
Пример №1
Метровая линейка, весом которой можно пренебречь, положена средним делением на подставку и нагружена гирями (рис. 2.40). Какого направления и значения сила должна быть приложена на делении 1 м для того, чтобы линейка находилась в равновесии? Какой будет сила реакции опоры, если приложить эту силу?
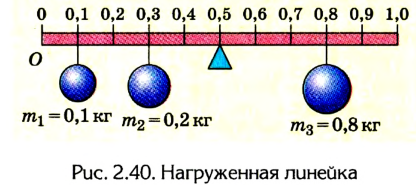
Решение:
Выполняем рисунок в соответствии с условием задачи (рис. 2.41), указав силы и их плечи. Линейка под действием моментов сил может вращаться вокруг неподвижной оси О, которая проходит через точку О. Будем считать положительными все моменты, вращающие систему по часовой стрелке. В задаче это момент силы 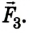 Отрицательные моменты создают силы
Отрицательные моменты создают силы 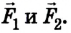
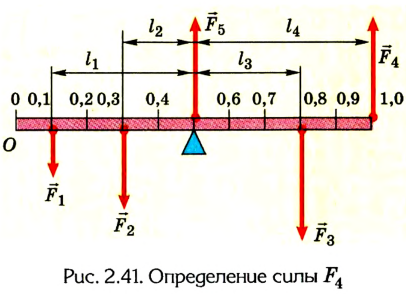
Для упрощения вычислений значение ускорения свободного падения будем считать равным 10 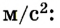
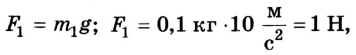
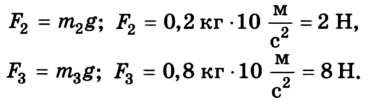
Предположим, что для равновесия системы на конце линейки 1 м должна быть приложена сила 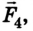 направленная вертикально вверх. Если же мы ошиблись в выборе направления этой силы, то в ответе значение силы получится со знаком “-“. Для решения задачи воспользуемся вторым условием равновесия тела:
направленная вертикально вверх. Если же мы ошиблись в выборе направления этой силы, то в ответе значение силы получится со знаком “-“. Для решения задачи воспользуемся вторым условием равновесия тела:
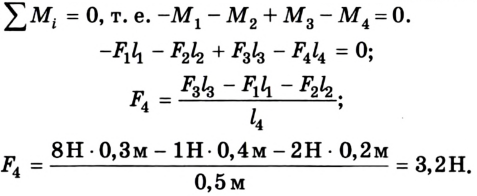
Ответ: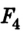 = 3,2H, направление силы выбрано правильно.
= 3,2H, направление силы выбрано правильно.
Пример №2
Метровая линейка, весом которой можно пренебречь, положена крайними точками на две опоры и нагружена гирями, как в предыдущей задаче. Нужно определить силы реакции опор 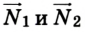 (рис. 2.42).
(рис. 2.42).

Решение:
Чтобы определить силу реакции опоры 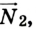 можно воспользоваться таким приемом. Если опору забрать, то для равновесия системы на отметке 1 м необходимо приложить силу, направленную вертикально вверх. Иначе система будет вращаться вокруг оси в точке О линейки по часовой стрелке. Теперь можно применить правило моментов:
можно воспользоваться таким приемом. Если опору забрать, то для равновесия системы на отметке 1 м необходимо приложить силу, направленную вертикально вверх. Иначе система будет вращаться вокруг оси в точке О линейки по часовой стрелке. Теперь можно применить правило моментов:
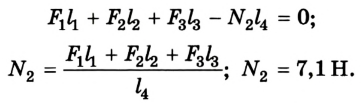
Чтобы определить силу реакции опоры 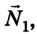 действуем аналогично. Теперь система будет вращаться вокруг оси против часовой стрелки, когда она проходит через отметку 1 м:
действуем аналогично. Теперь система будет вращаться вокруг оси против часовой стрелки, когда она проходит через отметку 1 м: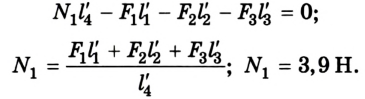
Чтобы найти силы реакции опор, можно воспользоваться правилом сложения параллельных сил. Им же можно пользоваться и для контроля найденных значений.
Ответ:  = 3,9 H;
= 3,9 H;  =7,1 Н.
=7,1 Н.
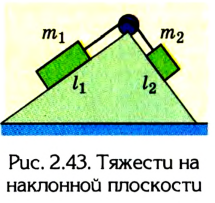
Оригинальный метод решения задач статики был предложен Симоном Сте-вином (1548-1620). Для случаев равновесия тел на наклонной плоскости он доказал, что массы тел соотносятся как длины плоскостей, которые их образуют (рис. 2.43):
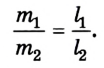
Он же установил принцип сложения статических сил (треугольник сил): три силы, действующие на одну точку, находятся в равновесии тогда, когда они бывают параллельны и пропорциональны трем сторонам плоского треугольника (рис. 2.44). Приведем пример решения одной из задач статики с применением треугольника сил.
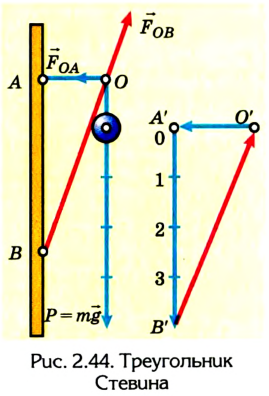
Пример №3
На кронштейне висит лампа весом 4 Н. Найти значение сил упругости в деталях ОА и ОВ.
Дано:
Р = 4 Н
 – ?
– ?
Решение:
Выбираем масштаб построения треугольника. Пусть 1 см на рисунке соответствует значению силы 1 Н. Теперь строим сторону треугольника
А’В’, длина которой известна: 4 см = 4 Н. Эта сторона параллельна направлению силы тяжести, действующей на лампу. Из точки А’ проводим линию, параллельную направлению действия силы в подвесе ОА, а потом из точки В’ – параллельную направлению действия силы в упоре ОВ. На пересечении линий находится точка О’. Таким образом мы получили замкнутый треугольник сил. Зная масштаб, при помощи линейки измеряем значения силы упругости в подвесе ОА (О’А’) и силы реакции в упоре ОВ (О’В’).
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
Момент силы. Условия равновесия рычага
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
 |
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.

На рисунке (l_1) – плечо силы (F_1, l_2) – плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) – по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы – Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
$$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
 |
Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) – по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |
 Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |
 Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |
 Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Рычаги третьего рода
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы. 
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
(frac{l_1}{l_2}=frac 15)
(m_1=2,5 text{кг})
__________________
(m_2-?)

По правилу моментов begin{gather*} F_1l_1=F_2l_2 end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin{gather*} m_1gl_1=m_2gl_2\[7pt] m_2=frac{m_1l_1}{l_2} end{gather*} Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
(F_1=15 text{Н})
(F_2=60 text{Н})
(l_1+l_2=1 text{м})
__________________
(l_1, l_2-?)

По правилу моментов begin{gather*} F_1l_1=F_2l_2. end{gather*} Получаем систему уравнений begin{gather*} left{ begin{array}{l l} 15l_1=60l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 4l_2+l_2=1 end{array} right. Rightarrow \[7pt] Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 5l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=0,8 \ l_2=0,2 end{array} right. end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text{м/с}^2). Ответ запишите в килоньютонах.
Дано:
(m=500 text{кг})
(gapprox 10 text{м/с}^2)
(OB=4OA)
__________________
(F_A, F_B-?)

Сила тяжести (F_{text{т}}=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin{gather*} F_A+F_B=mg end{gather*} По правилу моментов при равновесии begin{gather*} F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac{mg}{5} end{gather*} Получаем: begin{gather*} F_B=frac{500cdot 10}{5}=1000 text{Н}=1 text{кН}, F_A=4cdot 100=4000 text{Н}=4 text{кН} end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
begin{gather*} M_1=M_2\[7pt] F_1l_1=F_2l_2 end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text{Н}. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text{Н}. $$
Относительные погрешности измерений: $$ delta_l=frac{Delta_l}{l}, delta_F=frac{Delta_F}{F}, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Погрешности определения отношений сил и плечей: begin{gather*} r_F=frac{F_1}{F_2}, delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}, Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}\[7pt] r_l=frac{l_2}{l_1}, delta_{rF}=delta_{rl}frac{Delta_l}{l_1}+frac{Delta_l}{l_2}, Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl} end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac{F_1}{F_2}) и плеч (frac{l_2}{l_1}) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text{Н}) | (l_1, text{см}) | (F_2, text{Н}) | (l_2, text{см}) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text{мм}=0,2 text{см}, Delta_F=0,05 text{Н} $$ Найдем моменты сил и погрешности вычислений: begin{gather*} M_1=F_1cdot l_1=2,9cdot 5=14,5 (text{Н}cdot text{м})\[7pt] delta_{M1}=frac{Delta_l}{l_1}+frac{Delta_F}{F_1}=frac{0,2}{5}+frac{0,05}{2,9}approx 0,04+0,017=0,057=5,7text{%} \[7pt] Delta_{M1}=M_1cdot delta_{M1}=14,5cdot 0,057approx 0,8 (text{Н}cdot text{м})\[7pt] M_1=(14,5pm 0,8) text{Н}cdot text{м}\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (text{Н}cdot text{м})\[7pt] delta_{M2}=frac{Delta_l}{l_2}+frac{Delta_F}{F_2}=frac{0,2}{15}+frac{0,05}{1,0}approx 0,013+0,05=0,063=6,3 text{%} \[7pt] Delta_{M2}=M_2cdot delta_{M2}=15,0cdot 0,063approx 0,9 (text{Н}cdot text{м})\[7pt] M_2=(15,0pm 0,9) text{Н}cdot text{м} end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac{F_1}{F_2}) begin{gather*} delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}=frac{0,05}{2,9}+frac{0,05}{1,0}approx 0,017+0,05=0,067=6,7text{%}\[7pt] Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}=2,9cdot 0,067approx 0,2\[7pt] frac{F_1}{F_2}=2,9pm 0,2 end{gather*}
Погрешность вычислений для (frac{l_2}{l_1}) begin{gather*} delta_{rl}=frac{Delta_l}{l_1}+frac{Delta_l}{l_2}=frac{0,2}{5}+frac{0,2}{15}approx 0,04+0,013=0,053=5,3text{%}\[7pt] Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl}=3,0cdot 0,053approx 0,2\[7pt] frac{l_2}{l_1}=3,0pm 0,2 end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ frac{F_2}{F_2}=frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) text{Н}cdot text{м}, M_2=(15,0pm 0,9) text{Н}cdot text{м} $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) – правило моментов выполняется.
Отношения сил и плечей равны begin{gather*} frac{F_1}{F_2}=2,9pm 0,2, frac{l_2}{l_1}=3,0pm 0,2 end{gather*}
Таким образом, с учетом вычисленных погрешностей (frac{F_1}{F_2}=frac{l_2}{l_1}) – правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
