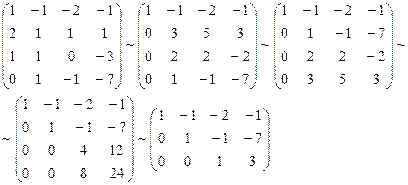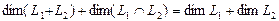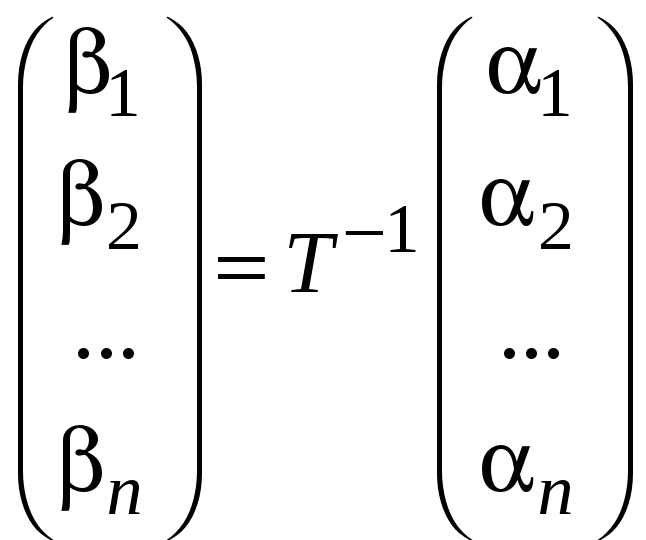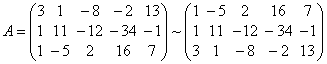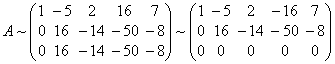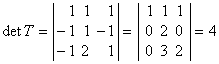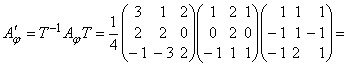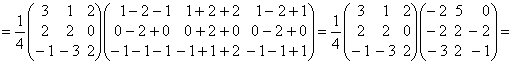Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1
1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1
1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 – x 1 ) · e ( 1 ) + ( x
2 – x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 – x 2 ) , . . . , ( x
n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 – 1 1 3 2 – 5 2 1 – 3
1 – 1 1 0 5 – 8 0 3 – 5
1 – 1 1 0 5 – 8 0 0 – 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x
1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x
1 ∆ = – 1 – 1 = 1 ∆ x
2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x
2 ∆ = – 1 – 1 = 1 ∆ x
3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Линейные оболочки и подпространства
Определение. Подпространством 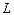

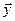
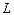
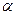
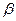
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 

Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств 



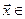
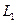
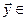

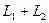
Утверждение. Сумма и пересечение подпространств 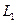

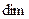
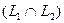
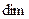
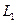
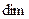

Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами 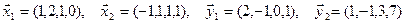
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства 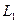
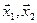
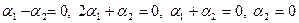
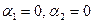
независимы и размерность подпространства 
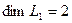

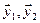
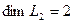
Вычислим теперь размерность пересечения подпространств 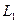


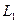
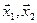
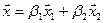

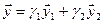
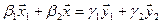
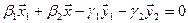

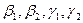
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим 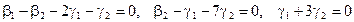
откуда 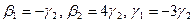
Полагая свободное неизвестное 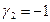
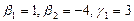
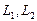
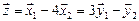
Размерность пересечения 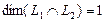
размерность суммы подпространств 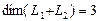
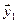
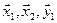
Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами 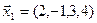
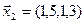

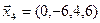
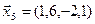
3.40. Найти размерность и какой-либо базис линейной оболочки векторов 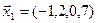
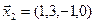
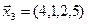
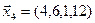
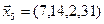
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале 
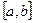
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;
б) векторов из пространства R n , координаты которых удовлетворяют уравнению 
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве 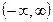
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а) 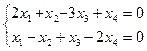
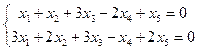
в) 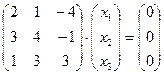
3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению 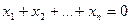
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами 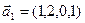
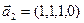
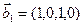
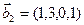
3.46. Найти размерность суммы и пересечения линейных оболочек векторов 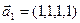
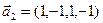
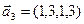

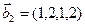
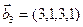
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 
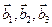
а) 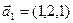
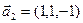
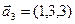
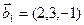
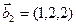
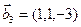
б) 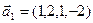
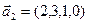
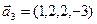
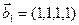
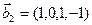
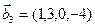
3.48. Найти базис суммы и пересечения линейных оболочек 
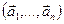

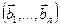
а) 
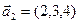
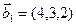
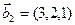
б) 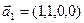
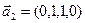
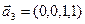
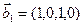
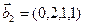
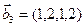
Является ли прямой сумма этих подпространств?
[spoiler title=”источники:”]
http://lektsii.org/10-6017.html
[/spoiler]
Лекция
11
Связь
между базисами линейного пространства.
Линейные
подпространства
|
Матрица перехода от
подпространства. |
11.1. Связь между
базисами линейного пространства
Пусть
–
линейное пространство,
(I)
и
(II)
– два базиса в
.
Так как (I)
– базис, любой вектор из
,
в частности любой вектор системы (II),
можно представить в виде линейной
комбинации векторов системы (I),
т.е. найдутся такие числа
,
что
……………………………….
(11.1)
Определение 1.
Матрица
называется матрицей перехода от базиса
(I) к базису (II).
Замечание
1. Столбцы матрицы перехода
,
являются координатами в разложении
векторов
по базису (I).
Справедливость
этого замечания непосредственно следует
из равенств (11.1).
Замечание
2. Матрица перехода от
базиса к базису является невырожденной
матрицей.
Доказательство
этого факта опустим.
Справедливо
следующее утверждение.
Теорема 1. Пусть
– линейное пространство,
(I) и
(II) – два базиса в
,
– матрица перехода от (I)
к (II),
,
и
,
тогда
.
(11.2)
Доказательство.
Подставим в разложение
по базису (II) выражения
из (11.1), получим
.
Последнюю сумму
запишем развернуто:
.
По условию
,
используя теорему о единственности
разложения вектора по базису (теорема
3 в лекции 10), получим
,
,
……………………………………
,
что в матричном
виде выглядит как равенство

Отсюда следует

Теорема доказана.
Пример
1.
– линейное пространство всех геометрических
векторов плоскости,
(I)
– произвольный декартов базис,
(II)
– декартов базис, полученный поворотом
векторов
и
на угол
против хода часовой стрелки. Найти
матрицу перехода от (I) к
(II) и связь координат
одного и того же вектора в (I)
и (II).
Имеем
,
(рис. 11.1). Тогда

– матрица перехода
от (I) к (II).
Найдем
.
и
.
Формула (11.2) в этом
случае имеет вид
,
где
– координаты произвольного вектора
в базисе (I), а
– координаты этого же вектора в базисе
(II).
(Сравните с формулами
(5.24) в Лекции 5).
Пример
2.
– произвольное линейное пространство,
.
Векторы
,
и
заданы своими координатами в некотором
базисе
.
Доказать, что система
– базис в
,
и найти координаты вектора
в базисе
.
Сначала докажем,
что система
– базис. Рассмотрим линейную комбинацию
векторов
и
,
равную нулевому вектору
:
.
Покоординатно
последнее равенство запишется в виде
системы двух уравнений:
(11.3)
Определитель
системы (11.3)
,
следовательно, система (11.3) имеет
единственное решение
.
Итак, допустив,
что линейная комбинация векторов
и
равна
,
мы с необходимостью получили, что
коэффициенты этой линейной комбинации
равны нулю. Это означает, что система
векторов
линейно независима, а так как
,
векторы
являются базисом в
.
Обозначим этот базис (II).
Найдем матрицу
перехода от (I) к (II).
В силу определения
1
(координаты векторов
и
в (I) располагаем по
столбцам).
Обозначим через
координаты
вектора
в (II).
Воспользуемся
теоремой 1. Найдем
.
Имеем
,
и по формуле (11.2)
получим
.
Итак,
.
Упражнения.
1.

– линейное пространство многочленов
степени
 .
.
Доказать, что система многочленов

образует базис в
 .
.
Найти матрицу перехода от базиса

к этому базису и координаты многочлена

в нем.
2. В произвольном
линейном пространстве векторы
и
заданы своими координатами в некотором
базисе
:
,
,
,
.
Доказать, что система векторов
– базис в
,
и найти координаты
в этом базисе.
3. В произвольном
линейном пространстве
векторы
(I)
и
(II)
заданы своими координатами в некотором
базисе
,
,
,
,
,
.
Доказать, что системы (I)
и (II) являются базисами в
,
и найти матрицу перехода от (I)
к (II).
11.2. Линейные
подпространства
Определение 2.
Пусть
– линейное пространство. Непустое
подмножество
линейного пространства
()
называется линейным подпространством
в
,
если выполняются два условия:
1)
;
2)
при любом вещественном числе
.
Пример
3. Пусть
– линейное пространство всех
арифметических
-мерных
векторов
;
– совокупность всех векторов, у которых
первая и последняя компоненты равны
нулю, т.е. векторов вида
.
– подпространство в
.
Действительно,
пусть
и
,
следовательно, по определению
и
.
По правилу сложения векторов в
и, таким образом, сумма любых двух
векторов из
принадлежит
.
Пусть
и
– произвольное вещественное число.
Но
(так как
),
следовательно, по правилу умножения
вектора на число в
и вместе с любым вектором произведение
его на
тоже принадлежит
.
В соответствии с определением 2 это
означает, что
– линейное подпространство в
.
Замечание.
Если
– линейное
подпространство в
,
то
само является
линейным пространством относительно
введенных в
операций
сложения и умножения на число.
Действительно,
требования 1) и 2) в определении 2 означают,
что в
определены операции сложения векторов
и умножения вектора на число.
Аксиомы 1 и 2
выполняются в
,
так как они имеют место в
.
Убедимся в справедливости аксиомы 3.
Пусть
,
,
следовательно, согласно условию 2)
,
но по следствию 5 из аксиом в
,
таким образом,
и в
справедлива аксиома 3.
Пусть
,
.
Следовательно, согласно условию 2)
,
но по следствию 8 из аксиом в
,
таким образом,
и в
справедлива аксиома 4.
Аналогично
проверяется справедливость аксиом 5 –
8, следовательно,
– линейное пространство.
Пусть
– произвольное линейное пространство,
– некоторая система векторов в
.
Рассмотрим совокупность всех векторов
вида
,
где
принимают всевозможные вещественные
значения. Обозначим множество этих
векторов
.
называется линейной оболочкой
векторов
.
является подпространством в
.
Действительно,
(так как, например, сами векторы
,
,
принадлежат
).
Пусть
,
,
следовательно, по определению
такие, что
,
.
Имеем
и
.
Пусть
,
– произвольное вещественное число.
Имеем
и
.
Таким образом,
выполняются условия 1) и 2) определения
2 и
является линейным подпространством
в
.
Говорят, что
порождено системой векторов
или
“натянуто” на систему
.
Заметим, что само
линейное пространство
может рассматриваться как линейная
оболочка любого своего базиса.
Пример
4.
Найти
размерность и базис линейной оболочки
векторов
,
,
.
Найдем ранг матрицы,
строками которой являются данные векторы
,
,
:



Минор второго
порядка
,
следовательно, первые две строки матрицы
линейно независимы. Значит, векторы
и
составляют линейно независимую систему
векторов в
,
а следовательно, и в линейной оболочке
,
и вектор
через них линейно выражается. Тогда
любой вектор
тоже линейно выражается через
и
.
Векторы
и
являются базисом в
,
.
Упражнение.
–
линейное пространство арифметических
векторов
.
Найти размерность и все
базисы линейной оболочки векторов
,
,
,
.
143
Рассмотрим L – линейное пространство.
– Сколько в L линейно независимых векторов.
– Какой из смысл.
Определение: Линейное пространство L называется N-мерным, а число N – размерностью, если в L существует N линейно независимых векторов, причём любые N+1 векторов линейно зависимы.
Определение: В N-мерном линейном пространстве L любая совокупность(система) N линейно независимых векторов называется базисом.
,
– базисные векторы.
Определение: если – базис в
, то для любого
существуют числа
:
. Это разложение вектора по базису.
Теорема 8: В данном базисе координаты вектора определены однозначно
Доказательство(от противного): Пусть в базисе два набора чисел для вектора
Так как линейно независимы, то все
Если в L существует любое число линейно независимых векторов, то L называется бесконечномерным линейным пространством.
Примеры базисов:
1)
2)
Базис Вейля
3)
.
4)
Подпространство и линейная оболочка
Пусть
L – множество
M – подмножество
Кроме того
L – линейное пространство
Тогда M – подпространство в L, если
Рассмотрим систему векторов .
Определение: Линейной оболочкой системы векторов называется множество всевозможных линейных комбинаций этих векторов. То есть:
. Очевидно, что
и является подпространством.
Пример: найти размерность и базис линейной оболочки , где

линейно независимы.
Операции над линейными пространствами.
– линейные пространства.
А)
Б)
А) Что такое .
Определение: линейное пространство L является прямой суммой и
, если: выполняется одно из условий:
1)
2)
Теорема 9: Для того, чтобы , достаточно, чтобы
1)
2)
Тогда чтобы доказать, что, необходимо доказать, что – базис в L.
Рассмотрим:
Тогда .
Так как , то 0=0
| < Предыдущая | Следующая > |
|---|
Исследование системы векторов на линейную зависимость. Определение координат вектора в базисе. Определение размерности линейного пространства решений системы
Страницы работы
Фрагмент текста работы
Координатные столбцы –
линейно независимы, следовательно, векторы тоже
линейно независимы и значит –
базис в линейном пространстве решений системы уравнений.
Найдем ранг матрицы системы
(поменяли
местами первую и третью строки).
Вычтем элементы первой строки из
соответствующих элементов второй строки, а затем элементы первой строки умножим на –3 и прибавим к
элементам третьей строки, получим
(при
последнем преобразовании вычли элементы третьей строки из соответствующих
элементов четвертой строки). Ранг матрицы системы равен двум, значит
размерность пространства решений системы равна .
Исходная система равносильна системе
,
Полагая в этой системе сначала ; затем
; а потом
, находим три линейно
независимых решения:
а) ,
,
б) ,
,
в) ,
,
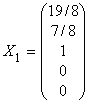
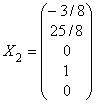
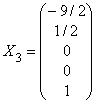
Таким образом, базисом пространства решений
будут, например, векторы:
,
здесь, для упрощения, координаты первых двух векторов умножены на 8, а
координаты последнего – на 2.
Пример 8.4. Найти размерность и базис
линейного подпространства, являющегося линейной оболочкой векторов.
Решение. Составим из координат векторов
системы матрицу и с помощью элементарных преобразований определим ее ранг. Ранг
этой матрицы будет совпадать с числом линейно независимых векторов в системе и
значит, равен размерности оболочки векторов (см. раздел 1). Матрица из
координат векторов имеет вид:
здесь,
сначала элементы первой строки прибавили к соответствующим элементам второй и
третьей строк, потом элементы первой строки умножили на два и прибавили к
соответствующим элементам пятой строки, после чего элементы второй строки разделили
на два и результат вычли из третьей, четвертой и пятой строк. Таким образом
ранг матрицы равен двум, т.е. в системе два линейно независимых вектора, значит
размерность линейной оболочки векторов равна двум. В качестве базиса можно
взять, например векторы .
Пример 8.5. Пусть Являются ли линейными
следующие преобразования?
Решение. Преобразование будет линейным, если
все координаты образов векторов будут линейными комбинациями координат вектора . Здесь в преобразовании
вторая координата равная
не является линейной
комбинацией, в преобразовании –
аналогично, кроме того третья координата имеет вид ,
что так же не является линейной комбинацией координат вектора . Значит эти преобразования
не являются линейными. Преобразование является
линейным.
Пример 8.6. Найти матрицу линейного
преобразования в базисе
если она задана в базисе
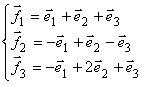
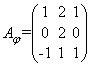
Решение. При переходе от базиса e к
базису f матрица линейного преобразования, в соответствии с
определением, будет иметь вид (см. (4.1)) ,
где T матрица перехода, которая находится из равенства f = eT.
Здесь 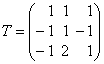
Найдем определитель матрицы:
(прибавили к элементам второй и третьей
строк соответствующие элементы первой строки и записали формулу разложения
определителя по первому столбцу).
Найдем алгебраические дополнения к элементам
матрицы T и обратную матрицу по формуле :
.
Таким образом, обратная матрица будет 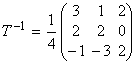
Пример 8.7. Определить ранг и дефект линейного
преобразования, а также найти базисы образа и ядра при преобразовании
.
.
Решение. Пусть в выбран базис
, тогда в этом базисе матрица
преобразования будет иметь
вид:
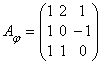
По определению вектор принадлежит
образу при преобразовании
в том и только том
случае, когда найдется вектор такой,
что , или в координатной
записи по формуле (3.4):
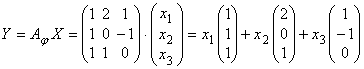
Это равенство означает, что образ совпадает с линейной оболочкой системы
векторов , так как
. Следовательно,
ранг оператора , который
совпадает с рангом его матрицы, равен двум. В качестве базиса можно взять любой
базис линейной оболочки векторов , например,
– они линейно независимы.
Аналогично вектор принадлежит
ядру тогда и только тогда, когда , или,
в координатной записи:
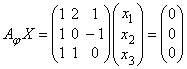
Это однородная система линейных уравнений, ранг которой равен двум,
значит, она эквивалентна следующей системе:
, полагая
в которой, например, , получаем
, т.е. базис ядра
состоит из одного вектора .
При этом по
теореме 3.5, размерность ядра равна:
.
Пример 8.8. Доказать линейность, найти матрицу, область значений
и ядро оператора:
а) проектирования на плоскость ;
б) зеркального отражения относительно
плоскости .
Решение. Рассмотрим произвольный вектор . Отложим его от начала
координат, тогда координаты точки конца вектора будут . Проекцию этого вектора
на плоскость обозначим
, а зеркально отраженный
Похожие материалы
- Решение задач по дифференциальным уравнениям и рядам
- Функциональные ряды (Понятие функционального ряда. Степенные ряды и их свойства. Ряды Тейлора и Маклорена. Применение степенных рядов. Ряды Фурье)
- Решение задач на поверхностные интегралы, компоненты векторного поля, формулу Остроградского-Гаусса
Информация о работе
Найти базис и размерность линейной оболочки векторов
Пример1)
Найти базис и размерность линейной оболочки векторов a1=(1, 2, 3, 4), a2=( -1, 3, 2, 1),
a3=(- 1, 8, 7, 6), a4=(1, 4, -2, 5).
По определению базис максимальный набор линейно независимых векторов.
А) проверим, что вектора < a1, a2,a3, a4>–линейно независимы?
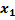

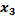


С помощью элементарных преобразований приводим матрицу к треугольному виду:
Выписываем решение….. Получаем, что вектора линейно зависимы значит вектора < a1, a2,a3, a4>не базис.
В) Из набор вектора < a1, a2,a3, a4>уберем один вектор, например a3.Проверим, что вектора < a1, a2, a4>образуют базис.
Дата добавления: 2015-09-07 ; просмотров: 2766 . Нарушение авторских прав
Сайт о разделе высшей математики — линейной алгебре
п.5. Вычисление ранга матрицы и нахождение базиса линейной оболочки ее системы строк (столбцов).
Для вычисления ранга матрицы часто применяют метод Гаусса приведения матрицы к ступенчатому виду. Метод Гаусса основан на элементарных преобразованиях строк матрицы, которые, как мы уже знаем, не изменяют ранга системы строк, а значит не изменяют и ранга матрицы.
Таким образом, ранг данной матрицы равен рангу получившейся после преобразований ступенчатой матрицы. В свою очередь, ранг ступенчатой матрицы легко вычисляется, так как легко увидеть ее максимальный ненулевой минор и его порядок.
Пример. Вычислить ранг матрицы 
1-й шаг: умножим первую строку на 2 и прибавим ко второй строке:

2-й шаг: прибавим к третьей строке первую, умноженную на (–3):

3-й шаг: прибавим ко второй строке 3-ю, умноженную на (–1):

4-й шаг: умножаем вторую строку на (–3) и прибавляем к третьей строке:

Ранг последней матрицы равен 3, так как в первых трех столбцах стоит ненулевой минор 3-го порядка

Приведенные преобразования не изменяют величину определителя, построенного на первых трех столбцах матрицы А, поэтому он отличен от нуля и, следовательно, его столбцы линейно независимые и образуют максимальную линейно независимую подсистему системы столбцов матрицы А. Отсюда можно сделать вывод, что первые три столбца матрицы А образуют базис линейной оболочки натянутой на столбцы матрицы А, т.е. 

Ответ: 



Определение. Любой ненулевой минор матрицы А максимального порядка называют базисным минором матрицы А.
Из этого определения следует, что порядок базисного минора матрицы А равен рангу матрицы А.
Замечание. Максимальную линейно независимую подсистему системы строк матрицы, которая образует базис линейной оболочки системы строк матрицы, мы будем, для краткости, называть базисными строками матрицы. И то же самое для столбцов.
Из приведенного примера можно сделать вывод, что если, вычисляя ранг матрицы, мы не переставляем строки и столбцы матрицы, то найдя базисный минор матрицы и определив номера строк и столбцов на которых он построен, мы, тем самым, находим номера базисных строк и столбцов исходной матрицы.
Так в примере, базисный минор матрицы А построен на первых трех строках и первых трех столбцах, следовательно именно они и образуют базисы системы строк и столбцов матрицы А.
Определения размерности и базиса
Линейное пространство [math]V[/math] называется n-мерным , если в нем существует система из [math]n[/math] линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число [math]n[/math] называется размерностью (числом измерений) линейного пространства [math]V[/math] и обозначается [math]operatornameV[/math] . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве [math]V[/math] найдется система, состоящая из [math]n[/math] линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: [math]operatornameV=infty[/math] ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность [math]n[/math] линейно независимых векторов ( базисных векторов ).
Теорема 8.1 о разложении вектора по базису. Если [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис n-мерного линейного пространства [math]V[/math] , то любой вектор [math]mathbfin V[/math] может быть представлен в виде линейной комбинации базисных векторов:
и притом единственным образом, т.е. коэффициенты [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства [math]V[/math] равна [math]n[/math] . Система векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] линейно независима (это базис). После присоединения к базису любого вектора [math]mathbf[/math] , получаем линейно зависимую систему [math]mathbf_1,mathbf_2,ldots,mathbf_n, mathbf[/math] (так как это система состоит из [math](n+1)[/math] векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
Следствие 1. Если [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис пространства [math]V[/math] , то [math]V=operatorname (mathbf_1,mathbf_2, ldots,mathbf_n)[/math] , т.е. линейное пространство является линейной оболочкой базисных векторов.
В самом деле, для доказательства равенства [math]V=operatorname (mathbf_1,mathbf_2, ldots, mathbf_n)[/math] двух множеств достаточно показать, что включения [math]Vsubset operatorname(mathbf_1,mathbf_2, ldots,mathbf_n)[/math] и [math]operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)subset V[/math] выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. [math]operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)subset V[/math] . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. [math]Vsubset operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)[/math] . Отсюда следует равенство рассматриваемых множеств.
Следствие 2. Если [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — линейно независимая система векторов линейного пространства [math]V[/math] и любой вектор [math]mathbfin V[/math] может быть представлен в виде линейной комбинации (8.4): [math]mathbf=v_1mathbf_1+ v_2mathbf_2+ldots+v_nmathbf_n[/math] , то пространство [math]V[/math] имеет размерность [math]n[/math] , а система [math]mathbf_1,mathbf_2, ldots,mathbf_n[/math] является его базисом.
В самом деле, в пространстве [math]V[/math] имеется система [math]n[/math] линейно независимых векторов, а любая система [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] из большего количества векторов n)”>[math](k>n)[/math] линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] . Значит, [math]operatorname V=n[/math] и [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис [math]V[/math] .
Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему [math]k[/math] векторов n-мерного линейного пространства [math](1leqslant k можно дополнить до базиса пространства.
В самом деле, пусть [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] — линейно независимая система векторов n-мерного пространства [math]V
(1leqslant k . Рассмотрим линейную оболочку этих векторов: [math]L_k=operatorname(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] . Любой вектор [math]mathbfin L_k[/math] образует с векторами [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно зависимую систему [math]mathbf_1,mathbf_2,ldots,mathbf_k,mathbf[/math] , так как вектор [math]mathbf[/math] линейно выражается через остальные. Поскольку в n-мерном пространстве существует [math]n[/math] линейно независимых векторов, то [math]L_k
e V[/math] и существует вектор [math]mathbf_in V[/math] , который не принадлежит [math]L_k[/math] . Дополняя этим вектором линейно независимую систему [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , получаем систему векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k,mathbf_[/math] , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что [math]mathbf_in operatorname(mathbf_1, mathbf_2, ldots,mathbf_k)=L_k[/math] , а это противоречит условию [math]mathbf_
otin L_k[/math] . Итак, система векторов [math]mathbf_1,mathbf_2,ldots, mathbf_k, mathbf_[/math] линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: [math]L_=operatorname (mathbf_1, mathbf_2,ldots, mathbf_k, mathbf_)[/math] . Если [math]L_=V[/math] , то [math]mathbf_1,mathbf_2, ldots,mathbf_k, mathbf_[/math] — базис и теорема доказана. Если [math]L_
e V[/math] , то дополняем систему [math]mathbf_1,mathbf_2, ldots,mathbf_k,mathbf_[/math] вектором [math]mathbf_
otin L_[/math] и т.д. Процесс дополнения обязательно закончится, так как пространство [math]V[/math] конечномерное. В результате получим равенство [math]V=L_n=operatorname (mathbf_1,ldots,mathbf_k,ldots,mathbf_n)[/math] , из которого следует, что [math]mathbf_1,ldots,mathbf_k,ldots,mathbf_n[/math] — базис пространства [math]V[/math] . Теорема доказана.
1. Базис линейного пространства определяется неоднозначно. Например, если [math]mathbf_1,mathbf_2, ldots, mathbf_n[/math] — базис пространства [math]V[/math] , то система векторов [math]lambda mathbf_1,lambda mathbf_2,ldots,lambda mathbf_n[/math] при любом [math]lambda
e0[/math] также является базисом [math]V[/math] . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.
2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.
4. Если множество [math]mathbb[/math] является линейной оболочкой [math]operatorname(mathbf_1,mathbf_2,ldots,mathbf_k)[/math] , то векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] называют образующими множества [math]mathbb[/math] . Следствие 1 теоремы 8.1 в силу равенства [math]V=operatorname (mathbf_1,mathbf_2,ldots,mathbf_n)[/math] позволяет говорить, что базис — это минимальная система образующих линейного пространства [math]V[/math] , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора [math]mathbf_1, mathbf_2,ldots,mathbf_n[/math] ) без нарушения равенства [math]V=operatorname( mathbf_1,mathbf_2,ldots,mathbf_n)[/math] .
5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] . Количество базисных векторов определяет размерность пространства . Разумеется, что эти определения эквивалентны приведенным выше.
Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.
1. Нулевое линейное пространство [math]<mathbf>[/math] не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: [math]dim<mathbf>=0[/math] . Это пространство не имеет базиса.
2. Пространства [math]V_1,,V_2,,V_3[/math] имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства [math]V_1[/math] , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства [math]V_1[/math] коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, [math]dim=1[/math] , а базисом пространства [math]V_1[/math] является любой ненулевой вектор. Аналогично доказывается, что [math]dim=2[/math] и [math]dim=3[/math] . Базисом пространства [math]V_2[/math] служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства [math]V_3[/math] являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в [math]V_1[/math] является единичный вектор [math]vec[/math] на прямой. Стандартным базисом в [math]V_2[/math] считается базис [math]vec,,vec[/math] , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве [math]V_3[/math] считается базис [math]vec,,vec,,vec[/math] , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.
3. Пространство [math]mathbb^n[/math] содержит не более, чем [math]n[/math] , линейно независимых векторов. В самом деле, возьмем [math]k[/math] столбцов из [math]mathbb^n[/math] и составим из них матрицу размеров [math]n imes k[/math] . Если n”>[math]k>n[/math] , то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, [math]dim<mathbb^n>leqslant n[/math] . В пространстве [math]mathbb^n[/math] не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы
линейно независимы. Следовательно, [math]dim<mathbb^n>=n[/math] . Пространство [math]mathbb^n[/math] называется n-мерным вещественным арифметическим пространством . Указанный набор векторов считается стандартным базисом пространства [math]mathbb^n[/math] . Аналогично доказывается, что [math]dim<mathbb^n>=n[/math] , поэтому пространство [math]mathbb^n[/math] называют n-мерным комплексным арифметическим пространством .
4. Напомним, что любое решение однородной системы [math]Ax=o[/math] можно представить в виде [math]x=C_1varphi_1+C_2varphi_2+ldots+C_varphi_[/math] , где [math]r=operatornameA[/math] , a [math]varphi_1,varphi_2,ldots,varphi_[/math] — фундаментальная система решений. Следовательно, [math]=operatorname (varphi_1,varphi_2,ldots,varphi_)[/math] , т.е. базисом пространства [math][/math] решений однородной системы служит ее фундаментальная система решений, а размерность пространства [math]dim=n-r[/math] , где [math]n[/math] — количество неизвестных, а [math]r[/math] — ранг матрицы системы.
5. В пространстве [math]M_<2 imes3>[/math] матриц размеров [math]2 imes3[/math] можно выбрать 6 матриц:
которые линейно независимы. Действительно, их линейная комбинация
равна нулевой матрице только в тривиальном случае [math]alpha_1=alpha_2= ldots= alpha_6=0[/math] . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из [math]M_<2 imes3>[/math] линейным образом выражается через выбранные 6 матриц, т.е. [math]M_<2 imes>= operatorname (mathbf_1,mathbf_2,ldots,mathbf_6)[/math] . Следовательно, [math]dim>=2cdot3=6[/math] , а матрицы [math]mathbf_1, mathbf_2,ldots,mathbf_6[/math] являются базисом (стандартным) этого пространства. Аналогично доказывается, что [math]dim>=mcdot n[/math] .
6. Для любого натурального [math]n[/math] в пространстве [math]P(mathbb)[/math] многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены [math]mathbf_1=1,[/math] [math]mathbf_2=z,[/math] [math]mathbf_3=z^2,,ldots,[/math] [math]mathbf_n=z^[/math] линейно независимы, так как их линейная комбинация
равна нулевому многочлену [math](o(z)equiv0)[/math] только в тривиальном случае [math]a_1=a_2=ldots=a_n=0[/math] . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство [math]P(mathbb)[/math] бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства [math]P(mathbb)[/math] многочленов с действительными коэффициентами. Пространство [math]P_n(mathbb)[/math] многочленов степени не выше, чем [math]n[/math] , конечномерное. Действительно, векторы [math]mathbf_1=1,[/math] [math]mathbf_2=x,[/math] [math]mathbf_3=x^2,,ldots,[/math] [math]mathbf_=x^n[/math] образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из [math]P_n(mathbb)[/math] можно представить в виде линейной комбинации этих векторов:
7. Пространство [math]C(mathbb)[/math] непрерывных функций является бесконечно мерным. Действительно, для любого натурального [math]n[/math] многочлены [math]1,x,x^2,ldots, x^[/math] , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).
В пространстве [math]T_<omega>(mathbb)[/math] тригонометрических двучленов (частоты [math]omega
e0[/math] ) с действительными коэффициентами базис образуют одночлены [math]mathbf_1(t)=sinomega t,
mathbf_2(t)=cosomega t[/math] . Они линейно независимы, так как тождественное равенство [math]asinomega t+bcosomega tequiv0[/math] возможно только в тривиальном случае [math](a=b=0)[/math] . Любая функция вида [math]f(t)=asinomega t+bcosomega t[/math] линейно выражается через базисные: [math]f(t)=a,mathbf_1(t)+b,mathbf_2(t)[/math] .
8. Пространство [math]mathbb^X[/math] действительных функций, определенных на множестве [math]X[/math] , в зависимости от области определения [math]X[/math] может быть конечномерным или бесконечномерным. Если [math]X[/math] — конечное множество, то пространство [math]mathbb^X[/math] конечномерное (например, [math]X=<1,2,ldots,n>[/math] ). Если [math]X[/math] — бесконечное множество, то пространство [math]mathbb^X[/math] бесконечномерное (например, пространство [math]mathbb^N[/math] последовательностей).
9. В пространстве [math]mathbb^<+>[/math] любое положительное число [math]mathbf_1[/math] , не равное единице, может служить базисом. Возьмем, например, число [math]mathbf_1=2[/math] . Любое положительное число [math]r[/math] можно выразить через [math]mathbf_1[/math] , т.е. представить в виде [math]alphacdot mathbf_1colon[/math] [math]r=2^<log_2r>=log_2rast2=alpha_1ast mathbf_1[/math] , где [math]alpha_1=log_2r[/math] . Следовательно, размерность этого пространства равна 1, а число [math]mathbf_1=2[/math] является базисом.
10. Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис вещественного линейного пространства [math]V[/math] . Определим на [math]V[/math] линейные скалярные функции [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] , положив:
При этом, в силу линейности функции [math]mathcal_i[/math] , для произвольного вектора [math]mathbf=v_1 mathbf_1+v_2 mathbf_2+ldots+v_n mathbf_n[/math] получаем [math]mathcal(mathbf)=sum_^v_j mathcal(mathbf_j)=v_i[/math] .
Итак, определены [math]n[/math] элементов (ковекторов) [math]mathcal_1, mathcal_2, ldots, mathcal_n[/math] сопряженного пространства [math]V^<ast>[/math] . Докажем, что [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] — базис [math]V^<ast>[/math] .
Во-первых, покажем, что система [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов [math](alpha_1 mathcal_1+ldots+alpha_nmathcal_n)(mathbf)=[/math] и приравняем ее нулевой функции
forall mathbfin V)colon
forall mathbfin V.[/math]
Подставляя в это равенство [math]mathbf=mathbf_i,
i=1,ldots,n[/math] , получаем [math]alpha_1=alpha_2cdot= alpha_n=0[/math] . Следовательно, система элементов [math]mathcal_1,mathcal_2,ldots,mathcal_n[/math] пространства [math]V^<ast>[/math] линейно независима, так как равенство [math]alpha_1mathcal_1+ldots+ alpha_nmathcal_n =mathbf[/math] возможно только в тривиальном случае.
Во-вторых, докажем, что любую линейную функцию [math]fin V^<ast>[/math] можно представить в виде линейной комбинации ковекторов [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] . Действительно, для любого вектора [math]mathbf=v_1 mathbf_1+v_2 mathbf_2+ldots+v_n mathbf_n[/math] в силу линейности функции [math]f[/math] получаем:
т.е. функция [math]f[/math] представлена в виде линейной комбинации [math]f=eta_1 mathcal_1+ldots+eta_nmathcal_n[/math] функций [math]mathcal_1,mathcal_2,ldots, mathcal_n[/math] (числа [math]eta_i=f(mathbf_i)[/math] — коэффициенты линейной комбинации). Следовательно, система ковекторов [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] является базисом сопряженного пространства [math]V^<ast>[/math] и [math]dim>=dim[/math] (для конечномерного пространства [math]V[/math] ).