Все формулы медианы треугольника
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, ( M ):
Формула длины медианы через две стороны и угол между ними, ( M ):
Определение и свойства медианы треугольника
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см 2 ⋅ 6 = 30 см 2 .
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .
Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .
Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
[spoiler title=”источники:”]
[/spoiler]
Все формулы медианы треугольника
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
- Подробности
-
Автор: Administrator
-
Опубликовано: 08 октября 2011
-
Обновлено: 13 августа 2021
Здравствуйте, уважаемые читатели. В этой статье рассмотрим простейшие задания по геометрии на применение свойств медианы и биссектрисы в треугольнике.
Что такое медиана треугольника?
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Другими словами, медиана треугольника делит противоположную сторону на два равных отрезка.
Задача №1
В этой задаче длина медианы ВМ является лишней и для решения не используются. Для решения нужно взять длину стороны АС. Чтобы найти АМ нужно, по свойству медианы треугольника, разделить сторону АС на 2 и получим отрезок АМ.
Задача №2
Что такое биссектриса ?
Биссектриса угла – это луч, исходящий из вершины угла и делящий этот угол на два равных.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части.
Теперь решим задачу.
Задача №3
В условии задачи, точка М – середина стороны АВ, значит СМ – медиана. Вспомним свойство медианы в прямоугольном треугольнике проведенной из вершины прямого угла:
Медиана в прямоугольном треугольнике, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы (значение гипотенузы делим на 2). Значит для решения задачи этой задачи нам нужно знать только значение отрезок АВ (гипотенузы), а значение отрезка ВС дано лишним.
Задача №4
Так как точка М является серединой АВ (АМ= МВ) и точка N является серединой ВС (BN=NC), то отрезки СМ и AN являются медианами в треугольнике АВС. Для решения этой задачи полезно знать свойство медиан треугольника:
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Решим задачу на части:
Весь отрезок AN = 15, но он поделен точкой О на два отрезка. Один отрезок равен две части, второй отрезок равен одной части.
Задача №5
Здесь представлены на вид 6 разных задач, но если внимательно прочитать, то можно заметить, что они одинаковые. Решить такие задачи можно как по теореме Пифагора, так и с помощью свойства медиан в треугольнике и вписанной окружности.
Для решения этих задач с помощью свойств медиан в треугольнике, вспомним свойство равностороннего треугольника и вписанной окружности в треугольник.
1) В равностороннем треугольнике медианы, биссектрисы и высоты совпадают и пересекаются в одной точке.
2) Центром вписанной окружности в треугольник является точка пересечения биссектрис. Значит в разностороннем треугольнике центром вписанной окружности является пересечение биссектрис, медиан и высот.
3) Свойство медиан в треугольнике: Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Рассмотрим решение такой задачи:
Для нахождения стороны или высоты равностороннего (правильного) треугольника, воспользуемся формулами, которые есть в справочном материале, выдаваемое на экзамене:
Так как в нашей задаче биссектриса равностороннего треугольника является медианой, найдем чему будет равна одна часть, т.е. радиус вписанной окружности:
Аналогично решаются задачи, где дана медиана или высота равностороннего (правильного) треугольника.
Решим второй тип подобной задачи:
Так как биссектриса в равностороннем треугольнике является медианой и высотой, то мы можем найти высоты по формуле
Можно эту задачу решить через свойство медиан треугольника:
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
У этого термина существуют и другие значения, см. Медиана.
Треугольник и его медианы.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине.
Иногда медианой называют также прямую, содержащую этот отрезок, а иногда длину этого отрезка.
Точка пересечения медианы со стороной треугольника называется основанием медианы.
Если 












Связанные определения[править | править код]
Точка пересечения медиан делит каждую медиану на два отрезка.
Отрезок от вершины до точки пересечения называется предмедианой, а отрезок от точки пересечения до противоположной стороны постмедианой[1].
В частности можно сказать, что в любом треугольнике отношение предмедианы к постмедиане равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Если медианы равнобедренного треугольника, проведённые к боковым сторонам, пересекаются под прямым углом, то косинусы углов при основании этого треугольника равны 

Свойства оснований медиан[править | править код]
- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема[2]. Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (то есть 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Медиана делит пополам любой отрезок, параллельный стороне, к которой проведена эта медиана.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
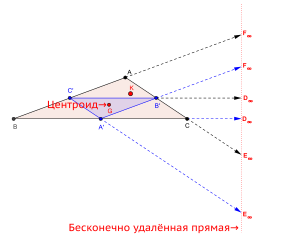
Бесконечно удаленная прямая — трилинейная поляра центроида
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
- где
— медианы к сторонам треугольника
соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
.
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
- где
— медианы к соответствующим сторонам треугольника,
— стороны треугольника.
Площадь 
- где
— полусумма длин медиан.
Вариации и обобщение[править | править код]
- Чевиана — отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне.
См. также[править | править код]
- Биссектриса
- Высота треугольника
- Инцентр
- Симедиана
- Центроид
- Чевиана
Примечания[править | править код]
- ↑ Стариков В. Н. 10-е исследование по геометрии (§ До- (пред-)- и пост-чевианы)// Научный рецензируемый электронный журнал МГАУ «Наука и образование». 2020. № 1. 7 с.// http://opusmgau.ru/index.php/see/article/view/ 1604
- ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 16.
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.
Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.
Задача.
Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

BC=a, AC=b, AB=c,
сторона AC — наибольшая,
BO- медиана.
Найти: BO.
Решение:
1) На луче BO отложим отрезок OD, OD=BO.
2) Проведем отрезки AD и CD.
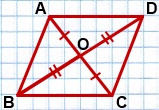
3) Рассмотрим четырехугольник ABCD.
AO=CO (так как BO — медиана треугольника ABC по условию);
BO=DO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
4) По свойству диагоналей параллелограмма,
так как BO=1/2 BD (по построению),
Если ввести обозначение
формула для нахождения медианы треугольника по его сторонам примет вид:
Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.
Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.
Соответственно, формулы для нахождения длины медианы в этих случаях:
Приём, который применили для решения задачи — метод удвоения медианы.