Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
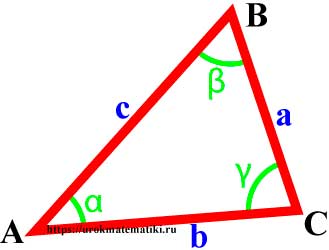
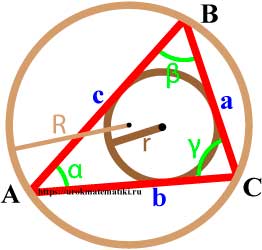
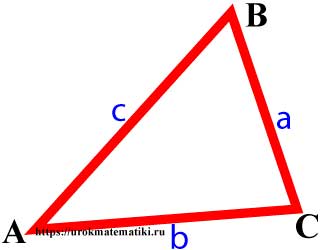
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
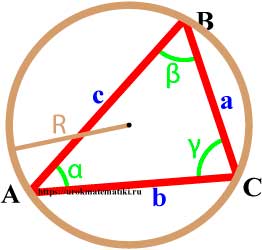
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 – 2 bc · cos α
b 2 = a 2 + c 2 – 2 ac · cos β
c 2 = a 2 + b 2 – 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
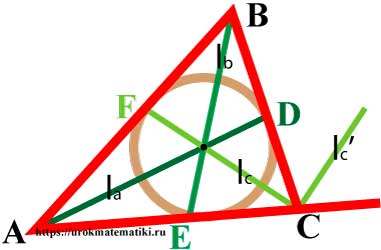
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 – a 2
mb = 1 2 √ 2 a 2 +2 c 2 – b 2
mc = 1 2 √ 2 a 2 +2 b 2 – c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p – a ) b + c
lb = 2√ acp ( p – b ) a + c
lc = 2√ abp ( p – c ) a + b
где p = a + b + c 2 – полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
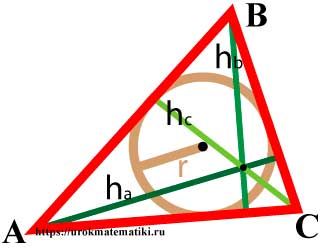
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
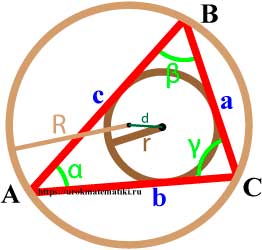
Связь между вписанной и описанной окружностями треугольника
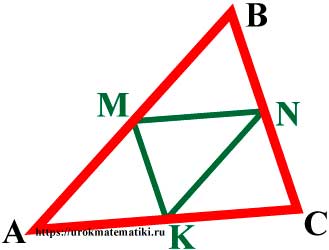
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
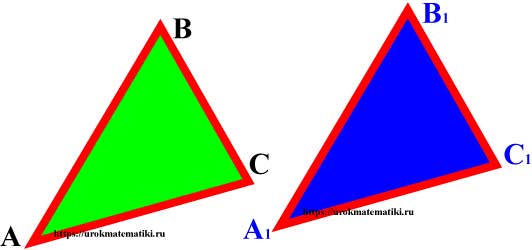
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
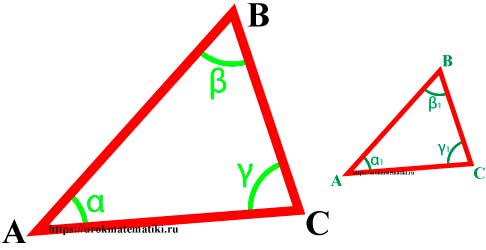
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k – коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Формулы треугольника
Для расчёта всех основных параметров треугольника воспользуйтесь калькулятором.
Виды треугольников
-
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°. -
Прямоугольный треугольник – это треугольник, содержащий прямой угол.
Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).
-
Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.(по числу равных сторон) -
Равносторонний (правильный) треугольник – это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°). -
Равнобедренный тругольник – это треугольник, у которого два угла и две стороны равны. -
Разносторонний треугольник – это треугольник, в котором все углы, а значит и все стороны попарно различны.
Свойства треугольника, применимые к любому треугольнику:
- Против большей стороны лежит больший угол, и наоборот.
- Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)
- Сумма углов треугольника равна 180° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60°).
- Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.
- Любая сторона треугольника меньше суммы двух других сторон и больше их разности:
- $$ AB BC – CA $$
- $$ BC AB – CA $$
- $$ CA AB – BC $$
Признаки равенства треугольников
Произвольные треугольники равны, если:
Три стороны одного треугольника равны трем сторонам другого треугольника (по трем сторонам).
AB = DE и BC = EF и AC = DF
Две стороны одного треугольника равны двум сторонам другого треугольника и углы между этими сторонами также равны (по двум сторонам и углу между ними).
AB = DE и BC = EF и ∠ABC = ∠DEF;
BC = EF и AC = DF и ∠BCA = ∠EFD;
AB = DE и AC = DF и ∠CAB = ∠FDE;
Три угла одного треугольника равны трем углам другого треугольника (по трем углам).
∠ABC = ∠DEF и ∠BCA = ∠EFD и ∠CAB = ∠FDE;
Два угла одного треугольника равны двум углам другого треугольника, и любая сторона первого треугольника равна соответствующей стороне другого треугольника.
∠ABC = ∠DEF и ∠BCA = ∠EFD;
∠BCA = ∠EFD и ∠CAB = ∠FDE;
∠CAB = ∠FDE и ∠ABC = ∠DEF;
AB = DE или BC = EF или AC = DF
Прямоугольные треугольники равны, если равны:
-
Гипотенуза и острый угол.
BC = EF и ∠ABC = ∠DEF
BC = EF и ∠BCA = ∠EFD;
Катет и противолежащий угол.
AB = DE и ∠BCA = ∠EFD
AC = DF и ∠ABC = ∠DEF
Катет и прилежащий угол.
AB = DE и ∠ABC = ∠DEF
AC = DF и ∠BCA = ∠EFD
AB = DE и AC = DF
Гипотенуза и катет.
AB = DE и BC = EF
AC = DF и BC = EF
Подобные треугольники
Два треугольника являются подобными, если углы одного треугольника равны, углам тругого треугольника, а стороны подобны
Признаки подобия треугольников
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны.
- Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.
Свойства подобных треугольников.
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия (Kподобия) $$ over S_<ΔDEF>> = К_<подобия>^2 $$
- Отношение периметров и длин биссектрис, медиан, высот, серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.
Подобие в прямоугольных треугольниках.
- Треугольники, образованные высотой, опущенной из прямого угла, являются подобными друг другу
- Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
- Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
- Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
Площадь треугольника
| Где: | AB,BC,AC – стороны треугольника |
| h – высота треугольника | |
| α, β, γ– углы треугольника | |
| P – полупериметр | |
| AC – основание треугольника |
Площадь произвольного треугольника
Площадь треугольника по формуле Герона
Площадь треугольника по углу и двум сторонам
$$ S = <1 over 2>* AB * AC * sin(α) $$ $$ S = <1 over 2>* AB * BC * sin(β) $$ $$ S = <1 over 2>* AC * BC * sin(γ) $$
Площадь треугольника по двум углам и стороне
Площадь прямоугольного треугольника по катетам
| Где: | AB,AC – катеты треугольника |
$$ S = <1 over 2>* AB * AC $$
Площадь равнобедренного треугольника
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника |
$$ S = * sqrt <4 * AB^2 – AC^2>$$
Площадь равностороннего треугольника
| Где: | AB,BC,AC – равные стороны треугольника |
| h – высота треугольника |
$$ S = <sqrt<3>over 4> * AB^2 $$ $$ S = > $$
Стороны треугольника
| Где: | AB,BC,AC – стороны треугольника |
| h – высота треугольника | |
| α, β, γ– углы треугольника | |
| P – полупериметр | |
| AC – основание треугольника |
Сторона треугольника по двум сторонам и углу
Сторона треугольника по стороне и двум углам
Сторона прямоугольного треугольника
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника |
$$ AC = BC * cos(β) = BC * sin(α) = AB * tg(α) $$ $$ AB = BC * cos(α) = BC * sin(β) = AC * tg(β) $$ $$ BC = = $$ $$ BC = = $$
Сторона прямоугольного треугольника по теореме Пифагора.
Сторона равнобедренного треугольника
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника |
$$ AC = 2 * AB * sin(<β over 2>) = AB * sqrt <2 – 2 * cos(β)>$$ $$ AC = 2 * AB * cos(α) $$ $$ AB = = > $$ $$ AB = $$
Высота треугольника
Высота – это перпендикуляр, выходящий из любой вершины треугольника, к противоположной стороне или её продолжению для треугольника с тупым углом. Высоты треугольника пересекаются в одной точке
| Где: | AB,BC,AC – стороны треугольника |
| h – высота треугольника | |
| P – полупериметр $$ P = $$ | |
| α, β, γ – углы треугольника | |
| R – радиус описанной окружности | |
| S – площадь треугольника |
Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формула длины высоты через сторону и угол
Высота на сторону АС, hAC
$$ h_ = AB * sin(α) = BC * sin(γ) $$
Высота на сторону AB, hAB
$$ h_ = BC * sin(β) = AC * sin(α) $$
Высота на сторону BC, hBC
$$ h_ = AC * sin(γ) = AB * sin(β) $$
Формула длины высоты через сторону и площадь
Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формула длины высоты через стороны и радиус
Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формулы высоты из прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| BD, DC – отрезки полученные от деления гипотенузы, высотой | |
| α, β– углы треугольника |
Формула длины высоты через гипотенузу и острые углы
$$ h = BC * sin(α) * cos(α) = BC * sin(β) * cos(β) $$
Формула длины высоты через катет и угол
$$ h = AB * sin(α) = AC * sin(β) $$
Формула длины высоты через составные отрезки гипотенузы
Биссектрисы в треугольнике
Биссектриса – это отрезок, который делит угол пополам из которого выходит. Точка пересечения всех трех биссектрис треугольника совпадает с центром вписанной окружности.
| Где: | AB,BC,AC – стороны треугольника |
| AA1,BB1,CC1 – биссектрисы в треугольнике | |
| α, β, γ– углы треугольника | |
| P – полупериметр $$ P = $$ |
Длина биссектрисы через две стороны и угол
Длина биссектрисы через полупериметр и стороны
Длина биссектрисы через три стороны
Длина биссектрисы через стороны и отрезки, на которые делит биссектриса
Формула длины биссектрис в прямоугольном треугольнике
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| β, γ– острые углы треугольника |
Длина биссектрисы из прямого угла, через катеты.
Длина биссектрисы из прямого угла, через гипотенузу и угол
Длина биссектрисы через катет и угол
Длина биссектрисы через катет и гипотенузу
Длина биссектрисы равнобедренного треугольника
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника | |
| α – равные углы при основании треугольника | |
| β – угол образованный равными сторонами треугольника |
Длина биссектрисы через стороны и угол, равнобедренного треугольника
$$ BB_1 = AB * sin(α) = * tg(α) = AB * cos(<β over 2>) $$ $$ BB_1 = AB * sqrt <<1 + cos(β)>over 2> $$
Длина биссектрисы через стороны, равнобедренного треугольника
Длина биссектрисы равностороннего треугольника
| Где: | AB,BC,AC – равные стороны треугольника |
$$ BB_1 = over 2> $$
Медиана в треугольнике
Медиана – это отрезок, который выходит из вершины и делит противоположную сторону пополам. Медиана делит треугольник на два равных по площади треугольника.
| Где: | AB,BC,AC – стороны треугольника |
| AA1,BB1,CC1 – медианы в треугольнике | |
| α, β, γ– углы треугольника |
Длина медианы через три стороны
Длина медианы через две стороны и угол между ними
Длина медианы в прямоугольном треугольнике, выходящая из прямого угла.
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| AA1,BB1,CC1 – медианы в треугольнике | |
| β, γ– острые углы треугольника |
Длина медианы в прямоугольном треугольнике, выходящая из прямого угла, равна радиусу описанной окружности, а середина гипотенузы является центром описанной окружности
Длина медианы через катеты
Длина медианы через катет и острый угол
Описанная окружность
Радиус описанной окружности произвольного треугольника по сторонам
| Где: | AB,BC,AC – стороны треугольника |
| P – полупериметр $$ P = $$ | |
| R – радиус описанной окружности |
$$ R = > $$
Радиус описанной окружности равностороннего треугольника по стороне или высоте
| Где: | AB,BC,AC – равные стороны треугольника |
| h – высота треугольника | |
| R – радиус описанной окружности |
$$ R = > $$ $$ R = <2 * h over 3>$$
Радиус описанной окружности равнобедренного треугольника по сторонам
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника | |
| h – высота треугольника | |
| R – радиус описанной окружности |
$$ R = > $$
Радиус описанной окружности прямоугольного треугольника по катетам
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| R – радиус описанной окружности |
$$ R = <1 over 2>* sqrt = $$
Длина окружности, L
Площадь окружности, S
Вписанная окружность
Радиус вписанной окружности произвольного треугольника по сторонам
| Где: | AB,BC,AC – стороны треугольника |
| P – полупериметр $$ P = $$ | |
| R – радиус вписанной окружности |
$$ R = sqrt <
over P> $$
Радиус вписанной окружности в равносторонний треугольник
| Где: | AB,BC,AC – равные стороны треугольника |
| R – радиус вписанной окружности |
$$ R = > $$
Радиус вписанной окружности равнобедренного треугольник
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника | |
| R – радиус вписанной окружности | |
| h – высота треугольника | |
| α – угол при основании треугольника |
$$ R = * sqrt <<2 * AB – AC over 2 * AB + AC>> $$ $$ R = AB * = AB * cos(α) * tan(<α over 2>) $$ $$ R = * = * tan(<α over 2>) $$ $$ R = > $$ $$ R = over AB + sqrt> $$
Радиус вписанной окружности в прямоугольном треугольнике
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://calc-online24.ru/formula/treyg
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Треугольник
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
- типы треугольников
- вершины углы и стороны треугольника
- медианы треугольника
- биссектрисы треугольника
- высоты треугольника
- окружность вписанная в треугольник
- окружность описанная вокруг треугольника
- связь между вписанной и описанной окружностями треугольника
- средняя линия треугольника
- периметр треугольника
- формулы площади треугольника
- равенство треугольников
- подобие треугольников
- прямоугольные треугольники
Типы треугольников
По величине углов
Остроугольный треугольник
— все углы треугольника острые.
Тупоугольный треугольник
— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник
— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник
— две стороны равны.
Равносторонний (правильный) треугольник
— все три стороны равны.
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
- если α > β, тогда a > b
- если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
asinα = bsinβ = csinγ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 – 2bc·cos α
b2 = a2 + c2 – 2ac·cos β
c2 = a2 + b2 – 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 232mb2+mc2-ma2b = 232ma2+mc2-mb2c = 232ma2+mb2-mc2
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
- В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD=
BOOE=COOF=21 - Медиана треугольника делит треугольник на две равновеликие частиS∆ABD=S∆ACDS∆BEA=S∆BECS∆CBF=S∆CAF
- Треугольник делится тремя медианами на шесть равновеликих треугольниковS∆AOF=S∆AOE=S∆BOF=S∆BOD=S∆COD=S∆COE
- Из векторов, образующих медианы, можно составить треугольник
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 122b2+2c2-a2mb = 122a2+2c2-b2mc = 122a2+2b2-c2
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника
- Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, – центре вписанной окружности.
- Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB=
ECBC - Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
Угол между
lc и lc’ = 90°
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
la = 2bcpp-ab+clb = 2acpp-ba+clc = 2abpp-ca+b
где p = a+b+c2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
la = 2bc cosα2b+clb = 2ac cosβ2a+clc = 2ab cosγ2a+b
Высоты треугольника
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
- Если в треугольнике две высоты равны, то треугольник — равнобедренный.
- ha:hb:hc=1a:1b:1c=
BC:AC:AB - 1ha:1hb:1hc=1r
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
ha = b sin γ = c sin βhb = c sin α = a sin γhc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь
ha = 2Sahb = 2Sbhc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности
ha = bc2Rhb = ac2Rhc = ab2R
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
r = Sp
Радиус вписанной в треугольник окружности через три стороны
r = a+b-cb+c-ac+a-b4a+b+c
Формулы высот треугольника через две стороны и радиус описанной окружности
1r=1ha+1hb+1hc
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
- Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
- Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
R = abc4S
Радиус описанной окружности через площадь и три угла
R = S2 sinα sinβ sinγ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
R =a2 sinα+b2 sinβ+c2 sinγ
Связь между вписанной и описанной окружностями треугольника
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
d2 = R2 – 2Rr
Радиус описанной окружности через площадь и три угла
rR = 4sinα2 sinβ2 sinγ2 = cosα + cosβ + cosγ
2Rr =abca+b+c
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
- Любой треугольник имеет три средних линии.
- Средняя линия треугольника параллельна основанию и равна его половине.
MN= 12AC; KN= 12AB; KM= 12BCMN || AC; KN || AB; KM || BC - Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника.
S∆MBN = 14S∆ABC; S∆MAK = 14S∆ABC;
S∆NCK = 14S∆ABC - При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN ~ ∆ABC;
∆AMK ~ ∆ABC;
∆KNC ~ ∆ABC;
∆NKM ~ ∆ABC
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон.
P = a + b + c
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S = 12 a · ha
,
S = 12 b · hb
,
S = 12 c · hc
,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
S = pp-ap-bp-c
,
где p — полупериметр треугольника: p = a + b + c2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 12 a · b · sinγ
,
S = 12 b · c · sinα
,
S = 12 a · c · sinβ
,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b,
α — угол между сторонами b и c,
β — угол между сторонами a и c.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a · b · c4R
,
a, b, c — стороны треугольника,
R – радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = p · r
,
где S — площадь треугольника,
r – радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c2
Равенство треугольников
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Теорема.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Теорема.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Теорема.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
∆АВС~∆MNK=> α=α1
,
β=β1
,
γ=γ1
и
ABMN=BCNK=ACMK=k
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK=k2
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1+∠ 2=90°.Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
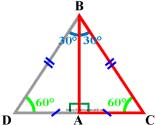
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK=k2
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
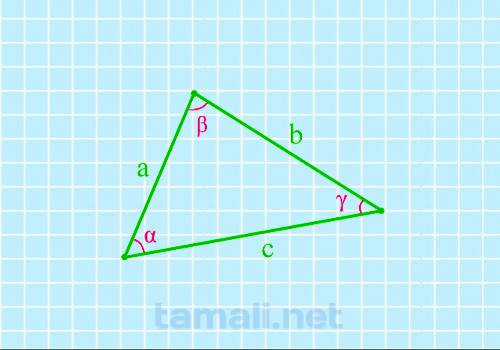
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
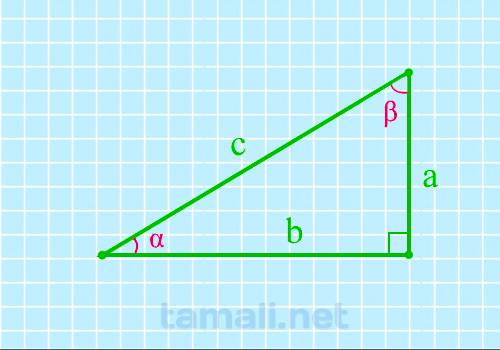
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
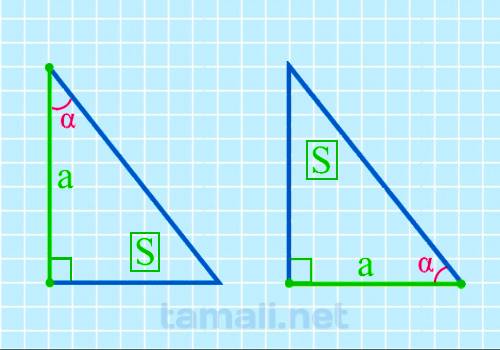
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
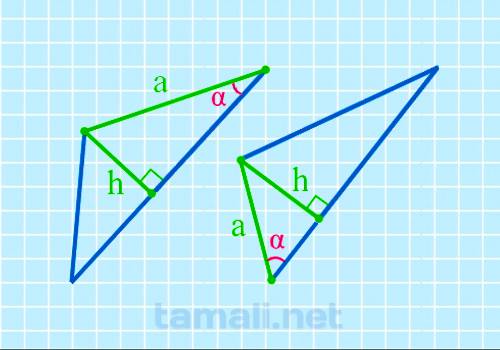
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
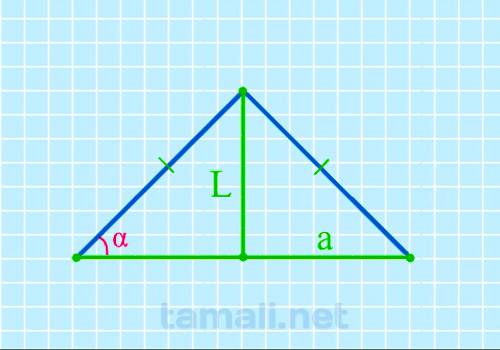
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
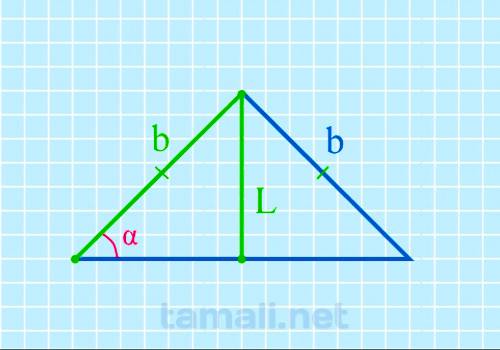
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
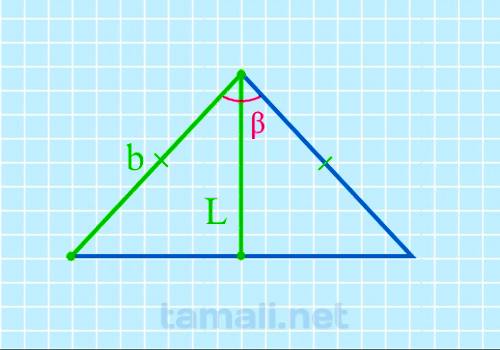
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
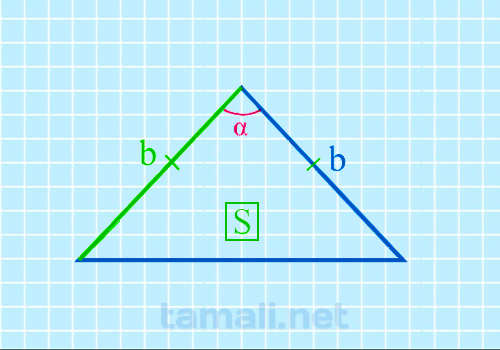
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
Содержание:
- Определение разностороннего треугольника
- Примеры решения задач
Определение разностороннего треугольника
Определение
Разносторонним называется треугольник, у которого все стороны имеют разную длину.
Свойства разносторонних треугольников
- Против большего угла лежит большая сторона, а против меньшего угла – меньшая сторона.
- Неравенство треугольника: $AB + BC > AC$
Примеры решения задач
Пример
Задание. Дан разносторонний треугольник со сторонами 3, 4, 6. Определить какой треугольник
(тупоугольный,
остроугольный или
прямоугольный)?
Решение. Предположим, что треугольник прямоугольный, тогда меньшие стороны
$AB$ и
$BC$ будут катетами, а
$AC$ – гипотенузой. Тогда по
теореме Пифагора имеем:
$$sqrt{A B^{2}+B C^{2}}=sqrt{3^{2}+4^{2}}=sqrt{9+16}=sqrt{25}=5 neq 6$$
Следовательно, данный треугольник не прямоугольный, а удлинение стороны на единицу автоматически увеличит и угол, он станет тупой.
Таким образом, треугольник, с заданными сторонами, тупоугольный.
Ответ. Треугольник тупоугольный.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Определить могут ли быть треугольники со сторонами:
1) $AB = 3, BC = 5, AC = 8$
2) $AB = 3, BC = 5, AC = 9$
3) $AB = 3, BC = 5, AC = 7$
Решение. Проверим, выполняется ли для каждого набора сторон неравенство треугольника
$AB + BC > AC$. Получим:
1) $3 + 5 = 8$ – не выполняется, треугольника с
такими сторонами не существует.
2) $3 + 5 < 9$ – не выполняется, треугольника
с такими сторонами не существует.
3) $3 + 5 > 7$ – выполняется, следовательно,
треугольник с такими сторонами существует.
Ответ. Из заданных наборов длин существует только треугольник со сторонами
$AB = 3, BC = 5, AC = 7$
Читать дальше: что такое остроугольный треугольник.