- Авторы
- Научный руководитель
- Файлы
- Литература
Ляховский К.С.
1
1 г. Котлас, ЧЧОУ «Школа-интернат № 1 среднего общего образования ОАО «Российские железные дороги», 4 класс
Бубнова Н.И. (Котлас, ЧОУ «Школа-интернат № 1 ;среднего общего образования ОАО «Российские железные дороги»)
1. Моро М.И., Волкова С.И. Для ;тех, кто любит математику. 4 ;класс ;/ Просвещение, 2017.
2. Волкова С.И. Математика и ;конструирование. 4 ;класс, 2014.
3. Атанасян Л.С., Бутузов В.Ф. Геометрия 7–9 ;классы: учеб. для ;образовательных учреждений. 5-е изд. – М.: Просвещение.
4. http://uslide.ru/geometriya/18852–razvyortki-kuba.html.
5. http://easyen.ru/load/m/3_klass/kub_ehlementy_kuba_grani_rebra_vershiny/377–1–0–13873.
6. https://ru.wikipedia.org/wiki.
Математика изучает объекты, явления, процессы окружающего мира во всех его проявлениях и взаимодействиях. Обустраивая окружающее пространство, человек всегда старается его упорядочить. Одна из часто встречаемых форм бытовых предметов – это прямоугольный параллелепипед. Его форму имеют: шкаф, телевизор, детские кубики, кусочки сахара… Длину, ширину и высоту прямоугольного параллелепипеда называют его измерением. Если все три измерения равны, то его называют кубом.
Знания о площади поверхности куба, его развертках, объёме полезны при расчётах количества обоев, паркета, краски при ремонте квартиры, кубометров леса при постройке дома… Поэтому тема «Куб и его развёртки» является актуальной.
Актуальность применения правил замощения плоскости подтверждает сказ о мастерах.
Двум мастерам было дано задание из одинаковых листов железа изготовить максимальное количество кубов, используя предложенную развертку куба. У первого мастера получилось 5 штук, второй же мастер, применив принципы замощения плоскости, сумел сделать в два раза больше кубов, тем самым показав возможность рационального использования материала
Цель исследования: получение новых знаний о кубе, его развертках и их практических применениях.
Задачи исследования:
1. Изучить элементы куба.
2. Исследовать развёртки куба.
3. Изготовить модели куба.
4. Выполнить замощение плоскости развёртками куба.
5. Изготовить пазлы.
Предмет исследования: куб.
Объект исследования: развёртки куба.
Гипотеза: знания о кубе и его развёртках помогают решать практические задачи.
Методы исследования: практический, наблюдение, опрос, анализ, обобщение, измерения, расчёты, изучение литературы и материалов сайтов.
Теоретический этап исследования
1. Куб и его элементы
По другому куб называют шестигранником или гексаэдром [6]. Куб имеет 6 граней Каждая грань куба – квадрат. У куба 8 вершин. Вершина куба – это самая отдалённая от центра куба точка, которая лежит на пересечении трёх его граней. Каждая вершина принадлежит только трём граням и только трём рёбрам. Куб имеет 12 рёбер. Ребро куба – это отрезок, образованный пересечением двух граней куба. Рёбра имеют одинаковую длину. Каждый конец ребра соединен с двумя соседними рёбрами под прямым углом [3].
Поверхность куба состоит из шести граней. Площадь поверхности куба – это сумма площадей всех граней.
Площадь одной грани куба при длине ребра «а» равна а2. Площадь поверхности куба можно выразить формулой S=6a2.
Площадь одной грани этого куба: 1 дм2, тогда площадь поверхности куба будет равна 6 дм2. Если разбить 1 дм2 на см2 и мм2, мы получим, что площадь поверхности данного куба будет равна 600см2 и 60 000мм2 соответственно.
Объём куба – это совокупность всех точек в пространстве, ограниченных гранями куба. Объём куба при длине ребра «а» можно выразить формулой V=a3.
Кубы с одинаковым размером граней, но сделанные из разных материалов имеют одинаковый объем, одинаковую площадь, но разную массу. Соответственно, кубы, изготовленные из разных материалов, но имеющие одинаковую массу, будут отличаться размерами.
Игральная кость – это популярный источник случайности, который широко применяется в азартных, настольных и ролевых играх.
Традиционная игральная кость – это кубик, который используется как средство генерирования случайных чисел. На каждую грань кубика нанесены числа от 1 до 6. Их принято располагать так, чтобы сумма чисел на противоположных гранях была равна семи. Целью кубика является демонстрация случайно определённого целого числа от одного до шести. Выпадение каждого числа является равновозможным благодаря правильной геометрической форме кубика.
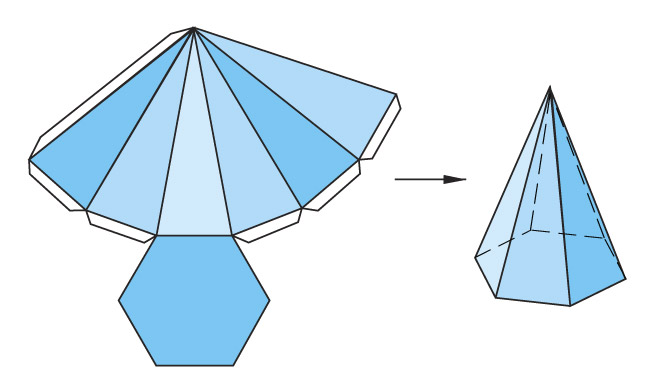
2. Развёртки куба
Развёртка куба – это оболочка, позволяющая увидеть куб со всех сторон. Развертка куба состоит из 6 равных квадратов.
Изучение возможных вариантов развёртки куба, показало, что их всего 11 видов [4].
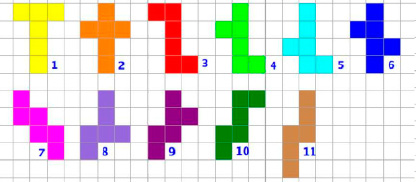
3. Замощение
Замощение – это покрытие всей плоскости или заполнение всего пространства неперекрывающимися фигурами [5].
Изучение куба показало, что плоскость можно покрыть целиком без пробелов его реберными развёртками одного вида. При этом несколько развёрток одного типа складываются в симметричный элемент орнамента, называемый плиткой, с помощью которой происходит замощение плоскости [2].
Выполнено замощение плоскости различными развёртками куба. Замощение плоскости развертками куба можно использовать при изготовлении пазлов.
Пазл – это увлекательная головоломка очень популярная у взрослых и незаменимый элемент в жизни каждого ребёнка. Пазлы для детей – это увлекательная игра, позволяющая развивать мелкую моторику, логическое мышление, воображение, память, усидчивость, терпение, целеустремленность.
Практический этап исследования
Практическая работа №1
Сделать модель куба из дерева с рёбрами 1 дм, из бумаги с ребром 1 дм. Из бумаги с ребром 1 см.
Заполнить таблицу.
|
Ребро |
Площадь поверхности |
Объём |
Масса |
|
|
Куб из дерева |
1 дм |
6 дм2 |
1 дм3 |
650 г |
|
Куб из бумаги |
1 дм |
6 дм2 |
1 дм3 |
50 г |
|
Куб из бумаги |
1 см |
6 см2 |
1 см3 |
0,5 г |
Вывод: площадь поверхности и объёма куба зависит от величины ребра и не зависит от материала. Масса куба зависит от размеров куба и материала, из которого он изготовлен (Приложение 1).
Практическая работа №2
Изготовить тренажёр по переводу единиц измерения площади. На бумажной модели куба разбить одну грань на квадратные сантиметры, на противоположной сделать надпись 100см2, другую грань разбить на квадратные миллиметры, на противоположной грани сделать надпись 10000 мм2. На пятой грани сделать надпись 1 дм2.
Результат: изготовлен тренажёр по переводу единиц измерения площади (Приложение 2).
Практическая работа №3
Изготовить 11 различных развёрток куба с длиной ребра 1дм. Обёртыванием бумажной модели куба убедиться, что все они являются развёртками куба.
Результат: даны названия развёрткам куба: «Буква Т», «Крестик», «Лежачая собачка», «Ружьё», «Стоячая собачка», «Пушка», «Загадочная», «Лесенки».
Проверено, что все 11 многоугольников являются развёртками куба (Приложение 3).
Практическая работа №4
Изготовить модель игральной кости с ребром 5 см. Подбрасыванием кости убедиться, что выпадение очков происходит с равной вероятностью.
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Выпадение очков |
5 |
1 |
4 |
5 |
6 |
3 |
3 |
1 |
2 |
6 |
3 |
5 |
6 |
4 |
2 |
1 |
6 |
2 |
4 |
5 |
Вывод: выпадение очков происходит с равной вероятностью (Приложение 4).
Практическая работа №5
Замостить плоскость различными развёртками куба. Сделать пазлы.
Результаты:
1. Выполнены рисунки по замощению плоскости развёртками куба.
2. Изготовлены пазлы (Приложение 5).
Задача о нахождении кратчайшего расстояния по поверхности куба
В точке А на поверхности куба находится паук, в точке В муха. Найти кратчайшее расстояние по поверхности куба от паука к мухе.
Развертки куба помогают при решении различных задач. Одна из таких задач была предложена для решения воспитанникам нашей школы. Необходимо было указать кратчайший путь от паука, сидящего в точке А, к мухе, находящейся в точке В.
Был проведён опрос воспитанников по нахождению самого короткого пути по поверхности куба.Предложенные варианты ответов изображены цифрами.
|
№ опыта |
Длина линии |
|
1 |
25 см |
|
2 |
23 см |
|
3 |
21 см 5 мм |
|
4 |
20 см 5 мм |
|
5 |
21 см 4 мм |
Произвели измерения и вычислили длины путей, самый короткий путь оказался четвёртый. Это подтверждает развёртка куба. Самый короткий путь на развёртке – это отрезок АВ. Двигаться надо к точке на ребре куба, отстоящей от нижней грани на четверть ребра (Приложение 6).
Заключение
В результате работы были сделаны следующие выводы:
1. Куб – это геометрическое тело, являющееся правильным шестигранником, каждая грань которого представляет собой квадрат.
2. Куб небольшого размера, на каждую грань которого нанесены числа от 1 до 6, используется как средство генерирования случайных чисел.
3. Развёртки куба позволяют находить решения различных задач.
4. Применение различных развёрток куба и правил замощения плоскости способствуют созданию разнообразных орнаментов и рациональному использованию материала.
5. Замощение плоскости развертками куба можно использовать при изготовлении пазлов для детей, способствующих их полноценному и всестороннему развитию.
Приложения
Приложение 1
Модели куба
Приложение 2
Поверхность куба
Приложение 3
Развёртки куба
Приложение 4
Игральная кость
Приложение 5
Замощение плоскости
Приложение 6
Нахождение кратчайшего пути
Библиографическая ссылка
Ляховский К.С. КУБ И ЕГО РАЗВЁРТКИ // Старт в науке. – 2018. – № 5-6.
;
URL: https://science-start.ru/ru/article/view?id=1223 (дата обращения: 16.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Чертежи развёрток поверхностей геометрических тел
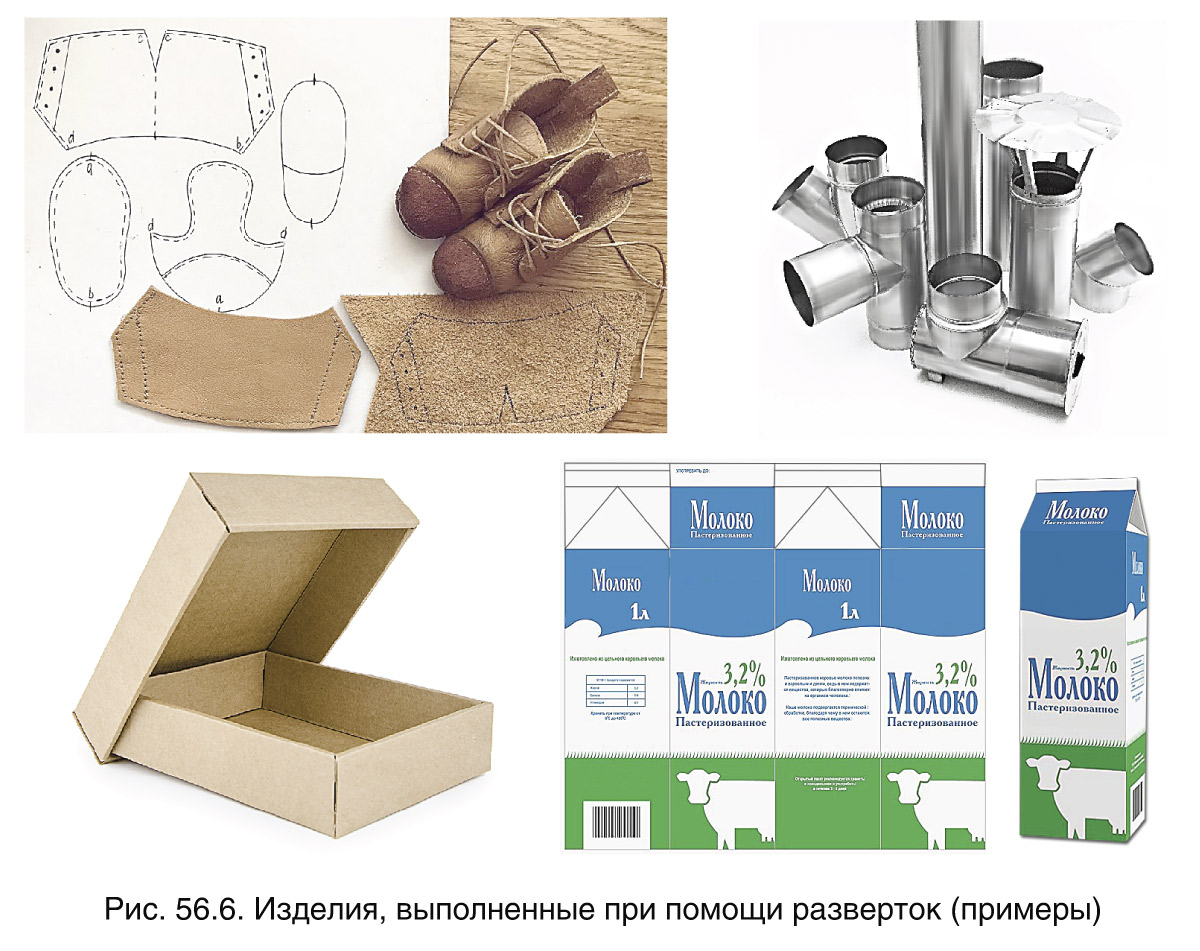
Некоторые предметы (упаковочные коробки, канцелярские папки, водосточные трубы и др.) изготавливаются из листового материала — жести, картона, плотной бумаги (рис. 56.6). Для их изготовления пользуются развёртками. Построение развёрток поверхностей имеет большое практическое значение при конструировании различных изделий.
Развёрткой называют плоскую фигуру, полученную путем совмещения всей поверхности, ограничивающей предмет, с одной плоскостью
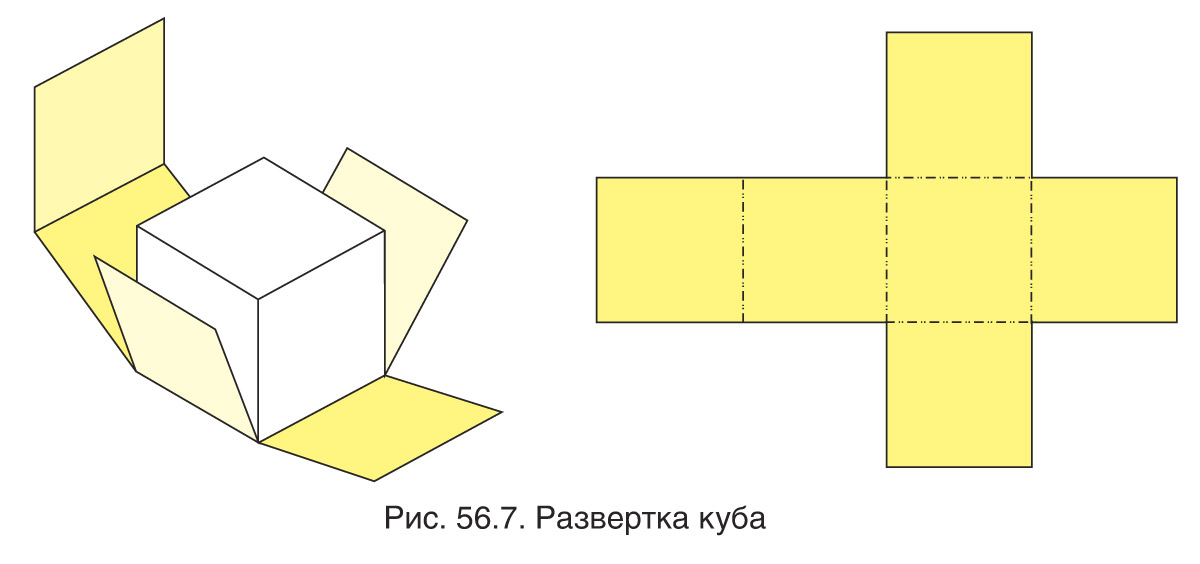
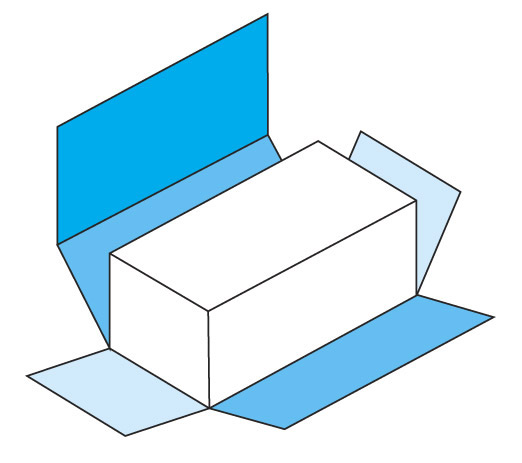
Техника выполнения развёрток используется конструкторами дизайнерами, которые разрабатывают дизайн коробок и пакетов. Делая чертежи развёртки, затем, вырезая ее и склеивая можно получить трехмерные модели. Например, развёртка куба (рис. 56.7).
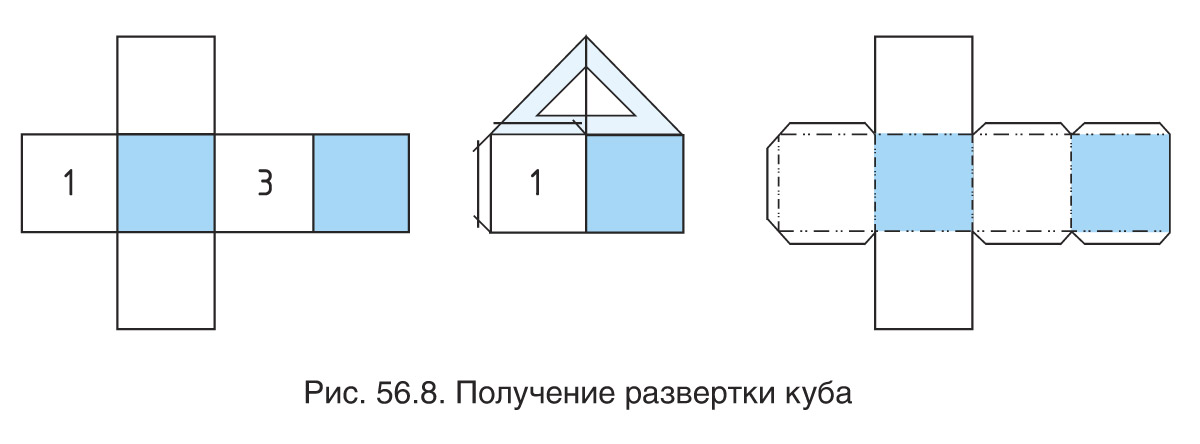
Куб имеет шесть квадратных граней с одинаковыми размерами. Все грани между ними образуют прямые углы. Для получения развертки сначала надо на бумаге сделать проекцию каждой грани куба, а затем вырезать и соединить их друг с другом (склеить) (рис. 56.8).
Особенности изображения и обозначения разверток. Для одних геометрических тел развёртки могут быть точными, для других – приближенными. Точные развёртки имеют все многогранники (призмы, пирамиды и др.), цилиндрические и конические поверхности и некоторые другие. Их поверхности называют развертывающимися. Приближенные развёртки имеют шар, тор и другие поверхности вращения с криволинейной образующей. Такие поверхности носят название неразвёртывающиеся.
При построении развёртки необходимо найти сначала истинные, натуральные размеры и форму отдельных элементов предмета на чертеже. Если необходимые геометрические фигуры на проекциях искажены, то перед построением развёртки определяют их натуральную величину. Конструкторы при разработке изделия стремится сделать развёртку более компактной, чтобы при изготовлении изделий израсходовать меньше материала.
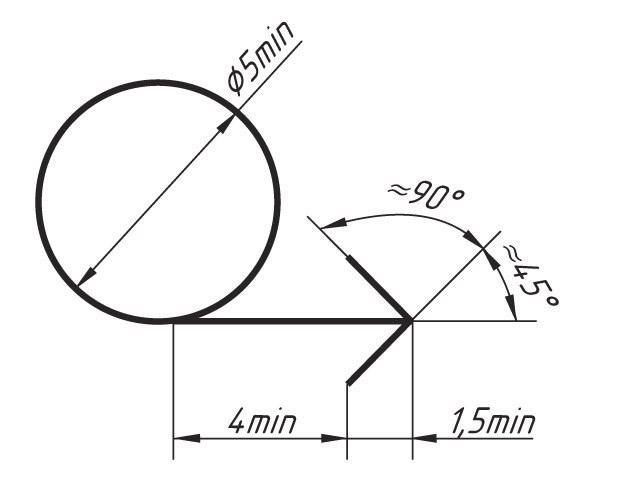На изображении развёртки наносят только те размеры, которые невозможно указать на изображении готовой детали. Над изображением развёртки располагают условное графическое изображение «Развертка».
Развертку изображают основными сплошными линиями, толщина которых должна быть равна толщине линий видимого контура на изображении детали.
При необходимости, на изображении развёртки наносят линии сгибов, выполняемые штрихпунктирной тонкой линией с двумя точками, с указанием на полке линии-выноски «Линия сгиба».
Вспомните и назовите, какой линией чертежа показывают место сгиба.
Несложно вычертить развертку простого геометрического тела, составленного из плоских граней, или развернуть на плоскость цилиндр и конус, сложнее построить точную развертку поверхности шара на плоскости.
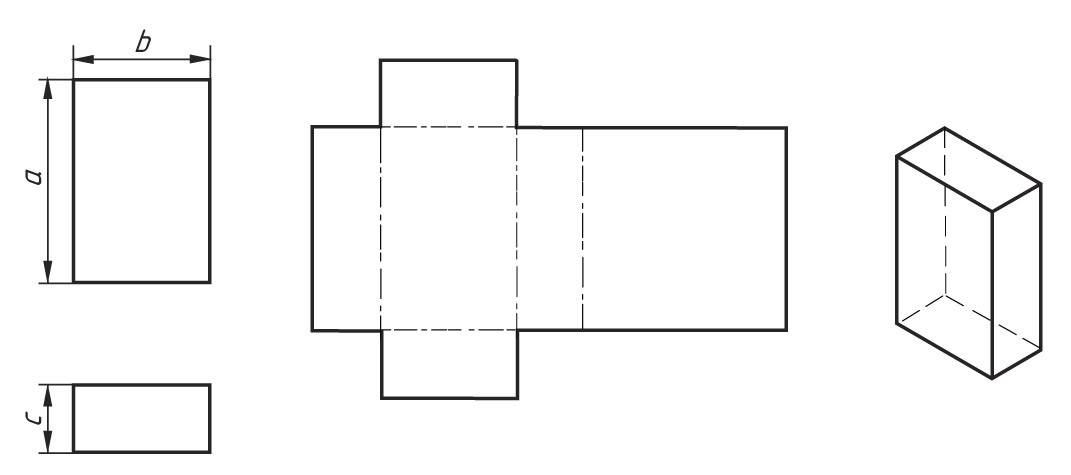
Построение развёртки призмы
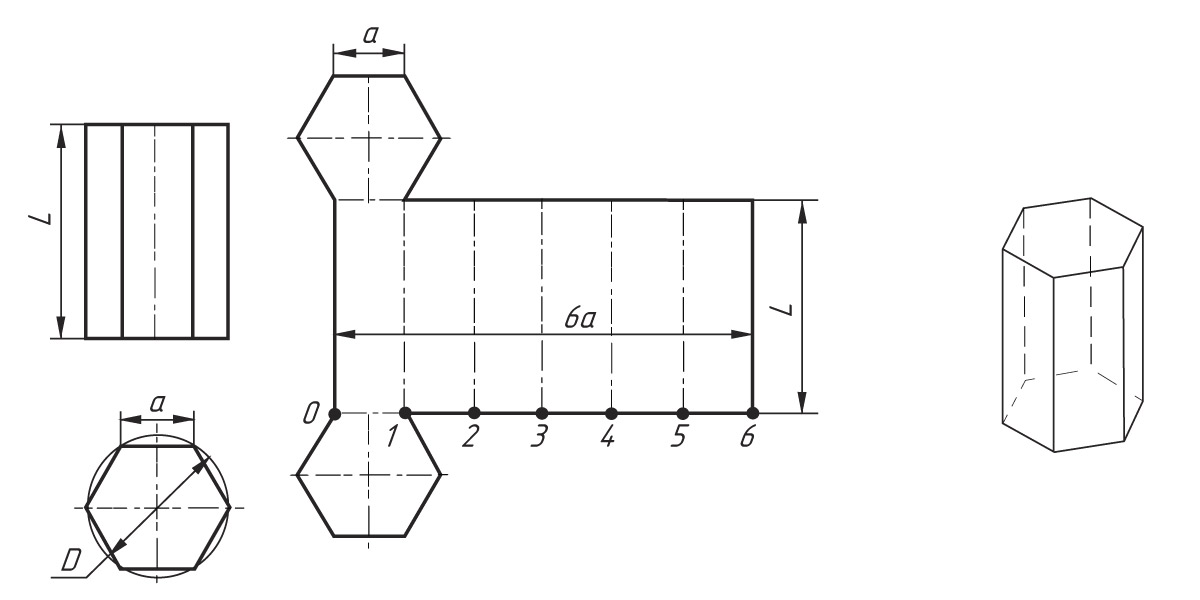
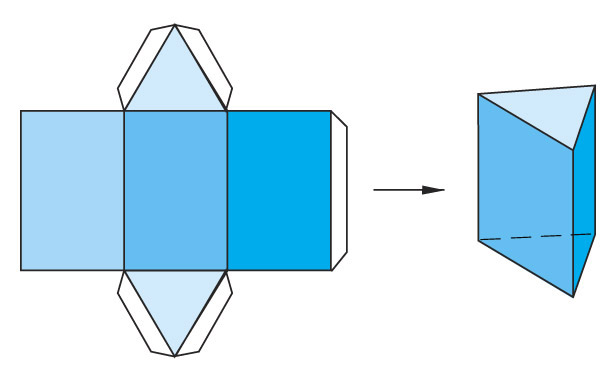
Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней – прямоугольников и двух равных между собой многоугольников, являющихся основаниями. Для построения развертки прямой призмы, достаточно знать три размера: длину (b), ширину (с) и высоту (а) призмы.
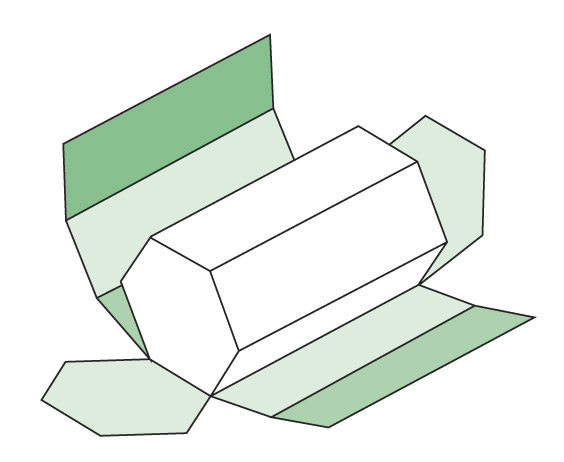Последовательность построения шестиугольной призмы
Все боковые грани призмы — прямоугольники, равные между собой по ширине а и высоте L; основания призмы — правильные шестиугольники со стороной, равной а.
1. На горизонтальной прямой из точки О последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т. е. 6а (точки 1,2,3,4,5,6).
2. Из полученных точек 1,2,3,4,5,6 восставляют перпендикуляры, равные высоте призмы L, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (L х 6а) является разверткой боковой поверхности призмы.
3. Затем на одной оси пристраивают фигуры оснований – два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба – штрихпунктирной с двумя точками.
Выполните чертеж развертки призмы, изображенной на рисунке. Какие величины вы будете использовать для ее построения?
Построение развёртки пирамиды
Развертка поверхности пирамиды представляет собой плоскую фигуру, составленную из боковых граней – равнобедренных или равносторонних треугольников и правильного многоугольника основания. При этом следует учесть, что неизвестна величина боковых граней пирамиды, т. к. ребра граней не параллельны ни одной из плоскостей проекций.
1. Построение начинают способом определения вращения истинной величины наклонного ребра Sa, равной s’a’1.
2. Из вершины S радиусом Sa проводят дугу до совмещения ее с горизонтальной осью в точке а1. S’a’1 — истинная величина ребра Sa.
3. Из произвольной точки О, как из центра, проводят дугу радиусом S’a’1. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину.
4. Найденные точки соединяют прямыми с точкой О. Получив развёртку боковой поверхности, к основанию одного из треугольников пристраивают квадрат, равный основанию пирамиды.
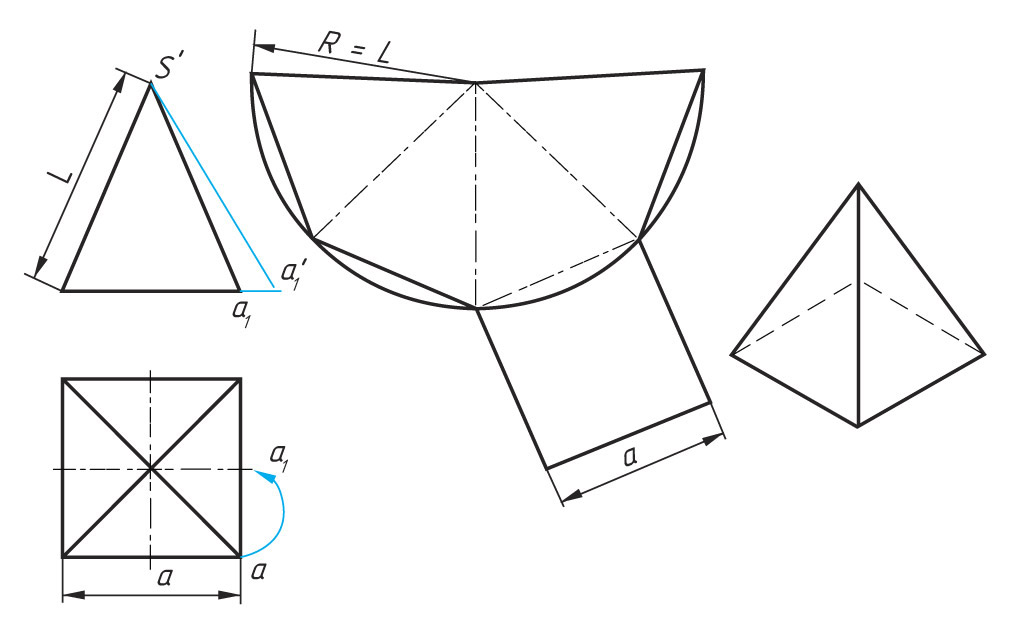
Определите величины боковых граней шестиугольной пирамиды. Выполните построение ее развертки.
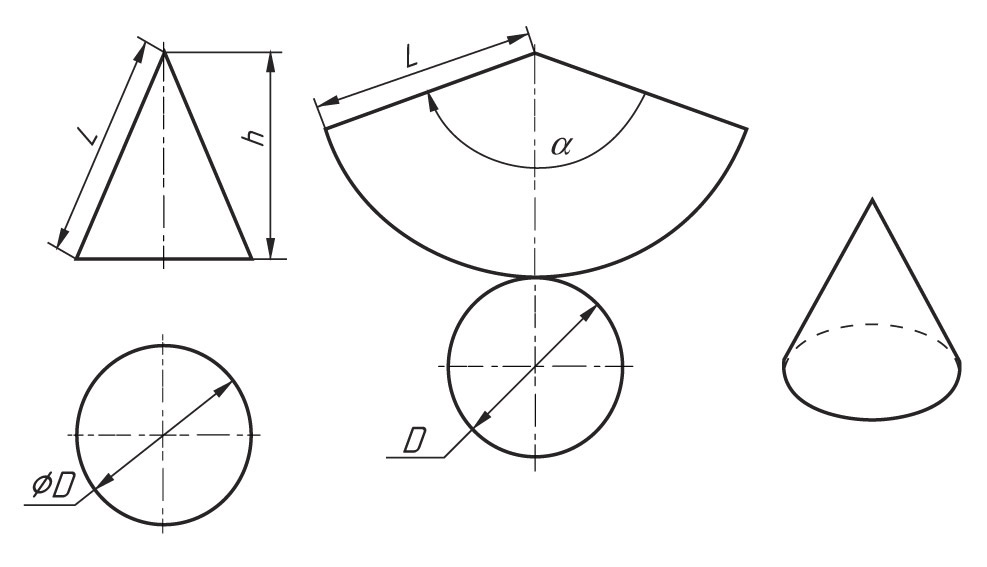
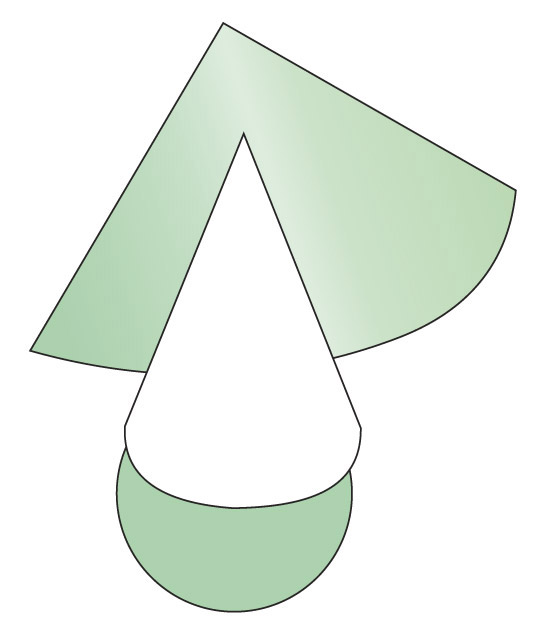Построение развертки конуса. Развёртка поверхности конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга.
1. Проводят осевую линию и из точки S, взятой на ней, как из центра, радиусом R1 равным образующей конуса L, очерчивают дугу окружности.
2. Затем подсчитывают угол сектора α по формуле
: где R — радиус окружности основания конуса; L — длина образующей боковой поверхности конуса. Этот угол строят симметрично относительно осевой линии с вершиной в точке S. К
полученному сектору пристраивают окружность с центром на осевой линии и диаметром, равным диаметру основания конуса.
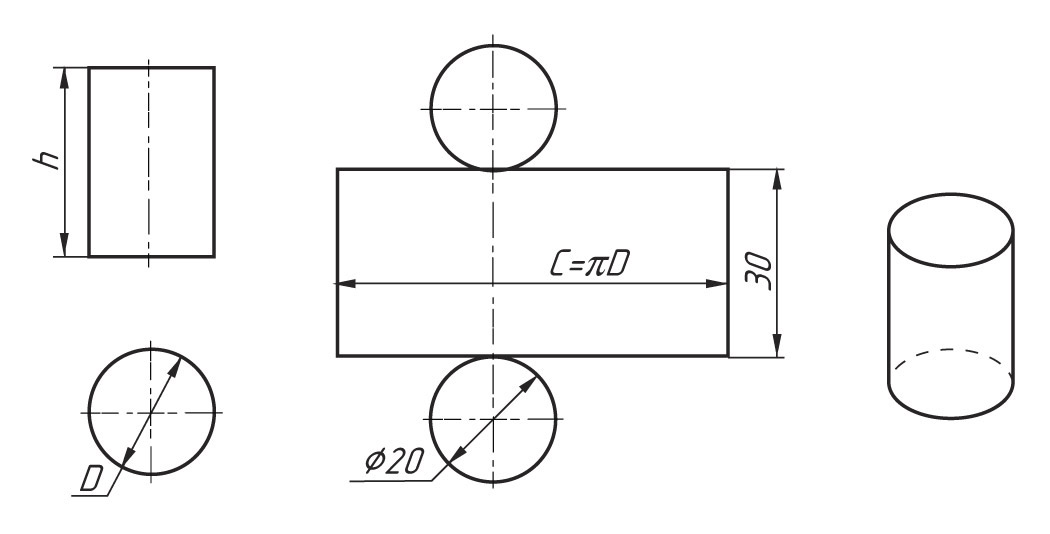
Построение развёртки цилиндра
Развёртка цилиндра представляет собой прямоугольник, одна сторона которого равна высоте цилиндра (h), а другая – развёрнутой длине окружности основания 2πR (или πD).
Проверим знания
1.Что называется развёрткой поверхности?
2.Какие надписи наносят на чертежах развёрток поверхностей предметов?
3.Какие типы линий используют на чертежах развёрток?
4.Определите, развертка какой фигуры изображена на рисунке.
5.На рисунке даны три варианта развёртки игрального кубика. Сумма очков на двух противоположных гранях всегда равняется семи. Для примера указана развертка кубика в виде буквы «Т». Расставьте правильно очки на двух остальных вариантах развёртки кубика. При этом надо сохранить порядок расположения очков, который принят на первой развёртке
.
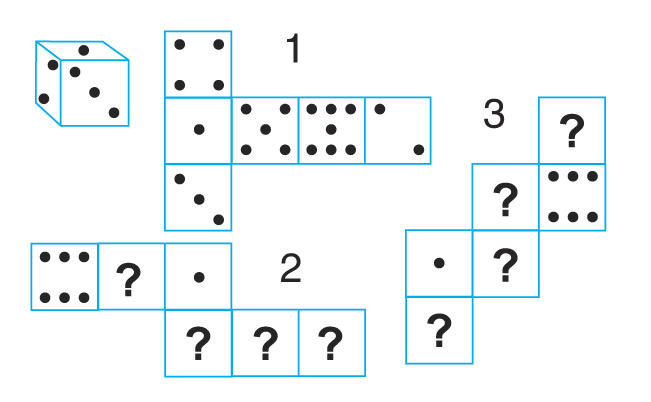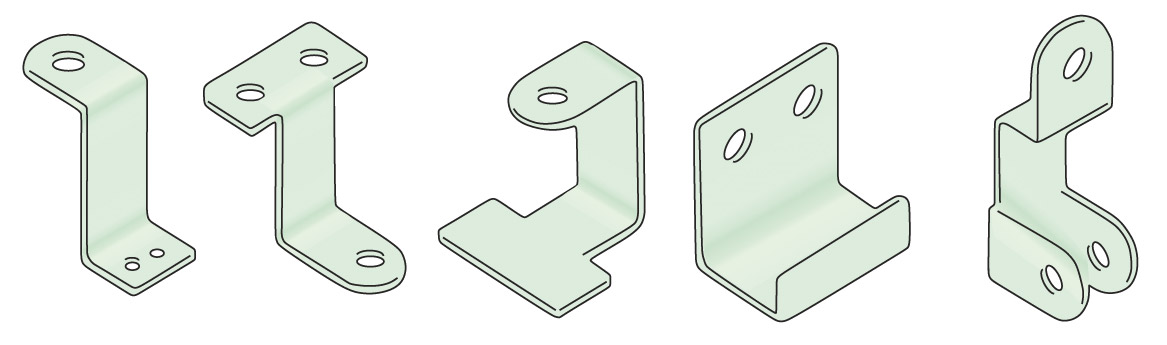
6. Выполните эскизы развёрток изделий, изображенных на рисунках.
Вопросы и задания повышенной сложности
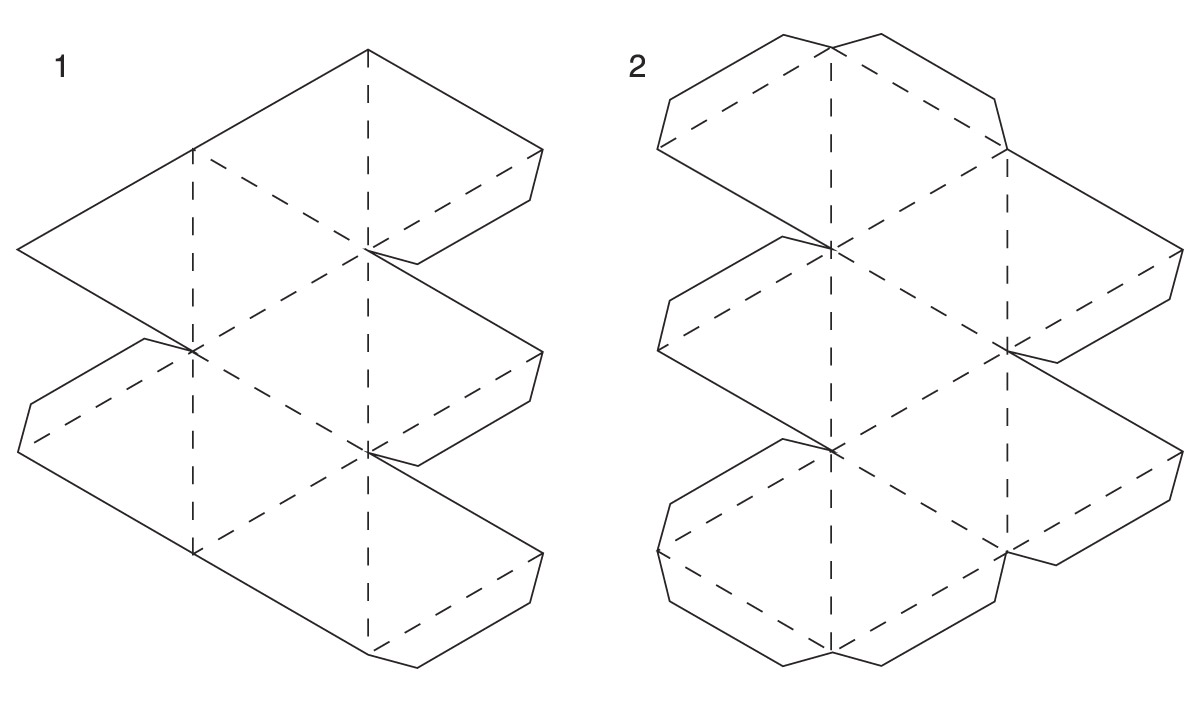
Используя чертежи 1 и 2 развёртки, определите, какая фигура здесь показана.
Графическая работа № 4.1. Развёртка
На формате А4 по чертежу и рисунку начертите развёртку детали из тонколистового металла.
Валерия Сирота
«Квантик» №8, 2022
В статье из «Квантика» № 7 за 2022 год мы научились рисовать четырёхмерный кубик. Может, теперь его сделать? Из подручных материалов.
Совсем сделать, конечно, не получится. Ведь у нас всё-таки нет здесь четырёхмерного пространства, в котором такой кубик можно было бы хранить. Но зато можно сделать выкройку — развёртку — и подождать, когда кто-нибудь четырёхмерный её сложит в куб.
Действительно, когда мы делаем трёхмерный бумажный кубик, мы сначала рисуем на бумаге плоскую развёртку из шести квадратов — например, латинский крест (рис. 1). И эта развёртка, заметьте, двумерная! Её могли бы сделать и плоские человечки, живущие на листе бумаги. Потом мы её сворачиваем в куб, а вот это плоские человечки уже не могут: мы используем наше третье измерение.
Трёхмерный куб мы собирали из двумерных граней. А из чего же собирать четырёхмерный? Из трёхмерных кубиков, конечно! В прошлый раз мы выяснили, что их понадобится 8 штук — столько, сколько 3-граней у 4-куба. И склеивать их нужно будет уже не рёбрами, как кубик, а гранями — ведь у двух соседних 3-граней есть общая двумерная (квадратная) грань. Всё, что можно, склеим у себя в трёхмерном пространстве, а остальное они уж там в своём четырёхмерном сложат.
Выкройки, как и для двумерного кубика, могут быть разные. Проще всего сделать «обобщение» латинского креста: ведь мы знаем, что в четырёхмерном кубе все двумерные грани должны соединять какие-то две 3-грани, «свободных» двумерных граней не должно оставаться; так же, как в трёхмерном кубе не болтаются ни к чему не приклеенные рёбра. Итак, берём 8 кубиков и склеиваем их — и вуаля! Развёртка готова (рис. 2).
Теперь нужно разобраться, как наша выкройка будет потом, в четырёхмерье, складываться. Тут придётся потренировать наше почти уже 4-мерное воображение!
Заметьте, что мы не можем разглядеть один из кубиков нашей развёртки ни с какой стороны — он полностью закрыт соседями. Так же и плоские человечки, когда смотрят на латинский крест, не видят центрального квадрата. Но можно сделать такую развёртку, чтобы им были видны все квадраты. Так же и мы — если захотим, можем переклеить одну из будущих 3-граней так, чтобы в новой развёртке нам были видны все кубики.
Из каждой развёртки обычного 3-куба можно получить много развёрток 4-куба: достаточно к каждому её квадрату приклеить кубик, получив похожий на латинский крест «плоский слой» (высотой в один кубик), потом к этому плоскому слою приклеить ещё два кубика: один с одной стороны (к любому кубику слоя!), второй — с другой (тоже к любому кубику). Так, например, получается развёртка на рисунке 2. Но бывают и такие развёртки 4-куба, которые из развёрток 3-куба не получишь.
Теперь, когда вы умеете рисовать и даже почти изготавливать четырёхмерные кубики, вы, конечно, понимаете, что можно рисовать и пятимерные, и шестимерные… А вдруг на самом деле мы живём в каком-нибудь таком «пространстве большей размерности», пяти- или там десятимерном? Так плоские человечки или одномерные червяки могли бы жить у нас в трёхмерии, сами того не замечая и ничего не видя снаружи от своей плоскости… Мы живём, а пятимерные существа иногда подходят и смотрят «оттуда» на наш трёхмерный мир? Что ж, такое не исключено…
А что, если в одном четырёхмерном пространстве находятся сразу два трёхмерных мира (говорят: подпространства)? Могут они там поместиться? А может быть, жителям этих миров можно как-нибудь переходить из одного в другой? Или хотя бы что-нибудь передавать?.. Подумайте: каким может быть такой «портал», соединяющий миры?
(Подсказка. Прежде чем придумывать про 4-мерье, можно «упростить задачу на одно измерение» и посмотреть, как это устроено в нашем трёхмерном пространстве. Какие пространства и как в него могут «помещаться»?)
И ещё. Двумерным человечкам не обязательно жить на плоскости. Они могут жить и на какой-нибудь изогнутой поверхности, например на сфере — на оболочке большого шара… Нам, смотрящим на них снаружи, это было бы хорошо видно. А как они могли бы догадаться об этом сами? Может, и наше трёхмерное пространство — какое-нибудь кривое? Как мы могли бы это проверить?
Художник Мария Усеинова.
Решение задачи 1
Решение задачи 2
А где белый кубик?
Решение задачи 3
Например, так:
Решение задачи 4
Например, можно последовательно переклеить все боковые кубики «латинского креста» друг на друга — оранжевый кубик на рисунке к задаче 2 отклеить от центрального и приклеить к розовому, розовый — к бежевому, бежевый — к фиолетовому. Получится так, как на рисунке.
Характеристики гексаэдра (куба)
Число сторон у грани – 4
Общее число граней – 6
Форма грани квадрат
Число рёбер, примыкающих к каждой вершине – 3
Общее число вершин – 8
Общее число ребер – 12
У каждого ребра (красный) имеется три параллельных ребра (синий).
Количество пар параллельных ребер можно определить, умножив общее количество ребер на 3.
В кубе 18 пар параллельных ребер.
У каждого ребра (красный) имеются 8 перпендикулярных ему рёбер (синий). Определить количество пар перпендикулярных ребер можно умножив общее количество рёбер на 8 и разделив на 2.
Всего куб имеет 48 пар перпендикулярных рёбер.
У каждого ребра (красный) имеются 4 скрещивающихся с ним ребра.
Определить количество пар скрещивающихся рёбер можно умножив общее количество рёбер на 4 и разделив на 2.
Всего куб имеет 24 пары скрещивающихся рёбер.
Количество пар параллельных граней – 3
Расстояние между противоположными рёбрами можно определить по формуле
,где а – длина стороны
Длину диагонали куба можно определить по формуле
Куб обладает центром симметрии
Куб имеет 9 осей симметрии.
Три оси симметрии это прямые проходящие через центр параллельных граней куба:
Шесть осей симметрии это прямые соединяющие центры противолежащих рёбер куба:
Куб имеет 9 плоскостей симметрии
Три плоскости проходят через центр параллельно граням
Шесть плоскостей проходят через центр по диагонали
Куб может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы куба
где a – длина стороны.
Сфера может быть вписана внутрь куба.
Радиус вписанной сферы куба
Сферу можно вписать в куб таким образом, что она коснется поверхностью всех рёбер куба. Такая сфера именуется – полувписанная в куб.
Радиус полувписанной сферы можно определить по формуле:
Площадь поверхности куба
Для наглядности площадь поверхности куба можно представить в виде площади развёртки.
Площадь поверхности можно определить как площадь одной из сторон куба (это площадь правильного четырехугольника – квадрата) умноженной на 6. Либо воспользоваться формулой:
Объем куба определяется по следующей формуле:
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
- многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
- прямая призма, все грани которой есть квадраты;
- прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями.
Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть.
Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать.
Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Перспективный рисунок куба
ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Чтобы научиться рисовать куб в перспективе, сначала изобразите куб в произвольном положении на основе горизонтального квадрата. Проанализируйте перспективные закономерности построения куба на примере вашего рисунка. Затем изобразите кубы в произвольном и заданном повороте, выше и ниже линии горизонта.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
Приступая к работе над рисунком, продумайте композицию листа. На нем должны разместиться 7 – 8 кубов (рис. 3.2). В верхней части листа изображайте кубы, на которые вы смотрите снизу, в нижней части листа – кубы, на которые вы смотрите сверху -так, как будто примерно посередине листа проходит линия горизонта. При желании можно действительно провести ее на рисунке, тогда раскрытие квадратов в основании кубов будет задано более точно. Обозначьте на листе место и приблизительный размер каждого куба легкими линиями.
Наилучшее представление о геометрическом теле дает анализ его ортогональных проекций. Рассмотрите перспективный рисунок куба на рис. 3.3 и его ортогональные проекции на рис. 3.4. Перспектива куба строится на перспективе квадратов, его образующих. Чувство перспективы квадрата, а также куба, должно быть развито у архитектора особенно хорошо, так как квадрат и куб являются основными модулями площади и объема для других плоских и пространственных форм.
Для выполнения задания внимательно изучите схемы построения куба в угловой и фронтальной перспективах. Сначала изобразите куб ниже линии горизонта в угловой перспективе. Рисунок куба начните с горизонтального квадрата верхнего основания. Квадрат постройте на основе эллипса (рис. 3.5). Проведите из вершин квадрата вертикальные ребра куба и отложите на ближнем вертикальном ребре высоту куба. Она, примерно, равна большой оси эллипса, вписанного в квадрат основания куба. Определив высоту куба, последовательно достраивайте недостающие ребра, сводя параллельные линии в точки схода на горизонте. Эти построения лучше совершать в определенной последовательности – в той, которая позволит вам постоянно контролировать ход работы и своевременно исправлять замеченные ошибки. Сначала из полученной точки в нижнем основании куба проведите горизонтальное ребро, достроив до квадрата ту вертикальную грань, которая имеет большее раскрытие (рис. 3.6). Визуально проверьте правильность этого квадрата и, если это необходимо, исправьте его, увеличив или уменьшив выбранную высоту куба. Направление второго горизонтального ребра легко определить, продлив его линию на рисунке и проверив, насколько она сходится в перспективе с горизонтальными ребрами верхнего основания куба (рис. 3.7). Третье ребро также проведите, ориентируясь на уже существующие линии параллельного направления (рис. 3.8). Последнее ребро нижнего основания соединяет две вершины, место которых на рисунке уже определено предыдущим построением (рис. 3.9). Изображенный куб должен выглядеть убедительно и правдиво – каждая его грань, вне зависимости от того, видим мы ее или нет, должна по ощущению быть похожа именно на квадрат. Проверьте это визуально, а затем графически, вписав в видимые нам вертикальные грани куба окружности (рис. 3.10).
Закончив рисунок, еще раз проанализируйте закономерности раскрытия граней куба и перспективных сокращений его ребер:
• горизонтальные параллельные линии, на которых лежат ребра куба, равномерно сходятся в точки схода на линии горизонта, а вертикальные ребра куба сохраняют на листе свое вертикальное направление (рис. 3.11);
• те горизонтальные ребра, что идут в точку схода, расположенную ближе к кубу, сходятся быстрее, чем те, что идут в точку схода, расположенную дальше (рис. 3.12);
• те ребра, которые расположены ближе к зрителю, на рисунке имеют больший размер по сравнению с ребрами, которые расположены дальше. Заметьте, что подобным образом можно сравнивать только те ребра, которые лежат на параллельных прямых. Так, например, из четырех вертикальных ребер куба наибольший размер имеет ближнее к нам ребро, а по мере удаления от зрителя размер ребер на рисунке уменьшается (рис. 3.13);
• верхняя горизонтальная грань куба, расположенная ближе к линии горизонта, раскрыта меньше, чем нижняя горизонтальная грань (рис. 3.14). Из двух параллельных вертикальных граней больше раскрыта та грань, которая расположена дальше от зрителя (рис. 3.15 и 3.16);
• из двух видимых вертикальных граней куба больше раскрыта та грань, точки схода горизонтальных ребер которой находятся дальше от куба, таким образом, больший угол при основании а соответствует менее раскрытой вертикальной грани куба, меньший угол р – более раскрытой грани (рис. 3.17);
• параллельные диагонали, проведенные в горизонтальных гранях куба, сходятся на линии горизонта (рис. 3.18).
Если вы обнаружили ошибки в своем рисунке, исправьте их. В следующих кубах старайтесь отслеживать перспективные закономерности в процессе рисунка, а не в конце, когда построение уже закончено.
На рисунке куба во фронтальной перспективе фронтальные грани куба изображаются как квадраты различного размера – в зависимости от того, ближе или дальше от зрителя они расположены. Ребра, ограничивающие фронтальные грани, имеют вертикальное и горизонтальное направления. Горизонтальные ребра куба, уходящие от зрителя, сходятся в точке схода на линии горизонта. Сначала изобразите верхнее основание куба – горизонтальный квадрат во фронтальной перспективе на основе эллипса (рис. 3.19). Опустите из вершин основания вертикальные ребра куба и достройте до квадрата переднюю вертикальную грань (рис. 3.20). Из нижних точек фронтальной грани проведите прямые в точку схода на линии горизонта. Точки пересечения этих прямых с дальними вертикальными ребрами определят на вашем рисунке размеры остальных граней куба (рис. 3.21). Завершите рисунок, вписав окружности во фронтальные грани куба (рис. 3.22).
Для того, чтобы нарисовать куб в определенном повороте, сначала необходимо изобразить в соответствующем повороте его горизонтальное основание. Вы можете самостоятельно задать этот поворот, определяя его как отношение проекций боковых граней куба на горизонтальную прямую (рис. 3.23). Выберите простые отношения – 1:2, 1:3, 1:4. Изображая куб в заданном положении, сначала, как обычно, изобразите эллипс, а затем опишите вокруг него квадрат, добиваясь заданного положения квадрата путем последовательных приближений. На основе квадрата постройте куб.
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
рисуем куб
Все окружающие нас вещи, которые мы хотели бы нарисовать, какими бы сложными по форме они нам не казались, всегда можно схематически представить с помощью простых геометрических фигур, таких как куб, цилиндр, шар. Поэтому, нужно понять, как правильно рисовать эти простейшие фигуры, и потом в рисовании более сложных фигур у вас будет гораздо меньше сложностей.
Для начала нужно построить куб. Чтобы понять, как будут изменяться пропорции куба в перспективе, рассмотрим рисунок, на котором изображен непрозрачный и прозрачный куб. Точка F на рисунке – точка схода.
Тут показано фронтальное положение куба в трех возможных случаях:
1) когда линия горизонта пересекает куб – значит, мы смотрим на прямо куб, находящийся на уровне наших глаз;
2) когда куб находится ниже линии горизонта – мы смотрим на куб прямо и немного сверху и
3) когда куб находится над линией горизонта – мы смотрим прямо и снизу. Вот всех этих случаях вся передняя грань куба находится на одинаковом расстоянии от наших глаз, поэтому она не изменится в перспективе. Чтобы построить куб во всех этих положениях, достаточно построить переднюю грань, провести линии из четырех углов в точку схода, отложить на этих линиях верхние и нижние ребра и соединить их между собой.
На рисунке 1 видно, что когда куб расположен на линии горизонта, его передние боковые ребра не подвергаются перспективным изменениям, а задние ребра кажутся короче передних, из-за этого верхние и нижние ребра, уходящие в глубину, кажутся не параллельными, и продлив их до линии горизонта, мы получим точку схода.
Если куб поставить ниже или выше линии горизонта (рис 2 и 3), то ребра, уходящие в глубину, поднимутся вверх или, соответственно, опустятся вниз, сходясь на линии горизонта.
Возможны еще случаи, когда линия горизонта проходит через верхнюю или нижнюю грани куба, такие положения построить тоже достаточно легко. Теперь рассмотрим вариант, если куб развернут к нам одним из своих боковых ребер, так же в трех положениях: на линии горизонта, ниже и выше линии горизонта. В этом случае точек схода будет две.
В первом случае, нам будут видны только две грани, расположенные под углом. Ближе всего к зрителю будет находиться переднее боковое ребро, и только оно не подвергнется перспективным сокращениям. Из углов куба проводим вправо и влево прямые, сходящиеся на линии горизонта, на них будут лежать верхние и нижние ребра куба.
Если поставить куб выше или ниже линии горизонта, то нам будет видна верхняя или нижняя грань. В этом упражнении мы будем рисовать куб, развернутый к нам одним из боковых ребер, расположенный ниже линии горизонта.
Вам нужно будет нарисовать линейный рисунок прозрачного куба, прорисовывая задние ребра. Во время рисования можно использовать линейку. Если вы выполняли упражнения на развитие моторики кисти, то, скорее всего, у вас вполне получится сделать это и без линейки, во всяком случае, хотя бы попробуйте. Вполне можно наметить все линии от руки, а потом нарисовать окончательный контур с помощью линейки. Пусть размен нашего куба будет 5х5 см. Наверняка вам придется вытирать черновые линии, поэтому возьмите лист ватмана. Карандаш подойдет любой от Н до 2В.
Начните с переднего бокового ребра, которое мы видим без перспективных искажений, и только это ребро будет иметь реальный размер 5 см. На уровне нижнего угла ребра проведите вспомогательную горизонтальную прямую, потом ее можно будет вытереть, она нужна нам, чтобы определить углы, под которыми мы будем строить боковые грани куба. Если они равны, обе боковые грани мы видим одинаково, но в нашем варианте это разные углы.
Чем больше угол, тем меньше открыта соответствующая боковая грань. Определившись с углами, проведите прямые, содержащие горизонтальные ребра. Для тренировки глазомера на листе бумаги желательно не располагать точки схода, и если вы разместите ваш рисунок на вертикально развернутом листе, то они просто не поместятся, главное, чтобы из рисунка было понятно, что эти прямые сойдутся, Но вполне можно довести прямые до точек схода и указать их на линии горизонта, так нарисовать куб будет проще. Теперь, помня о том ,что исходя из законов перспективы, чем дальше от нас что-то тем оно меньше, откладываем на прямых нижние и верхнее горизонтальные ребра.
Здесь можно проверить себя с помощью линейки. Все ребра, кроме переднего бокового должны быть меньше 5 см. Например, дальнее ребро, будет меньше противоположному ему ближнему, так как более удалено от зрителя.
После того, как куб будет построен, попробуйте придать линиям разную толщину, чтобы подчеркнуть этим перспективу. Самым тонким будет дальнее вертикальное ребро, а самым толстым – ближнее. На горизонтальных ребрах нужно сделать плавный переход от более тонкого (дальнего) угла к более толстому (ближнему). Так будет выглядеть ваш куб.
Градации светотени. Тоновый рисунок куба
Теперь, зная, как правильно построить куб, мы будем разбираться, как его нарисовать тоном. Чтобы правильно нарисовать даже простейшие геометрические фигуры, нам понадобится немного теории. Мы видим предметы, если они освещены. Лучи света по-разному попадают на разные участки поверхности предметов и вы видим его форму, сам предмет закрывает собой доступ для лучей света на какую-нибудь поверхность и образуется падающая тень. Светотеневые участки на любом предмете можно представить в виде нескольких градаций:
Свет – это участок поверхности предмета, получающий наибольший поток прямых лучей света.
Полутон – участок поверхности предмета, освещенных скользящими лучами света. Полутон делится на полутон света и полутон тени.
Тень (собственная тень) – участок поверхности предмета, куда прямые и скользящие лучи света не попадают. Это самый темный участок на поверхности предмета. Блик – бывает на блестящих или лакированных поверхностях, чаще всего на территории света.
Рефлекс – участок теневой поверхности предмета, получающий поток отраженных лучей света от окружающих предметов или от поверхности, на которой предмет расположен.
Цвет рефлекса зависит от цвета окружающих предметов, а яркость или светлота зависит от характера поверхности предмета: на блестящих объектах рефлексы более светлые и ярче выражены, чем на матовых. Падающая тень – это тень, отбрасываемая объектом на какую-нибудь поверхность. Падающая тень темнее, чем собственная, а наиболее темный участок падающей тени ближе всего к источнику света. Позже я сделаю дополнение к этому уроку о том, как правильно построить падающую тень. Источников света может быть несколько, мы рассмотрим вариант с одним источником света, расположенным вверху слева относительно объекта.
На стыках по-разному освещенных граней можно наблюдать так называемый краевой контраст. На границе светлого и темного светлое кажется светлее, а темное – темнее.
Для того, чтобы выполнить это упражнение, вам потребуется настольная лампа и гипсовый куб. Гипсовые геометрический фигуры продаются в магазинах для художников, но в домашних условиях вполне можно обойтись, сделав, например, бумажный кубик, вырезанный из белого листа ватмана или картона по такой схеме:
После того, как вы сделаете куб из бумаги, поставьте его на ровную горизонтальную поверхность справа от настольной лампы так, чтобы свет от нее был направлен на куб немного сверху и слева. Желательно, чтобы поверхность стола и фон сзади куба были однотонными, чтобы не отвлекать ваше внимание. Рассмотрите куб в различных положениях, о которых мы говорили в первой части этого урока, И подробнее остановимся на том положении, которой нам предстоит нарисовать. Обратите внимание, как распределяются светотеневые участки на гранях, как ведет себя падающая тень, если приближать или удалять куб от источника света, постарайтесь увидеть краевой контраст и рефлекс.
Дальше можно выполнять это упражнение по-разному. Более простой вариант – снова начертить линейный куб и раскрасить его тоном, а более сложный – сделать рисунок куба с натуры. При рисовании с натуры тоже начинаем с переднего бокового ребра, строим сходящиеся линии, необязательно доводить их до точки схода. После определяем углы. Можно применять визирование, этот метод помогает определять углы и расстояния. Прищурив один глаз, держа на вытянутой руке карандаш, используют его, для измерения. Например, замерив одну из граней куба карандашом, смотрим, на сколько процентов или частей другая грань больше или меньше. Чтобы измерить углы, держим карандаш горизонтально на вытянутой руке как бы образуя им вспомогательную линию, параллельную линии горизонта и проходящую через нижний угол передней грани куба.
При визировании обязательно рука всегда должна быть вытянутой, иначе все время будут получаться разные результаты. Визирование тормозит развитие глазомера, поэтому не стоит им пользоваться постоянно.
Старайтесь штриховать параллельно ребрам куба, плотно и аккуратно. В результате у вас получится примерно такой куб как на рисунке выше или ниже.
