Реакция заделки теоретическая механика как найти

Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.

В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

 В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (R_A), горизонтальная (H_A) и момент (M_A).

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

• если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;

• если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как H_A, R_A и R_B:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — H_A. Так как H_A направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда H_A будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила R_B поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30^°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что M_A, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции R_A:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

Пример решения задачи по расчету реакций опоры в жесткой (глухой) заделке стальной балки, нагруженной поперечной силой F, сосредоточенным моментом m и равномерно распределенной нагрузкой q.

Задача

Рассчитать величину и направление опорных реакций в жесткой заделке консольной балки нагруженной заданной системой внешних нагрузок.

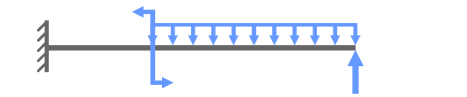
Другие примеры решений >
Помощь с решением задач >

Пример решения

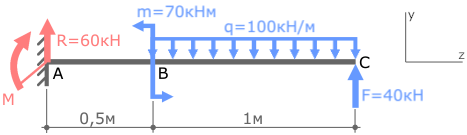
Покажем значения нагрузок и продольные размеры балки, обозначим ее характерные сечения буквами A, B и C.

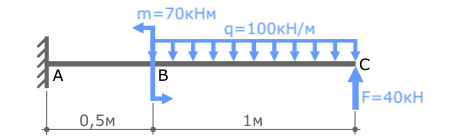
В случае плоского поперечного изгиба в жесткой заделке консольной балки могут иметь место только две опорные реакции:

1. Поперечная сила R
2. Изгибающий момент M

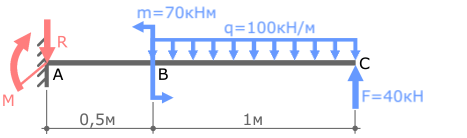
На данном этапе решения задачи эти реакции можно направить в любую сторону.

Короткое видео о реакциях в заделках:

Другие видео

Определим величину, а заодно и истинное направление опорных реакций.

Зададим систему координат y-z.

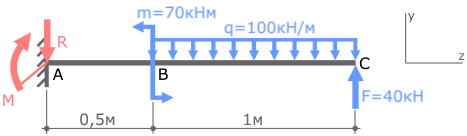
Для нахождения двух реакций нам понадобятся два уравнения равновесия.

Балка не перемещается вверх-вниз, поэтому сумма проекций всех сил на ось y должна равняться нулю.

Проецируя все силы на ось y получаем первое уравнение:

∑F(y)=0=-R-q∙1+F

Правило знаков для проекций сил.

Откуда находим величину реакции R

R=-q∙1+F=-100∙1+40=-60кН

Знак «-» в ответе говорит о том, что реальное направление реакции R противоположно выбранному вначале.

Поэтому изменим направление силы и соответственно ее знак на противоположные.

Второе уравнение статики получим из условия, что балка не вращается, так как сумма моментов приложенных к ней тоже равнв нулю.

Запишем уравнение суммы моментов, например, относительно точки A:

∑m_A=0=M-m+q∙1∙(0,5+0,5)-F(0,5+1)

Правило знаков для моментов.

Отсюда находим опорный момент M

M=m-q+F∙1,5=70-100+40∙1,5=30кНм

Положительный результат показывает, что выбранное наугад направление момента М оказалось верным, то есть перенаправлять его не нужно.

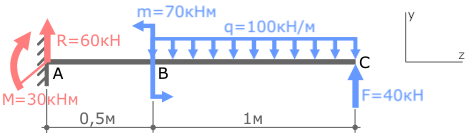
Полученные значения опорных реакций можно легко проверить.

Для этого запишем уравнение суммы моментов относительно точки B или C:

∑m_B=M+R∙0,5-m+q∙1∙0,5-F∙1

и подставив в него полученные значения, мы должны получить сумму равную нулю

∑m_B=30+60∙0,5-70+100∙1∙0,5-40∙1=0

Так и есть! Значит опорные реакции определены верно.

Расчет реакций в опорах простой двухопорной балки >
Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Реакция заделки.

Р

ассмотрим
балку один конец которой АВ заделан в
стену. Такое крепление конца балки АВ
называется заделкой в
точке В. Пусть на балку
действует плоская система сил. Определим
силы, которые надо приложить к точке В
балки, если часть балки АВ отбросить. К
сечению балки (В) приложены распределенные
силы реакции. Если эти силы заменить
элементарными сосредоточенными силами
и затем привести их к точке В, то в точке
В получим силу


(главный вектор сил реакции) и пару сил
с моментом М (главный вектор сил реакции
относительно точки В) . Момент М
называют моментом
заделки или
рективным моментом. Силу
реакции

можно заменить двумя составляющими



и

.

Заделка
в отличие от шарнира создает не только
неизвестную по величине и направлению
реакцию

, но еще и пару сил с неизвестным моментом
М в заделке.

Лекция 6

Краткое
содержание:
Центр параллельных сил. Параллельные
силы распределенные по отрезку прямой.
Центр тяжести твердого тела, поверхности
и линии. Способы определения координат
центра тяжести.

ЦЕНТР
ПАРАЛЛЕЛЬНЫХ СИЛ.

ЦЕНТР
ТЯЖЕСТИ.

Центр параллельных сил.

Для
системы параллельных сил введем понятие
центра параллельных
сил.

На тело
действует система параллельных сил

,
приложенных в точках

.
Выберем оси координат так, чтобы ось
Оz была параллельна силам.

,

,

–
проекция силы на ось
Oz.

Точка
С с координатами


называется центром
параллельных сил .

–
проекция силы на ось
Oz.

Свойства
центра параллельных
сил:

1. Сумма
   моментов всех сил

   
   относительно точки С равна нулю

2. Если
   все силы повернуть на угол , не меняя
   точек приложения сил, то центр новой
   системы параллельных сил будет той же
   точкой С.

Параллельные силы распределенные по отрезку прямой.

а)
общий случай

–
интенсивность
распределенной силы [Н/м],

–
элементарная сила.

l
– длина отрезка

Распределенная
по отрезку прямой сила интенсивности
q(x)
эквивалентна сосредоточенной силе

.
Сосредоточенная сила прикладывается
в точке С (центре параллельных сил) с
координатой

б)
постоянная интенсивность

в)
интенсивность, меняющаяся по линейному
закону

Центр тяжести.

Центром тяжести
тела называется геометрическая точка,
жестко связанная с этим телом, и являющаяся
центром параллельных сил тяжести,
приложенных к отдельным элементарным
частицам тела.

Координаты
центра тяжести неоднородного
твердого тела в выбранной
системе отсчета определяются следующим
образом:

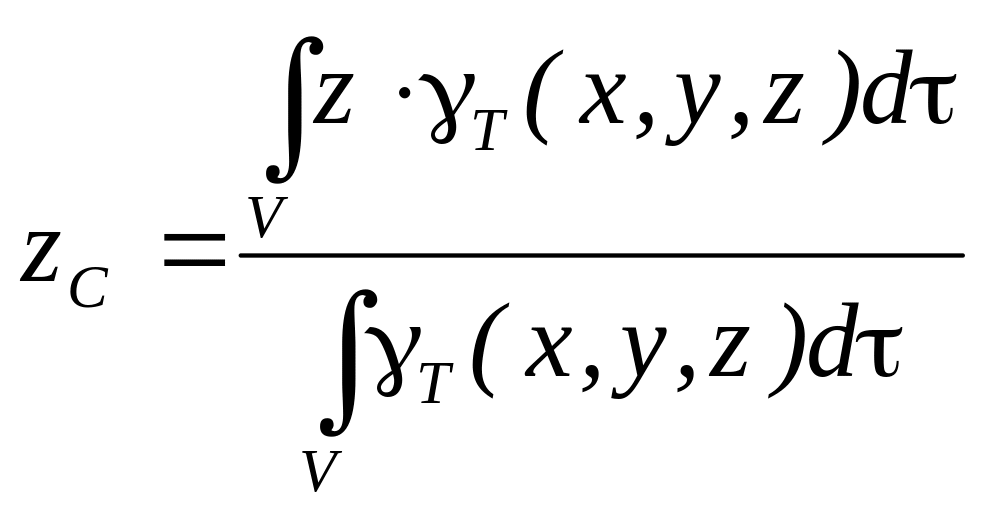
где

–
вес единицы объема тела (удельный вес)

–
Вес всего тела.

Для
однородного
твердого тела



и формулы получают вид:

–
Объем всего тела.

Если
твердое тело представляет собой
неоднородную поверхность,
то координаты центра
тяжести в выбранной системе отсчета
определяются следующим образом:

где



– вес единицы площади тела ,

– Вес
всего тела.

Для
однородной
поверхности



и формулы получают вид:

–
Площадь поверхности.

Если
твердое тело представляет собой
неоднородную линию, то
координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:

где

– вес единицы длины тела ,

–
Вес всего тела.

Для
однородной
линии


и формулы получают вид:

–
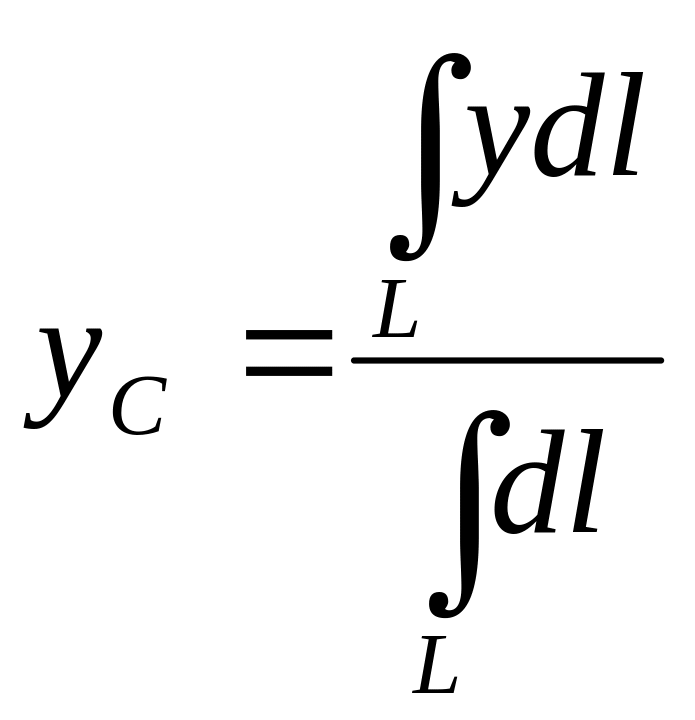
Длина линии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение опорных реакций

Способы определения опорных реакций изучаются в курсе теоретической механики. Остановимся только практических вопросах методики вычисления опорных реакций, в частности для шарнирно опертой балки с консолью (рис. 7.4).

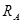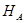Нужно найти реакции: , и 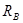. Направления реакций выбираем произвольно. Направим обе вертикальные реакции вверх, а горизонтальную реакцию – влево.

Нахождение и проверка опорных реакций в шарнирной опоре

Для вычисления значений реакций опор составим уравнения статики:

Сумма проекций всех сил (активных и реактивных) на ось z равна нулю: .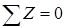

Поскольку на балку действуют только вертикальные нагрузки (перпендикулярные к оси балки), то из этого уравнения находим: горизонтальная реакция неподвижной шарнирной опоры .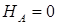

Сумма моментов всех сил относительно опоры А равна нулю:.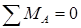

Правило знаков для момента силы: считаем момент силы положительным, если он вращает балку относительно точки против хода часовой стрелки.

Необходимо найти равнодействующую распределенной погонной нагрузки. Распределенная погонная нагрузка равна площади эпюры распределенной нагрузки 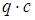и приложена в центре тяжести этой эпюры (посредине участка длиной ).

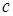Тогда

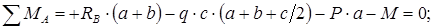
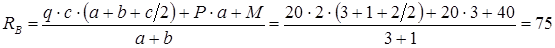кН.

Сумма моментов всех сил относительно опоры B равна нулю:.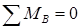

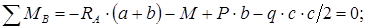
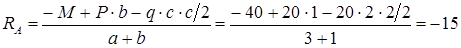кН.

Знак «минус» в результате говорит: предварительное направление опорной реакции 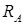было выбрано неверно. Меняем направление этой опорной реакции на противоположное (см. рис. 7.4) и про знак «минус» забываем.

Проверка опорных реакций

Сумма проекций всех сил на ось y должна быть равна нулю: .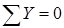

Силы, направление которых совпадает с положительным направлением оси y, проектируются на нее со знаком «плюс»:

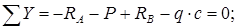
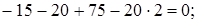
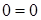(верно).

Нахождение опорных реакций в жесткой заделке

Найдем реакции опор в жесткой заделке. Для определения опорных реакций составляются уравнения статики:

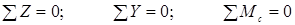
Из первого уравнения определяется реакция 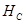(обычно равна нулю), из второго – 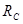и из третьего – момент в жесткой заделке .

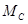Проверка, как правило, не производится.

Содержание:

1. Задача с решением 75-14.
2. Задача с решением 76-14;
3. Задача с решением 77-14.
4. Задача с решением 79-14.
5. Задача с решением 80-14*.
6. Задача с решением 82-14.
7. Определение реакций в общем случае
8. Пример с решением 58.
9. Пример с решением 59.

Как известно, любую плоскую систему сил можно привести к главному вектору и главному моменту

Если же система сил уравновешена (тело, находящееся под действием такой системы сил, либо неподвижно, либо равномерно вращается около неподвижной оси, либо находится в равномерном и прямолинейном поступательном движении), то и

Эти равенства выражают два необходимых и достаточных условия равновесия любой системы сил.

Для произвольной плоской системы сил из этих двух условий непосредственно получаем три уравнения равновесия:

Первое и второе выражения — уравнения проекций — образуются из условия — третье выражение – уравнение моментов – из условия

Если на тело действует система параллельных сил, то уравнений равновесия получится только два: уравнение проекций на ось, параллельную силам, и уравнение моментов

При решении некоторых задач одно или оба уравнения проекций целесообразно заменить уравнениями моментов относительно каких-либо точек, т. е. систему уравнений равновесия можно представить в таком виде:

или

В первом случае линия, проходящая через точки и не перпендикулярна к оси Во втором случае центры моментов и не лежат на одной прямой линии.

Для системы параллельных сил соответственно получаем два уравнения моментов:

В этом случае точки и не лежат на прямой, параллельной силам.

В задачах, решаемых при помощи уравнений равновесия, обычно рассматриваются тела, находящиеся в состоянии покоя, тогда система сил, действующих на это тело, уравновешена.

Возможно вам будут полезны данные страницы:

Силы, действующие на тело, делятся на две группы. Одна группа сил называется нагрузками (активные силы), вторая группа сил называется реакциями связей (пассивные силы).

Нагрузки, как правило, бывают заданы. Они имеют числовое значение, точку приложения к телу и направление их действия.

В рассматриваемых ниже задачах используются лишь три разновидности нагрузок: сосредоточенные силы, равномерно распределенные силы* и пары сил (статические моменты)**.

Сосредоточенными называются силы, приложенные к точке тела. Если, например, на тело действуют нагрузки или как показано

на рис. 91, а, действия этих нагрузок можно считать приложенными соответственно к точкам или тела и на расчетных схемах изобразить так, как это выполнено на рис. 91, б.

Равномерно распреде.генные нагрузки, например кирпичная кладка (рис. 92, а), или собственный вес однородного тела (бруса, балки) постоянного поперечного сечения по всей его длине задается при помощи двух параметров —интенсивности и длины па протяжении которой они действуют. На расчетных схемах эти нагрузки изображаются так, как показано на рис. 92, б.

• Пара сил (сосредоточенный момент), например, может быть образована двумя одинаковыми грузами действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.

Очень часто в каком-либо месте тела возникает совместное действие сосредоточенной силы и момента. Пусть, например, груз подвешен на конце бруса, жестко заделанного другим концом

в каком-либо теле (рис. 94, а). Если перенести действие силы в точку тела (рис. 94, б), то получим в ней совместное действие сосредоточенной силы и момента.

Как правило, в задачах по статике реакции связей —искомые величины. Для каждой искомой реакции связи обычно необходимо

знать ее направление и числовое значение (модуль).

Направления реакций идеальных связей —связей без трения — определяют в зависимости от вида связи по следующим правилам.

1. При свободном опирании тела на связь реакция связи направлена от связи к телу перпендикулярно либо к поверхности тела ( рис. 95), либо к поверхности связи ( рис. 95), либо к общей касательной обеих поверхностей ( рис. 95).

Во всех этих случаях связь препятствует движению тела в одном направлении —перпендикулярном к опорной поверхности.

2. Если связями являются нити, цепи, тросы (гибкая связь), то они препятствуют движению тела только будучи натянутыми.

Поэтому реакции нитей, цепей, тросов всегда направлены вдоль их самих в сторону от тела к связи ( и рис. 96).

3. Если связь тела с какой-либо опорной поверхностью осуществляется при помощи подвижного шарнира (рис. 97), то его реакция направлена перпендикулярно к опорной поверхности. Таким

образом, подвижный шарнир (т. е. шарнир, ось которого может передвигаться вдоль опорной поверхности) представляет собой конструктивный вариант свободного опирания.

4. Если соединение тела со связью осуществляется при помощи неподвижного шарнира (рис. 98), то определить непосредственно направление реакции нельзя, за исключением тех частных случаев, которые описаны ниже.

Шарнирное соединение препятствует поступательному перемещению тела во всех направлениях в плоскости, перпендикулярной к оси шарнира. Направление реакции неподвижного шарнира может быть любым в зависимости от направления действия остальных сил. Потому сначала определяют две взаимно перпендикулярные составляющие и (или и ) реакции шарнира, а затем, если нужно, по правилу параллелограмма или треугольника можно определить как модуль, так и направление полной реакции (или ).

Направление реакции неподвижного шарнира непосредственно определяют в двух следующих случаях:

а) если, кроме реакции шарнира, все остальные силы (нагрузки и реакция другой связи) образуют систему параллельных сил, то реакция неподвижного шарнира также параллельна всем силам;

б) если, кроме реакции шарнира, на тело действуют еще только две непараллельные силы, то линия действия реакции неподвижного шарнира проходит через ось шарнира и точку пересечения двух других сил (задачи 47-9 и 48-9).

5. Движение тела может быть ограничено жесткой заделкой в какой-либо опоре (рис. 99). В этом случае даже одна жесткая заделка обеспечивает равновесие тела при любых нагрузках.

Так же как и неподвижный шарнир, жесткая заделка препятствует поступательному перемещению тела. Поэтому направление

ее реакции заранее определить нельзя и сначала определяют составляющие и Кроме того, жесткая заделка препятствует повороту тела в плоскости действия сил, поэтому, кроме силы реакции, на тело действует еще момент заделки уравновешивающий стремление нагрузок повернуть тело (вывернуть тело из заделки).

Таким образом, если опорой тела является жесткая заделка, то со стороны последней на тело действуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки.

6. Иногда тело удерживается в равновесии при помощи жестких стержней, шарнирно соединенных с телом и с опорами (рис. 100). В отличие от гибкой связи (см. п. 2) такие стержни могут испытывать не только растяжение, но и сжатие.

Возможны и такие случаи, когда нельзя заранее установить, какие стержни растянуты, а какие сжаты. Поэтому при составлении уравнений равновесия исходят из того, что все стержни растянуты. Если же некоторые стержни окажутся в действительности сжатыми, tq в результате решения числовые значения реакций таких стержней получатся отрицательными.

Задача с решением 75-14.

На горизонтальную балку левый конец которой имеет шарнирно-неподвижную опору, а правый — шарнирно-подвижную, в точках и поставлены два груза: и (рис. 101, а). Определить реакции опор балки.

Решение.

1. Рассмотрим равновесие балки на которую в точках и действуют две вертикальные нагрузки и (рис. 101, б).

2. Освободив правый конец балки от связи и заменив ее действие реакцией направленной перпендикулярно к опорной поверхности, увидим, что на балку действует система

параллельных сил. Поэтому, если освободить и левый конец балки от шарнирно неподвижной опоры, то ее реакция будет также направлена вертикально (рис. 101, б).

3. Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку а для другого — точку

4. Решая уравнения, из (1) находим

из (2)

5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось

Подставляя в это уравнение числовые значения, получаем тождество

или

Значит задача решена правильно.

Реакции опор:

и

При решении задач рекомендуется не пренебрегать проверкой. От правильности определения реакций опор зависит правильность всего остального решения или расчета.

Задача с решением 76-14;

На консольную балку, имеющую в точке шарнирно-непод-вижную, а в точке шарнирно-под-вижную опору, действуют две сосредоточенные нагрузки: и как показано на рис. 102, а; угол Определить реакции опор балки.

Решение.

1. Рассматривая находящуюся в равновесии балку видим, что в точке на нее действует вертикально вниз нагрузка а в точке под углом к действует другая нагрузка (рис. 102, б).

2. Освобождаем балку от связей и заменим их действие реакциями. В месте шарнирно-подвижной опоры возникает вертикальная реакция Направление реакции шарнпрно-неподвиж-ной опоры в данном случае непосредственно определить нельзя, поэтому заменим эту реакцию се двумя составляющими и

3. Для полученной системы из пяти сил, произвольно расположенных в плоскости, составим систему уравнений равновесия вида (3), расположив ось вдоль балки, а за центры моментов приняв точки и

4. Решаем полученные уравнения. Из (1)

Так как

то из (2)

Замечая, что

из (3) получаем

Знак минус, получившийся в последнем случае, показывает, что — вертикальная составляющая реакция неподвижного шарнира—направлена вниз, а не вверх, как предполагалось перед составлением уравнения (3).

5. При необходимости реакцию шарнира легко определить (рис. 102, в).

Модуль реакции шарнира найдем из формулы

Направление реакции установим, определив угол

откуда

6. Проверим правильность решения задачи. Так как при решении не использовано уравнение проекций на ось то используем его для проверки:

Уравнение составлено по рис. 102, б.

После подстановки в это уравнение известных значений получим:

В данном случае, проверка решения при помощи уравнения проекций не дает возможности установить правильность определения полной реакции шарнира Чтобы проверить и этот этап решения, составим уравнение моментов относительно точки воспользовавшись рис. 102, в, на котором изображена реакция так, как она направлена в действительности:

Подставляем в это уравнение числовые значения, имея в виду, что

Расхождение в результатах, равное получается из-за округлений при вычислениях.

В следующих задачах проверка решения не приводится и ее рекомендуется производить самостоятельно.

Задача с решением 77-14.

Горизонтальная балка имеет в точке шарнирно-подвижную опору, плоскость которой наклонена к горизонту под углом (рис. 103, а), а в точке — шарнирно-неподвижную опору. Балка нагружена в точках и двумя сосредоточенными силами кн и Определить реакции опор.

Решение.

1. Так же как и в задаче 75-14, балка нагружена двумя параллельными силами, но в отличие от этой задачи здесь реакция подвижного шарнира направлена не параллельно вертикальным нагрузкам, а под углом к вертикали – перпендикулярно к опорной поверхности шарнира (рис. 103,6). Поэтому реакция неподвижного шарнира не будет направлена вертикально и, так же как в задаче 76-14, ее целесообразно заменить двумя составляющими и

2. Расположив оси и как показано на рис. 103, б, составляем уравнения равновесия вида (I):

3. Решаем полученные уравнения. Из уравнения (3) находим

Из уравнения (2) находим

Из уравнения (1) находим

Таким образом, реакция шарнира

а составляющие реакции шарнира

и

4. Проверку решения производим при помощи уравнения моментов относительно точки или

Следующую задачу рекомендуется решить самостоятельно.

Задача с решением 79-14.

На консольную балку, имеющую в точке шарнирно-неподвижную, а в точке шарнирно-подвижную опору, действуют две нагрузки (рис. 104, а): в точке — сосредоточенная нагрузка а на участке — равномерно распределенная нагрузка интенсивностью Определить реакции опор.

Решение.

1. В этой задаче, кроме сосредоточенной силы на участке действует равномерно распределенная сила, интенсивность которой Полная величина этой нагрузки (ее равнодействующая) равна и приложена в точке посредине участка (рис. 104,6), т. е.

2. Так же как в задаче 75-14, реакция подвижного шарнира направлена вертикально (перпендикулярно к опорной поверхности). Следовательно, и реакция неподвижного шарнира направлена вертикально. Таким образом, на балку действует система параллельных сил (см. рис. 104, б).

3. Составим два уравнения моментов относительно точек и

Из уравнения (1)

Отрицательное значение реакции означает, что она направлена вниз, а не вверх, как показано на рис. 104, б, потому что момент силы относительно опоры больше, чем момент равномерно распределенной нагрузки.

Из уравнения (2) находим

Таким образом, реакция шарнира равна и направлена вертикально вниз; реакция шарнира составляет и направлена вертикально вверх.

5. Для проверки решения можно использовать уравнение проекций на вертикальную ось.

Задача с решением 80-14*.

На двухконсольную балку с шарнирно-неподвижной опорой в точке и с шарнирно-подвижной в точке действуют, как показано на рис. 105,а, сосредоточенная сила сосредоточенный момент (пара сил) и равномерно распределенная нагрузка интенсивностью Определить реакции опор.

Решение.

1. В отличие от предыдущей задачи здесь, кроме сосредоточенной силы и равномерно распределенной-нагрузки, равнодействующая которой приложена в точке посредине участка на балку действует момент направленный по часовой стрелке (рис. 105, б).

2. После освобождения балки от связей и замены связей их реакциями и получаем уравновешенную систему, составленную из четырех параллельных сил и одной пары сил (момента).

3. Составим два уравнения моментов относительно точек и

4. Решая эти уравнения, находим, что

и

Задача с решением 82-14.

Жестко заделанная у левого конца консольная балка (рис. 107, а) нагружена равномерно распределенной нагрузкой интенсивностью сосредоточенной силой и моментом Определить реакции заделки.

Решение.

1. На балку действуют три нагрузки: в точке — вертикальная сосредоточенная сила по всей длине балки — равномерно распределенная нагрузка, которую заменим сосредоточенной силой приложенной в точке Правый конец балки нагружен моментом действующим против хода часовой стрелки (рис. 107, б).

2. Равновесие балки обеспечивается жесткой заделкой у точки Освободив балку от связи, заменим ее действие силой — реакцией связи и реактивным моментом Но так как реакцию заделки сразу определить нельзя (по тем же причинам, что и направление реакции неподвижного шарнира), заменим ее составляющими и совместив их с осями и (см. рис. 107, б).

3. Составим уравнения равновесия — уравнение проекции на оси и и уравнение моментов относительно точки

4. Из уравнения (1)

а это означает, что горизонтальная составляющая реакции заделки равна нулю, так как в данном случае нет усилий, смещающих балку в горизонтальном направлении. Из уравнения (2)

Выше найдено, что ; значит реакция заделки перпендикулярна к оси Следовательно,

Из уравнения (3)

Таким образом,

и

5. Проверку правильности решения можно произвести при помощи уравнения моментов относительно точки или В любое из них входят обе найденные величины.

Следующую задачу рекомендуется решить самостоятельно.

Определение реакций в общем случае

Один из способов определения реакций связей был уже рассмотрен при изучении уравнений равновесия с множителями Лагранжа, когда связи задаются неявными уравнениями или неравенствами. В общем же случае связи, наложенные на систему материальных точек, всегда могут быть заменены соответствующими силами реакций, действие которых эквивалентно действию связей. После такой замены система может рассматриваться как свободная от связей, но подверженная действию как активных, так и пассивных сил. Принцип Бернулли для такой свободной системы дает необходимые и достаточные условия равновесия в виде уравнения

где — проекции активных сил на неподвижные оси координат; — проекции сил реакции на те же оси. Величины теперь полностью произвольны, так что равенство (а) будет выполняться для всех возможных перемещений лишь в том случае, когда обращаются в нуль все коэффициенты при т. е.

Последние уравнения и служат для определения реакций связи. Если по условиям задачи требуется определять не все, а лишь некоторые силы реакции, то система освобождается только от тех связей, реакции которых необходимо определить. Освобождая систему от связей, тем самым добавляем ей возможные перемещения, которые раньше не допускались связями и на которых будут работать реакции освобожденных связей.

Подсчитывая сумму работ активных сил и сил реакции связей на освобожденном перемещении, получим условия для определения реакций связи.

Пример с решением 58.

Исследовать условия равновесия твердого тела, у которого закреплены две точки и и на которое действуют активные силы приложенные к точкам (рис. 138).

Решение. Выберем начало неподвижной системы координат в точке а ось направим по прямой Наложенные езязи допускают вращение твердого тела вокруг оси Подсчитывая работу активных сил на этом возможном перемещении, получим

где — угол поворота твердого тела вокруг оси Отсюда сразу же получаем условие равновесия твердого тела, которое сводится к равенству нулю суммы моментов всех активных сил, действующих на твердое тело, относительно оси

Для определения реакции в точке освободим твердое тело от связи в этой точке, заменив действие последней действием неизвестной силы Освобожденное от связи тело может вращаться как вокруг оси так и вокруг оси Сообщим твердому телу бесконечно малое возможное перемещение, повернув его вокруг оси на угол и подсчитаем работу всех сил на этом возможном перемещении. Возможные перемещения точек твердого тела определятся из матрицы

так что

Из принципа Бериулли для освобожденного твердого тела будем иметь

подставляя сюда значения вариаций координат, получим

или, после сокращения на

где — сумма моментов активных сил относительно оси a — расстояние

Точно таким же путем можно получить реакцию рассматривая поворот твердого тела вокруг оси Возможные перемещения в этом случае будут определяться из матрицы

так что

Подставляя найденные значения вариаций координат в общее уравнение статики, получим

или

Реакция таким способом не может быть найдена, потому что любое возможное перемещение точки твердого тела ортогонально направлению силы , и задача оказывается статически неопределимой.

Пример с решением 59.

На гладкой горизонтальной плоскости лежат несколько одинаковых однородных цилиндрических труб. Чтобы трубы не раскатывались, они подпираются двумя брусьями и как показано на рис. 139. Определить реакции брусьев.

Решение. Для определенности рассмотрим пятнадцать труб, расположенных, как указано на чертеже. Чтобы избежать рассмотрения статически неопределимой задачи, предположим, что расстояние между брусками и больше суммы диаметров нижних труб. Положение системы определим четырьмя параметрами и (углы, которые образуют прямые, соединяющие центры труб нижнего и верхнего ряда с горизонталью), которые связаны соотношением

где — сколь угодно малое число. Углы и подчиняются еще условиям

Будем предполагать сначала, что последние условия выполняются лишь в виде неравенств. Определив вертикальные координаты центров труб

Запишем принцип Торричелли для системы с удерживающими связями:

или, после подстановки значений

где величины и связаны соотношением

Определив из последнего уравнения

и подставив это значение в равенство (с), получим уравнение для независимых параметров

Приравнивая нулю коэффициенты при и приходим к следующим условиям равновесия системы:

которые можно переписать в виде

Принимая во внимание неравенства (b), получим условия равновесия

Величины и должны удовлетворять уравнению (а), которое перепишется в виде

При отсюда находим предельное значение для

В самом деле,

При уменьшении левая часть равенства (f) будет увеличиваться, а следовательно, будет возрастать и Таким образом, предполагая связи (Ь) в положении равновесия выполненными в виде неравенств, устанавливаем, что в положении равновесия должно быть

Лишь при выполнении этого неравенства нижине трубы в положении равновесия не будут касаться друг друга. Уменьшая мы вынуждены будем отказаться от предположения, что все связи (Ь) в положении равновесия выполняются в виде неравенств. Из условий (е) следует, что первыми переходят в равенство связи

и

Рассмотрим теперь только такие состояния системы, для которых выполняются условия

Уравнение связи для возможных перемещений (d) приобретает вид

Общее уравнение статики для рассматриваемой системы перепишем в виде

Система линейных относительно и уравнений (d’) и (с7) обладает ненулевым решением, если обращается в нуль определитель

или

Отсюда следует, что в положении равновесия должно быть

Тогда из уравнения связи (а) находим

Как видно из последнего соотношения, при получим

Для определения реакции в точке освободим систему от связи, убрав брус и заменив его действие силой реакции После такого освобождения системы параметры и можно изменять независимо друг от друга. При этом должно выполняться условие (при отличных от нуля или системе сообщается освобождающее перемещение, на котором будут совершать отличную от нуля работу силы реакции труб, находящихся при равнозесии в соприкосновении). Сообщим системе перемещение

и подсчитаем работу всех сил, в том числе и работу силы на возможном перемещении системы. Будем иметь

откуда следует

Если то и

Заметим, что на рассматриваемом перемещении опускаются вниз четыре трубы. У остальных труб вертикальные координаты не изменяются. Если обозначить через вес опускающихся труб (в нашем случае ), то предельное значение силы реакции будет равно