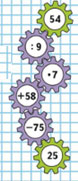
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.
reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 1. Страница 86. Номер №8
Решение 1
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
.
Решение 2
Способ 1.
AB = CD = 5 см;
BC = AD = 2 см;
S
A
B
C
D
=
A
B
∗
A
D
=
5
∗
2
=
10
(
с
м
2
)
.
Способ 2.
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
;
S
A
B
C
D
=
S
B
C
K
E
+
S
A
E
K
D
=
4
+
6
=
10
(
с
м
2
)
.
-
Главная
-
ГДЗ
- 3 класс
- Математика
-
Моро учебник
- Деление нуля на число
- Страница 87. Часть 1
Вернуться к содержанию учебника
Деление нуля на число
Вопрос
7. Реши уравнения.
| 75 + x = 90 | 80 – k = 42 | 6 • n = 54 |
Подсказка
Решить уравнение – это значит найти такое значение неизвестного числа, при котором это равенство станет верным.
Ответ
Вопрос
8. 1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.
Подсказка
Чтобы найти площадь прямоугольника ABCD, нужно сложить площади прямоугольников ВСКЕ и AEKD или измерить стороны прямоугольника ABCD и умножить длину на ширину.
Ответ
Вопрос
9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2).
2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD – и на сколько квадратных сантиметров.
Подсказка
Площадь прямоугольника равна произведению его длины и ширины.
Ответ
Вопрос
На сколько 9 меньше, чем 72?
Во сколько раз 6 меньше, чем 54?
Подсказка
Чтобы узнать, на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее – вычитание.
Чтобы узнать, во сколько раз одно число больше или меньше другого, нужно узнать, сколько раз маленькое число содержится в большом – деление.
Ответ
Вопрос
Цепочка:
Подсказка
Ответ
Вернуться к содержанию учебника
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
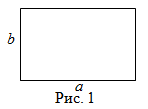
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
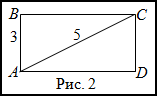
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
ГДЗ > 🧮 Математика > 5 класс > 📗 Математика 5 класс Виленкин, Жохов, Чесноков, Шварцбурд > 🧠 Задание 2. ПР-1. Площадь. Формула площади прямоугольника

Содержание
Авторы:Виленкин, Жохов, Чесноков, Шварцбурд
Год:2021
Тип:учебник
Часть:1, 2
Нужно другое издание?
Проверьте себя > 2. ПР-1. Площадь. Формула площади прямоугольника

Ошибка или идея? Сообщить 📤
Мне не нравится на сайте, измените:Сделайте так, чтобы можно было:Решение неправильно/опечатка
Бот с ответами МЭШ | Скайсмарт
Все номера
1. ПР-1. Формулы2. ПР-1. Площадь. Формула площади прямоугольника3. ПР-1. Единицы измерения площадей4. ПР-1. Прямоугольный параллелепипед5. ПР-1. Объемы. Объем прямоугольного параллелепипеда5. ПР-2. Объемы. Объем прямоугольного параллелепипеда
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие свойства площади фигуры вы знаете?
- Равные фигуры имеют равные площади.
- Площадь фигуры равна сумме площадей фигур, из которых она состоит.
2. Какой квадрат называют единичным?
Единичный квадрат — это квадрат, стороны которого равны единичному отрезку.
3. Какие единицы измерения площади вы знаете?
- мм² — квадратный миллиметр
- см² — квадратный сантиметр
- м² — квадратный метр
- км² — квадратный километр
4. Что означает измерить площадь фигуры?
Измерить площадь фигуры — это значит подсчитать, сколько единичных квадратов в ней помещается.
5. Чему равна площадь прямоугольника?
Площадь прямоугольника равна произведению длин его соседних сторон:
S = ab
6. По какой формуле вычисляют площадь квадрата?
S = a²
7. Сколько квадратных метров содержит 1 ар? 1 гектар?
1 ар = 100 м²
1 га = 10 000 м²
Решаем устно
1. Сколько сантиметров содержится в:
- 1 дм = 10 см
- 1 м 3 дм = 130 см
- 5 м 2 дм = 520 см
- 12 дм 5 см = 125 см
- 40 мм = 4 см
2. Лодка за 5 ч прошла 40 км. За сколько часов она пройдёт с той же скоростью 24 км?
1) 40 : 5 = 8 (км/ч) — скорость лодки.
2) 24 : 8 = 3 (ч) — потребуется дл преодоления 24 км.
Ответ: 3 часа.
3. Сколько литров воды может перекачать насос за 8 мин, если пять таких насосов за 6 мин перекачивают 450 л воды?
1) 450 : 6 = 75 (л/мин) — скорость работы пяти насосов.
2) 75 : 5 = 15 (л/мин) — скорость работы одного насоса.
3) 15 • 8 = 120 (литров) — воды перекачает один насос за 8 минут.
Ответ: 120 литров воды.
4. Какую цифру надо поставить вместо звёздочек, чтобы запись 1* + 3* + 5* = 111 стала верным равенством?
Вспомним таблицу умножения на 3 и подберём число, которое при умножении на 3 дает число, оканчивающееся на 1. Это число 7 (7 • 3 = 21).
Подставим цифру 7 в равенство:
17 + 37 + 57 = 111 — равенство верно.
Ответ: цифра 7.
Упражнения
564. 1) Сколько квадратных сантиметров содержит 1 дм²? 1 м²?
1 дм² = 10 см • 10 см = 100 см²
1 м²= 100 см • 100 см = 10 000 см²
2) Сколько квадратных метров содержит 1 км²?
1 км²= 1 000 м • 1 000 м = 1 000 000 м²
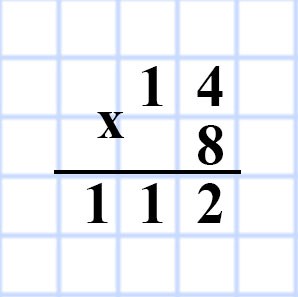
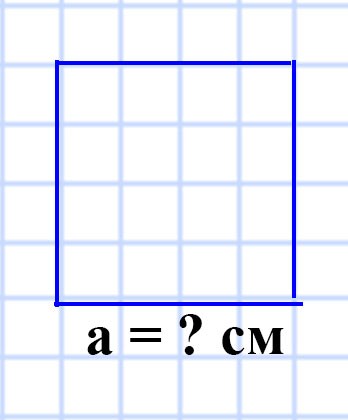
565. Вычислите площадь прямоугольника, соседние стороны которого равны 14 см и 8 см.
a = 14 см
b = 8 см
S = ?
S = ab
S = 14 • 8 = 112 (см²)
Ответ: S = 112 см²
566. Вычислите площадь квадрата со стороной 7 дм.
a = 7 дм
S = ?
S = a²
S = 7 • 7 = 49 (дм²)
Ответ: S = 49 дм²
567. Одна сторона прямоугольника равна 16 см, а соседняя сторона — на 6 см длиннее. Вычислите площадь прямоугольника.
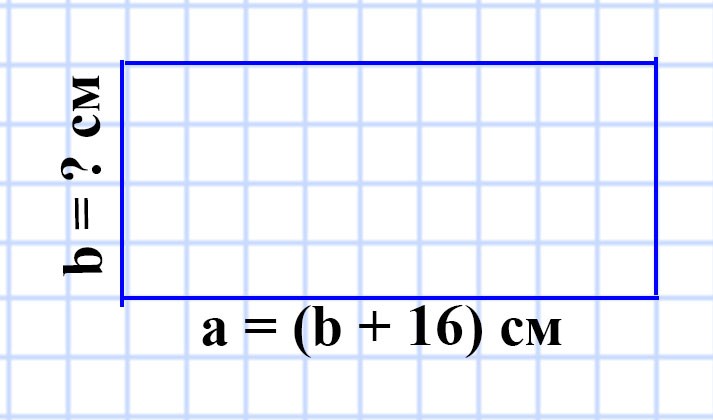
a = 16 см
b = (a + 6) см
S = ?
S = ab
S = 16 • (16 + 6) = 16 • 22 = 352 (см²)
Ответ: S = 352 см²
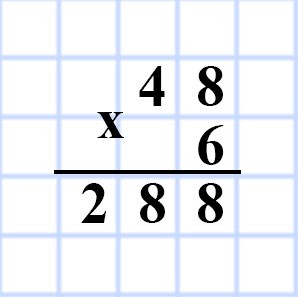
568. Одна сторона прямоугольника равна 48 см, а соседняя сторона — в 8 раз меньше. Вычислите площадь прямоугольника.
a = 48 см
b = (a : 8) см
S = ?
S = ab
S = 48 • (48 : 8) = 48 • 6 = 288 (см²)
Ответ: S = 288 см²
Внимание! Следующие 5 задач решены двумя способами!
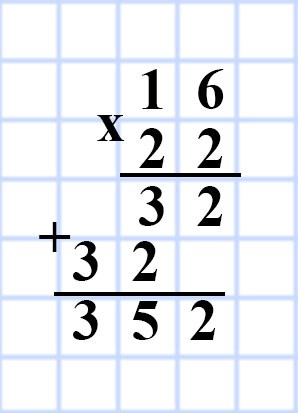
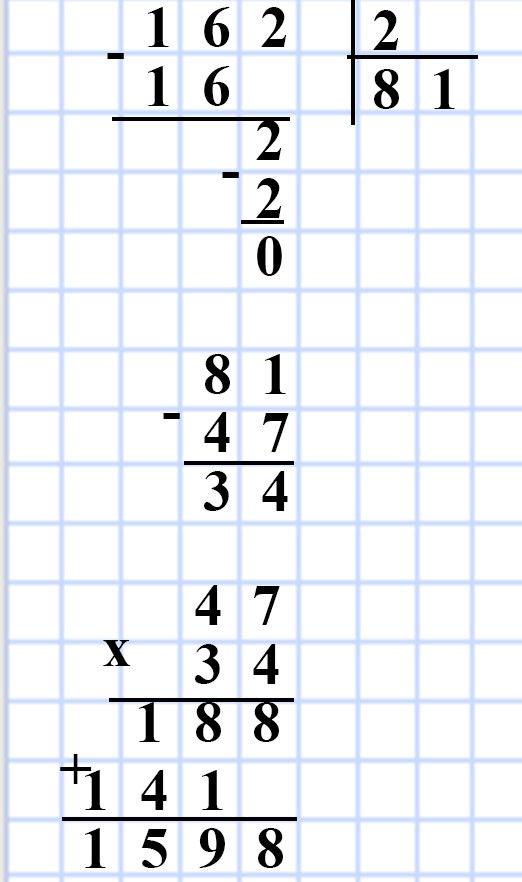
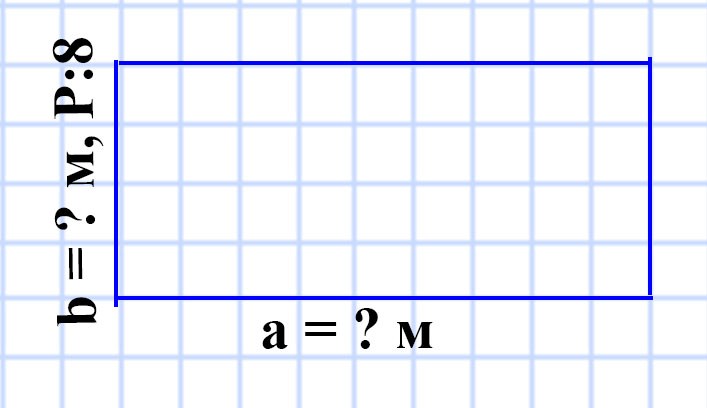
569. Периметр прямоугольника равен 162 дм, а одна из сторон — 47 дм. Найдите площадь прямоугольника.
Способ 1:
a = 47 дм
P = 162 дм
S = ?
P = (a + b) • 2
b = P : 2 — a
b = 162 : 2 — 47 = 81 — 47 = 34 (дм) — длина стороны b.
S = ab
S = 47 • 34 = 1 598 (дм²) — площадь прямоугольника.
Ответ: S = 1598 дм².
Способ 2:
1) 162 : 2 = 81 (дм) — сумма двух соседних сторон прямоугольника.
2) 81 — 47 = 34 (дм) — длина второй стороны прямоугольника.
3) 47 • 34 = 1 598 (дм²) — площадь прямоугольника.
Ответ: S = 1598 дм².
570. Периметр прямоугольника равен 96 м, и он в 8 раз больше одной из сторон прямоугольника. Найдите площадь прямоугольника.
Способ 1:
P = 96 м
a = (P : 8) м
S = ?
a = P : 8
a = 96 : 8 = 12 (м) — длина стороны a прямоугольника.
P = (a + b) • 2
b = P : 2 — a
b = 96 : 2 — 12 = 48 — 12 = 36 (м) — длина стороны b.
S = ab
S = 36 • 12 = 432 (м²) — площадь прямоугольника.
Ответ: S = 432 м².
Способ 2:
1) 96 : 8 = 12 (м) — длина одной стороны прямоугольника.
2) 96 : 2 = 48 (м) — сумма длин соседних сторон прямоугольника.
3) 48 — 12 = 36 (м) — длина второй стороны прямоугольника.
4) 36 • 12 = 432 (м²) — площадь прямоугольника.
Ответ: S = 432 м².
571. Найдите площадь квадрата, периметр которого равен 96 см.
Способ 1:
P = 96 см
a = ? см
S = ?
a = P : 4
a = 96 : 4 = 24 (см) — длина стороны квадрата.
S = a²
S = 24 • 24 = 576 (см²) — площадь прямоугольника.
Ответ: S = 576 см².
Способ 2:
1) 96 : 4 = 24 (см) — длина стороны квадрата.
2) 24² = 24 • 24 = 576 (см²) — площадь прямоугольника.
Ответ: S = 576 см².
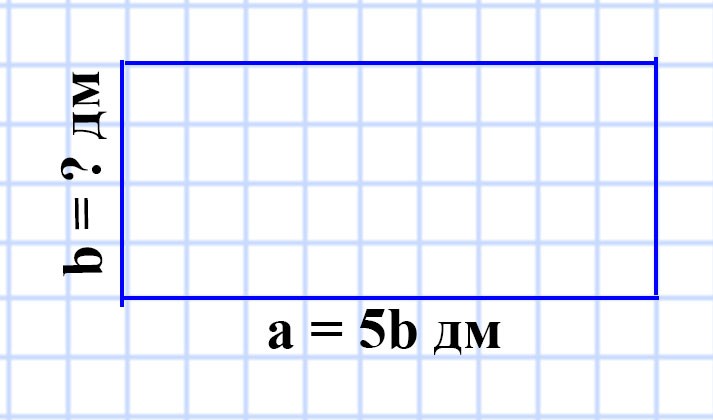
572. Периметр прямоугольника равен 4 м 8 дм, одна из его сторон в 5 раз больше соседней стороны. Найдите площадь прямоугольника.
Способ 1:
P = 4 м 8 дм
a = 5b
S = ?
4 м 8 дм = 48 дм
P = (a + b) • 2 и a = 5b. Составим уравнение:
48 = (5b + b) • 2
5b + b = 48 : 2
6b = 24
b = 24 : 6
b = 4 (дм) — длина стороны b прямоугольника
a = 5b = 5 • 4 = 20 (дм) — длина стороны a прямоугольника
S = ab
S = 20 • 4 = 80 (дм²) — площадь прямоугольника.
Ответ: S = 80 дм².
Способ 2:
4 м 8 дм = 48 дм
1) 48 : 2 = 24 (дм) — сумма длин соседних сторон прямоугольника.
2) 24 : 6 = 4 (дм) — длина одной стороны прямоугольника.
3) 4 • 5 = 20 (дм) — длина другой стороны прямоугольника.
4) 20 • 4 = 80 (дм²) — площадь прямоугольника.
Ответ: S = 80 дм².
573. Периметр прямоугольника равен 6 дм 8 см, одна из его сторон на 1 дм 6 см меньше соседней стороны. Найдите площадь прямоугольника.
Способ 1
P = 6 дм 8 см
a = b + 1 дм 6 см
S = ?
6 дм 8 см = 68 см
1 дм 6 см = 16 см
P = (a + b) • 2 и a = b + 16 см. Составим уравнение:
68 = (b + 16 + b) • 2
b + 16 + b = 68 : 2
2b + 16 = 34
2b = 34 — 16
2b = 18
b = 18 : 2
b = 9 (см) — длина стороны b прямоугольника
a = b + 16 = 9 + 16 = 25 (см) — длина стороны a прямоугольника
S = ab
S = 25 • 9 = 225 (см²) — площадь прямоугольника.
Ответ: S = 225 см².
Способ 2:
6 дм 8 см = 68 см
1 дм 6 см = 16 см
1) 68 : 2 = 34 (см) — сумма длин двух соседних сторон прямоугольника.
2) 34 — 16 = 18 (см) — сумма длин двух коротких сторон прямоугольника.
3) 18 : 2 = 9 (см) — длина короткой стороны прямоугольника.
4) 34 — 9 = 25 (см) — длина длинной стороны прямоугольника.
5) 25 • 9 = 225 (см²) — площадь прямоугольника.
Ответ: S = 225 см².
574. Выразите:
1) в арах:
- 12 га = 1 200 а
- 45 га = 4 500 а
- 6 га 28 а = 600 а + 28 а = 628 а
- 14 га 68 а = 1 400 а + 68 а = 1468 а
- 32 400 м² = 324 а
- 123 800 м² = 1 238 а
- 2 км² 14 га 5 а = 20 000 а + 1 400 а + 5 а = 21 405 а
- 4 км² 72 га 16 а = 40 000 а + 7 200 а + 16 а = 47216 а
2) в квадратных метрах:
- 5 а = 500 м²
- 17 а = 1 700 м²
- 8 га = 80 000 м²
- 63 га = 630 000 м²
- 5 га 72 а = 50 000 м² + 7 200 м² = 57 200 м²
- 14 га 43 а = 140 000 м² + 4 300 м² = 144 300 м²
3) в гектарах и арах:
- 530 а = 5 га 30 а
- 1 204 а = 12 га 4 а
- 16 300 м² = 10 000 м² + 6 300 м² = 1 га 63 а
- 85 200 м² = 80 000 м² + 5 200 м² = 8 га 52 а
575. Выразите:
1) в квадратных сантиметрах:
- 8 дм² = 800 см²
- 16 дм² = 1 600 см²
- 4 м² = 40 000 см²
- 38 м² = 380 000 см²
- 16 м² 19 дм² = 160 000 см² + 1 900 см² = 161 900 см²
- 74 м² 3 дм² = 740 000 см² + 300 см² = 740 300 см²
2) в гектарах:
- 340 000 м² = 34 га
- 5 830 000 м² = 583 га
- 53 км² = 5 300 га
- 14 км² = 1 400 га
- 5 км² 18 га = 500 га + 18 га = 518 га
- 24 км² 6 га = 2 400 га + 6 га = 2 406 га
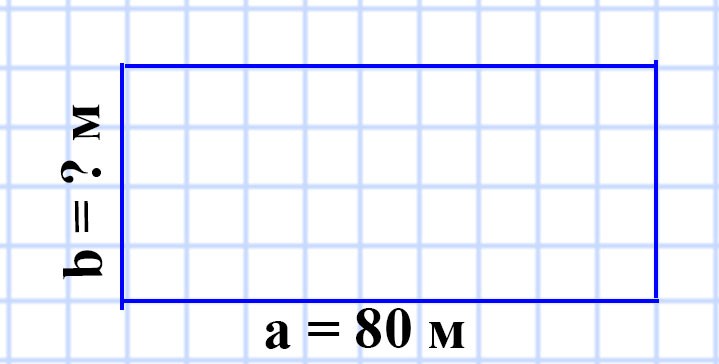
576. Поле прямоугольной формы имеет площадь 56 а, его длина — 80 м. Вычислите периметр поля.
a = 80 м
S = 56 а
P = ? м
56 а = 5 600 м²
S = ab
b = S : a = 5 600 : 80 = 70 (м) — ширина поля.
P = (a + b) • 2 = (70 + 80) • 2 = 150 • 2 = 300 (м) — периметр поля
Ответ: P = 300 м.
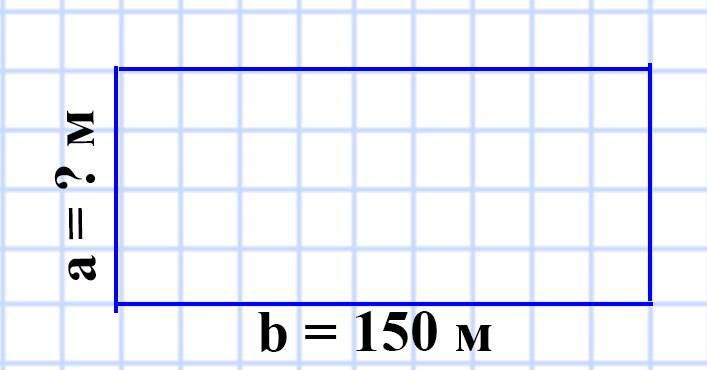
577. Поле прямоугольной формы имеет площадь 48 а, его ширина — 150 м. Вычислите периметр поля.
b = 150 м
S = 48 а
P = ? м
48 а = 4 800 м²
S = ab
a = S : b = 4 800 : 150 = 32 (м) — длина поля.
P = (a + b) • 2 = (32 + 150) • 2 = 182 • 2 = 364 (м) — периметр поля
Ответ: P = 364 м.
578. Вычислите периметр и площадь фигуры, изображённой на рисунке 149 (размеры даны в сантиметрах).
а)
1) Проведём вспомогательную линию и разделим фигуру на два прямоугольника.
2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:
- 15 — 5 = 10 (см) — длина части большого прямоугольника, не обозначенная на схеме и не равная стороне этого прямоугольника.
P = 15 + 18 + 10 + 8 + 5 + 8 + 18 = 82 (см) — периметр всей фигуры.
3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Найдём площадь маленького прямоугольника: S = ab = 8 • 5 = 40 (см²).
- Найдём площадь большого прямоугольника: S = ab = 18 • 15 = 270 (см²).
Значит площадь всей фигуры: S = S (маленького прямоугольника) + S (большого прямоугольника) = 40 + 270 = 310 (см²).
Ответ: P = 82см, S = 310 см².
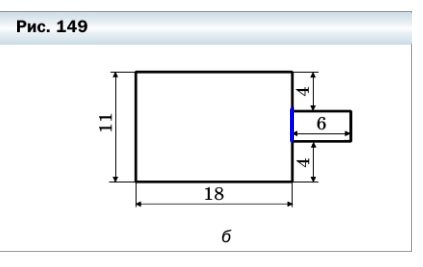
б)
1) Проведём вспомогательную линию и разделим фигуру на два прямоугольника.
2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:
- 11 — (4 + 4) = 3 (см) — ширина маленького прямоугольника.
P = 18 + 4 + 6 + 3 + 6 + 4 + 18 + 11 = 70 (см) — периметр всей фигуры.
3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Найдём площадь маленького прямоугольника: S = ab = 6 • 3 = 18 (см²).
- Найдём площадь большого прямоугольника: S = ab = 18 • 11 = 198 (см²).
Значит площадь всей фигуры: S = S (маленького прямоугольника) + S (большого прямоугольника) = 18 + 198 = 216 (см²).
Ответ: P = 70 см, S = 216 см².
579. Вычислите периметр и площадь фигуры, изображённой на рисунке 150 (размеры даны в сантиметрах).
1) Проведём вспомогательную линию(синюю) и разделим фигуру на три прямоугольника.
2) Периметр фигуры равен сумме длин всех её сторон. Мы помним, что противоположные стороны прямоугольника равны. Значит:
- 12 + 6 + 12 = 30 (см) — длина большого прямоугольника.
- 18 — 4 = 14 (см) — ширина большого прямоугольника.
P = 12 + 4 + 6 + 4 + 12 + 18 + 30 + 18 = 104 (см) — периметр всей фигуры.
3) Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Найдём площадь первого маленького прямоугольника: S = ab = 12 • 4 = 48 (см²).
- Найдём площадь второго маленького прямоугольника: S = ab = 12 • 4 = 48 (см²).
- Найдём площадь большого прямоугольника: S = ab = 30 • 12 = 420 (см²).
Значит площадь всей фигуры: S = S (маленького первого прямоугольника) + S (маленького второго прямоугольника) + S (большого прямоугольника) = 48 + 48 + 420 = 516 (см²).
Ответ: P = 104 см, S = 516 см².
Комментарий: Площадь данной фигуры удобнее находить другим способом. Для этого надо провести вторую вспомогательную линию (красную) и из площади получившегося в результате построения большого прямоугольника вычесть площадь маленького прямоугольника:
- Найдём площадь большого прямоугольника: S = ab = 30 • 18 = 540 (см²).
- Найдём площадь маленького прямоугольника: S = ab = 6 • 4 = 24 (см²).
Значит площадь всей фигуры: S = S (большого прямоугольника) — S (маленького прямоугольника) = 540 — 24 = 516 (см²).
580. Хватит ли 5 т гороха, чтобы засеять им поле, имеющее форму прямоугольника со сторонами 500 м и 400 м, если на 1 га земли надо высеять 260 кг гороха?
5 т = 5 000 кг
1) 500 • 400 = 200 000 м² = 20 га — площадь поля.
2) 260 • 20 = 5 200 (кг) — гороха потребуется для засеивания поля.
3) 5 200 кг >5 000 кг — значит 5т гороха не хватит для засеивания поля.
Ответ: Нет, не хватит.
581. Отец решил облицевать кафелем стену кухни, длина которой равна 4 м 50 см, а высота — 3 м. Хватит ли ему 20 ящиков кафеля, если одна плитка имеет форму квадрата со стороной 15 см, а в одном ящике находится 30 плиток?
- 4м 50 см = 450 см — длина стены
- 3 м = 300 см — высота стены
1) 15 • 15 = 225 (см²) — площадь 1 плитки.
2) 450 • 300 = 135 000 (см²) — площадь стены.
3) 135 000 : 225 = 600 (шт) — плиток потребуется на облицовку стены.
4) 30 • 20 = 600 (шт) — плиток находится в 20 ящиках.
5) 600 шт = 600 шт — значит 20 ящиков плитки хватит для облицовки стены.
Ответ: Да, хватит.
582. Фермер Пётр Трудолюб посадил в теплице огурцы. Длина теплицы равна 16 м 50 см, а ширина — 12 м. Сколько килограммов огурцов соберёт фермер в своей теплице, если с 1 м² собирают 30 кг огурцов?
- 16 м 50 см = 1 650 см
- 12 м = 1 200 см
1) 1 650 • 1 200 = 1 980 000 см² = 198 м² — площадь теплицы.
2) 198 • 30 = 5 940 (кг) — огурцов соберёт фермер.
Ответ: 5 940 кг огурцов.
583. Расход эмалевой краски на однослойное покрытие составляет 180 г на 1 м². Хватит ли 3 кг эмали, чтобы покрасить стену длиной 6 м и высотой 3 м?
3 кг = 3 000 г
1) 6 • 3 = 18 (м²) — площадь стены.
2) 18 • 180 = 3 240 (г) — краски потребуется на однослойное покрытие стены.
3) 3 240 г > 3 000 г — значит 3 кг краски не хватит на окраску данной стены.
Ответ: Нет, не хватит.
584. Квадрат со стороной 12 см и прямоугольник, длина которого равна 18 см, являются равновеликими. Найдите периметр прямоугольника.
1) 12 • 12 = 144 (см²) — площадь квадрата = площадь прямоугольника.
2) 144 : 18 = 8 (см) — длина стороны b прямоугольника.
3) (18 + 8) • 2 = 26 • 2 = 52 (см) — периметр прямоугольника.
Ответ: 52 см.
585. Квадрат и прямоугольник являются равновеликими, соседние стороны прямоугольника равны 3 см и 12 см. Найдите периметр квадрата.
1) 12 • 2 = 36 (см²) — площадь прямоугольника = площадь квадрата.
2) Подберём число, квадрат которого равен 36. Это число 6 (6 • 6 = 36). Значит сторона квадрата равна 6 см.
3) 6 • 4 = 24 (см) — периметр квадрата.
Ответ: 24 см.
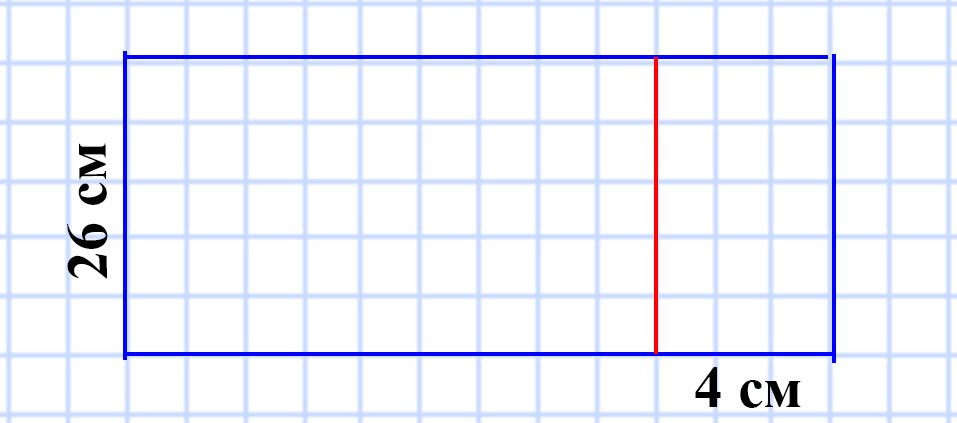
586. Ширина прямоугольника равна 26 см. На сколько квадратных сантиметров увеличится площадь этого прямоугольника, если его длину увеличить на 4 см?
Для того, чтобы узнать на сколько квадратных сантиметров увеличится площадь этого прямоугольника, надо найти площадь маленького прямоугольника, полученного в результате увеличения длины на 4 см.
Мы знаем, что противоположные стороны прямоугольника равны.
26 • 4 = 104 (см²) — площадь, на которую увеличиться площадь исходного прямоугольника.
Ответ: на 104 см².
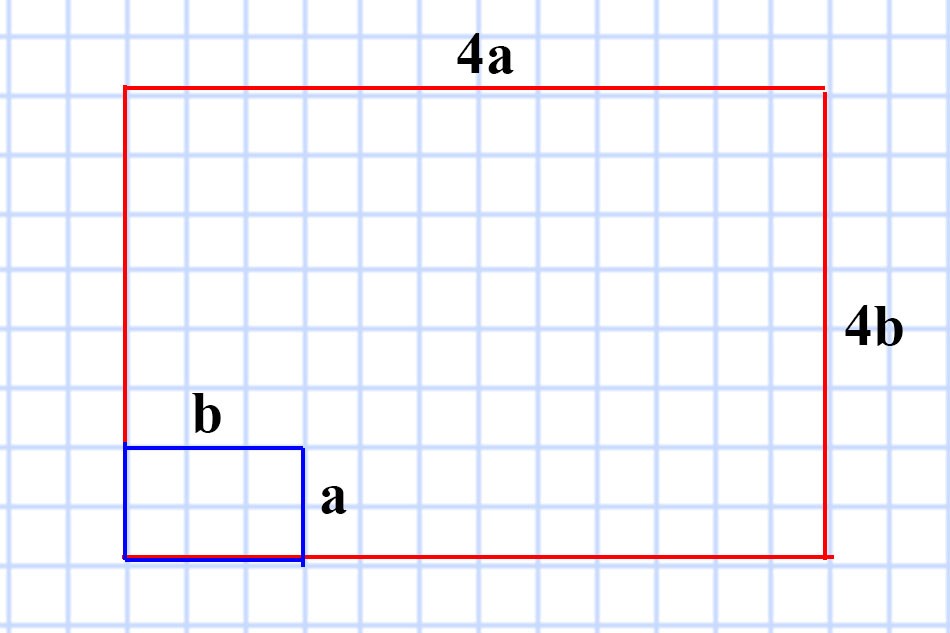
587. Во сколько раз увеличатся периметр и площадь прямоугольника, если каждую его сторону увеличить в 4 раза?
Посчитаем, во сколько раз увеличится периметр прямоугольника, если каждую его сторону увеличить в 4 раза.
- P (исходного прямоугольника) = (a + b) • 2 = 2(a + b)
- P (увеличенного прямоугольника) = (4a + 4b) • 2 = 8(a + b)
8(a + b) : 2(a + b) = 4 (раза) — увеличился периметр прямоугольника.
Посчитаем, во сколько раз увеличится площадь прямоугольника, если каждую его сторону увеличить в 4 раза.
- S (исходного прямоугольника) = ab
- S (увеличенного прямоугольника) = 4a • 4b = 16ab
16ab : ab = 16 (раз) — увеличится площадь прямоугольника.
Ответ: Периметр увеличится в 4 раза, а площадь увеличится в 16 раз.
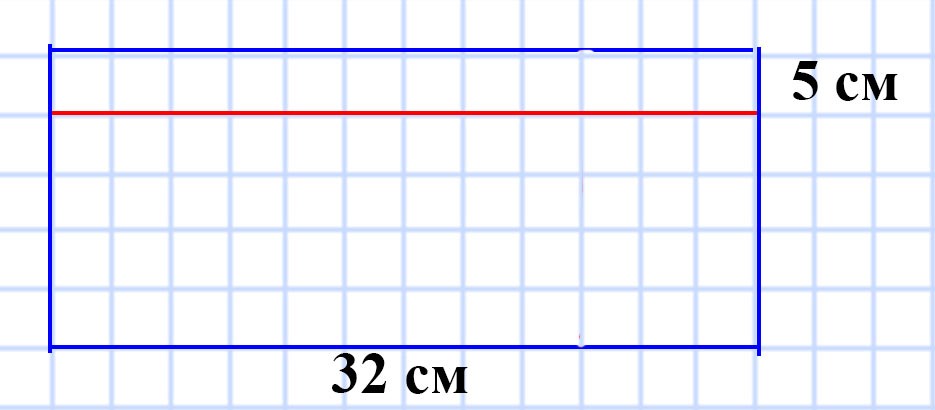
588. Длина прямоугольника равна 32 см. На сколько квадратных сантиметров уменьшится площадь этого прямоугольника, если его ширину уменьшить на 5 см?
Для того, чтобы узнать на сколько квадратных сантиметров увеличится площадь этого прямоугольника, надо найти площадь маленького прямоугольника, полученного в результате увеличения ширины на 5 см.
Мы знаем, что противоположные стороны прямоугольника равны.
32 • 5 = 160 (см²) — площадь, на которую увеличиться площадь исходного прямоугольника.
Ответ: на 160 см².
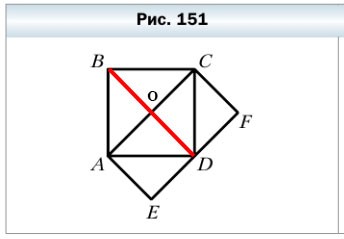
589. Площадь квадрата ABCD равна 16 см² (рис. 151). Чему равна площадь прямоугольника ACFE?
1) Проведём в квадрате ABCD ещё одну диагональ BD. Каждая из диагоналей делит квадрат ABCD на 2 равные части, а две диагонали AC и BD делят квадрат ABCD на 4 равных треугольника. Значит:
SAOB = SBOC = SCOD = SAOD = 16 : 4 = 4 см²
2) AODE — квадрат, так как две его соседние стороны AO и OD равны. Диагональ AD делит квадрат AODE на 2 равных треугольника. Значит:
SADE = SAOD = 4 см²
2) OCFD — квадрат, так как две его соседние стороны OD и OC равны. Диагональ CD делит квадрат OCFD на 2 равных треугольника. Значит:
SCFD = SOCD = 4 см²
3) SACFE = SAOD + SADE + SOCD + SCFD = 4 + 4 + 4 + 4 = 16 см².
Ответ: площадь прямоугольника ACFE равна 16 см².
590. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 12 см². Сколько квадратов площадью 4 см² можно вырезать из этого прямоугольника?
1) Если площадь листа равна 12 см², то лист может быть следующих форматов:
- 1 см х 12 см
- 2 см х 6 см
- 3 см х 4 см
2) Если площадь квадрата равна 4 см², то его сторона может быть равна только 2 см, так как 2 • 2 = 4 см².
3) Из листа со сторонами 1 см х 12 см невозможно вырезать ни одного квадрата со стороной 2 см.
4) Из листа со сторонами 2 см х 6 см можно вырезать 3 квадрата со стороной 2 см, так как:
- по длине 6 : 2 = 3
- по ширине 2 : 2 = 1
- 3 • 1 = 3
5) Из листа со сторонами 3 см х 4 см можно вырезать 2 квадрата со стороной 2 см, так как:
- по длине 4 : 2 = 2
- по ширине 3 : 2 = 1 (остаток 1).
- 2 • 1 = 2
Ответ: из листа площадью 12 см² можно вырезать 3 квадрата площадью 4 см², если стороны листа равны 2 и 6 см, либо 2 квадрата площадью 4 см², если стороны листа равны 3 и 4 см.
591. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 18 см². Сколько квадратов со стороной 3 см можно вырезать из этого листа?
1) Если площадь листа равна 18 см², то лист может быть следующих форматов:
- 1 см х 18 см
- 2 см х 9 см
- 3 см х 6 см
2) Из листа со сторонами 1 см х 18 см невозможно вырезать ни одного квадрата со стороной 3 см.
3) Из листа со сторонами 2 см х 9 см невозможно вырезать ни одного квадрата со стороной 3 см.
4) Из листа со сторонами 3 см х 6 см можно вырезать 2 квадрата со стороной 2 см, так как:
- по длине 6 : 3 = 2
- по ширине 3 : 3 = 1.
- 2 • 1 = 2
Ответ: из листа площадью 18 см² можно вырезать 2 квадрата со стороной 3 см, если стороны листа равны 3 и 6 см.
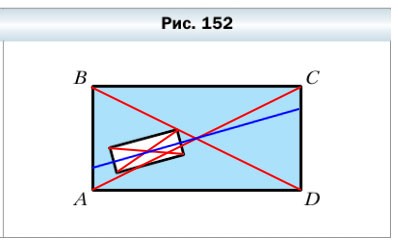
592. Внутри прямоугольника ABCD (рис. 152) вырезали отверстие прямоугольной формы. Как одним прямолинейным разрезом разделить полученную фигуру на две фигуры с равными площадями?
- Проведём две вспомогательные линии (красные) и найдём точку пересечения диагоналей малого прямоугольника.
- Проведём две вспомогательные линии (красные) и найдём точку пересечения диагоналей большого прямоугольника.
- Проведём прямую (синяя) через две точки:
- точку пересечения диагоналей малого прямоугольника
- точку пересечения диагоналей большого прямоугольника.
- Вдоль данной прямой выполним разрез и получим две фигуры с равными площадями.
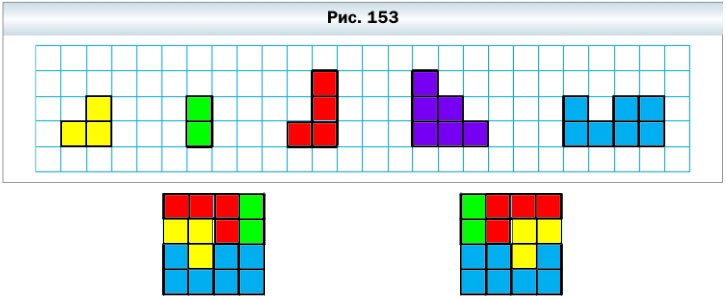
593. Используя четыре из пяти изображённых на рисунке 153 фигур, составьте квадрат.
594. Можно ли разрезать квадрат на несколько частей так, чтобы потом из них можно было составить два квадрата, длины сторон которых выражаются целым числом сантиметров, если сторона данного квадрата равна:
1) 5 см
Да, можно, так как площадь квадрата со стороной 5 см равна 5² = 25 см, а число 25 можно выразить суммой двух квадратов целых чисел: 25 = 4² + 3².
Например, можно разрезать квадрат со стороной 5 см на 4 квадрата со стороной по 2 см и 9 квадратов со стороной 1 см, а затем сложить из них одни квадрат со стороной 4 см и один квадрат со стороной 3 см.
2) 6 см
Нет, такие квадраты составить нельзя, так как число площадь квадрата со стороной 6 см равна 6² = 36 см, а число 36 нельзя выразить суммой двух квадратов целых чисел.
Упражнения для повторения
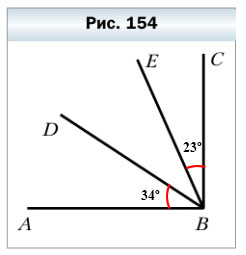
595. Из вершины прямого угла ABC (рис. 154) провели лучи BD и BE так, что угол АВЕ оказался больше угла DBE на 34º, а угол CBD больше угла DBE на 23º. Какова градусная мера угла DBE?
∠ABC= 90º — прямой
∠АВЕ — ∠DBE = 34º
∠CBD — ∠DBE = 23º
∠DBE = ?
1) ∠ABD = ∠АВЕ — ∠DBE = 34º
2) ∠EBC ∠CBD — ∠DBE = 23º
3) ∠DBE = ∠ABC — ∠ABD — ∠EBC = 90º — 34º — 23º = 33º
Ответ:∠DBE = 33º
596. Выполните действия:
Задача от мудрой совы
597. Расстояние между городами А и В равно 30 км. Из города А в город В выехал велосипедист и двигался со скоростью 15 км/ч. Одновременно из города В в направлении города А вылетела птица со скоростью 30 км/ч. Встретившись с велосипедистом, птица развернулась и полетела назад. Прилетев в город В, она снова развернулась и полетела навстречу велосипедисту. Встретившись с ним, птица развернулась и полетела назад в город В и т. д. Сколько километров пролетела птица за то время, пока велосипедист ехал из города А в город В?
1) 30 : 15 = 2 (часа) — потребуется велосипедисту, чтобы доехать из города А в город В.
Птица летала до места встречи с велосипедистом и обратно несколько раз все эти два часа, причём скорость полёта птицы была неизменна — 30 км/ч.
2) 30 • 2 = 60 (км) — пролетела птица в то время, пока велосипедист ехал из города А в город В.
Ответ: 60 км.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта