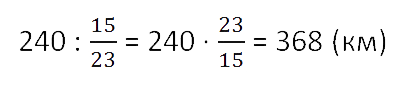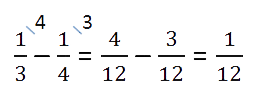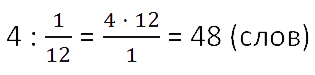Если известно сколько составляет часть от целого, то по известной части можно “восстановить”
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
|
Как найти целое, если известна его часть? Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт?
Нахождение целого по его части Если у нас известна какая-либо часть (доля) от целого, то можно всегда “восстановить” целое. При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента. Рассмотрим оба случая. 1) Часть числа – это обыкновенная дробь. В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь. Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель. _ Пример 1: Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника. Решение: Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей. Значит, сотрудник получает зарплату 30000 рублей в месяц. _ Пример 2: Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля. Решение: Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров. 2) Часть числа представлена в процентах. Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции. _ Пример: Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально. Решение: Так как скидка = 20%, то от исходной цены апельсинов осталось 100% – 20% = 80%. 80% – 120 рублей. 100% – x рублей. 0,8x = 120 рублей. x = 120 / 0,8 = 150 рублей. Таким образом, до скидки апельсины стоили 150 рублей. модератор выбрал этот ответ лучшим
Алиса в Стране 3 года назад Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например. Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое. Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части. Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36. Ну и в итоге решим задачку автора из его вопроса: 300 граммов делим на 3/8 получаем 800 граммов.
smile6008 3 года назад В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении. Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах – это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получаем 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт.
[пользователь заблокирован] 5 лет назад Для лучшего понимания процесса можно делать так (хотя математически это нерационально). Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3. 300 делим на 3, получаем 300/3=100 Это одна восьмая часть. Целое – это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800 Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же. Узнаём, чему равна одна тысячная часть 300/375=0.8 Ну, а далее узнаём чему равно само целое 0.8*1000=800
Эл Лепсоид 5 лет назад В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) – неизвестную “х”. Но, поскольку, у нас во второй части пропорции стоит “1”, то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800. Таким образом, весь торт будет весить 800 грамм.
СТА 1106 3 года назад 3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак: 3 части – 300 грамм. 8 частей – Х грамм. Решаем пропорцию. 8 × 300 ÷ 3 = 800 грамм. Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей. Второй вариант решения задачи. 300 : 3 × 8 = 800 грамм. Ответ. 800 грамм , в обоих вариантах таз решения задачи.
Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть. Пример: Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 – это и будет целое. Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести.
Master-Margarita 5 лет назад Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм. То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель – 3, а знаменатель – 8.
Рина19 5 лет назад Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей. На данном примере. Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г. Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт. 100*8=800 г
Бекки Шарп 3 года назад Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм. Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм. Приведем еще пример как найти целое число, если известна часть. В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе? Решить задачу можно так: 27 : 3/4 = 36 человек. Знаете ответ? |
Математика
5 класс
Урок № 50
Нахождение целого по его части
Перечень рассматриваемых вопросов:
- обыкновенная дробь;
- числитель, знаменатель обыкновенной дроби;
- сократимая, несократимая дробь;
- задачи на дроби.
Тезаурус
Дробь в математике – это число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя.
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
«Без знания дробей никто не может быть сведущим в математике», – однажды сказал древнеримский философ Марк Туллий Цицерон. И трудно с ним не согласиться, ведь дроби в нашей жизни встречаются очень часто.
Убедимся в этом, решая задачи на нахождение целого по его части.
В окружающем нас мире очень часто приходится находить не только часть от чего-либо, но и, наоборот, целое по его части. Например, мы можем услышать в прогнозе погоды такую фразу «Сегодня выпало 20 миллиметров осадков, что составляет половину месячной нормы». А сколько тогда составляет месячная норма? Если половина нормы это 20 миллиметров, тогда норма в два раза больше, т. е. 40 миллиметров.
А теперь немного изменим условие задачи. Найдём всю месячную норму, если известно, что за день выпало 20 миллиметров, что составляет 
месячной нормы.
Для решения этой задачи воспользуемся следующими рассуждениями.
Будем считать, что месячная норма это 
. По условию, её 
равны 20 миллиметрам. Сначала найдём 
нормы, а потом и 
.
20 : 2 = 10 мм – одна треть нормы. 10 мм · 3 = 30 мм – три трети нормы.
Ответ: месячная норма равна 30 мм.
Итак, сформулируем правило нахождения целого по его части: если часть искомого целого выражена дробью, то чтобы найти целое, можно эту часть разделить на числитель дроби, а результат умножить на её знаменатель.
Решим задачу.
Два путешественника отправились в поход, который длился несколько дней. В первый день они преодолели 
от всего маршрута. Во второй день они прошли 
от того, что прошли в первый день.
Какой путь должны преодолеть путешественники, если во второй день они прошли 20 км?
Решение.
Составим схему, на основе которой будем выполнять решение этой задачи.
Нам известно, что 20 километров это четыре пятых маршрута, пройденного в первый день. Соответственно, найдём длину маршрута в первый день.
20 : 4 · 5 = 25 км – расстояние, пройденное за 1 день.
Теперь, зная, что 25 = 
от всего маршрута, найдём весь пройденный путешественниками путь: 25 : 5 · 13 = 65 км.
Ответ: весь путь равен 65 км.
Решим задачу. Младшей сестре исполнилось 9 лет, что составляет 
от возраста её старшей сестры. А возраст старшей сестры составляет 
от возраста их матери. Сколько лет старшей сестре и матери?
Решение: для решения этой задачи составим следующую схему.
По известному возрасту младшей сестры найдём возраст старшей.
9 : 3 · 5 =15 (лет) – возраст старшей из дочерей.
Теперь найдём возраст матери.
15 : 5 · 12 = 36 (лет) – возраст матери.
Ответ: 15 лет; 36 лет.
Тренировочные задания
№ 1. За один день бригада заасфальтировала 5 км дороги, что составило 
всей работы. Сколько километров должна заасфальтировать бригада?
Решение: для решения этой задачи нужно использовать правило нахождения части от целого: чтобы найти целое по части, нужно эту часть разделить на числитель дроби, а результат умножить на её знаменатель.
Т. е. 5 : 5 · 7 = 7 км
Ответ: 7 км.
№ 2. Первая сторона треугольника равна 12 см, что составляет 
от его периметра, другая составляет 
от первой стороны. Чему равна третья сторона треугольника?
Решение: для решения этой задачи сначала нужно вспомнить, что периметр – это сумма длин всех сторон треугольника, т. е. сумма длин трёх сторон.
Теперь найдём периметр, исходя из условия задачи.
1) 12 : 3 · 10 = 60 см – периметр.
12 : 2 · 3 = 18 см – вторая сторона.
Теперь от периметра отнимем сумму длин двух сторон и получим третью сторону.
40 – (18 + 12) = 10 см – третья сторона. Ответ: 10 см.
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Цикл статей “Дроби”
Первая часть Вторая часть Третья часть
Четвертая часть Пятая часть Шестая часть Седьмая часть
ТРИ ТИПА ПРОСТЕЙШИХ ЗАДАЧ с ДРОБЯМИ
Здравствуйте, уважаемые читатели.
Вашему вниманию предлагается статья о простейших задачах на дроби. Сразу оговорюсь, что к этой теме мы в будущем вернёмся ещё не раз, поскольку эта статья предназначена для учащихся 4-5 классов, которые ещё не изучали такие действия с дробями, как их сложение, вычитание, умножение и деление.
Тем не менее полученные ими знания уже позволяют решать простые, даже можно сказать — простейшие, задачи с дробями.
К таковым следует отнести такие задачи, в которых участвуют три величины:
- Число, которое принимается за целую величину — обозначим его буквой А;
- Число, являющееся частью целой величины А — обозначим его буквой а;
- Дробь
Все введённые величины (исключая значение d), учитывая предназначение статьи, будем считать натуральными.
Простейшими задачами с тремя величинами считаются такие задачи, в которых по двум данным величинам требуется найти третью.
К первому типу автор относит следующую задачу:
I. НАХОЖДЕНИЕ ДРОБИ, ВЫРАЖАЮЩЕЙ ДАННУЮ ЧАСТЬ от ДАННОГО ЦЕЛОГО.
Руководствуясь определением обыкновенной дроби эта задача решается следующим образом:
ПРИМЕР 1. Масса тортика — 800 г, за ужином было съедено 600 г. Какая часть тортика была съедена за ужином?
РЕШЕНИЕ
II. НАХОЖДЕНИЕ ЧАСТИ, ВЫРАЖЕННОЙ ДАННОЙ ДРОБЬЮ
Чтобы найти часть а, выраженную данной дробью
следует целую величину А разделить на знаменатель дроби n и полученное частное умножить на числитель m.
ПРИМЕР 2. Купили тортик массой 800 г и за ужином съели ¾ его. Сколько граммов тортика съедено за ужином?
РЕШЕНИЕ.
800:4 × 3 = 200 ×3 = 600 (г).
ОТВЕТ. 600 г.
III. НАХОЖДЕНИЕ ЦЕЛОГО по ЕГО ЧАСТИ, ВЫРАЖЕННОЙ ДРОБЬЮ
Для нахождения целого следует его часть разделить на числитель дроби и полученное частное умножить на знаменатель данной дроби, выражающей эту часть.
ПРИМЕР 3. За ужином съели 600 грамм купленного тортика, что составляет ¾ его массы. Найдите массу тортика.
РЕШЕНИЕ.
600 : 3 × 4 = 200 × 4 = 800 (г).
ОТВЕТ. 800 г.
Желаю девочкам и мальчикам успехов в изучении дробей, и не только их!
Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_математика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Цикл статей “Дроби”
1 статья 2 статья 3 статья 4 статья 5 статья 6 статья
7статья 8 статья [Текущая]
Как найти целое дробей
Определение целой части у дробного числа производится визуально, то есть достаточно только посмотреть на число и, зная ряд простейших правил, отделить его дробную часть от целой.
Инструкция
Если данное число является дробью десятичной, а такие дроби записываются в строчку и всегда имеют знак запятой, то именно по этому знаку и определяется, где целая, а где дробная составляющая данного числа. Тогда число, которое расположено слева от запятой, и есть искомая целая часть, а то, что написано справа – дробная. Пример 1. У десятичной дроби 56,89 целая часть – 56 (пятьдесят шесть целых), а дробная – 89 (восемьдесят девять сотых). Читается это число как: «пятьдесят шесть целых восемьдесят девять сотых».Пример 2. 0,4 – дробь ноль целых четыре десятых не имеет целой части, так как она равна нулю.
Если надо отделить целую часть у обыкновенной дроби, которая пишется в столбик (см. рисунок) или в строчку через дробь «/», например, 47 2/3 (сорок семь целых две третьих), то в этом случае целая составляющая числа пишется отдельно от его дробной части. Если целая часть равна нулю, то она просто не пишется.Пример 3. На рисунке: целая часть первой дроби равна сорока семи, у второй дроби она равна нулю.Пример 4. У числа 47 2/3, «47» – целая часть. У дроби 5/9 – целой части нет или она равна нулю.
Если обыкновенная дробь записана в неправильном виде (это когда в числителе значение больше, чем в знаменателе), к примеру, 6/4, то целую часть выделить нужно путем математического действия. Следует разделить в столбик числитель на знаменатель числа. В ответе получится десятичная дробь, а выделение целой части такого числа, указано в первом шаге данной статьи.Пример 5. Чтобы выделить целую часть у числа 5/2, разделите в столбик 5 на 2 (см. рисунок). В ответе видно, что эта дробь равна десятичной 2,5. Значит целая часть этого числа равна двум. Это число в обыкновенной дроби запишется как 2 5/10 = 2 ½.Если при делении числитель нацело не делится на знаменатель, то дробь запишется в следующем алгоритме: целая часть ответа – это целая часть составляемой дроби, остаток деления – числитель дроби, а делитель – это знаменатель результативной дроби (см рисунок).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
