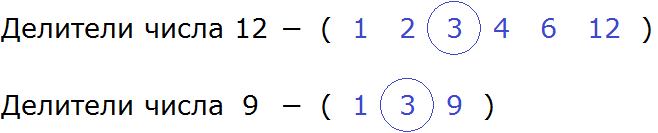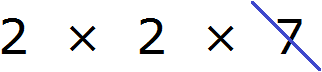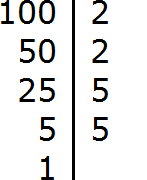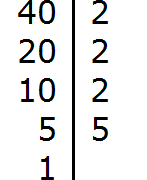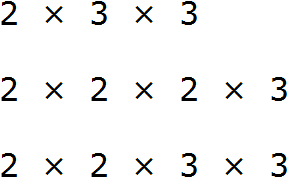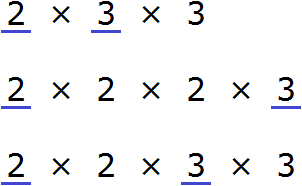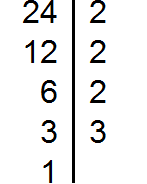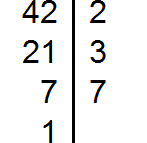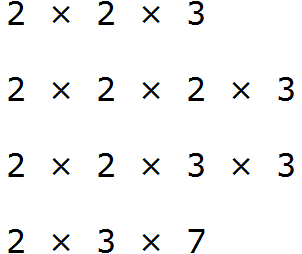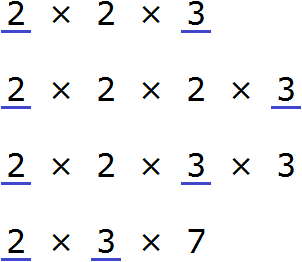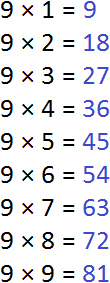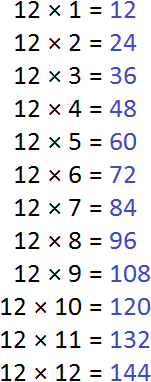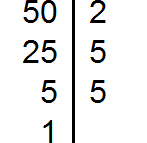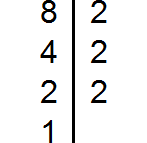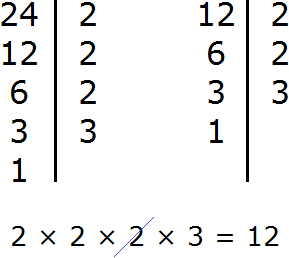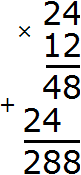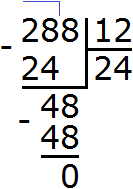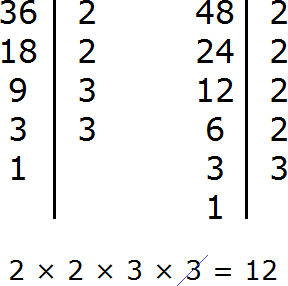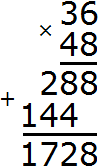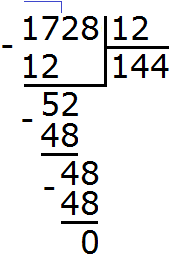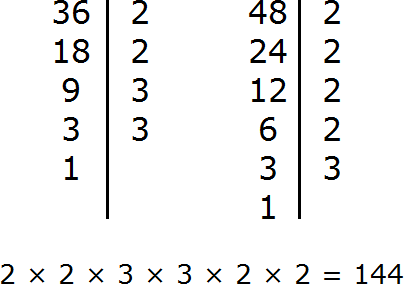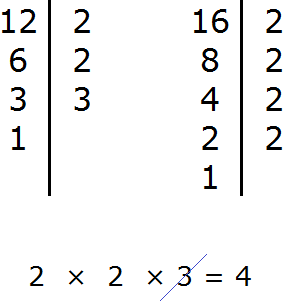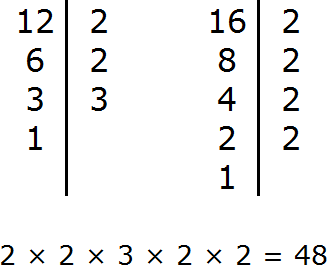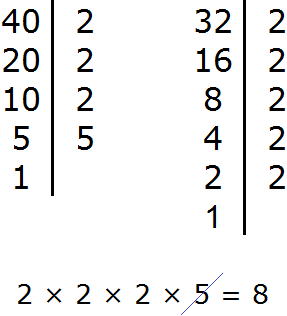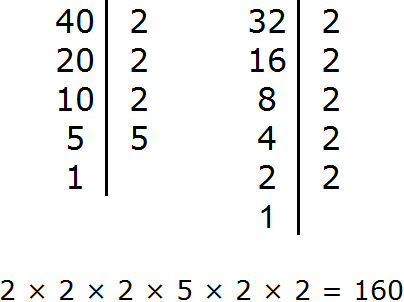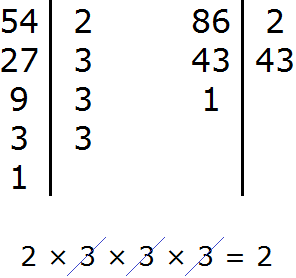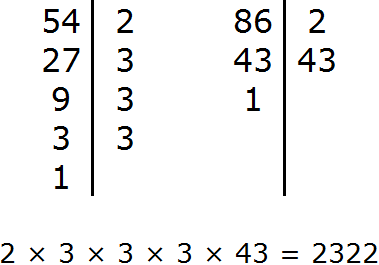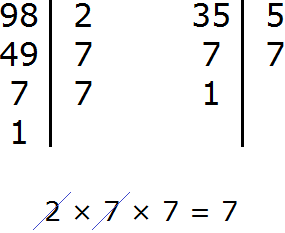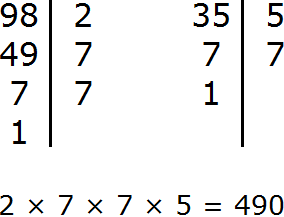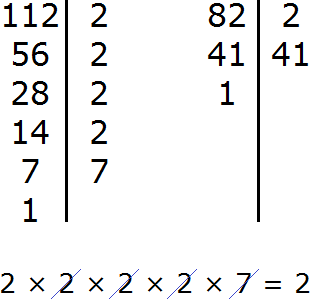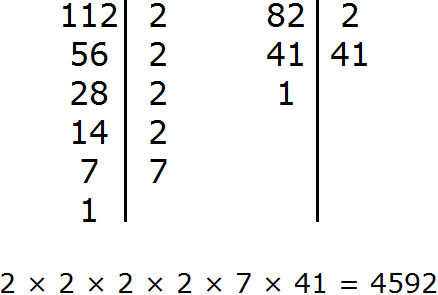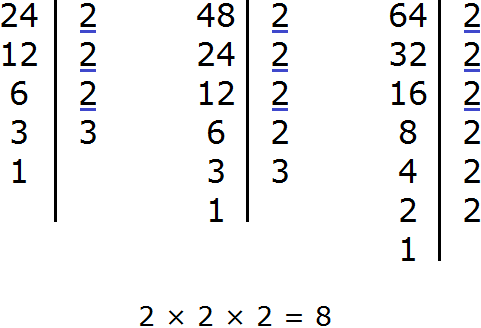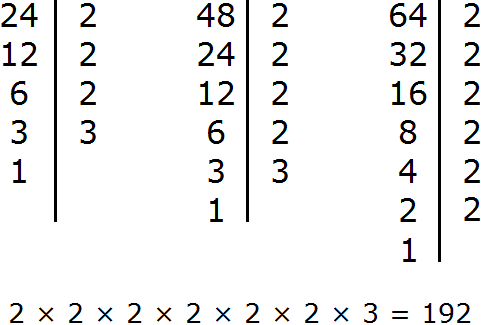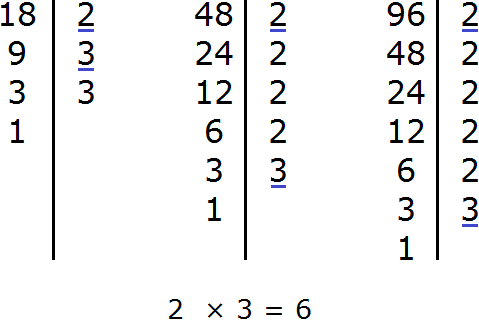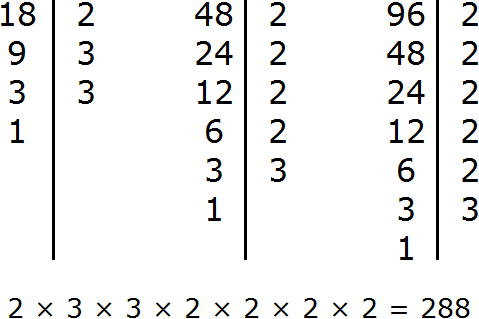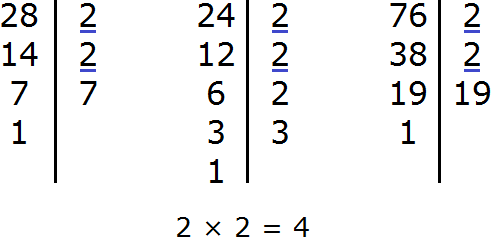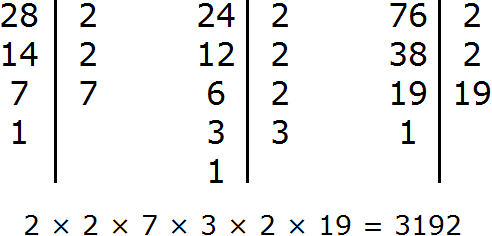Как найти НОД
- Нахождение путём разложения на множители
- Алгоритм Евклида
Рассмотрим два способа нахождения наибольшего общего делителя.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.
Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.
Пример 1. Найти НОД (84, 90).
Решение: Раскладываем числа 84 и 90 на простые множители:
Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой:
2 · 3 = 6.
Таким образом, НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
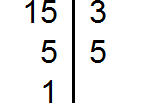
Решение: Раскладываем 15 и 28 на простые множители:
Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.
НОД (15, 28) = 1.
Алгоритм Евклида
Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.
Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.
Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.
Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно:
НОД (27, 9) = 9.
В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:
- Из двух данных чисел большее число делят на меньшее.
- Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
- Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
- Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
- Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.
Пример 2. Найдём наибольший общий делитель чисел 140 и 96:
1) 140 : 96 = 1 (остаток 44)
2) 96 : 44 = 2 (остаток 8)
3) 44 : 8 = 5 (остаток 4)
4) 8 : 4 = 2
Последний делитель равен 4 — это значит:
НОД (140, 96) = 4.
Последовательное деление так же можно записывать столбиком:
Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
- Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
- Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
- Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.
Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа — 48:
48 : 4 = 12
48 делится на 4 без остатка. Таким образом:
НОД (140, 96, 48) = 4.
Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.
Как найти НОД?
Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
- выбрать одинаковые множители, входящие в оба разложения;
- найти их произведение.
Примеры нахождения наибольшего общего делителя
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОД 12 и 8
1. Раскладываем 12 и 8 на простые множители:
2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2
3. Перемножаем эти множители и получаем: 2 · 2 = 4
Ответ: НОД (8; 12) = 2 · 2 = 4.
Пример 2: найти НОД 75 и 150
Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:
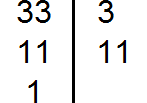
1. Раскладываем 75 и 150 на простые множители:
2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5
3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75
Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.
Частный случай или взаимно простые числа
Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:
Пример 3: найти НОД 9 и 5
1. Раскладываем 5 и 9 на простые множители:
Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.
Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.
Алгоритм Евклида для нахождения НОД
Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».
Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:
a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1
Мы можем закончить деление тогда, когда rk+1=0, при этом rk=НОД(a, b).
Найдите наибольший общий делитель чисел 64 и 48.
Решение
Введем обозначения: a=64, b=48.
На основе алгоритма Евклида проведем деление 64 на 48.
Получим 1 и остаток 16. Получается, что q1=1, r1=16.
Вторым шагом разделим 48 на 16, получим 3. То есть q2=3, а r2=0. Таким образом число 16 – это наибольший общий делитель для чисел из условия.
Ответ: НОД(64, 48)=16.
Чему равен НОД чисел 111 и 432?
Решение
Делим 432 на 111. Согласно алгоритму Евклида получаем цепочку равенств 432=111·3+99, 111=99·1+12, 99=12·8+3, 12=3·4.
Таким образом, наибольший общий делитель чисел 111 и 432 – это 3.
Ответ: НОД(111, 432)=3.
Найдите наибольший общий делитель чисел 661 и 113.
Решение
Проведем последовательно деление чисел и получим НОД(661, 113)=1. Это значит, что 661 и 113 – это взаимно простые числа. Мы могли выяснить это до начала вычислений, если бы обратились к таблице простых чисел.
Ответ: НОД(661, 113)=1.
Нахождение НОД с помощью разложения чисел на простые множители
Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.
Если мы разложим числа 220 и 600 на простые множители, то получим два произведения: 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими в этих двух произведениях будут множители 2,2 и 5. Это значит, что НОД(220, 600)=2·2·5=20.
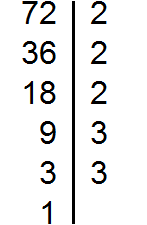
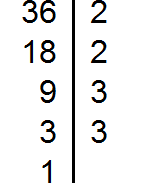
Найдите наибольший общий делитель чисел 72 и 96.
Решение
Найдем все простые множители чисел 72 и 96:
72361893122233
96482412631222223
Общими для двух чисел простые множители: 2, 2, 2 и 3. Это значит, что НОД(72, 96)=2·2·2·3=24.
Ответ: НОД(72, 96)=24.
Правило нахождения наибольшего общего делителя двух чисел основано на свойствах наибольшего общего делителя, согласно которому НОД(m·a1, m·b1)=m·НОД(a1, b1), где m– любое целое положительное число.
Нахождение НОД трех и большего количества чисел
Независимо от количества чисел, для которых нам нужно найти НОД, мы будем действовать по одному и тому же алгоритму, который заключается в последовательном нахождении НОД двух чисел. Основан этот алгоритм на применении следующей теоремы: НОД нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3, НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.
Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.
Решение
Введем обозначения: a1=78, a2=294, a3=570, a4=36.
Начнем с того, что найдем НОД чисел 78 и 294: d2=НОД(78, 294)=6.
Теперь приступим к нахождению d3=НОД(d2, a3)=НОД(6, 570). Согласно алгоритму Евклида 570=6·95. Это значит, что d3=НОД(6, 570)=6.
Найдем d4=НОД(d3, a4)=НОД(6, 36). 36 делится на 6 без остатка. Это позволяет нам получить d4=НОД(6, 36)=6.
d4=6, то есть, НОД(78, 294, 570, 36)=6.
Ответ: НОД(78, 294, 570, 36)=6.
А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.
Вычислите НОД чисел 78, 294, 570 и 36.
Решение
Произведем разложение данных чисел на простые множители: 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.
Для всех четырех чисел общими простыми множителями будут числа 2 и 3.
Получается, что НОД(78, 294, 570, 36)=2·3=6.
Ответ: НОД(78, 294, 570, 36)=6.
Нахождение НОД отрицательных чисел
Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.
Найдите НОД отрицательных целых чисел −231 и −140.
Решение
Для выполнения вычислений возьмем модули чисел, данных в условии. Это будут числа 231 и 140. Запишем это кратко: НОД(−231, −140)=НОД(231, 140). Теперь применим алгоритм Евклида для нахождения простых множителей двух чисел: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Получаем, что НОД(231, 140)=7.
А так как НОД(−231, −140)=НОД(231, 140), то НОД чисел −231 и −140 равен 7.
Ответ: НОД(−231, −140)=7.
Определите НОД трех чисел −585, 81 и −189.
Решение
Заменим отрицательные числа в приведенном перечне на их абсолютные величины, получим НОД(−585, 81, −189)=НОД(585, 81, 189). Затем разложим все данные числа на простые множители: 585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими для трех чисел являются простые множители 3 и 3. Получается , что НОД(585, 81, 189)=НОД(−585, 81, −189)=9.
Ответ: НОД(−585, 81, −189)=9.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
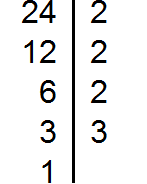
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
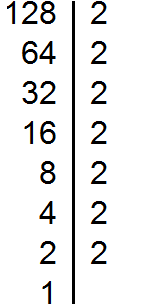
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
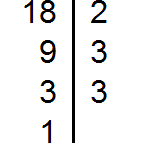
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
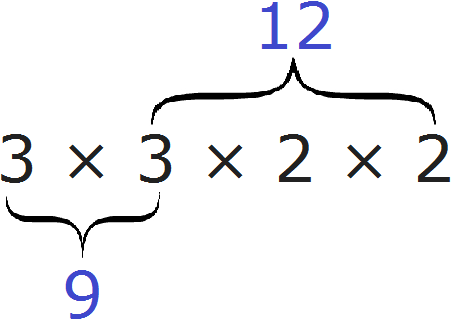
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
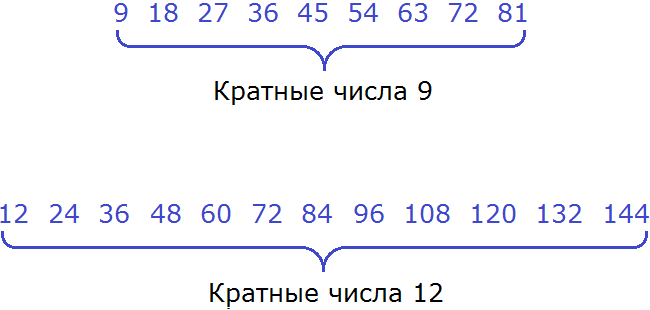
Теперь выпишем кратные обоих чисел:
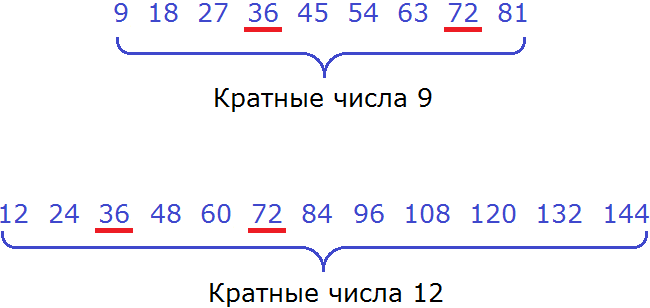
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
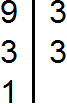
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
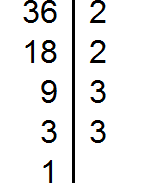
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
Задание 2. Найдите НОК чисел 12 и 16
Решение:
Задание 3. Найдите НОД чисел 40 и 32
Решение:
Задание 4. Найдите НОК чисел 40 и 32
Решение:
Задание 5. Найдите НОД чисел 54 и 86
Решение:
Задание 6. Найдите НОК чисел 54 и 86
Решение:
Задание 7. Найдите НОД чисел 98 и 35
Решение:
Задание 8. Найдите НОК чисел 98 и 35
Решение:
Задание 9. Найдите НОД чисел 112 и 82
Решение:
Задание 10. Найдите НОК чисел 112 и 82
Решение:
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
Задание 13. Найдите НОД чисел 18, 48, 96
Решение:
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Наибольший общий делитель

4.3
Средняя оценка: 4.3
Всего получено оценок: 222.
4.3
Средняя оценка: 4.3
Всего получено оценок: 222.
Наибольший общий делитель – это еще один показатель, позволяющий упростить работу с дробями. Очень часто в результате вычислений получаются дроби с очень большими значениями числителя и знаменателя. Сокращать поэтапно такие числа можно, но это крайне долго, поэтому проще сразу найти НОД и сократить на него. Разберемся в теме подробнее.
Что такое НОД?
Наибольший общий делитель (НОД) ряда чисел – это наибольшее число, на которое можно без остатка разделить каждое из чисел ряда.
Это значение чаще всего используется для ряда из двух чисел. Просто потому, что сокращаются обычно два числа: числитель и знаменатель дроби. Нахождение НОД для большего количества значений не всегда оправдано, но вырабатывает навык.
Как найти НОД?
Для того, чтобы найти НОД необходимо каждое из чисел разложить на простые множители и выделить общую часть.
Специальной формулы для этого не придумали, зато есть алгоритм вычисления.
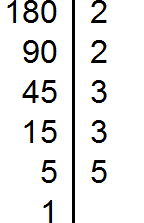
Приведем пример нахождения наибольшего общего делителя двух натуральных чисел: 540 и 252. Разложим 640 на простые множители. Последовательность действий такова:
- Делим число на наименьший из возможных простых чисел. То есть, если число можно разделить на 2, 3 или 5, то сначала нужно делить на 5. Просто, чтобы не запутаться.
- Получившийся результат делим на наименьшее из возможных простых чисел.
- Повторяем деление каждого полученного результата, пока не получим простое число.
Теперь проведем ту же процедуру на практике.
- 540 : 2=270
- 270:2=135
- 135 : 3 =45
- 45 : 3=15
- 15 : 5 = 3
Запишем результат в виде равенства 540=2*2*3*3*3*5. Для того, чтобы записать результат, нужно последнее получившееся число умножить на все делители.
Аналогично поступим с числом 252:
- 252 : 2=126
- 126: 2=63
- 63 : 3=21
- 21 : 3 = 7
Запишем результат: 252=2*2*3*3*7.
В каждом разложении есть одинаковые числа. Найдем их, это два числа 2 и два числа 3. Отличаются только 7 и 3*5.
Для того, чтобы найти НОД нужно перемножить общие множетели. То есть в произведении будет две двойки и две тройки.
НОД=2*2*3*3=36
Как можно это использовать?
Задача: сократить дробь $$252over540$$.
НОД для двух этих чисел мы уже находили, теперь просто воспользуемся уже посчитанным значением.
НОД = 36
Сократим числитель и знаменатель дроби на 36 и получим ответ.
$${252over540} ={7over15}$$ – чтобы быстро сократить, достаточно посмотреть на разложение чисел.
Если 540=2*2*3*3*3*5, а НОД=36=2*2*3*3, то 540 = 36*3*5. И если мы поделим 540 на 36, то получим 3*5=15.
Без НОД нам пришлось бы в одну длинную строку писать сокращения. К тому же, бывают случаи, когда непонятно, можно ли сократить дробь вообще. Для таких ситуаций в математике и придумали разложение чисел на простые множители и НОД.
Что мы узнали?
Мы узнали, что такое наибольший общий делитель пары чисел, разобрались, как можно использовать показатель на практике, решили задачу на нахождение НОД и применение НОД для сокращения дробей. Поняли, что с использованием НОД можно проще и быстрее сократить громоздкие дроби, найдя НОД для числителя и знаменателя.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 222.
А какая ваша оценка?