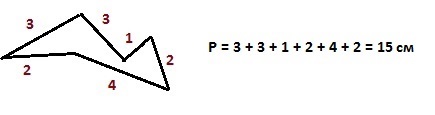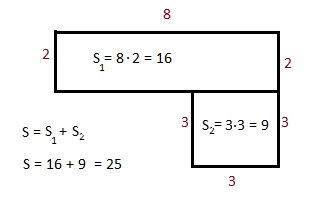Решение задач по математике как найти площадь

Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8-9 класс. Задачи на нахождение площади треугольника. Они встречаются в 15 задании ОГЭ по математике.

В статье будут рассмотрены несколько формул вычисления площади треугольника.

Первая теорема

Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена.

Задача №1

Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника

Решение

Задача №2

У треугольника со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?

Решение

Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена. Поэтому площадь треугольника в каждом случае будет одинаковой.

Задача №3

На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.

Решение

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла, делит треугольник на два треугольника, площади которых относятся как m:n:

Отрезок AD относиться к отрезку DC как 6:10. Значить площадь треугольника ABD составляет 6 частей от площади треугольника АВС, а площадь треугольника DBC – 10 частей. Вся площадь треугольника ABC равна 16 частей. По условию площадь треугольника АВС равна 48. Значит площадь треугольника ВСD=(48/16)*10=30.

Ответ 30

Задача №4

Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.

Решение

Вторая теорема

Площадь прямоугольного треугольника равна половине произведения его катетов.

Ответ 20

Задача №5

В прямоугольном треугольнике один из катетов равен 4, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника

Решение:

Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.

Значит в треугольнике катеты равны 4 ( a=b=4). Найдем площадь равнобедренного прямоугольного треугольника:

Ответ 8

Задача №6

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.

Решение

Вспомним что такое катет и гипотенуза.

Стороны прямоугольного треугольника, которые образуют прямой угол, называются катеты, а третья сторона – гипотенуза.

Чтобы вычислить площадь прямоугольного треугольника, необходимо вычислить второй катет. Для этого воспользуемся теоремой Пифагора.

Теорема Пифагора

Квадрат гипотенузы равен сумме квадратов катетов.

Зная оба катета прямоугольного треугольника, вычислим его площадь:

Ответ 60

Задача №7

Катеты прямоугольного треугольника равны 21 и 72. Найдите высоту, проведенную к гипотенузе.

Решение

В этой задаче, чтобы найти высоту, проведенную к гипотенузе, необходимо воспользоваться двумя формулами нахождения площади треугольника. Первая формула (для прямоугольного треугольника): половина произведения его катетов. Вторая формула: половина произведения высоты на сторону, к которой эта высота проведена. Площадь, вычисленная разными формулами одной фигуры, одинаковая. Для решения, нам понадобятся размеры гипотенузы. Вычислим ее:

Теперь найдем, чему будет равна высота:

Ответ 20,16

Задача №8

Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.

Решение.

В этой задаче, площадь треугольника найдем по формуле Герона. Для этого нужно знать полупериметр (периметр, деленный на 2) треугольника и длину каждой стороны.

В равнобедренном треугольнике, боковые стороны равны. Найдем периметр треугольника. Периметр треугольника – это сумма всех длин сторон треугольника

Ответ 168

Задача №9

В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.

Решение

Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.

В нашем случает получается треугольник прямоугольный и равнобедренный т.е. катеты треугольника равны. Найдем катеты прямоугольного треугольника через теорему Пифагора.

Пусть катеты прямоугольного треугольника это Х

Ответ 1681

Задача №10

Решение

Третья теорема. Теорема о площади треугольника (9 класс)

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Ответ 50

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог

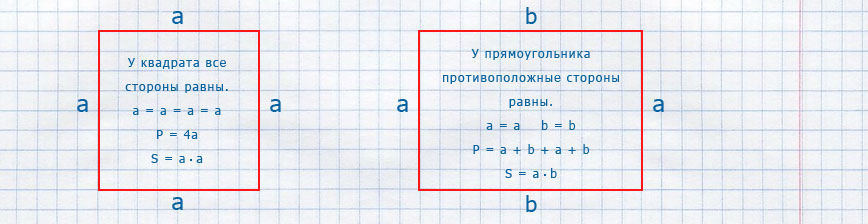
Примеры решения задач разной сложности на нахождение периметра и площади

Условные обозначения и формулы

• a — длина
• b — ширина
• P — периметр
• S — площадь

Квадрат → определение

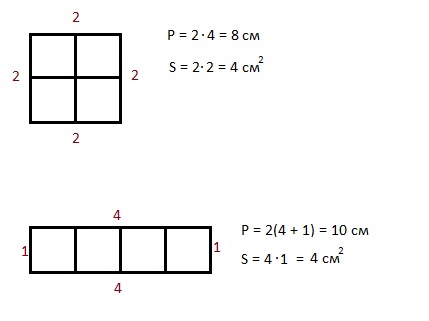
P = a + a + a + a; P = a · 4 — периметр квадрата

S = a · a; S = a² — площадь квадрата

Прямоугольник → определение

P = a + b + a + b; P = 2a + 2b; P = (a + b) · 2 – периметр прямоугольника

S = a ·  b — площадь прямоугольника

Задачи

Треугольник → определение

S = ½ · a · h – площадь треугольника

P = a + b + c – периметр треугольника

Задачи

Круг → определение

P = πD; P = 2πR — длина окружности

S = πR2; S = πD2 : 4 – площадь круга

Задачи

30 задач – от простого к сложному

Задача №1

Найди периметр квадрата со стороной 8 см.

Решение:

8 · 4 = 32 (см)

Ответ: периметр квадрата 32 см.

Задача №2

Найди периметр квадрата со стороной 16 см.

Решение:

16 · 4 = 64 (см)

Ответ: периметр квадрата 64 см.

Задача №3

Периметр квадрата 16 см. Найди его сторону.

Решение:

16 : 4 = 4 (см)

Ответ: сторона квадрата 4 см.

Задача №4

Найди периметр прямоугольника со сторонами 9 и 6 см.

Решение:

(9 + 6) · 2 = 30 (см)

Ответ: периметр прямоугольника 30 см.

Задача №5

Найди периметр прямоугольника со сторонами 7 и 8 см.

Решение:

(7 + 8) · 2 = 30 (см)

Ответ: периметр прямоугольника 30 см.

Задача №6

Найди длину прямоугольника, если его ширина 7 см, а периметр равен 40 см.

Решение:

Вариант Ⅰ

У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.

Если одна ширина (сторона) 7 см, то и другая (противоположная) тоже 7 см.

7 + 7 = 14 (см)

Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон (длин) будет равна:

40 – 14 = 26 (см)

Теперь узнаем длину одной стороны:

26 : 2 = 13 (см)

Ответ: длина прямоугольника 13 см.

или

Вариант Ⅱ

P = (a + b) · 2 — периметр прямоугольника

или

(a + b) · 2 = P, где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.

Составим уравнение:

(а + 7) · 2 = 40

2а + 14 = 40

2а = 40 – 14

2а = 26

а = 26 : 2

а = 13

Ответ: длина прямоугольника 13 см.

Задача №7

Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.

Решение:

Вариант Ⅰ

У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.

Если одна длина (сторона) 10 см, то и другая (противоположная) тоже 10 см.

10 + 10 = 20 (см)

Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон будет равна:

30 – 20 = 10 (см)

Теперь узнаем ширину одной стороны:

10 : 2 = 5 (см)

Ответ: ширина прямоугольника 5 см.

или

Вариант Ⅱ

P = (a + b) · 2 — периметр прямоугольника

или

(a + b) · 2 = P, где a — длина = 10 см, b — ширина = ?, P — периметр = 30 см.

Составим уравнение:

(10 + b) · 2 = 30

20 + 2b = 30

2b = 30 – 20

2b = 10

b = 10 : 2

b = 5

Ответ: ширина прямоугольника 5 см.

Задача №8

Ширина прямоугольника 14 см. Длина на 5 см больше. Найди его периметр и площадь.

Решение:

14 + 5 = 19 (см)

(19 + 14) · 2 = 66 (см)

19 · 14 = 266 (см²)

Ответ: периметр прямоугольника 66 см; площадь прямоугольника 266 см².

Задача №9

Длина прямоугольника 7 см. Ширина на 3 см меньше. Найди его периметр и площадь.

Решение:

7 – 3 = 4 (см)

(7 + 4) · 2 = 22 (см)

7 · 4 = 28 (см²)

Ответ: периметр прямоугольника 22 см; площадь прямоугольника 28 см².

Задача №10

Периметр квадрата 24 см. Найди его площадь.

Решение:

24 : 4 = 6 (см)

6 · 6 = 36 (см²)

Ответ: площадь квадрата 36 см².

Задача №11

Периметр квадрата 36 см. Найди его площадь.

Решение:

36 : 4 = 9 (см)

9 · 9 = 81 (см²)

Ответ: площадь квадрата 81 см².

Задача №12

Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.

На сколько см² он ошибся?

Решение:

5 · 9 = 45 (см²)

6 · 8 = 48 (см²)

48 – 45 = 3 (см²)

Ответ: он ошибся на 3 см².

Задача №13

Ученику нужно было начертить прямоугольник со сторонами 10 см и 8 см, а он начертил его со сторонами 8 см и 6.

На сколько см² он ошибся?

Решение:

10 · 8 = 80 (см²)

8 · 6 = 48 (см²)

80 – 48 = 32 (см²)

Ответ: он ошибся на 32 см².

Задача №14

Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.

Решение:

4 + 4 = 8 (см)

36 – 8 = 28 (см)

28 : 2 = 14 (см)

14 · 4 = 56 (см²)

Ответ: площадь прямоугольника 56 см².

Задача №15

Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.

Решение:

6 · 4 = 24 (см)

3 + 3 = 6 (см)

24 – 6 = 18 (см)

18 : 2 = 9 (см)

Ответ: длина прямоугольника 9 см.

Задача №16

Сторона квадрата 18 см. Найди длину прямоугольника с таким же периметром и шириной 14 см.

Решение:

18 · 4 = 72 (см)

14 + 14 = 28 (см)

72 – 28 = 44 (см)

44 : 2 = 22 (см)

Ответ: длина прямоугольника 22 см.

Задача №17

Площадь прямоугольника 40 см². Ширина его 4 см.

Чему равен периметр прямоугольника?

Решение:

40 : 4 = 10 (см)

(10 + 4) · 2 = 28 (см)

Ответ: периметр прямоугольника 28 см.

Задача №18

Площадь прямоугольника 40 см². Длина его 8 см.

Чему равен периметр прямоугольника?

Решение:

40 : 8 = 5 (см)

(8 + 5) · 2 = 26 (см)

Ответ: периметр прямоугольника 26 см.

Задача №19

Ширина прямоугольника 15 см, длина 20 см.

Найди длину другого прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.

Решение:

в первом действии узнаём площадь по формуле a · b = S

15 · 20 = 300 (см²) — S  одного и другого прямоугольника

теперь ширину второго

15 : 3 = 5 (см) — ширина другого прямоугольника

и отвечаем на вопрос задачи применив формулу S : a = b

300 : 5 = 60 (см)

Ответ: длина другого прямоугольника 60 см.

Задача №20

Длина прямоугольника b = 32 см. Ширина a = 4 см.

Найди длину другого прямоугольника с такой же площадью, если его ширина в 2 раза больше ширины первого прямоугольника.

Решение:

узнаем площадь прямоугольников по формуле a · b = S

32 · 4 = 128 (см²) — S  первого прямоугольника

теперь ширину второго прямоугольника

4 · 2 = 8 (см) — ширина другого прямоугольника

применив формулу S : a = b узнаем длину другого

128 : 8 = 16 (см)

Ответ: длина другого прямоугольника 16 см.

Задача №21

Какой участок земли потребует большую ограду: прямоугольный размерами 32 м и 2 м или квадратный, имеющий ту же площадь?

Решение:

Ⅰ. Прямоугольный участок

32 · 2 = 64 (м²) — S прямоугольного участка = 64 (м²)  

(32 + 2) · 2 = 68 (см) — P прямоугольного участка = 68 (см)

Ⅱ. Квадратный участок (имеющий площадь прямоугольного = 64 м²) 

Если  S квадрата = a · a,  тогда, из формулы, узнаем сторону квадратного участка S : a = a

(у квадрата все стороны равны, тогда a · a = S —  таблицу умножения мы знаем, подберём значения  a  и заменим их —  8 · 8 = S  или  8 · 8 = 64  или  64 = 8 · 8   или  64 : 8 = 8) 

64 : 8 = 8 (м) — любая сторона квадратного участка = 8 (м)

8 · 4 = 32 (м) — периметр квадратного участка = 32 (м) 

Ⅲ. P прям. – P квадр. = разница периметров

68 – 32 = 36 (м) — разница периметров

Ответ: потребует большую ограду прямоугольный на 36 м.

Задача №22

Какая комната потребует больше плинтуса: прямоугольная размерами 4 м и 9 м или квадратная, имеющая ту же площадь?

Решение:

(4 + 9) · 2 = 26 (м) — P периметр прямоугольной комнаты

4 · 9 = 36 (м²) — S площадь прямоугольной комнаты

(из условия задачи квадратная комната имеет ту же площадь 36 м², а из определения площади квадрата знаем, что все стороны равны a = a = a = a, смотрим таблицу умножения и видим 6 · 6 = 36, то есть любая из сторон a = 6

запишем (приведём) формулу площади квадрата S = a · a в форму нахождения её стороны S : a = a

36 : 6 = 6 (м) — любая из сторон квадратной комнаты

6 · 4 = 24 (м) — P периметр квадратной комнаты

26 – 24 = 2 (м)

Ответ: потребует больше плинтуса прямоугольная на 2 м.

Задача №23

Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.

Решение:

Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.

У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).

Если S = a · a — площадь квадрата, тогда

S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6

2 · 2 · 6 = 24 (см²)

Ответ: площадь всех граней куба равна 24 см².

Задача №24

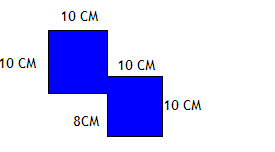
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Решение:

Для решения потребуются формулы:

S = a · a; S = a² — площадь квадрата (у квадрата все стороны равны)

S = a · b — площадь прямоугольника (у прямоугольника противоположные стороны равны)

Далее всё очень просто:

Квадрат A.

S = a · a или a · a = S — формула площади квадрата, тогда

8 · 8 = 64 — площадь квадрата

S = a · a или a · b = S — формула площади прямоугольника, тогда

4 · 1 = 4 — площадь вырезанного прямоугольника

из площади квадрата вычтем площадь вырезанного прямоугольника

64 – 4 = 60

Ответ: площадь получившейся фигуры равна 60.

Квадрат B.

S = a · a или a · a = S — формула площади квадрата, тогда

7 · 7 = 49 — площадь квадрата

S = a · a или a · b = S — формула площади прямоугольника, тогда

4 · 2 = 8 — площадь вырезанного прямоугольника

из площади квадрата вычтем площадь прямоугольника

49 – 8 = 41

Ответ: площадь получившейся фигуры равна 41.

Квадрат C.

S = a · a или a · a = S — формула площади квадрата, тогда

7 · 7 = 49 — площадь квадрата

S = a · a или a · b = S — формула площади прямоугольника, тогда

5 · 1 = 5 — площадь вырезанного прямоугольника

из площади квадрата вычтем площадь прямоугольника

49 – 5 = 44

Ответ: площадь получившейся фигуры равна 44.

Задача №25

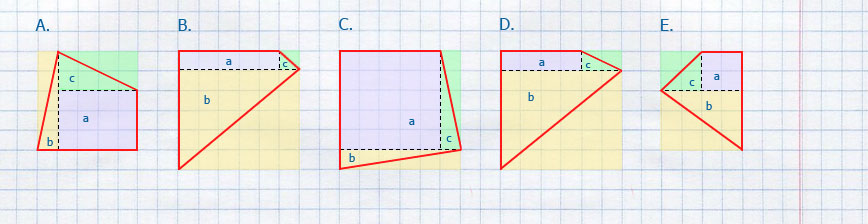
1. Найдите площадь фигуры, изображённой на рисунке A.
2. Найдите площадь фигуры, изображённой на рисунке B.
3. Найдите площадь фигуры, изображённой на рисунке C.
4. Найдите площадь фигуры, изображённой на рисунке D.
5. Найдите площадь фигуры, изображённой на рисунке E.

(!) Фигуры расположены на листе в клетку, где каждая клетка – квадрат со стороной равной 1см.

Определение:

Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.

Решение:

разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.

Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу

Фигура A.

S = a · b — формула площади прямоугольника, тогда

3 · 4 = 12 см² — площадь прямоугольника a

S = ½ · a · h — формула площади треугольника, тогда

½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b

S = ½ · a · h — формула площади треугольника

½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c

теперь сложив полученные площади узнаем полную площадь фигуры A

12 + 2,5 + 4 = 18,5 см²

Ответ: площадь фигуры A 18,5 см²

Фигура B.

S = a · b — формула площади прямоугольника, тогда 

5 · 1 = 5 см² — площадь прямоугольника a

S = ½ · a · h — формула площади треугольника, тогда

½ · 6 · 5 = 15 см² — площадь прямоугольного треугольника b

S = ½ · a · h — формула площади треугольника, тогда

½ · 1 · 1 = 0,5 см² — площадь прямоугольного треугольника c

теперь сложив полученные площади узнаем полную площадь фигуры B 

5 + 15 + 0,5 = 18,5 см²

Ответ: площадь фигуры B 20,5 см²

Фигура C.

S = a · a; S = a² — формула площади квадрата, тогда

5 · 5 = 25 см² — площадь квадрата a

S = ½ · a · h — формула площади треугольника, тогда

½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b

S = ½ · a · h — формула площади треугольника, тогда

½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c

теперь сложив полученные площади узнаем полную площадь фигуры C

25 + 3 + 2,5 = 30,5 см²

Ответ: площадь фигуры C 30,5 см²

Фигура D.

S = a · b — формула площади прямоугольника, тогда

3 · 4 = 12 см² — площадь прямоугольника a

S = ½ · a · h — формула площади треугольника, тогда

½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b

S = ½ · a · h — формула площади треугольника, тогда

½ · 2 · 4 = 4 см² — площадь прямоугольного треугольника c

теперь сложив полученные площади узнаем полную площадь фигуры D

12 + 2,5 + 4 = 18,5 см²

Ответ: площадь фигуры A 18,5 см²

Фигура E.

S = a · a; S = a² — формула площади квадрата, тогда

2 · 2 = 4 см² — площадь квадрата a

S = ½ · a · h — формула площади треугольника, тогда

½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b

S = ½ · a · h — формула площади треугольника, тогда

½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c

теперь сложив полученные площади узнаем полную площадь фигуры E

4 + 6 + 2 = 12 см²

Ответ: площадь фигуры E 12 см².

Задача №26

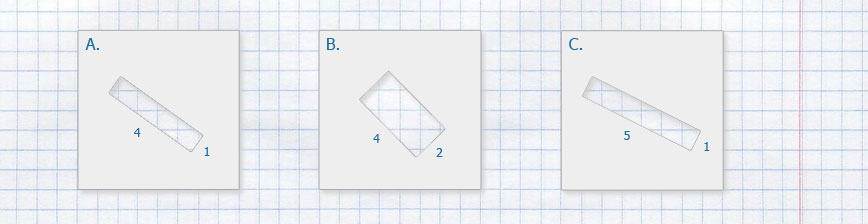
Найдите площади и периметры фигурок. Сделайте вывод.

Определение:

Периметр – сумма длин всех сторон фигуры выраженый в милиметрах, сантиметрах, дециметрах, метрах и т.д.

Площадь фигуры – геометрическое понятие, размер плоской фигуры выраженый в мм², см², дм², м² и т.д.

Пусть каждая из сторон клетки равна 1 см, тогда

применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²

Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда

1 · 4 = 4 см² — площадь фигуры;

фигура A имеет четыре стороны, тогда

1 + 4 + 1 + 4 = 10 см — периметр фигуры.

Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда

1 · 4 = 4 см² — площадь фигуры;

фигура B имеет четыре стороны, тогда

2 + 2 + 2 + 2 = 8 см — периметр фигуры.

Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда

1 · 4 = 4 см² — площадь фигуры;

фигура C имеет шесть сторон, тогда

3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда

1 · 4 = 4 см² — площадь фигуры;

фигура D имеет восемь сторон, тогда

1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда

1 · 4 = 4 см² — площадь фигуры;

фигура E имеет восемь сторон, тогда

1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.

Вывод:

Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат.

У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.

Задача №27

Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см

Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²

Решение:

6² + 8² = c²

6 · 6 + 8 · 8 = c²

36 + 64 = с²

с² = 36+64

с² = 100

с = 10

Найдём периметр прямоугольного треугольника по формуле: p = a + b + c

p = 6 + 8 + 10 = 24

Ответ: периметр прямоугольника равен 24 см.

см. Площадь треугольника

Задача №28

Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (гипотенуза) с = 10 см

Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²

Решение:

6² + b² = 10²

6 · 6 + b² = 10 · 10

36 + b² = 100

b² = 100 – 36

с² = 64

с = 8

Найдём периметр прямоугольного треугольника по формуле: p = a + b + c

p = 6 + 8 + 10 = 24

Ответ: периметр прямоугольника равен 24 см.

см. Площадь треугольника

Задача №29

В треугольной пластине abc у которой один из углов 90°, сторона a равна 20 сантиметрам, а сторона b равна 10 сантиметрам просверлили отверстие диаметром 3 сантиметра. Какую оставшуюся площадь пластины нужно покрасить?

Решение:

Мы знаем что площадь – S треугольника равна половине – ½ произведения его основания – a умноженная на высоту – h,
то есть S = ½ · a · h, а Формула площади круга S = πd² : 4, число π ≈ 3,14.

1) По условию задачи пластина имеет форму прямоугольника со сторонами abc, в данном случае сторона b является высотой треугольника.

Тогда формула будет выглядеть так – S = ½ · a · b

подставим значения в эту формулу

½ · 10 · 20 = 100 (см²) — площадь треугольника

2) Подставим значения в формулу и узнаем площадь круга S = πd² : 4

3,14 · 3² : 4  =  3,14 · 9 : 4 = 7,065 (см²)

3) Теперь мы можем ответить на вопрос поставленный в задаче

100 – 7,065 = 92,935 см² — оставшуюся площадь пластины

Ответ: нужно покрасить 92,935 см².

Задача №30

На садовом участке Петя построил для цыплят круглый вольер радиусом 5 метров. Участок имеет прямоугольную форму с длинной 120 метров и шириной равной 8 диаметрам вольера. Сколько потребуется метров металлической сетки чтобы огородить участок и вольер?

Решение:

Для решения задачи нам потребуются вычислить периметры участка и вольера.

1) В первом действии узнаем диаметр вольера, нам известен радиус 5 метров, тогда по формуле диаметр равен двум радиусам D = 2R

5 · 2 = 10 (м) — диаметр вольера

2) Если ширина участка равна 8 диаметрам вольера, тогда

10 · 8 = 80 м — ширина участка

3) Далее по формуле P = (a + b) · 2 — периметр прямоугольника

120 + 80 · 2 = 400 (м)

4) Теперь по формуле P = 2πR — длина окружности (периметр) вольера

2 · 3,14 · 5  =  2 · 3,14 · 5 = 31,4 (м)

5) В последнем действии сложим периметры участка и вольера ответим на вопрос задачи

400 + 31,4 = 431,4 (м)

Ответ: потребуется 431,4 метров металлической сетки.

Рене Декарт

математик, философ

Дата рождения: 31 марта 1596 г.

Место рождения: Декарт, Турень, Абсолютная монархия во Франции

Дата смерти: 11 февраля 1650 г. (53 года), Стокгольм, Швеция

Биография

Родился 31 марта 1596 года в городе Ла-Э-ан-Турен (ныне Декарт), департамент Эндр и Луара, Франция. Декарт происходил из старинного, но обедневшего дворянского рода, был младшим (третьим) сыном в семье. Начальное образование Декарт получил в иезуитском колле́же Ла Флеш, где его учителем был Жан Франсуа.

В коллеже Декарт познакомился с Мареном Мерсенном (тогда — учеником, позже — священником), будущим координатором научной жизни Франции, и Жаком Валле де Барро. Религиозное образование только укрепило в молодом Декарте скептическое отношение к тогдашним философским авторитетам. Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.

В 1612 году Декарт закончил коллеж, некоторое время изучал право в Пуатье, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем он поступил на военную службу (1617) — сначала в революционной Голландии (в те годы — союзнице Франции), затем в Германии, где участвовал в недолгой битве за Прагу (Тридцатилетняя война).

В Голландии в 1618 году Декарт познакомился с выдающимся физиком и натурфилософом Исааком Бекманом, оказавшим значительное влияние на его формирование как учёного. Несколько лет Декарт провёл в Париже, предаваясь научной работе, где, помимо прочего, открыл принцип виртуальных скоростей, который в то время никто ещё не был готов оценить по достоинству.

Затем — ещё несколько лет участия в войне (осада Ла-Рошели). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.

В 1634 году он заканчивает свою первую, программную книгу под названием «Мир» (Le Monde), состоящую из двух частей: «Трактат о свете» и «Трактат о человеке». Вскоре, однако, одна за другой, появляются другие книги Декарта.

Кардинал Ришельё благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции. Протестантские же богословы Голландии наложили на них проклятие (1642)

В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины (с которой много лет активно переписывался) и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер.

Его труды:

• Сформулировал (хотя и не доказал) основную теорему алгебры
• Методы решения алгебраических уравнений
• Классификация алгебраических кривых
• Сформулировал точное «правило знаков» для определения числа положительных корней уравнения
• Исследовал алгебраические функции (многочлены)
• Исследования Декарта в области к механики, оптики и общему строению Вселенной
• Математически вывел закон преломления света
• Понятие о рефлексе
• Классическое построение философии рационализма
• Теория близкодействия
• Метод радикального сомнения
• Картезианский дуализм

В память о Декарте:

• Великий физиолог И. П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
• В честь учёного названы его родной город
• Назван кратер на Луне
• Назван астероид (3587) Descartes
• Декартова система координат
• Декартов лист
• Декартов овал
• Декартово дерево
• Декартово произведение

***

Цитата: У одного человека зачастую больше шансов сделать открытие, нежели у нескольких, занимающихся одной проблемой.

ПЕРИМЕТР

Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.

Чаще всего периметр обозначается буквой P.

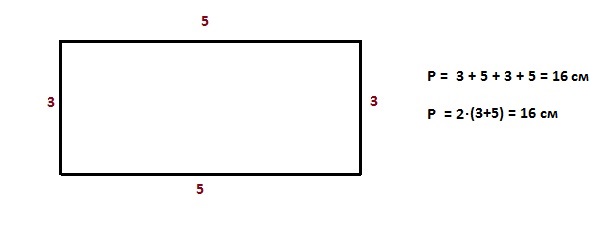
Периметр прямоугольника – удвоенная сумма длины и высоты – 2∙(a+b)

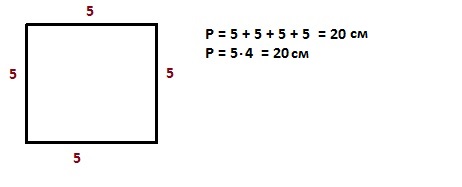
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.

ПЛОЩАДЬ

Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.

В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.

Чаще всего площадь обозначается буквой S.

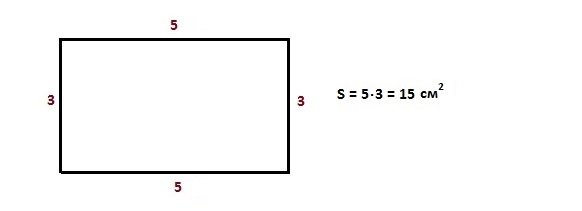
Площадь прямоугольника – произведение длины на высоту.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

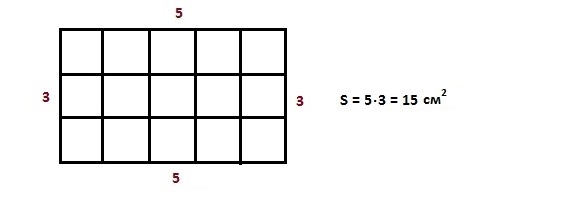
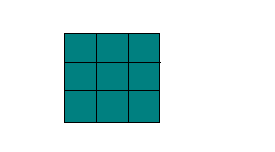
Разделим этот прямоугольник на квадраты

Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.

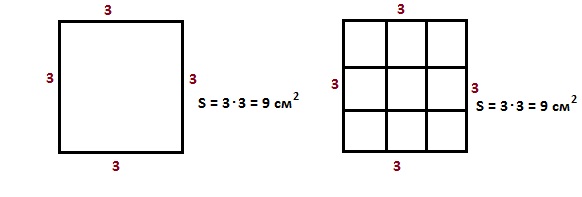
Площадь квадрата – произведение длины стороны на саму себя.

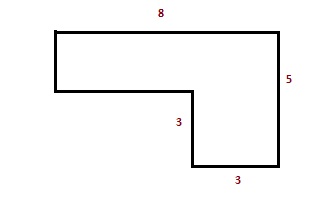
СОСТАВНЫЕ ФИГУРЫ

Разделим эту фигуру на прямоугольник и квадрат

Высота прямоугольника составит 5 – 3 = 2

СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА

Фигуры с одной и той же площадью могут иметь разный периметр

Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?

Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.

Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.

ОБЪЁМ

Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.

1 л = 1 дм³

Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.

Чаще всего объём обозначается буквой V.

Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.

Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты

Зная объём и две стороны, мы можем найти третью сторону:

c = (V:a):b = V:S

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

ЗАДАЧИ

Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.

x = 10 см – ширина

1. Найдём длину

y = 10 + 6 = 16 см

2. Найдём периметр

P = 2∙(10+16) = 52 см

3. Найдём площадь

S = 10∙16 = 160 см²

Ответ: P = 52 см, S = 160 см²

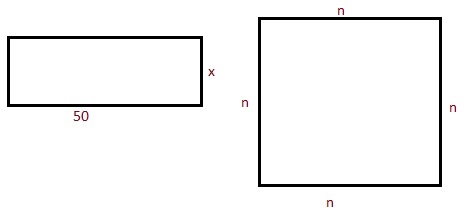
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?

1. Вычислим сторону квадрата

4∙n = 80 – периметр

n = 20 см

2. Вычислим площадь квадрата

20∙20 = 400 см²

3. Вычислим ширину прямоугольника

50∙x = 400 см²

x = 8 см

Ответ: 8 см

Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?

1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм

1. Переведём длину прямоугольника в дм

x = 15∙10 = 150 дм

2. Найдём ширину прямоугольника

150∙y = 7500

y = 7500:150 = 50 дм

Ответ: 50 дм

Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.

1. Найдите площадь этого прямоугольника.

2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.

3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.

1. Найдём ширину прямоугольника

x = 60:3 = 20 см

2. Найдём площадь прямоугольника

S = 60∙20 = 1200 см

2. Найдём периметр прямоугольника

P = 2∙(60+20) = 160 см

3. Найдём сторону квадрата

y = 160:4 = 40 см

4. Найдём площадь квадрата

Sкв = 40∙40 = 1600 см²

5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:

Sкв₂ = 1200:12 = 100 см²

6. Найдём сторону такого квадрата

Площадь квадрата = 100 см²

Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см

7. Найдём периметр такого квадрата

P = 10∙4 = 40 см

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

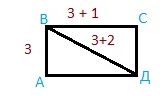
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.

1. Найдём сторону ВС

ВС = 3+1 = 4

2. Найдём диагональ ВД

ВД = 3+2 = 5

3. Найдём периметр АВСД

P = 2∙(3+4) = 14 см

4. Найдём площадь АВСД

Sавсд = 3∙4 = 12 см²

5. Найдём периметр треугольника АВД

Pавд = 3 + 5 + 4 = 13 см

6. Найдём площадь треугольника АВД

Треугольник АВД занимает половину площади прямоугольника АВСД

Sавд = Sавсд:2

Sавд = 12:2 = 6 см²

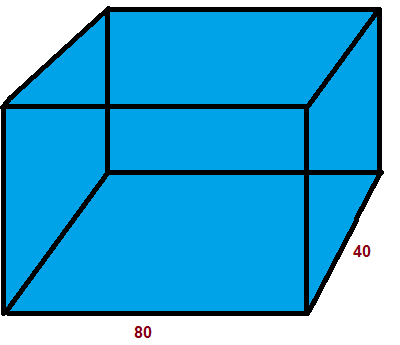
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?

Решение

1. Переведём литры в кубические дециметры

1 л = 1 дм³, 160 л = 160 дм³

2. Переведём стороны аквариума в дециметры

1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм

3. Найдём высоту аквариума

V = a∙b∙c, a = 8, b = 4

c = (V:a):b

c = (160:8):4 = 5 дм

c = 5∙10 = 50 см

Ответ: 50 см

Примеры решения задач разной сложности на нахождение периметра и площади

Задача 1

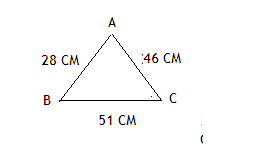
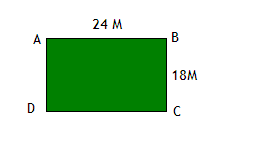
Каков периметр треугольника ABC?

Ответ: периметр треугольника равен 125 см.

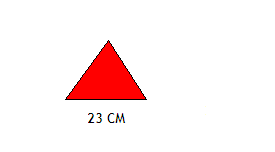
Задача 2

Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?

Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.

Задача 3

Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?

Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 – 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.

Задача 4

У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?

Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.

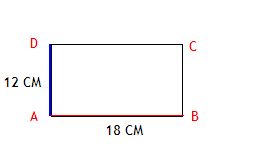
Задача 5

В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?

Ответ: Периметр прямоугольника равен 60 см.

Задача 6

Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?

Ответ: Площадь прямоугольника 56 м².

Задача 7

Площадь витрины квадратной формы 64м². Узнай ее периметр.

Ответ: Периметр витрины равен 32 м.

Задача 8

Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.

Ответ: Площадь прямоугольника равна 630 см².

Задача 9

Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?

Ответ: 42 дерева.

Задача 10

Каков периметр синей фигуры?

Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.

Задача 11

Два прямоугольных участка имеют одинаковую площадь. Длина первого – 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?

Ответ: Длина второго участка 40 м.

Задача 12

Найди периметр квадрата со стороной 8 см.


Ответ: Периметр квадрата 32 см.

Задача 13

Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.

Решение:

6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)

Ответ: Длина прямоугольника 9 см.

Задача 14

Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.

Решение:

120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)

Ответ: Периметр бассейна 46 метров

Задача 15

Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.

Решение:

8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)

Ответ: Периметр прямоугольника 16 см.

Задача 16

Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?

Решение:

5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)

Ответ: Ученик ошибся на 3 см²

Задача 17

Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.

Решение:

4·2=8 (дм) -длина окна
8·4=32 (дм²)

Ответ: Площадь окна 32 дм²

Задача 18

Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.

Ответ: Ширина другого участка 24 м.

Задача 19

У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?

Ответ: Площадь квадрата больше на 4 см.

Задача 20

Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.

Задача 21

У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.

Задача 22

Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?

Решение:

1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36

Ответ: Незабудками засажено 36 м².

Задача 23

Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?

Решение:

1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18

Ответ: Площадь прямоугольника 18 м².

Задача 24

Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?

Решение:

1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см

Ответ: Периметр стола 280 см.

Задача 25

Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?

Решение:

1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75

Ответ: Площадь прямоугольника 75 см².

Задача 26

Площадь квадрата 49 кВ дм. Узнайте его периметр.

Решение:

1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)

Ответ: Периметр квадрата равен 28 дм.

Задача 27

Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

Решение:

1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32

Ответ: Площадь окна равна 32 м².

Задача 28

Длина участка земли 54 м. ширина – 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?

Решение:

1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152

Ответ: Капустой засадили 1152 м².

Задача 29

Найди периметр квадрата со стороной 16 см.

Ответ: Периметр квадрата 64 см.

Задача 30

Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.

Решение:

P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,

где a —  длина = ?, b —  ширина = 7 см, P —  периметр = 40 см.

Составим уравнение:

(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 – 14
2а = 26
а = 26 : 2
а = 13

Ответ: Длина прямоугольника 13 см.

Задача 31

Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.

Ответ: Ширина прямоугольника 5 см.

Задача 32

Периметр квадрата 24 см. Найди его площадь.

Решение:

24 : 4 = 6 (см)
6 · 6 = 36 (см²)

Ответ: Площадь квадрата 36 см².

Задача 33

Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.

Ответ: Площадь прямоугольника 56 см².

Задача 34

Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?

Решение:

40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)

Ответ: Периметр прямоугольника 28 см.

Задача 35

Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.

Решение:

Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.

У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).

Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)

Ответ: Площадь всех граней куба равна 24 см².

Задача 36

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Ответ: Площадь получившейся фигуры равна 44.

Задача 37

Площадь одной клетки равна 1см.

• Найдите площадь фигуры, изображённой на рисунке A.
• Найдите площадь фигуры, изображённой на рисунке B.
• Найдите площадь фигуры, изображённой на рисунке C.
• Найдите площадь фигуры, изображённой на рисунке D.
• Найдите площадь фигуры, изображённой на рисунке E.

Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².

Задача 38

Найдите площади и периметры фигурок. Сделайте вывод.

Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²

Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.

Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.

Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.

Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат. 

Задача 39

Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник – периметр 15 см. Каков периметр красной фигуры?

Ответ: Периметр красной фигуры равен 27 см.

Задача 40

Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?

Ответ: Периметр равен 36 см.

Задача 41

Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?

Ответ: Длина прямоугольника равна 12 см. а ширина – 6 см.

Задача 42

Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.

Ответ: Периметр прямоугольника равен 24 см.

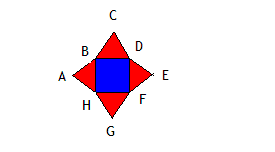
Задача 43

Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?

Ответ: Расстояние пройденное улиткой будет равно 28 см.

Задача 44

В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?

Ответ: 2400 плиток.

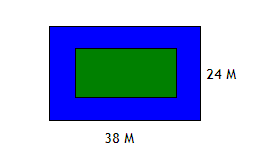
Задача 45

Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?

Ответ: Периметр зеленой зоны равен 100 метров.