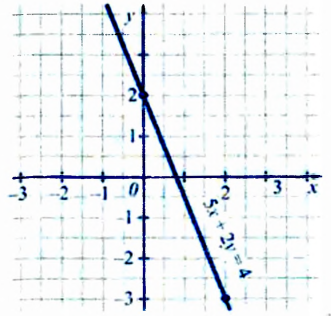
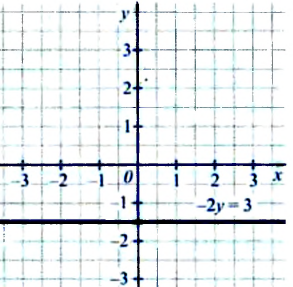
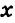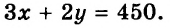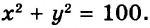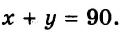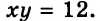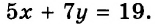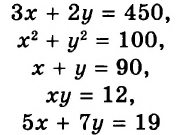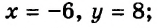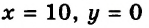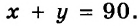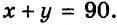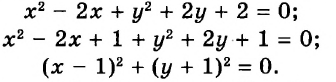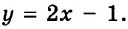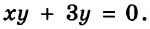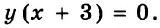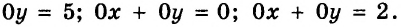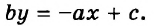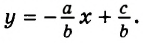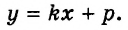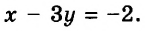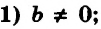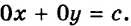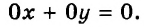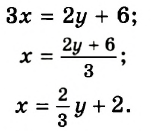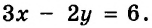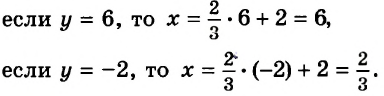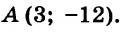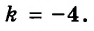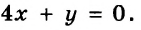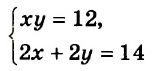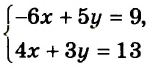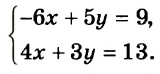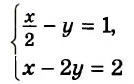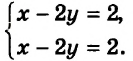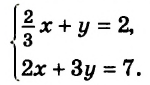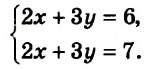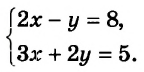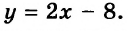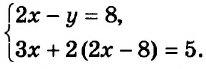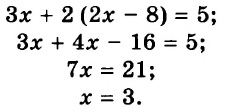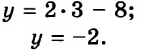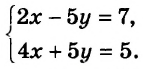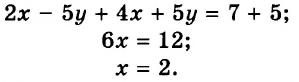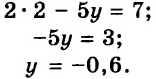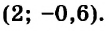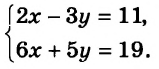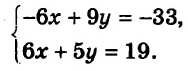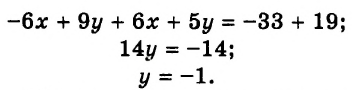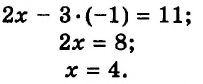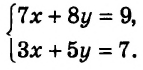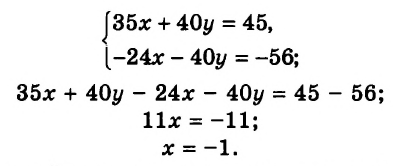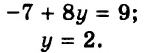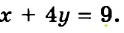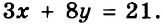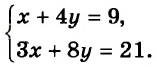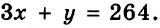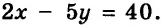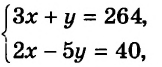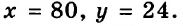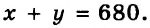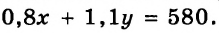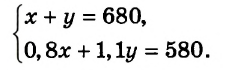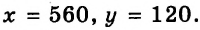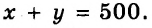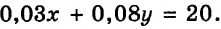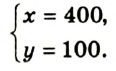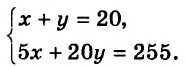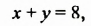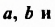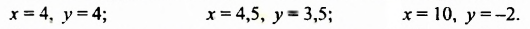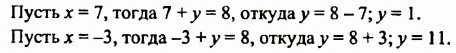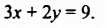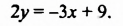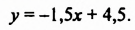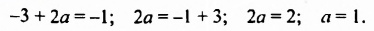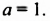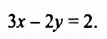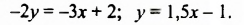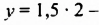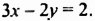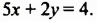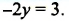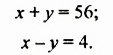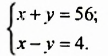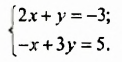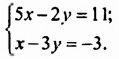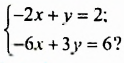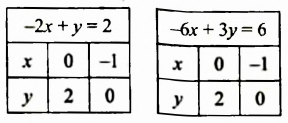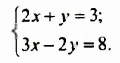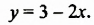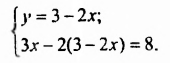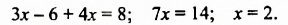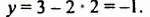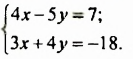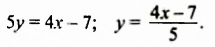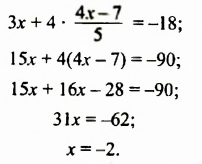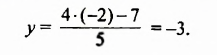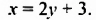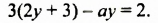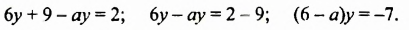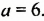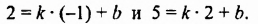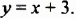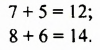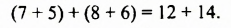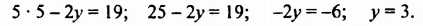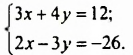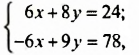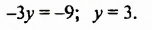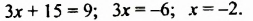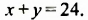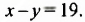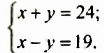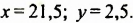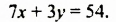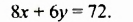Содержание:
Системы линейных уравнений с двумя переменными
- В этом параграфе вы познакомитесь с уравнениями с двумя переменными и их системами. Изучите некоторые методы их решения.
- Вы узнаете, что уравнение с двумя переменными может служить математической моделью реальной ситуации.
- Овладеете новым эффективным методом решения текстовых задач.
Уравнения с двумя переменными
Рассмотрим несколько примеров реальных ситуаций.
Пример:
Расстояние между Киевом и Харьковом равно 450 км. Из Киева в Харьков со скоростью
Построим математическую модель этой ситуации.
Путь, пройденный вторым автомобилем до встречи, равен 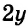
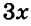
Имеем:
Это равенство с двумя переменными является математической моделью вышеописанной реальной ситуации.
Рассмотрим еще несколько примеров ситуаций, математическими моделями которых служат равенства с двумя переменными.
Пример:
Площадь квадрата со стороной 10 см равна сумме площадей двух других квадратов.
Если длины сторон этих квадратов обозначить 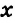
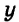
Пример:
Дан прямоугольный треугольник.
Если градусные меры его острых углов обозначить 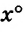
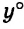
Пример:
Дан прямоугольник, площадь которого равна 12 см2. Обозначим длины его сторон 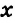
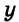
Пример:
Купили 5 ручек и 7 тетрадей. За всю покупку заплатили 19 руб.
Если одна ручка стоит 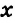
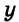
Как видим, все полученные в примерах 1-5 равенства
содержат по две переменные 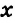
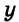
Если, например, в уравнение 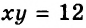
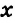
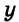
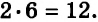
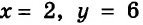
Определение. Пару значений переменных, обращающую уравнение в верное равенство, называют решением уравнения с двумя переменными.
Так, для уравнения 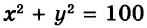
является его решением, а, например, пара 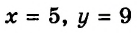
Обратим внимание на то, что данное определение похоже на определение корня уравнения с одной переменной. В связи с этим распространена ошибка: называть каждое число пары или саму пару, являющуюся решением, корнем уравнения с двумя переменными.
Тот факт, что пара 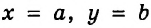
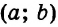
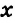
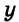
Используя такое обозначение, можно, например, записать, что каждая из пар чисел 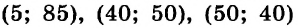
Три указанные пары далеко не исчерпывают все решения этого уравнения. Если вместо переменной 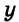
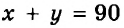
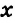
Уравнение с двумя переменными не обязательно имеет бесконечно много решений. Например, уравнение 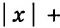
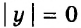
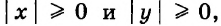
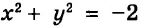
Заметим, что мы решили каждое из уравнений 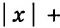
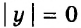
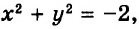
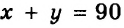
Решить уравнение с двумя переменными — это значит найти все его решения или показать, что оно не имеет решений.
Свойства уравнений с двумя переменными запомнить легко: они аналогичны свойствам уравнений с одной переменной, которые вы изучали в б классе.
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же решения, что и данное.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же решения, что и данное.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же решения, что и данное.
Рассмотрим уравнение 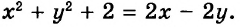
Поскольку 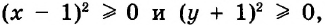
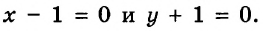
Изучая какой-то объект, мы стремимся не только описать его свойства, но и составить о нем наглядное представление. График функции — характерный тому пример. Поскольку решением уравнения с двумя переменными является пара чисел, например 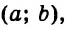
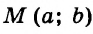
Определение. Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Например, графиком уравнения 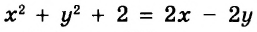
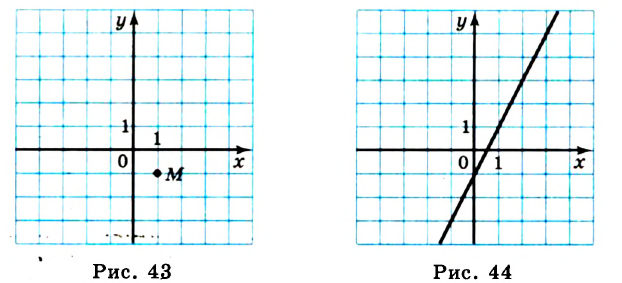
На рисунке 44 изображен график функции 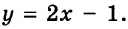
Подчеркнем, что если какая-то фигура является графиком уравнения, то выполняются два условия:
1) все решения уравнения являются координатами точек, принадлежащих графику;
2) координаты любой точки, принадлежащей графику, — это пара чисел, которая является решением данного уравнения.
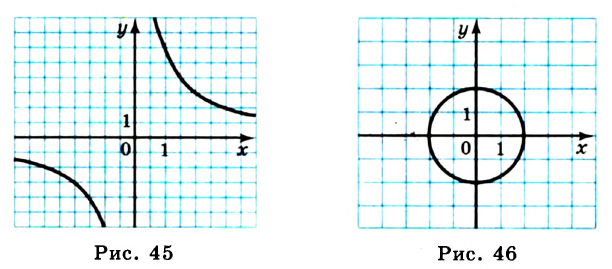
Семейства графиков уравнений очень разнообразны. Изучая курс алгебры, вы будете знакомиться с их представителями. Например, в 8 классе вы узнаете, что графиком рассмотренного в начале пункта уравнения 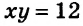
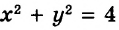
Пример:
Постройте график уравнения
Запишем данное уравнение в виде
Следовательно, решениями данного уравнение являются все пары чисел вида 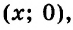
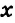
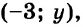
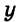
Все точки, координаты которых имеют вид 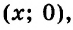
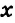
Все точки, координаты которых имеют вид 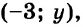
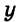
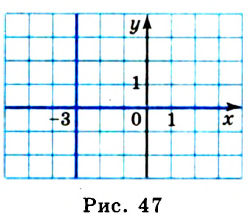
Следовательно, графиком данного уравнения является пара прямых, изображенных на рисунке 47.
Линейное уравнение с двумя переменными и его график
Определение. Линейным уравнением с двумя переменными называют уравнение вида 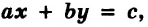
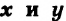
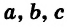
Уравнения 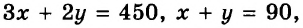
Выясним, какая фигура является графиком линейного уравнения. Для этого рассмотрим три случая.
СЛУЧАЙ 1
Рассмотрим линейное уравнение 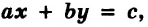
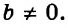
Поскольку 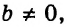
Введем обозначения: 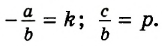
Мы получили формулу, задающую линейную функцию. Следовательно, графиком уравнения 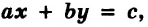
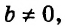
Пример:
Постройте график уравнения
Решение:
Мы уже знаем, что графиком этого уравнения является прямая. Поэтому достаточно определить координаты двух любых ее точек. Имеем: если 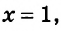
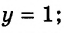
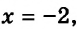
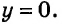
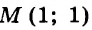
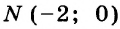
Эта прямая и является искомым графиком.
СЛУЧАЙ 2
Пусть есть линейное уравнение 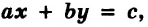
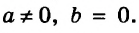
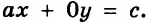
Пример:
Постройте график уравнения
Решение:
Легко найти несколько решений этого уравнения. Вот, например, четыре его решения: 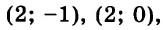
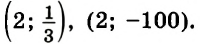
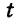
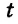
При этом координаты любой точки этой прямой — пара чисел, являющаяся решением данного уравнения. А значит, указанная прямая и является искомым графиком.
Рассуждая аналогично, можно показать, что графиком уравнения 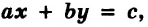
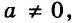
Теперь можно сделать такой вывод: в каждом из двух случаев: 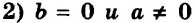
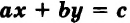
Часто, например, вместо предложения «дано уравнение 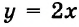
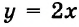
СЛУЧАЙ 3
Пусть 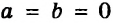
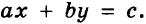
Если 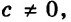
Если 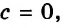
Любая пара чисел является его решением. Значит, в этом случае график уравнения — вся координатная плоскость. Следующая таблица подытоживает материал, рассмотренный в этом пункте.
Пример:
Выразите из уравнения 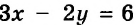
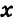
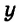
Решение:
Имеем:
Придавая переменной 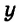
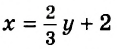
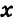
Например,
Пример:
Постройте график уравнения
Решение:
Запишем данное уравнение в виде 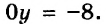
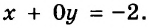
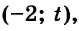
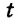
Пример:
Составьте линейное уравнение с двумя переменными, графиком которого является прямая, проходящая через начало координат и точку
Решение:
Так как график искомого уравнения проходит через точки 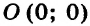
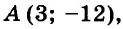
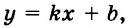
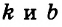
Из того, что график проходит через начало координат, следует, что 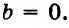
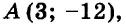
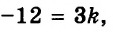
Значит, искомое уравнение имеет вид 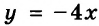
Ответ:
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь уже в древности люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения местоположения объектов на поверхности Земли.
Лишь в XIV в. французский ученый Никола Орем (около 1323—1392) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбит ваш тетрадный листок) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты только в XVII в. в работах выдающихся французских математиков Пьера Ферма (1601 — 1665) и Рене Декарта (1596— 1650). В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то, что П. Ферма опубликовал свое сочинение годом раньше, чем Р. Декарт, ту систему координат, которой мы сегодня пользуемся, называют декартовой. Это связано с тем, что Р. Декарт в своей работе «Рассуждения о методе» изобрел новую удобную буквенную символику, которой с небольшими изменениями мы пользуемся и сегодня. Вслед за ним мы обозначаем переменные последними буквами латинского алфавита 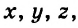
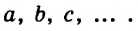
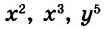
Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными
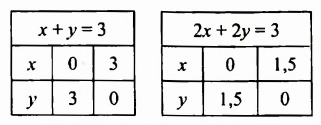
Легко проверить, что пара чисел 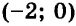
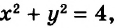
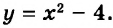
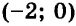
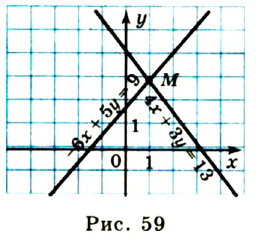
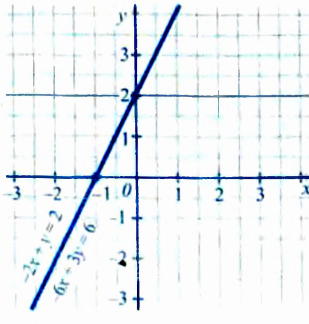
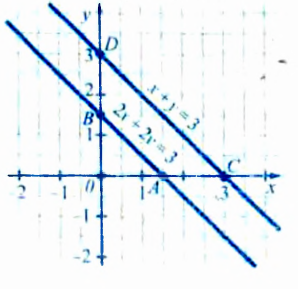
На рисунке 59 изображены графики уравнений 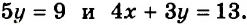
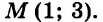
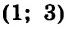
Если поставлена задача найти стороны прямоугольника, площадь которого равна 12 см2, а периметр 14 см, то понятно, что надо найти общее решение уравнений 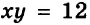
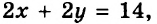
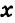
Если требуется найти все общие решения нескольких уравнений, то говорят, что нужно решить систему уравнений.
Систему уравнений записывают с помощью фигурной скобки.
Так, запись
является математической моделью задачи о поиске сторон прямоугольника, площадь которого равна 12 см2, а периметр 14 см.
Система
— это математическая модель задачи о поиске координат общих точек двух прямых (рис. 59).
Оба уравнения этой системы являются линейными. Поэтому эту систему называют системой двух линейных уравнений с двумя переменными.
Определение. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение в верное равенство.
Из примера, приведенного в начале пункта, следует, что пара чисел 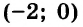
Однако это совершенно не означает, что данная система решена.
Определение. Решить систему уравнений — значит найти все ее решения или доказать, что решений нет.
Пара чисел 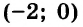
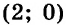
мы можем решить уже сейчас. Очевидно, что первое уравнение этой системы решений не имеет, а значит, не существует и общего решения уравнений, входящих в систему. Отсюда следует вывод: система решений не имеет.
Также можно считать решенной систему
Действительно, графики уравнений системы пересекаются в точке 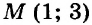
Описанный метод решения системы уравнений называют графическим. Его суть состоит в следующем:
Графический метод эффективен в тех случаях, когда требуется определить количество решений системы. Например, на рисунке 60 изображены графики некоторых функций 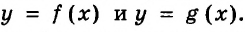
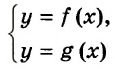
Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение;
- если прямые совпадают, то система имеет бесконечно много решений;
- если прямые параллельны, то система решений не имеет. Случай, когда система имеет единственное решение, мы уже рассмотрели. Теперь обратимся к примерам, которые иллюстрируют две другие возможности.
Так, если в системе
обе части первого уравнения умножить на 2, то решения этого уравнения, а значит, и всей системы не изменятся.
Имеем:
Очевидно, что решения этой системы совпадают с решениями уравнения 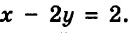
Действительно, умножим обе части первого уравнения системы на 3. Получим:
Понятно, что не существует такой пары значений 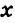
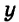
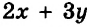
Подчеркнем, что именно графический метод нам подсказал, что не существует системы линейных уравнений, имеющей, например, ровно 2, или ровно 3, или ровно 100 и т. п. решений?
Решение систем линейных уравнений методом подстановки
Если математикам встречается новая задача, то, как правило, они пытаются ее решение свести к уже известной задаче.
Покажем, как решение системы линейных уравнений с двумя переменными можно свести к решению линейного уравнения с одной переменной. А последняя задача вам хорошо знакома.
Решим систему уравнений
Из первого уравнения выразим переменную 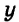
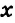
Подставим во второе уравнение системы вместо переменной 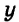
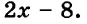
Эта и исходная системы имеют одни и те же решения. Примем здесь этот факт без обоснований. Вы можете рассмотреть доказательство этого факта на занятиях математического кружка.
Второе уравнение последней системы является уравнением с одной переменной. Решим его:
Подставим найденное значение переменной 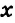
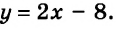
Пара чисел 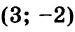
Описанный здесь способ решения системы называют методом подстановки.
Итак, чтобы решить систему линейных уравнений методом подстановки, нужно:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение другой переменной;
- записать ответ.
Эту последовательность действий, состоящую из шести шагов, можно назвать алгоритмом решения системы двух линейных уравнений с двумя переменными методом подстановки.
Решение систем линейных уравнений методом сложения
Рассмотрим еще один способ, позволяющий свести решение системы двух линейных уравнений с двумя переменными к решению линейного уравнения с одной переменной.
Решим систему уравнений
Поскольку в этой системе коэффициенты при переменной 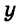
Подставим найденное значение переменной 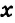
Итак, решением системы является пара чисел
Описанный способ решения системы называют методом сложения.
Этот метод, как и любой другой математический метод, нуждается в обосновании его законности. Примем без доказательства, что метод сложения дает верные результаты. Вы можете рассмотреть доказательство этого факта на занятии математического кружка.
Решим еще одну систему:
Если мы сложим почленно левые и правые части уравнений системы, то вновь получим уравнение с двумя переменными. Данная система еще «не готова» к применению метода сложения.
Умножим обе части первого уравнения на -3. Получим систему, решения которой совпадают с решениями исходной системы:
Для такой системы метод сложения уже является эффективным:
Подставим найденное значение 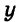
Пара чисел (4; -1) — искомое решение.
Рассмотрим систему, в которой сразу два уравнения нужно подготовить к применению метода сложения:
Чтобы исключить переменную 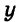
Подставив найденное значение 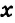
Следовательно, пара чисел (-1; 2) — решение данной системы.
Алгоритм решения системы уравнений методом сложения можно записать так:
- подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициенты при одной из переменных стали противоположными числами;
- сложить почленно левые и правые части уравнений, полученных на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение другой переменной;
- записать ответ.
Решение задач с помощью систем линейных уравнений
Рассмотрим задачи, в которых системы двух линейных уравнений с двумя переменными используют как математические модели реальных ситуаций.
Пример:
На пошив одного платья и 4 юбок пошло 9 м ткани, а на пошив 3 таких же платьев и 8 таких же юбок — 21 м ткани. Сколько ткани требуется для пошива одного платья и одной юбки отдельно?
Решение:
Пусть на одно платье идет 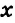
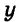
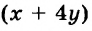
На 3 платья и 8 юбок требуется 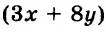
Имеем систему уравнений:
Решив эту систему, получаем: 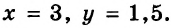
Пример:
Из города А в город В, расстояние между которыми 264 км, выехал мотоциклист. Через 2 ч после этого навстречу ему из города В выехал велосипедист, который встретился с мотоциклистом через 1 ч после своего выезда. Найдите скорость каждого из них, если за 2 ч мотоциклист проезжает на 40 км больше, чем велосипедист за 5 ч.
Решение:
Пусть скорость мотоциклиста равна 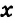
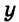
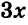
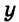
Велосипедист за 5 ч проезжает 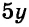
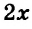
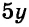
Получили систему уравнений:
решением которой является пара чисел
Следовательно, скорость мотоциклиста равна 80 км/ч, а велосипедиста — 24 км/ч.
Ответ: 80 км/ч, 24 км/ч.
Пример:
Стол и стул стоили вместе 680 руб. После того как стол подешевел на 20 %, а стул подорожал на 10 %, они стали стоить вместе 580 руб. Найдите первоначальную цену стола и первоначальную цену стула.
Решение:
Пусть первоначальная цена стола составляла 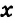
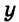
Новая цена стола составляет 80 % первоначальной и равна 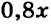
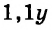
Получили систему уравнений:
Решением этой системы является пара
Следовательно, первоначальная цена стола была 560 руб., а стула — 120 руб.
Ответ: 560 руб., 120 руб.
Пример:
Сколько граммов 3 % -ного и сколько граммов 8 % -ного растворов соли надо взять, чтобы получить 500 г 4 %-ного раствора?
Решение:
Пусть первого раствора надо взять 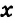
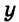
В 3 % -ном растворе содержится 0,03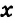
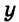
Составим систему уравнений:
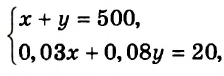
Значит, надо взять 400 г 3 %-ного раствора и 100 г 8 %-ного раствора.
Ответ: 400 г, 100 г.
Пример:
У Петра были купюры по 5 руб. и по 20 руб. Он говорит, что купил велосипед за 255 руб., отдав за него 20 купюр, а Василий говорит, что такого быть не может. Кто прав?
Решение:
Пусть было 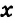
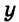
Решением этой системы является пара 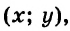
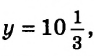
Ответ: прав Василий.
—7 класс
Системы линейных уравнений с двумя переменными
Существует немало задач, решая которые, получают уравнения, содержащие не одну, а несколько переменных.
В данном разделе мы выясним, что такое линейное уравнение с двумя переменными и его решение, что такое система двух линейных уравнений с двумя переменными и ее решение, каковы основные способы решения систем линейных уравнений с двумя переменными.
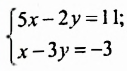
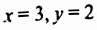
Уравнения с двумя переменными
Вы уже умеете решать линейные уравнения с одной переменной и уравнения, приводимые к линейным. Напомним, что линейное уравнение с одной переменной — это уравнение вида 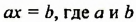

Рассмотрим пример, который приводит к уравнению с двумя переменными.
Пусть известно, что сумма некоторых двух чисел равна 8. Если одно из чисел обозначить через 
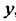
которое содержит две переменные: 
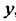
Уравнения
также являются уравнениями с двумя переменными. Первые два из этих уравнений являются уравнениями вида 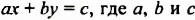
Определение:
Линейным уравнением с двумя переменными называют уравнение вида 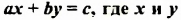
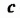
Решения уравнения с двумя переменными
Рассмотрим уравнение 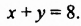
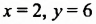
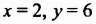
Определение:
Решением уравнения с двумя переменными называют пару значений переменных, при которых уравнение превращается в верное числовое равенство.
Решениями уравнения 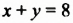
Сокращенно эти решения записывают так: (4; 4); (4,5; 3,5); (10;-2). В этих записях на первом месте пишут значение переменной 
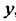

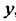
Чтобы найти решение уравнения с двумя переменными, можно подставить в уравнение любое значение одной переменной и, решив полученное уравнение с одной переменной, найти соответствующее значение другой переменной. Для примера найдем несколько решений уравнения
Мы нашли два решения (7; 1) и (-3; 11). Выбирая другие значения переменной 
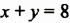
Искать решения уравнений с двумя переменными можно иным способом, который обусловливается свойствами уравнений.
Свойства уравнений с двумя переменными
Свойства уравнений с двумя переменными такие же, как и уравнений с одной переменной, а именно:
- В любой части уравнения можно выполнить тождественные преобразования выражений (раскрыть скобки, привести подобные слагаемые).
- Любое слагаемое можно перенести из одной части уравнения в другую, изменив его знак на противоположный.
- Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Рассмотрим уравнение
Используя свойства уравнений, выразим из этого уравнения одну переменную через другую, например, 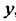

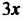
Разделим обе части полученного уравнения на 2:
Используя формулу 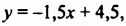

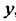

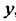
Пары чисел каждого столбика — решения уравнения
Примеры решения упражнений:
Пример №161
Найти все значения коэффициента 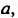
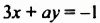
Решение:
Если пара чисел (-1; 2) является решением уравнения 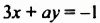
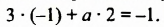
Ответ.
График линейного уравнения с двумя переменными
Рассмотрим уравнение
Решениями этого уравнения являются, например, пары чисел (0;-1) и (2; 2). Этим решениям на координатной плоскости соответствуют точки с координатами (0;-1) и (2; 2). Если на координатной плоскости отметим все точки, координаты которых являются решениями уравнения 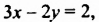
График уравнения с двумя переменными образуют все точки координатной плоскости, координаты которых являются решениями данного уравнения.
Чтобы выяснить, что является графиком уравнения 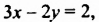
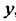

Формулой 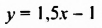
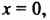
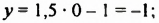
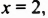
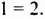
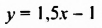
Вообще, графиком уравнения 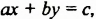
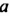
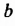
Чтобы построить график такого уравнения, можно: 1) выразить переменную 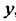

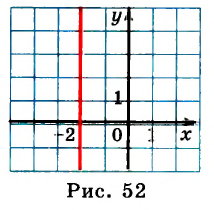
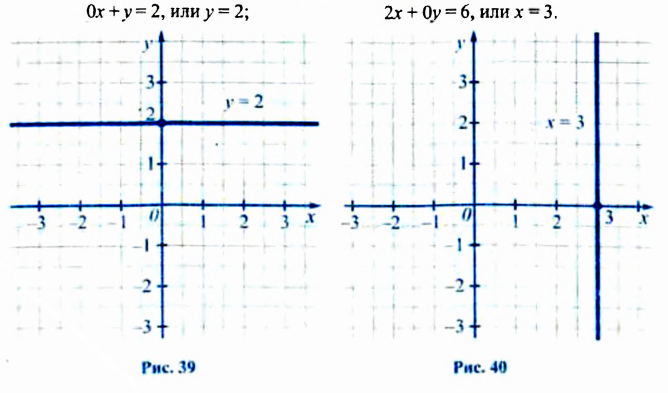
На рисунках 39 и 40 изображены графики линейных уравнений, в которых один из коэффициентов при переменных равен 0:
Графиком уравнения 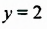
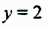

Решениями уравнения 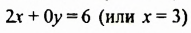
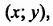
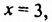
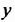
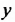
Для тех, кто хочет знать больше
Уравнение 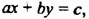
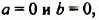
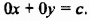
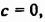
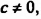
Примеры решения упражнений:
Пример №162
Построить график уравнения
Решение:
Сначала найдем два решения уравнения.
Пусть 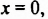
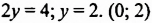
Пусть 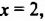
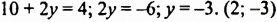
Решения уравнения можно представлять в виде таблицы.
На координатной плоскости отмечаем точки (0; 2) и (2; -3) и проводим через них прямую. Эта прямая является искомым графиком.
Пример №163
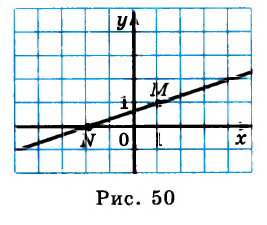
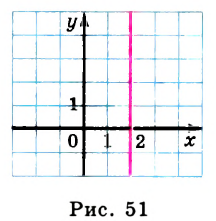
Построить график уравнения
Решение:
Данное уравнение содержит одну переменную 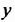

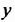

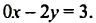
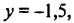

Системы линейных уравнений с двумя переменными и их решении
Рассмотрим задачу.
В 7-А и 7-Б классах вместе 56 учеников, причем в 7-А классе на 4 ученика больше, чем в 7-Б. Сколько учеников в каждом классе?
Для решения задачи обозначим количество учеников 7-А класса через 
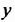
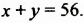
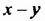
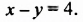
И в первом, и во втором уравнениях переменные обозначают одни и те же величины — количество учеников 7-А и 7-Б классов. Поэтому нужно найти такие значения переменных, которые обращают в верное числовое равенство и первое, и второе уравнения, то есть нужно найти общие решения этих уравнений.
Если нужно найти общие решения двух уравнений, то говорят, что эти уравнения образуют систему уравнений.
Систему уравнений записывают с помощью фигурной скобки. Систему линейных уравнений с двумя переменными, составленную по условию нашей задачи, записывают гак:
Общим решением обеих уравнений этой системы является пара значений переменных 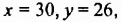
Определение
Решением системы двух уравнений с двумя переменными называют пару значений переменных, при которых каедое уравнение сисгемы превращается в верное числовое равенство.
Решить систему уравнений — значит найти все ее решения или доказать, что решений нет.
Решение систем линейных уравнений графическим способом
Решим систему уравнений
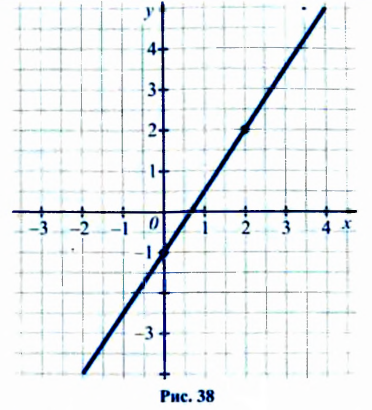
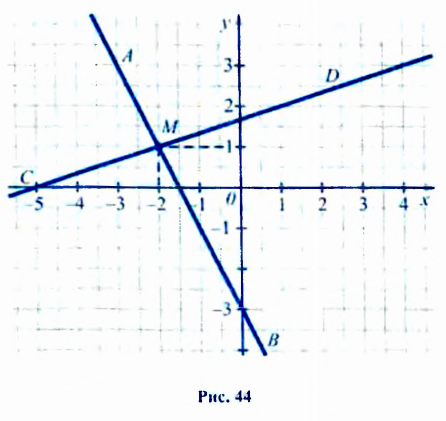
Построим в одной системе координат графики обоих уравнений системы. На рисунке 44 прямая АВ — график уравнения 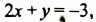
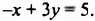
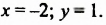
Способ решения систем линейных уравнений, который мы только что использовали, называют графическим.
Чтобы решить систему линейных уравнений графическим способом, нужно построить графики уравнений системы в одной системе координат и найти координаты общих точек этих графиков.
Если в каждом из уравнений системы хотя бы один из коэффициентов при переменных не равен нулю, то графиками таких уравнений являются прямые. Поскольку прямые могут пересекаться, совпадать или быть параллельными, то такие системы уравнений могут иметь одно решение, бесконечно много решений или не иметь решений.
- Заказать решение задач по высшей математике
Примеры решения упражнений:
Пример №164
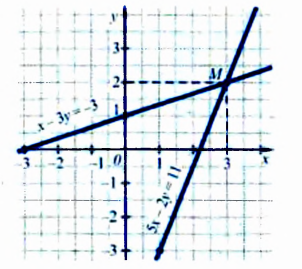
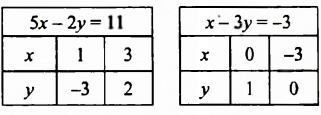
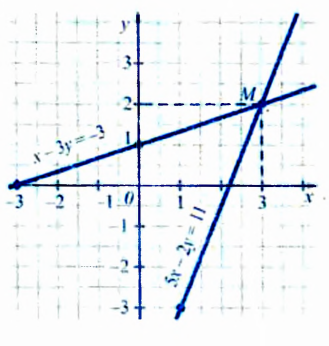
Решить графически систему уравнений
Решение:
Построим графики обоих уравнений системы.
Графики пересекаются в единственной точке — точке М(3; 2). Следовательно, система уравнений имеет единственное решение (3; 2).
Примечание. Чтобы не ошибиться, определяя по графикам координаты точки М, следует проверить, действительно ли найденные координаты являются решением системы. Проверим: если 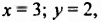
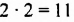
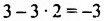
Пример №165
Сколько решений имеет система уравнений
Решение:
Построим графики уравнений системы.
Графики совпадают. Система уравнений имеет бесконечно много решений.
Пример №166
Сколько решений имеет система уравнений
Решение:
Построим графики уравнений системы.
Графиками уравнений являются параллельные прямые (поскольку 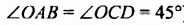
Решение систем линейных уравнений способом подстановки
Рассмотрим верное равенство 7 + 2 = 9. Если в этом равенстве число 2 заменить числовым выражением 2(3 – 2), значение которого равно 2, то получим верное равенство 7 + 2(3 – 2) = 9. Наоборот, если в верном равенстве 7 + 2(3 – 2) = 9 выражение 2(3 – 2) заменить его значением 2, то получим верное равенство 7 + 2 = 9.
На этих свойствах числовых равенств базируется решение систем линейных уравнений способом подстановки. Рассмотрим пример.
Пусть нужно решить систему уравнений
Из первого уравнения системы выразим переменную 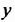

Подставим во второе уравнение системы вместо 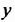
Получим систему
Системы (1) и (2) имеют одни и те же решения (доказательство в рубрике «Для тех, кто хочет знать больше»). Второе уравнение системы (2) имеет только одну переменную 
В первое уравнение системы (2) подставим вместо 
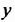
Пара чисел (2; -1) — решение системы (2), а также и системы (1).
Способ, использованный при решении системы (1), называют способом подстановки.
Чтобы решить систему линейных уравнений способом подстановки, нужно:
- выразить из какого-нибудь уравнения системы одну переменную через другую;
- подставить в другое уравнение системы вместо этой переменной полученное выражение;
- решить полученное уравнение с одной переменной;
Для тех, кто хочет знать больше
Докажем, что системы (1) и (2) имеют одни и те же решения.
Пусть пара чисел 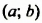
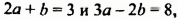
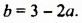
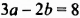
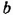
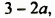
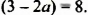
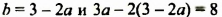
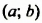
Наоборот, пусть пара чисел 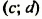
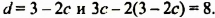
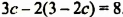
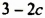
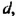
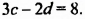
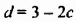
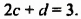
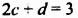
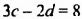
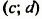
Таким образом, системы (1) и (2) имеют одни и те же решения.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Следовательно, решая систему уравнений (1), мы заменили ее равносильной системой (2).
Примеры решения упражнений:
Пример №167
Решить систему уравнений
Решение:
Выразим из первого уравнения переменную 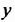

Подставим во второе уравнение системы вместо 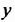
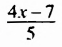
Найдем соответствующее значение переменной 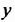
Ответ. (-2; -3).
Пример №168
При каких значениях коэффициента 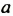
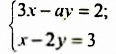
Решение:
Выразим из второго уравнения переменную 
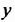
Подставив в первое уравнение системы вместо 
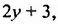
Далее получаем:
Последнее уравнение не имеет корней только в случае, если коэффициент при 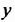
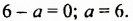
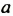
Ответ.
Пример №169
Графиком функции является прямая, проходящая через точки 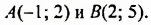
Решение:
Прямая является графиком линейной функции. Пусть искомая линейная функция задается формулой 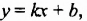
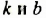
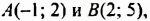
Решив систему уравнений 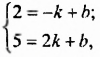
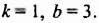
Решение систем линейных уравнений способом сложения
Рассмотрим два верных равенства:
Сложим почленно эти равенства: левую часть с левой и правую с правой:
Снова получили верное равенство. Это свойство верных числовых равенств лежит в основе способа решения систем уравнений, который называют способом сложения.
Рассмотрим пример:
Пусть нужно решить систему уравнений
Сложим почленно левые и правые части уравнений:
Заменим одно из уравнений системы (1), например, первое, уравнением 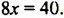
Системы (1) и (2) имеют одни и те же решения (доказательство в рубрике «Для тех, кто хочет знать больше»). Решим систему (2). Из первого уравнения находим: 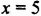
Пара чисел (5; 3) — решение системы (2), а также и системы (1). Решая систему (1), мы воспользовались тем, что в уравнениях коэффициенты при переменной 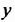

Решим еще одну систему уравнений
В этой системе уравнений коэффициенты при переменной 
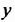
в которой коэффициенты при 
Подставив значение 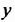
Следовательно, решением системы (3) является пара чисел (-4; 6).
Чтобы решить систему линейных уравнении способом сложения, нужно:
- умножить обе части уравнений системы на такие числа, чтобы коэффициенты при одной из переменных в обеих уравнениях системы стали противоположными числами;
- сложить почленно левые и правые части уравнений;
- решить полученное уравнение с одной переменной;
- найти соответствующее значение другой переменной.
Для тех, кто хочет знать больше
Докажем, что системы (1) и (2) имеют одни и те же решения.
Пусть пара чисел 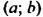
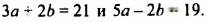
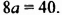
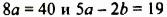
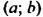
Наоборот, пусть пара чисел 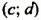
Таким образом, системы (1) и (2) имеют одни и те же решения.
Примеры решения упражнений:
Пример №170
Решить способом сложения систему уравнений
Решение:
Умножим обе части первого уравнения системы на -2. Получим систему
Почленно сложив уравнения последней системы, получим:
Подставим в первое уравнение системы вместо 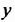
Ответ. (-2;3)
Решение задач с помощью систем уравнений
Вы уже решали задачи с помощью уравнений с одной переменной. Решим задачу, составив систему уравнений.
Задача:
Скорость моторной лодки по течению реки 24 км/ч, а против течения — 19 км/ч. Каковы скорость лодки в стоячей воде и скорость течения реки?
Решение:
Пусть скорость лодки в стоячей воде 
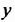
Скорость лодки против течения реки (19 км/ч) равна разности скорости лодки в стоячей воде и скорости течения реки, поэтому
Чтобы ответить на вопрос задачи, нужно найти такие значения 
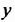
Решив систему, получим:
Ответ. Скорость лодки в стоячей воде 21,5 км/ч; скорость течения реки 2,5 км/ч.
Эту задачу можно было бы решить, составив уравнение с одной переменной. Однако для составления такого уравнения пришлось бы провести более сложные рассуждения.
Чтобы решить задачу с помощью систем уравнений, поступают так:
- обозначают некоторые две неизвестные величины буквами;
- используя условие задачи, составляют два уравнения с выбранными неизвестными;
- записывают систему этих уравнений и решают ее;
- отвечают на поставленные в задаче вопросы.
Примеры решения упражнений:
Пример №171
Если открыть кран теплой воды на 7 мин, а потом кран холодной — на 3 мин, то в ванную нальется 54 л воды. Если же открыть кран теплой воды на 8 мин, а потом кран холодной — на 6 мин, то в ванную нальется 72 л воды. Сколько литров воды наливается в ванную через каждый кран за минуту?
Решение:
Пусть за 1 мин через первый кран (теплой воды) наливается 
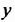
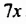
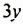
Во втором случае за 8 мин через первый кран нальется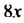
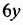
Получили систему уравнений
Решим эту систему способом сложения:
Из первого уравнения системы находим 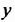
Ответ. 6 л; 4 л.
Интересно знать
В книге «Геометрия», вышедшей в 1637 году, известный французский математик Рене Декарт (1596-1650) предложил новый метод математических исследований — метод координат. Суть этого метода в том, что каждой геометрической фигуре на координатной плоскости ставят в соответствие уравнение или неравенство, которые удовлетворяют координаты каждой точки фигуры и только они. Так, каждой прямой ставят в соответствие уравнение этой прямой вида 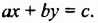
Рене Декарт родился в департаменте Турень (Франция) в семье дворян. После получения образования служил офицером в армии Мориса Оранского, принимал участие в Тридцатилетней войне. Завершив военную службу, Декарт поехал в Голландию, где написал большую часть своих научных трудов и завоевал славу великого ученого.
Декарт сделал ряд открытии, которые стали поворотными пунктами во всей математике. Он ввел понятия переменной величины и функции, прямоугольной системы координат, которую мы на его честь называем еще прямоугольной декартовой системой координат.
С уравнениями с несколькими переменными связана одна из самых известных математических теорем, о которой длительное время ведутся разговоры и в среде, далекой от математики. Речь идет о Великой теореме Ферма. Эта теорема утверждает, что уравнение с тремя переменными вида 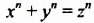
Как выяснилось, в этом простом, на первый взгляд, математическом утверждении скрыта чрезвычайная сложность. Причина же огромного ажиотажа, разгоревшегося вокруг теоремы Пьера Ферма, такова.
В 1636 году в книге Диофанта Александрийского (III в.) «Арифметика», которую Ферма часто перечитывал, делая пометки на ее широких полях, и которую сохранил для потомков его сын, была сделана запись, что он, Ферма, имеет доказательство теоремы, но оно слишком большое, чтобы его можно было разместить на полях.
С этого времени начался поиск доказательства, поскольку в других материалах Ферма его так и не обнаружили.
Кто только не пробовал доказать теорему. Практически каждый математик считал своим долгом заняться Великой теоремой, но усилия были тщетными. За доказательство брались и самые известные математики XVII-XX веков. Эйлер доказал теорему для степеней 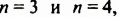
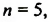
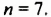
В начале XX в. (1907) зажиточный немецкий любитель математики Вольфекель завещал сто тысяч марок тому, кто предложит полное доказательство теоремы Ферма. Через некоторое время появились доказательства для показателя степени 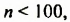
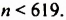
Были и попытки опровергнуть Великую теорему путем поиска хотя бы одного решения уравнения 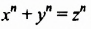
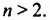
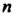
Только в 1995 году английскому профессору математики из Принстонского университета (США) Эндрю Уайлсу удалось доказать Великую теорему. Доказательство было напечатано в одном из ведущих математических журналов и заняло весь номер — более ста листов.
Таким образом, только в конце XX в. весь мир признал, что на 360 году своей жизни Великая теорема Ферма, которая на самом деле все это время была гипотезой, стала-таки доказанной теоремой.
К своему триумфу Уайлс шел более тридцати лет. О теореме Ферма случайно узнал в десятилетнем возрасте, и с тех пор заветная мечта доказать ее не оставляла Эндрю ни на минуту. К счастью, у него хватило здравого смысла, чтобы не пойти путем тысяч упрямых энтузиастов, которые настойчиво старались решить проблему элементарными средствами. Только через двадцать лет, имея уже докторскую степень и занимая должность профессора математики в Принстоне, Уайлс решил отложить все дела и заняться осуществлением своей мечты. Ему удалось доказать Великую теорему Ферма и тем самым решить самую популярную математическую головоломку последних веков.
Отечественные математики
Феофан Прокопович — один из известнейших мыслителей конца XVII – начала XVIII в., профессор и ректор Киево-Могилянской академии, общественный и церковный деятель. Философ и математик, поэт и публицист, он оставил после себя большое количество работ. Писал на латыни, на украинском, русском, польском языках, делал переводы книг и комментировал их.
Феофан Прокопович был одним из наиболее образованных людей своего времени. Его библиотека насчитывала около 30 тысяч книг, написанных на разных языках.
Родился Феофан Прокопович в Киеве 7 июня 1681 года в семье купца. Он рано потерял родителей, и его опекуном стал дядя по матери, ректор Киево-Могилянской академии Феофан Прокопович. Дядя отдал своего семилетнего племянника в начальную школу при Киево-Братском монастыре, а через три года — в Киево-Могилянскую академию. Во время учебы юноша был одним из лучших учеников, не раз побеждал в научных диспутах.
Стремясь углубить свои знания, семнадцатилетний Феофан Прокопович отправился в лрадиционное для того времени научное путешествие. Два года находился во Львове, читал студентам лекции по поэтике и риторике. После этого поехал в Рим, где поступил в коллегию св. Афанасия.
В 1702 году Феофан Прокопович возвращается в Украину. С 1704 года он преподает философию в Киево-Могилянской академии. Его любимым предметом была математика. Поэтому в курс философии он включил два математических курса — арифметику и геометрию, написав оригинальные учебники по этим предметам.
В 1707 году Феофана Прокоповича избирают заместителем ректора, с 1711 по 1715 год он был ректором Киево-Могилянской академии. В 1715 году по приказу царя Феофан Прокопович отправился в Петербург, где принимал участие в создании Петербургского университета и Российской академии наук.
Самым весомым математическим трудом Феофана Прокоповича является курс лекций по математике, теоретические сведения в котором на то время были самыми полными в царской России.
Почетное место в истории математики занимает наш соотечественник Михаил Остроградский. Он был членом Туринской, Петербургской, Римской, Американской и Французской Академий Наук. Слава его была настолько велика, что родители, желая поощрить своих детей к обучению, убеждали их словами: «Учись, и будешь, как Остроградский».
Михаил Остроградский родился в 1801 году в Полтавской губернии в семье помещика. Уже в детские годы он проявлял удивительную любознательность, и наблюдательность, но учился в Полтавской гимназии, куда его отдали в девять лет, посредственно по всем предметам. Михаил мечтал о карьере военного и очень обрадовался, когда отец решил забрать его из гимназии и устроить в один из гвардейских полков. В последний момент по совету одного из родственников, который заметил большие способности мальчика, было решено продолжить учебу. В шестнадцать лет Остроградский стал студентом Харьковского университета.
В 1818 году Остроградский сдал экзамены за курс университета, а в 1820 году — экзамены на звание кандидата наук. Но университетские власти, считая Остроградского «неблагонадежным», отказались присудить ему ученую степень и даже лишили диплома об окончании университета.
И все же Остроградский стал известным ученым, академиком. Неудача только разожгла в нем желание упорно работать. Он едет в Париж и там посещает лекции Коши, Лапласа, Пуассона и других выдающихся математиков. Общение с французскими учеными, изучение их работ приводит Остроградского к собственным открытиям. Его работы публикуются в журнале Парижской Академии наук. Слухи о больших успехах Остроградского дошли и на родину.
В 1828 году Остроградский вернулся в царскую Россию. В Петербурге он преподавал математику в Главном педагогическом институте, Морском кадетском корпусе и в Михайловском артиллерийском училище.
Михаил Остроградский написал много математических работ, среди которых есть работы по алгебре и теории чисел, он является автором нескольких учебников, а теоремы и формулы Остроградского изучают студенты математических специальностей всех университетов мира.
Дмитрий Граве родился в 1863 году в городе Кириллове около Вологды (Россия), окончил физико-математический факультет Петербургского университета (1885).
Будучи студентом, Дмитрий Граве занимался научной работой, был инициатором издания журнала «Записки физико-математического кружка Петербургского университета», где были напечатаны его первые работы.
После защиты магистерской роботы в 1889 году Граве становится приват-доцентом Петербургского университета.
В 1897 году Дмитрий Граве защитил докторскую диссертацию и переехал в Украину. Сначала он работал профессором Харьковского университета и Харьковского технологического института.
В 1902 году профессор Граве возглавил кафедру чистой математики Киевского университета, где и продолжалась почти вся eго научно-педагогическая деятельность.
В 1905-1915 годах Дмитрий Граве разработал несколько учебных курсов, относящиеся в основном к алгебре и теории чисел, наиболее весомыми из которых являются «Элементарный курс теории чисел» и «Элементы высшей алгебры». Он развил на математическом отделении Киевского университета семинарскую форму занятий со студентами.
В конце 1933 года был организован Институт математики Академии наук УССР, первым директором которого стал Граве.
Большой заслугой Дмитрия Граве является создание первой всемирно признанной алгебраической школы.
Работы Михаила Кравчука, которых он написал более 180, относятся к разным разделам математики, в частности к алгебре и теории чисел. Введенные им специальные многочлены сейчас известны математикам как многочлены Кравчука. Он является автором важных работ по истории математики, многих учебников для высшей и средней школ. Много сил, энергии, таланта отдал Михаил Кравчук образованию, сделал важный вклад в развитие украинской математической терминологии.
Михаил Кравчук родился 30 сентября 1892 года в селе Човницы (теперь Волынская область) в семье землемера.
В 1910 году золотой медалист Луцкой гимназии становится студентом физико-математического факультета Киевского университета им. св. Владимира.
В 1915-1917 годах Кравчук выезжает в Москву на специальные студии, где сдает магистерские экзамены. В 1918 году его избирают приват-доцентом Киевского университета.
В 1924 году Михаил Кравчук защищает докторскую диссертацию. На протяжении 1927-1938 гг. работает в высших учебных заведениях Киева. Со времени образования в Киеве Института математики (1933 г.) и до начата 1938 года возглавляет в нем отдел математической статистики.
Михаил Кравчук был организатором первой математической олимпиады школьников (1935 г.).
В сентябре 1938 года Кравчук был арестован сталинским режимом, его обвинили в украинском буржуазном национализме. Приговор — тюремное заключение сроком на 20 лет. Далее — Магадан, где в марте 1942 года Михаил Кравчук и умер.
- Рациональные выражения
- Квадратные корни
- Квадратные уравнения
- Неравенства
- Одночлены
- Многочлены
- Формулы сокращенного умножения
- Разложение многочленов на множители
§ 2. Системы линейных уравнений
Решение многих задач сводится к решению систем линейных уравнений.
Системой двух линейных уравнений с двумя неизвестными `x` и `y` называется система уравнений вида
$$ left{begin{array}{l}{a}_{1}x+{b}_{1}y={c}_{1},\ {a}_{2}x+{b}_{2}y={c}_{2},end{array}right.$$
где `a_1`, `b_1`, `c_1`, `a_2`, `b_2`, `c_2` – некоторые числа.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение в верное числовое равенство.
Например, пара чисел `(2;3)` является решением системы уравнений
$$ left{begin{array}{l}2x+3y=13,\ x+5y=17,end{array}right.$$
а пара чисел `(1;1)` не является решением системы, т. к. эта пара не является решением каждого из уравнений системы.
Обозначим множество решений первого уравнения буквой `A`, а множество решений второго уравнения – `B`. Множество решений системы этих уравнений составляет пересечение множеств `A` и `B` (рис. 9). При этом возможны случаи, когда пересечение двух множеств является пустым (рис. 10) или совпадает с каждым из множеств `A` и `B` (рис. 11).
Графиком линейного уравнения `ax+by=c`, где `a^2+b^2>0`, является прямая. Следовательно, решение системы линейных уравнений с двумя неизвестными для указанного случая сводится к нахождению на координатной плоскости общих точек двух прямых линий. А две прямые на плоскости могут:
1) пересекаться, т. е. иметь единственную общую точку;
2) быть параллельными, т. е. не иметь общих точек;
3) совпадать, т. е. иметь бесконечно много общих точек.
Значит, система двух линейных уравнений с двумя неизвестными может либо иметь единственное решение, либо вообще не иметь решения, либо иметь бесконечное множество решений.
Сколько решений имеет система уравнений
$$ left{begin{array}{l}2y+3x=8,\ y-x=-1?end{array}right.$$
Запишем первое уравнение системы в виде `y=-3/2x+4`, а второе уравнение системы в виде `y=x-1`. Мы получили две линейные функции, графиками которых являются прямые с разными угловыми коэффициентами у первой `k_1=-3/2`, а у второй `k_2=1`. Вам известно, что такие прямые пересекаются в одной точке. Чтобы найти координаты точки пересечения прямых, приравняем значения для `y`. Получаем
`-3/2x+4=x-1`, `-3/2x-x=-4-1`, `-5/2x=-5`, `x=2`,
тогда `y=2-1=1`.
Таким образом, система имеет единственное решение `(2;1)`.
Решите систему уравнений
$$ left{begin{array}{l}2x+y=5,\ 4x+2y=10.end{array}right.$$
Из первого уравнения следует, что `y=5-2x`, а из второго уравнения получим `y=5-2x`. Графики этих уравнений совпадают. Уравнению удовлетворяет любая пара чисел `(x,5-2x)`, где `x` любое число, а `y=5-2x`. Система уравнений имеет бесконечно много решений.
Решите систему уравнений
$$ left{begin{array}{l}x+y=7,\ 2x+2y=10.end{array}right.$$
Запишем первое уравнение системы в виде `y=-x+7` и второе уравнение системы в виде `y=-x+5`. Графиками этих уравнений являются две параллельные прямые, которые не пересекаются, т. к. `-x+7=-x+5`, `x*0=-2`, а это уравнение не имеет решений.
При решении систем применяют метод подстановки, метод сложения и метод введения новых переменных.
1. В одном из уравнений выразить одно неизвестное через другое.
2. Подставить вместо этого неизвестного полученное выражение в другое уравнение системы.
3. Решить полученное во втором пункте уравнение с одним неизвестным.
4. Воспользовавшись найденным значением одного неизвестного, вычислить значение второго неизвестного.
5. Записать ответ.
Покажем на конкретном примере, как применяется метод подстановки.
Решите систему уравнений
$$ left{begin{array}{l}2x+y=4,\ 5x+3y=11.end{array}right.$$
Из первого уравнения выражаем `y=4-2x`, и это значение для `y` подставляем во второе уравнение системы, получаем:
`5x+3(4-2x)=11`, `5x+12-6x=11`, `-x=-1`, `x=1`.
Подставляем это значение `x` в выражение для `y`, получаем: `y=4-2=2`. Пара чисел `(1;2)` является единственным решением системы уравнений.
1. Умножить или разделить одно (или оба) уравнения системы на некоторое число, не равное 0, так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях стали противоположными числами (или совпали).
2. Сложить (вычесть) уравнения.
3. Решить полученное во втором пункте уравнение с одним неизвестным.
4. Воспользовавшись найденными значениями одного неизвестного, вычислить значение второго неизвестного.
5. Записать ответ.
Теперь приведём пример, где применяется метод сложения.
Решите систему уравнений
$$ left{begin{array}{l}3x-2y=5,\ 2x+2y=10.end{array}right.$$
В этих уравнениях коэффициенты при переменной `y` отличаются знаком. Сложив уравнения системы, получаем
`3x-2y+2x+2y=5+10`, `5x=15`, `x=3`.
Подставляем найденное значение `x`, например, в первое уравнение системы, получаем:
`3*3-2y=5`, `-2y=-4`, `y=2`.
Система имеет единственное решение `(3;2)`.
Решите систему уравнений
$$ left{begin{array}{l}4x+3y=11,\ 3x+7y=13.end{array}right.$$
Сделаем коэффициенты при $$ x$$ обоих уравнений противоположными числами, для этого умножим обе части первого уравнения на `3` и обе части второго уравнения на `(-4)`, получим систему
$$ left{begin{array}{l}12x+9y=33,\ -12x-28y=-52.end{array}right.$$
Сложим уравнения системы:
`12x+9y-12x-28y=33-52`, `-19y=-19`, `y=1`.
Подставляем это значение для `y` в первое уравнение системы, получаем:
`12x+9=33`, `12x=24`, `x=2`.
Пара чисел `(2;1)` является единственным решением системы.
Метод введения новых переменных позволяет упростить вид системы.
Покажем на конкретном примере, как применяется метод введения новых переменных.
Решите систему уравнений
$$ left{begin{array}{l}{displaystyle frac{1}{2x-y}}+{displaystyle frac{9}{3x+y}}=2,\ {displaystyle frac{7}{2x-y}}-{displaystyle frac{18}{3x+y}}=5.end{array}right.$$
Введём новые переменные: `u=1/(2x-y)`, `v=1/(3x+y)`.
Для переменных `u` и `v` получим систему уравнений
$$ left{begin{array}{l}u+9v=2,\ 7u-18v=5.end{array}right.$$
Умножим обе части первого уравнения на `2`, получим систему
$$ left{begin{array}{l}2u+18v=4,\ 7u-18v=5.end{array}right.$$
Сложим уравнения системы, получим `9u=9`, `u=1`. Из первого уравнения при `u=1` следует, что `v=1/9`.
Из условия `1/(2x-y)=1` следует, что `2x-y=1`, а из условия `1/(3x+y)=1/9` следует, что `3x+y=9`. Решаем систему уравнений
$$ left{begin{array}{l}2x-y=1,\ 3x+y=9.end{array}right.$$
Сложим уравнения системы: `5x=10`, `x=2`, из первого уравнения получаем `4-y=1`, `y=3`.
`(2;3)`.
Мы рассмотрели системы двух уравнений с двумя неизвестными, теперь рассмотрим систему из трёх уравнений с тремя неизвестными.
С помощью способа сложения сводим систему трёх уравнений с тремя неизвестными к системе двух уравнений с двумя неизвестными. Покажем это на примере.
Решите систему уравнений
$$ left{begin{array}{l}10x-5y-3z=-9,\ 6x+4y-5z=-1,\ 3x-4y-6z=-23.end{array}right.$$
Уравняем коэффициенты при `x` в первом и втором уравнениях, для этого умножим обе части первого уравнения на `3`, а второго уравнения – на `5`, получаем:
$$ left{begin{array}{l}30x-15y-9z=-27,\ 30x+20y-25z=-5.end{array}right.$$
Вычитаем из второго уравнения полученной системы первое уравнение, получаем:
`35y-16z=22`.
Из второго уравнения исходной системы вычитаем третье уравнение, умноженное на `2`, получаем:
`4y+8y-5z+12z=-1+46`, `12y+7z=45`.
Теперь решаем новую систему уравнений:
$$ left{begin{array}{l}35y-16z=22,\ 12y+7z=45.end{array}right.$$
К первому уравнению новой системы, умноженному на `7`, прибавляем второе уравнение, умноженное на `16`, получаем:
`35*7y+12*16y=22*7+45*16`,
`245y+192y=154+720`, `437y=874`, `y=2`.
Подставляем `y=2` в уравнение `12y+7z=45`, получаем:
`24+7z=45`, `7z=21`, `z=3`.
Теперь подставляем `y=2`, `z=3` в первое уравнение исходной системы, получаем:
`10x-5*2-3*3=-9`, `10x-10-9=-9`, `10x=10`, `x=1`.
`(1;2;3)`.
При решении задач могут получаться системы уравнений с большим количеством неизвестных, их решение осуществляется аналогичным образом.
Если несколько линейных уравнений с одними теми же неизвестными рассматривают совместно, то говорят, что это система линейных уравнений с несколькими неизвестными.
Пример:
|
а) (begin{cases}x-2y=5\3x+2y=7end{cases}) |
г) (begin{cases}3(5-x)-4y=0\y-2x+4=0 end{cases}) |
|
б)(begin{cases}3b=13-2a\5a=5-2b end{cases}) |
д)(begin{cases}frac{p}{3} + frac{m-6}{2} = 1-9m \11p+3(m-p-1)=-2(m+1) end{cases}) |
|
в)(begin{cases}3x-8=2y\x+y=6end{cases}) |
е)(begin{cases}0,02y=1,25-3,21x \1,5x-frac{3}{4}=4-0,1yend{cases}) |
Решить систему с двумя неизвестными – это значит найти все пары значений переменных, которые удовлетворяют каждому из заданных уравнений. Каждая такая пара называется решением системы.
Пример:
Пара значений (x=3);(y=-1) является решением первой системы, потому что при подстановке этих тройки и минус единицы в вместо (x) и (y), оба уравнения превратятся в верные равенства (begin{cases}3-2cdot (-1)=5 \3 cdot 3+2 cdot (-1)=7 end{cases})
А вот (x=1); (y=-2) – не является решением первой системы, потому что после подстановки второе уравнение «не сходится» (begin{cases}1-2cdot(-2)=5 \3cdot1+2cdot(-2)≠7 end{cases})
Отметим, что такие пары часто записывают короче: вместо “(x=3); (y=-1)” пишут так: ((3;-1)).
Как решить систему линейных уравнений?
Есть три основных способа решения систем линейных уравнений:
- Способ подстановки.
-
Возьмите любое из уравнений системы и выразите из него любую переменную.
(begin{cases}x-2y=5\3x+2y=7 end{cases})(Leftrightarrow) (begin{cases}x=5+2y\3x+2y=7end{cases})(Leftrightarrow)
-
Полученное выражение подставьте вместо этой переменной в другое линейное уравнение системы.
(Leftrightarrow) (begin{cases}x=5+2y\3(5+2y)+2y=7end{cases})(Leftrightarrow)
-
Равносильными преобразованиями уравнений найдите по очереди каждое неизвестное.
(Leftrightarrow) (begin{cases}x=5+2y\15+6y+2y=7end{cases})(Leftrightarrow)(begin{cases}x=5+2y\8y=-8end{cases})(Leftrightarrow)(begin{cases}x=5+2y\y=-1end{cases})(Leftrightarrow)(begin{cases}x=5-2\y=-1end{cases})(Leftrightarrow)(begin{cases}x=3\y=-1end{cases})
-
Ответ запишите парой чисел ((x_0;y_0))
Ответ: ((3;-1))
- Способ алгебраического сложения.
-
Равносильно преобразовывая каждое уравнение в отдельности, запишите систему в виде:(begin{cases}a_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end{cases}).
(begin{cases}3y=13-2x\5x=5-2yend{cases})(Leftrightarrow)(begin{cases}2x+3y=13\5x+2y=5end{cases})(Leftrightarrow)
-
Теперь нужно сделать так, чтоб коэффициенты при одном из неизвестных стали одинаковы (например, ((3) и (3)) или противоположны по значению (например, (5) и (-5)). В нашем примере уравняем коэффициенты при игреках. Для этого первое уравнение домножим на (2), а второе – на (3).
(begin{cases}2x+3y=13 |cdot 2\ 5x+2y=5 |cdot 3end{cases})(Leftrightarrow)(begin{cases}4x+6y=26\15x+6y=15end{cases})(Leftrightarrow)
-
Сложите (или вычтите) почленно обе части уравнения так, чтобы получилось уравнение с одним неизвестным.
- Найдите неизвестное из полученного уравнения.
(-11x=11) (|∶(-11))
(x=-1) - Подставьте найденное значение неизвестного в любое из исходных уравнений и найдите второе неизвестное.
(3y=13-2x)
(3y=13-2·(-1))
(3y=15)
(y=5) -
Ответ запишите парой чисел ((x_0;y_0)).
Ответ: ((-1;5))
- Графический способ.
-
Приведите каждое уравнение к виду линейной функции
(y=kx+b).(begin{cases}3x-8=2y\x+y=6end{cases})(Leftrightarrow)(begin{cases}2y=3x-8 |:2\y=6-xend{cases})(Leftrightarrow)(begin{cases}y=frac{3}{2}x-4\y=-x+6end{cases})
-
Постройте графики этих функций. Как? Можете прочитать здесь.
- Найдите координаты ((x;y)) точки пересечения графиков и запишите их в ответ в виде ((x_0;y_0 )).
Ответ: ((4;2))
Замечание к шагу 1: нет никакой разницы какую переменную и из какого уравнения выражать. Обычно более удобно выражать ту переменную, перед которой нет коэффициента или, говоря точнее, коэффициент которой равен единице (в примере выше это был икс в первом уравнении).
Почему так? Потому что во всех остальных случаях у нас при выражении переменной получилась бы дробное выражение. Попробуем, например, выразить икс из второго уравнения системы:
(begin{cases}x-2y=5\3x+2y=7 end{cases})(Leftrightarrow) (begin{cases}x=5+2y\3x=7-2yend{cases})(Leftrightarrow)(begin{cases}x=5+2y\x=frac{7-2y}{3}end{cases})
И сейчас нам нужно будет эту дробь
подставлять в первое уравнение и решать то, что получиться. До верного ответа мы бы всё равно дошли, но идти было бы неудобнее
Замечание к шагу 3: В каком случае уравнения складывают, а в каком вычитают? Ответ прост – делайте так, чтоб пропала переменная: если «уравненные» коэффициенты имеют один и тот же знак – вычитайте, а если разные – складывайте.
Пример. Решите систему уравнений: (begin{cases}12x-7y=2\5y=4x-6end{cases})
Решение:
|
(begin{cases}12x-7y=2\5y=4x-6end{cases}) |
Приводим систему к виду (begin{cases}a_1 x+b_1 y=c_1\a_2 x+b_2 y=c_2end{cases}) преобразовывая второе уравнение. |
|
|
(begin{cases}12x-7y=2\-4x+5y=-6end{cases}) |
«Уравняем» коэффициенты при иксах. Для этого домножим второе уравнение на (3). |
|
|
(begin{cases}12x-7y=2\-12x+15y=-18end{cases}) |
Знаки при иксах разные, поэтому чтоб иксы пропали, уравнения надо сложить. |
|
|
(0·x+8y=-16) |
Делим уравнение на (8), чтобы найти (y). |
|
|
(y=-2) |
Игрек нашли. Теперь найдем (x), подставив вместо игрека (-2) в любое из уравнений системы. |
|
|
(12x-7·(-2)=2) |
Икс тоже найден. Пишем ответ. |
Ответ: ((-1;-2))
Матхак. Если сомневаетесь в правильности ответа (неважно каким способом вы решали), проверьте подстановкой значений (x_0) и (y_0) в каждое уравнение. Если оба уравнения превратятся в верные равенства, то ответ правильный.
Пример: решая систему (begin{cases}3x-8=2y\x+y=6end{cases}), мы получили ответ ((4;2)). Проверим его, подставив вместо икса (4), а вместо игрека (2).
(begin{cases}3cdot 4-8=2cdot 2\4+2=6end{cases})(Leftrightarrow)(begin{cases} 12-8=4\6=6end{cases})(Leftrightarrow)(begin{cases} 4=4\6=6end{cases})
Оба уравнения сошлись, решение системы найдено верно.
Пример. Решите систему уравнений: (begin{cases}3(5x+3y)-6=2x+11\4x-15=11-2(4x-y)end{cases})
Решение:
|
(begin{cases}3(5x+3y)-6=2x+11\4x-15=11-2(4x-y)end{cases}) |
Раскроем скобки в уравнениях. |
|
|
(begin{cases}15x+9y-6=2x+11\4x-15=11-8x+2yend{cases}) |
Перенесем все выражения с буквами в одну сторону, а числа в другую. |
|
|
(begin{cases}15x-2x+9y=11+6\4x+8x-2y=11+15end{cases}) |
Приведем подобные слагаемые. |
|
|
(begin{cases}13x+9y=17\12x-2y=26end{cases}) |
Во втором уравнении каждое слагаемое – четное, поэтому упрощаем уравнение, деля его на (2). |
|
|
(begin{cases}13x+9y=17\6x-y=13end{cases}) |
Эту систему линейных уравнений можно решить любым из способов, но мне кажется, что способ подстановки здесь удобнее всего. Выразим y из второго уравнения. |
|
|
(begin{cases}13x+9y=17\y=6x-13end{cases}) |
Подставим (6x-13) вместо (y) в первое уравнение. |
|
|
(begin{cases}13x+9(6x-13)=17\y=6x-13end{cases}) |
Первое уравнение превратилась в обычное линейное. Решаем его. Сначала раскроем скобки. |
|
|
(begin{cases}13x+54x-117=17\y=6x-13end{cases}) |
Перенесем (117) вправо и приведем подобные слагаемые. |
|
|
(begin{cases}67x=134\y=6x-13end{cases}) |
Поделим обе части первого уравнения на (67). |
|
|
(begin{cases}x=2\y=6x-13end{cases}) |
Ура, мы нашли (x)! Подставим его значение во второе уравнение и найдем (y). |
|
|
(begin{cases}x=2\y=12-13end{cases})(Leftrightarrow)(begin{cases}x=2\y=-1end{cases}) |
Запишем ответ. |
Ответ: ((2;-1))
Скачать статью
Система двух линейных уравнений и её решение
Несколько уравнений образуют систему , если они имеют общее решение.
Общее решение при подстановке в каждое из уравнений системы преобразует его в тождество.
Решить систему уравнений означает найти все её общие решения.
Система двух линейных уравнений имеет вид:
$$ {left{ begin{array}{c} a_1 x+b_1 y = c_1\ a_2 x+b_2 y = c_2 end{array} right.} $$
Общее решение системы двух линейных уравнений – это упорядоченная пара $(x_*,y_* )$, которая при подстановке в каждое из двух уравнений превращает его в тождество.
Например: Система уравнений $ {left{ begin{array}{c} x+y = 3\ 2x-3y = 1 end{array} right.} $ имеет общее решение (2;1), т.е.
$2+1 ≡ 3,2 cdot 2-3 cdot 1 ≡ 1$ – оба уравнения превращаются в тождества.
Примеры
Пример 1. Какие из пар чисел (1;-1),(2;3),(-3;2) являются решениями системы уравнений:
а) $ {left{ begin{array}{c} x-y = 2\ 2x+3y = -1 end{array} right.} $
$ (1;-1): {left{ begin{array}{c}1-(-1) ≡ 2\ 2cdot1+3cdot(-1) ≡ -1end{array} right.} Rightarrow решение (1;-1)$
б) $ {left{ begin{array}{c} x-y = 5\ 2x+3y = 0 end{array} right.} $
$ (1;-1): {left{ begin{array}{c}1-(-1) neq -5\ 2cdot1+3cdot(-1) neq 0end{array} right.} $
$ (2;3): {left{ begin{array}{c}2-3 neq -5\ 2cdot2+3cdot3 neq 0end{array} right.} $
$ (-3;2): {left{ begin{array}{c}-3-2 ≡ -5\ 2cdot(-3)+3cdot2≡0end{array} right.} Rightarrow решение (-3;2)$
Пример 2.Составьте систему линейных уравнений, решением которой является пара чисел
а) $(7;1) : {left{ begin{array}{c} 2x+y = 15\x-5y = 2end{array} right.} $
б) $(-4;6) : {left{ begin{array}{c} 2x+y = -2\x-5y = -34end{array} right.} $
Пример 3.Найдите точку пересечения графиков x+y=5 и 2x-3y=5.
Покажите, что координаты это точки являются решением соответствующей системы уравнений.
x+y = 5 и 2x-3y = 5
Точка пересечения (4;1)
$ {left{ begin{array}{c}x+y = 5 \ 2x-3y = 5 end{array} right.} $
$ (4;1): {left{ begin{array}{c}4+1 ≡ 5\ 2cdot4-3cdot1 ≡ 5end{array} right.}$
Координаты точки пересечения являются решением системы уравнений.
Конспект урока
Алгебра
7 класс
Урок № 48
Решение систем двух линейных уравнений с двумя неизвестными
Перечень вопросов, рассматриваемых в теме:
- Систематизация решений систем уравнений.
- Использование отношений коэффициентов при решении систем уравнений.
- Практическое применение теоремы.
Тезаурус:
Теорема.
Пусть дана система уравнений:
где все коэффициенты отличны от нуля.
Тогда система:
а) имеет единственное решение, если ;
б) не имеет решений, если ;
в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Решение систем двух линейных уравнений с двумя неизвестными.
Пусть дана система двух линейных уравнений с двумя неизвестными.
Перенеся все члены правых частей этих уравнений в левые части, и приведя подобные члены, получим равносильную данной систему вида:
где ─ некоторые числа.
Мы уже знаем, как решать такую систему, когда все коэффициенты при неизвестных отличны от нуля. Мы знаем так же, что если коэффициенты при неизвестных непропорциональны, то решение системы существует и единственно; если же коэффициенты при неизвестных системы пропорциональны, то либо решений бесконечно много, либо нет ни одного решения.
Нам остаётся рассмотреть те случаи, когда некоторые коэффициенты при неизвестных равны нулю. Рассмотрим это на характерных примерах.
Пример 1. Решим систему уравнений:
Второе уравнение этой системы имеет отличные от нуля коэффициенты при неизвестных, а первое уравнение имеет коэффициент при , отличный от нуля, и коэффициент при , равный нулю.
Эту систему проще решить методом подстановки. Найдем из первого уравнения:
И подставим его во второе. Получим:
Откуда
Таким образом, пара чисел есть единственное решение системы.
Пример 2. Решим систему уравнений:
Система есть частный случай системы , где
Единственным решением этой системы является пара чисел
Пример 3. Решим систему уравнений:
Из каждого уравнения системы получим
Так как систему мы рассматриваем как частный случай системы , где то система может быть записана так:
Здесь может быть любым числом, а .
Таким образом, решения системы записываются в виде пар чисел , где ─ любое число.
Пример 4. Решим систему уравнений
Эта система противоречива (не имеет решений), потому что не может одновременно равняться и 1, и .
Пример 5. Решим систему уравнений:
Если , то эта система противоречива, потому что никакая пара чисел не удовлетворяет второму уравнению системы
Если , то второе уравнение обращается в верное равенство при любых Остаётся только первое уравнение. Оно уже рассматривалось. Следовательно, все решения первого уравнения являются решениями системы.
О количестве решений системы двух уравнений первой степени с двумя неизвестными.
Теорема
Пусть дана система уравнений:
где все коэффициенты отличны от нуля.
Тогда система :
а) имеет единственное решение, если ;
б) не имеет решений, если ;
в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.
Доказательство.
Из первого уравнения системы получим, что:
. Подставив полученное выражение вместо во второе уравнение системы и учитывая, что получим уравнение:
Здесь возможны три случая.
- Если:
то уравнение имеет единственный корень, поэтому и система имеет единственное решение.
Так как и то условие можно записать в виде
- Если:
то уравнение не имеет корней и система не имеет решений.
Так как то условия можно записать в виде
- Если:
то уравнение имеет бесконечно много корней, поэтому и система имеет бесконечно много решений.
Так как то условия можно записать в виде
Итак:
если то система имеет единственное решение;
если то система не имеет решений;
если то система имеет бесконечно много решений, и эти решения задаются парами , где любое число.
Теорема доказана.
Пример 1. Определим число решений системы уравнений:
а) б) в)
Решение.
а) Так как выполняется условие , то система имеет единственное решение.
б) Так как выполняется условие , то система имеет бесконечно много решений.
в) Так как выполняется условие то система не имеет решений.
Ответ: а) единственное решение; б) бесконечно много решений; в) нет решений.
Пример 2. При каком значении система
не имеет решений?
Решение.
Система не имеет решений, если выполняется условие
. Условие выполняется лишь при При этом условие также выполняется. Следовательно, система не имеет решений при
Ответ: при
Пример 3. Существует ли значение , при котором система не имеет решений?
Решение.
Система не имеет решений, если выполняется условие . Условие выполняется лишь при При этом условие не выполняется. Следовательно, таких не существует.
Ответ: не существует.
Разбор решения заданий тренировочного модуля.
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Впишите пропущенные элементы при решении системы.
Задание:
Перенесем из первого уравнения в правую часть 4, получим
Найдем отношение коэффициентов при х и у в системе:
‑ так как отношения __ равны, значит, система имеет одно решение. Решим систему способом подстановки:
Ответ: ( ___; ___ ).
Решение.
Перенесем из первого уравнения в левую часть 4, получим:
Найдем отношение коэффициентов при х и у в системе:
‑ так как отношения не равны, значит, система имеет одно решение. Решим систему способом подстановки:
Ответ: (4; 16).
№2. Тип задания: восстановление последовательности элементов горизонтальное / вертикальное.
Задание:
Решите систему двух уравнений:
Варианты ответов:
Ответ: (1; 0).
Значит, система имеет единственное решение.
Так как отношение коэффициентов равно –
Значит, система имеет единственное решение.
Решение:
Так как отношение коэффициентов равно –
Значит, система имеет единственное решение.
Перенесем в первом уравнении из левой части в правую 4:
Ответ: (1; 0).