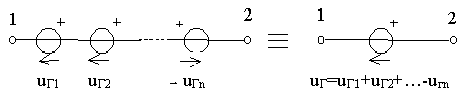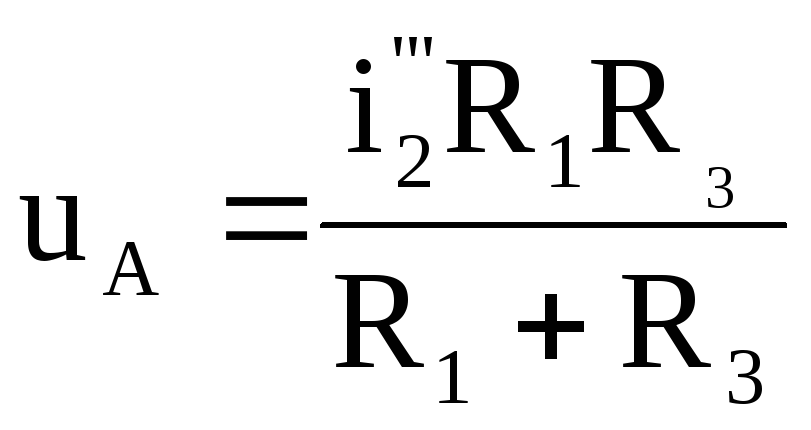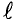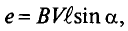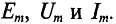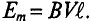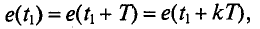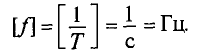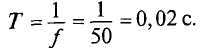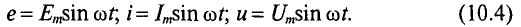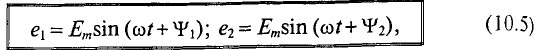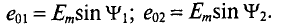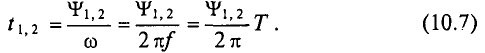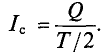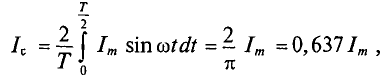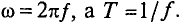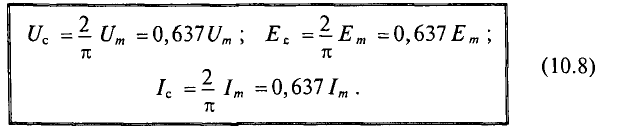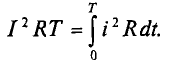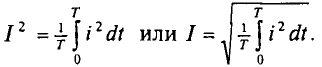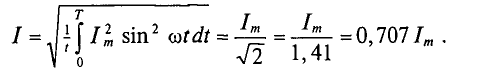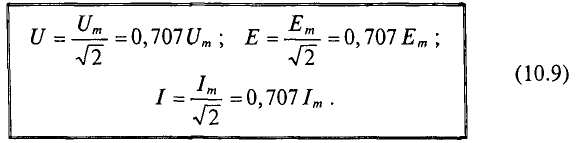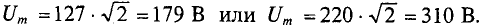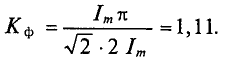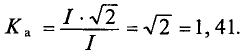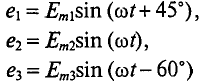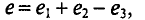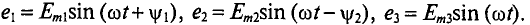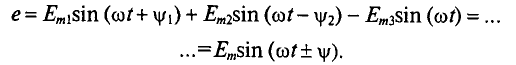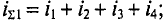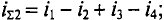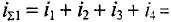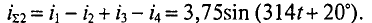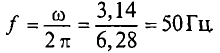1.2.1
Законы Кирхгофа
Законы Кирхгофа
являются основными в теории цепей.
Первый
закон
– закон токов Кирхгофа (ЗТК) формулируется
по отношению к узлам электрической цепи
и отражает тот факт, что в узлах не могут
накапливаться заряды.
Он гласит: алгебраическая
сумма токов ветвей, сходящихся в любом
узле электрической цепи, равна нулю.
Формально это записывается так:
,
(2.1)
где m
– число ветвей, сходящихся в узле.
В этом уравнении
токи,
одинаково ориентированные относительно
узла, имеют одинаковые знаки.
Например,
знаки
выходящих токов можно считать
положительными, а входящих – отрицательными.
Число
независимых уравнений, составляемых
по ЗТК, равно числу независимых узлов
электрической цепи.
Второй
закон
– закон
напряжений Кирхгофа
(ЗНК) формулируется
по отношению к контурам
и гласит: алгебраическая
сумма напряжении ветвей в любом контуре
цепи равна нулю.
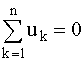
(2.2)
где n
– число ветвей, входящих в контур.
В этом уравнении
напряжения,
совпадающие с направлением обхода
контура, записываются со знаком “+”,
а не совпадающие – со знаком “-“.
Иллюстрация
законов Кирхгофа
Рассмотрим
пример,
в котором рассчитываются токи ветвей
схемы резистивной цепи, изображенной
на рис. 2.1, по методу уравнений Кирхгофа.
Схема имеет nу
= 4 узла, nв
= 6 ветвей. Выберем узел 4 в качестве
базисного и составим nу
– 1 = 3 уравнения по ЗТК: для 1-го узла -i1
+ i3
+ i4
= 0; для 2-го узла -i2
– i3
+ i5
= 0; для 3-го узла i2
– i4
+ i6
= 0. По ЗНК составляем nв
– nу
+ 1 = 3 уравнения для контуров, показанных
на рисунке стрелками: для 1-го контура
-uг1
+ u1
+ u3
+ u5
= 0; для 2-го контура uг2
+ u2
– u3
+ u4
= 0; для 3-го контура -uг2
– u2
+ u6
– u5
= 0. Или с учетом закона Ома:
Рисунок
2.1 – Схема, отражающая применение ЗТК и
ЗНК
-uг1
+R1i1
+ R3i3
+ R5i5
= 0 ;
uг2
+ R2i2
– R3i3
+ R4i4
= 0 ;
–uг2
–R2i2
+ R6i6
– R5i5
= 0 .
Решая
совместно эти системы уравнений, находят
искомые токи.
1.2.2
Преобразование электрических схем
Преобразования
электрических схем применяются для
упрощения расчетов.
Наиболее типичные методы преобразования
следующие.
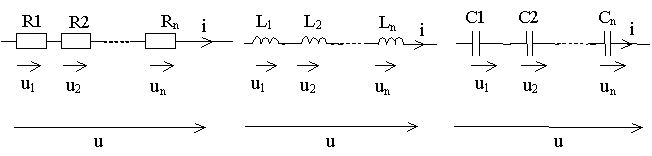
Последовательное
соединение элементов.
Согласно ЗТК при
последовательном соединении элементов
через них протекает один и тот же ток
(рисунок 2.2).
Рисунок
2.2 – Последовательное соединение элементов
Согласно ЗНК
напряжение,
приложенное ко всей цепи:

(2.3)
Тогда для
последовательного соединения резистивных
элементов
R1,
R2,
…, Rn
будем иметь:
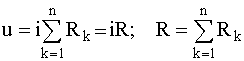
(2.4)
Для последовательного
соединения индуктивных элементов
(рисунок 2.2):
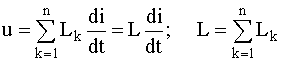
(2.5)
Для последовательного
соединения емкостных элементов:
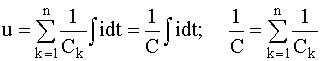
(2.6)
Таким
образом,
цепь
из n
последовательно
соединенных резистивных, индуктивных
или емкостных элементов может
быть заменена одним эквивалентным
резистивным, индуктивным или емкостным
элементом.
Причем при нахождении эквивалентного
сопротивления или эквивалентной
индуктивности необходимо суммировать
сопротивления и индуктивности отдельных
резистивных и индуктивных элементов,
а для
нахождения эквивалентной обратной
емкости – суммировать величины, обратные
емкости отдельных емкостных элементов.
При n = 2:
С = С1C2/(С1
+ С2).
(2.7)
При последовательном
соединении независимых источников
напряжения
они заменяются
одним эквивалентным источником напряжения
с задающим напряжением uг,
равным
алгебраической
сумме
задающих напряжений отдельных источников.
Причем со
знаком “+” берутся задающие напряжения
совпадающие с задающим напряжением
эквивалентного источника,
а со знаком “-” – несовпадающие (рисунок
2.3).
Рисунок
2.3 – Последовательное соединение
источников напряжения
Параллельное
соединение элементов.
При параллельном
соединении элементов
согласно ЗНК к
ним будет приложено одно и то же напряжение
(рисунок 2.4). Согласно ЗТК для
тока каждой из схем,
изображенных на рисунке 2.4, можно
записать:
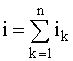
(2.8)
Рисунок
2.4 – Параллельное соединение пассивных
элементов
На основании этого
уравнения для
параллельного соединения резистивных
элементов
получаем:
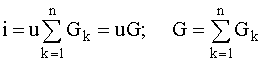
(2.9)
Для параллельного
соединения емкостных элементов:
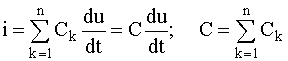
(2.10)
Для параллельного
соединения индуктивных
элементов:
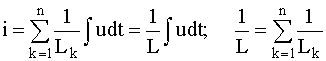
(2.11)
Следовательно,
цепь из
n
параллельно
соединенных резистивных, индуктивных
или емкостных элементов можно заменить
одним
эквивалентным
резистивным, индуктивным или емкостным
элементом.
Таким
образом,
при
параллельном
соединении резистивных, емкостных и
индуктивных элементов для нахождения
эквивалентных проводимости
и емкости цепи проводимости или емкости
отдельных элементов складываются.
Эквивалентная
обратная индуктивность
цепи находится
суммированием обратных индуктивностей
отдельных индуктивных элементов. В
частности, при n = 2:
R
= R1R2/(R1
+ R2);
L
= L1L2/(L1
+ L2)
. (2.12)
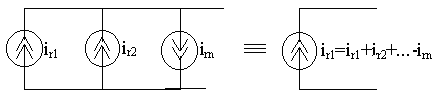
Параллельно
соединенные независимые источники
тока
можно заменить
одним эквивалентным источником тока с
задающим током, равным алгебраической
сумме задающих токов отдельных источников.
Причем со
знаком “+” берутся задающие токи,
совпадающие по направлению с задающим
током эквивалентного источника,
а со знаком “-” – не совпадающие (рисунок
2.5).
Рисунок 2.5 –
Параллельное соединение источников
тока
При расчете
электрических цепей часто
возникает необходимость преобразования
источника напряжения с параметрами uг
и
Rг,
в эквивалентный источник тока с
параметрами iг
и Gг,
или наоборот – преобразование источника
тока в эквивалентный источник напряжения.
Эти преобразования
осуществляются в соответствии с формулами
iг
= uг/Rг
; Gг
= 1/Rг
.
(2.13)
Пример
преобразования
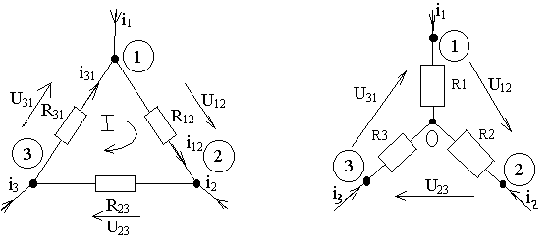
“звезда—треугольник”.
Кроме последовательного и параллельного
соединений элементов весьма
распространенными являются соединения
элементов треугольником и звездой
(рисунок 2.6).
Рисунок
2.6 – Соединения треугольником и звездой
Существуют
формулы преобразования соединения
треугольника
в звезду:
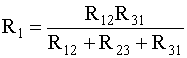
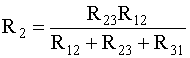
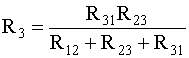
(2.14)
Обратный
переход можно получить по формулам,
которые получены из предыдущих:
R12
= R1
+ R2
+ R1R2/R3
; R23
= R2
+ R3
+ R2R3/R1
; R31
= R3
+ R1
+ R3R1/R2
.
(2.15)
Аналогично
существуют формулы преобразования
“звезда—треугольник” индуктивных и
емкостных элементов [1, с. 23-24].
1.2.3
Принцип наложения
Принцип наложения
(суперпозиции)
имеет важнейшее значение в теории
линейных электрических цепей. Подавляющее
число методов анализа линейных цепей
базируется на этом принципе. Если
рассматривать напряжения и токи
источников как задающие воздействия,
а напряжение и токи в отдельных ветвях
цепи как реакцию (отклик) цепи на эти
воздействия, то
принцип наложения можно сформулировать
следующим образом:
реакция
линейной цепи на сумму воздействий
равна сумме реакций от каждого воздействия
в отдельности.
Принцип наложения
можно
использовать
для нахождения реакции в
линейной цепи,
находящейся как под
воздействием нескольких источников,
так
и при сложном произвольном воздействии
одного источника.
Рассмотрим случай,
когда в линейной цепи действует несколько
источников.
В соответствии с
принципом наложения для нахождения
тока
i
или
напряжения
u
в заданной ветви осуществим
поочередное воздействие каждым источником
и найдем соответствующие частные реакции
ik
и uk
на эти воздействия.
Тогда результирующая реакция определится
как
,
(2.16)
где n
– общее число источников.
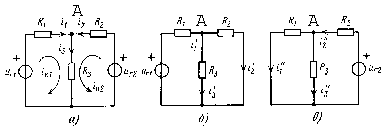
Проиллюстрируем
принцип наложения (суперпозиции) на
примере
резистивной цепи,
изображенной на рисунке 2.7, а.
Рисунок
2.7 – Иллюстрация принципа суперпозиции
Найдем
ток в резистивном элементе
R3.
Положим вначале,
что в цепи действует
только один источник uг1:
второй
источник напряжения исключается и
зажимы его закорачиваются.
При этом получаем частичную
схему, изображенную на рисунке 2.7,б.
Определим
ток i3‘
от воздействия напряжения uг1,
учитывая, что
и
:
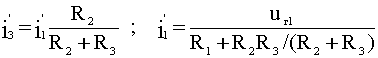
(2.17)
Теперь
полагаем,
что в
цепи действует только источник uг2.
Исключив источник uг1,
получим
вторую частичную схему.
Ток
i3”
от воздействия uг2
определится
как, учитывая, что
и
:
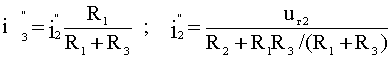
(2.18)
Результирующий
ток i3
найдем как
алгебраическую сумму частных токов:
i3
= i3‘
+ i3”
.
При определении результирующих токов
знак “+” берут у частных токов, совпадающих
с выбранным положительным направлением
результирующего тока, и знак “—” – у
несовпадающих. Как следует из рассмотренного
примера, при
составлении частичных электрических
схем исключаемые идеальные источники
напряжения закорачиваются.
В случае, если
в цепи действуют источники напряжения
с внутренними сопротивлениями Rг,
при их исключении они
заменяются своими внутренними
сопротивлениями Rг.
При наличии
идеальных источников тока соответствующие
ветви исключаемых источников размыкаются,
а при наличии реальных источников они
заменяются своими внутренними
проводимостями Gг.
Если в линейной
цепи приложено напряжение сложной
формы,
применение принципа наложения позволяет
разложить
это воздействие на
сумму простейших
и найти
реакцию цепи на каждое
из них в отдельности с
последующим наложением полученных
результатов.
Методы
контурных токов, узловых напряжений и
эквивалентного генератора
Соседние файлы в папке Лекции по ТОЭ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Результирующий ток
Cтраница 1
Результирующий ток через / 7-л-переход носит название прямого тока. Если U 0 ( обратное смещение), то барьер увеличивается ( рис. 9.21, в), диффузионный ток уменьшается, дрейфовый ток остается неизменным. Результирующий ток называется обратным током.
[1]
Результирующий ток поступает на усилитель; прибор откалиброван на единицы, показывающие общее содержание окислителей.
[2]
Результирующий ток в первичных обмотках выходного трансформатора Тр2, а также ток во вторичной его обмотке синусоидальны.
[3]
Результирующий ток на горизонте будет циркулировать вокруг дыры, как показано на рисунке.
[5]
Результирующий ток через р – – переход /, который в этом случае называется прямым, с ростом прямого напряжения будет расти экспоненциально.
[6]
Результирующий ток через переход складывается из двух встречных потоков электронов. Из р – в n – область валентные электроны переходят на свободные уровни в зоне проводимости, а из п-в р-об-ласть электроны проводимости переходят на свободные уровни валентной зоны.
[8]
Результирующий ток, проходящий через параллельные цепи индуктивного выключателя, слагается из токов в индуктивной ветви и ja – в емкостной ветви.
[9]
Результирующий ток во вторичной обмотке УТП возрастает при уменьшении коэффициента мощности нагрузки, как об этом было сказано выше.
[11]
Результирующий ток, таким образом равен нулю.
[12]
Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников. Для того чтобы результирующие токи совпадали с действительными направлениями, целесообразно выбирать положительные направления результирующих токов после определения токов от всех источников.
[13]
Результирующий ток теоретически может измениться в ту или другую сторону, но, как правило, ток увеличивается, т.е. возрастают потери в обмотках.
[14]
Результирующий ток, получающийся на выходе фотоэлемента, создает на сопротивлении, ( фиг. Со входа третьего каскада усиленное напряжение подается на вход лампы Л3, включенной по схеме фазочувствительного детектора.
[15]
Страницы:
1
2
3
4
5
Подобным образом поступают столько раз, сколько имеется в цепи источников.
Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников.
Для того чтобы результирующие токи совпадали с действительными направлениями, целесообразно выбирать положительные направления результирующих токов после определения токов от всех источников.
Метод наложения весьма удобен для анализа явлений, происходящих в электрических цепях при изменении их параметров.
Например, используя метод наложения, нетрудно определить характер изменения токов ветвей в цепи (см. рис. 13) при увеличении ЭДС E 1 до E 1′ .
Рис. 13. Схема электрической цепи
Действительно, предположим, что при некоторых параметрах цепи до увеличения E 1 установились токи, действительные направления которых совпадают с указанными на рисунке 13. Для решения задачи заменим мысленно увеличение ЭДС E 1 введением в первую ветвь дополнительного источника с r 0доп = 0 и Е доп = E 1′ – E 1. После этого удалим из цепи все источники, кроме источника с ЭДС Е доп, и определим действительные направления дополнительных токов от этого источника, которые очевидны.
Поскольку дополнительный ток первой ветви I 1доп будет совпадать по направлению с током I 1, для определения результирующего тока первой ветви следует воспользоваться формулой I 1′ = I 1 + I 1доп. На основании данной формулы можно сделать вывод о том, что при увеличении Е 1 ток I 1 будет возрастать.
К такому же выводу можно прийти и в отношении токов других ветвей, кроме третьей.
Так как дополнительный ток третьей ветви I 3доп направлен против тока I 3, то для определения результирующего тока нужно использовать формулу I 3′ = I 3 + I 3доп. В отношении результирующего тока третьей ветви можно сделать такой вывод: при увеличении ЭДС Е 1 ток I 3 будет сначала уменьшаться, при некотором значении Е 1 окажется равным нулю, а при дальнейшем увеличении Е 1 изменит направление ( I 3 < 0) и по абсолютному значению будет возрастать.
11. МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Метод эквивалентного генератора дает возможность упростить анализ и расчет электрических цепей в том случае, когда требуется определить ток, напряжение или мощность лишь одной ветви.
Рис. 14. Схема электрической цепи эквивалентного генератора
Предположим, что требуется найти ток I ветви amb некоторой электрической цепи (рис. 14а), остальные элементы которой сосредоточены в предела прямоугольника, представляющего собой активный двухполюсник А .
Согласно методу наложения ток I не изменится, если в данную ветвь ввести два источника, ЭДС которых Е 1 и Е Э равны и направлены в разные стороны (рис. 14б).
Ток I можно определить как разность двух токов: I = I Э + I 1,
где I 1 – ток, вызванный всеми источниками двухполюсника А и ЭДС Е 1 (рис. 14в);
I Э – ток, вызванный только ЭДС Е Э (рис. 14г).
Если выбрать ЭДС Е 1 таким образом, чтобы получить I 1 = 0, то ток I будет равен:
где r 0Э – эквивалентное сопротивление двухполюсника А относительно выводов а и b .
Так как при I 1 = 0 (рис. 14в) активный двухполюсник А будет работать относительно ветви amb в режиме холостого хода, то между выводами a и b установится напряжение холостого хода U = Ux и по второму закону Кирхгофа получим E 1 = I 1 r + Ux . Но по условию Е Э = Е 1, поэтому и Е Э = Ux . Учитывая это, формулу для определения тока I можно записать в такой форме:
В соответствии с последней формулой электрическая цепь (рис. 14а) может быть заменена эквивалентной цепью (рис. 14д), в которой Е Э = Ux и r 0Э следует рассматривать как ЭДС и внутреннее сопротивление некоторого эквивалентного генератора.
В результате возможности такой замены и возникло название изложенного метода.
Значения Е Э = Ux и r 0Э можно определить как расчетным, так и экспериментальным путем. Для расчетного определения Ux и r 0Э необходимо знать параметры элементов активного двухполюсника А и схему их соединения. При определении сопротивления r 0Э необходимо удалить из схемы двухполюсника все источники, сохранив все резистивные элементы, в том числе и внутренние сопротивления источников ЭДС. Внутренние сопротивления источников с указанными напряжениями следует принять равными нулю.
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
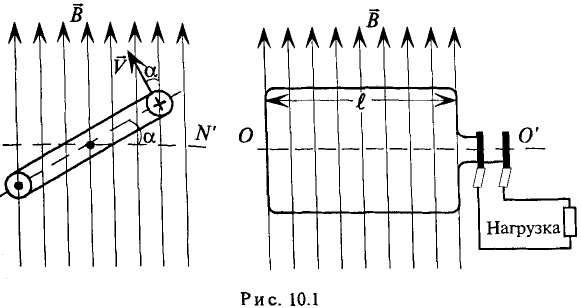
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной
где а – угол, под которым активный проводник рамки пересекает магнитное поле (угол между 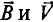
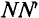
Плоскость 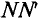
как 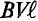
Синусоидальная ЭДС 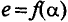
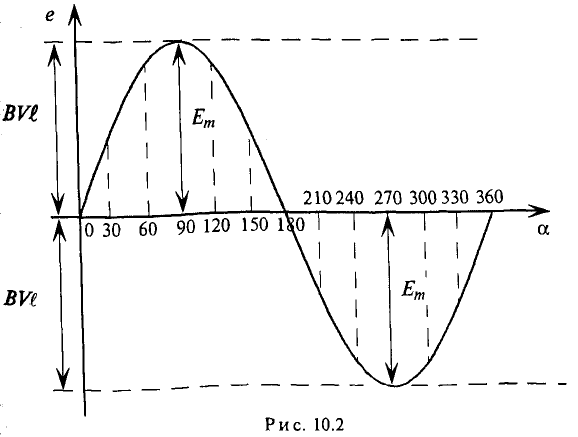
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е.
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 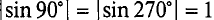
Тогда
Период – это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 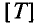
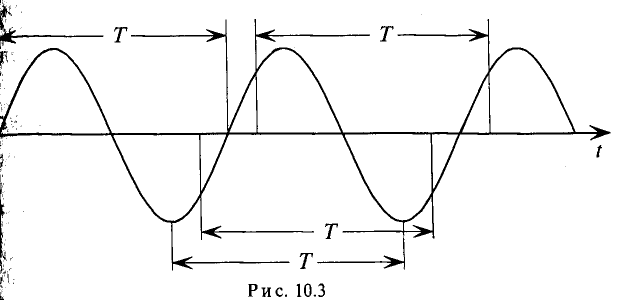
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
где к – целое число.
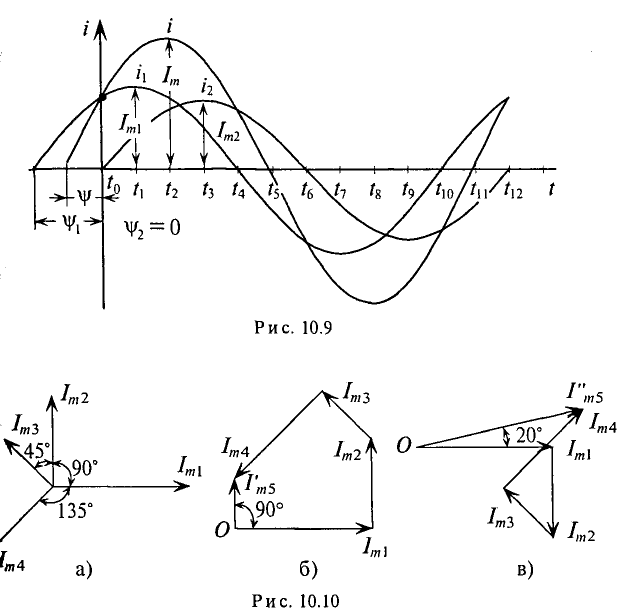
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота – число периодов в единицу времени, т. е. величина, обратная периоду.
Обозначается частота буквой 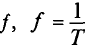
Стандартной частотой в электрических сетях России является частота 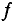
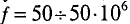
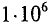
При частоте 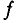
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 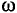
Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:
Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 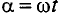
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Фаза и сдвиг фаз
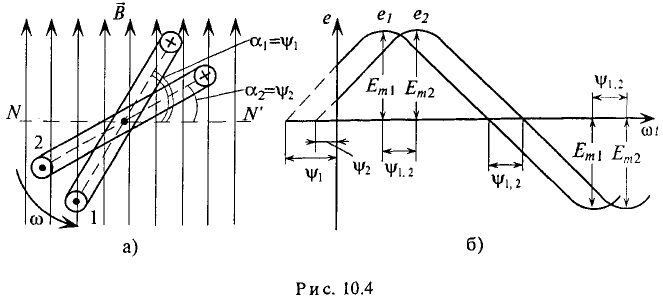
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 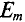
где 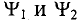
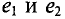
Поэтому эти углы 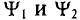
Начальные фазы 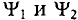
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 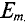

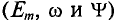


Величина 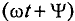
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:
При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 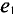
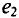
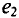
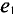
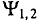
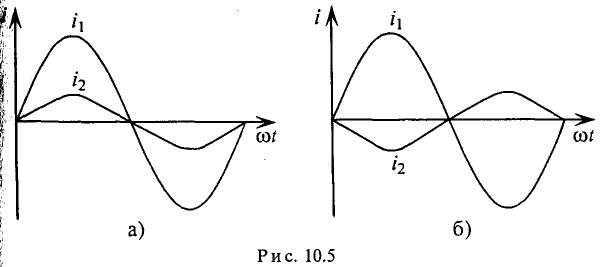
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 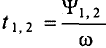
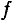
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 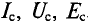
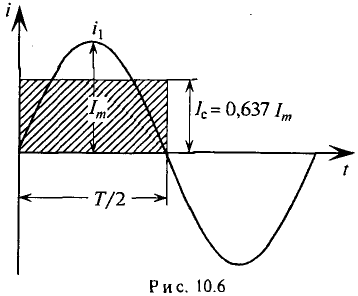
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 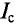
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
Из выражения (2.1) значение переменного тока 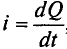
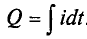
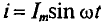
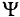
где
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
Откуда действующее значение переменного тока
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 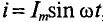
Действующее значение синусоидального тока в 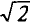
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 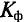
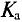
Коэффициент формы 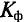
Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
Коэффициент амплитуды 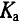
Для синусоидальных величин коэффициент амплитуды равен
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 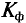
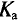
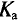
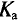
График прямоугольной формы имеет коэффициент амплитуды 1.
Векторные диаграммы
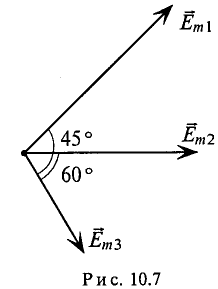
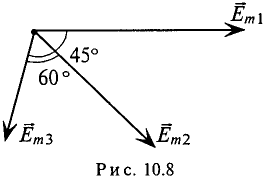
Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте со этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени (t = 0), то они подвижны. Длина вектора в выбранном масштабе определяется амплитудой синусоиды, а угол поворота вектора против часовой стрелки относительно положительного направления оси абсцисс начальной фазе синусоиды. Таким образом, вектор учитывают все значения, характеризующие синусоидальную величину – амплитуду, угловую частоту и начальную фазу, пример, три синусоидальные ЭДС одинаковой частоты
можно изобразить векторами (рис. 10.7).
Совокупность нескольких векторов, изображающих синусоидальные величины одинаковой частоты в начальный момент времени, называется векторной диаграммой.
На векторной диаграмме (рис. 10.7) на-ю видны величины синусоид (ампли-), их начальные фазы и углы сдвига между ними. Очевидно, наибольшую амплитуду имеет ЭДС 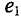
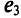
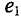
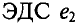
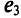
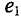

При этом амплитуды ЭДС и углы сдвига фаз остаются неизменными (как и угловая частота), а меняются только начальные фазы синусоид, изображенных на векторной диаграмме (рис. 10.7). В расчетах, если специально не оговорено, начальные фазы не играют роли.
Сложение синусоидальных величин
Сложение и вычитание синусоидальных величин одинаковой частоты можно осуществлять аналитически и графически. В результате такого сложения (вычисления) получается синусоида с той же частотой, с определенной амплитудой и определенной начальной фазой.
Аналитическое сложение предусматривает сложение мгновенных значений синусоидальных величин, выраженных аналитически, т. е.
где
Тогда
Математический анализ позволяет определить суммарную ЭДС е и ее аналитическое выражение.
Графическое сложение можно осуществлять по: 1) волновым (временном) диаграммам и 2) векторным диаграммам.
1. Графическое сложение по временным диаграммам (рис. 10.9) осуществляется следующим образом: ординаты суммарной синусоиды определяются сложением ординат слагаемых синусоид в различные моменты времени.
Как видно, в рассматриваемом примере амплитуда суммарной синусоиды не равна алгебраической сумме амплитуд слагаемых синусоид. Начальная фаза суммарной синусоиды также не является результатом арифметических действий, т.е. по временным диаграммам производятся только графические действия.
2. Графическое сложение по векторным диаграммам осуществляется в следующей последовательности. Прежде всего необходимо построить векторную диаграмму слагаемых синусоидальных величин (рис. 10.10а).
Определение вектора, изображающего суммарную синусоиду, осуществляется сложением векторов слагаемых синусоид по правилу многоугольника, т. е. из какой-либо точки О изображают вектор, соответствующий первой слагаемой синусоиде 10.106), из конца этого вектора изображают вектор, соответствующий второй слагаемой синусоиде, и т.д.
Вектор, соответствующий суммарной синусоиде, проводят из и О к концу последней слагаемой синусоиды.
Тот вектор (рис. 10.106), в масштабе изображения слагаемых синусоид, соответствует амплитуде суммарной синусоиды 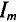
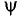
Вычитание синусоидальной величины равносильно умножение этой величины на отрицательную единицу (—1), что соответствует повороту вектора этой величины на 180″ (рис. 10.10 в).
Сложение и вычитание синусоидальных величин по векторный диаграммам рассматривается в примере 10.1.
Пример 10.1
Заданы мгновенные значения четырех токов:
Определить:
1)суммарный ток при условии
2)суммарный ток при условии
3)частоту f всех синусоид.
Решение
Для построения векторной диаграммы слагаемых токов задаются определенным масштабом токов 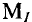
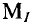
1. Для определения суммарного тока производится сложение векторов по правилу многоугольника (рис. 10.106). Суммарный ток в результате сложения будет равен 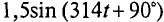
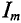
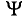
2. Построение многоугольника для заданного условия показано на рис. 10.10в. Из многоугольника определяется результирующий ток
3. Частота слагаемых и результирующих токов будет равна
В заключение можно сделать вывод, что самым удобным и, следовательно, распространенным методом сложения синусоидальных величин является метод графического сложения по векторным диаграммам. Этот метод и будет использован при расчете электрических цепей однофазного и трехфазного тока, изменяющегося по синусоидальному закону.
Так как действующие значения синусоидальных величин пропорциональны их амплитудным значениям (см. (10.9)), то вектор, отражающий в определенном масштабе амплитудное значение, в этом масштабе представляет действующее значение той же вены. Исходя из этого, в дальнейшем на векторных диаграммах будут изображаться векторы, в определенном масштабе представляющие не амплитудное, а действующее значение синусоидальной вены, которое чаще всего используется при расчетах цепей переменного тока.
- Однофазные цепи синусоидального тока
- Законы и правила Кирхгофа для электрических цепей
- Линии с распределенными параметрами
- Идеализированные пассивные элементы
- Закон Ома для замкнутой цепи
- Энергия и мощность электрического тока
- Закон Джоуля — Ленца для тока
- Режимы работы электрических цепей
Содержание
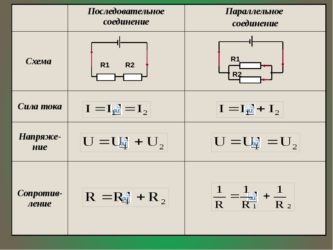
- 1 Сила тока при последовательном соединении
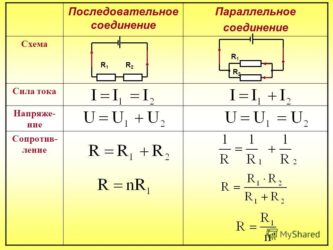
- 1.1 Последовательное и параллельное соединение сопротивлений
- 1.2 Законы последовательного и параллельного соединения проводников
- 2 Суммарная мощность при параллельном соединении. Расчет результирующего сопротивления при последовательно-параллельном соединении
- 2.1 Соединяем последовательно
- 2.2 Включаем параллельно
- 3 Расчет мощности при последовательном соединении — Все об электричестве
- 3.1 Последовательное соединение
- 3.2 Применение
- 3.3 Параллельное соединение
- 3.4 Работа тока
- 3.5 Мощность тока
- 3.6 Влияние схемы соединения на новогоднюю гирлянду
- 3.7 Последовательное и параллельное соединение для конденсаторов
- 3.8 Смешанное соединение проводников
- 3.9 Теперь используем формулу расчета сопротивления:
- 4 Последовательное и параллельное соединения проводников – FIZI4KA
- 4.1 Часть 1
- 4.2 Часть 2
- 4.3 Ответы
- 5 Параллельное и последовательное соединение проводников: теория, формулы, подключение и расчет силы тока
- 5.1 Взаимная зависимость электрических величин
- 5.2 Схемы с несколькими проводниками
- 5.3 Параллельное соединение проводников
- 5.4 Последовательное соединение
- 5.5 Смешанное соединение
- 5.6 Ответ на задачу о елочной гирлянде
Сила тока при последовательном соединении
В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом.
То есть, начало одного резистора соединяется с концом второго, а начало второго – с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках.
Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.
Последовательное и параллельное соединение сопротивлений
Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.
В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии – нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3.
Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь. То есть начало R1 соединяется с концом R2, а начало R2 – с концом R3 и так далее. В такой цепочке может быть любое количество резисторов.
Эти символы используют в расчетах последовательные и параллельные соединения.
Сила тока на всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет напряжение при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.
При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.
Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.
Для того чтобы отобразить эти свойства, вновь понадобится закон Ома. В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n.
Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться.
В виде формул все характеристики отображаются следующим образом: сила тока – I = I1 + I2 + I3, напряжение – U = U1 = U2 = U3, сопротивление – 1/R = 1/R1 + 1/R2 + 1/R3.
При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.
В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как смешанное соединение. Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.
Законы последовательного и параллельного соединения проводников
Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке.
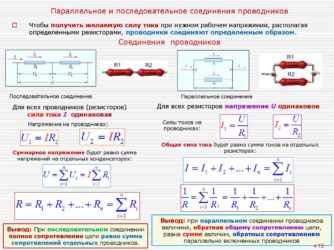
В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке.
Отсюда выводится и формула последовательного соединения.
Более сложные вычисления с участием других величин требуют применения правила Кирхгофа. Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них.
Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n.
Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.
В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.
Источник: https://electric-220.ru/news/sila_toka_pri_posledovatelnom_soedinenii/2017-04-11-1227
Суммарная мощность при параллельном соединении. Расчет результирующего сопротивления при последовательно-параллельном соединении
Это хотя и довольно простая тема, но очень важная. Правила всего два: при последовательном соединении складываются сопротивления резисторов, а при параллельном складываются их проводимости, которые, по определению из главы /, есть величины, обратные сопротивлению (см. рис. 5.3).
Понять, почему правила именно таковы, можно, если рассмотреть течение токов в обоих случаях — при последовательном соединении ток I через резисторы один и тот же, поэтому падения напряжения на них складываются, что равносильно сложению сопротивлений. При параллельном соединении, наоборот, равны падения напряжений U, а складывать приходится токи, что равносильно сложению проводимостей.
Если вы не поняли вышесказанное, то посидите над рис. 5.3 с карандашом и бумагой и выведите выражения закона Ома для каждого из случаев — и все станет на свои места.
Рис. 5.3. Последовательное и параллельное соединение резисторов
Из этих определений вытекает несколько практических правил, которые полезно заучить:
При последовательном соединении:
Пара резисторов имеет сопротивление всегда больше, чем сопротивление резистора с большим номиналом (правило «больше большего»);
Если номиналы резисторов равны, то суммарное сопротивление ровно вдвое больше каждого номинала;
Если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно большему номиналу (типичный случай упоминался в главе 1: в примере на рис. 1.4 мы игнорируем сопротивление проводов, так как оно много меньше сопротивления резисторов);
При параллельном соединении:
Пара резисторов имеет сопротивление всегда меньше, чем сопротивление резистора с меньшим номиналом (правило «меньше меньшего»);
Если номиналы резисторов равны, то суммарное сопротивление ровно вдвое меньше каждого номинала;
Если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно меньшему номиналу (это также можно проиллюстрировать на примере рис. 1.4, где мы игнорируем наличие вольтметра, включенного параллельно R2, так как его сопротивление намного больше сопротивления резистора).
Знание этих правил поможет вам быстро оценивать схему, не занимаясь алгебраическими упражнениями и не прибегая к помощи калькулятора. Даже если соотношение сопротивлений не попадает под перечисленные случаи, результат все равно можно оценить «на глаз» с достаточной точностью.
При параллельном соединении, которое представляет большую сложность при расчетах, для такой оценки нужно прикинуть, какую долю меньшее сопротивление составляет от их арифметической суммы- приблизительно во столько раз снизится их общее сопротивление по отношению к меньшему. Проверить это легко: пусть одно сопротивление имеет номинал 3,3 кОм, второе — 6,8 кОм.
В соответствии с изложенным мы будем ожидать, что общее сопротивление должно быть на 30% меньше, чем 3,3 кОм, то есть 2,2 кОм (3,3 составляет примерно одну треть от суммы 3,3+6,8, то есть общее сопротивление должно быть меньше, чем 3,3, на треть от этого значения, равную 1,1 — в результате и получаем 2,2).
Если мы проверим результат, полученный такой прикидкой в уме, точным расчетом, то мы получим в результате очень близкое значение 2,22 кОм.
В большинстве случаев нам такой точности и не требуется — помните, что и сами сопротивления имеют разброс по номиналу, и в большинстве обычных схем допуски на номиналы стандартных компонентов могут быть довольно велики (по крайней мере, в правильно составленных схемах).
Если же схема в некоторых случаях должна все же иметь какие-то строго определенные параметры, то с помощью стандартных компонентов вы все равно этого не добьетесь — параметры будут «гулять» (в пределах допусков, естественно) от дуновения ветерка из форточки, и в таких случаях надо применять прецизионные резисторы и конденсаторы, а во времязадающих цепях использовать кварцевые резонаторы.
Но составлять схему так, чтобы она теряла работоспособность от замены резистора 1 кОм на резистор 1,1 кОм — не наш метод!
Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. (10+)
Расчет параллельно / последовательно соединенных резисторов, конденсаторов и дросселей
Параллельное или последовательное соединение (включение) применяется обычно в нескольких случаях. Во-первых, если нет резистора номинала. Во-вторых, если есть потребность получить резистор большей мощности.
В-третьих, Если необходимо точно подобрать номинал детали, а устанавливать подстроечник нецелесообразно из соображений надежности. Большинство радиодеталей имеют допуски. Чтобы их компенсировать, например для резистора, последовательно с большим резистором устанавливают меньший в разы.
Подбор этого меньшего резистора позволяет получить точно нужное значение сопротивления.
Соединяем последовательно
= += [Сопротивление первого резистора, кОм] * [Сила тока, мА] 2 / 1000= [Сопротивление второго резистора, кОм] * [Сила тока, мА] 2 / 1000Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт.
Включаем параллельно
1 / (1 / [Сопротивление первого резистора, кОм] + 1 / [Сопротивление второго резистора, кОм])Эта формула интуитивно понятна, да и формально может быть выведена из следующего соображения. При заданном напряжении на резисторах через каждый из них независимо идет ток, равный напряжению, деленному на сопротивление. Итоговое сопротивление равно напряжению, деленному на суммарный ток. В формулах значение напряжения счастливым образом сокращается, и получается приведенная формула.[Мощность, рассеиваемая первым резистором, Вт] = [Напряжение на резисторах, В] 2 / [Сопротивление первого резистора, кОм] / 1000[Мощность, рассеиваемая вторым резистором, Вт] = [Напряжение на резисторах, В] 2 / [Сопротивление первого резистора, кОм] / 1000Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе.Если что-то непонятно, обязательно спросите!
Понятия и формулы
Последовательно-параллельное, или смешанное, соединение представляет собой сложное соединение трех и более сопротивлений. Результирующее сопротивление при смешанном соединении рассчитывается поэтапно с применением формул расчета сопротивлений при последовательном и параллельном соединениях.
Примеры
Сначала заменим параллельно соединенные сопротивления r2 и r3 результирующим сопротивлением r(2-3):
r(2-3)=(r2∙r3)/(r2+r3)=(10∙20)/30=6,6 Ом.
Результирующее сопротивление всей схемы r=r1+r(2-3)=5+6,6=11,6 Ом.
Рис. 1.
2. Какой ток протекает по цепи (рис. 2) в случаях разомкнутого и замкнутого P? Как изменяется напряжение на сопротивлении r2 в обоих случаях?
Рис. 2.
а) Рубильник разомкнут. Результирующее сопротивление последовательно включенных сопротивлений r1 и r2
r(1-2)=r1+r2=25 Ом.
Ток I(1-2)=U/r(1-2) =100/25=4 А.
Падение напряжения на сопротивлении r2
U2=I(1-2)∙r2=4∙5=20 В.
б) Рубильник замкнут. Результирующее сопротивление параллельно включенных сопротивлений r1 и r3
r(1-3)=(r1∙r3)/(r1+r3)=(20∙10)/(20+10)=200/30=6,6 Ом.
Общее сопротивление всей схемы r=r(1-3)+r2=6,6+5=11,6 Ом.
Ток I=U/r=100/11,6=8,62 А.
Падение напряжения на сопротивлении r2 в этом случае равно: U2=I∙r2=8,62∙5=43,25 В.
Во втором случае ток увеличился в результате подключения параллельного сопротивления R3. Больший ток создает большее на сопротивлении r2.
3. Каким должно быть rд, чтобы две параллельно соединенные лампы на напряжение 120 В и ток 0,2 А могли быть включены в сеть напряжением U=220 В (рис. 3)?
Рис. 3.
Напряжение на лампах должно быть равно 120 В. Остальное напряжение (100 В) падает на дополнительном сопротивлении rд. Через сопротивление rд проходит ток двух ламп I=0,4 А.
По закону Ома rд=Uд/I=100/0,4=250 Ом.
4. Электронные лампы с напряжением накала 1,2 В и током накала 0,025 и 0,05 А подключены последовательно к источнику постоянного тока напряжением 4,5 В. Какими должны быть добавочное сопротивление rд и к лампе, имеющей меньший ток накала (рис. 4)?
Рис. 4.
Сопротивления в схеме должны быть подобраны так, чтобы протекал ток накала второй лампы I=0,05 А. Напряжение на нитях накаливания электронных ламп будет равно 1,2+1,2=2,4 В. Вычтя эту величину из напряжения батареи, получим величину падения напряжения на добавочном сопротивлении rд: Uд=4,5-2,4=2,1 В.
Отсюда дополнительное сопротивление rд=(Uд)/I=2,1/0,05=42 Ом.
Ток накала 0,05 А не должен весь протекать через нить первой электронной лампы. Половина этого тока (0,05-0,025=0,025 А) должна пройти через шунт r. Напряжение на шунте такое же, как и на нити лампы, т. е. 1,2 В. Отсюда сопротивление шунта равно: r=1,2/0,025=48 Ом.
5. Каковы результирующие сопротивление цепи и ток в ней в схеме на рис. 5?
Рис. 5.
Прежде всего, определим результирующее сопротивление параллельно соединенных сопротивлений:
r(1-2)=(r1∙r2)/(r1+r2)=(2∙4)/(2+4)=8/6=1,3 Ом;
r(4-5)=(r4∙r5)/(r4+r5)=(15∙5)/(15+5)=75/20=3,75 Ом.
Результирующее сопротивление цепи равно:
r=r(1-2)+r3+r(4-5)=1,3+10+3,75=15,05 Ом.
Результирующий ток при напряжении U=90,5 В
I=U/r=90,5/15,05=6 А.
Рис. 6.
Результирующая проводимость параллельно включенных сопротивлений
1/r(3-4-5) =1/r3 +1/r4 +1/r5 =1/5+1/10+1/20=7/20 сим;
r(3-4-5)=20/7=2,85 Ом.
Сопротивление цепи из r1 и r2 равно:
r(1-2)=r1+r2=15+5=20 Ом.
Результирующая проводимость и сопротивление между точками А и В соответственно равны: 1/rAB =1/r(3-4-5) +1/r(1-2) =7/20+1/20=8/20 сим; rAB=20/8=2,5 Ом.
Результирующее сопротивление всей схемы r=rAB+r6=2,5+7,5=10 Ом.
Результирующий ток I=U/r=24/10=2,4 А.
Напряжение между точками А и В равно напряжению источника U за вычетом падения напряжения на сопротивлении r6
UAB=U-I∙r6=24-(2,4∙7,5)=6 В.
На это напряжение включено сопротивление r4, поэтому ток, проходящий через него, будет равен:
I4=UAB/r4 =6/10=0,6 А.
Сопротивления r1 и r2 имеют общее падение напряжения UAB, поэтому ток, проходящий через сопротивление r1, равен:
I1=UAB/r(1-2) =6/20=0,3 А.
Падение напряжения на сопротивлении r1
Ur1=I1∙r1=0,3∙15=4,5 В.
7. Каковы результирующее сопротивление и ток в схеме на рис. 7, если напряжение источника U=220 В?
Рис. 7.
Начинаем с контура, расположенного справа от узлов 3 и 3. Сопротивления r7, r8, r9 соединены последовательно, поэтому
r(7-8-9)=r7+r8+r9=30+40+20=90 Ом.
Параллельно этому сопротивлению включено сопротивление r6, поэтому результирующее сопротивление в узле 3 и 3 (разрез a)
ra=(r6∙r(7-8-9))/(r6+r(7-8-9))=(20∙90)/(20+90)=1800/110=16,36 Ом.
Последовательно с сопротивлением ra включены сопротивления r4 и r5:
r(4-5-a)=10+20+16,36=46,36 Ом.
Результирующее сопротивление в узлах 2 и 2 (разрез b)
rb=(r(4-5-a)∙r3)/(r(4-5-a)+r3)=(46,36∙30)/(46,36+30)=1390,8/76,36=18,28 Ом.
Результирующее сопротивление всей цепи r=r1+rb+r2=40+18,28+10=68,28 Ом.
Результирующий ток I=U/r=220/68,28=3,8 А.
Источник: https://homele.ru/electrician/total-power-with-parallel-connection-calculation-of-the-resulting-resistance-in-a-seriesparallel-connection/
Расчет мощности при последовательном соединении — Все об электричестве
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой.
Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка.
Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторов
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Источник: https://contur-sb.com/raschet-moschnosti-pri-posledovatelnom-soedinenii/
Последовательное и параллельное соединения проводников – FIZI4KA
ОГЭ 2018 по физике ›
1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).
Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.
При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: ( I_1=I_2=I ).
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: ( R_1=R_2=R ). Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: ( U_1=IR_1 ), ( U_2=IR_2 ), а общее напряжение равно ( U=I(R_1+R_2) ). Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: ( U=U_1+U_2 ).
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).
Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: ( U_1=U_2=U ).
При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: ( I=I_1+I_2 ).
В соответствии с законом Ома ( I=frac{U}{R} ), ( I_1=frac{U_1}{R_1} ), ( I_2=frac{U_2}{R_2} ). Отсюда следует: ( frac{U}{R}=frac{U_1}{R_1}+frac{U_2}{R_2} ). Так как ( U_1=U_2=U ), ( frac{1}{R}=frac{1}{R_1}+frac{1}{R_2} ). Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление ( r ), то их общее сопротивление равно: ( R=r/2 ). Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.
- Примеры заданий
- Ответы
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ( R_1 ) и ( R_2 ). Напряжения на резисторах соответственно ( U_1 ) и ( U_2 ).
По какой из формул можно определить напряжение U на участке АВ?
1) ( U=U_1+U_2 )
2) ( U=U_1-U_2 )
3) ( U=U_1=U_2 )
4) ( U=frac{U_1U_2}{U_1+U_2} )
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ( R_1 ) и ( R_2 ). Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) ( I=I_1=I_2 )
2) ( I=I_1+I_2 )
3) ( U=U_1+U_2 )
4) ( R=R_1+R_2 )
3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R} и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) ( U=U_1+U_2 )
2) ( I=I_1+I_2 )
3) ( U=U_1=U_2 )
4) ( R=frac{R_1R_2}{R_1+R_2} )
4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ( R_1 ) и ( R_2 ). Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) ( U=U_1=U_2 )
2) ( I=I_1+I_2 )
3) ( I=I_1=I_2 )
4) ( R=frac{R_1R_2}{R_1+R_2} )
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ( R_1 ). По какой из формул можно определить общее сопротивление цепи ( R )?
1) ( R=R_1{}2 )
2) ( R=2R_1 )
3) ( R=frac{R_1}{2} )
4) ( R=sqrt{R_1} )
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ( R_1 ) и ( R_2 ) равны. Чему равно сопротивление каждого резистора?
1) 81 Ом 2) 18 Ом 3) 9 Ом
4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?
1) 1/3 Ом 2) 3 Ом 3) 9 Ом
4) 27 Ом
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ( R_1 ) = 1 Ом, ( R_2 ) = 10 Ом, ( R_3 ) = 10 Ом, ( R_4 ) = 5 Ом?
1) 9 Ом 2) 11 Ом 3) 16 Ом
4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ( R_1 ) = 1 Ом, ( R_2 ) = 3 Ом, ( R_3 ) = 10 Ом, ( R_4 ) = 10 Ом?
1) 9 Ом 2) 10 Ом 3) 14 Ом
4) 24 Ом
10. Если ползунок реостата (см. схему) переместить влево, то сила тока
1) в резисторе ( R_1 ) уменьшится, а в резисторе ( R_2 ) увеличится 2) увеличится в обоих резисторах
3) в резисторе ( R_1 ) увеличится, а в резисторе ( R_2 ) уменьшится
4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?
Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА A) сопротивление реостата 2 Б) сила тока в цепи
B) напряжение на резисторе 1
ХАРАКТЕР ИЗМЕНЕНИЯ 1) увеличивается 2) уменьшается
3) не изменяется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов ( R_1 ) и ( R_2 ). Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе ( R_1 ) и ( R_2 )
Б) напряжение на резисторе ( R_2 )
B) общее напряжение на резисторах ( R_1 ) и ( R_2 )
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ( R_1 ) = 10 Ом, ( R_2 ) = 5 Ом, ( R_3 ) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?
Ответы
Источник: https://fizi4ka.ru/ogje-2018-po-fizike/posledovatelnoe-i-parallelnoe-soedinenija-provodnikov.html
Параллельное и последовательное соединение проводников: теория, формулы, подключение и расчет силы тока
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы.
Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой.
Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
- Электрическое напряжение, согласно научному определению, это разность потенциалов между двумя точками электрической цепи. Измеряется в вольтах (В). Между клеммами бытовой розетки, к примеру, оно равно 220 В, на батарейке вольтметр покажет 1,5 В, а зарядное устройство вашего планшета или смартфона выдает 5 В. Напряжение бывает переменным и постоянным, но в нашем случае это несущественно.
- Электрический ток – упорядоченное движение электронов в электрической цепи. Ближайшая аналогия – ток воды в трубопроводе. Измеряется в амперах (А). Если цепь не замкнута, ток существовать не может.
- Электрическое сопротивление. Величина измеряется в омах (Ом) и характеризует способность проводника или электрической цепи сопротивляться прохождению электрического тока. Если продолжить аналогию с водопроводом, то новая гладкая труба будет иметь маленькое сопротивление, забитая ржавчиной и шлаками – высокое.
- Электрическая мощность. Эта величина характеризует скорость преобразования электрической энергии в любую другую и измеряется в ваттах (Вт). Кипятильник в 1000 Вт вскипятит воду быстрее стоваттного, мощная лампа светит ярче и т.д.
Взаимная зависимость электрических величин
Теперь необходимо определиться, как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.
- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.
Схема люстры с тремя лампами
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ. – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Последовательно соединенная нагрузка
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет. Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Последовательное соединение трех ламп в гирлянду
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3.
То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше.
Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.
- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ.23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ.245).
Ну а дальше все очевидно, поскольку остались R1, R6 и найденное нами Rобщ.2345, соединенные последовательно:
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Схема елочной гирлянды из миниатюрных ламп накаливания
Источник: https://220v.guru/fizicheskie-ponyatiya-i-pribory/tok-provodnikov-v-parallelnom-i-posledovatelnom-soedinenii.html