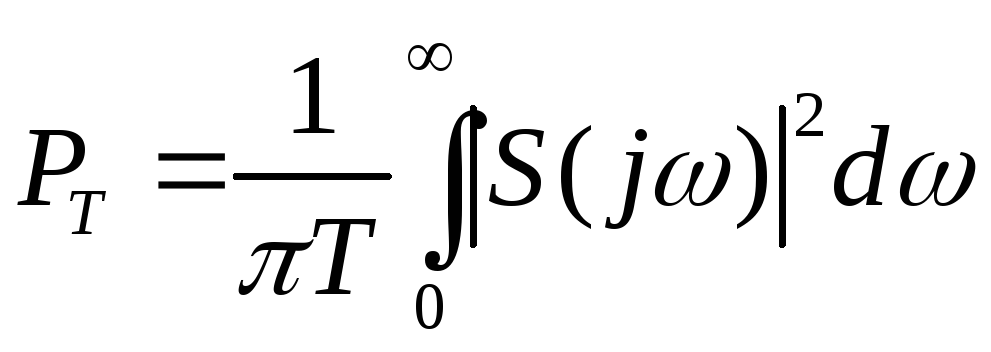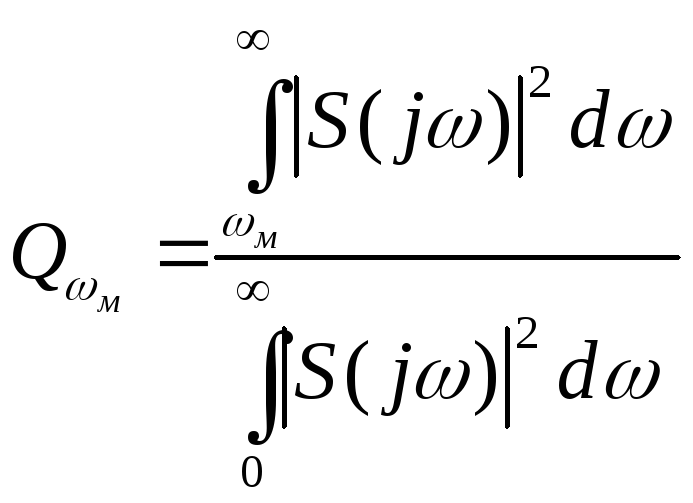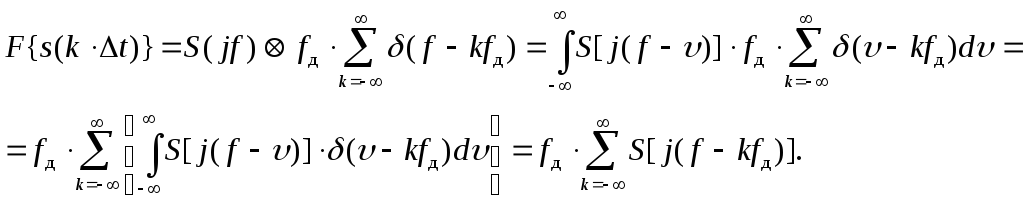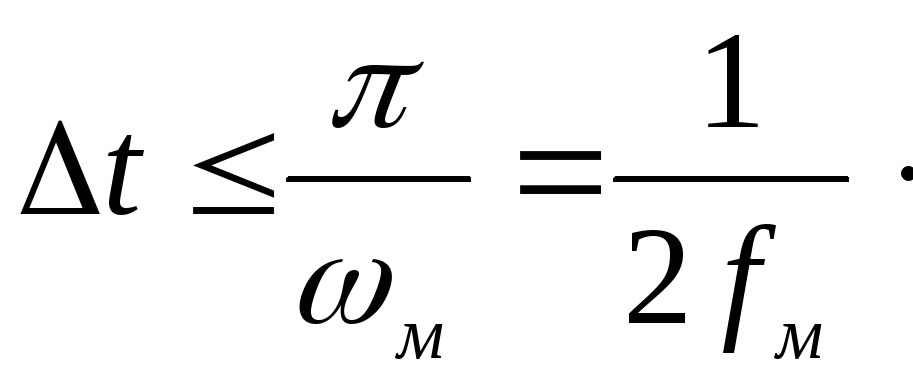Шаг дискретизации как найти

3.1.1.1. Дискретизация.

В основу дискретизации
положена принципиальная возможность
представления непрерывных сигналов в
виде взвешенных сумм:

(3.1)

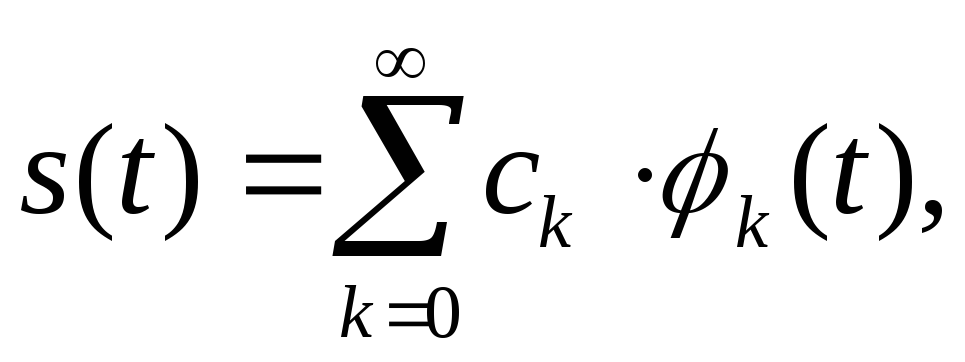
где

– некоторые коэффициенты или отсчеты,
характеризующие исходный сигнал в
дискретные моменты времени,

– набор элементарных
функций, с помощью которых происходит
восстановление сигнала по его отсчетам.

Очевидно, что по
дискретным значениям

исходную функцию

можно восстановить с некоторой
погрешностью. Часто функцию, полученную
в результате восстановления (интерполяции)
по значениям
,
называют воспроизводящей и обозначают
каким-либо другим, отличным от исходного
сигнала
,
символом, например

/4/ .

Понятно, что при
обработке сигналов дискретизация по
времени должна производиться таким
образом, чтобы по отсчетным значениям

можно было бы получить воспроизводящую
функцию
,
которая с заданной точностью отображает
исходную функцию
.

Как уже отмечалось,
при дискретизации приходится решать
вопрос о том, как часто следует брать
отсчеты функции, т.е. каким должен быть
шаг дискретизации

При малом

количество отсчетов преобразуемого
сигнала на интервале обработки будет
большим и точность воспроизведения –
высокой. Однако при отсчетах, взятых в
слишком близко расположенных точках,
будут получаться коррелированные
данные, число которых будет избыточно
велико, что неизбежно вызовет увеличение
как объема, так и стоимости расчетов. С
другой стороны, при больших

количество отсчетов уменьшится, но при
этом, как правило, снижается точность
восстановления и, кроме того, при
дискретизации реальных сигналов может
привести к явлению наложения (маскировки)
низко- и высокочастотных составляющих.
Оптимальной является такая дискретизация,
которая обеспечивает представление
исходного сигнала с заданной точностью
при минимальном числе выборок,
обусловленными необходимостью адекватного
представления существенной информации,
содержащейся в высокочастотной части
спектра сигнала.

Наиболее
распространенной является равномерная
дискретизация, при которой шаг (интервал)
дискретизации остается постоянным:

Величина, обратная
интервалу дискретизации,

называется частотой дискретизации.

Методы равномерной
дискретизации нашли широкое применение
вследствие того, что алгоритмы
дискретизации и восстановления сигналов,
а также соответствующая аппаратура,
реализующая их, в этом случае достаточно
просты.

Равномерная
дискретизация, как известно, основывается
на разложении исходного непрерывного
сигнала в ряд Котельникова. Это разложение
составляет основу теоремы Котельникова
(за рубежом ее называют теоремой Шеннона,
или просто теоремой отсчетов). Суть
теоремы отсчетов состоит в следующем:
непрерывная функция времени
,
не содержащая частот выше
,
полностью определяется отсчетами
мгновенных значений

в точках, отстоящих друг от друга на
интервал
.

В формулировке
автора эта теорема звучит так: любую
функции
,
состоящую из частот от

до
,
можно непрерывно передавать с любой
точностью при помощи чисел, следующих
друг за другом через

с.

В этом случае
исходный сигнал

может быть восстановлен без погрешностей
по точным значениям выборок

в виде

(3.2)

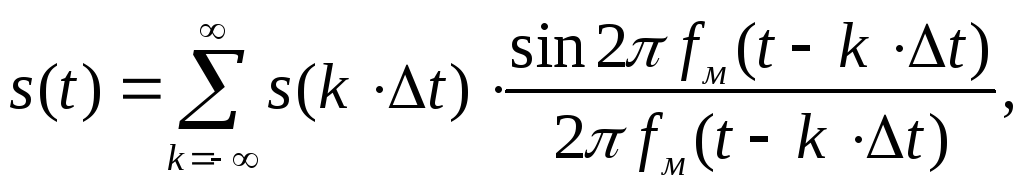
где

– шаг (интервал) дискретизации.

Из выражения (3.2)
видно, что непрерывная функция

представляется суммой (бесконечной)
произведений, один из сомножителей
которых есть выборка функции, а другой
– так называемая функция отсчетов

(3.3)

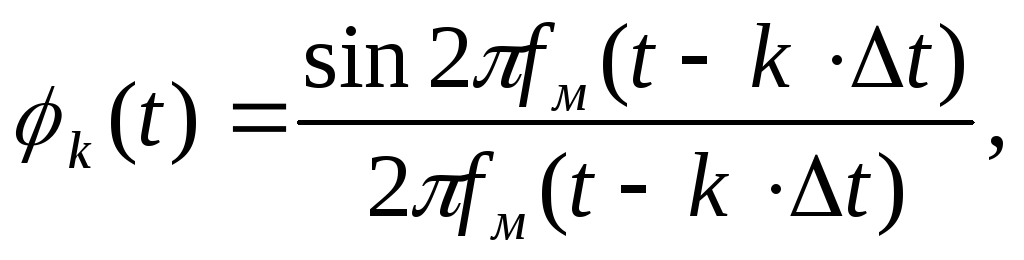
график которой
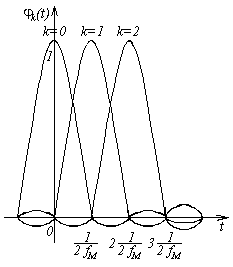
приведен на рис.3.4.

Рис.3.4. Функции отсчетов

Свойства функции
отсчетов:

1) в момент времени

функция

достигает своего наибольшего значения,
равного единице;

2) в моменты времени

,
где

– любое целое положительное число,
функция

обращается в нуль;

3) функции отсчетов
ортогональны с весом единица на
бесконечном интервале времени;

4) ширина лепестка
функций отсчетов на нулевом уровне
равна
.

Каждое слагаемое
ряда (3.2) можно рассматривать как отклик
идеального фильтра нижних частот с
верхней граничной частотой
,
когда на вход фильтра поступает
–
импульс, тождественный выборке временной
функции в момент
.Следует
отметить, что идеальный фильтр физически
не реализуем.

При практическом
применении теоремы отсчетов возникают
некоторые дополнительные погрешности
представления. Наиболее существенными
из них являются следующие. Теорема
отсчетов относится к сигналам с
ограниченным спектром. Реальные сигналы,
являющиеся носителями информации, имеют
ограниченную длительность. Следовательно,
точное разложение (3.2) заменяется
следующим приближенным:

(3.4)

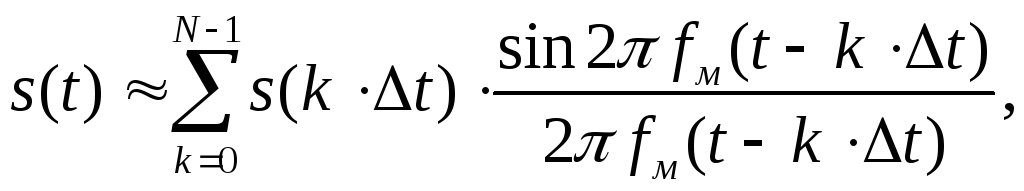
Причем, общее число
независимых параметров, т.е. значений

равно
,
если учитывать отсчеты на концах
интервала обработки
.
Обычно

и

полагают равным
.

Очевидно, что
погрешность представления будет в этом
случае тем больше, чем меньше число
членов разложения участвует в
восстановлении функции
.

Другая причина,
вызывающая погрешность при представлении
реальных сигналов рядом Котельникова,
состоит в том, что из-за конечной
длительности их частотный спектр не
ограничен. Если ограничить реальный
спектр сигнала, простирающийся от нуля
до бесконечности, некоторым диапазоном
частот от нуля до
,
в котором сосредоточена основная часть
энергии, то дисперсия приведенной
погрешности будет определяться выражением
/5/:

(3.5)

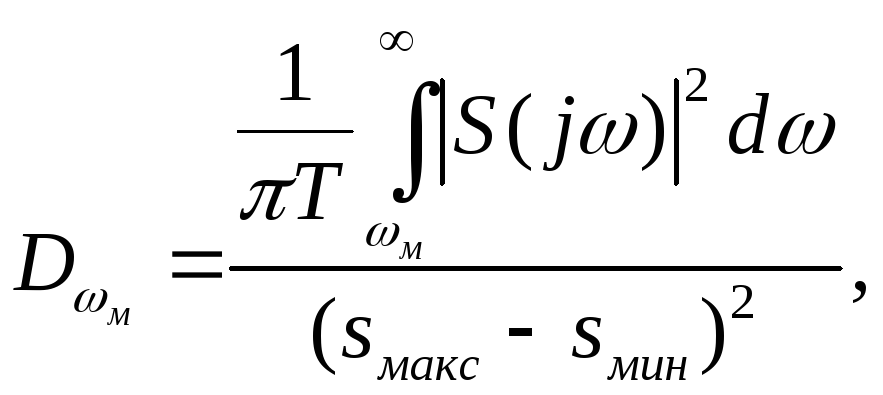
где

– преобразование Фурье исследуемого
сигнала,

Т –
длительность функции s(t),

– пиковые значения
функции s(t).

Нетрудно заметить,
что числитель выражения (3.5) определяет
среднюю мощность отсекаемой части
частотного спектра функция s(t).

Для удобства
расчётов (3.5) можно представить в виде

(3.6)

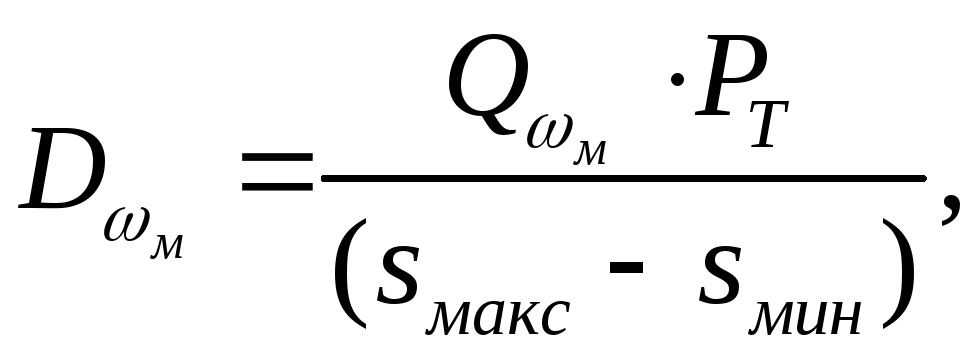
где

– средняя мощность сигнала,

–
относительная площадь отсекаемого
участка энергетического спектра сигнала
s(t).

Выражение (3.6) по
заданной величине

и при известных

и спектре функции s(t)
позволяет определить частоту
,
ограничивающую спектр.

Теорема отсчетов
может быть обобщена и на случай сигналов,
спектр которых начинается не с нулевой
частоты.

В идеальном случае
процесс дискретизации можно представить
как произведение исходного сигнала
s(t)
на последовательность единичных
импульсов (дельта-импульсов):

(3.7)

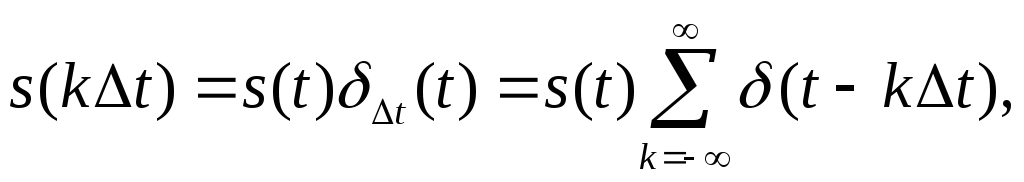
где

– интервал дискретизации,

(t)
– дельта-функция Дирака.

Найдем преобразование
Фурье выражения (3.7). На основании теоремы
о свертке получим:

(3.8)

где

и
–
преобразование Фурье функций

и

соответственно,

– условное обозначение
операции свертки,

F – оператор
преобразования Фурье.

Так как

где

– частота дискретизации,

то выражение (3.8)
можно представить в виде:

Отсюда
видно, что спектр исходного сигнала

повторяется по частоте через интервал

Гц. Графически это выглядит следующим
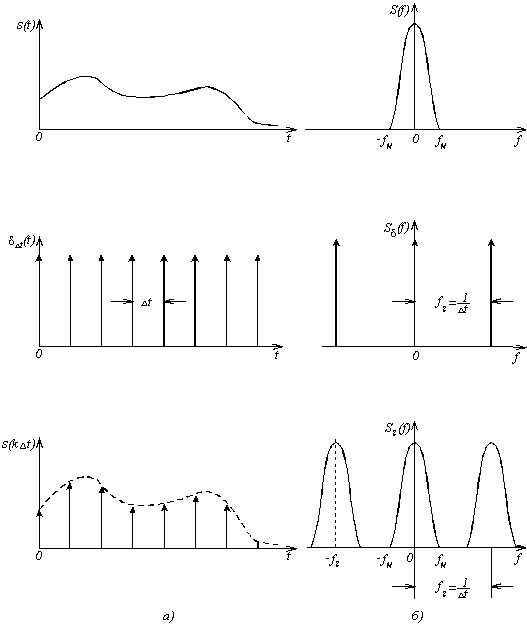
образом, рис.3.5.

Рис.3.5. Дискретизация сигналов с помощью
последовательности единичных импульсов;
а) – представление во временной области;
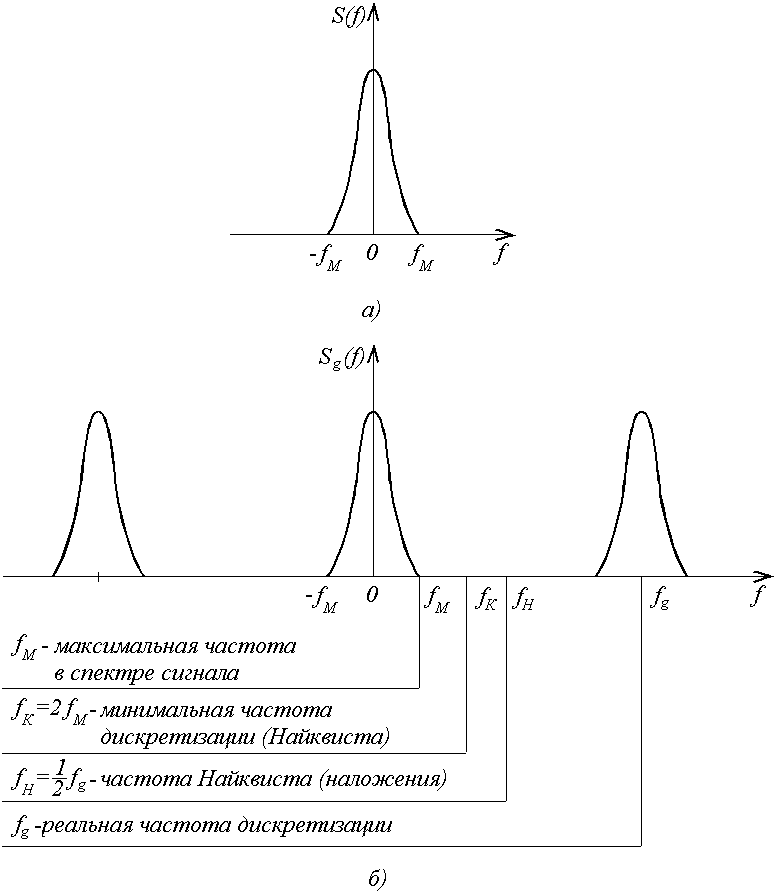
б) – представление в частотной области.

Как видно, спектр
исходного сигнала

повторяется периодически без взаимного
перекрытия, если

или, что тоже самое

Следующий рисунок
3.6 иллюстрирует различные соотношения
между частотой дискретизации и
максимальной частотной составляющей
в спектре преобразуемого сигнала.

Рис.3.6. Иллюстрация соотношения между
частотой дискретизации

и максимальной частотой

в спектре сигнала

Легко заметить из
первых двух рисунков, что форма спектра
сохраняется в диапазоне частот выше
удвоенной максимальной частоты в спектре
исходного сигнала, т.е. при выборе частоты
дискретизации

(в том случае, когда спектр преобразуемого
сигнала резко ограничен частотой
).
При неправильном выборе частоты
дискретизации составляющие спектра,
превышающие частоту

нельзя будет отличить от составляющих,
лежащих в интервале частот от 0 до
,
что приводит к возникновению эффекта,
известного как наложение спектров
(aliasing).

В самом деле,
нетрудно показать, что

если выборка
осуществляется в моменты времени
.
В этом случае для любой частоты

из диапазона 0 –

имеется набор частот, замаскированных
под

Например, если

=200
Гц, то составляющие с частотой 30 Гц будут
неотделимы от составляющих с частотами
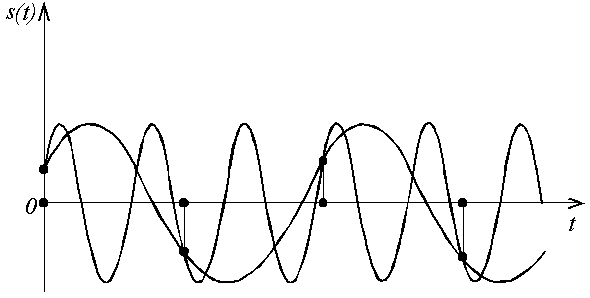
170, 230, 370, 430 и т.д. Эти составляющие будут
неотделимы в том смысле, что в точках
дискретизации они имеют одинаковые
значения, рис.3.7.

Рис.3.7. Частотные искажения (эффект
наложения), связанные с дискретизацией

Влияние дискретизации
будет проявляться в том, что энергия
составляющих с частотами выше

будет отражена в главный диапазон
энергетического спектра симметрично
относительно
,
рис.3.8.

Рис.3.8. Влияние дискретизации на
энергетический спектр преобразуемых
сигналов: а) – энергетический спектр
непрерывного сигнала; б) – энергетический
спектр после дискретизации

Это явление известно
из кино и телевидения. По мере того как
колеса телеги вращаются все быстрее и
быстрее, нам кажется, что они замедляют
свое движение и затем останавливаются.
Если частота вращения продолжает
увеличиваться, то будет казаться, что
колеса вращаются назад, останавливаются,
вращаются вперед и так последовательно
несколько раз. Очевидно, что эти эффекты
связаны с дискретизацией изображения
кинокамерой.

Таким образом,
явление наложения или маскировки частот,
несвойственное аналоговым методам
обработки, является источником
специфической погрешности, которую
необходимо учитывать при практическом
применении цифровых методов обработки
сигналов.

В заключение
уточним некоторые термины теории
дискретизации, встречающиеся в литературе.
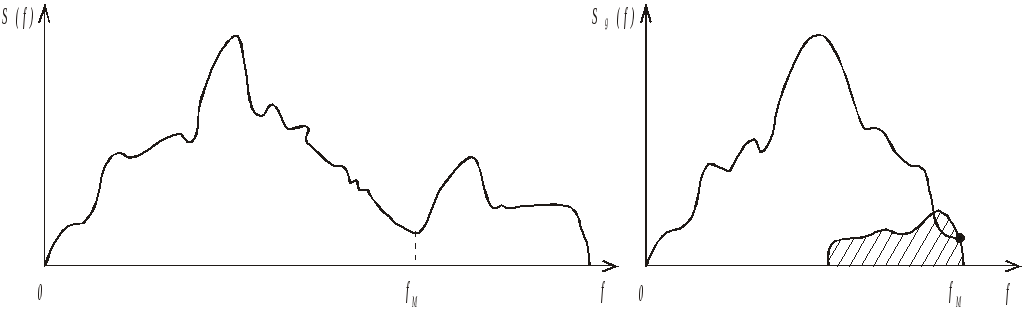
Для этого обратимся к рисунку 3.9.

Рис.3.9. Наглядное представление некоторых
терминов теории дискретизации: а) –
спектр исходного сигнала; б) – спектр
сигнала после дискретизации

Наивысшая частота

,
присутствующая в спектре сигнала, иногда
называется частотой Котельникова.
Частота

является наименьшей частотой, при
которой можно дискретизировать сигнал,
а затем восстановить его по дискретным
отсчетам. Интервал
–
интервал Котельникова (Найквиста).
Частота

– это частота дискретизации, выбранная
в конкретной (реальной) системе обработки.
Величина, обратная реальной частоте
дискретизации,

называется интервалом (шагом) дискретизации.
Частотой Найквиста (наложения) обычно
называют половину реальной частоты
дискретизации.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

9. Дискретные сигналы

Мы рассмотрели в предыдущих разделах методы описания аналоговых сигналов и ряд способов их преобразования: модуляцию, детектирование и фильтрацию. После осуществления модуляции сигнала, его усиления, высокочастотной фильтрации, демодуляции и низкочастотной фильтрации формируется сигнал постоянного тока, пропорциональный первичному сообщению. В таком виде сигнал может быть выведен на отчетное устройство или на самописец с целью его регистрации.

Теперь обратимся к другому классу сигналов – к дискретным сигналам и способам их преобразований. Аналоговый сигнал преобразуют в дискретный сигнал с целью его ввода в цифровой процессор. Здесь можно осуществить в цифровой форме самую изощренную обработку сигналов с целью выделения из них максимума информации, необходимой для решения поставленных перед Вами целей.

9.1 Аналого-цифровое и цифро-аналоговое преобразования

Обобщенная структура системы цифровой обработки сигналов представлена на рис. 9.1.

На вход поступает аналоговый сигнал x(t).

АЦП – аналого-цифровой преобразователь. На его выходе образуется сигнал, дискретизированный по времени и квантованный по уровню, то есть цифровой сигнал. Этот сигнал является потоком чисел, который в форме параллельного или последовательного кода поступает на цифровой процессор.

ЦП – цифровой процессор, который выполняет различные математические операции с поступающими числами. Наличие памяти позволяет запоминать и использовать в текущих расчетах ранее полученные значения сигналов. Результатом работы процессора является новая последовательность чисел. Они являются отчетами значений выходного аналогового сигнала.

ЦАП – цифро-аналоговый преобразователь, осуществляющий восстановление выходного сигнала по его отчетам, образованным цифровым процессором. В результате получается ступенчатый сигнал, который еще нужно сгладить.

Рекомендуемые материалы

ФНЧ – фильтр нижних частот, осуществляющий сглаживание выходного сигнала и таким образом его преобразование в настоящий аналоговый сигнал.

В цифровой форме, то есть в цифровом процессоре, можно реализовать самые различные устройства и процедуры:

– анализаторы спектров,

– цифровые фильтры,

– нелинейные преобразования сигналов (логарифмирование, возведение в степень и т.д.), компенсация нелинейностей характеристик измерительных преобразователей,

– линейные преобразования, такие как интегрирование или дифференцирование сигналов,

– именно в цифровой форме осуществляется наиболее надежная передача данных на расстояние по каналам связи.

9.2 Дискретизация измерительных сигналов

Различные параметры физических процессов перед их вводом в любую информационную систему вначале преобразуются датчиками в электрические сигналы. В большинстве случаев эти сигналы являются непрерывно изменяющимися токами или напряжениями.

Наиболее развитыми средствами информационной техники являются цифровые устройства, работающие с дискретными сигналами. Поэтому непрерывные сигналы необходимо уметь преобразовывать в дискретные. Это достигается тем, что непрерывные сигналы подвергаются операциям квантования по времени (дискретизации) и квантования по уровню.

В результате дискретизации реализация  (рис. 9.2-а) непрерывного измерительного сигнала  преобразуется в функцию дискретного времени, представленную последовательностью значений величин, называемых координатами сигнала. С помощью этих координат исходная функция непрерывного времени может быть может быть восстановлена с заданной точностью.

Координатами могут быть, например, мгновенные значения сигнала, отсчитанные в дискретные моменты времени (рис. 9.2-б).

При квантовании по уровню осуществляется преобразование величины (или координат сигнала) с непрерывной областью значений в значения величины с дискретной областью значений. Это преобразование реализуется путем замены мгновенного значения сигнала одним из конечного множества разрешенных значений или уровней квантования (рис. 9.2-в).

Если провести нумерацию уровней, то значению сигнала (или его координатам) будет поставлено в соответствие некоторое число (например, – от -18 до +16 на рис. 1в), которое может быть выражено в двоичном или другом коде. Тогда каждое значение сигнала представляется последовательностью сигналов двух уровней, где наличие или отсутствие импульса на определенном месте соответствует нулю или единице в данном разряде двоичного числа. Так получается цифровая форма представления сигнала.

9.3 Общие сведения о методах дискретизации сигналов.

В самом общем виде дискретизацию реализации непрерывного сигнала  на интервале времени  совокупностью координат сигнала  и последующее восстановление по ним исходного сигнала в виде его оценки  можно записать в виде:

где  – оператор представления сигнала  совокупностью координат,

 – оператор восстановления сигнала путем получения его оценки  по совокупности координат.

Разность

образует погрешность дискретизации и восстановления сигнала.

Операторы представления и восстановления могут быть линейными или нелинейными, причем одному и тому же оператору представления можно поставить в соответствие различные операторы восстановления и наоборот. Решение задачи дискретизации заключается в совместном выборе пары операторов  и , которые при известных статистических свойствах сигнала  обеспечивают заданную погрешность дискретизации.

Линейные операторы в большей степени соответствуют требованиям простоты схемной реализации, поэтому в дальнейшем ограничимся только линейной дискретизацией. Линейные операторы представления и восстановления в самом общем виде должны иметь следующий вид:

Здесь  – весовые функции, определяющие значимость различных координат сигнала,

 – базисные или координатные функции.

Здесь необходимо отметить, что координаты сигнала получаются путем взвешенного (в соответствии с весовыми функциями) интегрирования сигнала по интервалу дискретизации . Это приводит к уменьшению влияния шумов за счет их усреднения за тот же интервал времени. Плохо, однако, то, что координаты сигнала получаются с некоторой задержкой во времени, по крайней мере, на время дискретизации. Для устранения этого недостатка используются специальные алгоритмы экстраполяции сигнала.

В зависимости от выбора весовых функций координаты сигнала могут представлять собой различные образования.

а) Коэффициенты некоторого ряда, аппроксимирующего изменения сигнала в каждом периоде дискретизации. Это обобщенная дискретизация. В частном случае может быть . Тогда координаты сигнала – это спектральные коэффициенты сигнала в системе базисных функций , определяющих разложение сигнала  на интервалах дискретизации  в обобщенный ряд Фурье. Вместо самого сигнала дальнейшим преобразованиям подвергается теперь последовательность его координат.

На рис. 9.3, сверху, изображена реализация сигнала  на интервале времени Т от нуля до 0.5 с. В средней части рисунка построены две копии отрезка сигнала на малом интервале времени от 0.2 до 0.25 с.

Внизу слева дискретизированный сигнал на каждом шаге дискретизации  представлен двумя координатами, двумя первыми спектральными коэффициентами разложения сигнала на шаге дискретизации в ряд по системе базисных функций Лежандра.

б) Текущие мгновенные значения сигнала, то есть выборки его значений через промежутки времени .

Весовыми функциями в этом случае являются смещенные дельта – импульсы

в моменты отсчета сигнала . Выражение

определяет при этом дискретизацию выборками.

На рис. 9.3 внизу (справа) представлен результат дискретизации сигнала выборками при шаге дискретизации  с моментами отсчета . Из рисунка ясно видно различие в этих двух видах дискретизации.

в) Конечные разности, то есть приращения значений сигнала в моменты отсчета. Используются разности различных порядков:

– разности первого порядка n = I:

– разности второго порядка (n = 2), то есть разности разностей первого порядка:

– разности n-того порядка, то есть разности разностей n-1-го порядка.

В этом общем случае весовыми функциями будут линейные комбинации d – функций:

,

где  – число возможных сочетаний из n по k. При дискретизации разностями 1-го порядка

.

Восстановление сигнала ведется в два этапа. На первом этапе по конечным разностям вычисляются значения последовательных выборок, а затем по выборкам находится оценка исходного сигнала.

Разностная дискретизация удобна тем, что разности лежат в меньших диапазонах, чем сам сигнал. При очень малых интервалах дискретизации разности могут не превышать шага квантования сигнала по уровню. В этом случае разности говорят только о знаке изменения сигнала и могут принимать только два значения: -1 или +1. Здесь мы получаем следующий вид дискретизации.

г) Дельта – дискретизация разностями n -того порядка.

Такого рода дискретизация обладает целым рядом очевидных преимуществ, однако здесь появляются две новых составляющих погрешности дискретизации, связанных:

– с накоплением раз допущенных ошибок;

– с возможностью появления сигналов с аномально высокой скоростью изменения.

Восстановление сигнала при любых операторах представления осуществляется обобщенным полиномом

По отношению к исходному сигналу этот полином называется аппроксимирующим. В частном случае, когда в качестве координат сигнала используются выборки, а базисные функции выбраны так, что значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, этот полином называется интерполирующим.

При выбранном операторе представления задача восстановления сигнала сводится к выбору аппроксимирующего или интерполирующего полинома. При обобщенной дискретизация восстановление обычно ведется на основе аппроксимации, а при дискретизации по выборкам или разностям – путем интерполяции.

9.4 Оценка погрешности дискретизации

Погрешность дискретизации будем характеризовать дисперсией, усредненной по интервалу дискретизации :

где  – значения координат сигнала с учетом воздействия шума, вызванного, например, квантованием по уровню или другими внешними и внутренними воздействиями в устройствах преобразования и передачи сигналов. Шум подвергается дискретизации вместе с полезным сигналом, поэтому можно считать импульсным шумом .

После возведения в квадрат в результате интегрирования получаем:

Подставим сюда . Если сигнал  и шум  не коррелированны, то погрешность дискретизации можно представить в виде суммы двух составляющих.

Одна из этих составляющих – собственная погрешность дискретизации по не зашумленным координатам:

Вторая составляющая вызывается действием шума и ее дисперсия составляет:

,

или, после некоторых преобразований,

Если  – реализация случайного стационарного сигнала с нулевым математическим ожиданием, то первое слагаемое собственной погрешности дискретизации равно его дисперсии

а входящее в третье слагаемое математическое ожидание произведения координат  и  можно выразить через корреляционную функцию сигнала. Для этого преобразуем вначале математическое ожидание произведения координат к виду:

.

Но произведение двух интегралов можно представить в форме двойного интеграла. Поэтому

.

Операция взятия математического ожидания линейна. Поэтому знаки интегрирования и взятия математического ожидания можно поменять местами. В результате получаем:

.

Математическое ожидание, входящее во второе слагаемое собственной погрешности дискретизации, можно преобразовать аналогичным образом:

Теперь, с учётом стационарности измерительного сигнала , собственная погрешность дискретизации может быть представлена в виде:

Выражение для шумовой погрешности дискретизации значительно упрощается, если предположить, что шум  является белым шумом с нулевым математическим ожиданием. Тогда, по аналогии  с выражением для , имеем:

Поэтому окончательно имеем

.

Входящая в последнее выражение величина  называется коэффициентом фильтрующей способности выбранной системы базисных функций по отношению к внешним помехам типа белого шума.

9.5 Оптимальная дискретизация.

Задача оптимальной дискретизации состоит в отыскивании такой системы весовых  и базисных  функций, которая обеспечивала бы получение минимальной собственной погрешности дискретизации  при заданном числе N+1 координат сигнала, или получение минимального числа N+1 координат при заданной собственной погрешности дискретизации.

Карунен и Лоэв показали, что если – это реализация случайного стационарного сигнала с корреляционной функцией, то число координат N+1 будет минимальным, если в качестве координат используются коэффициенты обобщенного ряда Фурье (все – ортогональны и нормированы) и функции  удовлетворяют интегральному уравнению Фредгольма второго рода

где

являются дисперсиями i- тых координат сигнала.

Уравнение в общем случае решить невозможно, однако оно позволяет выявить близость к оптимальной различных систем координатных функций.

Если выбранная система координатных функций удовлетворяет вышеприведенному уравнению Фредгольма, то погрешность дискретизации может быть вычислена по формуле

где  – дисперсия дискретизируемого сигнала. Поскольку все  зависят от времени дискретизации , то, используя полученное соотношение, можно по заданной допустимой погрешности дискретизации определить конкретное значение шага дискретизации.

Реализация метода оптимальной дискретизации очень сложна. Поэтому для практических целей желательно иметь универсальные координатные функции, применение которых возможно при не очень сложной аппаратуре, но которые в то же время обеспечивали бы близость дискретизации к оптимальной.

9.6 Обобщенная дискретизация по полиномам Лежандра

Для дифференцируемых случайных сигналов координатными функциями, близкими к оптимальным, являются полиномы Лежандра. Полиномы Лежандра, ортогональные на интервале (-1, +1), имеют вид:

Полиномы Лежандра, ортогональные на интервале , где  – шаг дискретизации, получаются заменой переменных . Тогда получим координатные функции:

Мощность этих полиномов равна . Поэтому ортонормированные полиномы имеют вид . Такими же должны быть и весовые функции .

Расчёты погрешности дискретизации по формулам, приведенным в предыдущем параграфе, существенно упрощаются, если предположить, что шаг дискретизации  значительно меньше интервала корреляции исходного сигнала. В этом случае корреляционную функцию  можно представить рядом Тейлора по степеням  вблизи нуля и при интегрировании ограничиться несколькими первыми членами разложения.

Пример

Дискретизации подвергается случайный сигнал, имеющий спектральную плотность  квазибелого шума с граничной частотой . Корреляционная функция такого сигнала имеет вид:

Представим её в виде степенного ряда:

Предположим, что все  координат сигнала передаются одновременно как одна обобщенная координата с частотой  или , где  – шаг дискретизации.

Рассмотрим случаи использования различного числа координат сигнала.

I.        используется только одна координата

На каждом шаге дискретизации  определяется среднее значение сигнала, которое и используется в качестве координаты сигнала и применяется затем для его восстановления:

После восстановления сигнал представляется ступенчатой линией (рис.9.4), причём высота ступеней на каждом шаге дискретизации равна среднему значению сигнала в пределах этого шага. Вертикальными линиями отмечены границы интервалов дискретизации. Погрешность дискретизации  характеризуется дисперсией

причём

Подставляя сюда корреляционную функцию в виде ряда по степеням и учитывая, что  и , получим:

Погрешность дискретизации

Если задана допустимая погрешность дискретизации в долях стандартного отклонения измерительного сигнала, то, пользуясь этим выражением, можно найти допустимое значение шага дискретизации

Так если ширина спектра

то

II       N+1=2, используются две координаты сигнала:

– первая координата

– вторая координата

На каждом шаге дискретизации определяются теперь эти две координаты, последовательности которых и используются затем для восстановления сигнала:

Восстановленный сигнал (рис. 9.5, сравни с рис. 9.4) на каждом шаге дискретизации представляет собой отрезок прямой линии, наиболее близкий к исходной кривой. Такая аппроксимация называется кусочно-линейной.

Погрешность дискретизации составляет теперь

где дисперсия  уже определена, а  вычисляется как

Учитывая, что

,

получим следующее выражение для дисперсии второй координаты:

Теперь вычислим погрешность дискретизации и восстановления

При известной дисперсии собственной погрешности дискретизации шаг дискретизации теперь должен определяться как

При тех же условиях, что и в первом примере, шаг дискретизации должен теперь составлять

В условиях предыдущего примера  то есть той же погрешности восстановления сигнала можно добиться при шаге дискретизации, в шесть раз большем, чем при ступенчатой аппроксимации.

III      N+1=3, используя три координаты сигнала, две из которых  и  уже были определены. Третья координата находится как

С помощью этих трех координат сигнал на каждом шаге интегрирования приближается параболами второй степени:

Погрешность дискретизации после аналогичных вычислений принимает вид

Отсюда можно вновь найти шаг дискретизации при прочих равных условиях:

Шаг дискретизации увеличился еще почти в два раза.

Этот пример демонстрирует общее положение – увеличение числа координат приводит к увеличению допустимого шага дискретизации, но по мере роста числа координат – всё в меньшей и меньшей степени. Поэтому на практике число координат выбирают равным одному или двум и крайне редко N+1 принимается равным трем.

Дискретизация и восстановление сигнала с помощью полиномов Лежандра в большинстве случаев близка к оптимальной дискретизации, однако требует довольно сложных технических средств для своей реализации. Большее распространение в измерительных информационных системах получила дискретизация выборками, то есть представление сигнала в виде последовательности отчетов, которые берутся через определенный промежуток времени Т.

Этот интервал времени называется шагом дискретизации, а соответствующая ему частота

– круговой или, соответственно, линейной частотой дискретизации. Если частота дискретизации равна 1 кГц, то это означает, что в единицу времени, то есть в секунду, берется тысяча отчетов.

В дальнейшем мы будем более подробно заниматься именно сигналами, представленными последовательностями отчетов.

9.7 Описание сигналов, представленных выборками

9.7.1 Спектр дискретного сигнала

При шаге дискретизации  и круговой частоте дискретизации , соответствующей линейной частоте , дискретный сигнал , полученный после дискретизации выборками из аналогового сигнала , определяется как , где  – моменты взятия отчетов аналогового сигнала, –  последовательные номера отчетов сигнала.

В результате дискретизации аналоговый сигнал  преобразуется в дискретный сигнал (решетчатую функцию) , который мы будем часто обозначать просто, как . Аналогом преобразования Фурье для непрерывных сигналов является дискретное преобразование Фурье, которое определяется не как интеграл, а как сумма

Полученное выражение является комплексным, его модуль определяет спектральную плотность амплитуд или амплитудный спектр дискретного сигнала, а его аргумент – фазовый спектр сигнала.

Пример.

Задан аналоговый сигнал, представленный на рис. 9.6:

.

Сигнал является суммой экспоненциального всплеска, гармоники с амплитудой 2мВ на частоте 20 рад/с и гармоники с амплитудой 0.5мВ на частоте 150 рад/ с, которую можно рассматривать как шумовую составляющую.

Амплитудный спектр такого сигнала должен содержать:

– низкочастотную область, соответствующую экспоненциальному всплеску,

– δ – образным импульсам на частотах двух гармонических составляющих сигнала: высокий импульс на частоте 20 рад / с и более низкий импульс на частоте 150 рад / с.

Амплитудный спектр сигнала, вычисленный как модуль спектральной функции

изображен на рис. 9.7.

Характер амплитудного спектра полностью соответствует сделанным ранее предположениям. Он действительно включает в себя низкочастотную часть протяженностью от 0 до ~70 рад/ с. Кроме того, спектр содержит два δ – подобных всплеска на частотах 20 и 150 рад / с, причем последний всплеск лежит за границами низкочастотной части спектра.

Проведем дискретизацию сигнала на частоте . Период дискретизации составит при этом  Дискретизированный сигнал принимает вид:

.

Дискретный сигнал в виде последовательности отчетов в моменты времени  изображен на рис. 9.8. Огибающая этого сигнала в некотором приближении повторяет исходный аналоговый сигнал (рис. 9.6), хотя некоторые его подробности могут быть и потеряны.

Дискретный сигнал должен иметь, конечно, гораздо более широкий спектр, который вычисляется по вышеприведенной формуле:

.

Спектр сигнала, вычисленный таким образом, представлен на рис. 9.9.

На рисунке четко прослеживаются основные особенности спектра дискретного сигнала и его взаимосвязь со спектром исходного аналогового сигнала. Эти особенности не связаны с конкретной формой сигнала и имеют общее значение, выходящее за рамки рассматриваемого примера.

1. Спектр дискретного сигнала периодический с периодом, равным частоте дискретизации (в нашем случае 400 рад/с).

2. В пределах половины частоты дискретизации спектр дискретного сигнала повторяет спектр исходного аналогового сигнала. Поэтому, если спектр аналогового сигнала укладывается в полосе частот, равной половине частоты дискретизации, то он без искажений повторяется с периодом, равным частоте дискретизации.

3. В этих условиях аналоговый сигнал может быть восстановлен без искажений с помощью идеального фильтра низких частот, полоса пропускания которого равна половине частоты дискретизации.

4. Если ширина спектра аналогового сигнала больше половины частоты дискретизации, то сдвинутые на период копии спектра исходного сигнала перекрывают друг друга и поэтому даже идеальный фильтр нижних частот не поможет восстановить исходный сигнал из дискретного сигнала.

На рис 9.10 представлен спектр дискретного сигнала, полученного после дискретизации того же аналогового сигнала, но при частоте дискретизации 200 рад/с, то есть вдвое меньшей, чем на рис. 9.9. Здесь пары δ – всплесков, соответствующие более высокой гармоники аналогового сигнала и находящиеся на рис. 9.9 на частотах 150 рад/с и 400 – 150=250 рад/с, поменялись местами и располагаются теперь на частотах 150 рад/с и 200 – 150=50 рад/с.

Восстановление аналогового сигнала с помощью идеального фильтра нижних частот с частотой среза 100 рад/с, равной половине частоты дискретизации, приведет к существенному искажению сигнала.

9.7.2 Теорема Котельникова

Возможность восстановления аналогового сигнала из последовательности его отчетов при достаточно высокой частоте дискретизации с помощью идеального фильтра нижних частот, которая была подробно рассмотрена в предыдущем разделе,  формализуется теоремой Котельникова (в англоязычной литературе – теоремой Найквиста).

Теорема Котельникова звучит следующим образом. Можно со сколь угодно высокой точностью восстановить случайный аналоговый сигнал по его равномерным дискретным отчетам при соблюдении следующих условий:

– сигнал имеет ограниченный по протяженности (финитный) спектр, например от 0 до ;

– реализация сигнала наблюдается бесконечно долго как в прошлом, так и в будущем;

– дискретный сигнал формируется в виде последовательности отчетов аналогового сигнала с частотой дискретизации ;

– восстановление сигнала осуществляется по его точным (не зашумленным) отчетам с помощью обобщенного ряда Фурье  по функциям отчета (функциям Котельникова):

.

Функции отчета замечательны тем, что каждая k – тая из них принимает значение, равное единице, в момент взятия k – того отчета, и значение, равное нулю, в моменты любого другого отчета. Поэтому в моменты взятия отчетов восстановленный из дискретного сигнала аналоговый сигнал всегда совпадает с исходным аналоговым сигналом.

В качестве примера на рис. 9.11 представлена реализация некоторого аналогового сигнала x(t), а на рис. 9.12 – спектральная плотность амплитуд этой реализации. Граничная частота спектра сигнала имеет порядок 300 рад / с, поэтому частоту дискретизации сигнала можно принять равной 600 рад / с. Для простоты расчетов примем ее равной 628 рад/ с, тогда шаг дискретизации будет составлять 2π / 628=0,01 с.

На рис. 9.13 изображен небольшой фрагмент аналогового сигнала x(t) на интервале времени от 0,075 с до 0,15 с. Здесь же вертикальными отрезками представлены отчеты сигнала в моменты времени, разделенные шагами дискретизации

Ряд Котельникова представлен тремя функциями отчета (тонкие линии на рис. 9.13), умноженными на значения отчетов, в моменты времени . Их сумма  на этом интервале (0,10 – 0,12 с) уже очень близка к исходному сигналу. Степень близости восстановленного сигнала к исходному сигналу будет безгранично возрастать по мере учета все большего числа членов ряда Котельникова, если только выполняются условия ее справедливости.

Следует всегда помнить, что теорема Котельникова дает лишь предельные, потенциально возможные соотношения для определения частоты дискретизации в идеализированных условиях, основными из которых является ограниченность спектра сигнала и бесконечная протяженность времени наблюдения сигнала. Однако эти соотношения практически никогда не выполняются.

Восстановление реальных аналоговых сигналов с неограниченным спектром по его отчетам, взятым за ограниченное время наблюдения, всегда связано с определенной погрешностью дискретизации, как и в случае дискретизации по полиномам Лежандра. Поэтому частоту дискретизации всегда следует выбирать гораздо большей, чем . Погрешность дискретизации всегда имеет место, независимо от того, используются ли для восстановления сигнала функции Котельникова, или другие, более простые интерполяционные формулы.

9.7.3 Z – преобразование дискретного сигнала

Вернемся к формуле дискретного преобразования Фурье:

.

В теории дискретных систем принято использовать несколько иную форму записи, связанную с введением Z – преобразования. Сделаем такую подстановку:

.

Тогда вышеприведенная формула значительно упростится:

.

Вновь полученная функция X(z) переменной z называется Z – изображением или Z – образом дискретного сигнала x(k).

Z – преобразования для дискретных сигналов и систем играют ту же роль, что и преобразование Лапласа для аналоговых систем. Поэтому рассмотрим ряд примеров определения Z – изображений некоторых типичных дискретных сигналов.

1. Единичный импульс (рис. 9.14) является дискретным аналогом δ – импульса и представляет собой единичный отчет с единичным значением:

Z – преобразование единичного импульса находится как

как и для δ – импульса Дирака.

2. Дискретный единичный скачок (рис. 9.15) – это полный аналог функции включения Хевисайда:

Z – образ единичного скачка найдется как

Полученная сумма – это сумма членов бесконечной геометрической прогрессии с начальным членом, равным 1, и знаменателем . Сумма членов ряда составляет:

.

3. Дискретная экспонента (рис. 9.16) – это сигнал, определяемый выражением:

При  дискретная экспонента является убывающей (рис. 9.16), при  – возрастающей, при  – знакопеременной. Z – образ такой экспоненты

Как и в предыдущем случае, мы получили геометрическую прогрессию с нулевым членом, равным единице, но со знаменателем . Бесконечная сумма членов прогрессии определяет Z – образ экспоненты:

4. Дискретная затухающая гармоника. В противоположность предыдущим примерам запишем ее в общем виде:

где    α – коэффициент затухания гармоники,

         ω – частота гармоники,

         φ – начальная фаза колебаний,

          – период дискретизации.

Введем следующие обозначения:

На рис.9.17 представлен график дискретной затухающей гармоники при следующих данных: а=0.9, , φ=π/9. С учетом принятых обозначений выражение для дискретной затухающей гармоники можно представить в виде:

.

При получении Z – образа гармоники следует выразить функцию косинуса через сумму двух комплексных экспонент. Тогда, проделав целый ряд алгебраических и тригонометрических преобразований, в конце концов, можно будет получить следующее выражение:

.

Из приведенных примеров видно, что Z – образы большинства дискретных сигналов представляют собой дробно-рациональные функции от переменной . Происхождение Z – преобразования от преобразования Лапласа и Фурье приводит к тому, что Z – преобразование имеет и похожие свойства.

1. Линейность.

Z – преобразование линейно, так что если имеются два сигнала , то сумма этих сигналов  имеет Z – образ .

2. Временная задержка дискретного сигнала.

Если дискретный сигнал x(k), имеющий Z – образ X(z), задержать на m шагов дискретизации , то задержанный сигнал y(k)=x(k-m) имеет Z – образ . Выражение  можно рассматривать как оператор задержки сигнала на один шаг дискретизации.

3. Свертка дискретных сигналов.

По аналогии со сверткой аналоговых сигналов

,

Фурье – образ которой равен произведению Фурье – образов сворачиваемых сигналов, свертка двух дискретных сигналов определяется как

.

Z – образ свертки двух сигналов равен произведению Z – образов исходных дискретных сигналов

4. Умножение на дискретную экспоненту.

Если дискретный сигнал , имеющий Z – образ , умножается на экспоненту , то Z – образ произведения примет вид .

Рассмотренные свойства Z – преобразования позволяют во многих случаях без особого труда найти Z – образ заданного сигнала или решить обратную задачу – по известному Z – образу сигнала найти его представление во времени.

9.8 Цифровые фильтры

Под цифровым (или дискретным) фильтром понимается система преобразования дискретных сигналов, отвечающая требованиям линейности и стационарности. Линейность означает, что реакция системы на сумму сигналов равна сумме реакций на эти сигналы, подаваемые на вход системы по отдельности. Свойство стационарности системы требует того, чтобы задержка входного сигнала на произвольное число тактов (интервалов дискретизации сигнала) приводила бы только к такой же задержке выходного сигнала, никак не изменяя его форму.

Существуют, правда, и нелинейные фильтры и фильтры с переменными параметрами, например, адаптивные фильтры, характеристики которых изменяются при изменении статистических свойств входных сигналов. Но в дальнейшем анализе мы ограничимся классом только линейных стационарных фильтров.

Понятие «фильтр» необходимо ассоциируется в нашем сознании с устройствами для подавления гармоник с частотами, лежащими в одних диапазонах, и пропускания гармоник с другими частотами. Цифровые фильтры также обладают частотно – зависимыми свойствами, однако область применения цифровых фильтров гораздо шире и охватывает вообще все виды дискретных преобразований.

Наиболее полной характеристикой фильтра является его разностное уравнение. Разностное уравнение цифрового фильтра устанавливает зависимость выходного дискретного сигнала фильтра в текущий момент времени

– от значения входного сигнала в тот же момент времени,

– от предыдущих значений входного сигнала,

– от предыдущих значений выходного сигнала.

При соблюдении требований линейности выходной сигнал фильтра должен быть линейной комбинацией предыдущих значений входного и выходного сигналов:

Здесь  – коэффициенты разностного уравнения фильтра, которые полностью описывают его свойства, то есть реализуемый фильтром алгоритм преобразования входного сигнала.

Разностное уравнение фильтра можно записать в форме, очень похожей на запись линейного дифференциального уравнения стационарной аналоговой системы:

Отличие заключается лишь в том, что на месте производных входного или выходного сигналов соответствующих порядков здесь стоят сигналы, задержанные по времени на такие же числа шагов дискретизации.

Теперь подвергнем разностное уравнение фильтра Z – преобразованию:

Вынося за скобки в результаты Z – преобразования выходного и входного сигналов в обеих частях разностного уравнения, можно получить выражение для их отношения:

.

Полученное выражение носит название системной функции или функции передачи цифрового фильтра и является аналогом передаточной функции аналоговой динамической системы. Функция передачи физически реализуемой дискретной системы выражается отношением полиномов по отрицательным степеням переменной z. Функция передачи позволяет сразу же получить выражение для выходного сигнала фильтра через входной сигнал .

Для полного описания аналоговых линейных динамических систем Вы пользовались также импульсной функцией, которая представляет собой реакцию системы на входное воздействие в виде δ – импульса Дирака. Для цифровых фильтров ту же роль играет импульсная характеристика  – реакция фильтра на единичный импульс. Функция передачи цифрового фильтра является результатом Z – преобразования его импульсной характеристики .

Подстановкой  функция передачи цифрового фильтра превращается в его комплексный коэффициент передачи, то есть в амплитудно-фазовую частотную характеристику . Модуль комплексного коэффициента передачи образует амплитудно-частотную характеристику фильтра, а его аргумент – фазовую частотную характеристику:

Пример

Цифровой фильтр определяет среднее арифметическое из текущего и двух предыдущих значений входного сигнала. Разностное уравнение такого фильтра:

Функция передачи фильтра получается после Z – преобразования правой и левой частей этого уравнения:

и составляет:

.

Вычислим путем непосредственного подсчета импульсную функцию фильтра:

Импульсная функция равна 1/3 и остается постоянной в течении трех тактов отчета. После этого она становится равной нулю. Это означает, что импульсная функция фильтра является конечной.

Такого рода фильтры носят название КИХ-фильтры в противоположность БИХ–фильтрам, фильтрам с бесконечно – протяженной импульсной функцией.

Комплексный коэффициент передачи получается из функции передачи фильтра подстановкой  и составляет:

После проведения ряда тригонометрических преобразований это выражение приводится к виду:

Теперь просто определить АЧХ и ФЧХ фильтра:

Вам также может быть полезна лекция “57 Методика расследования причинения телесных повреждений”.

Графики АЧХ и ФЧХ фильтра, вычисляющего значение каждого отчета как среднее арифметическое из трех предыдущих значений входного дискретного сигнала, представлены на рис.9.18. Частота дискретизации была при этом принята равной , так что интервал дискретизации равнялся 0,0157 с.

Из построенных графиков можно сделать следующие выводы относительно формы частотных характеристик цифровых фильтров:

1. Амплитудно – частотная характеристика цифрового фильтра является периодической функцией частоты, период повторения АЧХ равен частоте дискретизации.

2. Форма АЧХ цифрового фильтра определяется только выражением для функции передачи фильтра, но конкретный график АЧХ фильтра зависит от частоты дискретизации входного сигнала. Получается парадоксальный результат: свойства фильтра зависят от свойств входного сигнала. Во избежание этого парадокса частотные характеристики цифровых фильтров приходится рассматривать в функции безразмерной частоты . Именно в такой комбинации частота входит в выражение для комплексного коэффициента передачи фильтра.

3. график ФЧХ строится в виде, изображенном на графике рис. 9.18 только для того, чтобы уместить его в ограниченном пространстве рисунка. На самом деле скачков фазы на угол , конечно, нет. Запаздывание по фазе выходного сигнала относительно входного непрерывно растет линейно с ростом частоты.

4. Форма первого лепестка АЧХ полностью определяется видом функции передачи фильтра или его разностного уравнения. Подбирая соответствующим образом коэффициенты разностного уравнения фильтра можно построить фильтры нижних частот, фильтры высоких частот, полосовые и режекторные фильтры с заданными полосами прозрачности и непрозрачности.

Как-то так:
1. Аналогово-цифровой преобразователь (АЦП) . Преобразует либо напряжение в цифровой код, либо другие характеристик сигнала.
2. Шаг это то, как часто мы замеряем сигнал. Частота это то, сколько получится замеров за 1 секунду. То есть при частоте 48000 Гц мы берем сигнал 48 тысяч раз в секунду. Соответственно, шаг будет 60 / 48000 = 0,00125с (Это время между двумя замерами) .
3. Если время между замерами (шаг) 0,005 , то обратим формулу и получим: 60 / Х = 0,005 => Х = 60 / 0.005 = 12000 Гц
4. Меняем формулу: теперь 60 / 1000 Гц = Х => X = 0.06с .
5. Разряд показывает, в целом, сколько значений можно хранить в переменной. Соответственно, разряд дискретизации показывает насколько точные значения могут быть записаны за один шаг. В 2 байта можно записать меньше чем в 4 байта.
6. Решается, вычислением логарифма по основанию 2. = 10