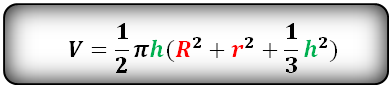Шаровой слой как найти объем

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем шарового слоя (среза шара), а также пример решения задачи для демонстрации их практического применения.

• Определение шарового слоя

• Формула для нахождения объема шарового слоя

• Пример задачи

Определение шарового слоя

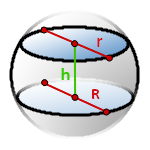
Шаровый слой (или срез шара) – это часть шара, оставшаяся между двумя  пересекающими его параллельными плоскостями. На рисунке ниже окрашен в желтый цвет.

• R – радиус шара;
• r₁ – радиус первого основания среза;
• r₂ – радиус второго основания среза;
• h – высота шарового слоя; перпендикуляр от центра первого основания до центра второго.

Формула для нахождения объема шарового слоя

Чтобы найти объем шарового слоя (среза шара), необходимо знать его высоту, а также радиусы двух его оснований.

Эта же формула может быть представлена слегка в другом виде:

Примечания:

• если вместо радиусов оснований (r₁ и r₂) известны их диаметры (d₁ и d₂), последние нужно поделить на 2 для получения соответствующих им радиусов.
• число π обычно округляется до 3,14.

Пример задачи

Найдите объем шарового слоя, если радиусы его оснований равны 3,4 см и 5,2 см, а высота составляет 2 см.

Решение

Все что нам нужно сделать в данном случае – это подставить известные значения в одну из формул, приведенных выше (в качестве примера выберем вторую):

Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями. Для
вычисления объема шарового слоя достаточно знать радиусы кругов, ограничивающих шаровой слой, и
расстояние между ними (высота шарового слоя). Объем вычисляется по формуле:

V = (π / 6) * h * (3R² + 3r² + h²)

где R, r — радиусы, h — высота.

Пример. Требуется найти объём шарового слоя зная что радиусы R = 3 см, r = 6 см,
высота h = 4 см. Подставим в формулу и получим: V = (3,14 / 6) * 4 * (3 * 3² + 3 * 6² + 4²) = 316 см³.

Примечательно, что для вычисления этого объема не требуется радиус самого шара. Требуются только
радиусы ограничивающих его кругов. Если секущие плоскости отодвинуть к полюсам шара, то высота h
станет равна диаметру шара, а радиусы кругов примут нулевые значения: R=0, r=0. Тогда формула примет
вид: V = π / 6 D³ = (4π / 3) * Rшара³. Это формула для вычисления объема
шара. Максимальный объем шарового слоя равен объему шара.

Актуально вычисление шарового слоя при устройстве сферических резервуаров, применяемых в химической
промышленности. Сферическая емкость применяется в тех случаях, когда давление в ней высокое.
Резервуар может иметь вид полной сферы или шарового слоя. Если в шаровом резервуаре находится
жидкость, заполняющая только часть объема, то по положению ее уровня можно определить высоту
шарового слоя и радиус ограничивающего круга, а потом посчитать объем жидкости. Сферические сосуды
используются и в быту. Примером может служить аквариум, выполненный в виде усеченного шара (шарового
слоя). Расчет его объема нужен для правильного оборудования среды обитания для аквариумных жителей.
Части конструкций в виде шарового слоя встречаются в машиностроении, архитектуре, столярном деле.
Вычисление объемов – необходимая часть конструкторской разработки.

Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар^[1].

Связанные определения[править | править код]

• Основания шарового слоя — это сечения шара, образовавшиеся в результате пересечения шара двумя параллельными плоскостями.
• Высота шарового слоя — это расстояние между основаниями слоя.

Свойства[править | править код]

• Объём шарового слоя можно найти как разность объёма двух шаровых сегментов:
      
  где  — объём шарового слоя,  — высота большего шарового сегмента,  — высота меньшего шарового сегмента,  — радиус шара.
• Площадь сферической части поверхности шарового слоя (так называемый сферический пояс) зависит только от высоты слоя и радиуса шара^[2]:

  

где  — площадь сферического пояса,  — высота шарового слоя,  — радиус шара.

Вариации и обобщения[править | править код]

• В физике под шаровым слоем часто понимают слой, ограниченный сферами радиуса и , для маленького . Объем шарового слоя в этом случае с точностью до O равен .

См. также[править | править код]

• Сферический слой

Примечания[править | править код]

Объем шарового слоя

На этом уроке мы введём понятия шарового сегмента,
шарового слоя и шарового сектора. А также выведем формулы для вычисления их объёмов.

Прежде чем приступить к рассмотрению данной темы,
давайте вспомним, что такое шар.

Определение:

Итак, шар
– это совокупность всех точек пространства, находящихся от данной точки на
расстоянии, не больше данного. Причём, данная точка называется центром
шара, а данное расстояние – радиусом шара.

Самой простой фигурой, которую можно начертить,
используя шар, является шаровой сегмент.

Определение:

Шаровым сегментом
называется часть шара, отсекаемая от него какой-нибудь плоскостью.

На экране вы видите, как секущая плоскость ,
проходящая через точку ,
разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется
основанием каждого из этих сегментов, а длины отрезков  и
 диаметра
,
перпендикулярного к секущей плоскости, называются высотами
сегментов.

Верно следующее утверждение: если радиус шара равен ,
а высота сегмента равна ,
то объем  шарового
сегмента можно вычислить по формуле:

Докажем это утверждение. Доказывать
будем с помощью определённого интеграла.

Проведём ось  перпендикулярно
к плоскости .
Тогда площадь ,

при .

Вычислим объём шарового сегмента с помощью основной
формулы объёма тела. Вспомним её: .

Итак, применим основную формулу для вычисления объёмов
тел получаем, что объём шарового сегмента равен .

Что и требовалось доказать.

Заметим, что если высоту  в
формуле объема шарового сегмента  заменить
на ,
то получим формулу для нахождения объёма шара:

А если заменить высоту  на
радиус ,
то получим формулу для нахождения объёма полушара.

Кстати, в жизни нас также окружают некоторые объекты,
имеющие форму очень близкую к форме шарового сегмента.

В современной авиации наиболее популярны парашюты в
виде сегмента.

Форму шарового сегмента нередко используют и в
архитектуре, интерьере, декоре.

Перейдём к шаровому слою.

Определение:

Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.

На экране вы видите изображение шарового слоя.

Круги, получившиеся в сечении шара плоскостями,
называются основаниями шарового слоя, а расстояние между
плоскостями – высотой шарового слоя.

Нетрудно заметить, что объём шарового слоя можно
вычислить, как разность объёмов двух шаровых сегментов.

Объём шарового слоя, изображённого на экране, равен
разности объёмов шаровых сегментов, высоты которых равны  и
.

Если высота шарового слоя равна ,
а радиусы  и
 –
радиусы оснований шарового слоя соответственно, то объем шарового слоя можно
вычислить по формуле:

Декоративная свеча может служить примером шарового
слоя в жизни.

И теперь перейдём к шаровому сектору.

Определение:

Шаровым сектором
называется тело, которое получается при вращении кругового сектора с углом,
меньшим 90^о, вокруг прямой, содержащей один из ограничивающих круговой
сектор радиусов.

Обратите внимание, шаровой сектор состоит из шарового
сегмента и конуса. Причём шаровой сегмент имеет высоту ,
а конус высоту ,
где  –
радиус шара.

Понятно, что шаровая поверхность пересекается с
конусом по окружности. Радиус этой окружности равен .

Если радиус шара равен ,
а высота шарового сегмента равна ,
то объем  шарового
сектора можно найти по формуле:

Для того чтобы получить данную формулу необходимо
сложить объём конуса (с вершиной O), лежащего под плоскостью, и объём шарового сегмента,
лежащего над плоскостью.

Большой воздушный шар имеет форму близкую к форме
шарового сектора в жизни.

Перейдём к задачам.

Задача: радиус
шара равен  см.
Вычислите объем шарового сегмента, если его высота равна  см.

Решение: запишем
формулу для вычисления объёма шарового сегмента.

И подставим в неё радиус шара и высоту шарового
сегмента.

Запишем ответ.

Задача: по
разные стороны от центра шара проведены два параллельных сечения с площадью  и
 см².
Расстояние между сечениями равно  см.
Определите объём получившегося шарового слоя.

Решение: запишем
формулу для вычисления объема шарового слоя.

Чтобы найти объём шарового слоя нам необходимо знать
его высоту и радиусы двух его оснований.

По условию задачи нам дано расстояние между сечениями,
как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .

Теперь найдём чему равны радиусы оснований шарового
слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга
вычисляется по формуле .
Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания
равен  (см),
радиус второго основания равен  (см).

Подставим радиусы оснований и высоту шарового слоя в
формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен .

Не забудем записать ответ

Задача: радиус
шара равен  см.
Найдите объем шарового сектора, если высота шарового сегмента равна  см.

Решение: запишем
формулу для вычисления объёма шарового сектора.

Подставим в неё радиус шара и высоту шарового
сегмента. Посчитаем. Получим, что объём данного шарового сектора равен .

Запишем ответ.

Итоги:

На этом уроке мы ввели понятия шарового сегмента,
шарового слоя и шарового сектора. Узнали, что шаровым сегментом называется
часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.
Шаровым сектором называется тело, которое получается при вращении кругового
сектора с углом, меньшим 90^о, вокруг прямой, содержащей один из ограничивающих
круговой сектор радиусов. А также вывели формулы для вычисления объёмов этих
тел.