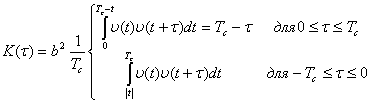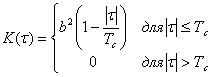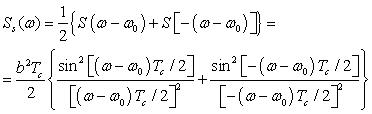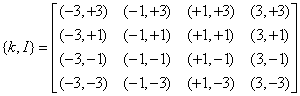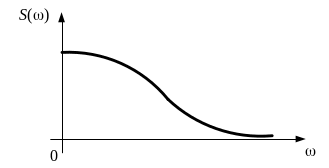
Ширина спектра сигнала как найти - Сайт, где вы сможете решить свои вопросы

Ширина спектра сигналов

Рис.1.21

На рисунке 1.21 приведен график
амплитудно-частотного спектра, произвольно
выбранного некого одиночного сигнала,
причем модуль спектральной плотности
монотонно убывает с ростом значения
частоты.

Для большинства одиночных сигналов
характерно такое распределение модуля
спектральной плотности от частоты.

Вычислив интегралы

получим
значения, пропорциональные соответственно
полной энергии сигнала W₀,
и энергии сигнала W(ω),
сосредоточенной в полосе частот от 0 до

.

Отношение

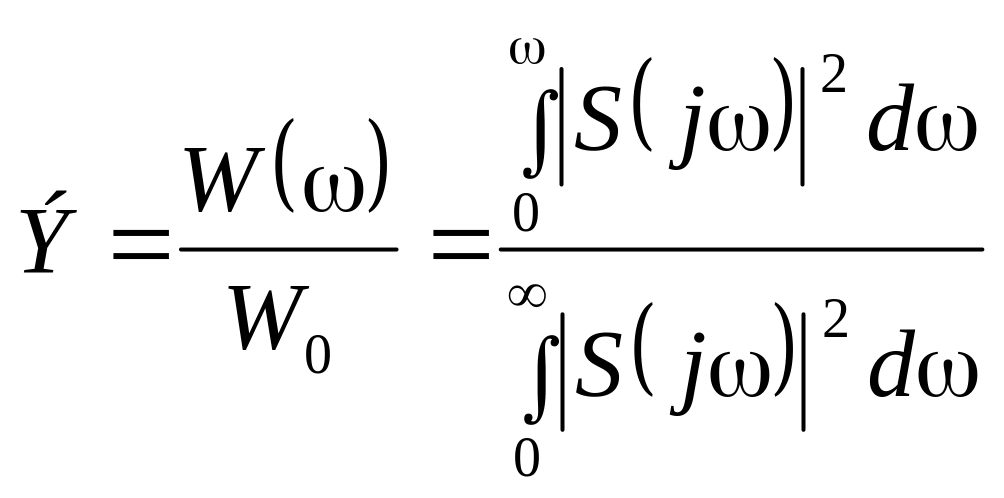
показывает,
какая часть всей энергии сигнала
сосредоточена в диапазоне частот от 0
до

Шириной спектра сигнала со сплошным
спектром называют область частот (от 0
до

или от

до

),
в пределах которой заключена основная
часть (принята величина 90 %) энергии
сигнала.

Рис.1.22

На рисунке 1.22 показан амплитудно-частотный
спектр некого периодического сигнала,
причем амплитуды спектральных составляющих
монотонно или немонотонно убывают с
ростом частоты.

Энергия сигналов, обладающих дискретным
спектром, пропорциональна:

где

 постоянная
составляющая;

 действующее значение
k-й составляющей.

Если вычислить

получим
значение, пропорциональное энергии
сигнала в полосе частот от 0 до некоторой
частоты

.

Отношение

показывает,
какая часть энергии сигнала с дискретным
спектром сосредоточена в диапазоне
частот от 0 до

.

Шириной спектра сигналов с дискретным
спектром называют область частот (от 0
до

или от

до

),
в пределах которой заключена основная
часть (не менее 90%) энергии сигнала.

Сравнивая определения ширины спектра
сигналов со сплошным спектром и с
дискретным спектром, можно заметить
отличие (“90% и не менее 90%”),
обусловленное дискретным характером
изменения величины

.

Спектры видеосигналов сосредоточены
в области низких частот, радиосигналов
– в области частот несущего колебания.

Важнейшей характеристикой сигналов в
радиотехнике является база сигнала
(коэффициент широкополостности), равная
произведению длительности сигнала (τ_с)
на ширину его спектра (Δƒ_с) n=τ_cΔf_c.

Сигналы, у которых база сигнала порядка
1, называют простыми (узкополосными)
сигналами. К простым сигналам относят
одиночные и периодические последовательности
импульсов без внутриимпульсной модуляции.

У сложных (широкополосных) сигналов

сложными сигналами являются радиосигналы
с внутриимпульсной частотной или
фазо-кодовой модуляцией, а также, пачки
видео и радиоимпульсов.

1.2. Одиночные сигналы и их спектры

1.2.1. Одиночные видеосигналы и их спектры

Рассмотрим спектры некоторых простейших
видеосигналов.

Спектр дельта-функции

Дельта-функцией называется сигнал вида
(рис. 1.23):

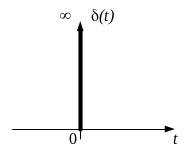
Рис. 1.23

Спектральную плотность получим путем
вычисления интеграла

Такой результат является следствием
так называемого фильтрующего свойства
дельта-функции(1.24), которое заключается
в следующем

,
т. к.

,
то

,

поэтому

,
.

График спектра показанный на рисунке
1.25. Амплитудно-частотный спектр на всех
частотах одинаков и равен 1. Фазо-частотный
спектр на всех частотах равен 0. АЧС
является сплошным и ширина спектра
бесконечна.

Рис.1.24

Рис.1.25

Начальные фазы всех гармонических
колебаний (рис. 1.26) одинаковы и равны 0.
Это значит, что в момент времени

= 0 все составляющие, изменяющиеся по
косинусоидальному закону, проходят
через амплитудное значение. В этот
момент их сумма образует бесконечную
величину.

Рис.1.26

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Практическая ширина спектра определяется либо по уровню половинной мощности, либо по нулям главного лепестка спектральной плотности.

____________

А теперь относительно Вашего вопроса. Если Вы имеете в виду синусоиду с бесконечной длительностью реализации, то её спектральная плотность — это дельта-функция Дирака, у которой ширина нулевая. А у прямоугольного видеоимпульса ширина спектра обратна его длительности. Поэтому конечно спектр прямоугольного видеоимпульса шире, чем у синусоиды. А вот если Вы имеете в виду гармонический сигнал с конечной длительностью реализации, то спектр уже не будет дельтой, он будет таким же, как у прямоугольного видеоимпульса, только разнесённый на частоту гармонического колебания (которое и называется несущим) и ширина спектра будет также обратна длительности реализации. Если Вы возьмёте радиоимпульс и видеоимпульс равной длительности, то и ширина спектра у них будет равной. Запомните простое правило — ширина спектра (для сигналов без внутриимпульсной модуляции), при условии равненства огибающих (а видеоимпульс — это огибающая радиоимпульса), тем больше, чем короче реализация, и наоборот.

Источник

2.4.1. Определение понятия “ширина спектра”

2.4.2. Метод прямого расширения спектра

2.4.3. Ортогональное частотное разделение со многими поднесущими (OFDM)

2.4.4. Примеры реализации BPSK, QPSK и QAM видов модуляции

При передаче информации с помощью радиосигнала осуществляют модуляцию какого-либо параметра высокочастотных колебаний (колебаний несущей частоты). Как правило, в качестве колебаний несущей частоты используется гармонический сигнал высокой частоты

Несложно видеть, что имеются всего лишь три параметра гармонического колебания (амплитуда, частота и фаза), которые можно менять пропорционально значению передаваемого сообщения. Поэтому говорят, что есть три основных метода модуляции: амплитудная модуляция (AM), частотная (ЧМ) и фазовая (ФМ). А способов их реализации и законов соответствия передаваемого (полезного) сообщения и модулируемого параметра ВЧ-колебания предложено такое количество, что даже трудно перечислить. Весьма обширна практическая реализация этих способов и их разновидностей в виде аппаратных, схемотехнических и программных средств. Разнообразие методов и способов реализации позволяет выбирать оптимальные варианты применительно к конкретным условиям передачи, системам связи, условиям распространения, требуемому качеству связи и т. п.

Существуют и общие факторы, происходящие из физических закономерностей, которые справедливы для любых способов модуляции:

увеличение скорости передачи приводит к увеличению частоты появления ошибок;
уменьшение длительности бита (символа) позволяет увеличить скорость передачи, одновременно приводит к расширению спектра занимаемых частот;
увеличение отношения сигнал/шум уменьшает вероятность появления ошибок;
увеличение занимаемой полосы частот позволяет увеличить скорость передачи.

Аксиома из теории спектрального анализа: уменьшение длительности импульса приводит к “расширению” спектра и, наоборот, импульсы большей длительности обладают более узким спектром. Одновременно сузить спектр и уменьшить длительность импульсного сигнала невозможно. Иное дело, что в конкретных случаях можно выбрать оптимальный вариант модуляции и, например, пойти на некоторое расширение спектра занимаемых частот; зато, уменьшив длительность посылок, можно повысить скорость передачи или, увеличив длительность посылок, можно уменьшить занимаемую область частот. Одновременно изменится и частота появления ошибок.

При использовании только одной несущей частоты существуют три “базовых” метода расширения спектра полезного сигнала: метод прямого расширения DS (Direct Spectrum) с помощью псевдослучайной последовательности (ПСП); метод расширения скачками по частоте FH (Frequency Hopping) и метод расширения скачками по времени ТН (Time Hopping). Используют также и различные комбинации этих методов.

На практике используют методы расширения спектра с помощью ансамбля из многих модулированных поднесущих, занимающих весь отведенный диапазон частот. Каждая поднесущая может модулироваться своей битовой последовательностью. Различение спектра модулированных колебаний на каждой поднесущей в цепях приемника осуществляется с помощью соответствующих канальных фильтров. Для устранения взаимного перекрытия частотных полос между спектрами на поднесущих используют защитные частотные интервалы при формировании сигнала на передачу. Такой метод расширения спектра называют широкополосной модуляцией с частотным разделением FDM (Frequency Division Multiple). У такого метода недостатком является необходимость иметь защитные частотные интервалы, что снижает эффективность использования отведенного диапазона частот.

Значительно большей эффективностью использования отведенного диапазона частот является применение технологии с ортогональным частотным разделением OFDM (Orthogonal Frequency Division Multiplexing). В этом случае спектр передаваемого радиосигнала формируется таким образом, что спектры соседних поднесущих перекрывают друг друга на половину своей ширины так, что на частотах максимума спектральной плотности любой поднесущей будут нулевые значения спектральной плотности от любых других поднесущих. В этом смысле спектры модулированных поднесущих ортогональны друг другу, следовательно, их можно разделить на приемной стороне с помощью цифрового преобразования Фурье.

Рассмотрим некоторые особенности вышеназванных методов получения радиосигналов с расширенным спектром.

В методе прямого расширения исходная битовая последовательность передаваемого сигнала перемножается с импульсами псевдослучайной последовательности (ПСП). Последовательность ПСП является как бы цифровой несущей для битовых импульсов. Импульсы ПСП имеют вид прямоугольных импульсов одинаковой амплитуды и длительностью, много меньшей длительности бита передаваемого сообщения, так, что за время длительности бита генерируется много импульсов ПСП. Моменты появления импульсов ПСП определяются псевдослучайным законом, который известен и на передающей, и на приемной сторонах. Поскольку импульсы ПСП короче битовых, то их спектр много шире спектра битовых посылок. В результате перемножения получается импульсный сигнал с широким спектром. Далее этим сигналом модулируют гармонический сигнал несущей частоты и получают радиосигнал с расширенным спектром.

В методе расширения спектра скачками по частоте спектр одного канала узкополосный, но его положение в пределах выделенного диапазона частот меняется по псевдослучайному закону путем скачкообразного изменения частоты несущей. При использовании диапазона многими пользователями каждый ведет передачу/прием в пределах узкополосного канала, но в разные моменты времени на разных частотах несущей. Смена частот несущих у всех пользователей производится синхронно. В результате по псевдослучайному закону окажется заполненным весь выделенный диапазон.

В методе расширения спектра скачками по времени спектр одного канала также узкополосный, но его положение в пределах выделенного на цикл времени меняется по псевдослучайному закону путем скачкообразного изменения момента включения радиосигнала.

В настоящее время наиболее часто применяют метод прямого расширения спектра. Именно такой метод используется, например, в системе сотовой связи CDMA (one) и в системе WiMAX стандартов 802.16 и 802.16—2004 в режиме с одной несущей SC (Single Carrier). Стандартом 802.16—2004 для условий прямой видимости используется метод прямого расширения с одной несущей, а для условий непрямой видимости более эффективным является многочастотная технология OFDM. Поэтому далее рассмотрены оба метода, применяемые в WiMAX.

Понятно, что уже на самых ранних этапах проектирования любой цифровой системы связи важнейшим становится компромиссный многокритериальный выбор метода модуляции, его схемотехническая, аппаратная и программная реализация. Разработчикам приходится искать компромисс между желанием иметь высокую скорость передачи, узкую полосу занимаемых частот, простоту реализации, низкую стоимость, невысокие требования к вычислительным ресурсам, быстродействие, относительно невысокое отношение сигнал/шум и многое другое, чаще всего исключающее друг друга. Лишь определив область использования системы связи, его связь с другими системами, условия применения и т. п., можно выбрать наиболее подходящий способ модуляции и технологию его применения. Одним из ключевых понятий, используемых при выборе типа модуляции, является ширина спектра сигнала и полоса частот, занимаемая сигналом.

2.4.1. Определение понятия “ширина спектра”

При построении систем связи с подвижными объектами всегда стремятся использовать радиосигналы с возможно меньшей шириной спектра. Теперь очевидно, что форма спектра радиосигналов при таких способах модуляции определяется формой одиночного символа.

Дефицит частотных полос, выделяемых на ту или иную систему радиосвязи, накладывает ограничения на ширину спектра частот, используемых в системе. Разработчики связной радиоаппаратуры всегда стремились минимизировать ширину спектра радиосигнала в канале с целью разместить в выделенной полосе как можно больше радиоканалов. Ширина спектра полезного сигнала должна быть много меньше частоты несущих колебаний. Такие радиоканалы принято называть узкополосными. На время сеанса связи узкополосный канал выделяется одному абоненту. Однако опыт использования широкополосных сигналов, применяемых в последние годы, показал, что можно построить эффективные системы с расширенной полосой частот в радиоканале. Занимаемая каналом ширина полосы частот может быть более 1 МГц. При этом вся ширина канала может быть предоставлена сразу многим пользователям. Разработаны способы модуляции с расширенным спектром, позволяющие при одновременной работе нескольких абонентов в одной и той же полосе частот сделать их взаимное влияние незначительным. Число таких абонентов можно увеличивать до некоторого предела, в результате чего спектральная эффективность таких систем оказывается значительно выше эффективности систем с узкополосной модуляцией.

Важнейшим параметром радиоканала является занимаемая им полоса радиочастот . При прочих равных условиях (скорость передачи информации, качество передачи и т. д.) систему считают тем лучше, чем меньше полоса частот, занимаемая одним радиоканалом. Полоса радиочастот, требующаяся для одного радиоканала, определяется формой спектра радиосигнала, который должен быть передан по данному каналу. Форма спектра радиосигнала зависит как от свойств модулирующего сигнала, так и от вида используемой модуляции. При этом получается разным соотношение сигнал/шум для разных видов модуляции и связанная с ним вероятность ошибок в принимаемом сигнале.

Заметим, что термин “форма спектра радиосигнала” является не совсем ростым, по крайней мере, по двум причинам. Во-первых, формы наиболее привлекательных модулирующих сигналов оказываются достаточно сложными. В результате чего процесс вычисления их спектров оказывается затруднительным. Во-вторых, модулирующие сигналы приходится рассматривать как специфические случайные процессы, поскольку они отображают случайные последовательности битов, передаваемые в цифровых системах по радиоканалам. Поэтому более правильным является термин “спектральная плотность мощности” модулирующего сигнала или радиосигнала. Часто для краткости термин “спектр” употребляют вместо термина “спектральная плотность”. Обычно из контекста понятно, о каком значении спектра говорится. Пояснение физического смысла спектральной плотности мощности для произвольного стационарного случайного процесса можно найти в учебниках по курсу “Радиотехнические цепи и сигналы”.

Теоретически спектр (и спектральная плотность), как модулирующих импульсов, так и модулированного радиосигнала, имеет по оси частот неограниченное значение, т. е. ширина спектра равна бесконечности. При этом с ростом частоты уровни спектральных составляющих неограниченно уменьшаются, стремясь к нулевому уровню. На практике нет смысла учитывать спектральные составляющие, уровень которых ниже уровня шумов. Прохождение сигнала через фильтрующие устройства и через среду с ограниченной полосой пропускания также ограничивает ширину спектра. Поэтому на практике определяют ширину спектра, как некоторую область частот Δf, в пределах которой ведут учет спектральных составляющих. Само же понятие ширины спектра определить единственным способом невозможно. Исходя из общих свойств модулирующих цифровых сигналов, их можно считать квазислучайными последовательностями. Будем рассматривать модулирующий сигнал общего вида на достаточно больших промежутках времени. Для этого сигнала в качестве его математической модели можно использовать случайный процесс U(t)с вещественными значениями, реализации которого доступны наблюдению, регистрации и обработке на всей оси времени (−∞< t <+∞). Обычно считают, что этот процесс является стационарным, и его математическое ожидание M{U(t)} постоянно и равно нулю для всех модулирующих сигналов. В этом случае ковариационная функция процесса U(t)определяется равенством:

, ( < < ),

где функция — совместная плотность вероятности значений процесса U(t)в два момента времени: tи t+τ.Для стационарных процессов эта функция зависит только от разности рассматриваемых моментов времени.

Если процесс является эргодическим, то можно применить иное определение ковариационной функции:

, ( < < ),

которое часто используется для практического вычисления ковариационной функции процесса U(t)по одной единственной реализации и этого процесса, полученной на достаточно большом интервале времени. Здесь верхний индекс k указывает на номер реализации.

Спектральная плотность мощности случайного процесса U(t)теперь может быть найдена как прямое преобразование Фурье ковариационной функции:

, ( < < ). (2.1)

За ширину спектральной плотности мощности можно принять полосу частот, в которой сосредоточено 95% мощности модулирующего сигнала.

Следует обратить внимание, что функция S(ώ) определена как для положительных, так и для отрицательных значений угловой частоты ώ=0.

Поскольку ковариационная функция К(х)является вещественной симметричной относительно нуля функцией, то спектральная плотность мощности S(ώ) также является вещественной и симметричной относительно точки ώ = 0 функцией. Для всех модулирующих сигналов в системах связи с подвижными объектами это свойство сохраняется. Физические спектры этих сигналов существенно отличны от нуля в окрестности нулевой частоты; их значения уменьшаются с ростом частоты , но, к сожалению, не становятся равными нулю.

Одно из определений ширины спектра можно сформулировать следующим образом: в качестве ширины Δf_оп основной полосы спектра (2.1) принимается интервал частот, на котором сосредоточено 95% мощности модулирующего сигнала:

(2.2)

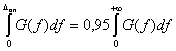
или, что эквивалентно,

. (2.3)

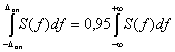
При любом способе модуляции спектр модулирующего сигнала переносится в область высоких радиочастот. Если для радиосигнала использовать обозначение s[t;U(t)], то очевидно, что подводимый к излучающей антенне сигнал передатчика является узкополосным случайным процессом, для которого могут быть использованы определения, аналогичные приведенным, с той лишь разницей, что спектр модулированного сигнала сосредоточен около частоты (или f₀) несущего колебания. Ширину спектра этого радиосигнала будем определять соотношениями, аналогичными (2.2) или (2.3):

;

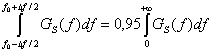
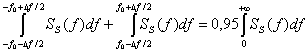
Следует обратить внимание еще на одно важное понятие — мощность внеполосного излучения, которую обычно определяют выражением:

. (2.4)

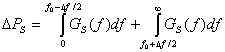
Часто используемой мерой ширины спектра сигнала является полоса частот, на которой спектральная плотность мощности превышает половину максимального значения, т. е. значение спектра на граничных частотах на 3 дБ ниже его максимального значения. Иногда используют и более жесткое определение ширины спектра — это полоса частот между нижней и верхней граничными частотами, такими, что только 0,5% мощности сигнала попадает в область выше верхней границы и 0,5% — ниже нижней границы; так что 99% мощности сигнала попадает в полосу частот, которая принимается в качестве ширины спектра.

Из многолетнего опыта использования различных радиосистем стало понятно, что из-за более широкой занимаемой полосы частот амплитудная модуляция (AM) уступает частотной и фазовой модуляции. Уступает и помехозащищенность. Поэтому практически во всех современных системах цифровой радиосвязи используют частотную или фазовую модуляцию. Правда, достижения цифровой техники последних лет позволили изменить представление о методах АМ-модуляции. Оказалось, за счет дополнительной обработки можно избежать слишком широкого спектра АМ-сигнала и использовать АМ-модулированные сигналы наряду с частотно- или фазомодулированными сигналами. По-видимому, и в дальнейшем возможны улучшения характеристик модулированных сигналов. Подробности различных способов цифровой модуляции хорошо описаны в [25, 27], а в [28] помимо различных способов модуляции приводятся спектральные характеристики модулированных сигналов.

По ширине занимаемой полосы частот все системы цифровой связи можно условно разделить на системы с узкополосными сигналами и системы с широкополосными и сверхширокополосными сигналами. Использование узкополосных сигналов основывается на желании иметь как можно меньшую полосу занимаемых частот. При этом можно избежать (при надлежащем исполнении полосовых фильтров на входе приемника и на выходе передатчика) попадания в приемник сигналов соседних каналов или от других систем, в то же время не создавая своей работой помех другим системам. При узкой полосе пропускания входных цепей на вход приемника попадает меньше шумов, меньше интерференции. В радиосвязи всегда ставятся жесткие ограничения на диапазон и ширину занимаемой сигналом полосы частот. Это связано с наличием в мире множества различных радиоэлектронных средств, а частотные ресурсы практически во всех странах почти исчерпаны. В каждой стране имеются государственные органы надзора за распределением и использованием имеющегося радиочастотного ресурса по регионам.

Получение разрешения на ту или иную полосу частот в необходимом диапазоне сопряжено с длительным изучением возможностей и требует заметных финансовых затрат. И не всегда вопрос может быть решен положительно, поскольку требуемые частоты могут уже использоваться другими системами. При использовании узкополосных систем в отведенном диапазоне может работать большее количество радиооборудования.

Если модулировать несущую частоту непосредственно битовыми импульсами, имеющими, как правило, прямоугольную форму, то при амплитудной модуляции спектр модулирующих прямоугольных импульсов будет перенесен в область несущей частоты. Примерно 90% энергии радиосигнала будет сосредоточено в первом лепестке спектральной плотности. Ширина этого лепестка обратно пропорциональна длительности модулирующего импульса . Чем меньше длительность импульса, тем шире занимаемая радиосигналом полоса частот при любом виде модуляции. Столь широкая полоса занимаемых частот не всегда приемлема. Поэтому в системах цифровой связи принимают меры по ограничению полосы частот спектра. В принципе полосу можно ограничить, пропуская модулированный сигнал через полосовой фильтр с центральной частотой, равной частоте несущих колебаний. Однако габаритные размеры фильтров и их стоимость достаточно велики, к тому же любые реальные фильтры имеют конечную крутизну скатов в области задержания. Поэтому во всех методах цифрой модуляции ограничивают спектр самого модулирующего импульса, т. е. модулировать необходимо не прямоугольными импульсами, а импульсами такой формы, спектр которых был бы минимальным. В цифровых системах передачи форма битовых импульсов не несет информации. Информация заложена лишь в наличии или отсутствии импульса и его полярности. Можно поставить вопрос: импульс какой формы имеет минимальную ширину спектра? Этому условию отвечает импульсный сигнал, описываемый функцией:

, (2.5)

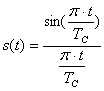
где — время передачи символа. Спектр такого сигнала прямоугольный с шириной полосы занимаемых частот , и у него нет боковых составляющих спектра. К сожалению, такой импульс физически нереализуем, поскольку он не ограничен во времени. Он должен начинаться в −∞ и длиться бесконечно долго. Любое ограничение такого импульса по времени приводит к расширению полосы пропускаемых частот. Форма частотной характеристики фильтра отклоняется от прямоугольной и приобретает колоколообразный вид с плавно нарастающими и спадающими фронтами. На практике реализуют фильтры с частотной характеристикой типа приподнятого косинуса или фильтры с гауссовской характеристикой. В системе GSM принята фазовая манипуляция с минимальным сдвигом GMSK, где модулирующие прямоугольные импульсы вначале пропускают через гауссовский фильтр. За счет этого удается сузить спектр модулированного сигнала по сравнению с модуляцией прямоугольными импульсами более чем в 1,2 раза.

На практике чаще всего применяют спектрально эффективные фазовые способы модуляции BPSK, QPSK, GMSK, частотные виды модуляции FSK. GFSK и другие их разновидности или комбинации. Подробности об этих видах модуляции можно найти в [25, 28].

Широкополосные системы связи обладают рядом преимуществ и недостатков по сравнению с узкополосными системами. К преимуществам можно отнести:

использование отведенного спектра частот сразу многими пользователями;
малая чувствительность как к узкополосным, так и широкополосным помехам (естественным или искусственным);
малая чувствительность к интерференционным помехам в условиях многолучевого распространения;
меньшая чувствительность к селективным замираниям;
возможности шифрования сигнала с целью обеспечения безопасности информации;
более эффективное использование отведенного спектра, так как появляется возможность передавать более 1 бита на 1 Гц частоты;
возможность получения высоких скоростей передачи.

К недостаткам можно отнести необходимость выделения дефицитного частотного ресурса сразу в широкой области частот, сравнительно высокую стоимость и сложность оборудования.

Опыт эксплуатации показал, что во многих случаях применение широкополосных сигналов экономически выгоднее, так как отведенный спектр используется более эффективно. Выбор систем передачи (узкополосные или широкополосные) определяется технологией использования модулированных сигналов. Например, в системе сотовой связи стандарта GSM используются узкополосные частотные каналы шириной 200 кГц с разновидностью фазовой модуляции GMSK, называемой гауссовской частотной манипуляцией с минимальным сдвигом (ГММС), а в системе сотовой связи CDMA используется широкополосный сигнал (1,225 МГц), получаемый методом прямого расширения спектра и использованием QPSK.

При разработке WiMAX как системы, обеспечивающей высокоскоростные каналы передачи, был выбран путь использования широкополосных сигналов. Такие сигналы обладают наибольшим преимуществом в условиях многолучевого распространения и многопользовательского применения. Стандартами IEEE 802.16 и IEEE 802.16a предусматривается использование расширенного спектра на одной несущей частоте SC (Single Carrier). При этом пользовательские станции имеют фиксированное положение антенн (мобильности нет). В этом случае при частотно-территориальном планировании, дополненном реальными измерениями, можно найти наилучшее решение по размещению антенн, их диаграмм направленности, выборе мощностей передатчиков для уменьшения интерференции и уменьшить попадание на антенну приемника многих отраженных сигналов. Для обеспечения мобильности в условиях многолучевого распространения подходит другая технология, основанная на ортогональном уплотнении с частотным разделением OFDM (Orthogonal Frequency Division Multiplexing), иногда называемая еще модуляцией с множественными несущими.

2.4.2. Метод прямого расширения спектра

Важным свойством метода прямого расширения спектра можно считать то, что ширина спектра сигнала, модулирующего опорную частоту, а значит, и радиосигнала, определяется главным образом не скоростью передачи полезной информации, а параметрами ПСП. Элементарный импульс ПСП называют чипом. Каждый информационный бит после перемножения с ПСП будет отображаться многими чипами. (Например, один информационный бит отображается 128 чипами ПСП.) Скорость в радиоканале определяется, как произведение скорости передачи на выходе канального кодера и количества чипов за интервал одного бита. Обычно скорость передачи в радиоканале измеряют в мегачипах в секунду (Мчип/с).

Сигналы с расширенным спектром являются псевдослучайными, т. е. имеют свойства, аналогичные свойствам случайного процесса или шума, хотя формируются по вполне детерминированным алгоритмам. ПСП чаще всего является бинарной с элементами 0 и 1 и обладает свойствами, схожими со свойствами случайной бинарной последовательности. Например, если на любом конечном интервале число нулей примерно равно числу единиц, то автокорреляционная функция такой последовательности близка к автокорреляционной функции случайной бинарной последовательности, в частности, имеет малые значения коэффициента корреляции между сдвинутыми друг относительно друга копиями одной и той же последовательности и т.д. Это свойство используется для распознавания ПСП.

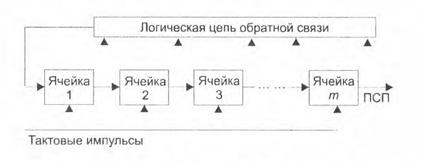
Псевдослучайные последовательности обычно формируются с помощью логических цепочек, реализующих детерминированные алгоритмы. На рис. 2.5 приведен пример такой цепи [25], которая содержит регистр сдвига из последовательно соединенных элементов с двумя устойчивыми состояниями и некоторую логическую схему в цепи обратной связи.

Рис. 2.5. Генератор ПСП

Двоичная последовательность символов 0 и 1, хранящаяся в регистре, смещается вправо по регистру при подаче очередного тактового импульса; символ из последней ячейки регистра выдается на выход в качестве очередного символа последовательности; символы всех или некоторых ячеек регистра подаются в логическую цепь обратной связи, в которой формируется символ обратной связи, передаваемый в первую ячейку регистра.

Период следования тактовых импульсов определяет длительность элементарного символа (чипа) последовательности. Если логическая цепь обратной связи содержит только элементы типа “исключающее ИЛИ”, которые применяются наиболее часто, данное устройство называется генератором линейной псевдослучайной последовательности (ПСП). В этом случае значение очередного символа на выходе цепи обратной связи определяется следующим рекуррентным соотношением:

, (2.6)

где символ “+” обозначает суммирование по модулю 2, а коэффициенты и символы принимают значения 0 или 1. Логическая цепь обратной связи в этом случае представляет собой сумматор по модулю 2.

Начальное состояние ячеек регистра и структура логической цепи обратной связи полностью определяют последующее состояние ячеек регистра. Если принять некоторое состояние регистра сдвига за исходное, то через N тактов это состояние вновь повторится. Если при этом регистрировать последовательность символов на выходе ячейки с номером I, то длина этой последовательности будет равна N. На последующих N тактах эта последовательность вновь повторится и т. д.

Число N называется периодом последовательности. Значение N при фиксированной длине регистра m зависит от числа ненулевых весовых коэффициентов с и расположения соответствующих отводов в регистре. Например, из равенства (2.6) следует, что если в какой-то момент времени состояние всех ячеек регистра оказывается равным 0, то все последующие элементы последовательности на выходе регистра будут нулевыми. Существует разных ненулевых состояний регистра сдвига. Следовательно, период линейной ПСП, формируемой регистром сдвига с m ячейками, не может превышать символов. ПСП с периодом , формируемые регистром сдвига с линейной обратной связью, называются последовательностями максимальной длины или, более коротко, М-последовательностями. Длительность периода повторения ПСП может составлять десятки-сотни часов.

Устройство, функциональная схема которого представлена на рис. 2.5, можно назвать цифровым автоматом. Если формируемая им последовательность описывается уравнением (2.6), то такие автоматы принято задавать характеристическим многочленом:

где и . Значение вектора полностью определяет структуру автомата формирования ПСП: если коэффициент , то это означает, что выход ячейки с номером I к цепи обратной связи не подключен; при I-й выход подключен.

Известно достаточно большое число способов формирования псевдослучайных последовательностей, статистические свойства которых хорошо изучены. У них автокорреляционная функция имеет ярко выраженный максимум, а взаимокорреляционная функция носит случайный шумоподобный характер с малым уровнем значений. Новые способы реализации ПСП получают и в настоящее время.

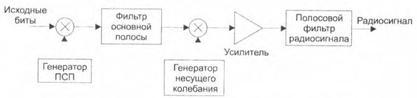
Можно использовать два способа получения радиосигнала с расширенным спектром. Например, сначала перемножить исходную битовую последовательность с выхода кодера канала на сигнал ПСП, тем самым расширить спектр. Затем полученным сигналом промодулировать колебания несущей частоты. При второй модуляции можно использовать методы фазовой модуляции (BPSK, QPSK) или амплитудно-фазовой (QAM). Пример построения такого способа формирования радиосигнала с расширенным спектром приведен на функциональной схеме рис. 2.6.

Рис. 2.6. Функциональная схема формирования радиосигнала с расширенным спектром

Фильтр основной полосы в этой схеме предназначен для получения модулирующего сигнала с требуемой формой спектральной плотности мощности и требуемой полосой частот. Однако теперь на входе фильтра сигнал имеет в раз более широкий спектр, так что и радиосигнал имеет в В раз более широкий спектр, чем обычный узкополосный радиосигнал.

Аналогичный результат получится, если вначале промодулировать битовой последовательностью колебания несущей частоты методами BPSK, QPSK или QAM, а затем осуществить модуляцию полученного радиосигнала импульсами ПСП.

Прямое расширение спектра осуществляется путем перемножения информационного сигнала на сигнал ПСП , формируемый из псевдослучайной последовательности в течение всего сеанса связи. В результате модулирующий сигнал можно записать:

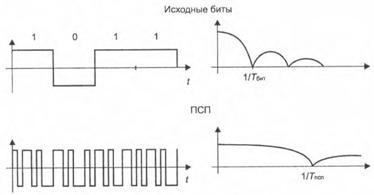
На рис. 2.7 показан примерный вид участка исходной битовой последовательности, сигнала ПСП и их соответствующие спектры.

Рис. 2.7. Примерный вид соотношения битовой последовательности и ПСП

Сигналы с расширенным спектром имеют интересную особенность. При первом перемножении битовой последовательности с сигналом ПСП (в передатчике) происходит расширение спектра до полосы . В приемнике входной радиосигнал с расширенным спектром поступает на первый демодулятор, на который также подается такая же ПСП, что и была использована в передатчике. В результате перемножения входного радиосигнала с сигналом ПСП на выходе первого демодулятора получается радиосигнал, спектр которого вновь сужается и становится равным по ширине спектру канальной битовой последовательности. Важно заметить, что при первом перемножении (в передатчике) битовой последовательности с сигналом ПСП происходит расширение спектра, а второе перемножение (в демодуляторе приемника) с такой же ПСП, вновь сужает спектр до исходного спектра канальных битов. Это свойство сигналов с расширенным спектром играет весьма полезную роль в уменьшении негативного влияния помех. 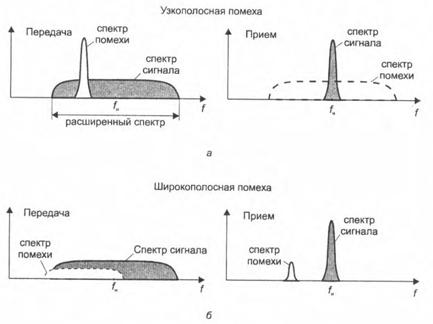Допустим, что в радиоканале имеется узкополосная (преднамеренная или случайная) помеха, спектр которой находится в пределах расширенного спектра сигнала. При попадании помехи совместно с сигналом на вход приемника на первом демодуляторе сигнал подвергнется второму умножению на ПСП, его спектр сузится, а помеха подвергнется первому перемножению с ПСП и его спектр расширится и его энергия окажется “размазанной” по широкой области частот (см. рис. 2.8, а). При выделении полосовым фильтром (например, на промежуточной частоте) спектра полезного сигнала в его полосу будет попадать лишь малая доля энергии помехи. Поэтому даже сравнительно сильная узкополосная помеха окажет незначительное влияние.

Рис. 2.8. Воздействие помехи:

а – узкополосная помеха; б – широкополосная помеха

При попадании на вход приемника широкополосной помехи совместно с полезным сигналом (рис. 2.8, б) после перемножения с ПСП пропорционально сузятся спектры и сигнала, и помехи. Если они имели разные полосы и разные центральные частоты, то помеха и сигнал могут быть разделены полосовым фильтром. Такая невосприимчивость к помехам делает привлекательным использование сигналов с расширенным спектром в условиях наличия помех.

В условиях многолучевого распространения сигнала отраженные копии будут приходить на вход приемника с запозданием относительно основного сигнала. Если задержка копий будет более длительности чипа, то их можно отделить от основного сигнала. В узкополосном сигнале, модулированном битовыми импульсами, длительность битовой посылки довольно велика, и отраженные копии сигнала успевают наложиться на основной сигнал. Длительность чиповых импульсов намного меньше, поэтому отраженные сигналы могут не накладываться на основной сигнал.

Следует обратить внимание еще на одно свойство сигналов с расширенным спектром. Поскольку ширина расширенного спектра радиосигнала одного канала значительно больше ширины спектра сигнала, полученного при частотном разделении каналов (узкополосных), то при одинаковой излучаемой мощности этих радиосигналов спектральная плотность мощности сигнала с расширенным спектром оказывается намного меньше и может даже не превышать спектральную плотность мощности шума. Это обеспечивает хорошую скрытность широкополосных сигналов.

Важным для систем подвижной связи является также отсутствие необходимости решать проблему распределения частот между различными абонентами, поскольку все абоненты используют одну и ту же полосу частот. Для узкополосных методов модуляции решение задачи частотного планирования обязательно.

Важной характеристикой широкополосного сигнала является его база, смысл которой заключается в относительном увеличении полосы частот передаваемого сигнала в радиоканале по сравнению с полосой частот битового (исходного) сигнала. Величина базы сигнала: . Обычно базу сигнала определяют в децибелах: . На практике удобнее определять базу сигнала как произведение ширины спектра исходного сигнала на длительность элементарного символа ПСП (чипа): . По многим причинам удобно использовать такую длительность чипа ПСП, чтобы база сигнала с расширенным спектром была целым числом. На приемной стороне удобно использовать понятие выигрыш обработки, величина которой численно равна величине базы сигнала и означает выигрыш за счет обратного сужения спектра от расширенного к исходному: .

Перечислим коротко некоторые свойства сигналов с прямым расширением спектра, наиболее важные с точки зрения организации множественного доступа в системах связи с подвижными объектами.

· Множественный доступ. Если одновременно несколько абонентов используют канал передачи, то в канале одновременно присутствуют несколько сигналов с прямым расширением спектра. Каждый из этих сигналов занимает всю полосу канала. В приемнике сигнала конкретного абонента осуществляется обратная операция — свертывание сигнала этого абонента путем использования того же псевдослучайного сигнала, который был использован в передатчике этого абонента, Эта операция концентрирует мощность принимаемого широкополосного сигнала снова в узкой полосе частот, равной ширине спектра информационных символов. Если взаимная корреляционная функция между псевдослучайными сигналами данного абонента и других абонентов достаточно мала, то при когерентном приеме в информационную полосу приемника абонента попадет лишь незначительная доля мощности сигналов остальных абонентов. Сигнал конкретного абонента будет принят верно.

· Многолучевая интерференция. Если псевдослучайный сигнал, используемый для расширения спектра, имеет идеальную автокорреляционную функцию, значения которой вне интервала равны нулю, и если принимаемый сигнал и копия этого сигнала в другом луче сдвинуты во времени на величину, большую , то при сворачивании сигнала его копия может рассматриваться как мешающая интерференция, вносящая лишь малую долю мощности в информационную полосу.

· Узкополосная помеха. При когерентном приеме в приемнике осуществляется умножение принятого сигнала на копию псевдослучайного сигнала, используемого для расширения спектра в передатчике. Следовательно, в приемнике будет осуществляться операция расширения спектра узкополосной помехи, аналогичная той, которая выполнялась с информационным сигналом в передатчике. Следовательно, спектр узкополосной помехи в приемнике будет расширен в В раз, где В — коэффициент расширения, так что в информационную полосу частот попадет лишь малая доля мощности помехи, в В раз меньше исходной мощности помехи.

· Вероятность перехвата. Так как сигнал с прямым расширением спектра занимает всю полосу частот системы в течение всего времени передачи, то его излучаемая мощность, приходящаяся на 1 Гц полосы, будет иметь очень малые значения. Следовательно, обнаружение такого сигнала является очень трудной задачей.

Применение широкополосных сигналов имеет свои достоинства и недостатки, в целом присущие любому способу их формирования.

Достоинства широкополосных сигналов:

генерирование необходимых псевдослучайных сигналов может быть обеспечено простыми устройствами (регистрами сдвига);
операция расширения спектра может быть реализована простым умножением или сложением цифровых сигналов по модулю 2;
генератор несущего колебания является простым, так как необходимо генерировать гармоническое несущее колебание только с одной частотой;
может быть реализован когерентный прием сигнала с прямым расширением спектра;
нет необходимости обеспечивать синхронизацию между абонентами системы.

Недостатки широкополосных сигналов:

выравнивание и поддержание синхронизации между генерируемым в приемнике и содержащимся в принимаемом сигнале псевдослучайными кодами является трудной задачей. Синхронизация должна поддерживаться с точностью до малой доли длительности элементарного символа;
правильный прием информации обеспечивается только при высокой точности временной синхронизации, когда ошибка составляет малую долю длительности элементарного символа, что ограничивает возможность уменьшения длительности этого символа и, следовательно, возможность расширения полосы лишь до 10…20 МГц. Таким образом, существует ограничение на увеличение коэффициента расширения спектра;
мощность сигнала, принимаемого от близких к БС абонентов, намного превышает мощность сигнала далеких абонентов. Следовательно “близкий” абонент постоянно создает очень мощную помеху “далекому” абоненту, часто делая прием его сигнала невозможным. Эта проблема “близкий — далекий” может быть решена применением системы управления мощностью, излучаемой пользовательской станцией и базовой станцией в направлении пользовательской. Цель управления — обеспечить одинаковую среднюю мощность сигналов разных пользователей на входе приемника базовой станции.

2.4.3. Ортогональное частотное разделение со многими поднесущими (OFDM)

OFDM есть метод модуляции, уже используемый и хорошо зарекомендовавший себя в беспроводных компьютерных сетях (WLAN), таких как IEEE 802.11 в США, ETSI BRAN в Европе, ARIB ММАК в Японии, в мобильной связи, а также в цифровых аудио- и видеовещании. Концепция данного метода модуляции [22, 26, 7], в основном, базируется на известном с середины 1950-х гг. методе модуляции со многими поднесущими (Multicarrier modulation — МСМ), однако учитывает новейшие достижения последних десятилетий в области цифровых методов передачи информации и высокоэффективных методов модуляции, обеспечивающих высокие качественные характеристики систем связи при наличии помех, доплеровских смещений частот, замираний сигналов и т. д.

Амплитудно-частотные характеристики (АЧХ) реальных каналов передачи не равномерны в полосе частот для разных поднесущих частот и не постоянны во времени. Спектральная плотность мощности аддитивного гауссовского шума также может быть не постоянной. Согласно К. Шеннону, максимальная скорость передачи информации по таким каналам достигается, когда спектральная плотность мощности передаваемого сигнала во всей полосе удовлетворяет условию

, (2.7)

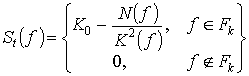
где константа выбирается из условия

— средняя мощность передатчика.

Один из способов повышения эффективности использования полосы частот состоит в разделении её на N поддиапазонов шириной

. (2.8)

Выбор величины достаточно малой позволяет аппроксимировать отношение константой в каждом поддиапазоне и передавать сигналы с оптимальным распределением мощности , а будучи закодированными, индивидуально; сигналы при этом дают возможность достичь максимальной скорости передачи информации.

Метод OFDM позволяет реализовать указанные возможности. В этом методе весьма эффективно используется разбиение последовательности символов данных на параллельный поток с увеличением длительности каждого символа.

При OFDM символы данных часто берутся из алфавитов рассмотренных

далее так называемых m-ичных систем модуляции (m-позиционных) PSK, BPSK, QPSK QAM и т. п. Эти символы передаются поднесущими, отстоящими

друг от друга на интервал Гц, где — длительность символа, что обеспечивает их ортогональность при прямоугольной форме модулирующих видеоимпульсов, несмотря на случайные фазы, обусловленные модуляцией данными. Выбор другой формы огибающей модулирующих видеоимпульсов дает возможность получить более компактной спектральную плотность мощности, однако влечет за собой нарушение ортогональности поднесущих и увеличение вероятности появления ошибок.

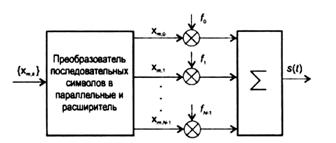
Передаваемая последовательность символов данных разбивается на блоки из N символов. Каждый блок из _N последовательных символов преобразуется в блок из N параллельных символов длительностьюкаждый. Полученные символы модулируют N соответствующих поднесущих частот (рис. 2.9 и 2.10).

Рис. 2.9. Формирование группового OFDM-сигнала

Рис. 2.10. Взаимное расположение ортогональных поднесущих частот

При этом комплексную огибающую сигнала OFDM на интервале Т можно представить в форме

_{, (2.9)}

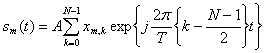
где: — помер блока данных;—амплитуда; – поднесущая частота,

_(2.10)

множитель, обеспечивающий центрирование полосового сигнала относительно поднесущей частоты_.

Если длина блокавыбрана так, что >>где — длительность импульсной характеристики канала поднесущей частоты (подканала), то межсимвольная интерференция (наложение соседних блоков друг на друга) значительно снижается. Она может быть исключена полностью за счет небольшого снижения пропускной способности, если между последовательно модулированными OFDM-блоками вставить защитный интервал .

Из (2.7) следует, что передаваемая мощность должна быть большой, когда отношение велико, и наоборот. Это подразумевает, что в реальных системах связи с заданной вероятностью ошибки необходимо использование большего алфавита сигналов в тех подканалах, где больше. Такой метод OFDM получил название “дискретной многотональной модуляции” (ДМТ).

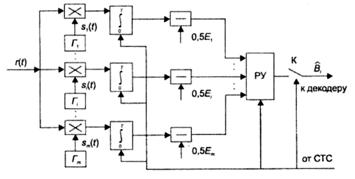
В рассматриваемом варианте метода OFDM структурная схема оптимального демодулятора достаточно сложна, так как для каждого из подканалов она должна совпадать с известной структурной схемой оптимального демодулятора полностью известных сигналов (рис. 2.11) и быть достаточно гибкой, чтобы учесть возможное разнообразие (в том числе изменяющееся) алфавитов сигналов на поднесущих частотах.

Главным достоинством метода OFDM, обусловившим его широкое применение, является то обстоятельство, что модуляция и демодуляция сигналов могут быть выполнены в дискретной форме с использованием дискретного (ДПФ), а, следовательно, и быстрого (БПФ) преобразования Фурье.

Рис. 2.11. Структурная схема оптимального демодулятора

Рассматривая в (2.9) (в качестве примера) блок с номером m=0 и пренебрегая частотным смещением (2.10), комплексную огибающую OFDM сигнала можно записать в виде

(2.11)

и выполнить ее дискретизацию с шагом в моменты , где _.Тогда для момента времени из (2.7) получим:

_{. (2.12)}

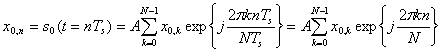
Выражение (2.12) есть обратное дискретное преобразование Фурье от вектора которое эффективно вычисляется с помощью алгоритма обратного быстрого преобразования Фурье (Inverse Fast Fourier Transform — IFFT).

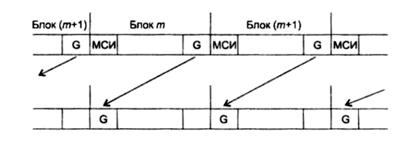
Другим важным преимуществом метода OFDM является простота снижения влияния межсимвольной интерференции (МСИ). Это достигается за счет введения защитного интервала, добавляемого к исходному блоку в виде циклического префикса длиной G интервалов отсчета. С учетом этого защитного интервала символы передаваемой последовательности определяются выражением (2.13):

, (2.13)

а для исключения снижения скорости передачи информации длительность символа, передаваемого по линии связи, уменьшается до величины

_(2.14)

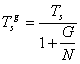
Полученная последовательность после цифроаналогового преобразователя (ЦАП) и модуляции несущего колебания (например, с использованием квадратурной амплитудной модуляции) может быть передана по линии связи.

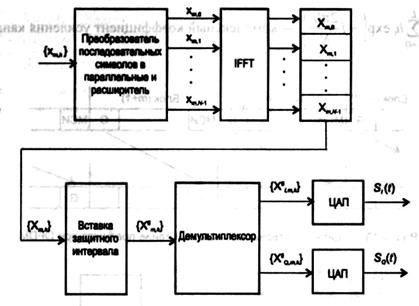
Структурная схема OFDM-модулятора с использованием IFFT представлена на рис. 2.12.

Комбинация ЦАП, линии связи с импульсной характеристикой , фильтра предварительной селекции и аналогоцифрового преобразователя эквивалентна каналу связи с дискретным временем с импульсной характеристикой, определяемой множеством ее выборочных значений, где , и эффективной длительностью _.

Элементы последовательности отсчетов на выходе канала с дискретным временем принятого сигнала представимы дискретной сверткой

_(2.15)

Рис. 2.12. Структурная схема OFDM-модулятора с использованием IFFT

Когда очередной блок принят, первые G ≥ L символов могут быть искаженными за счет межсимвольной интерференции (на рис. 2.13 обозначены МСИ — межсимвольная интерференция), порожденной предшествующим блоком. Влияние межсимвольной интерференции удается практически исключить циклической заменой искаженных (МСИ) отсчетов введенным ранее префиксом (символами защитного интервала G из последней части ранее переданного фрейма) согласно выражению:

(2.16)

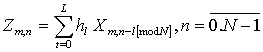
Схема замены искаженных символов символами префикса представлена на рис. 2.13.

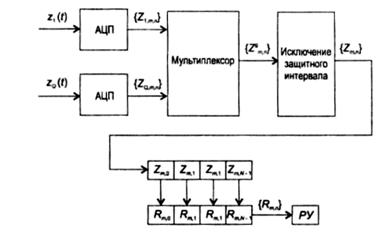
Структурная схема OFDM-демодулятора с использованием быстрого преобразования Фурье приведена на рис. 2.14.

Элементы выходной последовательности определяются выражением:

(2.17)

где — комплексный коэффициент усиления канала.

Рис. 2.13. Защитные интервалы и использование префикса при OFDM

Рис. 2.14. Структурная схема OFDM-демодулятора

Последовательность поступает на вход решающего устройства (РУ).

Вероятность ошибки Р_ош при приеме одиночного символа данныхопределяется используемыми алфавитом, разновидностью реализованного метода OFDM и видом модуляции несущего колебания.

Использование OFDM предусмотрено стандартом IEEE 802.16—2004 (старое название IEЕЕ 802.16 Revd). По этой технологии в разрешенной полосе частот (она может иметь ширину 1,5, 10, 20, 25 и 28 МГц) генерируются N поднесущих частот. Передаваемая информация, имеющая скорость передачи R бит/с, распараллеливается на потоки, число которых равно числу поднесущих. Длительность битового интервала . 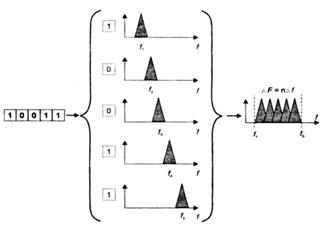Перед модуляцией каждый импульс параллельного потока растягивается во времени враз, так что длительность бита становится_NT_b_.Каждый импульс из параллельного потока модулирует “свою” поднесущую. На рис. 3.15 показан пример формирования спектра радиосигнала. Для упрощения рисунка взят кадр из 5-ти передаваемых бит.

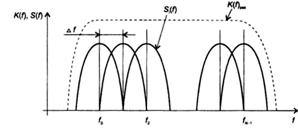
Рис. 2.15. Формирование спектра OFDM-сигнала

Обратите внимание, что в суммарном сигнале спектры частично перекрываются. Причем перекрытие спектра производится таким образом, что максимум спектральной плотности для любой поднесущей всегда соответствует минимальному значению (теоретически нулевому) первого лепестка соседних поднесущих и всех боковых лепестков. В этом случае скалярное произведение соседних спектров не равно нулю только на частотах максимальных значений спектров поднесущих. В этом смысл ортогональности, и это позволяет выделить спектральные компоненты поднесущих из общего сигнала с помощью преобразования Фурье. На практике в принятом сигнале всегда присутствуют шумы и всегда есть некоторая взаимная несогласованность стабильности частот ансамбля станций. Поэтому соответствие максимума спектральной плотности поднесущих нулевым значениям спектральной плотности остальных поднесущих на практике будет выполняться неточно. Говорят, что система связи с OFDM наиболее чувствительна к джиттеру (дрожанию) частот поднесущих и их фаз. Это и будет, в основном, ограничивать качество приема и распознавания. Модуляция на каждой поднесущей, в принципе, может производиться любым способом. Разумеется, целесообразно и в этом случае использовать спектральноэффективные способы с целью минимизировать ширину спектра каждой поднесущей. В WiMAX используют BPSK, QPSK и QAM.

2.4.4. Примеры реализации BPSK, QPSK и QAM видов модуляции

При формировании широкополосного радиосигнала в пределах отведенного диапазона частот модуляцию несущей (в системе с прямым расширением спектра на одной несущей) или поднесущих в системе OFDM осуществляют битовыми импульсами, поступающими с выхода кодера канала. В последовательности таких бит содержится и полезная информация, и служебная, и вся необходимая управляющая информация. Используют так называемые спектрально эффективные виды модуляции, с помощью которых за одну посылку удается передать информацию сразу об т битах. Такую посылку называют символом. Формируется минимально необходимая ширина спектра, определяемая видом модуляции. Спектрально эффективные виды модуляции, содержащие в одном символе информацию из т бит, относятся к m-позиционным (m-ичным) системам модуляции. К числу таких методов модуляции относятся BPSK, QPSK, QAM и различные их варианты.

Фазовая модулящия BPSK и QPSK

Радиосигнал при бинарной фазовой манипуляции (называемой также двоичной ФМ или ФМ-2) BPSK (Binary Phase Shift Keying) можно представить в виде:

То есть модулированный сигнал имеет вид гармонических колебаний, фаза которых в зависимости от передаваемого символа +1 или -1 может меняться скачком на _.

Рассмотрим частный случай, как правило, используемый в цифровых системах передачи, когда форма символа является прямоугольной:

_(2.18)

Тогда

Таким образом,

Спектральную плотность мощности модулирующего процесса при форме символа (3.18) вычисляем как преобразование Фурье:

(2.19)

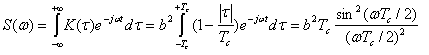
Поэтому спектральная плотность мощности радиосигнала может быть получена непосредственно из спектра модулирующего сигнала:

а физический спектр (т. е. только для положительных частот) ФМ-2 радиосигнала в рассматриваемом случае имеет вид:

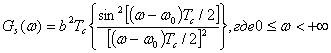
С целью последующего сравнения спектров для различных способов модуляции и увеличения диапазона возможных значений при построении соответствующих графиков введем нормировку спектра на его максимальное значение и используем логарифмический масштаб по оси ординат:

(2.20)

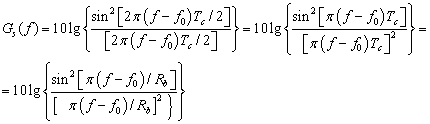
Здесь введено обозначение скорости передачи информации, так как

при ФМ-2 за время длительности символа (в секундах)передается 1 бит. Произведение является безразмерным и часто используется при построении графиков спектров для различных способов модуляции.

На рис. 2.16 представлен график функции физической спектральной плотности из (2.19) от нормированного значения (на графике для краткости обозначено буквой ). Для рассматриваемого примера график обозначен как и показан пунктиром.

Спектральная плотность мощности для сигнала с квадратурной фазовой модуляцией QPSK (Quadrature Phase Shift Keying) может быть получена аналогично спектральной плотности BPSK-сигнала. Запишем для общности сигнал QPSK в виде:

_, (2.21)

где функции

синфазная и квадратурная компоненты модулирующего сигнала; импульс теперь имеет длительность в два раза большую длительности импульса Последовательность содержит нечетные, а последовательность — четные символы исходной последовательности. Здесь, как и в предыдущем случае, будем полагать, что элементы исходной последовательности являются дискретными случайными величинами, принимающими с равной вероятностью значения b или – b; элементы с разными значениями индексов независимы.

Каждое слагаемое в (2.21) имеет вид, аналогичный виду ФМ-2 сигнала, и отличается только тем, что теперь длительность одного символа равна 2Тс. Если заменить в формуле спектральной плотности ФМ-2 сигнала v(t) на g(t) и Т_C на 2Т_C то получим выражение для спектральной плотности QPSK-сигнала:

_(2.21)

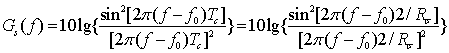
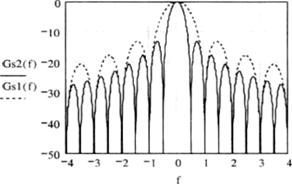
График этой функции представлен на рис. 2.16 сплошной линией и обозначен Gs2(f). Ширина лепестков спектра QPSK-сигнала в два раза меньше ширины спектра ФМ-2-сигнала при той же скорости передачи информации (поскольку аргумент синуса стал в два раза больше). Однако скорость убывания боковых лепестков остается такой же. Впрочем, важнее то, что ширина основного лепестка многопозиционного сигнала становится меньше.

Рис. 2.16. Зависимость спектральной плотности от нормированного значения (f~f₀)/R6

Подчеркнем, что в соответствии с последней формулой для определения G_s(f) максимальные значения боковых лепестков спектра убывают как 1/(f–f₀)². Первый боковой лепесток на 13 дБ ниже основного лепестка на частоте несущего колебания, второй — на 18 дБ и т. д. То есть спектральная плотность мощности убывает сравнительно медленно при отклонении от частоты несущего колебания. Поэтому мощность внеполосных излучений для этого способа модуляции при прямоугольной форме элементарного символа достаточно велика, что является недостатком данного типа радиосигнала.

В качестве ширины физического спектра ФМ-2 радиосигнала часто принимают ширину основного лепестка между ближайшими нулями, которая равна Δf= 2/Т_с, т. е. где (f-f₀)Tc = ±1. В этой полосе содержится примерно 95% мощности этого сигнала.

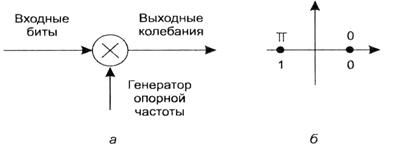
Схема модулятора получается наиболее простой (рис. 2.17, а). Модулирующие импульсы могут иметь значение +1 для передачи логической 1 и -1 — для передачи логического 0. Одному биту передаваемого сообщения соответствует один символ модулированного колебания в виде гармонического колебания с начальной фазой 0 или π. Такое состояние символа удобно изображать в виде созвездия состояний, как это показано на рис. 2.17, б.

Рис. 2.17. Схема модуляции BPSK (а) и сигнальное созвездие (б)

Модуляцию QPSK (Quadrature Phase Shift Keying) можно представить как сдвоенный метод BPSK, в котором одно BPSK имеет сдвиг фазы на +π /4 и на –π/4, а другое на +3π/4 и –3π/4 (или +π/4, +7π/4, +3π/4 и +5π/4 соответственно). Поэтому такой вид модуляции еще называют четырехуровневой PSK (ФМ-4). При таком способе модуляции каждой сигнальной посылке модулированного сигнала соответствуют два бита. Например, пусть:

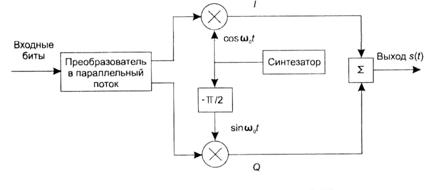
Такой способ удобно реализовать с помощью квадратурной схемы модуляции. Передаваемый последовательный поток битов преобразуют в параллельный (например, разделяя на нечетные и четные биты). Поток с нечетными битами подают на модулятор, куда также подаются с генератора (синтезатора) опорной частоты колебания несущей частоты cos(ω₀t). Этот канал модуляции называют синфазным и обозначают буквой I. Поток с четными битами подают на другой модулятор. На второй модулятор подают такую же опорную частоту, что и на первый модулятор, но сдвинутую по начальной фазе на -π/2, т. е. колебания . Поскольку косинус и синус являются ортогональными функциями, то о них говорят, что они находятся в квадратуре. Поэтому второй канал модуляции называют квадратурным и обозначают буквой Q. На практике колебания опорной частоты для обоих каналов модуляции получают от одного и того же синтезатора. Это гарантирует совместную стабильность опорной частоты в обоих каналах. На синфазный канал подаются косинусоидальные колебания, а на квадратурный канал подаются колебания с предварительной задержкой на четверть периода. При расчетах удобно считать амплитуды колебаний опорной частоты в обоих каналах равными 1/√2 с тем, чтобы амплитуда суммарных колебаний получилась равной 1. С выхода модуляторов обоих каналов сигналы суммируются, и получается выходной сигнал квадратурного модулятора. Схема модулятора приведена на рис. 2.18.

Рис. 2.18. Структурная схема модулятора QPSK

Поскольку входной поток разбит на два параллельных, то для сохранения прежней скорости потока длительности битовых импульсов в параллельных потоках растягиваются по времени вдвое, соответственно вдвое уменьшается скорость в параллельных каналах. Вдобавок для обеспечения скачков фазы на битовые импульсы в параллельных потоках делают двуполярными так, что, например, модулирующие импульсы будут иметь значение +1 для передачи логической 1 и -1 — для передачи логического 0. Обозначая амплитуды модулирующих импульсов в квадратурных каналах как и колебания на выходе QPSK модулятора можно записать:

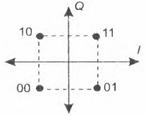
Поскольку за один символ передается два бита, то сигнальное созвездие будет иметь вид, показанный на рис. 2.19.

Рис. 2.19. Сигнальное созвездие при модуляции QPSK при m = 4

Следует отметить, что на сигнальном созвездии положения всех значений символов равноудалены от начала координат. Это означает равенство амплитуд всех символьных колебаний. В принципе, необязательно, чтобы значения символов располагались по углам квадрата. Они могут располагаться и по окружности. Можно также отметить, что можно еще больше усложнить способность модуляции, делая сдвиги фаз на меньший угол. Тогда в каждом символе будет передаваться большее количество бит и на сигнальном созвездии будет больше точек. Но тогда труднее будет в условиях воздействия шумов различать фазовые углы на приеме, поэтому возрастает вероятность ошибочного восстановления при приеме символов.

Квадратурная амплитудная модуляция QAM

Квадратурная амплитудная модуляция КАМ — QAM (Quadrature Amplityde Modulation) служи! примером модуляции с большим числом бит в символах. Следовательно, можно получить и большее число состояний. Название 16-QAM означает 16 состояний на сигнальном созвездии, а 64-QAM означает 64 состояния. КАМ совмещает в себе амплитудную и фазовую модуляции. Выходные колебания образуются сложением модулированных сигналов квадратурных каналов, как и при фазовой манипуляции, однако обе несущие теперь модулированы и по амплитуде. Импульсные сигналы в параллельном потоке однополярные. Логической 1 соответствует сигнал ±A_m. (знак минус соответствует смене фазы модулированных колебаний на π;), а логическому 0 соответствует нулевой уровень. Причем логическая 1 создает на выходе модулятора колебания с амплитудой A_m_, а логический 0 не создает колебаний. Выходной сигнал, таким образом, будет модулирован (точнее, манипулирован) и по фазе, и по амплитуде. Если входной поток битов после преобразования из последовательного в параллельный преобразовать в многоуровневый импульсный сигнал, то на выходе модулятора будут получаться фазоманипулированные многоуровневые по амплитуде колебания. Схема КАМ модулятора по принципу действия совпадает со схемой QPSK (см. рис. 2.15). Разница лишь в том, что в преобразователе потока из последовательного в параллельный производится многоуровневое преобразование битовых символов. К настоящему времени освоена техника создания QPSK-модуляторов, имеющих 256 и более состояний.

Один канальный символ сигнала при таком способе модуляции можно представить следующим равенством:

в котором является комплексной амплитудой этого канального символа, т = 1, 2,…,М. При построении сигнального созвездия этого сигнала удобнее использовать вещественную и мнимую части комплексной амплитуды:

где а_m и b_m — координаты m-й точки сигнального созвездия КАМ-сигнала.

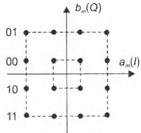
На рис. 2.20 представлено сигнальное созвездие КАМ-16 (большее число состояний усложнит рисунок).

Рис. 2.20. Сигнальное созвездие КАМ-сигнала

Необходимо отметить, что разные канальные символы этого сигнала имеют разную энергию; расстояние между разными сигнальными точками также оказывается различным. В результате вероятность перепутывания символов в приемнике для разных символов оказывается разной.

Один канальный символ такого сигнала может переносить n=log₂m информационных битов. В частности, при m=16 имеем n=4. Поэтому если по-прежнему считать, что длительность одного бита равна то длительность одного канального символа KAM-сигналa равна Т_KC = nТ_c, Следовательно, при формировании этого сигнала поток информационных битов должен группироваться в блоки по n битов. Каждому блоку должен быть поставлен в соответствие один канальный символ. Установление такого соответствия называется сигнальным кодированием.

На рис. 2.20 сигнальное созвездие имеет форму квадрата или квадратной решетки, в узлах которой располагаются сигнальные точки. Это не единственно возможная форма сигнального созвездия, и не всегда лучшая. Сигнальные созвездия могут иметь форму, например, креста, круга, что часто оказывается необходимым при больших значениях т. Удаление от центра координат соответствует уровню амплитуды колебаний. В современных системах связи значения этого параметра могут превышать 1024.

При больших значениях т задавать множества возможных координат сигнальных точек проще с помощью целых чисел, нумеруя сигнальные точки от начала координат. Например, для квадратной сигнальной решетки, изображенной на рис. 2.20, можно ввести обозначения a_min и b_min для координат точек ближайших к началу координат. Тогда, если все соседние точки имеют одинаковые расстояния между собой вдоль каждой оси, то координаты остальных точек можно выразить через значения координат ближайших точек с помощью соотношений:

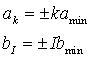
где индексы k и I принимают целочисленные значения. Например, для созвездия на рис. 2.20 значения индексов принадлежат множеству {-3, -1, +1, +3}. Совокупность всех точек этого сигнального созвездия может быть задана с помощью матрицы:

Ширина спектра КАМ-сигнала примерно такая же, как и m-ичного ФМ-сигнала. Однако данный способ модуляции может обеспечить меньшую вероятность ошибки на бит передаваемой информации и поэтому иногда оказывается более предпочтительным. Следует, однако, отметить, что, так как амплитуда КАМ-сигнала принимает различные значения, то применение этого способа модуляции сопровождается повышением требований к линейности канала передачи.

В силу ортогональности спектров наличие небольшого остатка боковых лепестков спектров поднесущих мало влияет на качество различимости, поэтому требования к фильтрам в каналах поднесущих, ограничивающим боковые лепестки, могут быть не столь жесткими, что упрощает их схемотехнику и уменьшает стоимость. Выделение поднесущих в приемнике из суммарного сигнала производится с помощью быстрого преобразования Фурье. Трафик пользователя, получившего малое число поднесущих, требует меньше вычислительных ресурсов на преобразование Фурье, что экономит время и стоимость передачи.

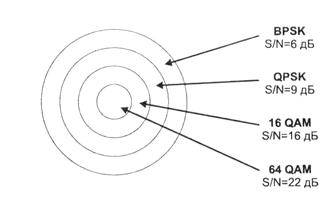
Разные способы модуляции позволяют получить разные скорости передачи при разных отношениях сигнал/шум. Использование обеспечивает более высокую скорость передачи, но требует обеспечения большей величины отношения сигнал/шум. Поэтому такой способ целесообразно применять для пользователей, находящихся вблизи базовой станции. На удалении применяют QPSK и BPSK, позволяющие работать при меньших значениях сигнал/шум, Система автоматически переходит с одного вида модуляции на другой при смене условий передачи (отношения сигнал/шум — S/N). Схематично области применения разных способов модуляции в зависимости от расстояния показаны на рис. 2.21.

Рис. 2.21. Условные зоны применения способов модуляции

Скорости кодирования при различных видах модуляции: BPSK— 1/2, QPSK — 1/2. 3/4, 16 QAM — 1/2, 2/3. 3/4, 64 QAM — 2/3, 3/4.

В табл. 2.1 приведены сравнительные данные по стандартам 802.16, 802.16-2004 и 802.16е.

Таблица 2.1. Сравнительные данныепо стандартам 802.16, 802.16—2004 и 802.16е

Параметры	802.16	802.16—2004	802.16е
Диапазон	10—66 ГГц	Ниже 11 ГГц	Ниже 11 ГГц
Условия использования	Прямая видимость	Прямая и непрямая видимость	Прямая и непрямая видимость
Скорость передачи	32,0—134,4 Мбит/с	1,0—75,0 Мбит/с
Вил модуляции	QPSK, 16 QAM. 64 QAM, одна несущая	QPSK, 16 QAM, 64 QAM, одна несущая. Или QPSK, 16 QAM. 64 QAM. 256 QAM, дополнительно BPSK OFDM
Дуплексный разнос	TDD/FDD	TDDA/DD	TDD/FDD
Ширина полосы	20,25 и 28 М1ц	Изменяемая 1.25—20 МГц	Изменяемая 1,25—20 МГц
Типовой радиус зоны покрытия	2—5 км	4—6 км	4—8 км

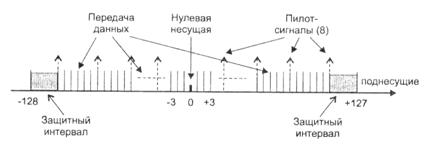
Пользователю могут быть предоставлены (теоретически) все поднесущие, что обеспечит максимально возможную в системе скорость (например. 75 или 134 Мбит/с). Следует понимать, что это максимальная скорость, которую может обеспечить система на передачу. Сюда входит и информационный трафик, и каналы управления и сигнализации, и т. п. Реальная скорость передачи трафика пользователя, конечно же, будет ниже. Например, при обеспечении 256 частотных поднесущих под трафик пользователей могут быть отданы лишь 192 поднесущих, 8 отводится под пилот-сигналы и 56 остаются пустыми в качестве защитного интервала. Уровень пилот-сигналов на 2.5 дБ выше, чем у остальных поднесущих. Распределение поднесущих в кадре из 256 поднесущих видно из рис. 2.22.

Рис. 2.22. Распределение поднесущих

На защитных интервалах несущие не излучаются и передача не ведется. В середине интервала частот поднесущих находится нулевая несущая DC (центральная несущая), означающая середину полосы частот. Излучения на ней нет.

Каждому пользователю может выделяться лишь часть поднесущих. Таким образом можно распределять поднесущие между пользователями (802.16— 2004) или динамически перераспределять их (802.16е), обеспечивая необходимые им скорости передачи.

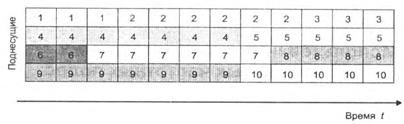
На рис. 2.23 показано возможное распределение трафика пользователей 1, 2, 3 и т. д. по времени и по поднесущим. Показано условное распределение поднесущих трафика без показа защитных интервалов, пилот-сигналов и пр.

Рис. 2.23. Распределение трафика по поднесущим и времени

В системе WiMAX предполагается, что один из видов оплаты пользования услугами как раз будет плата за предоставляемые полосы частот или за обеспечиваемую скорость передачи.

Применение OFDM — весьма эффективный способ борьбы с межсимвольной интерференцией, вызванной наложением отраженных и задержанных во времени копий сигнала. Поскольку длительность битовой посылки стала NT_б, то доля времени посылки, пораженной интерференцией, по сравнению с длительностью посылки стала намного меньше, чем в случае, когда при других способах модуляции длительность посылки была равна T_б. Энергия непораженной части посылки становится достаточной для ее правильного восстановления. Растяжение битовой посылки во времени выбирается значительно больше среднестатистического времени действия помехи.

OFDM-сигнал имеет несколько замечательных свойств. Во-первых, общая ширина полосы занимаемых частот является минимальной. Следовательно, в отведенной под систему полосе частот можно разместить максимальное число поднесущих. Во-вторых, спектр суммарного сигнала является широким, и такой сигнал обладает всеми свойствами широкополосных сигналов. Следовательно, в условиях многолучевого распространения можно эффективно бороться с интерференцией. На этом положительные стороны OFDM-сигнала не заканчиваются. Поскольку спектр широкий, то глубокому замиранию за счет интерференции может оказаться подверженным в каждый момент времени не весь спектр, а лишь небольшой участок. В этом случае ухудшение наступит лишь для тех символов, которые модулировали пораженные поднесущие, т. е. лишь часть информации. Если же организовать с некоторой частотой проверку качества канала (например, с помощью специальных бит, вводимых в процессе передачи), то можно иметь оперативную информацию о качестве канала в каждом частотном участке. Следовательно, можно корректировать мощность на каждой поднесущей, значительно уменьшая негативное влияние интерференции или селективной помехи.

Источник

Расчет спектров сигналов

Под спектром непериодического сигнала понимают функцию частоты , которую получают на основе прямого преобразования Фурье вида:

(1.1)

Для обратного преобразования используют формулу вида(1.2)

(1.2)

Модуль спектральной функции

(1.3)

называют спектром сигнала или спектральной плотностью сигнала.

Аналитическая запись задаваемых сигналов во временной области имеет вид:

(1.4)

где рад/с., В, 1/с.

Данный сигнал имеет вид, представленный на рис. 1.1, зависимость сведена в табл. 1.1.

, (1.5)

где В, с.

Данный сигнал имеет вид, представленный на рис. 1.2, зависимость сведена в табл. 1.2.

(1.6)

где В,

Данный сигнал имеет вид, представленный на рис. 1.3, зависимость сведена в табл. 1.3.

Запишем спектральную плотность для каждого сигнала :

, (1.7)

, (1.8)

. (1.9)

Модули спектральной плотности сигналов находятся по формуле (1.3) .

Графики спектров сигналов , , представлены на рис 1.4, рис 1.5, рис 1.6 соответственно.

Фазa спектральной плотности находятся следующим образом:

, 1.10)

Графики фазы спектральной плотности сигналов представлены на рис 1.7, рис.1.8 соответственно.

Таблица 1.1 – Зависимость

t·10-3, c	0	0,2	0,4	0,6	0,8	0,1	0,11
U1(t), В	0,25	0,132	0,065	0,028	0,011	0,0027	0,00079

Рисунок 1.1 -График сигнала 1

Таблица 1.2 – Зависимость

t·10-5, c	-2	-1,5	1	-0,5	0	0,5	1	1,5	2
U2(t), В	0	0,077	0,141	0,185	0,2	0,185	0,141	0,077	0

Рисунок 1.2 -График сигнала 2

Таблица 1.3 – Зависимость

t•10-6,c	-2	0	2	4	6	8	10	12
U3(t), В	0	0,2	0,2	0,2	0,2	0,2	0,2	0

Рисунок 1.3 – График сигнала 3

Рисунок 1.4 – График спектра сигнала 1

Рисунок 1.5 – График спектра сигнала 2

Рисунок 1.6 – График спектра сигнала 3

Рисунок 1.7 – График фазы сигнала 1

Рисунок 1.8 – График фазы сигнала 3

Расчёт практической ширины спектра сигнала

Расчёт полной энергии сигнала

Полная энергия сигнала рассчитывается по формуле:

(2.1)

Найдём полную энергию для каждого из сигналов , , , используя формулы (2.1) и (1.3, 1.4, 1.5), расчет производим в среде MathCad:

В/c. (2.2)

В/c. (2.3)

В/c (2.4)

Определение практической ширины спектра сигнала

Ограничение практической ширины спектра сигнала по верхнему значению частоты , по заданному энергетическому критерию осуществляется на основе неравенства: