Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
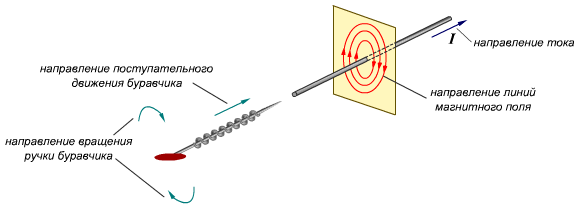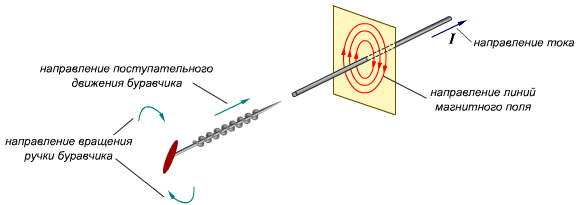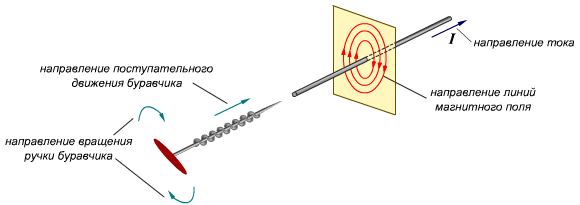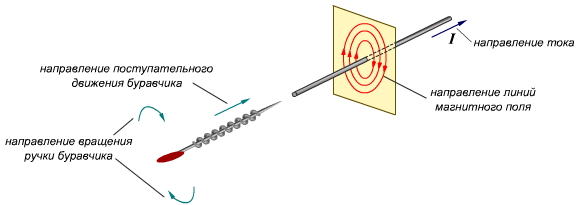
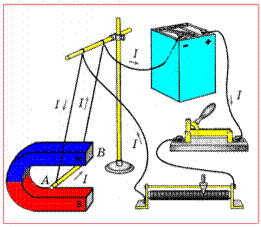
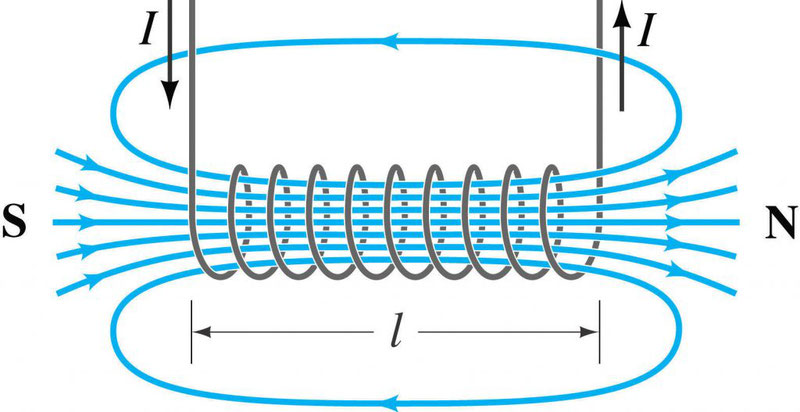
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
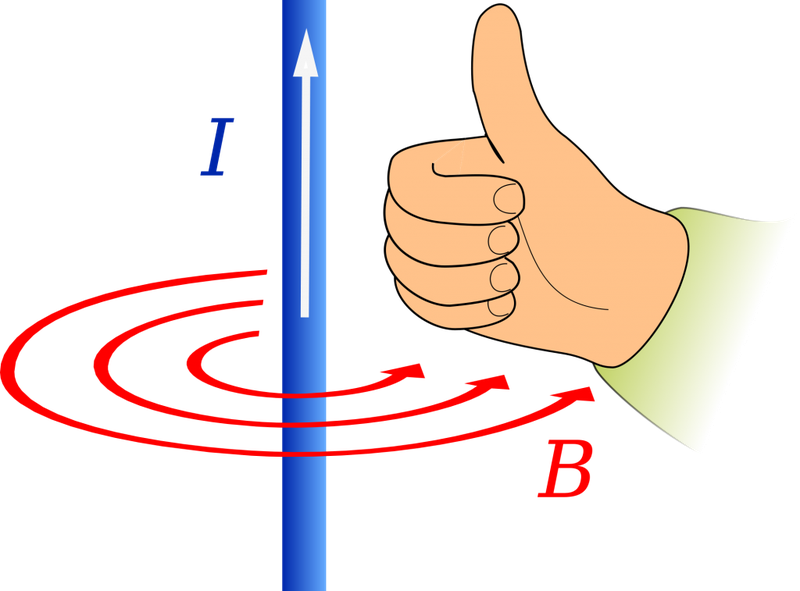
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
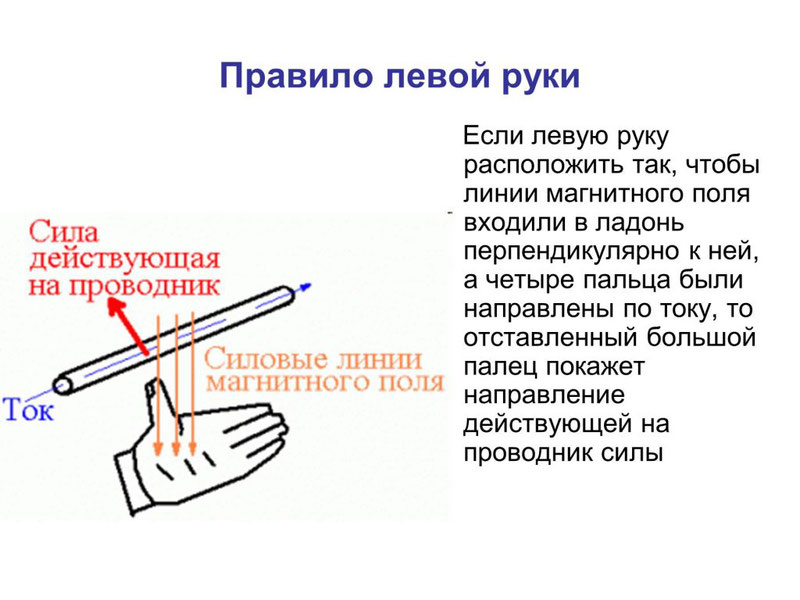
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
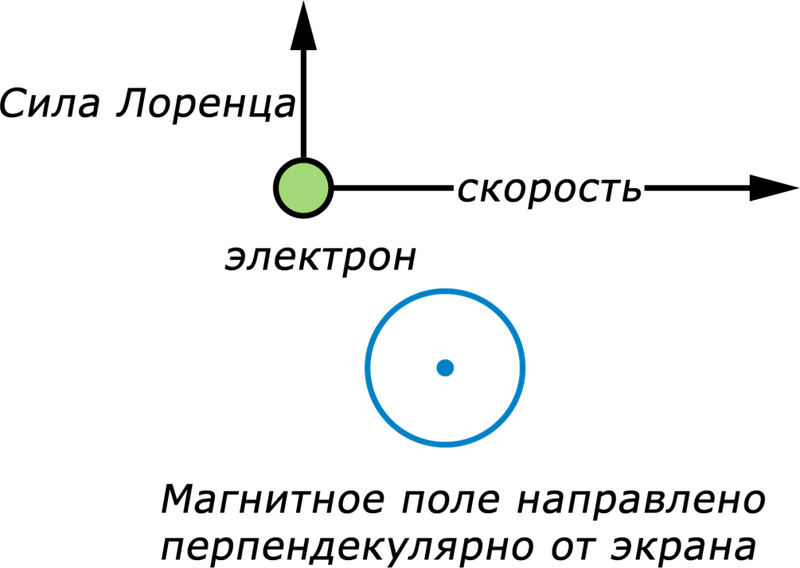
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
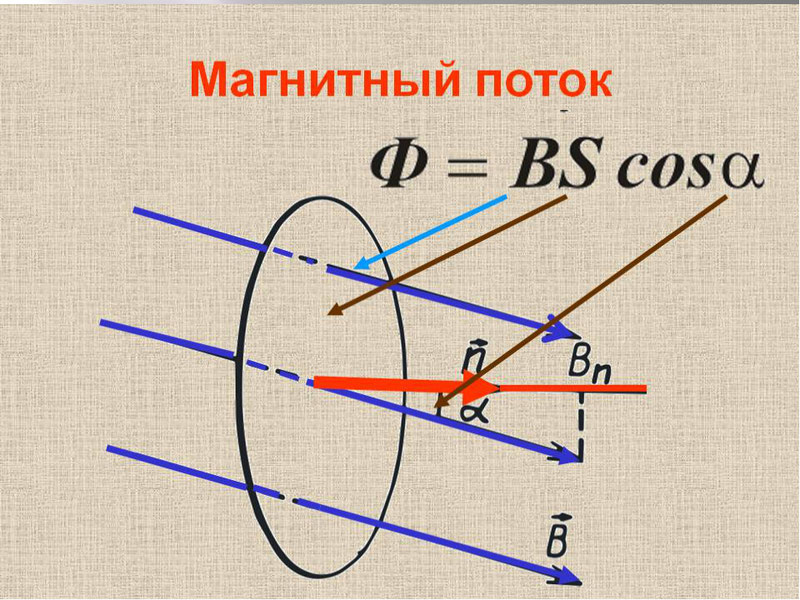
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].
Вектор индукции магнитного поля: главные понятия
Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.
Вектор магнитной индукции однородного поля и неоднородного
Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.
Вектор индукции магнитного поля: важные формулы
Важно!
Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.
Формула
Модуль вектора индукции однородного поля находят следующим образом:
[mathrm{B}=frac{mathrm{M}_{max }}{mathrm{P}_{mathrm{m}}}].
где [mathrm{M}_{max }] — вращающий момент в максимуме действует на контур с элементарным током, помещенный в магнитное поле, где в данном случае [mathrm{P}_{mathrm{m}}=mathrm{I} cdot mathrm{S}] — магнитный момент контура (S — площадь определенного контура).
Модуль вектора индукции магнитного поля: производные формулы
Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:
[B=frac{F_{max }}{I cdot L}]
В вакууме модуль индукции будет равен:
[mathrm{B}=mu 0 cdot mathrm{H}]
Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)
[vec{F}=B cdot q cdot v cdot sin alpha]
[B=frac{F}{sin alpha cdot q v}]
В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика. Под символом q подразумевается заряд в магнитном поле.
Интересно
В СИ единицей модуля магнитной индукции принимается 1 Тесла (кратко — Тл), где [1 Tл=frac{H}{Aм}]
Как определяется направление вектора индукции магнитного поля?
За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}] используют направление, в котором устанавливается под воздействием поля утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.
Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].
Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.
Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:
- Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.
- Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.
Задания по теме
Разберем примеры, в которых будет задействована данная формула и свойства.
Пример 1
Условие задачи:
Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.
Решение задачи следующее:
Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.
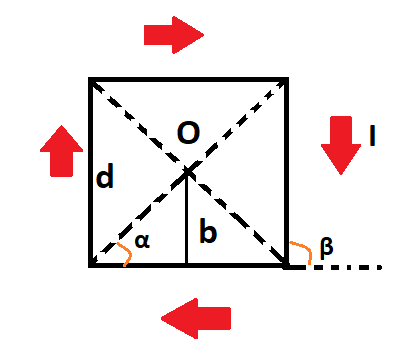
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B1+B2+B3+B4
Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B1
В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.
Чтобы формула подошла к данной задачи, ее применяют в следующем виде:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]
углы α и β, которые отмечены на рисунке:
[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]
Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]
Поскольку у нас квадратная форма, то следует заметить следующее:
[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]
Возьмем выведенные формулы и получим конечное выражение, то есть:
[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Нет времени решать самому?
Наши эксперты помогут!
Пример 2
Условие задачи:
Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.
Решение задачи:
В точке А получается из двух частей проводника, то есть:
[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]
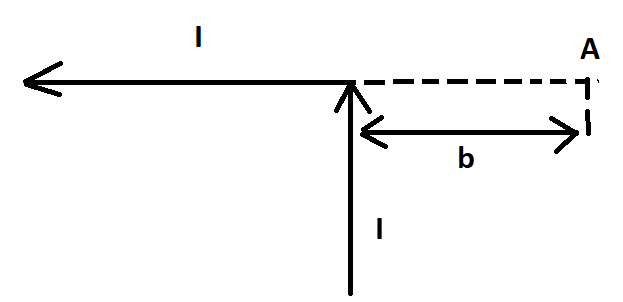
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.
Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:
[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]
В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].
Индукция бесконечного проводника в точке А была бы равна:
[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]
Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:
[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]
Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]
Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля. Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так. На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.
Определение и формула
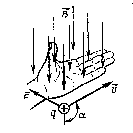
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
По закону Ампера:
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0<К<1, а n – порядок числа 10.
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Формула силы Лоренца при наличии магнитного и электрического полей
Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:
Тогда:
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).
Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.
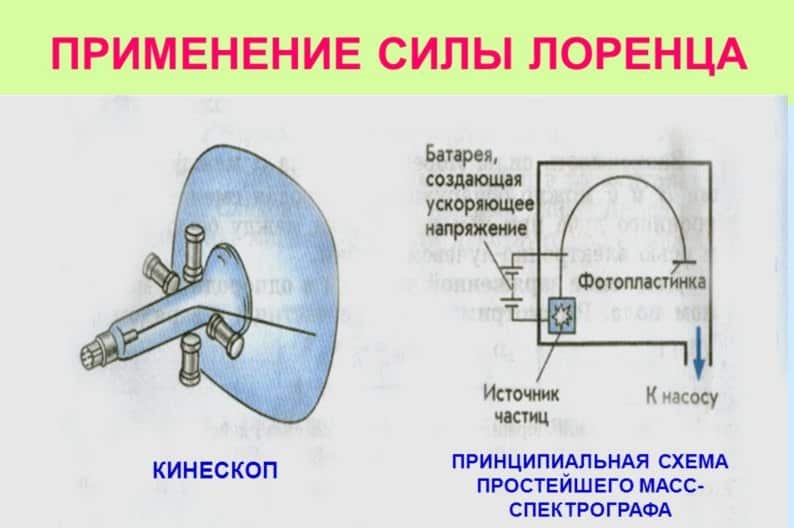
Применение на практике
Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.
Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.
На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.
Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).
Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.
Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.
На основании действия силы Лоренца создано много других устройств, используемых на практике.
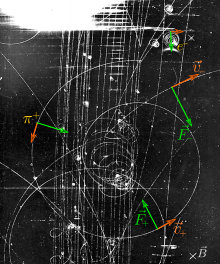
Сила Лоренца, действующая на быстро движущиеся заряженные частицы в пузырьковой камере, приводит к появлению траекторий положительного и отрицательного заряда, которые изгибаются в противоположных направлениях.
Си́ла Ло́ренца — сила, с которой электромагнитное поле, согласно классической (неквантовой) электродинамике[1], действует на точечную заряженную частицу[2][3]. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью 



![{displaystyle {vec {mathbf {F} }}=qleft({vec {mathbf {E} }}+[{vec {mathbf {v} }},{vec {mathbf {B} }}]right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b43e62949e6a7ef49afeafa25fee75314af2c10)
Электромагнитная сила, действующая на заряд q, представляет собой комбинацию силы, действующей в направлении электрического поля 


Историки науки предполагают, что этот закон подразумевался в статье Джеймса Клерка Максвелла, опубликованной в 1865 году[6]. Хендрик Лоренц привёл полный вывод этой формулы в 1895 г.[7], определив вклад электрической силы через несколько лет после того, как Оливер Хевисайд правильно определил вклад магнитной силы[8][9].
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется (это верно лишь при условии, что создающий поле магнит не рассматривается как часть системы). Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца[10].
Полный вывод такого утверждения требует определения понятия “импульс поля”, а едва ли не единственный способ сделать это – это теорема Эммы Нетер (и тесно связанное с ней понятие тензора энергии-импульса) в классической (не-квантовой) теории поля в лагранжевом формализме. Однако же характерный импульс поля/волны (“давление света”) в c раз меньше, чем его характерная энергия, где c – скорость света, и во многих реальных, технических применениях представляет собой исчезающе малую величину. Что означает справедливость ЗСИ для одного лишь заряженного вещества, и, в свою очередь, если вещество состоит из всего 2 материальных точек – справедливость третьего закона Ньютона (он равносилен ЗСИ для замкнутой системы, которая есть пара материальных точек/тел).
Сила Лоренца как определение E и B[править | править код]
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Во многих учебниках по электромагнетизму силу Лоренца используют в качестве определения электрического и магнитного полей E и B[11][12][13]. В частности, сила Лоренца понимается как следующее эмпирическое утверждение:
- Электромагнитная сила F, действующая на пробный заряд в данной точке и момент времени, является определённой функцией его заряда q и скорости v, которая может быть параметризована ровно двумя векторами E и B в функциональной форме :
-
.
Это выражение верно в том числе для случая движения частицы со скоростью близкой по величине к скорости света (v = | v | ≈ c).[14] Таким образом, два векторных поля E и B определяются во всём пространстве и времени, и они называются «электрическим полем» и «магнитным полем». Поля определены повсюду в пространстве и времени относительно силы, которую испытывает пробный заряд, помещённый в электромагнитное поле.
Как определение E и B, сила Лоренца является только определением в принципе, потому что реальная частица (в отличие от гипотетического пробного тела бесконечно малой массы и заряда) будет создавать свои собственные конечные поля E и B, изменяющие электромагнитную силу, которую он испытывает. Вдобавок, заряд в магнитном поле обычно движется по криволинейной траектории, то есть с ускорением — а значит, он испускает излучение и теряет кинетическую энергию (см., например, статьи тормозное излучение или синхротронное излучение). Эти эффекты возникают за счёт как прямого воздействия (так называемой силы реакции излучения), так и косвенного (путём воздействия на движение близлежащих зарядов и токов).
Уравнение[править | править код]
Заряженная частица[править | править код]
Сила F, действующая на частицу с электрическим зарядом q и мгновенной скоростью v из-за внешнего электрического поля E и магнитного поля B, определяется выражением (в единицах СИ):[15]
где знак × обозначает векторное произведение (все величины, выделенные жирным шрифтом, являются векторами). В декартовых компонентах
В общем случае, электрическое и магнитное поля зависят от координат и времени. Следовательно, в явном виде силу Лоренца можно записать как
,
где r — вектор положения заряженной частицы, t — время, а точка обозначает производную по времени.
Положительно заряженная частица будет ускоряться в том же направлении, что и поле E, но её траектория будет изгибаться перпендикулярно как вектору мгновенной скорости v, так и полю B в соответствии с правилом буравчика (если пальцы правой руки вытянуты так, чтобы указывать в направлении v, а затем изгибаются так, чтобы указывать в направлении B, тогда вытянутый большой палец будет указывать в направлении F).
Член q E называется электрической силой, а член q (v × B) — магнитной силой[16]. Согласно некоторым определениям, термин «сила Лоренца» относится конкретно к формуле для магнитной силы[17] а формуле с общей электромагнитной силой (включая электрическую силу), дано другое название. В дальнейшем термин «сила Лоренца» будет относиться к выражению для полной силы.
Магнитная составляющая силы Лоренца проявляется как сила, действующая на помещённый в магнитное поле проводник с током. В этом контексте эта сила также называется силой Лапласа.
Сила Лоренца — это сила воздействия электромагнитного поля на заряженную частицу, или. другими словами, скорость, с которой передаётся линейный импульс от электромагнитного поля частице. С ним связана мощность, которая представляет собой скорость, с которой энергия передаётся от электромагнитного поля частице:
.
Магнитное поле не совершает работы, потому что магнитная сила всегда перпендикулярна скорости частицы.
Непрерывное распределение заряда[править | править код]
Сила Лоренца (на единицу 3-х мерного объёма) f действующая на непрерывное распределение заряда (плотность заряда ρ) в движении. 3-хмерного плотность тока J соответствует движению элемента заряда dq в элементе объёма dV и изменяется по всему пространству.
Для непрерывного распределения заряда, находящегося в движении, уравнение для силы Лоренца принимает дифференциальный вид
,
где 


,
где 

,
так что непрерывным аналогом уравнения для силы Лоренца является выражение[18]
К полной силе можно прийти вычислив объемный интеграл по распределению заряда:
.
Устраняя 



В терминах 

,
где 
Плотность мощности, связанная с силой Лоренца в материальной среде, равна
.
Если разделить полный заряд и полный ток на их свободную и связанную части, получится, что плотность силы Лоренца равна
,
где 



Уравнение в единицах СГС[править | править код]
В приведённых выше формулах используются единицы СИ, которые являются наиболее распространёнными среди экспериментаторов, техников и инженеров. В системе СГС, которая более распространена среди физиков-теоретиков, сила Лоренца примет вид
,
где c — скорость света. Хотя это уравнение выглядит несколько иначе, оно полностью эквивалентно, поскольку новые величины связаны в двух системах единиц соотношениями
где ε 0 — диэлектрическая проницаемость вакуума, а μ 0 — магнитная проницаемость вакуума. На практике индексы «cgs» и «SI» всегда опускаются, и система единиц измерения должна быть понятна из контекста.
Частные случаи[править | править код]
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса 
| СГС | СИ |
|---|---|
|
|
|
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости 


| СГС | СИ |
|---|---|
|
|
|
Если заряженная частица движется в магнитном поле так, что вектор скорости 




| СГС | СИ |
|---|---|
|
|
История[править | править код]
Первые попытки количественного описания электромагнитной силы были предприняты в середине 18 века. Предполагалось Иоганн Тобиас Майер и другие в 1760 году[19] предполагали, что сила на магнитных полюсах как и электрически заряженные объекты, что установил Генри Кавендиш в 1762 году[20], подчиняются закону обратных квадратов. Однако в обоих случаях экспериментальное доказательство не было ни полным, ни окончательным. Только в 1784 году Шарль-Огюстен де Кулон, используя торсионные весы, смог окончательно экспериментально показать, что это правда.[21] Вскоре после открытия в 1820 году Хансом Кристианом Эрстедом того факта, что на магнитную стрелку действует электрический ток, Андре-Мари Ампер в том же году смог экспериментально получить формулу угловой зависимости силы между двумя элементами тока.[22][23] Во всех этих описаниях сила всегда описывалась в терминах свойств вещества и расстояний между двумя массами или зарядами, а не в терминах электрических и магнитных полей.[24]
Современная концепция электрических и магнитных полей впервые возникла в теориях Майкла Фарадея, особенно удачной оказалась его идея силовых линий, которая позже получила полное математическое описание лордом Кельвином и Джеймсом Клерком Максвеллом.[25] С современной точки зрения, в формулировке Максвелла 1865 г. его уравнений для электромагнитного поля можно получить уравнение для силы Лоренца по отношению к электрическим токам[6], хотя во времена Максвелла не было очевидно, как его уравнения связаны с силами при перемещении заряженных предметов. Дж. Дж. Томсон был первым, кто попытался вывести из уравнений Максвелла поля электромагнитные силы, действующие на движущийся заряженный объект, в терминах свойств объекта и внешних полей. Заинтересовавшийся поведением заряженных частиц в катодных лучах, Томсон опубликовал статью в 1881 году, в которой он дал определение силы, действующей на частицы, обусловленную внешним магнитным полем, в виде[8]
Томсон вывел правильную основную форму формулы, но из-за некоторых ошибок и неполного описания тока смещения перед формулой включил неверный масштабный коэффициент, равный половине. Оливер Хевисайд изобрёл современные векторные обозначения и переписал в их терминах полевые уравнения Максвелла; он также (в 1885 и 1889 годах) исправил ошибки вывода Томсона и пришел к правильному виду для магнитной силы действующей на движущуюся заряженную частицу.[8][25][26] Наконец, в 1895 году[7][27] Хендрик Лоренц пришёл к современному виду формулы для электромагнитной силы, которая включает вклады как электрического, так и магнитного полей. Лоренц вначале отказался от максвелловского описания эфира и проводимости. Вместо этого Лоренц указал на различия между материей и светоносным эфиром и записал уравнения Максвелла в микроскопическом масштабе. Используя версию уравнений Максвелла Хевисайда для неподвижного эфира и, применяя лагранжевую механику (см. Ниже), Лоренц пришёл к правильной и полной форме закона для электромагнитной силы, который теперь носит его имя.[25][28]
Траектории частиц под действием силы Лоренца[править | править код]
Заряженная частица дрейфует в однородном магнитном поле. (A) Нет возмущающей силы (B) В электрическом поле, E (C) С независимой силой, F (например, гравитация) (D) В неоднородном магнитном поле, grad H
Во многих случаях, представляющих практический интерес, движение в магнитном поле электрически заряженной частицы (например, электрона или иона в плазме) можно рассматривать как суперпозицию относительно быстрого кругового движения вокруг точки, которая дрейфует в направлении перпендикулярном электрическому и магнитным полям. Скорости дрейфа могут различаться в зависимости от их зарядового состояния, массы или температуры, что может привести к электрическим токам или химическому разделению.
Значение силы Лоренца[править | править код]
В то время как современные уравнения Максвелла описывают то, как электрически заряженные частицы и токи или движущиеся заряженные частицы вызывают электрические и магнитные поля, сила Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей.[15][29] Хотя сила Лоренца описывает действие E и B на точечный заряд, но такие электромагнитные силы не являются всей картиной. Заряженные частицы, возможно, связаны с другими силами, особенно с гравитацией и ядерными силами. Таким образом, уравнения Максвелла не отделены от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один из аспектов; генерация E и B токами и зарядами — другое.
В реальных материалах сила Лоренца неадекватно описывает коллективное поведение заряженных частиц как в принципе, так и с точки зрения вычислений. Заряженные частицы в материальной среде не только реагируют на поля E и B, но и создают эти поля сами. Для определения временной и пространственной реакции зарядов необходимо решать сложные уравнения переноса, например, уравнение Больцмана, уравнение Фоккера — Планка или уравнения Навье — Стокса . Например, см. Магнитогидродинамику, гидродинамику, электрогидродинамику, сверхпроводимость, звёздную эволюцию . Разработан целый физический аппарат для решения этих вопросов. См., Например, формулы Грина — Кубо и функцию Грина (теория многих тел) .
Сила на токоведущем проводе[править | править код]
Правило правой руки для токоведущего провода в магнитном поле B
Когда провод, по которому течёт электрический ток, помещается в магнитное поле, каждый из движущихся зарядов, составляющих ток, испытывает силу Лоренца, и вместе они могут создавать макроскопическую силу действующую на проводе (иногда называемую силой Лапласа). Комбинируя приведённый выше закон Лоренца с определением электрического тока, в случае прямого неподвижного провода получается следующее уравнение:[30]
где ℓ — вектор, величина которого равна длине провода, а направление — вдоль провода, совмещённое с направлением обычного тока I.
Если провод не прямой, а изогнутый, то силу, действующую на него, вычисляют, применив данную формулу к каждому бесконечно малому отрезку провода dℓ, а затем сложив все эти силы путём интегрирования . Формально результирующая сила, действующая на неподвижный жёсткий провод, по которому течёт постоянный ток I равна
Это полная сила. Кроме того, обычно возникает крутящий момент и другие эффекты, если проволока не совсем жёсткая.
Одним из применений этого является закон силы Ампера, который описывает, как два токоведущих провода притягиваться или отталкиваться друг от друга, в зависимости от направления тока, поскольку каждый из них испытывает силу Лоренца от магнитного поля создаваемого другим током.
ЭДС[править | править код]
Магнитная сила (qv × B) в выражении силы Лоренца отвечает за двигательную электродвижущую силу (или двигательную ЭДС), явление, лежащее в основе действия многих электрических генераторов. Когда проводник перемещается через область магнитного поля, магнитное поле оказывает противоположно направленные силы на электроны и ядра в проводе, и это создаёт ЭДС. Термин «двигательная ЭДС» применяется к этому явлению, поскольку ЭДС возникает из-за движения провода.
В других электрических генераторах магниты движутся, а проводники — нет. В этом случае ЭДС возникает из-за электрической силы (q E) в уравнении для силы Лоренца. Рассматриваемое электрическое поле создается изменяющимся магнитным полем, приводящим к возникновению индуцированной ЭДС, как описано уравнением Максвелла — Фарадея.[31]
Обе эти ЭДС, несмотря на их явно различное происхождение, описываются одним и тем же уравнением, а именно ЭДС — это скорость изменения магнитного потока через провод. Это закон электромагнитной индукции Фарадея, см. Ниже . Специальная теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами.[31] Фактически, электрическое и магнитное поля представляют собой разные грани единого электромагнитного поля (разные элементы единой матрицы тензора силы поля Fij), и при переходе от одной инерциальной системы отсчета к другой (то есть применении операции замены базиса к матрице Fij) часть электромагнитного векторного поля E можно полностью или частично заменить на B или наоборот .[32]
Сила Лоренца и закон индукции Фарадея[править | править код]
Сила Лоренца — изображение на стене в Лейдене
Для петли из провода находящуюся в магнитном поле, закон индукции Фарадея утверждает, что наведённая электродвижущая сила (ЭДС) в проводе равна:
где
— магнитный поток через петлю, B — магнитное поле, Σ (t) — поверхность, ограниченная замкнутым контуром ∂Σ (t), в момент времени t, dA — бесконечно малый элемент вектора площади Σ (t) (величина — это площадь бесконечно малого участка поверхности, направление вектора ортогонально этому участку поверхности).
Знак ЭДС определяется законом Ленца. Это справедливо не только для стационарного провода, но и для движущейся проволоки.
Из закона электромагнитной индукции Фарадея и уравнений Максвелла можно получить силу Лоренца. Верно и обратное: силу Лоренца и уравнения Максвелла можно использовать для вывода закона Фарадея.
Пусть Σ (t) — движущийся поступательно провод с постоянной скоростью v, а Σ (t) — внутренняя поверхность провода. ЭДС вокруг замкнутого пути ∂Σ (t) определяется выражением[33]
где
— электрическое поле, а d ℓ — бесконечно малый векторный элемент контура ∂Σ (t).
Направление dℓ, и dA неоднозначно. Чтобы получить правильный знак, используется правило правой руки, как описано в статье Теорема Кельвина — Стокса .
Приведённый выше результат можно сравнить с законом электромагнитной индукции Фарадея, который появляется в современных уравнениях Максвелла, называемый здесь уравнением Максвелла — Фарадея :
Уравнение Максвелла — Фарадея можно записать в интегральной форме с помощью теоремы Кельвина — Стокса .[34]
Уравнение Максвелла — Фарадея принимает вид
и закон Фарадея,
Эти два выражения эквивалентны, если провод не движется. Используя интегральное правило Лейбница и div B = 0, можно получить,
и, используя уравнение Максвелла Фарадея,
поскольку это справедливо для любого положения провода, то
Закон индукции Фарадея справедлив независимо от того, является ли проволочная петля жёсткой и неподвижной, либо она находится в движении, либо в процессе деформации, а также независимо от того, является ли магнитное поле постоянным во времени или изменяющимся. Однако бывают случаи, когда закон Фарадея либо неадекватен, либо его трудно использовать, и необходимо применять закон Лоренца.
Если магнитное поле не зависит от времени и проводящая петля движется через поле, магнитный поток Φ B, проникающий в петлю, может изменяться несколькими способами. Например, если магнитное поле меняется в зависимости от положения, и петля перемещается в другое положение с другим значением B, — ΦB изменится. В качестве альтернативы, если петля изменяет ориентацию по отношению к B, то дифференциальный элемент B ⋅ dA будет меняться из-за различного угла между B и dA, также изменится Ф B. В качестве третьего примера, если часть электрической схемы проходит через однородное, не зависящее от времени магнитное поле, а другая часть схемы остаётся неподвижной, то магнитный поток, связывающий всю замкнутую цепь, может измениться из-за относительного смещения положения составных частей схемы с течением времени (поверхность ∂Σ (t), зависящая от времени). Во всех трёх случаях закон индукции Фарадея предсказывает появление ЭДС, порождённую изменением ΦB.
Из уравнения Максвелла — Фарадея следует, что если магнитное поле B изменяется во времени, то электрическое поле E неконсервативно, и не может быть выражено как градиент скалярного поля, поскольку его ротор не равен нулю.[35][36]
Сила Лоренца в терминах потенциалов[править | править код]
Поля E и B можно заменить векторным магнитным потенциалом A и (скалярным) электростатическим потенциалом ϕ посредством
где ∇ — градиент, ∇⋅ — дивергенция, ∇ × — ротор .
Сила запишется в виде
Используя тождество для тройного произведения, это выражение можно переписать как,
![{displaystyle mathbf {F} =qleft[-nabla phi -{frac {partial mathbf {A} }{partial t}}+nabla left(mathbf {v} cdot mathbf {A} right)-left(mathbf {v} cdot nabla right)mathbf {A} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaeed018e78d24c910e10653ad0dd3c0627ed3d9)
Здесь координаты и компоненты скорости следует рассматривать как независимые переменные, поэтому оператор набла действует только на 


так что приведенное выше выражение принимает вид
.
При v = ẋ уравнение можно переписать в удобной форме Эйлера — Лагранжа
где введены обозначения

и

Сила Лоренца и аналитическая механика[править | править код]
Лагранжиан для заряженной частицы с массой m и зарядом q в электромагнитном поле описывает динамику частицы с точки зрения её энергии, а не силы, действующей на неё. Классическое выражение задается следующим образом:[37]
где A и ϕ — потенциальные поля, как указано выше. Величину
-
Вывод силы Лоренца из классического Лангранжана (единицы СИ) В поле A, частица двигающаяся со скоростью v = ṙ обладает импульсом , тогда её потенциальная энергия равна
. В поле ϕ, потенциальная энергия частицы равна
.
Полная потенциальная энергия записывается в виде
и кинетическая энергия:
Отсюда Лагранжан:
Уравнения Лагранжа
(аналогично для y и z компонент). Вычисление частных производных приводит к
уравнивая и упрощая выражение
и аналогично для y и z компонент. Уравнение для силы
Потенциальная энергия зависит от скорости частицы, поэтому сила зависит от скорости, и соответственно она не является консервативной.
Релятивистский лагранжиан
Действие — это релятивистская длина пути частицы в пространстве-времени, за вычетом вклада потенциальной энергии, плюс дополнительный вклад, который квантово-механически является дополнительной фазой, которую получает заряженная частица, когда она движется вдоль векторного потенциала.
-
Вывод силы Лоренца для релятивистского Лагранжиана (единицы СИ) Уравнения движения получающиеся из вариационного принципа для действия
соответствуют уравнениям движения Гамильтона:
которые эквиваленты следующему выражению в неканонической форме
Это выражение описывает силу Лоренца, — скорость с которой электромагнитное поле передаёт релятивистский импульс частице.
Релятивистская форма силы Лоренца[править | править код]
Ковариантная форма силы Лоренца.[править | править код]
Тензор поля[править | править код]
Используя сигнатуру метрики (1, −1, −1, −1), сила Лоренца для заряда q может быть записана в[39] ковариантной форме :
-
где p α — четырехмерный импульс, определяемый как
τ собственное время частицы, F αβ — контравариантный тензор электромагнитного поля
и U — ковариантная 4-скорость частицы, определяемая как:
где Лоренц-фактор
Поля преобразуются в систему, движущуюся относительно неподвижной системы с постоянной скоростью, с помощью:
где Λ μ α — тензор преобразования Лоренца.
Перевод в векторные обозначения[править | править код]
Компонента α = 1 (x -компонента) силы равна
Подставляя компоненты ковариантного тензора электромагнитного поля F, получаем
Используя компоненты ковариантных четырёхскоростей
Расчет для α = 2, 3 (компоненты силы в направлениях y и z) приводит к аналогичным результатам, поэтому объединение 3 уравнений в одно:
и поскольку дифференциалы по координатному времени dt и собственному времени dτ связаны между собой Лоренц-фактором,
в итоге можно записать
Это в точности закон Лоренца, однако p — это релятивистское выражение,
Сила Лоренца в алгебре пространства-времени (STA)[править | править код]
[проверить перевод!] Электрическое и магнитное поля зависят от скорости наблюдателя, поэтому релятивистскую форму закона Лоренца лучше всего можно продемонстрировать, исходя из не зависящего от координат выражения для электромагнитного и магнитного полей. 

и



(что показывает наш выбор метрики), а скорость равна
Правильная (инвариант — неадекватный термин, потому что никакое преобразование не было определено) форма закона Лоренца
Здесь порядок важен, потому что между бивектором и вектором скалярное произведение антисимметрично. При таком расщеплении пространства-времени можно получить скорость и поля, как указано выше, что дает обычное выражение.
Сила Лоренца в общей теории относительности[править | править код]
В общей теории относительности уравнение движения частицы с массой 



где 



Уравнение также можно записать как
куда 
куда 
Приложения[править | править код]
Сила Лоренца присутствует во многих устройствах, в том числе:
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы
Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
- Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД-генераторах.
- Сила Лоренца также используется в ускорителях заряженных частиц: она задаёт орбиту, по которой движутся эти частицы.
- Сила Лоренца используется в рельсотроне.
- Велосиметрия силой Лоренца заключается в бесконтактном измерении скорости движения проводящей жидкости.
- Циклотроны и другие ускорители частиц с круговым движением
- Масс-спектрометры
- Фильтры скорости
- Магнетроны
См. также[править | править код]
- Радиационное трение
Примечания[править | править код]
- ↑ Афанасьев, Г. Н. Старые и новые проблемы в теории эффекта Ааронова — Бома // Физика элементарных частиц и атомного ядра. — 1990. — Т. 21. — С. 172—250. Архивировано 12 февраля 2022 года.
- ↑ 1 2 Сила Лоренца / В. С. Булыгин // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ М. А. Миллер, Е. В. Суворов. Лоренца сила // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического, и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ H-поле измеряетс в амперах на метр (А/м) в ещиницах SI, и в эрстедах (Эр) в единицах СГС. International system of units (SI). NIST reference on constants, units, and uncertainty. National Institute of Standards and Technology. Дата обращения: 9 мая 2012. Архивировано 31 декабря 2016 года.
- ↑ 1 2 Huray, Paul G. Maxwell’s Equations. — Wiley-IEEE, 2010. — P. 22. — ISBN 978-0-470-54276-7. Архивная копия от 21 ноября 2021 на Wayback Machine
- ↑ 1 2 Per F. Dahl, Flash of the Cathode Rays: A History of J J Thomson’s Electron, CRC Press, 1997, p. 10.
- ↑ 1 2 3 Paul J. Nahin, Oliver Heaviside Архивная копия от 3 апреля 2021 на Wayback Machine, JHU Press, 2002.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43—44. — 260 с. Архивная копия от 14 марта 2022 на Wayback Machine
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
- ↑ See, for example, Jackson, pp. 777-8.
- ↑ J.A. Wheeler. Gravitation. — W.H. Freeman & Co, 1973. — ISBN 0-7167-0344-0.. These authors use the Lorentz force in tensor form as definer of the electromagnetic tensor F, in turn the fields E and B.
- ↑ I.S. Grant. Electromagnetism. — John Wiley & Sons, 1990. — P. 122. — ISBN 978-0-471-92712-9.
- ↑ I.S. Grant. Electromagnetism. — John Wiley & Sons, 1990. — P. 123. — ISBN 978-0-471-92712-9.
- ↑ 1 2 See Jackson, page 2. The book lists the four modern Maxwell’s equations, and then states, «Also essential for consideration of charged particle motion is the Lorentz force equation, F = q (E+ v × B), which gives the force acting on a point charge q in the presence of electromagnetic fields.»
- ↑ See Griffiths, page 204.
- ↑ For example, see the website of the Lorentz Institute Архивная копия от 17 декабря 2021 на Wayback Machine or Griffiths.
- ↑ 1 2 3 Griffiths, David J. Introduction to electrodynamics. — 3rd. — Upper Saddle River, New Jersey [u.a.] : Prentice Hall, 1999. — ISBN 978-0-13-805326-0.
- ↑
Delon, Michel. Encyclopedia of the Enlightenment. — Fitzroy Dearborn Publishers, 2001. — P. 538. — ISBN 157958246X. - ↑
Goodwin, Elliot H. The New Cambridge Modern History Volume 8: The American and French Revolutions, 1763–93. — Cambridge University Press, 1965. — P. 130. — ISBN 9780521045469. - ↑
Meyer, Herbert W. A History of Electricity and Magnetism. — Burndy Library, 1972. — P. 30–31. — ISBN 0-262-13070-X. - ↑
Verschuur, Gerrit L. Hidden Attraction : The History And Mystery Of Magnetism. — Oxford University Press, 1993. — P. 78–79. — ISBN 0-19-506488-7. - ↑
Darrigol Olivier. Electrodynamics from Ampère to Einstein. — Oxford University Press, 2000. — P. 9, 25. — ISBN 0-19-850593-0. - ↑
Verschuur, Gerrit L. Hidden Attraction : The History And Mystery Of Magnetism. — Oxford University Press, 1993. — ISBN 0-19-506488-7. - ↑ 1 2 3 Darrigol, 2000, p. 126–131, 139–144.
- ↑ Heaviside, Oliver (April 1889). “On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric”. Philosophical Magazine. Архивировано из оригинала 2021-02-21. Дата обращения 2021-03-15.
- ↑ Lorentz, Hendrik Antoon, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern, 1895.
- ↑
Whittaker E. T. A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century. — Longmans, Green and Co., 1910. — P. 420–423. — ISBN 1-143-01208-9. - ↑ See Griffiths, page 326, which states that Maxwell’s equations, «together with the [Lorentz] force law…summarize the entire theoretical content of classical electrodynamics».
- ↑ Physics Experiments (англ.). www.physicsexperiment.co.uk. Дата обращения: 14 августа 2018. Архивировано 8 июля 2018 года.
- ↑ 1 2 See Griffiths, pages 301-3.
- ↑ Tai L. Chow. Electromagnetic theory. — Sudbury MA : Jones and Bartlett, 2006. — P. 395. — ISBN 0-7637-3827-1. Архивная копия от 3 апреля 2021 на Wayback Machine
- ↑ Landau, L. D., Lifshitz, E. M., & Pitaevskiĭ, L. P. Electrodynamics of continuous media; Volume 8 Course of Theoretical Physics. — Second. — Oxford : Butterworth-Heinemann, 1984. — P. §63 (§49 pp. 205–207 in 1960 edition). — ISBN 0-7506-2634-8.
- ↑ Roger F. Harrington. Introduction to electromagnetic engineering. — Mineola, New York : Dover Publications, 2003. — P. 56. — ISBN 0-486-43241-6. Архивная копия от 3 апреля 2021 на Wayback Machine
- ↑ M N O Sadiku. Elements of electromagnetics. — Fourth. — NY/Oxford : Oxford University Press, 2007. — P. 391. — ISBN 978-0-19-530048-2. Архивная копия от 3 апреля 2021 на Wayback Machine
- ↑ Landau, 1984, p. §63.
- ↑ Classical Mechanics (2nd Edition), T.W.B. Kibble, European Physics Series, McGraw Hill (UK), 1973, ISBN 0-07-084018-0.
- ↑ Lanczos, Cornelius, 1893-1974. The variational principles of mechanics. — Fourth. — New York, January 1986. — ISBN 0-486-65067-7.
- ↑ Jackson, J.D. Chapter 11
- ↑ Hestenes. SpaceTime Calculus. Дата обращения: 15 марта 2021. Архивировано 9 мая 2021 года.
Литература[править | править код]
- Feynman, Richard Phillips. The Feynman lectures on physics (3 vol.) / Richard Phillips Feynman, Robert B. Leighton, Matthew L. Sands. — Pearson / Addison-Wesley, 2006. — ISBN 0-8053-9047-2.: volume 2.
- Griffiths, David J. Introduction to electrodynamics. — Prentice-Hall, 1999. — ISBN 0-13-805326-X.
- Jackson, John David. Classical electrodynamics. — Wiley, 1999. — ISBN 0-471-30932-X.
- Serway, Raymond A. Physics for scientists and engineers, with modern physics / Raymond A. Serway, John W., Jr. Jewett. — Thomson Brooks/Cole, 2004. — ISBN 0-534-40846-X.
- Srednicki, Mark A. Quantum field theory. — Cambridge University Press, 2007. — ISBN 978-0-521-86449-7.
Ссылки[править | править код]
- Определение направления силы Лоренца. Правило правого винта на YouTube
При прохождении тока по проводнику вокруг него образуется магнитное поле. Векторную характеристику магнитного поля называют вектором магнитной индукции . Это поле оказывает на рамку с током, помещенную в поле, ориентирующее действие. Такое действием магнитного поля на рамку с током или магнитную стрелку можно использовать для определения направления вектора магнитной индукции. За принимается направление, который показывает северный полюс N магнитной стрелки. Для определения направления вектора магнитной индукции поля, созданного прямолинейным проводником с током, пользуются правилом буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика указывает направление вектора магнитной индукции.
Если между полюсами подковообразного магнита поместить проводник с током, то он будет втягиваться или выталкиваться из поля магнита. Закон, определяющий силу, действующую на отдельный небольшой участок проводника, был установлен в 1820 г. А. Ампером.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F=B.I.ℓ. sin α — закон Ампера.
- Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
- Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
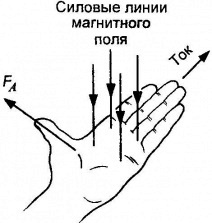
Макроскопическим проявлением силы Лоренца является сила Ампера. Запишем силу, действующую на одну частицу. Если заряженная частица влетает в магнитное поле со скоростью , на нее со стороны магнитного поля действует сила, которую называют силой Лоренца:
, a – угол между векторами
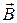
Если расположить левую руку так, чтобы составляющая магнитной индукции , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда, то отогнутый на 900 большой палец укажет направление действующей на заряд силы Лоренца Fл
.
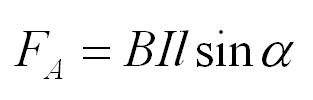
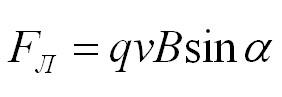
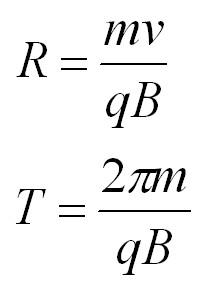
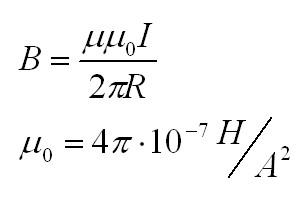
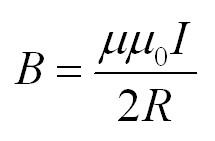
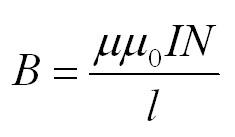
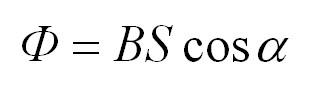
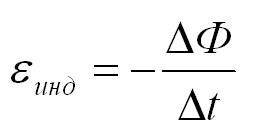
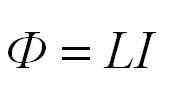
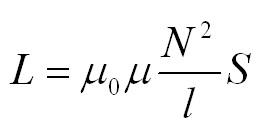
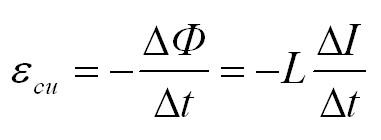
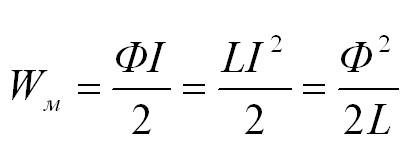











![{displaystyle {vec {mathbf {F} }}=q({vec {mathbf {E} }}+[{vec {mathbf {v} }},{vec {mathbf {B} }}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e262ee2534b1e76495eb6d7b4e28bfabb94182cc)



![{displaystyle mathbf {F} left(mathbf {r} ,mathbf {dot {r}} ,t,qright)=qleft[mathbf {E} (mathbf {r} ,t)+mathbf {dot {r}} times mathbf {B} (mathbf {r} ,t)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3b3f938e06038c39102023765843951b26b28b1)








































![{displaystyle mathbf {F} =qleft[-nabla phi -{frac {partial mathbf {A} }{partial t}}+mathbf {v} times (nabla times mathbf {A} )right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb4e9a877320ef94bcaaf59ed4b4cdcc3b46ac3)

![{displaystyle mathbf {F} =qleft[-nabla (phi -mathbf {v} cdot mathbf {A} )-{frac {mathrm {d} mathbf {A} }{mathrm {d} t}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb9e8796afe27fcf2150aa20fd5574bf7da85484)
![{displaystyle mathbf {F} =qleft[-nabla _{mathbf {x} }(phi -{dot {mathbf {x} }}cdot mathbf {A} )+{frac {mathrm {d} }{mathrm {d} t}}nabla _{dot {mathbf {x} }}(phi -{dot {mathbf {x} }}cdot mathbf {A} )right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9949c2ff8130b2afa9bc01498342a043eda8540)












![{displaystyle {begin{aligned}F_{x}&=-qleft({frac {partial phi }{partial x}}+{frac {partial A_{x}}{partial t}}right)+qleft[{dot {y}}left({frac {partial A_{y}}{partial x}}-{frac {partial A_{x}}{partial y}}right)+{dot {z}}left({frac {partial A_{z}}{partial x}}-{frac {partial A_{x}}{partial z}}right)right]\&=qE_{x}+q[{dot {y}}(nabla times mathbf {A} )_{z}-{dot {z}}(nabla times mathbf {A} )_{y}]\&=qE_{x}+q[mathbf {dot {r}} times (nabla times mathbf {A} )]_{x}\&=qE_{x}+q(mathbf {dot {r}} times mathbf {B} )_{x}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9dcaf925c2a01000291d1859fe864745ce0daa3)














![{displaystyle {frac {mathrm {d} p^{1}}{mathrm {d} tau }}=qleft[U_{0}left({frac {E_{x}}{c}}right)+U_{2}(-B_{z})+U_{3}(B_{y})right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa294150a56ff4b26e8662034d72dad77daacbca)
![{displaystyle {begin{aligned}{frac {mathrm {d} p^{1}}{mathrm {d} tau }}&=qgamma left[cleft({frac {E_{x}}{c}}right)+(-v_{y})(-B_{z})+(-v_{z})(B_{y})right]\&=qgamma left(E_{x}+v_{y}B_{z}-v_{z}B_{y}right)\&=qgamma left[E_{x}+left(mathbf {v} times mathbf {B} right)_{x}right],.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f7d8724e880bc6726e6b8bbdb9d6e7b329aab15)