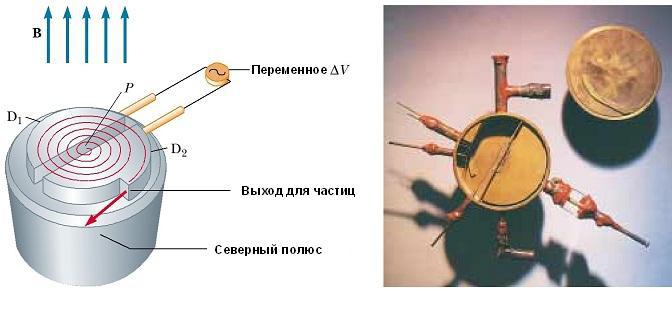
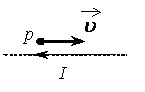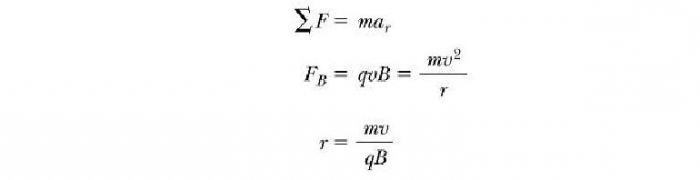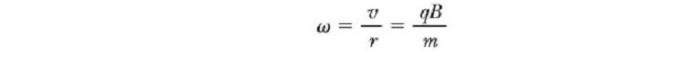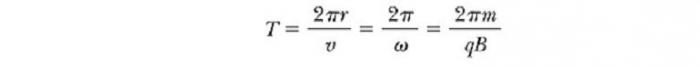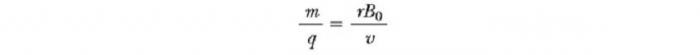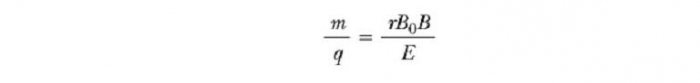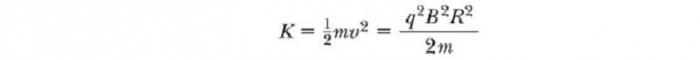Сила Лоренца, действующая на быстро движущиеся заряженные частицы в пузырьковой камере, приводит к появлению траекторий положительного и отрицательного заряда, которые изгибаются в противоположных направлениях.
Си́ла Ло́ренца — сила, с которой электромагнитное поле, согласно классической (неквантовой) электродинамике[1], действует на точечную заряженную частицу[2][3]. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью 



![{displaystyle {vec {mathbf {F} }}=qleft({vec {mathbf {E} }}+[{vec {mathbf {v} }},{vec {mathbf {B} }}]right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b43e62949e6a7ef49afeafa25fee75314af2c10)
Электромагнитная сила, действующая на заряд q, представляет собой комбинацию силы, действующей в направлении электрического поля 


Историки науки предполагают, что этот закон подразумевался в статье Джеймса Клерка Максвелла, опубликованной в 1865 году[6]. Хендрик Лоренц привёл полный вывод этой формулы в 1895 г.[7], определив вклад электрической силы через несколько лет после того, как Оливер Хевисайд правильно определил вклад магнитной силы[8][9].
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется (это верно лишь при условии, что создающий поле магнит не рассматривается как часть системы). Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца[10].
Полный вывод такого утверждения требует определения понятия “импульс поля”, а едва ли не единственный способ сделать это – это теорема Эммы Нетер (и тесно связанное с ней понятие тензора энергии-импульса) в классической (не-квантовой) теории поля в лагранжевом формализме. Однако же характерный импульс поля/волны (“давление света”) в c раз меньше, чем его характерная энергия, где c – скорость света, и во многих реальных, технических применениях представляет собой исчезающе малую величину. Что означает справедливость ЗСИ для одного лишь заряженного вещества, и, в свою очередь, если вещество состоит из всего 2 материальных точек – справедливость третьего закона Ньютона (он равносилен ЗСИ для замкнутой системы, которая есть пара материальных точек/тел).
Сила Лоренца как определение E и B[править | править код]
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Во многих учебниках по электромагнетизму силу Лоренца используют в качестве определения электрического и магнитного полей E и B[11][12][13]. В частности, сила Лоренца понимается как следующее эмпирическое утверждение:
- Электромагнитная сила F, действующая на пробный заряд в данной точке и момент времени, является определённой функцией его заряда q и скорости v, которая может быть параметризована ровно двумя векторами E и B в функциональной форме :
-
.
Это выражение верно в том числе для случая движения частицы со скоростью близкой по величине к скорости света (v = | v | ≈ c).[14] Таким образом, два векторных поля E и B определяются во всём пространстве и времени, и они называются «электрическим полем» и «магнитным полем». Поля определены повсюду в пространстве и времени относительно силы, которую испытывает пробный заряд, помещённый в электромагнитное поле.
Как определение E и B, сила Лоренца является только определением в принципе, потому что реальная частица (в отличие от гипотетического пробного тела бесконечно малой массы и заряда) будет создавать свои собственные конечные поля E и B, изменяющие электромагнитную силу, которую он испытывает. Вдобавок, заряд в магнитном поле обычно движется по криволинейной траектории, то есть с ускорением — а значит, он испускает излучение и теряет кинетическую энергию (см., например, статьи тормозное излучение или синхротронное излучение). Эти эффекты возникают за счёт как прямого воздействия (так называемой силы реакции излучения), так и косвенного (путём воздействия на движение близлежащих зарядов и токов).
Уравнение[править | править код]
Заряженная частица[править | править код]
Сила F, действующая на частицу с электрическим зарядом q и мгновенной скоростью v из-за внешнего электрического поля E и магнитного поля B, определяется выражением (в единицах СИ):[15]
где знак × обозначает векторное произведение (все величины, выделенные жирным шрифтом, являются векторами). В декартовых компонентах
В общем случае, электрическое и магнитное поля зависят от координат и времени. Следовательно, в явном виде силу Лоренца можно записать как
,
где r — вектор положения заряженной частицы, t — время, а точка обозначает производную по времени.
Положительно заряженная частица будет ускоряться в том же направлении, что и поле E, но её траектория будет изгибаться перпендикулярно как вектору мгновенной скорости v, так и полю B в соответствии с правилом буравчика (если пальцы правой руки вытянуты так, чтобы указывать в направлении v, а затем изгибаются так, чтобы указывать в направлении B, тогда вытянутый большой палец будет указывать в направлении F).
Член q E называется электрической силой, а член q (v × B) — магнитной силой[16]. Согласно некоторым определениям, термин «сила Лоренца» относится конкретно к формуле для магнитной силы[17] а формуле с общей электромагнитной силой (включая электрическую силу), дано другое название. В дальнейшем термин «сила Лоренца» будет относиться к выражению для полной силы.
Магнитная составляющая силы Лоренца проявляется как сила, действующая на помещённый в магнитное поле проводник с током. В этом контексте эта сила также называется силой Лапласа.
Сила Лоренца — это сила воздействия электромагнитного поля на заряженную частицу, или. другими словами, скорость, с которой передаётся линейный импульс от электромагнитного поля частице. С ним связана мощность, которая представляет собой скорость, с которой энергия передаётся от электромагнитного поля частице:
.
Магнитное поле не совершает работы, потому что магнитная сила всегда перпендикулярна скорости частицы.
Непрерывное распределение заряда[править | править код]
Сила Лоренца (на единицу 3-х мерного объёма) f действующая на непрерывное распределение заряда (плотность заряда ρ) в движении. 3-хмерного плотность тока J соответствует движению элемента заряда dq в элементе объёма dV и изменяется по всему пространству.
Для непрерывного распределения заряда, находящегося в движении, уравнение для силы Лоренца принимает дифференциальный вид
,
где 


,
где 

,
так что непрерывным аналогом уравнения для силы Лоренца является выражение[18]
К полной силе можно прийти вычислив объемный интеграл по распределению заряда:
.
Устраняя 



В терминах 

,
где 
Плотность мощности, связанная с силой Лоренца в материальной среде, равна
.
Если разделить полный заряд и полный ток на их свободную и связанную части, получится, что плотность силы Лоренца равна
,
где 



Уравнение в единицах СГС[править | править код]
В приведённых выше формулах используются единицы СИ, которые являются наиболее распространёнными среди экспериментаторов, техников и инженеров. В системе СГС, которая более распространена среди физиков-теоретиков, сила Лоренца примет вид
,
где c — скорость света. Хотя это уравнение выглядит несколько иначе, оно полностью эквивалентно, поскольку новые величины связаны в двух системах единиц соотношениями
где ε 0 — диэлектрическая проницаемость вакуума, а μ 0 — магнитная проницаемость вакуума. На практике индексы «cgs» и «SI» всегда опускаются, и система единиц измерения должна быть понятна из контекста.
Частные случаи[править | править код]
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса 
| СГС | СИ |
|---|---|
|
|
|
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости 


| СГС | СИ |
|---|---|
|
|
|
Если заряженная частица движется в магнитном поле так, что вектор скорости 




| СГС | СИ |
|---|---|
|
|
История[править | править код]
Первые попытки количественного описания электромагнитной силы были предприняты в середине 18 века. Предполагалось Иоганн Тобиас Майер и другие в 1760 году[19] предполагали, что сила на магнитных полюсах как и электрически заряженные объекты, что установил Генри Кавендиш в 1762 году[20], подчиняются закону обратных квадратов. Однако в обоих случаях экспериментальное доказательство не было ни полным, ни окончательным. Только в 1784 году Шарль-Огюстен де Кулон, используя торсионные весы, смог окончательно экспериментально показать, что это правда.[21] Вскоре после открытия в 1820 году Хансом Кристианом Эрстедом того факта, что на магнитную стрелку действует электрический ток, Андре-Мари Ампер в том же году смог экспериментально получить формулу угловой зависимости силы между двумя элементами тока.[22][23] Во всех этих описаниях сила всегда описывалась в терминах свойств вещества и расстояний между двумя массами или зарядами, а не в терминах электрических и магнитных полей.[24]
Современная концепция электрических и магнитных полей впервые возникла в теориях Майкла Фарадея, особенно удачной оказалась его идея силовых линий, которая позже получила полное математическое описание лордом Кельвином и Джеймсом Клерком Максвеллом.[25] С современной точки зрения, в формулировке Максвелла 1865 г. его уравнений для электромагнитного поля можно получить уравнение для силы Лоренца по отношению к электрическим токам[6], хотя во времена Максвелла не было очевидно, как его уравнения связаны с силами при перемещении заряженных предметов. Дж. Дж. Томсон был первым, кто попытался вывести из уравнений Максвелла поля электромагнитные силы, действующие на движущийся заряженный объект, в терминах свойств объекта и внешних полей. Заинтересовавшийся поведением заряженных частиц в катодных лучах, Томсон опубликовал статью в 1881 году, в которой он дал определение силы, действующей на частицы, обусловленную внешним магнитным полем, в виде[8]
Томсон вывел правильную основную форму формулы, но из-за некоторых ошибок и неполного описания тока смещения перед формулой включил неверный масштабный коэффициент, равный половине. Оливер Хевисайд изобрёл современные векторные обозначения и переписал в их терминах полевые уравнения Максвелла; он также (в 1885 и 1889 годах) исправил ошибки вывода Томсона и пришел к правильному виду для магнитной силы действующей на движущуюся заряженную частицу.[8][25][26] Наконец, в 1895 году[7][27] Хендрик Лоренц пришёл к современному виду формулы для электромагнитной силы, которая включает вклады как электрического, так и магнитного полей. Лоренц вначале отказался от максвелловского описания эфира и проводимости. Вместо этого Лоренц указал на различия между материей и светоносным эфиром и записал уравнения Максвелла в микроскопическом масштабе. Используя версию уравнений Максвелла Хевисайда для неподвижного эфира и, применяя лагранжевую механику (см. Ниже), Лоренц пришёл к правильной и полной форме закона для электромагнитной силы, который теперь носит его имя.[25][28]
Траектории частиц под действием силы Лоренца[править | править код]
Заряженная частица дрейфует в однородном магнитном поле. (A) Нет возмущающей силы (B) В электрическом поле, E (C) С независимой силой, F (например, гравитация) (D) В неоднородном магнитном поле, grad H
Во многих случаях, представляющих практический интерес, движение в магнитном поле электрически заряженной частицы (например, электрона или иона в плазме) можно рассматривать как суперпозицию относительно быстрого кругового движения вокруг точки, которая дрейфует в направлении перпендикулярном электрическому и магнитным полям. Скорости дрейфа могут различаться в зависимости от их зарядового состояния, массы или температуры, что может привести к электрическим токам или химическому разделению.
Значение силы Лоренца[править | править код]
В то время как современные уравнения Максвелла описывают то, как электрически заряженные частицы и токи или движущиеся заряженные частицы вызывают электрические и магнитные поля, сила Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей.[15][29] Хотя сила Лоренца описывает действие E и B на точечный заряд, но такие электромагнитные силы не являются всей картиной. Заряженные частицы, возможно, связаны с другими силами, особенно с гравитацией и ядерными силами. Таким образом, уравнения Максвелла не отделены от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один из аспектов; генерация E и B токами и зарядами — другое.
В реальных материалах сила Лоренца неадекватно описывает коллективное поведение заряженных частиц как в принципе, так и с точки зрения вычислений. Заряженные частицы в материальной среде не только реагируют на поля E и B, но и создают эти поля сами. Для определения временной и пространственной реакции зарядов необходимо решать сложные уравнения переноса, например, уравнение Больцмана, уравнение Фоккера — Планка или уравнения Навье — Стокса . Например, см. Магнитогидродинамику, гидродинамику, электрогидродинамику, сверхпроводимость, звёздную эволюцию . Разработан целый физический аппарат для решения этих вопросов. См., Например, формулы Грина — Кубо и функцию Грина (теория многих тел) .
Сила на токоведущем проводе[править | править код]
Правило правой руки для токоведущего провода в магнитном поле B
Когда провод, по которому течёт электрический ток, помещается в магнитное поле, каждый из движущихся зарядов, составляющих ток, испытывает силу Лоренца, и вместе они могут создавать макроскопическую силу действующую на проводе (иногда называемую силой Лапласа). Комбинируя приведённый выше закон Лоренца с определением электрического тока, в случае прямого неподвижного провода получается следующее уравнение:[30]
где ℓ — вектор, величина которого равна длине провода, а направление — вдоль провода, совмещённое с направлением обычного тока I.
Если провод не прямой, а изогнутый, то силу, действующую на него, вычисляют, применив данную формулу к каждому бесконечно малому отрезку провода dℓ, а затем сложив все эти силы путём интегрирования . Формально результирующая сила, действующая на неподвижный жёсткий провод, по которому течёт постоянный ток I равна
Это полная сила. Кроме того, обычно возникает крутящий момент и другие эффекты, если проволока не совсем жёсткая.
Одним из применений этого является закон силы Ампера, который описывает, как два токоведущих провода притягиваться или отталкиваться друг от друга, в зависимости от направления тока, поскольку каждый из них испытывает силу Лоренца от магнитного поля создаваемого другим током.
ЭДС[править | править код]
Магнитная сила (qv × B) в выражении силы Лоренца отвечает за двигательную электродвижущую силу (или двигательную ЭДС), явление, лежащее в основе действия многих электрических генераторов. Когда проводник перемещается через область магнитного поля, магнитное поле оказывает противоположно направленные силы на электроны и ядра в проводе, и это создаёт ЭДС. Термин «двигательная ЭДС» применяется к этому явлению, поскольку ЭДС возникает из-за движения провода.
В других электрических генераторах магниты движутся, а проводники — нет. В этом случае ЭДС возникает из-за электрической силы (q E) в уравнении для силы Лоренца. Рассматриваемое электрическое поле создается изменяющимся магнитным полем, приводящим к возникновению индуцированной ЭДС, как описано уравнением Максвелла — Фарадея.[31]
Обе эти ЭДС, несмотря на их явно различное происхождение, описываются одним и тем же уравнением, а именно ЭДС — это скорость изменения магнитного потока через провод. Это закон электромагнитной индукции Фарадея, см. Ниже . Специальная теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами.[31] Фактически, электрическое и магнитное поля представляют собой разные грани единого электромагнитного поля (разные элементы единой матрицы тензора силы поля Fij), и при переходе от одной инерциальной системы отсчета к другой (то есть применении операции замены базиса к матрице Fij) часть электромагнитного векторного поля E можно полностью или частично заменить на B или наоборот .[32]
Сила Лоренца и закон индукции Фарадея[править | править код]
Сила Лоренца — изображение на стене в Лейдене
Для петли из провода находящуюся в магнитном поле, закон индукции Фарадея утверждает, что наведённая электродвижущая сила (ЭДС) в проводе равна:
где
— магнитный поток через петлю, B — магнитное поле, Σ (t) — поверхность, ограниченная замкнутым контуром ∂Σ (t), в момент времени t, dA — бесконечно малый элемент вектора площади Σ (t) (величина — это площадь бесконечно малого участка поверхности, направление вектора ортогонально этому участку поверхности).
Знак ЭДС определяется законом Ленца. Это справедливо не только для стационарного провода, но и для движущейся проволоки.
Из закона электромагнитной индукции Фарадея и уравнений Максвелла можно получить силу Лоренца. Верно и обратное: силу Лоренца и уравнения Максвелла можно использовать для вывода закона Фарадея.
Пусть Σ (t) — движущийся поступательно провод с постоянной скоростью v, а Σ (t) — внутренняя поверхность провода. ЭДС вокруг замкнутого пути ∂Σ (t) определяется выражением[33]
где
— электрическое поле, а d ℓ — бесконечно малый векторный элемент контура ∂Σ (t).
Направление dℓ, и dA неоднозначно. Чтобы получить правильный знак, используется правило правой руки, как описано в статье Теорема Кельвина — Стокса .
Приведённый выше результат можно сравнить с законом электромагнитной индукции Фарадея, который появляется в современных уравнениях Максвелла, называемый здесь уравнением Максвелла — Фарадея :
Уравнение Максвелла — Фарадея можно записать в интегральной форме с помощью теоремы Кельвина — Стокса .[34]
Уравнение Максвелла — Фарадея принимает вид
и закон Фарадея,
Эти два выражения эквивалентны, если провод не движется. Используя интегральное правило Лейбница и div B = 0, можно получить,
и, используя уравнение Максвелла Фарадея,
поскольку это справедливо для любого положения провода, то
Закон индукции Фарадея справедлив независимо от того, является ли проволочная петля жёсткой и неподвижной, либо она находится в движении, либо в процессе деформации, а также независимо от того, является ли магнитное поле постоянным во времени или изменяющимся. Однако бывают случаи, когда закон Фарадея либо неадекватен, либо его трудно использовать, и необходимо применять закон Лоренца.
Если магнитное поле не зависит от времени и проводящая петля движется через поле, магнитный поток Φ B, проникающий в петлю, может изменяться несколькими способами. Например, если магнитное поле меняется в зависимости от положения, и петля перемещается в другое положение с другим значением B, — ΦB изменится. В качестве альтернативы, если петля изменяет ориентацию по отношению к B, то дифференциальный элемент B ⋅ dA будет меняться из-за различного угла между B и dA, также изменится Ф B. В качестве третьего примера, если часть электрической схемы проходит через однородное, не зависящее от времени магнитное поле, а другая часть схемы остаётся неподвижной, то магнитный поток, связывающий всю замкнутую цепь, может измениться из-за относительного смещения положения составных частей схемы с течением времени (поверхность ∂Σ (t), зависящая от времени). Во всех трёх случаях закон индукции Фарадея предсказывает появление ЭДС, порождённую изменением ΦB.
Из уравнения Максвелла — Фарадея следует, что если магнитное поле B изменяется во времени, то электрическое поле E неконсервативно, и не может быть выражено как градиент скалярного поля, поскольку его ротор не равен нулю.[35][36]
Сила Лоренца в терминах потенциалов[править | править код]
Поля E и B можно заменить векторным магнитным потенциалом A и (скалярным) электростатическим потенциалом ϕ посредством
где ∇ — градиент, ∇⋅ — дивергенция, ∇ × — ротор .
Сила запишется в виде
Используя тождество для тройного произведения, это выражение можно переписать как,
![{displaystyle mathbf {F} =qleft[-nabla phi -{frac {partial mathbf {A} }{partial t}}+nabla left(mathbf {v} cdot mathbf {A} right)-left(mathbf {v} cdot nabla right)mathbf {A} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaeed018e78d24c910e10653ad0dd3c0627ed3d9)
Здесь координаты и компоненты скорости следует рассматривать как независимые переменные, поэтому оператор набла действует только на 


так что приведенное выше выражение принимает вид
.
При v = ẋ уравнение можно переписать в удобной форме Эйлера — Лагранжа
где введены обозначения

и

Сила Лоренца и аналитическая механика[править | править код]
Лагранжиан для заряженной частицы с массой m и зарядом q в электромагнитном поле описывает динамику частицы с точки зрения её энергии, а не силы, действующей на неё. Классическое выражение задается следующим образом:[37]
где A и ϕ — потенциальные поля, как указано выше. Величину
-
Вывод силы Лоренца из классического Лангранжана (единицы СИ) В поле A, частица двигающаяся со скоростью v = ṙ обладает импульсом , тогда её потенциальная энергия равна
. В поле ϕ, потенциальная энергия частицы равна
.
Полная потенциальная энергия записывается в виде
и кинетическая энергия:
Отсюда Лагранжан:
Уравнения Лагранжа
(аналогично для y и z компонент). Вычисление частных производных приводит к
уравнивая и упрощая выражение
и аналогично для y и z компонент. Уравнение для силы
Потенциальная энергия зависит от скорости частицы, поэтому сила зависит от скорости, и соответственно она не является консервативной.
Релятивистский лагранжиан
Действие — это релятивистская длина пути частицы в пространстве-времени, за вычетом вклада потенциальной энергии, плюс дополнительный вклад, который квантово-механически является дополнительной фазой, которую получает заряженная частица, когда она движется вдоль векторного потенциала.
-
Вывод силы Лоренца для релятивистского Лагранжиана (единицы СИ) Уравнения движения получающиеся из вариационного принципа для действия
соответствуют уравнениям движения Гамильтона:
которые эквиваленты следующему выражению в неканонической форме
Это выражение описывает силу Лоренца, — скорость с которой электромагнитное поле передаёт релятивистский импульс частице.
Релятивистская форма силы Лоренца[править | править код]
Ковариантная форма силы Лоренца.[править | править код]
Тензор поля[править | править код]
Используя сигнатуру метрики (1, −1, −1, −1), сила Лоренца для заряда q может быть записана в[39] ковариантной форме :
-
где p α — четырехмерный импульс, определяемый как
τ собственное время частицы, F αβ — контравариантный тензор электромагнитного поля
и U — ковариантная 4-скорость частицы, определяемая как:
где Лоренц-фактор
Поля преобразуются в систему, движущуюся относительно неподвижной системы с постоянной скоростью, с помощью:
где Λ μ α — тензор преобразования Лоренца.
Перевод в векторные обозначения[править | править код]
Компонента α = 1 (x -компонента) силы равна
Подставляя компоненты ковариантного тензора электромагнитного поля F, получаем
Используя компоненты ковариантных четырёхскоростей
Расчет для α = 2, 3 (компоненты силы в направлениях y и z) приводит к аналогичным результатам, поэтому объединение 3 уравнений в одно:
и поскольку дифференциалы по координатному времени dt и собственному времени dτ связаны между собой Лоренц-фактором,
в итоге можно записать
Это в точности закон Лоренца, однако p — это релятивистское выражение,
Сила Лоренца в алгебре пространства-времени (STA)[править | править код]
[проверить перевод] Электрическое и магнитное поля зависят от скорости наблюдателя, поэтому релятивистскую форму закона Лоренца лучше всего можно продемонстрировать, исходя из не зависящего от координат выражения для электромагнитного и магнитного полей. 

и



(что показывает наш выбор метрики), а скорость равна
Правильная (инвариант — неадекватный термин, потому что никакое преобразование не было определено) форма закона Лоренца
Здесь порядок важен, потому что между бивектором и вектором скалярное произведение антисимметрично. При таком расщеплении пространства-времени можно получить скорость и поля, как указано выше, что дает обычное выражение.
Сила Лоренца в общей теории относительности[править | править код]
В общей теории относительности уравнение движения частицы с массой 



где 



Уравнение также можно записать как
куда 
куда 
Приложения[править | править код]
Сила Лоренца присутствует во многих устройствах, в том числе:
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы
Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
- Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД-генераторах.
- Сила Лоренца также используется в ускорителях заряженных частиц: она задаёт орбиту, по которой движутся эти частицы.
- Сила Лоренца используется в рельсотроне.
- Велосиметрия силой Лоренца заключается в бесконтактном измерении скорости движения проводящей жидкости.
- Циклотроны и другие ускорители частиц с круговым движением
- Масс-спектрометры
- Фильтры скорости
- Магнетроны
См. также[править | править код]
- Радиационное трение
Примечания[править | править код]
- ↑ Афанасьев, Г. Н. Старые и новые проблемы в теории эффекта Ааронова — Бома // Физика элементарных частиц и атомного ядра. — 1990. — Т. 21. — С. 172—250. Архивировано 12 февраля 2022 года.
- ↑ 1 2 Сила Лоренца / В. С. Булыгин // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ М. А. Миллер, Е. В. Суворов. Лоренца сила // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического, и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ H-поле измеряетс в амперах на метр (А/м) в ещиницах SI, и в эрстедах (Эр) в единицах СГС. International system of units (SI). NIST reference on constants, units, and uncertainty. National Institute of Standards and Technology. Дата обращения: 9 мая 2012. Архивировано 31 декабря 2016 года.
- ↑ 1 2 Huray, Paul G. Maxwell’s Equations. — Wiley-IEEE, 2010. — P. 22. — ISBN 978-0-470-54276-7. Архивная копия от 21 ноября 2021 на Wayback Machine
- ↑ 1 2 Per F. Dahl, Flash of the Cathode Rays: A History of J J Thomson’s Electron, CRC Press, 1997, p. 10.
- ↑ 1 2 3 Paul J. Nahin, Oliver Heaviside Архивная копия от 3 апреля 2021 на Wayback Machine, JHU Press, 2002.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43—44. — 260 с. Архивная копия от 14 марта 2022 на Wayback Machine
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
- ↑ See, for example, Jackson, pp. 777-8.
- ↑ J.A. Wheeler. Gravitation. — W.H. Freeman & Co, 1973. — ISBN 0-7167-0344-0.. These authors use the Lorentz force in tensor form as definer of the electromagnetic tensor F, in turn the fields E and B.
- ↑ I.S. Grant. Electromagnetism. — John Wiley & Sons, 1990. — P. 122. — ISBN 978-0-471-92712-9.
- ↑ I.S. Grant. Electromagnetism. — John Wiley & Sons, 1990. — P. 123. — ISBN 978-0-471-92712-9.
- ↑ 1 2 See Jackson, page 2. The book lists the four modern Maxwell’s equations, and then states, «Also essential for consideration of charged particle motion is the Lorentz force equation, F = q (E+ v × B), which gives the force acting on a point charge q in the presence of electromagnetic fields.»
- ↑ See Griffiths, page 204.
- ↑ For example, see the website of the Lorentz Institute Архивная копия от 17 декабря 2021 на Wayback Machine or Griffiths.
- ↑ 1 2 3 Griffiths, David J. Introduction to electrodynamics. — 3rd. — Upper Saddle River, New Jersey [u.a.] : Prentice Hall, 1999. — ISBN 978-0-13-805326-0.
- ↑
Delon, Michel. Encyclopedia of the Enlightenment. — Fitzroy Dearborn Publishers, 2001. — P. 538. — ISBN 157958246X. - ↑
Goodwin, Elliot H. The New Cambridge Modern History Volume 8: The American and French Revolutions, 1763–93. — Cambridge University Press, 1965. — P. 130. — ISBN 9780521045469. - ↑
Meyer, Herbert W. A History of Electricity and Magnetism. — Burndy Library, 1972. — P. 30–31. — ISBN 0-262-13070-X. - ↑
Verschuur, Gerrit L. Hidden Attraction : The History And Mystery Of Magnetism. — Oxford University Press, 1993. — P. 78–79. — ISBN 0-19-506488-7. - ↑
Darrigol Olivier. Electrodynamics from Ampère to Einstein. — Oxford University Press, 2000. — P. 9, 25. — ISBN 0-19-850593-0. - ↑
Verschuur, Gerrit L. Hidden Attraction : The History And Mystery Of Magnetism. — Oxford University Press, 1993. — ISBN 0-19-506488-7. - ↑ 1 2 3 Darrigol, 2000, p. 126–131, 139–144.
- ↑ Heaviside, Oliver (April 1889). “On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric”. Philosophical Magazine. Архивировано из оригинала 2021-02-21. Дата обращения 2021-03-15.
- ↑ Lorentz, Hendrik Antoon, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern, 1895.
- ↑
Whittaker E. T. A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century. — Longmans, Green and Co., 1910. — P. 420–423. — ISBN 1-143-01208-9. - ↑ See Griffiths, page 326, which states that Maxwell’s equations, «together with the [Lorentz] force law…summarize the entire theoretical content of classical electrodynamics».
- ↑ Physics Experiments (англ.). www.physicsexperiment.co.uk. Дата обращения: 14 августа 2018. Архивировано 8 июля 2018 года.
- ↑ 1 2 See Griffiths, pages 301-3.
- ↑ Tai L. Chow. Electromagnetic theory. — Sudbury MA : Jones and Bartlett, 2006. — P. 395. — ISBN 0-7637-3827-1. Архивная копия от 3 апреля 2021 на Wayback Machine
- ↑ Landau, L. D., Lifshitz, E. M., & Pitaevskiĭ, L. P. Electrodynamics of continuous media; Volume 8 Course of Theoretical Physics. — Second. — Oxford : Butterworth-Heinemann, 1984. — P. §63 (§49 pp. 205–207 in 1960 edition). — ISBN 0-7506-2634-8.
- ↑ Roger F. Harrington. Introduction to electromagnetic engineering. — Mineola, New York : Dover Publications, 2003. — P. 56. — ISBN 0-486-43241-6. Архивная копия от 3 апреля 2021 на Wayback Machine
- ↑ M N O Sadiku. Elements of electromagnetics. — Fourth. — NY/Oxford : Oxford University Press, 2007. — P. 391. — ISBN 978-0-19-530048-2. Архивная копия от 3 апреля 2021 на Wayback Machine
- ↑ Landau, 1984, p. §63.
- ↑ Classical Mechanics (2nd Edition), T.W.B. Kibble, European Physics Series, McGraw Hill (UK), 1973, ISBN 0-07-084018-0.
- ↑ Lanczos, Cornelius, 1893-1974. The variational principles of mechanics. — Fourth. — New York, January 1986. — ISBN 0-486-65067-7.
- ↑ Jackson, J.D. Chapter 11
- ↑ Hestenes. SpaceTime Calculus. Дата обращения: 15 марта 2021. Архивировано 9 мая 2021 года.
Литература[править | править код]
- Feynman, Richard Phillips. The Feynman lectures on physics (3 vol.) / Richard Phillips Feynman, Robert B. Leighton, Matthew L. Sands. — Pearson / Addison-Wesley, 2006. — ISBN 0-8053-9047-2.: volume 2.
- Griffiths, David J. Introduction to electrodynamics. — Prentice-Hall, 1999. — ISBN 0-13-805326-X.
- Jackson, John David. Classical electrodynamics. — Wiley, 1999. — ISBN 0-471-30932-X.
- Serway, Raymond A. Physics for scientists and engineers, with modern physics / Raymond A. Serway, John W., Jr. Jewett. — Thomson Brooks/Cole, 2004. — ISBN 0-534-40846-X.
- Srednicki, Mark A. Quantum field theory. — Cambridge University Press, 2007. — ISBN 978-0-521-86449-7.
Ссылки[править | править код]
- Определение направления силы Лоренца. Правило правого винта на YouTube
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
FЛ=FN
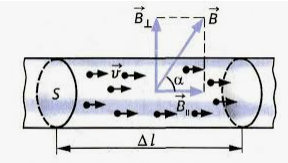
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля →B можно считать неизменным в пределах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I=qnvS
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F=|I|ΔlBsinα
Подставляя сюда выражение, полученное для силы тока, получим:
F=|qnvS|ΔlBsinα=|q|nvSΔlBsinα
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
N=nSΔlB
Тогда:
F=|q|vNBsinα
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
FЛ=FN=|q|vNBsinαN=|q|vBsinα
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.
FЛ=|q|vBsinα=0,005·200·0,3·√22≈0,2 (Н)
Направление силы Лоренца
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
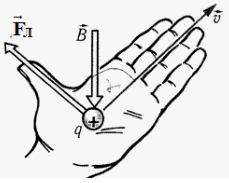
Если левую руку расположить так, чтобы составляющая магнитной индукции →B, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
Пример №2. Протон p имеет скорость →v, направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90о. Работа любой силы определяется формулой:
A=Fscosα
Но так как косинус 90о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила →Fэл, действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
→Fэл=q→E
Следовательно, полная сила, действующая на заряд, равна:
→F=→Fэл+→Fл=q→E+|q|→v→Bsinα
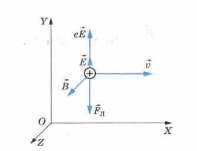
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна →E. Какова индукция →B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор →E направлен вдоль траектории движения протона. Тогда вектор →B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
- Векторы →E, →B и →v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
Заряд протона равен модулю заряда электрона — e. Сложим силы, действующие на протон по оси ОУ:
e→E+→FЛ=0
В скалярной форме:
eE−evB=0
Следовательно:
B=Ev
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Лоренца.
3.Выразить модуль вектора магнитной индукции.
4.Определить недостающие величины.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Напряжение на обкладках конденсатора: U = 2160 В.
• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.
• Масса протона: m = 1,673·10–27 кг.
• Заряд протона: q = 1,6·10–19 Кл.
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
Ответ: 33,6
pазбирался: Алиса Никитина | обсудить разбор
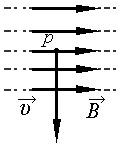
Задание EF17600
а) влево
б) вправо
в) к нам
г) от нас
Алгоритм решения
- Определить, каким способом можно найти направлений силы Лоренца, действующей на протон.
- Применить правила и найти направление силы Лоренца.
Решение
Силу Лоренца, действующую на заряженную частицу, можно найти с помощью правила левой руки. Для этого мысленно расположим четыре пальца левой руки в сторону, совпадающей с направлением движения положительной частицы (протона). Относительно рисунка пальца будут направлены вниз. Теперь развернем ладонь так, чтобы в нее входили линии магнитной индукции. Теперь отклоним на 90 градусов большой палец. Он будет направлен от плоскости рисунка к нам. Это и есть направление силы Лоренца, действующей на протон.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17749
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:
- увеличиться
- уменьшиться
- не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Записать формулу для определения силы Лоренца.
2.Установить, от чего зависят перечисленные в таблице физические величины.
3.Определить характер их изменения при изменении заряда.
Решение
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.
Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
|q|vBsinα=mv2R
Отсюда:
|q|Bsinα=mvR
R=mv|q|Bsinα
Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.
Частота обращения альфа-частицы связана с ее линейной скоростью формулой:
v=2πRν
Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.
Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).
Ответ: 121
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k
Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля. Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так. На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.
Определение и формула
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
По закону Ампера:
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
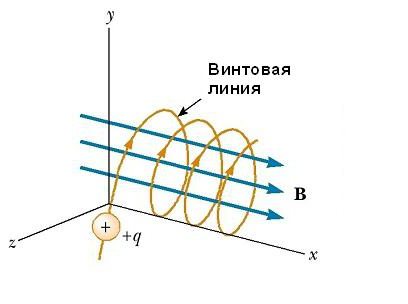
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0<К<1, а n – порядок числа 10.
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Формула силы Лоренца при наличии магнитного и электрического полей
Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:
Тогда:
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).
Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.
Применение на практике
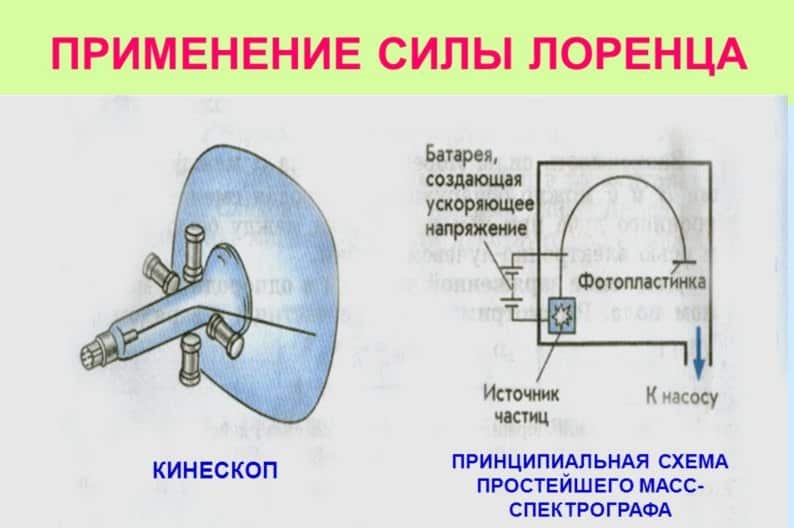
Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.
Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.
На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.
Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).
Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.
Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.
На основании действия силы Лоренца создано много других устройств, используемых на практике.
Как найти заряд частицы по окружности
Заряженная частица движется в магнитном поле по окружности со скоростью v = 10 6 м/с. Индукция магнитного поля B = 0,3 Тл. Радиус окружности R = 4 см. Найти заряд q частицы, если известно, что ее энергия W = 12 кэВ
Дано:
W = 12 кэВ = 1,92·10 -15 Дж
Решение:
На частицу, движущуюся в магнитном поле действует сила Лоренца
которая является центростремительной
Ответ:
Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле
Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы FB, которую поле оказывает на частицу при ее движении в нем со скоростью v.
Общие свойства магнитной силы
Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:
- Величина FB магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
- Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
- Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, FB перпендикулярна плоскости, образованной v и B (см.рис. ниже).
- Величина и направление FB зависит от скорости частицы и от величины и направления магнитного поля B.
- Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
- Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.
Сила Лоренца
Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде FB = qv х B.
Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца FB при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.
Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно FЛ = qE + qv х В. Его принято называть так: полная сила Лоренца.
Движение заряженных частиц в однородном магнитном поле
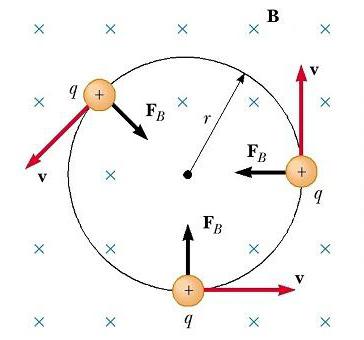
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.
Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила FB направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и FB изменяются непрерывно, как показано на рисунке. Так как FB всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.
Динамика кругового движения частицы
Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем FB центробежной силе, требуемой для сохранения круговой траектории движения:
То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы
Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:
Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.
Движение частицы под углом к вектору магнитного поля
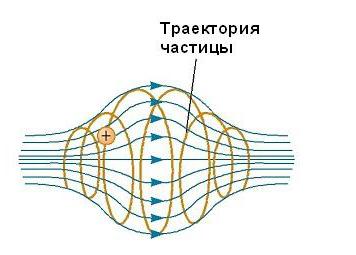
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы FB в этом направлении. В результате составляющая ускорения ax= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила FB = qv х В вызывает изменение во времени компонентов скорости vy и vz. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν⊥ = √(νу 2 + νz 2 ).
Неоднородное магнитное поле: как в нем движутся частицы
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.
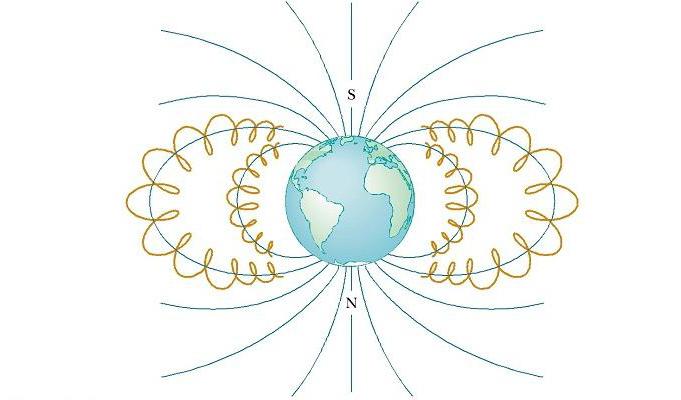
Как Земля влияет на движение космических частиц
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.
Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.
Селектор скоростей
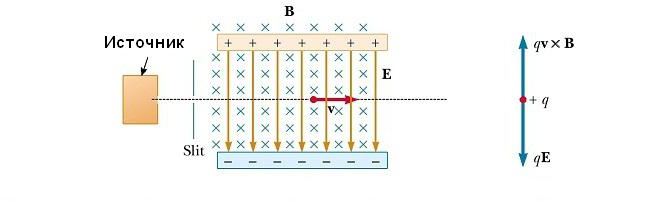
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).
Масс-спектрометр
Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B0, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q
и затем, используя уравнение v=E/B, мы находим, что
Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B0, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/mе для электронов.
Циклотрон
Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).
Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.
Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D2 получает более низкий электрический потенциал, чем D1 на величину qΔV, то ион ускоряется в зазоре перед входом в D2, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D2 по полукруглой траектории большего радиуса (потому что его скорость увеличилась).
Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия
Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.
Эффект Холла
Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.
Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.
Особенности формулы заряда q
Время на чтение:
Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.
Что такое электрический заряд q
Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.
Понятие из учебного пособия
Формула нахождения заряда
Определить искомую величину можно из физико-математической формулы силы тока. В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон.
Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.
Как вычислять с помощью законов
Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.
Закон сохранения
Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.
Закон сохранения
Закон Кулона
Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.
Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.
Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.
Образец решения задач по теме «Электрический заряд»
Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.
Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?
Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.
Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон. Задача состоит в определении первоначальных зарядов шаров.
Чтобы решить вторую задачу, нужно использовать ту же формулу Кулона, но немного видоизмененную: F=kq2/r2. Затем вывести из правила показатель q2. Он будет равен Fr2/k. Подставив известные значения и выполнив несложные расчеты, получится цифры в 10^-7 или 10 микрокулон.
Формула для решения
В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.
[spoiler title=”источники:”]
http://www.syl.ru/article/203046/new_dvijenie-zaryajennoy-chastitsyi-v-magnitnom-pole-formulyi-dvijenie-zaryajennyih-chastits-v-odnorodnom-magnitnom-pole
http://rusenergetics.ru/polezno-znat/formula-zaryada
[/spoiler]
Сила
Лоренца
— сила, с которой, в рамках классической
физики, электромагнитное поле действует
на точечную заряженную частицу. Иногда,
силой Лоренца называют силу, действующую
на движущийся со скоростью
заряд
лишь со стороны магнитного поля, нередко
же полную силу — со стороны электромагнитного
поля вообще иначе говоря, со стороны
электрического E
и магнитного B
полей в СИ:
Названа
в честь голландского физика Хендрика
Лоренца, который вывел выражение для
этой силы в 1892 году. За три года до Лоренца
правильное выражение было найдено
Хевисайдом
Частным
случаем силы Лоренца является сила
Ампера.
Сила
,
действующая на заряженную частицу,
движущуюся в магнитном поле:
При
движении заряженной частицы в
электромагнитном поле на неё будут
действовать и электрическое, и магнитное
поле, а полная сила есть сумма сил со
стороны первого и второго:
Движение
заряженной частицы в магнитном поле:
Формула
силы Лоренца дает возможность найти
ряд закономерностей движения заряженных
частиц в магнитном поле. Зная направление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле можно найти знак заряда
частиц, которые движутся в магнитных
полях.
Для
вывода общих закономерностей будем
полагать, что магнитное поле однородно
и на частицы не действуют электрические
поля. Если заряженная частица в магнитном
поле движется со скоростью v вдоль линий
магнитной индукции, то угол α между
векторами v и В равен 0 или π. Тогда сила
Лоренца равна нулю, т. е. магнитное поле
на частицу не действует и она движется
равномерно и прямолинейно.
В
случае, если заряженная частица движется
в магнитном поле со скоростью v, которая
перпендикулярна вектору В, то сила
Лоренца F=Q[vB] постоянна по модулю и
перпендикулярна к траектории частицы.
По второму закону Ньютона, сила Лоренца
создает центростремительное ускорение.
Значит, что частица будет двигаться по
окружности, радиус r которой находится
из условия QvB=mv^2/r , следовательно
Период
вращения частицы, т. е. время Т, за которое
она совершает один полный оборот,
Подствавив
(1), получим
т.
е. период вращения частицы в однородном
магнитном поле задается только величиной,
которая обратна удельному заряду (Q/m)
частицы, и магнитной индукцией поля, но
при этом не зависит от ее скорости (при
v<<c).
На этом соображении основано действие
циклических ускорителей заряженных
частиц.
Эффе́кт
Хо́лла —
явление возникновения поперечной
разности потенциалов (называемой также
холловским напряжением) при помещении
проводника с постоянным током в магнитное
поле. Открыт Эдвином Холлом в 1879 году в
тонких пластинках золота.
В
простейшем рассмотрении эффект Холла
выглядит следующим образом. Пусть через
металлический брус в слабом магнитном
поле B
течёт электрический ток под действием
напряжённости E.
Магнитное поле будет отклонять носители
заряда (для определённости электроны)
от их движения вдоль или против
электрического поля к одной из граней
бруса. При этом критерием малости будет
служить условие, что при этом электрон
не начнёт двигаться по циклоиде.
Таким
образом, сила Лоренца приведёт к
накоплению отрицательного заряда возле
одной грани бруска и положительного
возле противоположной. Накопление
заряда будет продолжаться до тех пор,
пока возникшее электрическое поле
зарядов E1
не скомпенсирует магнитную составляющую
силы Лоренца:
Скорость
электронов v можно выразить через
плотность тока:
где
n — концентрация носителей заряда. Тогда
Коэффициент
пропорциональности между E1 и jB называется
коэффициентом (или константой) Холла.
В таком приближении знак постоянной
Холла зависит от знака носителей заряда,
что позволяет определять их тип для
большого числа металлов. Для некоторых
металлов (например, таких, как свинец,
цинк, железо, кобальт, вольфрам), в сильных
полях наблюдается положительный знак
RH, что объясняется в полуклассической
и квантовой теориях твёрдого тела.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
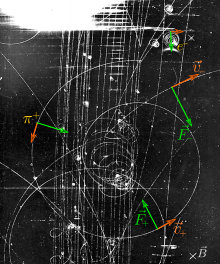


![{displaystyle {vec {mathbf {F} }}=q({vec {mathbf {E} }}+[{vec {mathbf {v} }},{vec {mathbf {B} }}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e262ee2534b1e76495eb6d7b4e28bfabb94182cc)



![{displaystyle mathbf {F} left(mathbf {r} ,mathbf {dot {r}} ,t,qright)=qleft[mathbf {E} (mathbf {r} ,t)+mathbf {dot {r}} times mathbf {B} (mathbf {r} ,t)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3b3f938e06038c39102023765843951b26b28b1)








































![{displaystyle mathbf {F} =qleft[-nabla phi -{frac {partial mathbf {A} }{partial t}}+mathbf {v} times (nabla times mathbf {A} )right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb4e9a877320ef94bcaaf59ed4b4cdcc3b46ac3)

![{displaystyle mathbf {F} =qleft[-nabla (phi -mathbf {v} cdot mathbf {A} )-{frac {mathrm {d} mathbf {A} }{mathrm {d} t}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb9e8796afe27fcf2150aa20fd5574bf7da85484)
![{displaystyle mathbf {F} =qleft[-nabla _{mathbf {x} }(phi -{dot {mathbf {x} }}cdot mathbf {A} )+{frac {mathrm {d} }{mathrm {d} t}}nabla _{dot {mathbf {x} }}(phi -{dot {mathbf {x} }}cdot mathbf {A} )right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9949c2ff8130b2afa9bc01498342a043eda8540)












![{displaystyle {begin{aligned}F_{x}&=-qleft({frac {partial phi }{partial x}}+{frac {partial A_{x}}{partial t}}right)+qleft[{dot {y}}left({frac {partial A_{y}}{partial x}}-{frac {partial A_{x}}{partial y}}right)+{dot {z}}left({frac {partial A_{z}}{partial x}}-{frac {partial A_{x}}{partial z}}right)right]\&=qE_{x}+q[{dot {y}}(nabla times mathbf {A} )_{z}-{dot {z}}(nabla times mathbf {A} )_{y}]\&=qE_{x}+q[mathbf {dot {r}} times (nabla times mathbf {A} )]_{x}\&=qE_{x}+q(mathbf {dot {r}} times mathbf {B} )_{x}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9dcaf925c2a01000291d1859fe864745ce0daa3)














![{displaystyle {frac {mathrm {d} p^{1}}{mathrm {d} tau }}=qleft[U_{0}left({frac {E_{x}}{c}}right)+U_{2}(-B_{z})+U_{3}(B_{y})right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa294150a56ff4b26e8662034d72dad77daacbca)
![{displaystyle {begin{aligned}{frac {mathrm {d} p^{1}}{mathrm {d} tau }}&=qgamma left[cleft({frac {E_{x}}{c}}right)+(-v_{y})(-B_{z})+(-v_{z})(B_{y})right]\&=qgamma left(E_{x}+v_{y}B_{z}-v_{z}B_{y}right)\&=qgamma left[E_{x}+left(mathbf {v} times mathbf {B} right)_{x}right],.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f7d8724e880bc6726e6b8bbdb9d6e7b329aab15)