Сила света как найти высоту

Как определить видимую высоту освещенной области на фасаде?

Дмитрий Сукачев, заместитель директора по развитию ООО «Марбел», приглашенный лектор Факультета ДПО НИУ ВШЭ, приглашенный лектор Факультета садоводства и ландшафтной архитектуры РГАУ-МСХА имени К. А. Тимирязева

пдф вариант

Введение

Нередко заказчики интересуются, какой высоты на фасаде «достигает» луч настенного светильника.

И чтобы ответить на этот вопрос, приходилось моделировать в Dialux. Расчеты занимали минут 20, однако хотелось упростить процесс и выполнять их быстрее. В результате пришел к этой формуле:

где h – видимая высота освещенной области на фасаде, м; r – расстояние от стены до продольной оси светильника, м; k – пороговый контраст яркости; I – сила света в направлении 3–6° КСС светильника, Кд; EФ – фоновая освещенность, лк.

Формула применима, если продольная ось светильники отстоит от стены на расстояние до 30 см, что справедливо для большинства настенных декоративных светильников. И видимая «длина луча» в темное время суток составляет 2 м и более (рис. 1).

Рис. 1. Видимая высота освещенной области на фасаде.

Рис. 2. КСС светильника

Например, для светильника, КСС которого приведена на рисунке 2, при фоновой освещенности 0,4 лк (полнолуние, луна освещает фасад) и расстоянии от продольной оси светильника до фасада r=0,2 м видимая высота освещенной светильником области составит:

Теперь, чтобы оценить видимую высоту освещенной области на фасаде, потребуется «научный калькулятор» на мобильном телефоне и 3–4 минуты. Особенности ночного зрения человека определяют, какой в темное время суток будет видимая высота освещенной области на фасаде. Рассмотрим эти особенности.

Особенности ночного зрения

Вечером в условиях темновой адаптации возможность зрительно обнаружить одноцветный с фоном объект наблюдения или различить его форму определяется пороговым значением яркостного контраста. Элементарное зрительное обнаружение или видимость объекта определяются минимальной (пороговой) разностью яркости ΔLпор двух смежных участков поля зрения наблюдателя. Отношение  ΔL пор к яркости фона называют пороговым контрастом яркости объекта наблюдения с фоном:

К_пор = ΔL_пор/Lф. (1)

K = (Lo – Lф)/Lф = ΔL/Lф, (2)

где Lo, Lф – яркости объекта и фона, ΔL – разность яркостей объекта и фона.

Условия обнаружения объекта, одноцветного с фоном, можно записать следующими неравенствами:

ΔL ≥ ΔL_пор или К ≥ К_пор. (3)

При низкой освещенности контрастная чувствительность резко уменьшается, для различения яркости смежных поверхностей необходимо, чтобы перепад между ними был не менее 55%, то есть яркости поверхностей должны отличаться одна от другой более чем в 1,5 раза [1].

Более точные значения К_пор приведены в диаграмме, опубликованной в учебнике «Архитектурная физика» [2] (рис. 3, 4).

Рис.3 Определение контраста между предметом и фоном для обеспечения его видимости в зависимости от условий природного освещения

Рис. 4. Яркости освещенной области на фасаде Lo и яркость фасада от фонового освещения

Яркость диффузно отражающей (далее по тексту – матовой) поверхности составляет:

где ρ – коэффициент отражения, Е – освещенность.

Для матовых поверхностей коэффициент отражения освещенной и темной областей фасада одинаковые, и яркость освещенной области составит:

где Lo – яркость освещенной области, Еф – фоновая освещенность, Есв – освещенность от светильника, ρ – коэффициент отражения поверхности.

где Еф – фоновая освещенность.

Запишем соотношение (2) с учетом выражений (5) и (6):

Однако гладкий и матовый фасад, имеющий полностью диффузное отражение, встречается довольно редко. Чаще всего мы имеем дело либо с текстурными или даже рельефными поверхностями, либо с глянцевыми отделочными материалами. Для таких материалов соотношение (7) не выполняется.

Виляние Текстуры на яркость Фасада

Текстурные или рельефные отделочные материалы, когда световой поток падает на них под малым углом к поверхности материала (или большим углом по отношению к нормали к поверхности материала), выглядят темнее по сравнению с гладкими материалами даже при одинаковом ρ.

Текстура и светлота неразрывно связаны между собой. Свет, падающий на текстурную поверхность, создает высокие контрасты между освещенными элементами текстуры и элементами в тени, относительные размеры и плотность текстурных элементов увеличивают или уменьшают светлоту пропорционально эффекту затенения [3] (рис. 5).

Рис. 5. Видимая яркость текстурных материалов с одинаковым коэффициентом отражения и разной текстурой при боковом освещении

Этот эффект хорошо виден на рисунке 4. Три образца с разной текстурой покрасили из аэрозольного баллончика серой краской. Влияние текстуры оказалось значительным. Левый, текстурный образец выглядит значительно темнее, правого гладкого.

Назовем этот эффект – эффектом текстурного затемнения.

Эффект текстурного затемнения зависит от угла падения светового потока на материал. Чем меньше угол падения светового потока к поверхности материала, тем сильнее тени и тем более темной будет выглядеть поверхность. Если световой поток направлен на материал под углами, близкими к нормали, теней на текстурных элементах не образуется и поверхность выглядит более светлой.

Свет от фасадного светильника падает на поверхность под малым углом, на текстурных элементах образуются глубокие тени, и поверхность выглядит темнее. Эффект текстурного затемнения учтем с помощью коэффициента текстурного затемнения kтекст.

Коэффициент отражения текстурной поверхности при падении светового потока под малым углом к поверхности запишем так:

где ρ – коэффициент диффузного отражения материала фасада.

Световой поток от фасадного светильника падает на фасад под малым углом к поверхности. Фоновое освещение, как правило, падает на фасад под значительно большими углами, близкими к нормали, и фоновое освещение теней на текстурных элементах почти не образует. Для фонового освещения эффектом текстурного затемнения можно пренебречь.

Для текстурных фасадов выражение (7) запишем следующим образом:

Исследований, определяющих kтекст, найти не удалось. При работе над проектами освещения фасадов, облицованных текстурными отделочными материалами, вместе с партнерами мы проверяли эту формулу и определили, что при значении kтекст = 0,7–0,8 оценка видимой высоты освещенной области на фасаде звучала «где-то примерно так».

Но видимая высота освещенной области на фасаде уменьшается не только на текстурных отделочных материалах. Глянцевые отделочные материалы также сокращают видимую высоту освещенной области

Рис. 6. Виды отражения света от поверхностей

Глянцевые Отделочные Материалы и коэффициент диффузного отражения

На глянцевых отделочных материалах присутствует смешанное (направленно-рассеянное) отражение. Более подробно направленно-рассеянное освещение рассмотрено в [4] (рис. 7).

Рис. 7. Смешанное отражение

При смешанном отражении часть падающего светового потока зеркально отражается и «улетает» в небо или в землю. А оставшийся световой поток отражается диффузно. Именно диффузное отражение светового потока светильника определяет видимую высоту освещенной области на фасаде.

Коэффициент зеркального отражения зависит от угла падения светового потока. Для стекла эта зависимость представлена на рисунке 8.

Рис.8. Зависимость коэффициента зеркального отражения светового потока на границе раздела «воздух-стекло» от угла падения (угол между направлением падающего светового потока и нормалью к плоскости раздела «воздух-стекло

Световой поток от светильника падает на стекло под острым углом (большим углом к нормали), например, если световой поток падает под углом 10° к поверхности, коэффициент зеркального отражения будет 0,4. Для глянцевых отделочных материалов таких графиков, увы, не существует. Но подобная зависимость для глянцевых отделочных материалов и материалов из полированного природного камня также выполняется.

При этом фоновое освещение падает на фасад под углами, близкими к нормали, коэффициент зеркального отражения не превышает 4%, и зеркальным отражением для фонового освещения можно пренебречь.

Таким образом, диффузно отражается только оставшаяся после зеркального отражения часть светового потока. Учтем это уменьшение коэффициентом kглянц.

Запишем выражение (7) с учетом потери части светового потока:

Уменьшения видимой высоты освещенной области на глянцевом фасаде оценивал, как и для текстурных фасадов, обсуждая результаты с партнерами. При значении kглянц = 0,7–0,8 оценка видимой высоты освещенной области на фасаде звучала «где-то примерно так».

Физика отражений на текстурном и глянцевом фасадах разная, но значения коэффициентов, учитывающих влияние отделочных материалов фасадов, одинаковые – 0,7–0,8.

Расчет Освещенности на Фасаде от Светильника

Теперь поговорим о расчете освещенности от светильника на фасаде (рис. 9).

Рис. 9. Определение вертикальной освещенности, создаваемой точечным источником света

Вертикальная освещенность на фасаде рассчитывается по следующей формуле [1]:

Ев = (I/d2) • sinα. (14)

Но она не очень удобна, поскольку в ней присутствует sinα. Чтобы упростить расчеты, лучше заменить его отношением сторон треугольника (рис. 10).

Рис. 10. Определение видимой высоты освещенной области на фасаде

У многих настенных светильников продольная ось отстоит от стены на 20–30 см.

Если высота освещенной области на фасаде равна 2 м и продольная ось светильника отстоит от фасада на 30 см, значение угла α составит arctg (0,3/2) = 8,5°.

Значения sinα и tgα для углов меньше 6°45’ различаются только четвертым знаком. А при значении до 10° есть незначительные различия в третьем знаке. Известно, что для инженерных расчетов достаточно точности до третьего знака, поэтому в формуле (14) для нашего частного случая можно заменить sinα на tgα.

Известно, что tgα = r/h, (15)

где α, r и h указаны (рис. 9).

Тогда формулу (14) можно записать:

Ев = (I/d2) • tgα = (I/d2) • (r/h) = Есв, (16)

где r – расстояние от продольной оси светильника до стены, h – высота видимой на фасаде освещенной области, а Есв – вертикальная освещенность от светильника на фасаде.

Вертикальные освещенности Есв в формулах (11) и (16), или (13) и (16) – это одна и та же величина. Поэтому:

Есв = K • Eф/kтекст (глянц) = (I/d2) • (r/h), (17)

где kтекст (глянц) – коэффициент, учитывающий уменьшение коэффициента диффузного отражения для текстурных или глянцевых фасадов, который, как раньше мы видели, составляет 0,7–0,8.

Преобразуем равенство (17) и получим:

h= (I/d²) • (r • kтекст (глянц))/(K • Eф). (18)

Определим d²:

Оценим вклад r и h для нашего случая, когда высота освещенной области на фасаде значительно больше, чем расстояние от продольной оси светильника до стены. Например, r = 0,3 м и h = 2 м: r2 = 0,09 и h2 = 4. d2 = 4,09,  а d = 2,02. Как видим, r значительно меньше h и для нашего частного случая им можно пренебречь. Тогда (18) можно записать:

где kтекст (глянц) = 0,75.

Это формула справедлива, когда светильник отстоит от стены не более чем на 30 см и отношение рассчитанной высоты освещенной области на фасаде к расстоянию продольной оси светильника от стены превышает 10.

Высоту освещенной области на фасаде на практике лучше оценивать следующим образом:

• рассчитываем видимую высоту освещенной области по формуле (22);
• умножаем результат на 0,8 и округляем в меньшую сторону;
• сообщаем заказчику, что видимая высота освещенной области будет от «…» до «…».

У всех людей зрение немного различается, и каждый увидит «свою» высоту освещенной области. Уменьшение/округление учитывает эти индивидуальные особенности. Формула позволяет оперативно оценить видимую высоту освещенной области на фасаде с достаточной точностью.

Литература:

1. Щепетков Н. и. Световой дизайн города. М.: архитектура-С, 2006.
2. Архитектурная физика. Под ред. Оболенского Н. В. М.: архитектура-С,  2007.
3. Michel L. Light: The Shape of Space. Designing with space and light. Jon Willey & Sons, New York, 1996.
4. Cuttle C. Lighting by design. Architectural press, London, 2003.

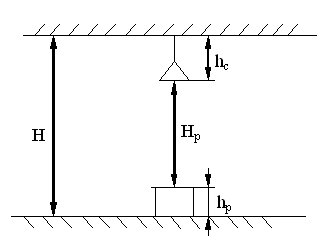
Высота
подвеса светильников над освещаемой
поверхностью (НР) – расчетная высота
подвеса светильников (Рисунок 3.1) в
значительной степени определяет
характеристику и технико-экономические
показатели проектируемой осветительной
установки. От ее величины зависит
установленная мощность источников
света, размещение светильников на плане;
высота подвеса определяет качественные
показатели освещения, выбор светильников
по светораспределению, экономическим
соображением [1].

Рисунок
3.1 – Размещение светильника по высоте
помещения:

Н
– высота помещения; Н_р
– высота подвеса светильника над

освещаемой
поверхностью; h_с
– высота свеса светильника;

h_р
– высота рабочей поверхности

Высота
подвеса определяется по выражению:

.
(3.1)

Определим
высоту подвеса светильников в механическом
цеху, предварительно приняв hc
= 0,3 м, а значение hp
= 0,8 м:

(м).

Расчет
высоты подвеса для остальных помещений
аналогичен. Результат расчета приведен
в таблице 3.2.

Таблица 3.2 – Расчетная
высота подвеса светильников

№	Наименование помещения	Тип светильника	H, м	hc, м	hp, м	Hp, м
1	Эксперементальный цех	РСП-08	7,5	0,3	0,8	6,4
2	КТП	НСП-17	3,4	0	0,8	2,6
3	Кабинет мастеров	ЛПО-06	1,9	0	0,8	1,1
4	Тамбур	НСП-17	2,7	0	0,8	1,9
5	Элекромастерская	ЛПО-06	2,1	0	0,8	1,3
6	Мехмастерская	ЛПО-06	2,1	0	0,8	1,3

3.3. Размещение светильников рабочего освещения

При
общем равномерном освещении, а по
возможности также и при локализованном
освещении, светильники рекомендуется
распола­гать по вершинам квадратных,
прямоугольных или ромбиче­ских полей.

Светильники
с люминесцентными лампами следует
преимуще­ственно размещать рядами,
параллельными стенам с окнами. Ряды
выполняются непрерывными или с разрывами.

В
производственных помещениях с типовыми
строительными модулями (в основном это
высокие помещения), светильники
размещаются обычно на фермах в виде
продольных рядов. Такое расположение
светильников не всегда дает воз­можность
достичь равномерности освещения, что,
в свою очередь, ведет к перерасходу
электроэнергии.

В
этих случаях рекомендуется применение
так называемых неравномерных схем
размещения светильников, которые
умень­шают неравномерность освещенности,
а, следовательно, и расход электроэнергии
[5].

4. Светотехнический расчёт системы общего равномерного освещения и определение единичной установленной мощности источников света в помещениях

Основной
светотехнического расчета освещения
являются три метода расчета: метод
коэффициента использования светового
потока, метод удельной мощности и
точечный метод.

Метод
коэффициента использования
светового потока применяется для расчета
общего равномерного освещения
горизонтальных поверхностей, в основном
для расчета светового потока источника
(источников) света. Этот метод позволяет
рассчитывать также среднюю освещенность
горизонтальной поверхности с учетом
всех падающих на нее потоков, как прямых,
так и отраженных. Он не применим при
неравномерном размещении светильников,
расчете освещенности в характерных
точках как негоризонтальных, так и
горизонтальных поверхностей.

Применим
данный метод для расчёта следующих
помещений: сварочный

цех,
кабинет
мастеров, электромастерская, мехмастеркая.

Метод
удельной мощности
на единицу освещаемой площади является
упрощенной формой метода коэффициента
использования светового потока.
Применяется этот метод для ориентировочных
расчетов общего равномерного освещения.

Применим
данный метод для расчёта следующих
помещений: КТП,тамбур.

Точечный
метод расчета
освещения позволяет определить
освещенность в любой точке поверхности
освещаемого помещения при любом
равномерном или неравномерном размещении
светильников. Он часто используется
как поверочный метод для расчета
освещенности в характерных точках
поверхности.[1].

Проведем
расчет механического цеха методом
коэффициента использования светового
потока.

Определяем
индекс помещения по формуле:

,

(4.1)

где
А – длина помещения, м;

В
– ширина помещения, м;

Н_р
– расчетная высота подвеса, м;

Примем
помещение, которому соответствуют
коэффициенты отражения:

ρ_п
= 70%, ρ_с
= 50%, ρ_р
= 10%.

По
Е_min,
i,
ρ_п,
ρ_с,
ρ_р
в соответствии с [1] определяем коэффициент
использования светового потока η, %:

η
= 78% или η = 0,78.

Определяем
световой поток, необходимый для создания
нормируемого уровня освещенности, по
формуле:

,
(4.2)

где
E­­­­­_min
– нормируемая
освещённость, лк;

k­_з
– коэффициент запаса;

Z
– коэффициент неравномерности освещения,
принимается 1,15 – для ЛН и ДРЛ, 1,1 – для
ЛЛ [1];

Sр
– общая площадь
помещения,
;

η
– коэффициент
использования светового потока.

(лм).

Определяем
количество ламп в помещении по выражению:

,
(4.3)

где
Ф
– общий световой поток, лм,

Фл
–
световой
поток лампы, лм; в данном случае лампы
ДРЛ мощностью 400 Вт.

(шт.).

Проведем
расчет комнаты отдыха методом
удельной мощности на единицу освещаемой
площади.

По
[1] принимаем величину Р_уд,
наиболее близко отвечающую заданным
условиям:

Р_уд
= 16,2
.

Определяем
установленную мощность источников
света в помещении по выражению:

Р
= Р_удS,
(4.4)

где
S
– площадь освещаемого помещения,
;

Р
= Р_уд

S
= 16,254
= 874,8 (Вт).

Определяем
количество светильников по формуле:

(4.5)

где
n
– количество ламп в светильнике, шт.;

р
– мощность одной лампы, Вт.

(шт.).

Расчет
остальных помещений аналогичен.
Результаты
расчетов приведены в таблице 4.1

Таблица 4.1 –
Результаты светотехнического расчета
освещения помещений

Номер	Наименование помещения	Индекс помещения i	Коэффициент помещения	Коэфф.испол. свет.потока η	Руд Вт/м	Треб. светотвого потока,Ф, лм	Фл,лм	Кол-во ламп и тип св.
gп	gс	gр
1	Эксперементальный цех	3,2	0,7	0,5	0,1	0,78	–	1096615.385	24000	45 РСП 08
2	КТП	–	–	–	–	–	16,2	874.8	2950	4 НСП 17
3	Кабинет мастеров	1,17	0,7	0,5	0,3	0,58	–	40965.51	4800	8 ЛПО 0,6
4	Тамбур	–	–	–	–	–	29,2	1051	2950	4 НСП 17
5	Элекромастерская	1,333	0,7	0,5	0,3	0,56	–	27578.57	4800	8 ЛПО 0,6
6	Мехмастерская	1,113	0,7	0,5	0,3	0,6	–	18385.71	4800	6 ЛПО 0,6

Соседние файлы в папке Вариант №14

• #
• #
• #

  15.04.201545.01 Кб5622_T-10.1_30s.bak

• #

  15.04.201564.97 Кб6322_T-10.1_30s.dwg

• #

  15.04.2015613 б55plot.log

• #
• #

  15.04.201586.62 Кб57СТАРЫЙl.bak

• #

  15.04.201593.78 Кб64СТАРЫЙl.dwg

Рассмотрим задачи на определение высоты звезд на небесной сфере. Небесной сферой мы называем представление о небе как о пустом глобусе с нашей планетой в центре и небесными объектами на его внутренней поверхности. Оно пришло к нам из древности и остается удобным. Когда мы смотрим на звезды, можно вообразить, что мы находимся внутри такого глобуса, внутри небесной сферы.

Так как земля вращается, то небесная сфера перемещается относительно поверхности земли: нам кажется, что звезды двигаются вокруг нас. При этом можно заметить, что некоторые из них восходят и заходят, то есть мы их то видим, то нет, а некоторые мы все время видим, только в разных частях небосклона. Есть и такие, о существовании которых мы знаем по книгам и картинкам  созвездий, но никогда не видели: просто они находятся «под» земным шаром, а мы, как наблюдатели, «сверху», и шар планеты заслоняет от нас такие звезды и созвездия.

Зенитом называется точка, расположенная прямо над головой наблюдателя. Математическим горизонтом называется большой круг небесной сферы, все точки которого отстоят от зенита на 90 градусов (вершиной угла будет сам наблюдатель).

Как на земле можно найти любую точку по ее координатам (зная широту и долготу места), так и на небесную сферу нанесли воображаемую сетку. Небесный экватор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и совпадает с плоскостью земного экватора. Небесный экватор делит небесную сферу на два полушария: северное полушарие, с вершиной в северном полюсе мира, и южное полушарие, с вершиной в южном полюсе мира.  Полюс мира — точка на небесной сфере, вокруг которой происходит видимое суточное движение звёзд из-за вращения Земли вокруг своей оси. Направление на северный полюс мира совпадает с направлением на географический север, а на Южный полюс мира — с направлением на географический юг. Северный полюс мира находится в созвездии Малой Медведицы и почти точно совпадает с  Полярной звездой, южный — в созвездии Октант. Полюсы мира соединены на небесной сфере линиями (окружностями), называемыми небесными меридианами подобно воображаемым линиям меридианов на земле. Один из этих меридианов проходит через зенит. Горизонтальные воображаемые линии – окружности, параллельные экватору, называются параллелями так же, как и параллели на земле.

На земле широту отсчитывают от экватора. Экватор является нулевой широтой и точкой отсчета. На небе

сной сфере «широту» отсчитывают от небесного экватора, и называют склонением. На рисунке показана звезда, склонение которой равно +30 градусам.

«Долготу» на небесной сфере отсчитывают от точки весеннего равноденствия и называют прямым восхождением. У нашей звезды прямое восхождение равно .

Еще раз рассмотрим рисунок

На нем хорошо видны «траектории» звезд. Звезды, имеющие на этом рисунке склонения от до никогда не заходят, а со склонениями от до – наоборот, никогда не восходят.

Земной шар вращается вокруг солнца. Плоскость, в которой движется планета в своем годовом обходе вокруг светила, называется плоскостью эклиптики. На небесной сфере это плоскость, в которой движется солнце. Но планета вращается и вокруг своей оси, и эта ось наклонена к плоскости эклиптики под углом в 23 градуса. Именно по этой причине солнечные лучи падают на Землю под разными углами. Точка весеннего равноденствия – положение солнца, когда оно пересекает небесный экватор, переходя из южной половины небесной сферы в северную.

Теперь поговорим о том, что такое высота светила.

Высота светила — угол между направлением на центр светила и плоскостью истинного горизонта. Отсчитывается в обе стороны от горизонта от 0 до со знаком (+), если светило над горизонтом, и (-), если оно под горизонтом.

Кульминация— прохождение центра светила через небесный меридиан в процессе его суточного движения. Иначе — прохождение центром светила точки пересечения суточной параллели светила и небесного меридиана.

В течение суток все светила дважды пересекают небесный меридиан. Различают верхнюю и нижнюю кульминации светила. В верхней кульминации высота светила наибольшая, а в нижней — наименьшая.  Для незаходящих светил обе кульминации происходят над горизонтом. Для восходящих и заходящих светил верхняя кульминация происходит над горизонтом, а нижняя под горизонтом. У невосходящих светил обе кульминации происходят под горизонтом и они недоступны наблюдениям.

На рисунке желтым показаны звезды в верхней кульминации, а красным – в нижней.

В каждом месте земной поверхности высота полюса мира всегда равна географической широте этого места, т. е. . Угол между полуденной линией и плоскостью небесного экватора равен .

Теперь нарисуем расположение звезды в случае и в случае . Из рисунка видно, как определить высоту звезды в обоих случаях для верхней кульминации.

Для нижней кульминации светила

И еще один рисунок, поясняющий, что такое зенитное расстояние.

Теперь попробуем решать задачи. Необходимо просто применять элементарные геометрические знания и помнить: высота не может быть больше 90 градусов по модулю, но может быть отрицательной.

Задача 1.

Определите высоту звезды Капеллы ( Возничего) в верхней кульминации на северном полярном круге (). Склонение Капеллы .

В ответе градусы и минуты запишите слитно без знаков, например, вместо укажите 4558.

В этой задаче , поэтому

Ответ: , в бланк запишем 6925.

Задача 2.

Определите высоту звезды Капеллы ( Возничего)  в нижней кульминации на северном полярном круге (). Склонение Капеллы .

В ответе градусы и минуты запишите слитно без знаков, например, вместо укажите 4558.

Для нижней кульминации считаем по формуле:

Ответ: , в бланк запишем 2231.

Задача 3.

На какой минимальной географической широте звезда Капелла ( Возничего)  не заходит за горизонт? Склонение Капеллы .

В ответе градусы и минуты запишите слитно без знаков, например, вместо укажите 4558.

Рассмотрим рисунок для нижней кульминации. Если высота светила будет положительна, тогда звезда не зайдет. Следовательно, необходимо, чтобы

Ответ: звезда не заходит севернее широты . В бланке ответ 4402.

Задача 4.

Определите полуденную высоту Солнца в Петрозаводске () в день летнего солнцестояния. В ответе градусы и минуты запишите слитно без знаков, например, вместо укажите 6147.

Так как склонение Солнца в день летнего солнцестояния равно (что меньше широты Петрозаводска), то

Ответ: , в бланк запишем 5140.

Задача 5.

Определите полуденную высоту Солнца в Петрозаводске ()  в день зимнего солнцестояния.

В ответе градусы и минуты запишите слитно без знаков, например, вместо укажите 6147.

Так как склонение Солнца в день зимнего солнцестояния равно (что меньше широты Петрозаводска), то

Ответ: , в бланк запишем 446.

Задача 6.

В некоторой местности в день летнего солнцестояния в полдень Солнце находится на юге на высоте . Определите полуденную высоту Солнца в этой местности в день зимнего солнцестояния.

В ответе градусы и минуты запишите слитно без знаков, например, вместо укажите 7250.

В день летнего солнцестояния склонение Солнца равно , а в день зимнего сонцестояния – . Солнце на Юге, следовательно, .

Сначала , или

В день зимнего солнцестояния также , поэтому

Ответ: , в бланке запишем 2556.

Задача 7.

Сириус ( Б. Пса) был в верхней кульминации на высоте . Чему равна широта места наблюдения?

Склонение Сириуса . Тогда

Ответ: .