Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
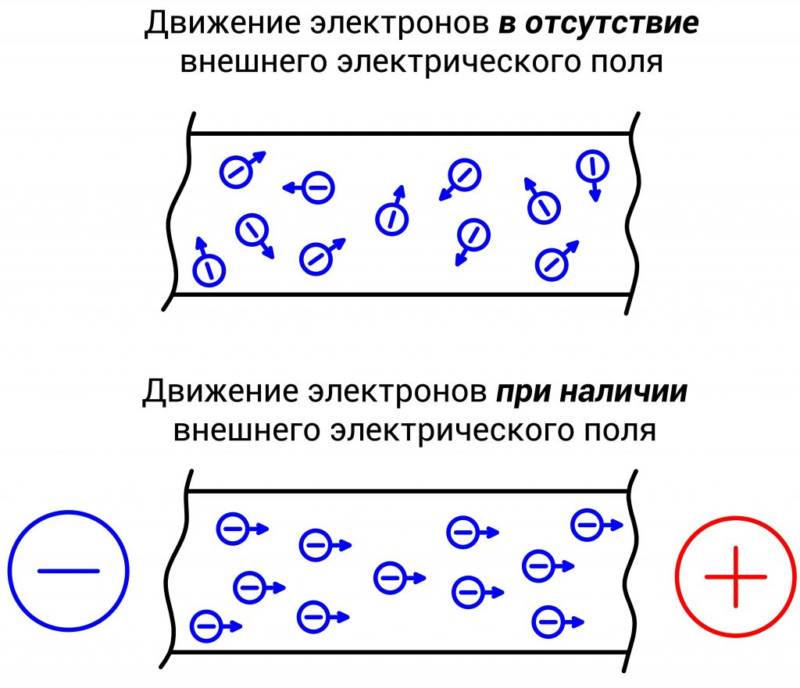
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.

Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I2R, откуда
![]()
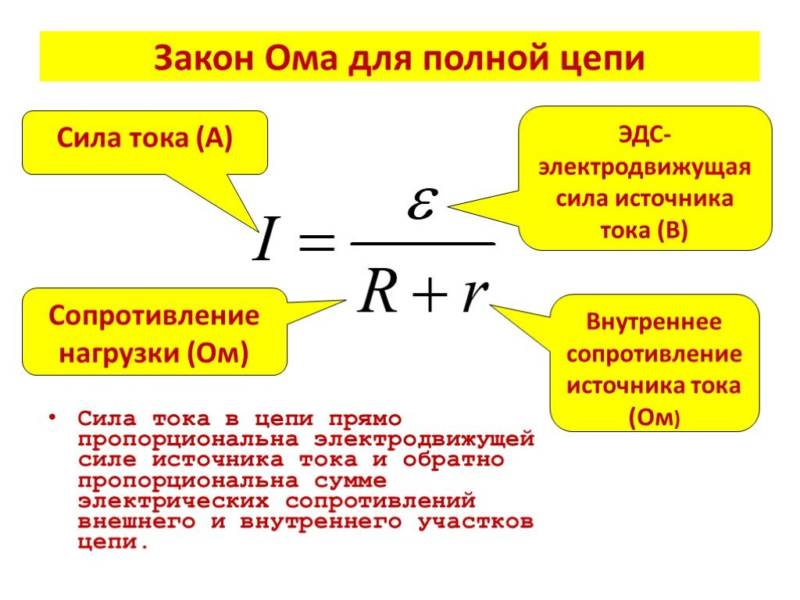
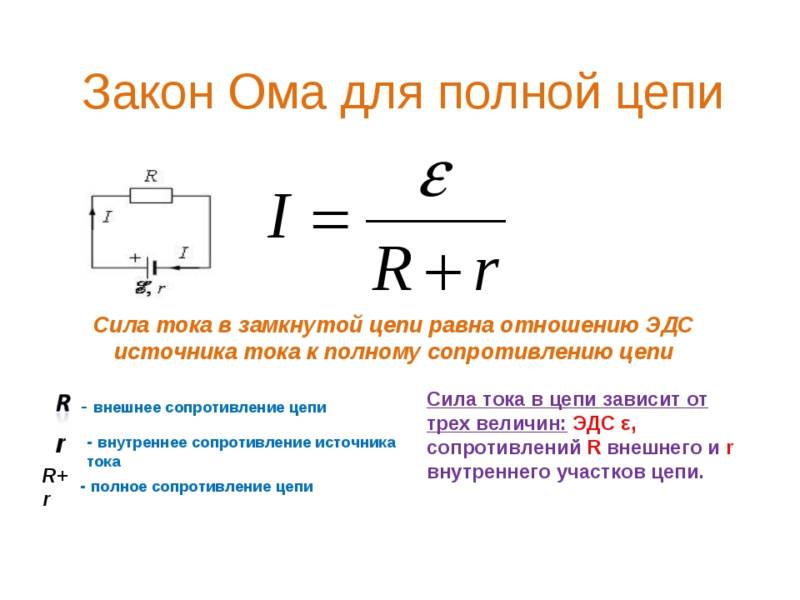
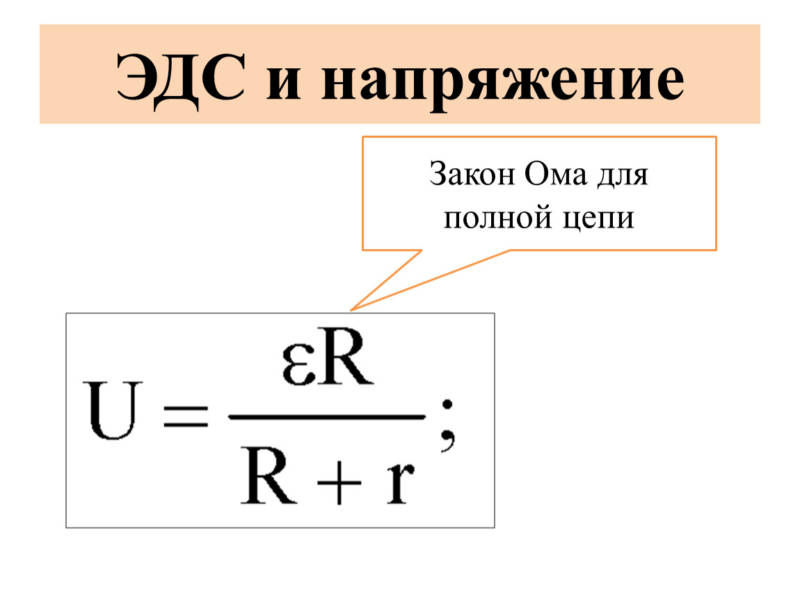
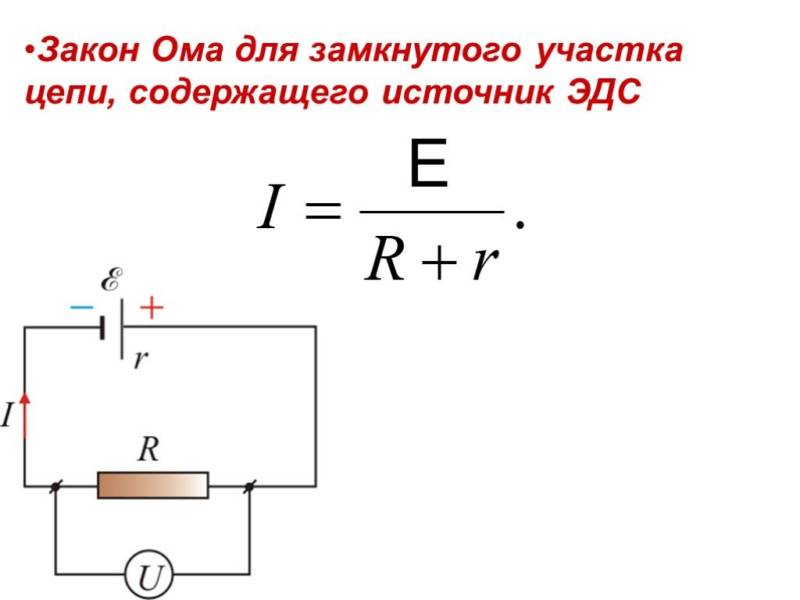
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
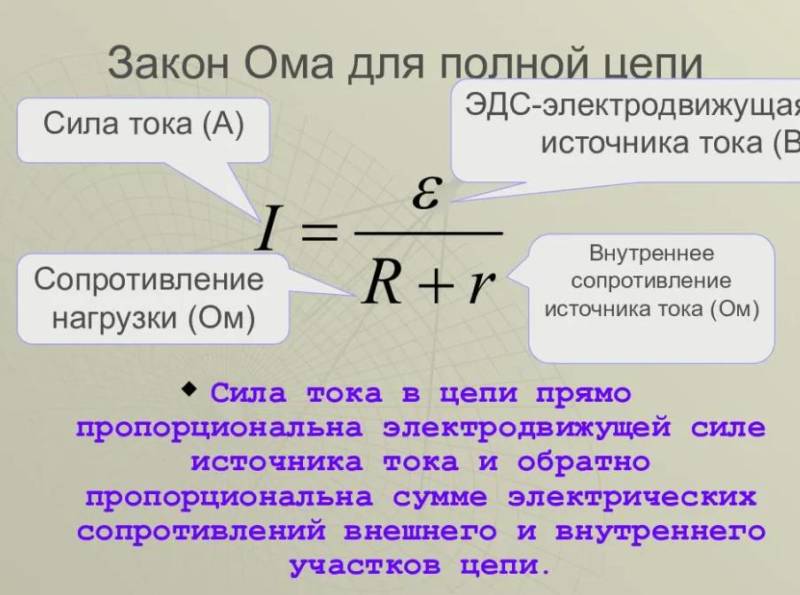
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.

Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:

Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
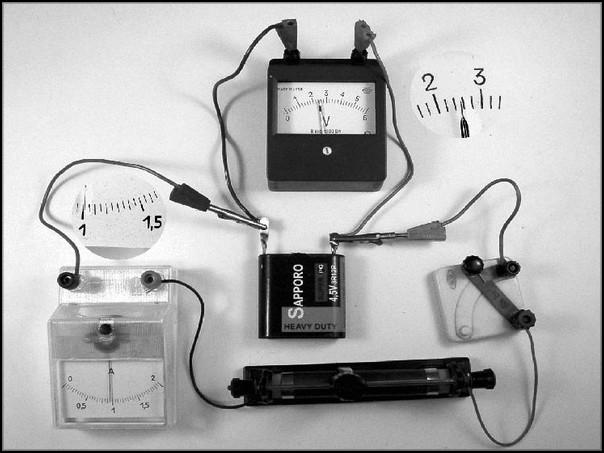
Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.

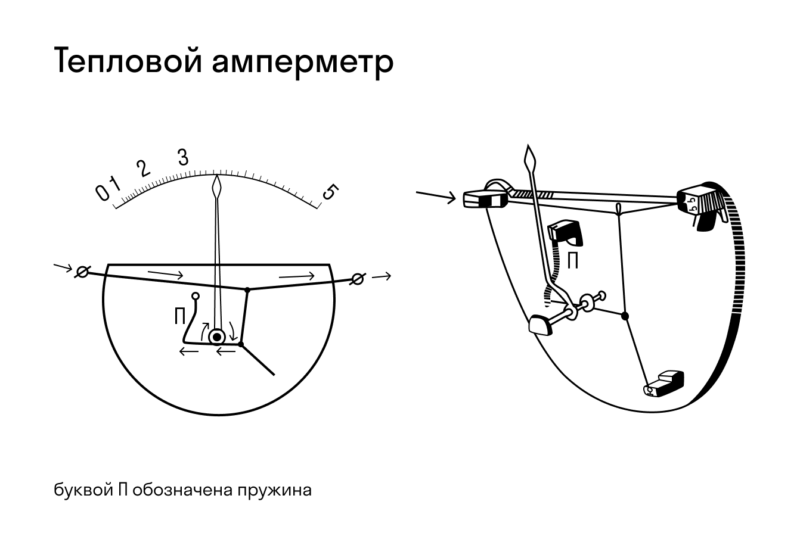
Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.

Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.
При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.
Мультиметром
Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.
Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.
Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.
Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.
Задача 1.
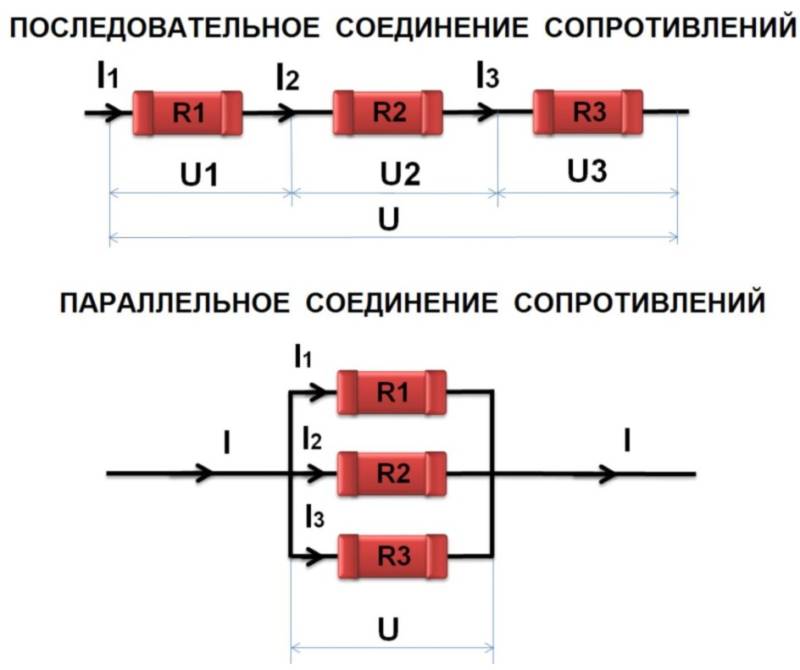
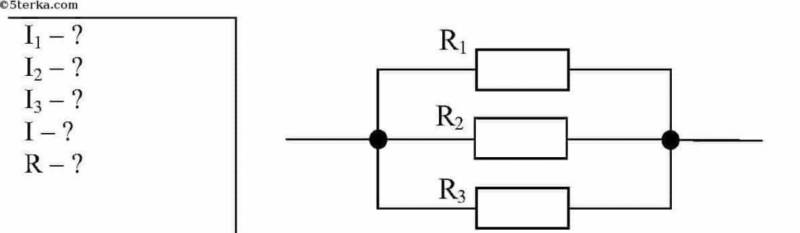
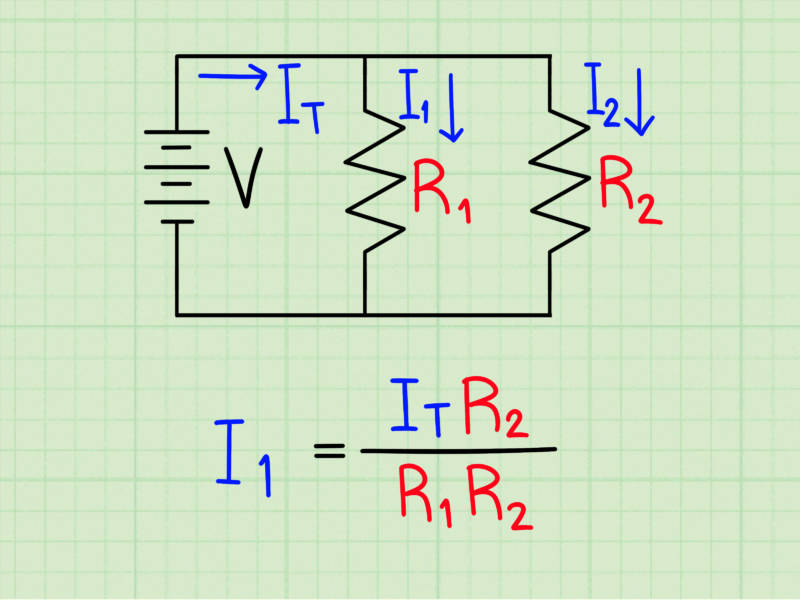
На участке цепи имеются три параллельно включенных резистора (см. рис. 5). Значения сопротивлений резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и на всём участке, если на нем поддерживается постоянное напряжение 100 В.

Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
- I1 = U/R1 =100/5 = 20 А;
- I2 = U/R2 =100/25 ≈ 4 А;
- I3 = U/R3 =100/50 = 2 А.
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:
![]()
Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
Ответ:
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Задача 2.
Мощность электрочайника 2 кВт. Чайник работает от городской сети под напряжением 220 В. Сколько электричества потребляет этот электроприбор?
Решение:
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Задача 3.
Вычислить силу тока в цепи, если известно, что сопротивление составляет 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление составляет 1 Ом.
Решение.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
I = 6 В / (5 Ом + 1 Ом) = 1 А.
Ответ: сила тока 1 А.
Задача 4.
Сколько энергии потребляет электроплита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?
Решение:
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U2/R)*t или
A = ((220 В)2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»

где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление
R = ρ · l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм2]
ρ — удельное сопротивление [Ом · мм2/м]
Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Таблица удельных сопротивлений различных материалов
|
Материал |
Удельное сопротивление ρ, Ом · мм2/м |
|
Алюминий |
0,028 |
|
Бронза |
0,095–0,1 |
|
Висмут |
1,2 |
|
Вольфрам |
0,05 |
|
Железо |
0,1 |
|
Золото |
0,023 |
|
Иридий |
0,0474 |
|
Константан (сплав NiCu + Mn) |
0,5 |
|
Латунь |
0,025–0,108 |
|
Магний |
0,045 |
|
Манганин (сплав меди марганца и никеля — приборный) |
0,43–0,51 |
|
Медь |
0,0175 |
|
Молибден |
0,059 |
|
Нейзильбер (сплав меди, цинка и никеля) |
0,2 |
|
Натрий |
0,047 |
|
Никелин (сплав меди и никеля) |
0,42 |
|
Никель |
0,087 |
|
Нихром (сплав никеля, хрома, железа и марганца) |
1,05–1,4 |
|
Олово |
0,12 |
|
Платина |
0,107 |
|
Ртуть |
0,94 |
|
Свинец |
0,22 |
|
Серебро |
0,015 |
|
Сталь |
0,103–0,137 |
|
Титан |
0,6 |
|
Хромаль |
1,3–1,5 |
|
Цинк |
0,054 |
|
Чугун |
0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:

В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:

Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
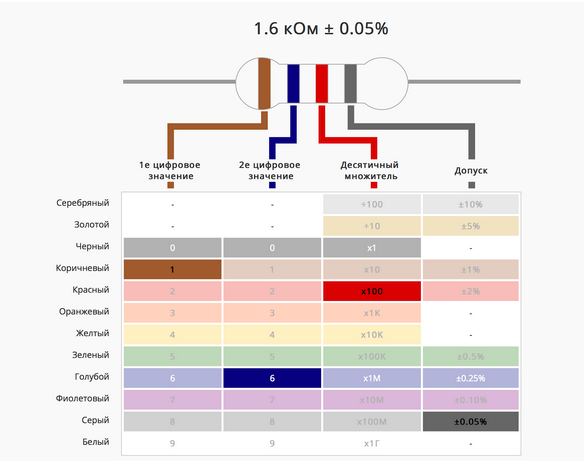
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
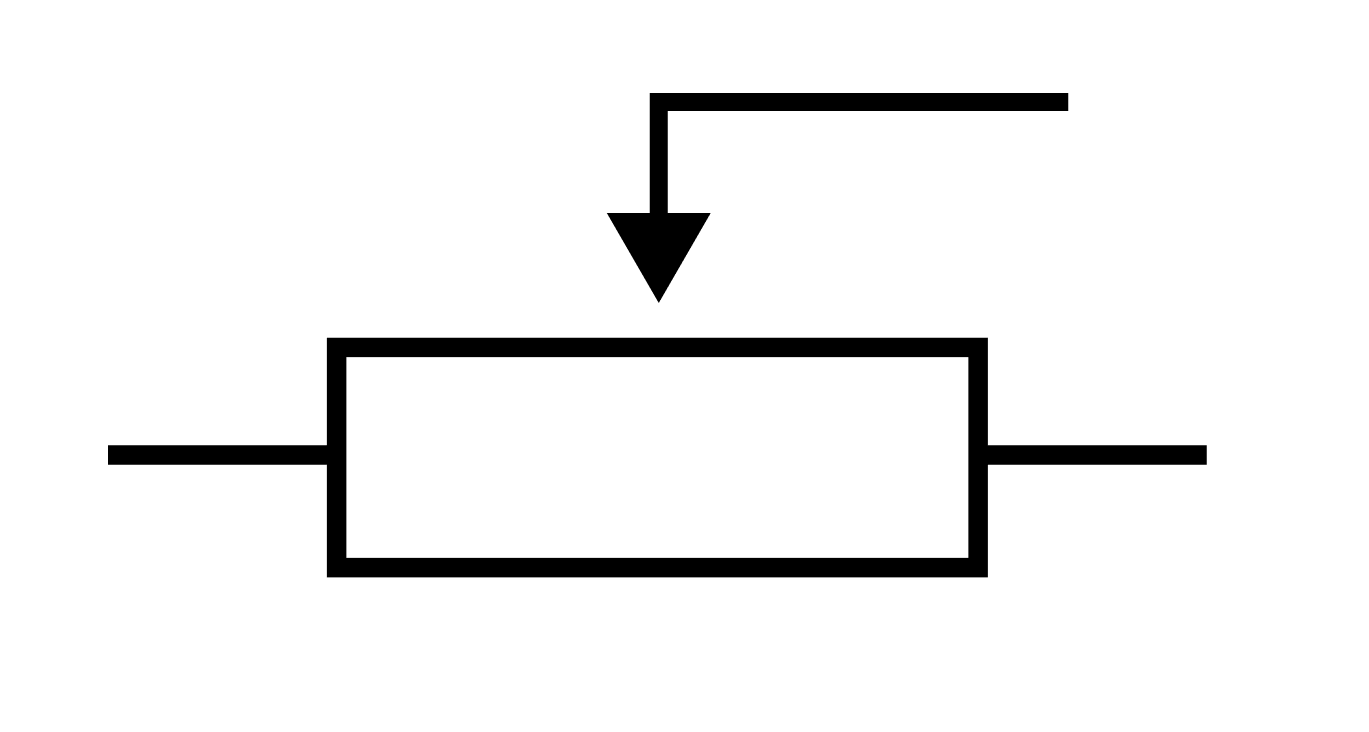
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление
R = ρ · l/S
R — сопротивление [Ом]
l — длина проводника [м]
S — площадь поперечного сечения [мм2]
ρ — удельное сопротивление [Ом · мм2/м]
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
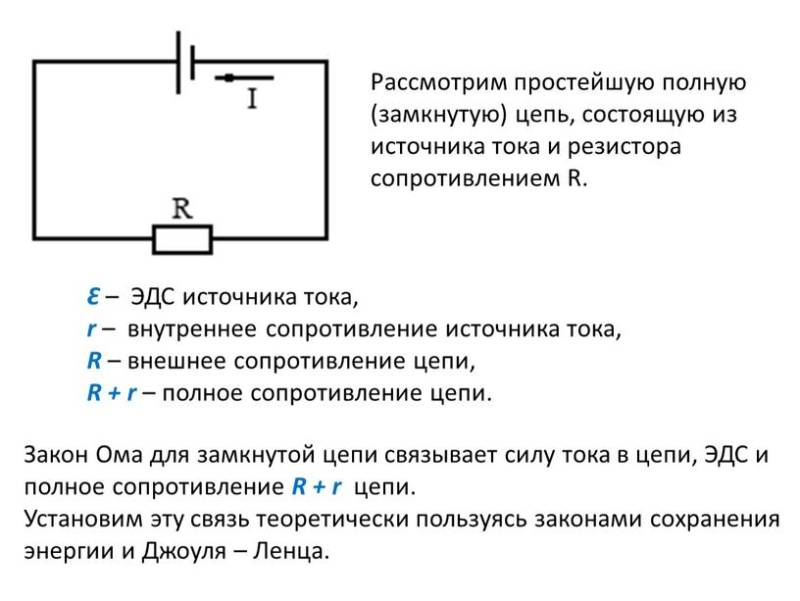
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи
I — сила тока [A]
ε — ЭДС [В]
R — сопротивление нагрузки [Ом]
r — внутреннее сопротивление источника [Ом]
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
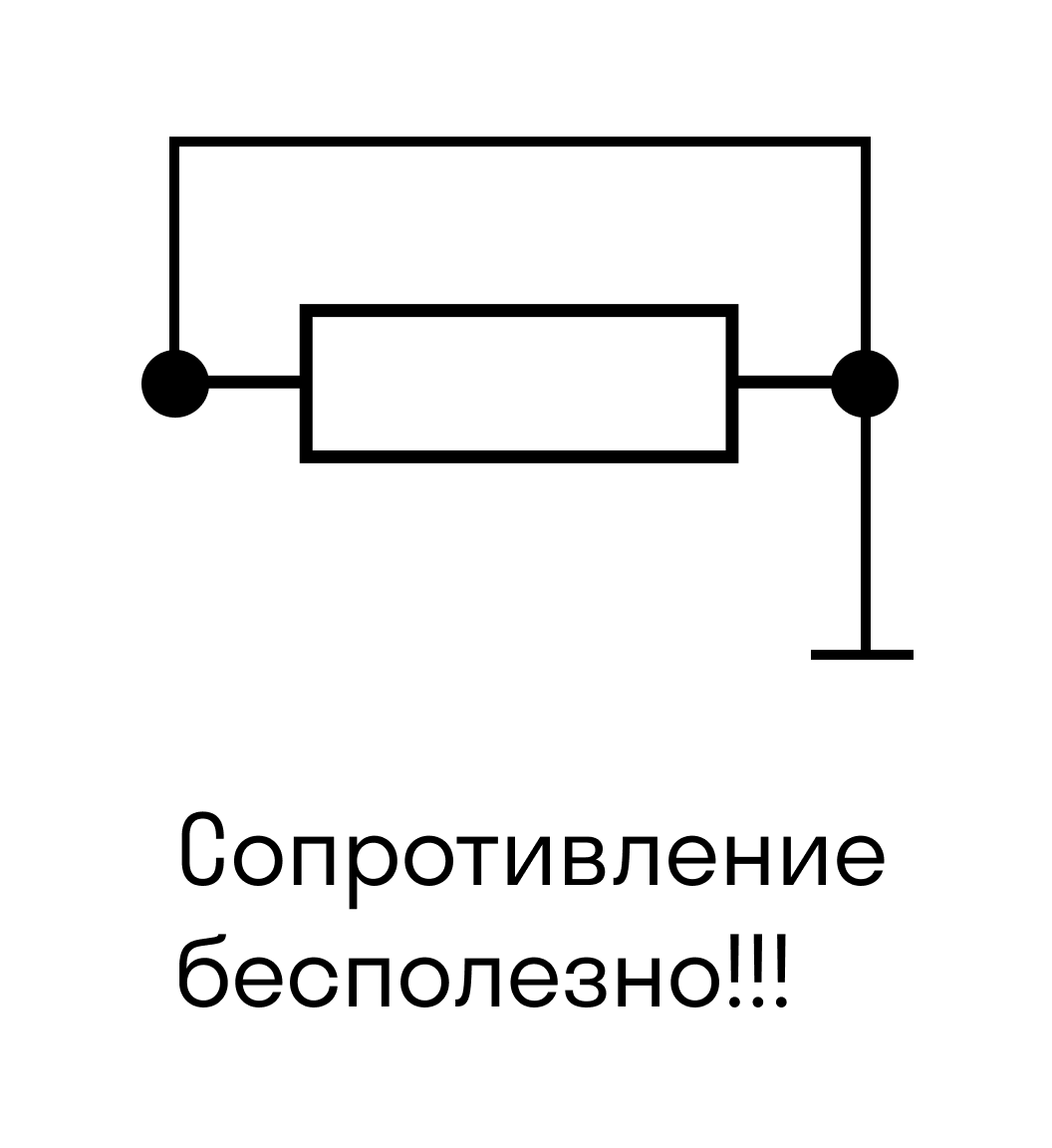
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
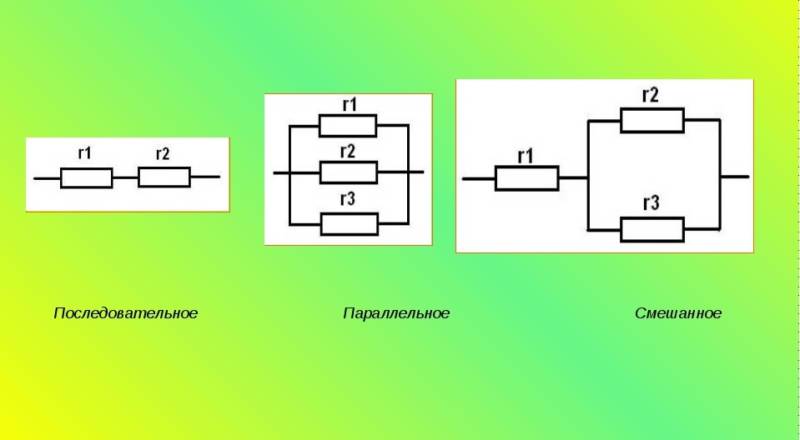
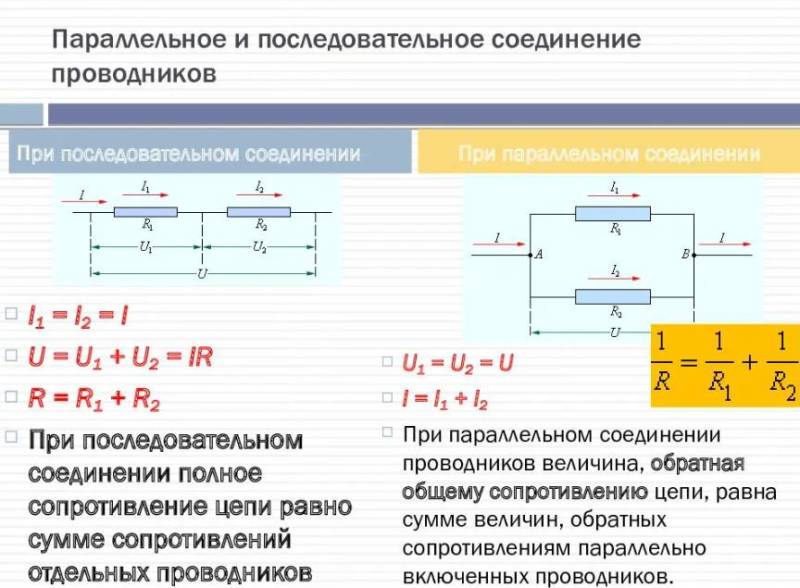
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?
Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.
Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
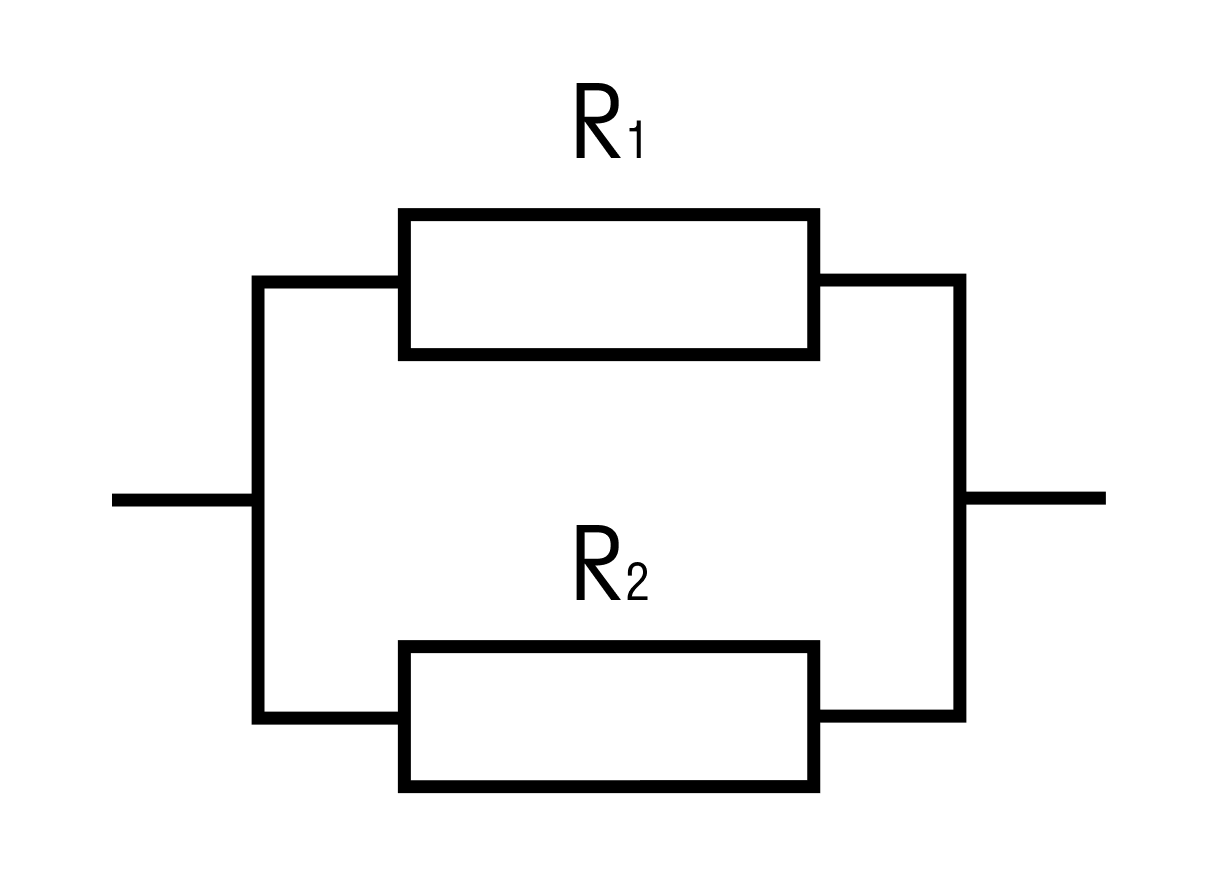
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Ответ: общее сопротивление цепи равно
Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
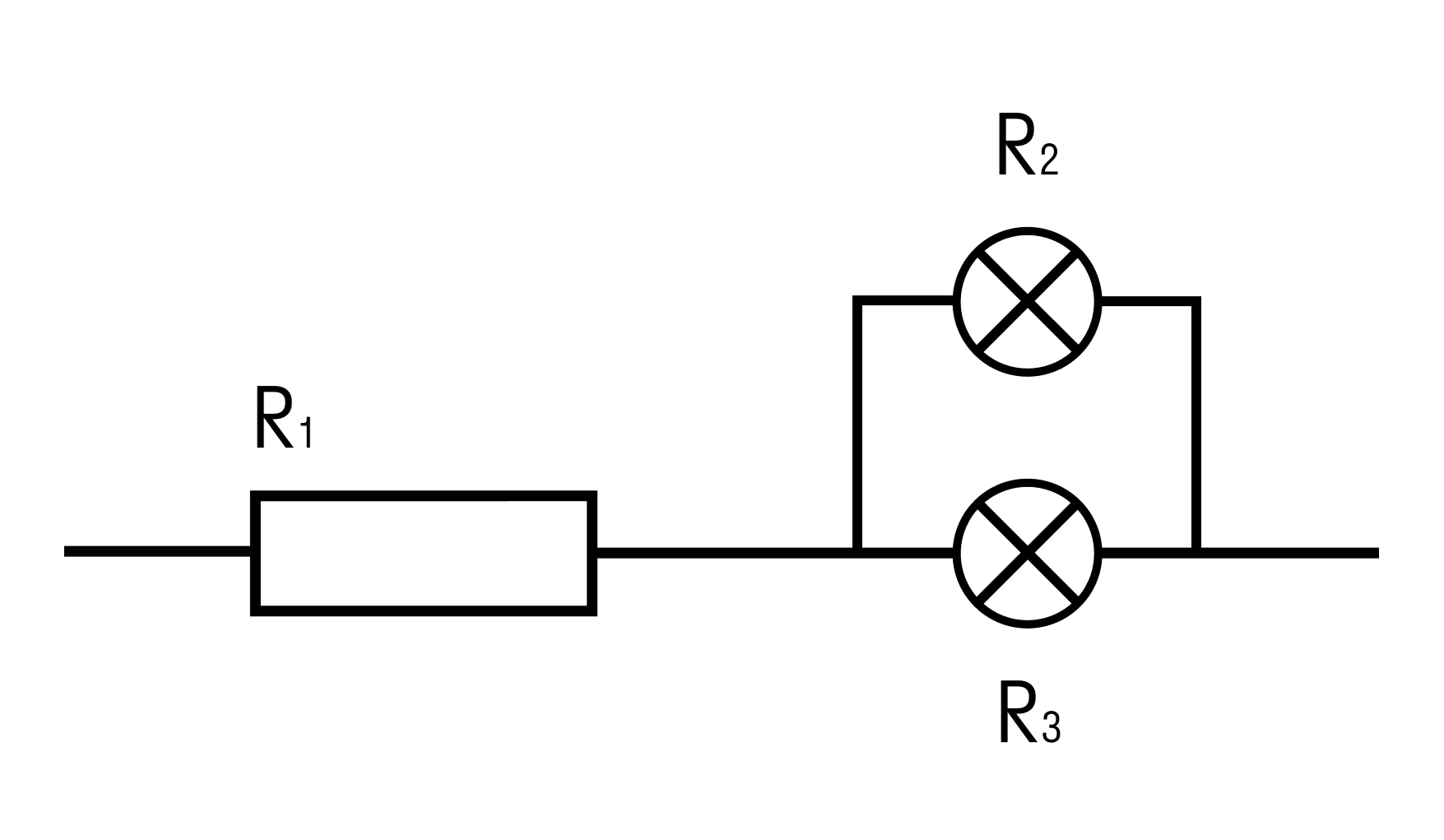
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соединены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
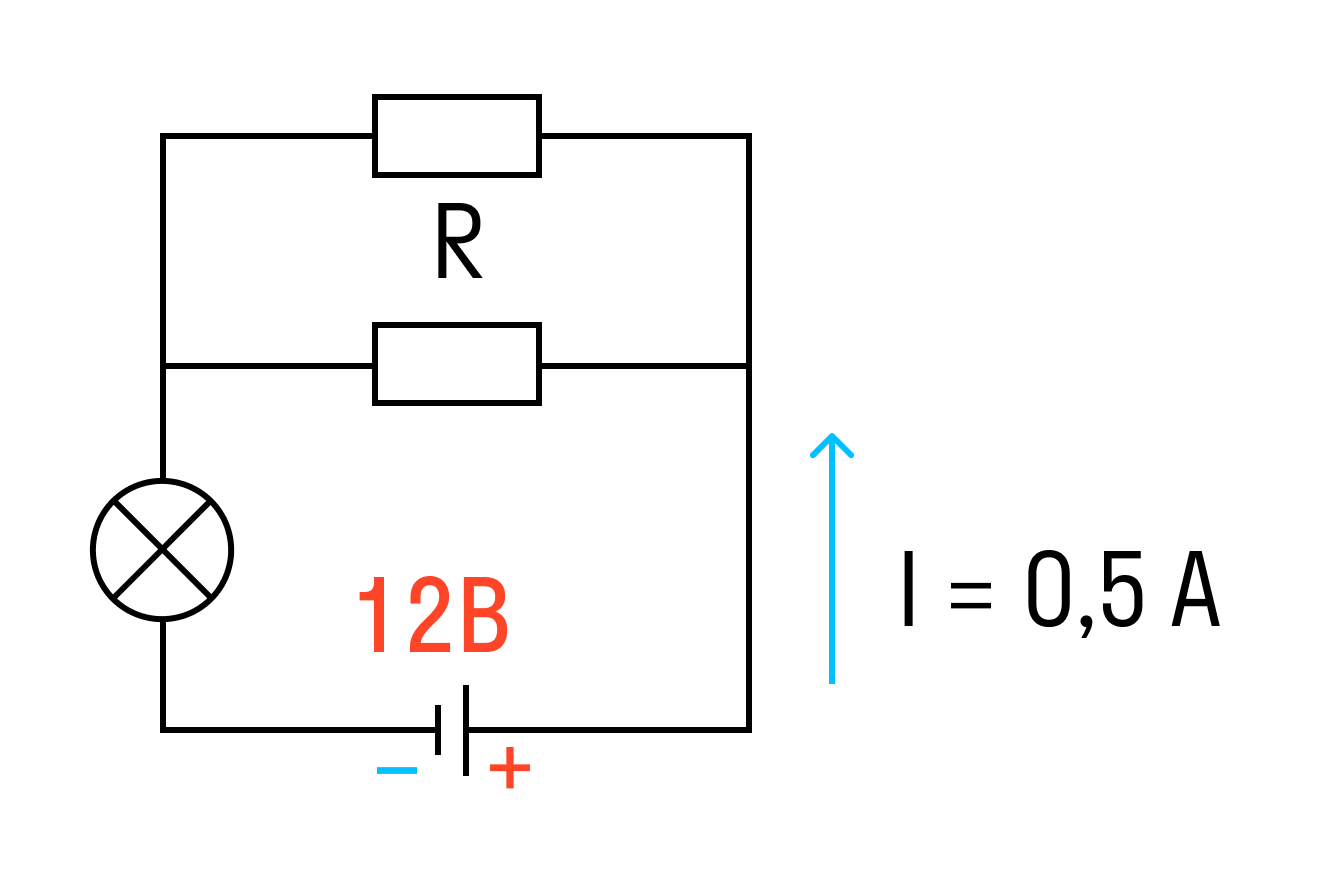
Решение:
Найдем сначала сопротивление лампы.
Rлампы = R/2 = 10/2 = 5 Ом
Теперь найдем общее сопротивление двух параллельно соединенных резисторов.
Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
R + r = ε/I
r = ε/I − R
Подставим значения:
r = 12/0,5 − 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Как найти силу тока — формула в физике через мощность и напряжение, при смешанном соединении, в резисторе, проводнике
Чтобы правильно построить электрические цепочки в физике необходим расчёт параметров электроэнергии. Поскольку цель использования электрического тока в электротехнической технике – выполнение током работы, то появляется вопрос о поиске значения силы тока.
Однако, помимо этого следует понимать различие между разными видами электрической мощности, а также знать несколько способов для их вычисления.

Содержание
Определения
Сила тока – физическая величина, являющаяся одной из главных характеристик электрического тока. Она определяется таким понятием как: направленное движение электрических частиц. Другими словами, сила тока равна заряду, который за одну единицу времени прошёл через сечение проводника. Обозначается сила тока: [ I ] и исчисляется в Амперах (А).

Электрическая мощность — физическая величина, которая показывает с какой скоростью преобразуется или передаётся энергия электричества. Данная величина – характеристика производительности прибора. Обозначается: [ P ] и измеряется в Ватт (Вт).

Интересно! Впервые «Ватт» стали использоваться только в 1882 году. Ранее данный термин заменялся «лошадиными силами» (которые, в некоторых сферах, таких как автомобилестроение, используются и сейчас).
Формулы
Для нахождения силы тока
Сила тока рассчитывается по следующим формулам:
I = q/t
- q – заряд, который проходит через сечение проводника,
- t – время в секундах.

Закон Ома:
I = P/U
- P – электрическая мощность,
- U – электрическое напряжение.
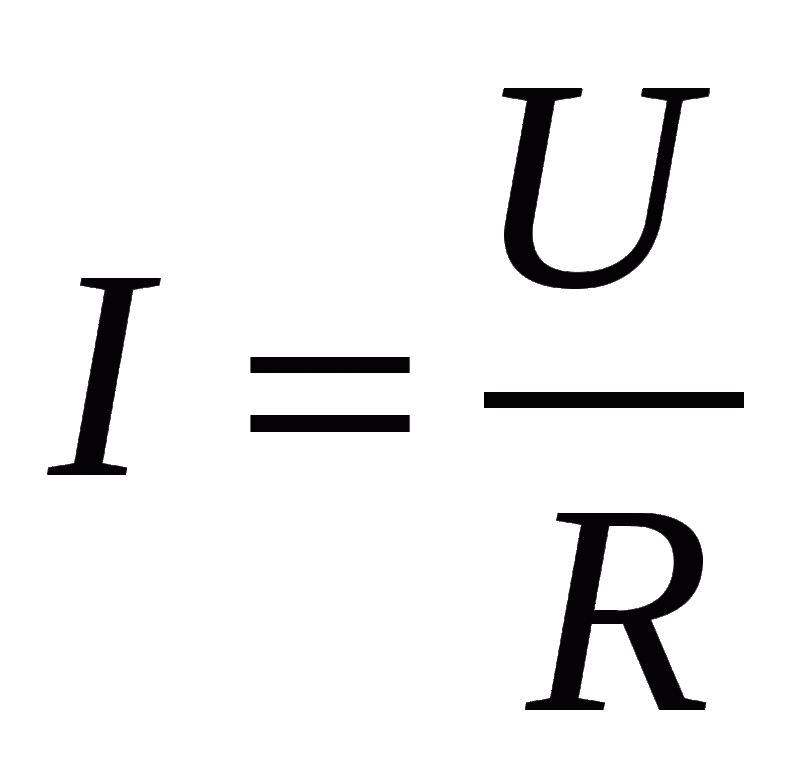
I = U/R
- U – электрическое напряжение,
- R – электрическое сопротивление.
Следствие закона Джоуля-Ленца:
I = корень из Q/Rt
- R – электрическое сопротивление,
- Q – количество теплоты,
- t – время.

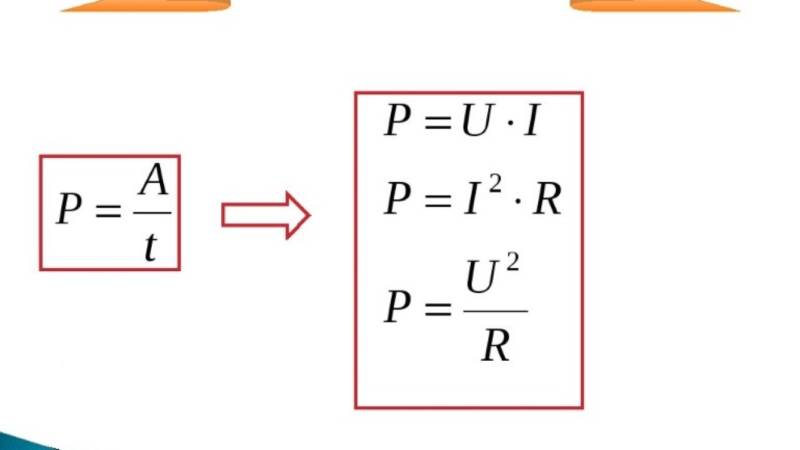
Для мощности электрического тока
P = A/t
- A – работа, которую выполняет электроприбор,
- t – время.

P = UxI
- U – электрическое напряжение,
- I – сила тока.

P = U2/R
- U – электрическое напряжение,
- R – электрическое сопротивление.

Нахождение силы тока при помощи приборов
Помимо формул, в некоторых случаях, гораздо удобнее использовать вычислительные приборы. Самое главное: правильно их использовать. При измерении следует соблюдать определенные правила и помнить о технике безопасности.
Амперметр
Амперметр – самый распространённый прибор для применения его в электрической цепи.

Единственным недостатком данного прибора является его собственное маленькое сопротивление, из-за чего он может сгореть или просто выключиться, если ему придется измерять силу тока, на которую он не рассчитан. Именно поэтому считается, что универсальность амперметра сильно ограничена.

Если появляется необходимость измерить постоянный ток, то для измерения прибором придется разорвать цепь, а также не забыть про полярность подключения. Данный процесс не всегда удобен и как следствие иногда вычисление по формулам является более предпочтительным.

Существует несколько видов амперметров, каждый из которых используется локально, то есть в определенных электрических цепочках. Наиболее популярными стали: тепловой, электромагнитный, магнитноэлектрический, электродинамический и индукционный амперметр.

Правила при работе с амперметром
- Клемму амперметра, на которой изображен «плюс» – соединяем с проводом, который идет от положительного полюса. Клемма с «минусом» – наоборот.
- Подключать амперметр в электрическую цепь, при отсутствии потребителя тока, нельзя.
- Подключается амперметр в цепи последовательно.
Мультиметром
Мультиметр является многофункциональным прибором, то есть он может измерять ток и постоянных, и переменных токов. Его подключение аналогично амперметру (при условии измерения силы тока).

Прежде чем включить мультиметр внутри цепи, важно проверить режим измерения, а также выбрать пределы измерения гораздо больше силы, которую Вы ожидаете увидеть (современные мультиметры имеют цифровое табло).

При нахождении значения переменного тока переключите прибор на нужный режим и записывайте значения только после того, как цифры на дисплее перестанут мигать.

Единицы измерения на практике
Единицы измерения, приведенные в формулах, порой могут оказаться неудобным на практике, и оттого считаются «теоретическими». Например, в паспортах различных электроприборах (лампочек, телевизоров) Вы не увидите электрическую мощность в Ваттах. Это связано с тем, что если преобразовать формулу, то мы получим, что один Ватт – это 1 Джоуль/1 секунду.
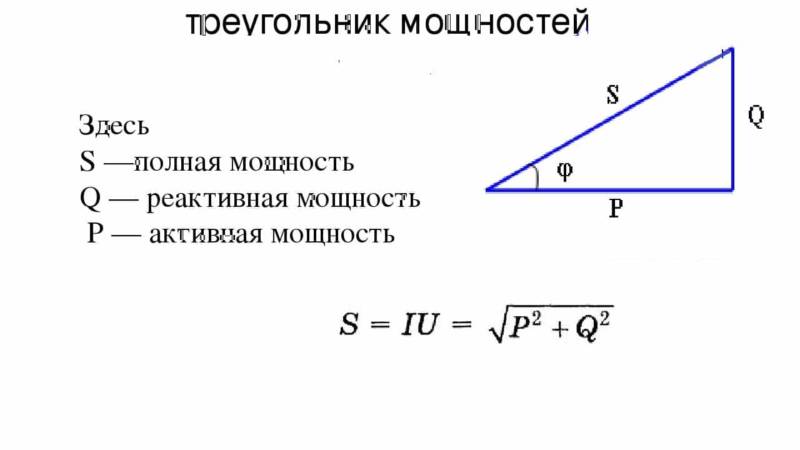
И такое выражение крайне неудобное, ведь электроприборы потребляют ток в течение долгого времени: несколько минут, часов, дней, а расчет электричества по электросчетчику проводится раз в месяц!
Такие расчеты не оправданы и, как следствие, на практике время стали выражать не в секундах, а в часах, из-за чего электрический ток больше не выражается в Ваттах, а в ватт-час (ВтхЧ) или киловатт-час (кВтхЧ).

Из-за введения разных терминов (единиц измерения) мощности, следует разобраться как отличать килоВатт от килоВатт в час. Понятие первое показывает непосредственную мощность электротехники. Другими словами, в виде числа показывает способность прибора преобразовывать энергию электричества. КилоВатт в час – это то, сколько килоВатт за единицу времени (один час) может потребить, например, лампочка.
Сама мощность прибора никак не зависит от времени, однако то, какую мощность он может потребить – напрямую зависит от времени.
Узнать мощность электротехники, без использования формул или специальных приборов, можно взглянув на паспорт (инструкцию) выбранного объекта или на наклейку на нем.
- Телевизор в среднем потребляет до 200 Вт.
- Компьютер – 550 Вт.
- Электрический чайник – 1200 Вт.
- Тостер – 1200 Вт.
- Электрообогреватель – 1400 Вт.
- Микроволновая печь (СВЧ) – 1800 Вт.
- Электроплита – 2500 Вт.
Связь мощности тока с действием тока в электрической цепи
Определить нагрузку на прибор в электрической цепи можно с помощью сравнения мощности тока и номинальной мощности электротехники.
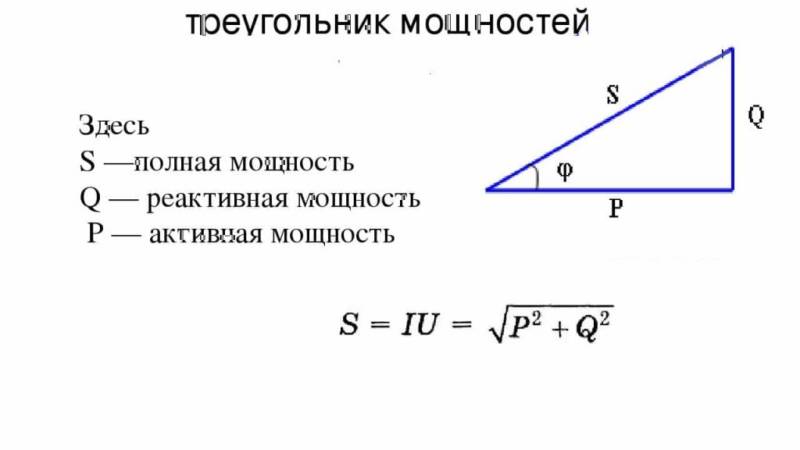
В случае, если мощность самого тока меньше, то его недостаточно или он в целом не проявляется. Это значит, что, если подключить мощный прибор – работать он не начнет.
Обратная ситуация, если сила тока слишком велика, то слабые приборы просто сгорят.

С помощью приведенных выше формул можно находить неизвестные переменные, которые используются в вычислительных задачах, связанных с электричеством. Самые распространенные величины в таких задачах: сопротивление, мощность, напряжение.

Каждый электроприбор имеет свою электрическую мощность и рассчитан на определенную силу тока. При избытке – прибор может сломаться, а при недостатке – не будет работать.

Иногда удобней будет использовать вычислительные «помощники», такие, как амперметр и мультиметр. Они изобретены для того, чтобы измерить силу тока в цепи, однако важно помнить об особенностях их использования.
Фото определения силы тока

















Об авторе: Эксперт в области электричества, общих вопросов
Задать вопрос
Что означает внутреннее сопротивление?
Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет. В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r.
Внутреннее сопротивление источника тока .
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Ток в замкнутой цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r.
В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до сотни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:


Цепляем лампочку


Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.


На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что


Далее






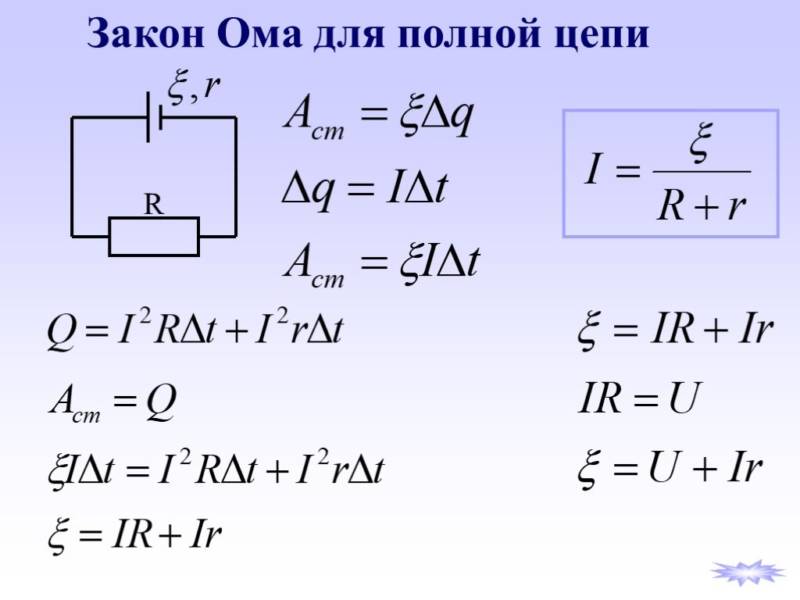
Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»


где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Как измеряется внутреннее сопротивление
Для определения значения рассматриваемой характеристики применяются измерения во время прямого замыкания клемм, которое называют коротким замыканием. Как известно, если закоротить клеммы источника, между ними протечёт значительный ток. Часто это является следствием неосторожности и приводит к обгоранию изоляции и расплавлению провода.
При коротком замыкании сопротивление цепи становится минимальным. Точно измерив силу тока в этой ситуации и зная величину напряжения на клеммах при отсутствии нагрузки, можно определить внутреннее сопротивление источника питания. Для этого понадобится следующая формула:
r = U / I(зам), где
- буквой r обозначено внутреннее сопротивление источника тока;
- U — разность потенциалов на клеммах батареи без подсоединения к электрической цепи;
- I(зам) — ток, который проходит при непосредственном замыкании клемм друг на друга.
Находить значение нагрузки таким образом не всегда возможно или целесообразно, поскольку короткое замыкание может стать причиной серьезной аварии.
Поэтому используются другие решения вопроса, как найти внутреннее сопротивление источника. Например, с помощью специальных измерительных приборов. Функцией измерения данного параметра снабжены оригинальные зарядные устройства iMax B6, ToolkinRC M8, M6, M600.
Зачем нужно знать внутреннее сопротивление
На первый взгляд может показаться, что наличие внутреннего сопротивления интересно только с теоретической точки зрения. На самом деле в некоторых ситуациях знать чему оно равно бывает жизненно важным.
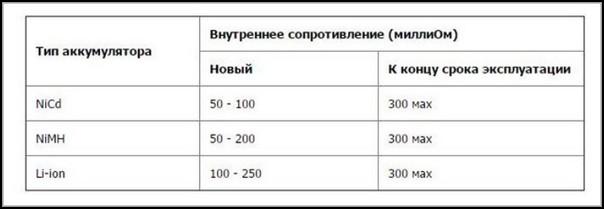
Одна из таких ситуаций — определение работоспособности автомобильного аккумулятора. Его внутреннее сопротивление не является постоянным. Оно изменяется под воздействием различных факторов и влияет на напряжение на клеммах. Чтобы быть уверенным в работоспособности оборудования, нужно не только уметь найти его внутреннее сопротивление, но и знать, какая его величина соответствует норме.

На внутреннее сопротивление источника питания могут оказывать влияние такие факторы:
- Температурные условия. Чем холоднее, тем с меньшей скоростью в аккумуляторе протекают химические процессы. Это приводит к увеличению внутреннего сопротивления и постепенному уменьшению напряжения на клеммах.
- Срок службы аккумулятора. У новых устройств внутреннее сопротивление имеет минимальную величину. Постепенно оно начинает расти. Это связано с тем, что в аккумуляторе происходит необратимый химический процесс. В некоторых случаях он относительно медленный, а в других может быть довольно заметным. Последнее, например, относится к свинцово-кислотным аккумуляторам.
- Емкость аккумулятора.
- Иногда на устройство может оказываться механическое воздействие, из-за которого появляются внутренние обрывы.
- Количество используемого электролита.
- Ток, который создаётся батареей, зависит от нагрузки цепи. В зависимости от него меняется сопротивление.
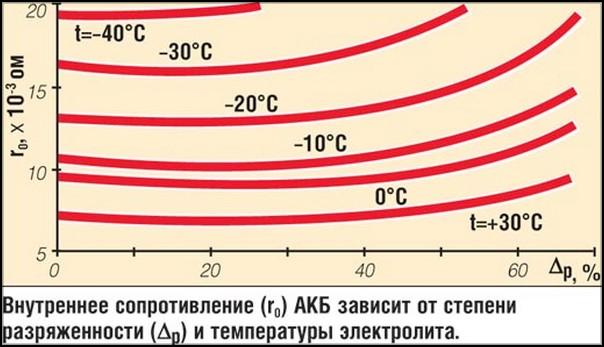
Влияние большого количества факторов приводит к тому, что в качестве нормального можно рассматривать различные значения внутреннего сопротивления. Однако его стандартным увеличением за год принято считать 5%. Если эта норма превышена, значит, на исправность аккумулятора нужно обратить особое внимание.
При анализе стоит принимать во внимание не только те значения, которые указаны в технической документации. Необходимо учитывать и то, насколько интенсивно происходят изменения сопротивления со временем. Это даст более точную информацию об исправности батареи и поможет понять, чего нужно добиваться, чтобы обеспечить работоспособность оборудования.
Один из наиболее простых способов измерения внутреннего сопротивления можно продемонстрировать на следующем примере. Его применение возможно при условии, что ЭДС аккумулятора известна.
ЭДС (ℰ, единица измерения — вольты, В) — это электродвижущая сила источника питания, равная отношению работы сторонних сил по перемещению заряда от отрицательного полюса источника к положительному к величине этого заряда: ℰ=A/q. Если к источнику питания не подключена нагрузка, то ЭДС по своему значению равно напряжению на его клеммах.
Будет рассмотрена ситуация, когда ЭДС равна 1.5 В. Составляется электрическая цепь, в которой выходы аккумулятора присоединяются к электрической лампочке. Измеряется падение напряжения на ней и ток, проходящий через цепь. Они, соответственно, равны 1.2 В и 0.3 А.
Цифры, которые здесь приводятся, являются условными. При измерении мастер может выбрать другой тип электрической нагрузки, если сочтёт это необходимым.
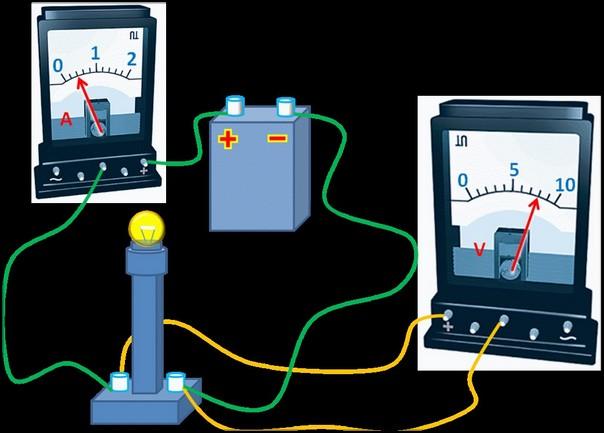
По закону Ома можно определить сопротивление лампочки:
R = U / I = 1.2 / 0.3 = 4 Ом.
В этой формуле буквой R обозначается полное сопротивление цепи. Его можно выразить, как сумму r + R, где r — внутреннее и R — обычное сопротивление.
Тогда: R + r = ℰ / I
Из этой формулы определяется r = ℰ / I − R = 1.5 / 0.3 − 4 = 1 Ом.
Важным условием нахождения значения r является знание величины электродвижущей силы. Эта характеристика имеет максимальное значение у новых и хорошо заряженных батарей. Те, что уже долго были в использовании, могут иметь значительно меньшую ЭДС вследствие разряда, износа, который часто связан с необратимыми химическими процессами в аккумуляторе.
Для определения ℰ необходимо отключить любую нагрузку от клемм источника питания и подключить вольтметр или мультиметр в режиме измерения напряжения. Прибор покажет значение ЭДС. Почему — это легко понять. По закону Ома для полной цепи:
I = ℰ / (R + r),
так как вольтметр имеет сопротивление R→∞, то ток I≈0. Следовательно напряжение на клеммах равно ЭДС:
U = I·R = ℰ – I·r = ℰ.
Также следует упомянуть, что нулевым внутренним сопротивлением «r» обладает только идеальный генератор напряжения. Также существуют элементы с большим внутренним сопротивлением — это разные датчики, источники сигналов, а r=∞ обладает только идеальный источник тока. Помимо этого, существуют двухполюсники с отрицательным значением r, его можно получить в схемах с обратной связью и в элементах с отрицательным дифференциальным сопротивлением. Расчеты применимы не только для аккумулятора, но и для любого другого источника тока, например, гальванической батареи, двухполюсника, петли фаза-нуль. Использовать эти знания можно для согласования источника и нагрузки, понижения высоких напряжений и минимизации шума.
Расчет внутреннего сопротивления источника напряжения
Реальные источники напряжения обладают собственным электрическим сопротивлением, которое называется «внутреннее сопротивление». Присоединенная на выводы источника нагрузка обозначается под названием «внешнее сопротивление» – R.
Батарея аккумуляторов генерирует ЭДС:
ε = E/Q, где:
- Е – энергия (Дж);
- Q – заряд (Кл).
Суммарная ЭДС аккумуляторного элемента является напряжением его разомкнутой цепи при отсутствии нагрузки. Его можно проконтролировать с хорошей точностью цифровым мультиметром. Разность потенциалов, измеренная на выходных контактах батареи, когда она включена на нагрузочный резистор, составит меньшую величину, чем ее напряжение при незамкнутой цепи, по причине протекания тока через нагрузочное внешнее и через внутреннее сопротивление источника, это приводит к рассеиванию энергии в нем как теплового излучения.
Внутреннее сопротивление аккумулятора с химическим принципом действия находится между долей ома и несколькими омами и в основном связано с сопротивлением электролитических материалов, используемых при изготовлении батареи.
Если резистор сопротивлением R подсоединить к батарее, ток в цепи I = ε/(R + r).
Внутреннее сопротивление – не постоянная величина. На него влияет род батареи (щелочная, свинцово-кислотная и т. д.), оно изменяется в зависимости от нагрузочного значения, температуры и срока использования аккумулятора. К примеру, у разовых батареек внутреннее сопротивление возрастает во время использования, а напряжение в связи с этим падает до прихода в состояние, непригодное для дальнейшей эксплуатации.
Если ЭДС источника – заранее данная величина, внутреннее сопротивление источника определяется, измеряя ток, протекающий через нагрузочное сопротивление.
- Так как внутреннее и внешнее сопротивление в приближённой схеме включены последовательно, можно использовать законы Ома и Кирхгофа для применения формулы:
- Из этого выражения r = ε/I — R.
Пример.
Аккумулятор с известной ЭДС ε = 1.5 В и соединен последовательно с лампочкой. Падение напряжения на лампочке составляет 1,2 В. Следовательно, внутреннее сопротивление элемента создает падение напряжения: 1,5 — 1,2 = 0,3 В. Сопротивление проводов в цепи считается пренебрежимо малым, сопротивление лампы не известно. Измеренный ток, проходящий через цепь: I = 0,3 А. Нужно определить внутреннее сопротивление аккумулятора.
- По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом;
- Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.
В случае короткого замыкания внешнее сопротивление падает почти до нуля. Ток может ограничивать свое значение только маленьким сопротивлением источника. Сила тока, возникающая в такой ситуации, настолько велика, что источник напряжения может быть поврежден тепловым воздействием тока, существует опасность возгорания. Риск пожара предотвращается установкой предохранителей, например, в цепях автомобильных аккумуляторов.
Внутреннее сопротивление источника напряжения – важный фактор, когда решается вопрос, как передать наиболее эффективную мощность подсоединенному электроприбору.
Важно!
Максимальная передача мощности происходит, когда внутреннее сопротивление источника равно сопротивлению нагрузки.
Однако при этом условии, помня формулу Р = I² x R, идентичное количество энергии отдается нагрузке и рассеивается в самом источнике, а его КПД составляет всего 50%.
Требования нагрузки должны быть тщательно рассмотрены для принятия решения о наилучшем использовании источника. Например, свинцово-кислотная автомобильная батарея должна обеспечивать высокие токи при сравнительно низком напряжении 12 В. Ее низкое внутреннее сопротивление позволяет ей это делать.
В некоторых случаях источники питания высокого напряжения должны иметь чрезвычайно большое внутреннее сопротивление, чтобы ограничить ток к. з.
Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.
Выразив отсюда r, получают формулу для его вычисления:
где:
- r – внутреннее сопротивление источника;
- ε – ЭДС источника;
- I – сила тока в полной цепи;
- R – сопротивление в полной цепи.
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.
Таблица удельных сопротивлений различных материалов
| Удельное сопротивление
ρ, Ом*мм2/м |
Удельное сопротивление
ρ, Ом*мм2/м |
| Алюминий | 0,028 |
| Бронза | 0,095 – 0,1 |
| Висмут | 1,2 |
| Вольфрам | 0,05 |
| Железо | 0,1 |
| Золото | 0,023 |
| Иридий | 0,0474 |
| Константан ( сплав Ni-Cu + Mn) | 0,5 |
| Латунь | 0,025 – 0,108 |
| Магний | 0,045 |
| Манганин (сплав меди марганца и никеля – приборный) | 0,43 – 0,51 |
| Медь | 0,0175 |
| Молибден | 0,059 |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 |
| Натрий | 0,047 |
| Никелин ( сплав меди и никеля) | 0,42 |
| Никель | 0,087 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 – 1,4 |
| Олово | 0,12 |
| Платина | 0.107 |
| Ртуть | 0,94 |
| Свинец | 0,22 |
| Серебро | 0,015 |
| Сталь | 0,103 – 0,137 |
| Титан | 0,6 |
| Хромаль | 1,3 – 1,5 |
| Цинк | 0,054 |
| Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
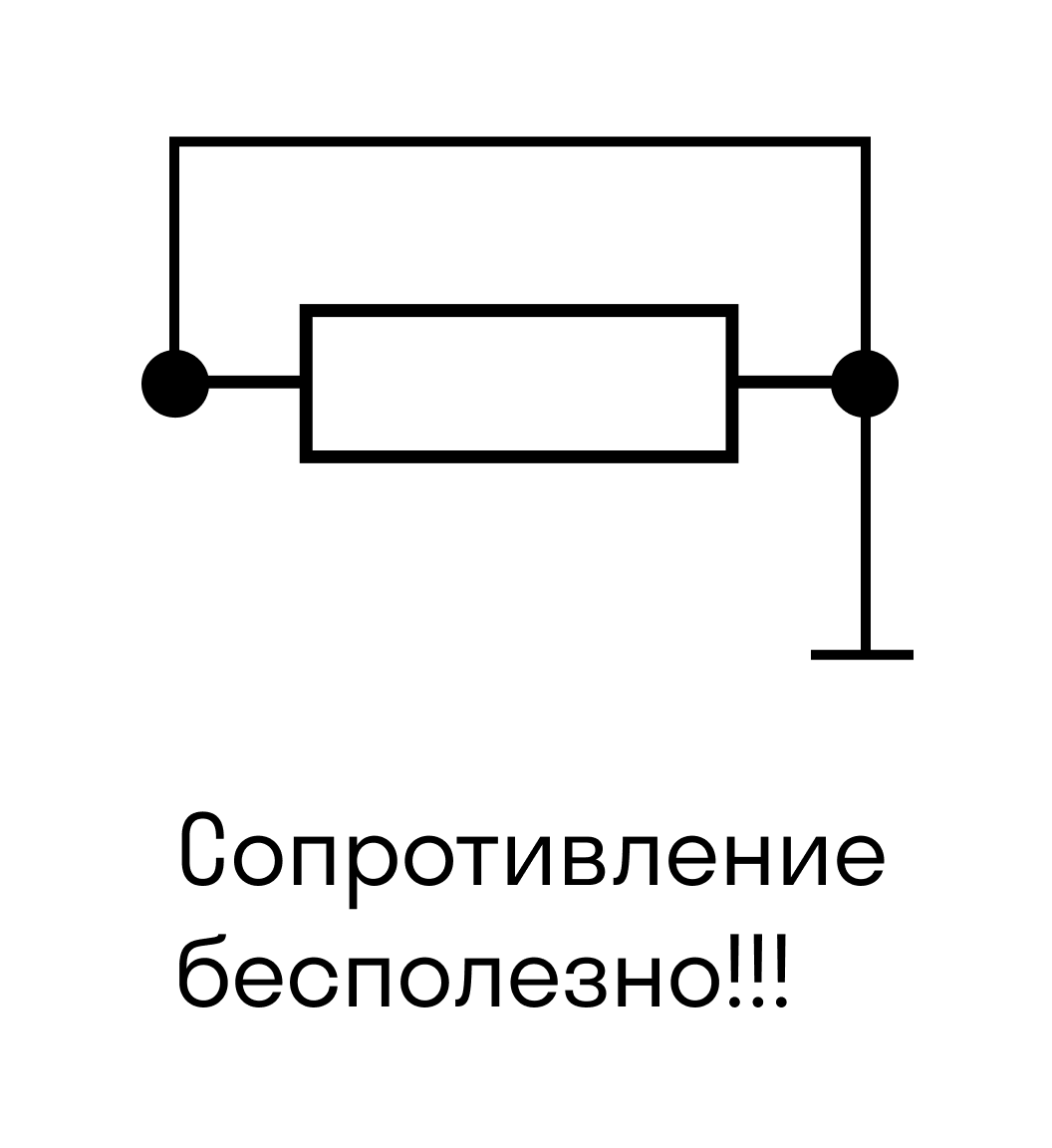
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Измерение внутреннего сопротивления.
Существует несколько методик измерения внутреннего сопротивления. Две из них прописаны в ГОСТ Р МЭК 61960-2007. Перед замером любым из приведенных ниже методов аккумулятор должен быть полностью заряжен. Испытания проводятся при температуре 20±5ºC.
Измерение внутреннего сопротивления методом переменного тока (а.с.)
С помощью этого метода измеряется импеданс, который на частоте 1000 Гц приблизительно равен сопротивлению.
Электрический импеданс (комплексное электрическое сопротивление) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Описание методики из ГОСТ
В течение одной – пяти секунд измеряем среднеквадратичное значение переменного напряжения Urms, возникающего при прохождении через аккумулятор переменного тока со среднеквадратичным значением Irms , следующего с частотой 1000 Гц. Внутреннее сопротивление Ra.c., Ом рассчитываем по формуле Ra.c.= Urms / Irms .
Irms (rms – Root Mean Square – среднеквадратичное значение).
Переменный ток должен иметь такое значение, чтобы пиковое напряжение не превышало 20 мВ.
Этот метод сложно воплотить в домашних условиях без специального оборудования. Популярный прибор YR1035 отлично справляется с измерениями с точностью 0,01 мОм. Зарядные устройства SKYRC MC3000 ,Opus BT-C3100V2.2, Liitokala Lii-500 также измеряют методом АС, но весьма с посредственной точностью.
Измерение внутреннего сопротивления методом постоянного тока (d.c.)
Этот метод возможно выполнить в домашних условиях с помощью обычных вольтметра и амперметра и пары подходящих нагрузочных сопротивлений. В качестве сопротивлений вполне можно использовать несколько автомобильных ламп накаливания или импровизированный резистор из нихромовой проволоки.
Описание метода из ГОСТ
- Разряжаем аккумулятор постоянным током I1= 0,2 Iн. На десятой секунде измеряем значение напряжения U1 на клеммах аккумулятора.
- Увеличиваем разрядный ток до значения I2=Iн. На следующей секунде измеряем значение напряжения U2 на клеммах аккумулятора.
Внутреннее сопротивление Rd.c., Ом рассчитываем по формуле Rd.c. = (U1-U2)/(I2-I1)
- Iн – номинальный ток разряда аккумулятора.
Схема для измерения внутреннего сопротивления по методике постоянного тока (d.c.)
Сопротивление R1 и R2 подбирается таким образом, чтобы протекали токи I1 и I2 нужной величины. Ориентироваться нужно на номинальный разрядный ток аккумулятора.
Вольтметр необходимо подключать непосредственно на полюса источника, чтобы исключить влияние от падения напряжения на проводах .
Идеальный источник тока
Идеальный источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах. Предполагается, что внутреннее сопротивление идеального источника тока бесконечно велико , и поэтому параметры внешней электрической цепи, от которых зависит напряжение на зажимах источника, не влияют на ток источника. Условные обозначения идеального источника тока приведены на рис. 1
Стрелка в источнике тока или знаки «+» и «—» указывают положительное направление тока i(t)
или полярность источника, т. е. направление перемещения положительных зарядов.
Сейчас принято обозначать источники тока буквой J, и чаще всего применяется нижнее условно графическое изображение.
Идеальный источник тока
По мере неограниченного увеличения сопротивления внешней электрической цепи, присоединенной к идеальном
у источнику тока, напряжение на его зажимах и соответственно мощность, развиваемая им, неограниченно возрастают.Поэтому идеальный источник тока, так же как и идеальный источник напряжения, рассматривается как источник бесконечной мощности.
Источник тока конечной мощности изображается в виде идеального источника тока с параллельно подключенным к его зажимам пассивным элементом который характеризует внутренние параметры источника и
Представляя собой теоретическое понятие, источник тока применяется в ряде случаев для расчета электрических цепей.
Некоторым подобием источника тока может служить устройство, состоящее из аккумулятора, соединенного последовательно с дополнительным большим сопротивлением Другим примером источника тока может являться пяти электродная усилительная электронная лампа (пентод). Имея внутреннее сопротивление несоизмеримо большее, чем сопротивление внешней электрической цепи, эти устройства отдают ток, почти не зависящий от изменения внешней нагрузки в широких пределах, и именно в этом отношении они аналогичны источнику тока.
Чему равно внутреннее сопротивление источника тока?
Внутреннее сопротивление источника тока r будет определяться формулой: r = ЭДС / I — R. Подставим данные из условия задачи: r = 10 В / 2 А — 4 Ом = 1 Ом. Ответ: источник тока имеет внутреннее сопротивление r = 1 Ом.
Как правильно пользоваться мультиметром: инструкция для чайников
Рассмотрим, как измерить несколько электрических характеристик.
Потенциал
Алгоритм для определения напряжения:
- Установить режим в позицию ACV или DCV в предполагаемом интервале.
- Черный провод подключить к коннектору СОМ, красный — к разъему VΩmA.
- Наконечники щупов соединить с контактами цепи. Например, ввести в отверстия розетки или на полюса батарейки.
- Провести измерение.
Высветившееся на дисплее число — величина напряжения в вольтах. Знак «минус» говорит о том, что полярность была нарушена. Если мультиметр поддерживает функцию удержания, значение можно зафиксировать кнопкой HOLD. Это удобно для большой цепочки измерений.
Сила тока
Эта характеристика измеряется только при последовательном подключении тестера в цепь и включенном питании. Большинство приборов дают возможность определить силу тока до 10 А, поскольку в быту большие значения используются редко.
Для проведения измерений в цепи устраивается разрыв. Дальнейшие действия по следующей схеме:
- Черный щуп — в гнездо СОМ.
- Красный — в разъем до 200 мА или 10А.
- Наконечниками осторожно прикоснуться к контактам.
- Считать с дисплея значение напряжения.
При работе с оголенными проводами необходимо соблюдать технику безопасности, чтобы не допустить удара током.
Сопротивление
Эту характеристику можно измерить без подачи питания. Исследуемый элемент просто замыкается между двумя щупами. Если проводимости нет, на экране высвечивается единица.
Последовательность действий:
- Установить режим Ω, выбрав максимальный диапазон.
- Щупы вставить в соответствующие коннекторы.
- Проверить состояние — замкнуть щупы друг на друга. Должен появиться 0 или небольшое число, которое нужно учитывать при измерении сопротивления цепи.
- Концы проводников набросить на контакты исследуемого объекта.
- На экране появится сопротивление элемента или участка цепи.
Для точных измерений рекомендуется провести 2-3 попытки.
Измерение транзисторов
Для проверки исправности pn-переходов и определения коэффициента усиления:
- Установить режим
- Вставить ножки транзистора в разъем в соответствии с цоколевкой, соблюдая зоны PNP и NPN.
- Отображением на дисплее будет значение усиления сигнала.
Диоды и простейшие транзисторы также измеряются при установленном режиме «диод». К базе подключается красный щуп (плюс), на эмиттер или коллектор черный (минус). При правильной полярности на экране высветится коэффициент передачи.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними


