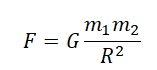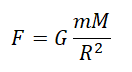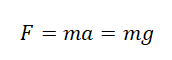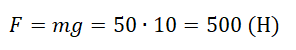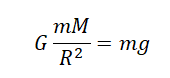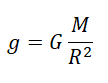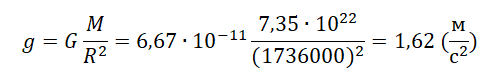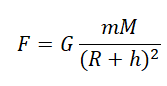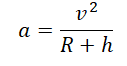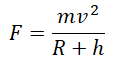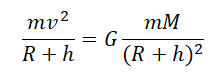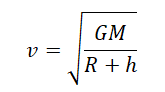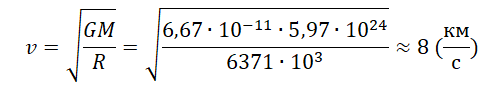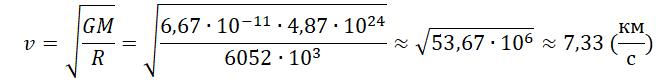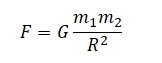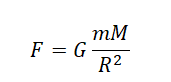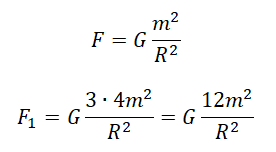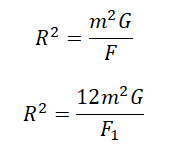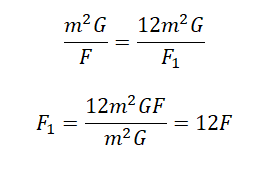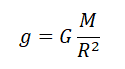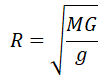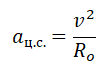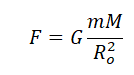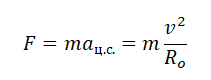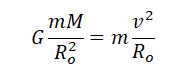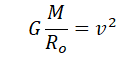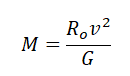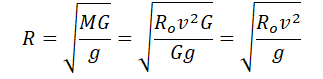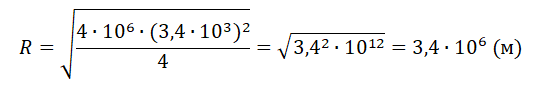Сила всемирного тяготения как найти расстояние - Сайт, где вы сможете решить свои вопросы

Закон всемирного тяготения Ньютона

Класси́ческая тео́рия тяготе́ния Нью́то́на (Зако́н всеми́рного тяготе́ния Нью́то́на) — закон, описывающий гравитационное взаимодействие в рамках классической механики. Этот закон был открыт Ньютоном около 1666 года, опубликован в 1687 году в «Началах» Ньютона.

Закон гласит, что сила гравитационного притяжения между двумя материальными точками с массами m_1 и m_2 , разделёнными расстоянием , действует вдоль соединяющей их прямой, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния^[1].

То есть:

${displaystyle F=Gcdot {m_{1}cdot m_{2} over r^{2}}}$

(1)

Здесь — гравитационная постоянная, равная^[2]: 6,67430(15)·10⁻¹¹ м³/(кг·с²).

Свойства ньютоновского тяготения[править | править код]

В ньютоновской теории каждое массивное тело порождает силовое поле притяжения к этому телу, называемое гравитационным полем.

Гравитационное взаимодействие в теории Ньютона распространяется мгновенно, так как сила тяготения зависит только от взаимного расположения притягивающихся тел в данный момент времени. Также для ньютоновских гравитационных сил справедлив принцип суперпозиции: сила тяготения, действующая на частицу со стороны нескольких других частиц, равна векторной сумме сил притяжения со стороны каждой частицы.

Ускорение, которое тело А приобретает под воздействием притяжения тела В, не зависит от массы тела А. Причина этого в том, что сила притяжения, действующая на тело А со стороны тела В, пропорциональна массе тела А – но ускорение, приобретаемое любым телом под действием любой силы, обратно пропорционально его массе по второму закону Ньютона; таким образом, увеличение массы тела А в равной мере увеличивает действующую на него силу и его сопротивление этой силе. В современной физике это свойство формулируют как равенство гравитационной и инертной масс.

В теории тяготения Ньютона ускорение точечного или маленького тела под действием гравитационной силы всегда в точности равно напряжённости гравитационного поля в точке, в которой находится тело^[3], определяемой как отношение

Сферически симметричное тело создаёт за своими пределами такое же поле, как материальная точка той же массы, расположенная в центре тела. Внутри сферически симметричной оболочки (имеющей сферическую полость или выделенной условно, являясь реально частью какого-то тела) поле, создаваемое ею^[4], имеет нулевую напряженность (и, соответственно, постоянный потенциал), то есть, сферически симметричная оболочка не притягивает находящиеся внутри неё тела, и вообще никак на них не действует посредством гравитации.

Сюда следует добавить и то, очевидное из сказанного выше и третьего закона Ньютона, утверждение, что на сферически симметричное тело гравитация сторонних источников также действует в точности как на точечное тело той же массы, расположенное в центре симметрии. А отсюда следует, что и два сферически симметричных тела конечных размеров притягиваются в точности так же, как точечные тела тех же масс, расположенные в их центрах. Это утверждение оказывается достаточно важным для небесной механики, ведь многие небесные тела имеют именно сферически симметричную форму (пусть и не точно), что, в дополнение к тому, что расстояния между небесными телами часто (обычно) во много раз превосходят их размеры, упрощает применение теории к ним, т.к. сила их взаимодействия (в соответствующем приближении, которое оказывается обычно очень хорошим), а соответственно и ускорение, вычисляется так же просто, как для материальных точек – т.е. просто по формуле (1).

Гравитационное поле в теории Ньютона является потенциальным, в связи с этим для его описания можно использовать гравитационный потенциал varphi. В случае, если поле создаётся расположенной в начале координат точечной массой , гравитационный потенциал определяется формулой:

${displaystyle varphi ({vec {r}})=-G{frac {M}{r}}}$

(1.1)

(здесь потенциал на бесконечности, как это делается обычно, принят равным нулю).

В общем случае, когда плотность вещества rho распределена произвольно, varphi удовлетворяет уравнению Пуассона:

{displaystyle Delta varphi ({vec {r}})=-4pi Grho ({vec {r}})}

(1.2)

Решение данного уравнения^[5] записывается в виде:

${displaystyle varphi ({vec {r}})=-Gint _{V^{prime }}{frac {rho ({vec {r}}^{prime })dV^{prime }}{|{vec {r}}-{vec {r}}^{prime }|}}+C}$

(1.3)

Здесь — радиус-вектор точки, в которой определяется потенциал, ${displaystyle {vec {r}}^{prime }}$ — радиус-вектор элемента объёма ${displaystyle dV^{prime }}$ c плотностью вещества ${displaystyle rho ({vec {r}}^{prime })}$ , а интегрирование охватывает все такие элементы; — произвольная постоянная; чаще всего ее принимают равной нулю, как это сделано в формуле выше для одного точечного источника.

Сила притяжения, действующая в гравитационном поле на материальную точку с массой , связана с потенциалом формулой:

{displaystyle {vec {F}}({vec {r}})=-mnabla varphi ({vec {r}})}

(1.4)

Если поле создаётся точечной массой , расположенной в начале координат, то на точку массой действует сила

${displaystyle {vec {F}}({vec {r}})=-G{frac {mM}{r^{3}}}cdot {vec {r}}}$

(1.5)

Величина этой силы зависит только от расстояния между массами, но не от направления радиус-вектора (см. формулу в преамбуле).

Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.

Аналогия с электростатикой[править | править код]

С точки зрения физики, гравитационное поле сильно отличается от электростатического — например, массы всегда притягиваются, а заряды могут и отталкиваться, в гравитации нет аналога таким эффектам, как электростатическая индукция и т. д. Однако классические математические модели обеих теорий во многом сходны, а в ряде случаев даже тождественны. В связи с этим для ньютоновской гравитации применимы по сути все те теоретические конструкции и методы решения задач, которые применяются в электростатике. В этом, формальном (но математически вполне содержательном) смысле, можно сказать, что теория одна^[6].

Среди теорем и методов, одинаково имеющих силу (и место для применения) в ньютоновской теории гравитации и электростатике, можно назвать теорему Гаусса, теорему Ирншоу, метод изображений, метод конформных отображений, полностью теорию потенциала, не говоря уже о принципе суперпозиции и других разного рода математических принципах и приёмах.

Ньютоновская гравитация гораздо более точно соответствует эксперименту, чем электростатика — она реже даёт существенную ошибку, и величина этой ошибки обычно гораздо меньше. Также можно заметить, что более общие теории для гравитации и электростатики (это соответственно ОТО и электродинамика) совершенно различны.

Точность закона всемирного тяготения Ньютона[править | править код]

Экспериментальная оценка степени точности закона тяготения Ньютона является одним из подтверждений общей теории относительности.^[7] Опыты по измерению квадрупольного взаимодействия вращающегося тела и неподвижной антенны показали^[8], что приращение delta в выражении для зависимости ньютоновского потенциала $r^{-(1+delta)}$ на расстояниях нескольких метров находится в пределах ${displaystyle (2,1pm 6,2)cdot 10^{-3}}$ . Другие опыты также подтвердили отсутствие модификаций в законе всемирного тяготения^[9].

Закон всемирного тяготения Ньютона в 2007 г. был проверен и на расстояниях, меньших одного сантиметра (от 55 мкм до 9,53 мм). С учетом погрешностей эксперимента в исследованном диапазоне расстояний отклонений от закона Ньютона не обнаружено^[10].

В 2021 г. закон всемирного тяготения Ньютона был проверен для тел с массой 90 мг на расстояниях от 3 до 5 мм.^[11]^[12].

Прецизионные лазерные дальнометрические наблюдения за орбитой Луны^[13] подтверждают закон всемирного тяготения на расстоянии от Земли до Луны с точностью $3cdot 10^{{-11}}$ .

Связь с геометрией евклидова пространства[править | править код]

Факт равенства с очень высокой точностью ( $10^{{-9}}$ ) показателя степени расстояния в знаменателе выражения для силы тяготения числу отражает евклидову природу трёхмерного физического пространства механики Ньютона. В трёхмерном евклидовом пространстве площадь поверхности сферы точно пропорциональна квадрату её радиуса^[14].

Исторический очерк[править | править код]

(См. также Ньютон, Исаак#Всемирное тяготение и астрономия).

Сама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие^[15]. Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире^[16]. Были, впрочем, догадки с правильной зависимостью от расстояния; Ньютон в письме к Галлею упоминает как своих предшественников Буллиальда, Рена и Гука^[17]. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера).^[18]. Кроме того, Ньютон пришел к пониманию того, что гравитация универсальна: другими словами, одна и та же сила заставляет и яблоко падать на землю, и Луну вращаться вокруг Земли^[19].

В своём основном труде «Математические начала натуральной философии» (1687) Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Он показал, что:

наблюдаемые движения планет свидетельствуют о наличии центральной силы;
обратно, центральная сила притяжения приводит к эллиптическим (или гиперболическим) орбитам.

Кроме того, Ньютон достиг существенного продвижения в таких практически значимых темах, связанных с тяготением, как проблема фигуры Земли, теория приливов, предварение равноденствий.

Отметим, что теория тяготения Ньютона уже не была, строго говоря, гелиоцентрической. Уже в задаче двух тел планета вращается не вокруг Солнца, а вокруг общего центра тяжести, так как не только Солнце притягивает планету, но и планета притягивает Солнце. Наконец, выяснилась необходимость учесть влияние планет друг на друга.

Теория Ньютона имела ряд существенных отличий от гипотез предшественников. Ньютон не просто опубликовал предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:

закон тяготения;
закон движения (второй закон Ньютона);
система методов для математического исследования (математический анализ).

В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел и тем самым создаёт основы небесной механики. До Эйнштейна никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить. Последующие исследователи достигли также существенного прогресса в небесной механике, и «астрономическая точность» расчётов вошла в поговорку.

В течение XVIII века закон всемирного тяготения был предметом активной дискуссии (против него выступали сторонники школы Декарта) и тщательных проверок. К концу века стало общепризнанным, что закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Генри Кавендиш в 1798 году осуществил прямую проверку справедливости закона тяготения в земных условиях, используя исключительно чувствительные крутильные весы^[20]. Важным этапом стало введение Пуассоном в 1813 году понятия гравитационного потенциала и уравнения Пуассона для этого потенциала; эта модель позволяла исследовать гравитационное поле при произвольном распределении вещества^[21]. После этого ньютоновский закон стал рассматриваться как фундаментальный закон природы.

Недостатки классической теории тяготения[править | править код]

В то же время ньютоновская теория содержала ряд трудностей. Главные из них следующие.

Необъяснимое дальнодействие: сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания.
Если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает неразрешимый гравитационный парадокс, который поставил под сомнение применимость ньютоновской теории в космологических масштабах.
В конце XIX века обнаружилась ещё одна проблема: расхождение теоретического и наблюдаемого смещения перигелия Меркурия^[22].

В течение XVIII—XIX веков делались неоднократные попытки модифицировать или обобщить классическую теорию тяготения — физики изменяли формулу ньютоновского закона, объясняли механизм тяготения участием мирового эфира. По мере осознания принципов теории относительности начались попытки построить релятивистское обобщение теории гравитации. По-видимому, первую чёткую формулировку проблемы опубликовал Анри Пуанкаре в 1905 году:

Возможно ли найти такой закон, который удовлетворил бы условиям, поставленным Лоренцем [имеются в виду преобразования Лоренца] и одновременно сводился к закону Ньютона во всех случаях, когда скорости небесных тел достаточно малы для того, чтобы можно было пренебречь их квадратами (а также произведениями ускорений на расстояния) по сравнению с квадратом скорости света?

Пуанкаре в статье «О динамике электрона» предложил два варианта релятивистского обобщения закона тяготения. Оба они исключали дальнодействие (скорость гравитации совпадала со скоростью света). Историк науки В. П. Визгин в своей монографии пишет^[23]:

Релятивистская теория тяготения, развитая Пуанкаре, не привлекла внимания физиков, хотя в принципиальном
отношении она была значительным шагом вперед в развитии гравитационной проблемы. Причины этого невнимания, с нашей точки зрения, таковы:

теория не объясняла аномальное смещение перигелия Меркурия;

большинство физиков в 1906—1908 годах не разделяло релятивистской программы;

формально-алгебраический метод построения теории отодвинул на задний план физические аспекты теории;

неоднозначность свидетельствовала о незаконченности теории;

в период преобладания электромагнитно-полевой программы настоящее обобщение ньютоновской теории тяготения требовало использования явного полевого подхода — теория же Пуанкаре не давала уравнений гравитационного поля, из которых можно было получить найденные им лоренц-инвариантные элементарные законы взаимодействия.

Далее наброски релятивистской теории тяготения опубликовали в начале 1910-х годов Макс Абрахам, Гуннар Нордстрём и Альберт Эйнштейн. Все они до создания ОТО не соответствовали данным наблюдений.

Дальнейшее развитие[править | править код]

Общая теория относительности[править | править код]

На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году — созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона, в полном согласии с принципом соответствия, оказалась приближением более общей теории, применимым при выполнении двух условий:

Гравитационный потенциал в исследуемой системе не слишком велик: $frac{varphi}{c^2} ll 1$ . В Солнечной системе это условие для большинства движений небесных тел можно считать выполненным — даже на поверхности Солнца отношение ${displaystyle |varphi |/c^{2}}$ составляет всего $2{,}12cdot 10^{{-6}}$ . Заметным релятивистским эффектом является только упомянутое выше смещение перигелия Меркурия^[24].
Скорости движения в этой системе незначительны по сравнению со скоростью света: $frac{v}{c} ll 1$ .

В слабых стационарных гравитационных полях уравнения движения переходят в ньютоновы (гравитационный потенциал). Для доказательства покажем, что скалярный гравитационный потенциал в слабых стационарных гравитационных полях удовлетворяет уравнению Пуассона

Известно, что в этом случае гравитационный потенциал имеет вид:

$Phi = - frac{1}{2}c^{2}(g_{44}+1)$

Найдём компоненту тензора энергии-импульса $T_{44}$ из уравнений гравитационного поля общей теории относительности:

$R_{ik} = - varkappa (T_{ik} - frac{1}{2}g_{ik}T)$

где $R_{ik}$ — тензор кривизны.
Для $T_{ik}$ мы можем ввести кинетический тензор энергии-импульса $rho u_{i} u_{k}$ . Пренебрегая величинами порядка u/c , можно положить все компоненты $T_{ik}$ , кроме $T_{44}$ , равными нулю. Компонента $T_{44}$ равна
$T_{44} = rho c^{2}$
и, следовательно $T = g^{ik} T_{ik} = g^{44} T_{44} = - rho c^{2}$ .
Таким образом, уравнения гравитационного поля принимают вид $R_{44}=-frac{1}{2} varkappa rho c^{2}$ . Вследствие формулы

$R_{ik} = frac{partial Gamma_{i alpha}^{alpha}}{partial x^{k}} - frac{partial Gamma_{ik}^{alpha}}{partial x^{alpha}} + Gamma_{i alpha}^{beta} Gamma_{k beta}^{alpha} - Gamma_{ik}^{alpha} Gamma_{alpha beta}^{beta}$

значение компоненты тензора кривизны $R_{44}$ можно взять равным $R_{44} = - frac{partialGamma^{alpha}_{44}}{partial x^{alpha}}$ и так как $Gamma^{alpha}_{44} approx - frac{1}{2}frac{partial g_{44}}{partial x^{alpha}}$ , $R_{44} = frac{1}{2} sum_{alpha} frac{partial^{2} g_{44}}{partial x_{alpha}^{2}} = frac{1}{2} Delta g_{44} = - frac{Delta Phi}{c^{2}}$ . Таким образом, приходим к уравнению Пуассона:

$Delta Phi = frac{1}{2} varkappa c^{4} rho$

, где $varkappa = - frac{8 pi G}{c^{4}}$

^[25]

Квантовая гравитация[править | править код]

Применение принципа корпускулярно-волнового дуализма к гравитационному полю показывает, что гравитационные волны можно рассматривать как поток квантов поля — гравитонов. В большинстве процессов во Вселенной квантовые эффекты гравитации очень малы. Они становятся существенными лишь вблизи сингулярностей поля тяготения, где радиус кривизны пространства-времени очень мал. Когда он становится близким к планковской длине, квантовые эффекты становятся доминирующими. Эффекты квантовой гравитации приводят к рождению частиц в гравитационном поле чёрных дыр и их постепенному испарению^[26]. Построение непротиворечивой квантовой теории гравитации — одна из важнейших нерешённых задач современной физики.

С точки зрения квантовой гравитации, гравитационное взаимодействие осуществляется путём обмена виртуальными гравитонами между взаимодействующими телами. Согласно принципу неопределенности, энергия виртуального гравитона обратно пропорциональна времени его существования от момента излучения одним телом до момента поглощения другим телом. Время существования пропорционально расстоянию между телами. Таким образом, на малых расстояниях взаимодействующие тела могут обмениваться виртуальными гравитонами с короткими и длинными длинами волн, а на больших расстояниях только длинноволновыми гравитонами. Из этих соображений можно получить закон обратной пропорциональности ньютоновского потенциала от расстояния. Аналогия между законом Ньютона и законом Кулона объясняется тем, что масса гравитона, как и масса фотона, равна нулю^[27]^[28]. Разница между законом ньютоновского тяготения и законом Кулона (существует два вида электрических зарядов и один вид «гравитационных зарядов» с притяжением между ними) объясняется тем, что спин фотона равен , а спин гравитона равен ^[29].

См. также[править | править код]

Закон Кулона
Гравитационная неустойчивость
Гравитационная модель внешней торговли

Примечания[править | править код]

↑ Всемирного тяготения закон // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 1. — С. 348. — ISBN 5-85270-034-7.
↑ CODATA Internationally recommended values of the Fundamental Physical Constants (англ.). Дата обращения: 7 марта 2020. Архивировано 27 августа 2011 года.
↑ Удобство использования физической величины напряженности связано с тем, что она не зависит от конкретного тела, помещаемого в данную точку, (будет одинаковой, если мы поместим в эту точку разные тела разной массы) и, таким образом, является характеристикой только самого поля, не зависящего непосредственно от тела, на которое оно действует (косвенная зависимость может быть за счёт действия самого этого тела на тела-источники поля, и только при изменении в результате этого воздействия их положения).
↑ То есть, речь не идет, конечно, об экранировке гравитационных полей, создаваемых другими источниками, которые могут находиться как внутри оболочки, так и вне её, а только лишь о том поле, которое создаётся самой оболочкой, именно его напряжённость равна нулю (а поля остальных источников тогда по принципу суперпозиции как раз останутся внутри сферической оболочки неизменными, как будто оболочки нет).
↑ Это решение естественно получается используя формулу решения с одним точечным источником, приведенную выше, и принцип суперпозиции – то есть просто сложением полей от (бесконечного) множества точечных источников, массой каждый, расположенных в соответствующих точках пространства.
↑ Это утверждение не столько дело вкуса, сколько указание на то, что можно достаточно свободно пользоваться методами и результатами одной теории применительно к другой, невзирая на то, на электростатическом или гравитационном языке всё описано, соблюдая, конечно, минимально необходимую осторожность, когда дело касается их немногочисленных отличий и особенностей.
↑ Д. Д. Иваненко, Г. А. Сарданашвили Гравитация, М.: Едиториал УРСС, 2004, ISBN 5-354-00538-8
↑ 10th International conference on General Relativity and Gravitation: Contribut. pap. — Padova, 1983. — Vol. 2, 566 p.
↑ Тезисы докладов Всесоюзной конференции «Современные теоретические и экспериментальные проблемы теории относительности и гравитации». — М.: МГПИ, 1984. — 308 с.
↑ Ю. Н. Ерошенко Новости физики в сети Internet (по материалам электронных препринтов) Архивная копия от 16 августа 2013 на Wayback Machine, УФН, 2007, т. 177, № 2, с. 230
↑ Tobias Westphal, Hans Hepach, Jeremias Pfaff, Markus Aspelmeyer Measurement of gravitational coupling between millimetre-sized masses Архивная копия от 22 августа 2021 на Wayback Machine // Nature volume 591, pages 225–228, 2021
↑ ArXiv.org Tobias Westphal, Hans Hepach, Jeremias Pfaff, Markus Aspelmeyer Measurement of gravitational coupling between millimetre-sized masses Архивная копия от 14 марта 2021 на Wayback Machine
↑ Турышев С. Г. «Экспериментальные проверки общей теории относительности: недавние успехи и будущие направления исследований» Архивная копия от 14 апреля 2015 на Wayback Machine, УФН, 179, с. 3-34, (2009)
↑ Бутиков Е.И., Кондратьев А.С. Физика. Книга 1. Механика. — М.: Наука, 1994. — 138 с.
↑ Архивированная копия. Дата обращения: 1 марта 2010. Архивировано из оригинала 12 февраля 2007 года.Архивированная копия. Дата обращения: 1 марта 2010. Архивировано из оригинала 12 февраля 2007 года.
↑ Спасский Б. И. История физики. — Т. 1. — С. 140—141.
↑ Ход их рассуждений легко восстановить, см. Тюлина И. А., указ. статья, стр. 185. Как показал Гюйгенс, при круговом движении центростремительная сила (пропорциональна) , где — скорость тела, — радиус орбиты. Но $vsim frac R T$ , где — период обращения, то есть $v^2sim frac {R^2} {T^2}$ . Согласно 3-му закону Кеплера, , поэтому $v^2sim frac {1} {R}$ , откуда окончательно имеем: $F sim frac {1} {R^2}$ .
↑ Точнее, никто не смог это сделать последовательно для эллиптических орбит. Для круговых, используя третий закон Кеплера и формулу Гюйгенса для центробежной силы, это было сделать довольно нетрудно, и сам Ньютон вспоминал, что сделал это довольно давно, но никому не сообщал, так как был не удовлетворен неудачей тогда с решением общей задачи. Это же, видимо, позже, сделал Гук (это его письмо сохранилось), побудивший Ньютона вернуться к общей задаче. Гук же обосновал второй закон Кеплера, применив методологически важный в тот момент прием суперпозиции свободного движения и движения с ускорением, направленным к центру. Однако только Ньютон решил в итоге задачу полностью, для некруговых орбит, впервые корректно и доказательно теоретически получив их форму, он же первый всё полно и систематически изложил.
↑ «Бог создал целые числа». Глава из книги. Архивная копия от 21 июня 2022 на Wayback Machine Elementy.ru, «Книжный клуб».
↑ Визгин В. П., 1981, с. 25.
↑ Визгин В. П., 1981, с. 27.
↑ Визгин В. П., 1981, с. 27—29.
↑ Визгин В. П., 1981, с. 69—75.
↑ Гинзбург В. Л. Гелиоцентрическая система и общая теория относительности (от Коперника до Эйнштейна) // Эйнштейновский сборник. — М.: Наука, 1973. — С. 63..
↑ В. Паули Теория относительности, ОГИЗ, 1947
↑ Ошибка в сносках^?: Неверный тег <ref>; для сносок Nov не указан текст
↑ Фриш Д., Торндайк А. Элементарные частицы. — М.: Атомиздат, 1966. — С. 98.
↑ Окунь Л. Б. Элементарное введение в физику элементарных частиц. — М.: Физматлит, 2009. — С. 105. — ISBN 978-5-9221-1070-9
↑ Киббл Т. «Квантовая теория гравитации» Архивная копия от 5 января 2016 на Wayback Machine, УФН, 96, с. 497—517, (1968)

Литература[править | править код]

Визгин, В. П. Релятивистская теория тяготения. Истоки и формирование. 1900-1915 гг. — М. : Наука, 1981. — 352 с.
Ньютон, И. Математические начала натуральной философии = Philosophiæ Naturalis Principia Mathematica : [пер. с лат.] / Исаак Ньютон ; ред. и предисл. Л. С. Полака ; пер. и комм. А. Н. Крылова. — М. : Наука, 1989. — 688 с. — (Классики науки). — ISBN 5-02-000747-1.
Тюлина, И. А. Об основах ньютоновой механики (к трехсотлетию «Начал» Ньютона) // История и методология естественных наук. — М. : МГУ, 1989. — Вып. 36. — С. 184—196.

Источник

Закон всемирного тяготения. Калькулятор силы притяжения, массы и расстояния онлайн.

Онлайн калькулятор закона всемирного тяготения (гравитации) вычислит силу притяжения двух материальных точек, массу и расстояния между ними, а также даст подробное решение.

Калькулятор содержит:
Калькулятор вычисления силы притяжения.
Калькулятор вычисления расстояния через массы и силу притяжения между двумя материальными точками.
Калькулятор вычисления массы материальной точки через массу второй материальной точки, силу и расстояние.

Калькулятор вычисления силы притяжения

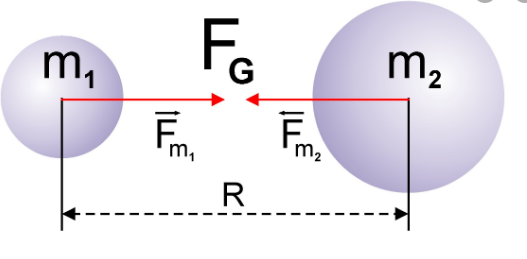
Сила притяжения между любыми двумя материальными точками m₁ и m₂ прямо пропорциональна произведению масс этих точек и обратна пропорциональна квадрату расстояния между ними.

Гравитационная постоянная G численно равна силе гравитационного притяжения между двумя телами, масса каждого тела равна 1 кг, находящимися на расстоянии 1 метра друг от друга.
G = 6.67 × 10^-11 Н × м² / кг²
Единицей измерения силы – Ньютон (Н, N)

Масса m1 =
Масса m2 =
Расстояние r =
Единица измерения силы F

Калькулятор вычисления расстояния через массы и силу притяжения между двумя материальными точками

По закону всемирного тяготения расстояние между двумя материальными точками равно квадратному корню из частного, в котором числителем выступает гравитационная постоянная G и произведение масс материальных точек, а знаменатель выражен силой притяжения между данными точками.

Гравитационная постоянная G численно равна силе гравитационного притяжения между двумя телами, масса каждого тела равна 1 кг, находящимися на расстоянии 1 метра друг от друга.
G = 6.67 × 10^-11 Н × м² / кг²
Единица измерения расстояния – Метр (м, m).

Масса m1 =
Масса m2 =
Сила F =
Единица измерения расстояния r

Калькулятор вычисления массы материальной точки через массу второй материальной точки, силу и расстояние.

По закону всемирного тяготения масса m1 одной из материальных точек, между которыми действует сила притяжения определяется как отношение произведения силы и квадрата расстояния на произведение гравитационной постоянной и массу m2 второй материальной точки.

Гравитационная постоянная G численно равна силе гравитационного притяжения между двумя телами, масса каждого тела равна 1 кг, находящимися на расстоянии 1 метра друг от друга.
G = 6.67 × 10^-11 Н × м² / кг²
Единица массы – килограмм, но также можно использовать и другие единицы, например грамм, тонна, миллиграмм и т.д.

Сила F =
Расстояние r =
Масса m2 =
Единица измерения массы m1

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Источник

Закон всемирного тяготения Как выразить расстояние из формулы всемирного тяготения?

Anna Mezentseva

Профи

(528),
на голосовании

8 лет назад

Голосование за лучший ответ

Карен Небесович

Мастер

(1040)

8 лет назад

Только смотрел фильм про астрономку – Епатия! Но больше всего мне понравилось её прекрасное тело, моя любовь=красота. У вас нет точки исхода – нет никакого всемирного тяготения.

Никита НовоселовЗнаток (453)

5 месяцев назад

Конченый

Гришка Я

Мастер

(1629)

8 лет назад

R=корень квадратный из (G*m1*m2)F, вроде так

Похожие вопросы

Источник

Главная Учёба Калькулятор расчётов по закону всемирного тяготения Ньютона

Калькулятор расчётов по закону всемирного тяготения Ньютона

Условные обозначения формулы: F – сила гравитации, m1,m2 – масса двух тел, G – гравитационная константа, приблизительно 6.67384 (80) x10^-11, R – расстояние между телами.

Формула расчёта силы гравитации: F=G*m1*m2/R2. Гравитационная константа, умноженная на массы двух тел и разделённая на расстояние в квадрате.

Формула расчёта массы одного из тел: m1=(F*R2*10^11)/(G/m2). Силу гравитации, умножаем на расстояние, в квадрате, на 10 в 11 степени, и делим на гравитационную константу умноженную на массу другого тела.

Формула расчёта расстояния между телами: R=[квадратный корень][(G*m1*m2)/(F*10^11)]. Гравитационную константу умноженную на массы тел, делим на силу гравитации, умноженную на 10 в 11 степени и извлекаем квадратный корень.

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Нет комментариев.

Источник

Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.

Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.

Закон всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.

F — сила всемирного тяготения, m₁ и m₂ — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10^–11Н ∙ м²/кг²).

Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.

Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m₁ = 1 кг и m₂ = 1 кг, то F = G.

G = 6,67∙10^–11Н ∙ м²/кг².

Сила тяжести

Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.

Сила тяжести — сила, с которой Земля притягивает к себе тела.

Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле

Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:

Вывод формулы ускорения свободного падения

Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.

Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.

Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:

Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:

Отсюда:

Формула расчета ускорения свободного падения

Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.

Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙10²² кг.

Переведем километры в метры: 1736 км = 1736000 м.

Первая космическая скорость

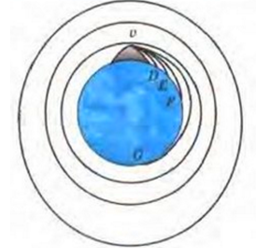
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.

ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Вывод формулы первой космической скорости

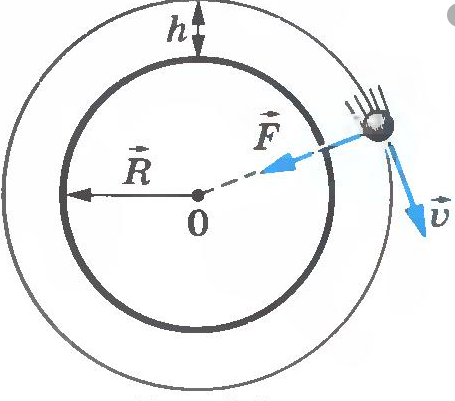
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:

Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:

Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:

Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:

Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:

Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.

Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:

8 км/с — первая космическая скорость Земли.

Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10²⁴ кг, а ее радиус равен 6052 км.

Задание EF18521

Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).

Алгоритм решения

Записать исходные данные.
Записать закон всемирного тяготения.
Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.

Решение

Запишем исходные данные:

Расстояние между двумя шарами в первом случае: R₁ = 2 м.
Расстояние между двумя шарами во втором случае: R₂ = 6 м.
Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.

Запишем закон всемирного тяготения:

Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m₁ и m₂.

R₂ больше R₁ втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3² раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.

Ответ: 1

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17569

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

а) 7F

б) 9F

в) 12F

г) 16F

Алгоритм решения

1.Записать закон всемирного тяготения.

2.Применить закон всемирного тяготения для первой и второй пары звезд.

3.Из каждого выражения выразить расстояние между звездами.

4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.

Решение

Закон всемирного тяготения выглядит так:

Примерим этот закон для первой и второй пары звезд:

Выразим квадраты радиусов, так как они в обоих случаях одинаковые:

Приравняем правые части выражений и выразим силу притяжения во втором случае:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18678

Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?

Для каждой величины определите соответствующий характер изменения:

1)	увеличилась
2)	уменьшилась
3)	не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость

спутника

Потенциальная энергия спутника

Алгоритм решения

1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.

2.Установить зависимость скорости от высоты спутника над поверхностью Земли.

3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.

Решение

На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:

F=maц=GmM(R+h)2

Отсюда центростремительное ускорение равно:

aц=GM(R+h)2

Но центростремительное ускорение также равно:

aц=v2(R+h)

Приравняем правые части выражений и получим:

GM(R+h)2=v2(R+h)

v2=MG(R+h)(R+h)2=MG(R+h)

Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.

Потенциальная энергия спутника определяется формулой:

E_p = mgh

Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.

Верная последовательность цифр в ответе: 21.

Ответ: 21

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17578

Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с². Чему равен радиус планеты? Ответ запишите в километрах.

Алгоритм решения

1.Записать исходные данные. Перевести единицы измерения в СИ.

2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.

3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.

4.Записать закон всемирного тяготения применительно к спутнику.

5.Вывести формулу для расчета радиуса планеты.

6.Подставить известные данные и произвести вычисление.

Решение

Запишем исходные данные:

• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙10³ м/с.

• Радиус орбиты спутника: R_о = 4000 км, или 4∙10⁶ м.

• Ускорение свободного падения у поверхности планеты: g = 4 м/с².