Скорость набегающего потока как найти

Цель работы – определение
аэродинамических коэффициентов С_x,
С_y, С_mz
и нахождение положения центра
давления относительно центра тяжести
осесимметричного оперенного тела
вращения в зависимости от угла атаки
α. Силовое воздействие потока на модель
тела вращения опреде­ляется с помощью
замера сил на аэродинамических весах.

Результаты измерений

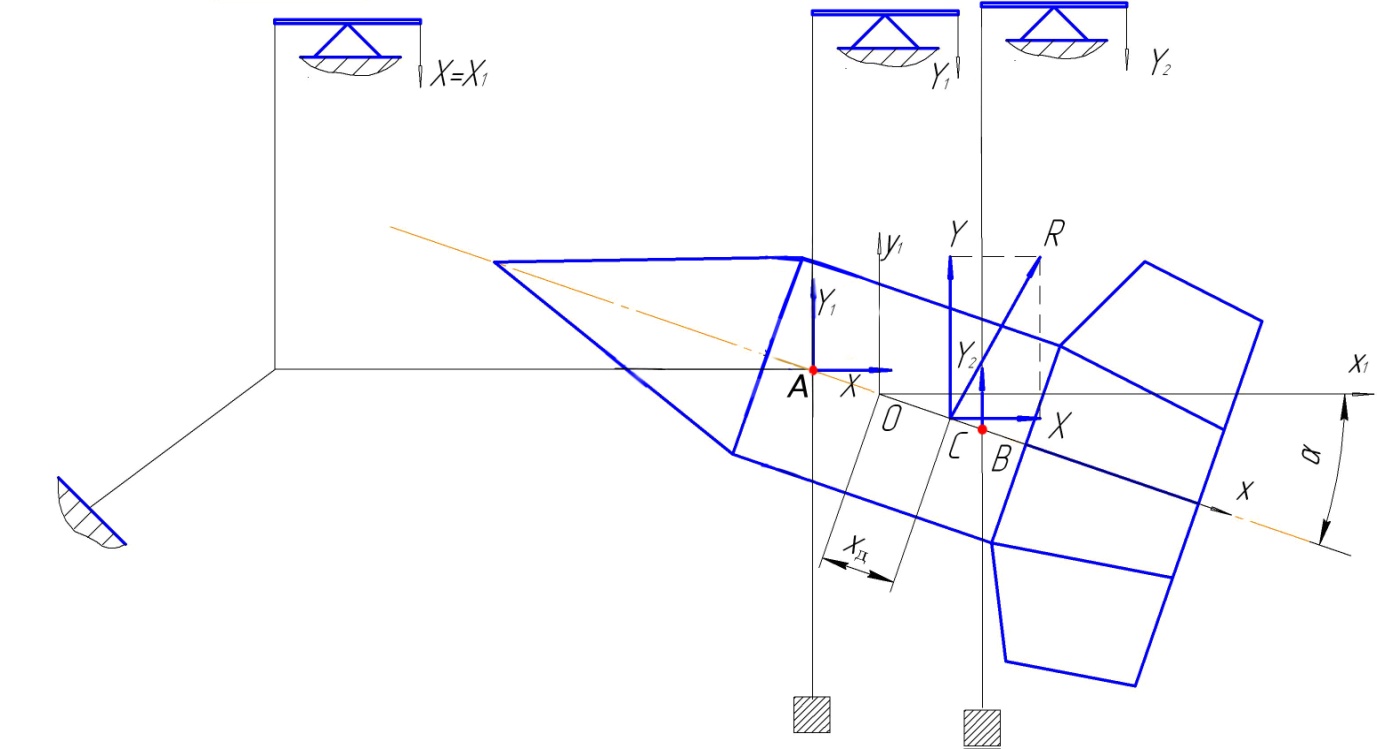
Рис.1. Схема сил и координатных осей

Модель тела вращения с «большим»
оперением подвешивается в рабочей части
аэродинамиче­ской трубы с помощью
проволочных растяжек, закрепленных на
модели в точках А и В (рис.1). Заданный
угол атаки α придается телу вращения
путем изме­нения высоты точки В. Нa
рисунке этот угол измеряется между
осями Ох₁ и Ox. где
точка О – центр тяжести тела вращения,
ось Ох связанной системы координат хОу
направлена по его оси, а ось Ox₁
скоростной системы коорди­нат х₁Оу₁
– по невозмущенной скорости натекающего
потока.

Так как проволочные растяжки закреплены
на рычажной системе аэро­динамических
весов, то при продувке модели можно
измерить в точке А силу сопротивления
X_изм и
составляющую подъемной силы Y_1изм,
а в точке В – дру­гую составляющую
подъемной силы Y_2изм.

Все три силы: X_изм,
Y_1изм, Y_2изм
– лежат в одной плоскости, проходящей
через ось вращения. Замер аэродинамических
сил в двух точках А и В позволяет найти
помимо коэффициентов С_x
и С_y еще и значение
коэффициента момента С_mz,
а также положение центра давления С.

В процессе проведения эксперимента при
различных углах атаки α определяются
массы грузов m_x,
m_y1,
m_y2,
уравновешивающих через систему рычагов
аэродинамические силы X_изм,
Y_1изм, Y_2изм.
Для каждого угла атаки трубкой Пито-Прандля
находится разность давлений P₀-P,
где P₀ – давление
заторможенного потока, а P
– статическое давление. Эта разность
фиксируется водяным дифференциальным
манометром в виде разницы высот Δh_пито
в сообщающихся трубках, к которым
подведены соответственно давления P₀
и P.

Результаты измерений сведём в Таблицу
1:

Таблица1

α, [град]	0°	4°	8°	12°
mx, [кг]	0,183	0,217	0,280	0,430
my1, [кг]	0	0,039	0,043	-0,033
my2, [кг]	0	0,263	0,680	1,210
Δhпито, [м]	0.152	0.152	0.150	0.147

Обработка результатов
измерений

В
соответствии с интегралом Бернулли для
потока с малой дозвуковой скоростью

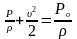
где
υ – скорость набегающего на модель
потока воздуха, Р – статическое давление,
Р₀ – давление заторможенного
потока,

имеем

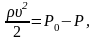
Разность
давлений Р₀-Р уравновешивается
весом столба жидкости (воды) в коленах
дифференциального манометра

,

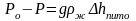
где
g=9.81 [м/с²] – ускорение
силы тяжести,

ρ_ж=1000
[кг/м³ ] – плотность воды,

Δh
[м]=0.001Δh [мм] – разность
уровней воды в коленах сообщающихся
сосудов.

Отсюда

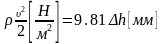
(1)

Для
нахождения υ используем уравнение (1) и
уравнение состояния

.

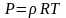
Примем:

P=10⁵
[Па],

R=287.1
[Дж/кг*°К],

T=300°К.

Тогда
ρ=1.161 кг/м³,

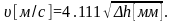
(2)

Результаты
вычислений

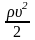
и υ сведем в Таблицу 2:

Таблица2

Значение скоростного напора и скорости
потока для различных углов атаки.

α, [град]	0°	4°	8°	12°
, [H/м2]	1491.1	1491.1	1471.5	1442.1
υ, [м/с]	50.68	50.68	50.35	49.84

2. Вычисление величин X, y1, y2 и y

Основные
соотношения: X=k_xgm_x;
Y₁=k_Ygm_y1;
Y₂=k_Ygm_y2;
Y=Y₁+Y_2
.

Переходные
коэффициенты для весов равны: k_x=2.5,
k_y=2.5
.

Результаты
вычислений сведём в Таблицу 3:

Таблица3

Значение
X_, Y_1,
Y_2,Y
для различных углов атаки.

α, [град]	0°	4°	8°	12°
X, [H]	4.488	5.322	6.867	10.546
Y1, [H]	0	0.956	1.055	-0.809
Y2, [H]	0	6.450	16.677	29.675
Y=Y1+Y2	0	7.407	17.732	28.866

3. Вычисление коэффициентов Сx ,Cy , Cy2.

Сила
лобового сопротивления Х, подъёмная
сила Y и составляющая
подъемной силы Y2
связаны с соответствующими безразмерными
коэффициентами С_x
,C_y ,
C_y2
соотношениями:

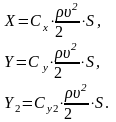
(3)

(4)

(5)

где площадь миделя S:

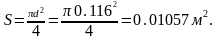
Подставляя
в зависимости (3), (4), (5) значения скоростного
напора

(Таблица 2) и сил X_,
Y_1, Y
(Таблица 3), получим величины коэффициентов
силы лобового сопротивления С_x
, коэффициентов подъёмной силы C_y
и составляющей подъёмной силы C_y2.

Сведём
результаты вычислений в Таблицу 4:

Таблица4

Значение
коэффициентов С_x
,C_y
, C_y2
при различных углах атаки α.

α, [град]	0°	4°	8°	12°
Сx	0.285	0.338	0.442	0.692
Cy2	0	0.409	1.072	1.947
Cу	0	0.470	1.140	1.894

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Скорость набегающего потока Калькулятор

Search
Дом	Инженерное дело ↺
Инженерное дело	Механический ↺
Механический	механика жидкости ↺
механика жидкости	Гиперзвуковой поток ↺
Гиперзвуковой поток	Вычислительно-гидродинамические решения ↺

Скорость набегающего потока Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Динамическая вязкость: 10.2 уравновешенность –> 1.02 паскаля секунд (Проверьте преобразование здесь)
Коэффициент излучения: 0.95 –> Конверсия не требуется
Плотность набегающего потока: 1.225 Килограмм на кубический метр –> 1.225 Килограмм на кубический метр Конверсия не требуется
Радиус носа: 0.52 метр –> 0.52 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

1.77424475010545 метр в секунду –> Конверсия не требуется

4 Вычислительно-гидродинамические решения Калькуляторы

Скорость набегающего потока формула

Скорость свободного потока = Динамическая вязкость/((Коэффициент излучения^2)*Плотность набегающего потока*Радиус носа)

V_∞ = μ_viscosity/((ε^2)*ρ_∞*r_nose)

Что такое излучательная способность?

Излучательная способность – это мера способности объекта излучать инфракрасную энергию. Излучаемая энергия указывает температуру объекта. Коэффициент излучения может иметь значение от 0

Важнейшими характеристиками потоков жидкости или газа (например при движении их в трубах) являются объемный расход и скорость потока.

Объемный расход

Объем жидкости, проходящей через заданную площадь за единицу времени. Измеряется в системе СИ в кубических метрах в секунду (м³/с). Обычно обозначается символом QQ.

Скорость потока

Скорость движения жидкости, которая численно равна отношению расхода жидкости Q к площади живого сечения.

Понятие расхода

Если через заданную площадь SS жидкость протекает с равномерно распределенной по площади скоростью VV под углом θθ к направлению скорости до перпендикуляра площади SS, то расход составит:

Q=V⋅S⋅cosθQ = V ⋅ S ⋅ cosθ

В частном случае, когда скорость потока перпендикулярна к площади SS, уравнение примет вид:

Q=V⋅SQ = V ⋅ S

Общий случай

Записанные выше уравнения обычно называют уравнениями непрерывности (для одномерных течений несжимаемой жидкости). Если скорость жидкости через заданную площадь неодинакова (или, если область не является плоской), то объемный расход потока жидкости может быть рассчитан с помощью интеграла по площади:

Q=∬Su⋅dωQ = ∬S u ⋅ dω,

где dωdω дифференциал поверхности, который записывается как:

dω=ndSdω = n dS,

где nn – единичный вектор нормали к поверхности; dSdS – дифференциал площади SS.

Полученное уравнение потока вектора скорости через поверхность SS является скалярной величиной. Физически поток вектора скорости представляет собой секундный объемный расход жидкости через поверхность SS.

Измерение скорости потока

Для измерения скорости потока жидкости или газа используется прибор, предложенный французским ученым А. Пито (1695-1771). Этот прибор имеет две трубки: одну с отверстием напротив потока и вторую с отверстием, параллельным потоку:

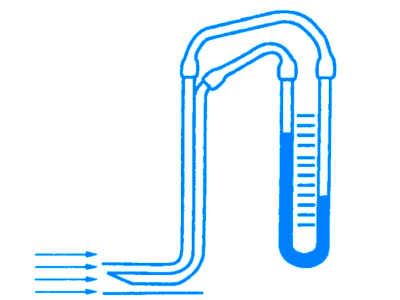
Трубки соединены с дифференциальным манометром:

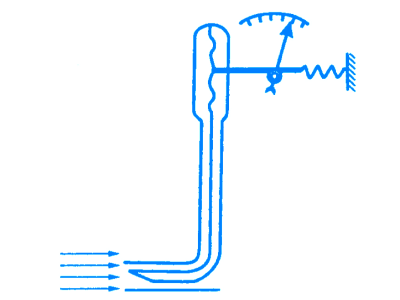
В отверстии первой трубки скорость жидкости или газа равна нулю, а в отверстии второй скорость потока сохраняется. Применив уравнение Бернулли для частиц потока в отверстиях трубок, получим:

p1=ρv22+p2{{p}_{1}}=frac{rho {{v}^{2}}}{2}+{{p}_{2}}

Составляющую ρv2/2ρv^2/2, имеющую размерность давления, называют динамическим давлениям, а составляющую р2р^2 – статичным.

Из уравнения определим скорость потока:

v=2(p1−p2)ρv=sqrt{frac{2({{p}_{1}}-{{p}_{2}})}{rho }}

Здесь ρρ – плотность вещества в потоке; (р1р_1 – р2р_2) находят по разнице высот жидкости в манометре. Согласно данной формуле можно проградуировать манометр в трубке Пито для измерения скорости потока.

Трубку Пито используют для измерения скорости кораблей и самолетов.

Скорость истечения жидкости из бака

Найдем скорость истечения жидкости из бака:

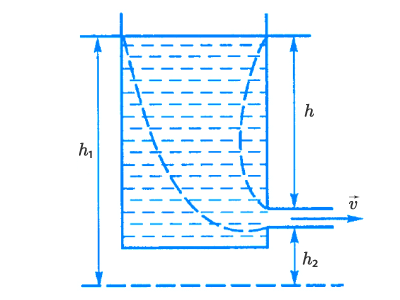
Для этого выделим в жидкости трубку потока (показанную штриховой линией) и применим к ее сечениям (взятых на поверхности жидкости в баке, и в отверстии утечки) уравнение Бернулли. Если при этом учесть, что давления в обоих сечениях одинаковы и равны атмосферному, а скорость в сечении на поверхности жидкости в баке приравнять к нулю, то получим:

ρgh1=ρv22+ρgh2rho g{{h}_{1}}=frac{rho {{v}^{2}}}{2}+rho g{{h}_{2}}

Отсюда находим vv – скорость истечения жидкости из бака:

v=2g(h1−h2)v=sqrt{2g({{h}_{1}}-{{h}_{2}})}

Поскольку h1−h2=hh_1 – h_2 = h – высота уровня жидкости в баке над отверстием истечения, окончательно:

v=2ghv=sqrt{2gh}

Эту формулу вывел итальянский ученый Э. Торричелли (1608-1647) в 1641 Из нее следует, что скорость истечения жидкости (идеальной) из сосуда такова, какова была бы скорость приобретенная телом, свободно падая с высоты hh.

Пример 1

Цилиндрический сосуд высотой hh = 70 см с площадью дна SS = 600 см2 заполнено водой. В дне сосуда образовалось отверстие S1S_1 = 1 см². За какое время вытечет вода из сосуда?

Решение

Приняв во внимание, что скорость истечения воды из сосуда со временем меняется, поскольку меняется уровень воды, определим сначала ее объем утечки за время dtdt:
dV=S1vdtdV = S_1vdt

где v=2ghv=sqrt{2gh} (hh – уровень воды в заданный момент времени); поэтому:

dV=S12ghdtdV={{S}_{1}}sqrt{2gh}dt

Этот объем утечки можно выразить через снижение уровня воды:
dV=−SdhdV = -Sdh

Если приравнять выражения и разделить переменные, то получим дифференциальное уравнение:

dhh=−S1S2gdtfrac{dh}{sqrt{h}}=-frac{{{S}_{1}}}{S}sqrt{2g}dt

Интегрируя обе части этого уравнения, получаем:

2h=−S1S2gdt+C2sqrt{h}=-frac{{{S}_{1}}}{S}sqrt{2g}dt+C

Найдем постоянную интегрирования. Поскольку при tt = 0, h=h0h = h_0, получим:

Тогда равенство примет вид:

h0−h=S12g2Stsqrt{{{h}_{0}}}-sqrt{h}=frac{{{S}_{1}}sqrt{2g}}{2S}t

В случае полного вытекания воды (hh = 0) равенство примет вид:

t=2SS1h02gt=frac{2S}{{{S}_{1}}}sqrt{frac{{{h}_{0}}}{2g}}

Подставив значения из условия получим
tt = 227 с.

Тест по теме «Скорость потока»

---

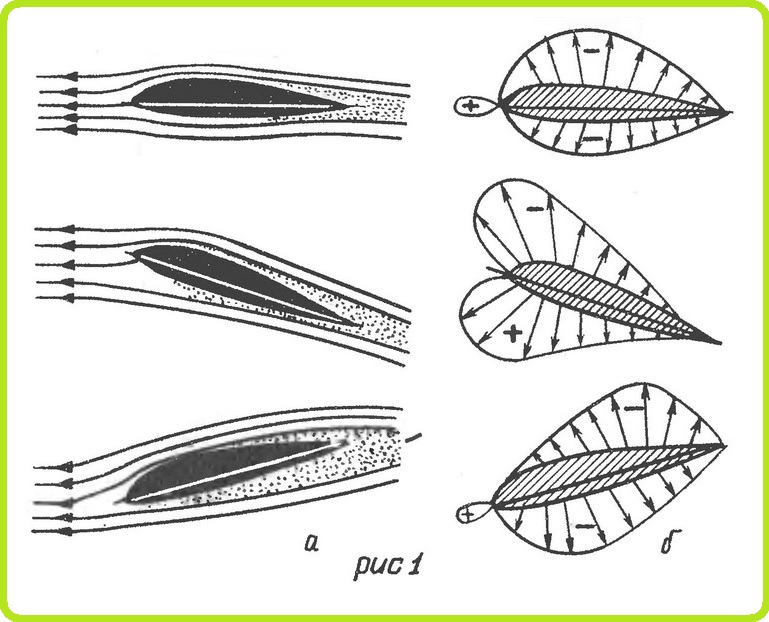
Аэродинамические характеристики крыла самолета

Похожие материалы  “Подъемная сила крыла” а так же, что такое “САХ” и как найти “центр тяжести”.

      ВСЯКАЯ несущая поверхность, помимо сопротивления, создает еще подъемную силу, обеспечивающую полет летательного аппарата. Единый поток перед крылом разделяется на два неодинаковых потока (рис. 1,а). В верхнем потоке струйки как бы сжимаются, скорость их увеличивается, в нижнем же потоке, наоборот, струйки расширяются и скорость их уменьшается. По закону Бернулли, чем выше скорость, тем меньше давление в струе. Следовательно, над крылом образуется область, давление в которой ниже, чем под крылом.

       В зависимости от скорости распределяется и давление по крылу (рис. 1,б). Каждый вектор давления на диаграммах представляет собой силу, которая действует на единицу площади поверхности крыла. Если все эти силы сложить, то получим полную аэродинамическую силу, воздействующую на крыло. Исключением в этом случае будут силы трения, которые по диаграмме распределения давления определить нельзя, так как они направлены по касательной к профилю.

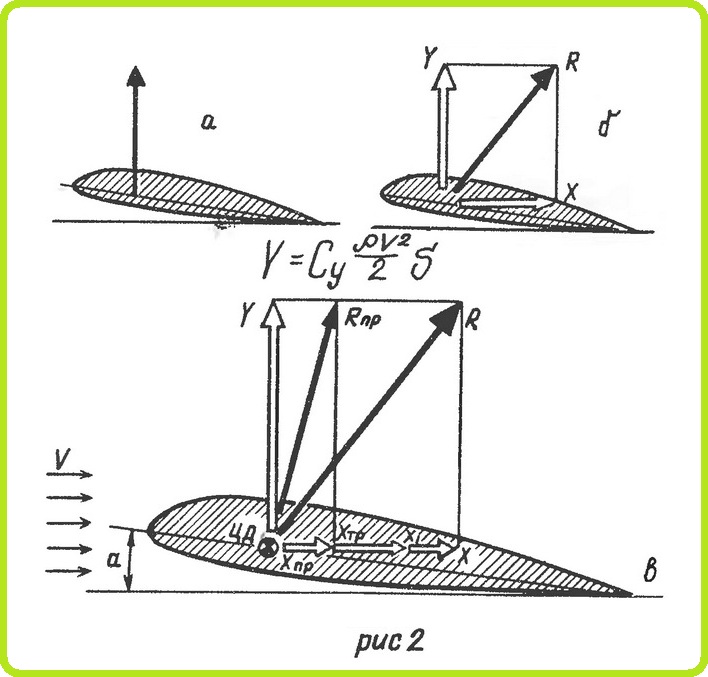
       Проекция полной аэродинамической силы на ось, перпендикулярную направлению потока, называется подъемной силой (рис. 2,а). Полную аэродинамическую силу R можно разложить на подъемную силу Y и силу лобового сопротивления X (рис. 2,б.)

     Подъемная сила крыла зависит от его геометрических размеров, положения относительно потока, скорости полета модели, плотности воздуха и несущей способности профиля крыла. Эту зависимость принято записывать в виде формулы:

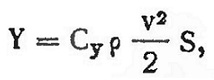
где Cy — коэффициент подъемной силы крыла, учитывающий несущую способность профиля.

       Этот коэффициент зависит от формы профиля и угла атаки α — угла между скоростью набегающего воздушного потока и хордой профиля (рис. 2в). Хорда профиля — это условная прямая линия, применяемая для построения профиля, проходящая, как правило, через носик и хвостовик профиля.

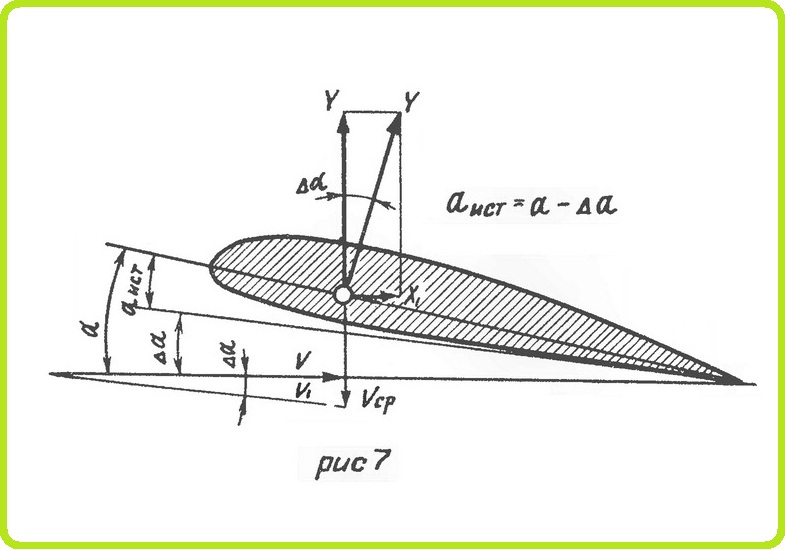
      Кроме сопротивления трения и формы, в коэффициент C_x входит еще один третий вид сопротивления — индуктивное. Дело в том, что крыло отбрасывает набегающий на него поток воздуха вниз со скоростью V_cp (рис. 7) так, что в итоге он направлен не по скорости v, a по скорости v₁. Это явление называется скосом потока. Угол отклонения потока ∆α называется углом скоса потока. Сложив геометрически скорости V и V_cp. получают действительное направление и величину скорости потока v1, обтекающего крыло. Изменение направления скорости вызывает, естественно, и изменение угла атаки

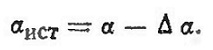
       Благодаря скосу потока истинный угол атаки меньше геометрического. Угол скоса потока определяется по формуле

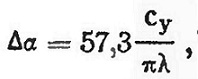
где  λ — удлинение крыла.

       Удлинение крыла λ определяется как отношение квадрата размаха крыла L к площади крыла Sкр

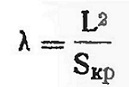
         Размах крыла L определяется как расстояние между двумя плоскостями, параллельными плоскости симметрии и касающимися концов крыла.

       Подъемная сила всегда направлена перпендикулярно к потоку, обтекающему крыло. Благодаря скосу потока подъемная сила отклонится назад на угол ∆α и будет перпендикулярна новому направлению скорости V₁

       Эта подъемная сила называется истинной. Ее можно разложить на две составляющие: перпендикулярную к направлению скорости полета V и параллельную направлению скорости. Эта составляющая, существование которой возможно только при наличии подъемной силы, направлена всегда против движения крыла.

        Коэффициент индуктивного сопротивления определяют по формуле

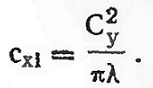
      Угол скоса потока и индуктивное сопротивление зависят от формы профиля крыла, удлинения и от угла атаки.

      Таким образом, полное лобовое сопротивление крыла конечного размаха состоит из сопротивления формы, сопротивления трения и индуктивного сопротивления (рис. 2в). Соответственно, коэффициент сопротивления крыла выражается формулой

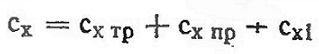
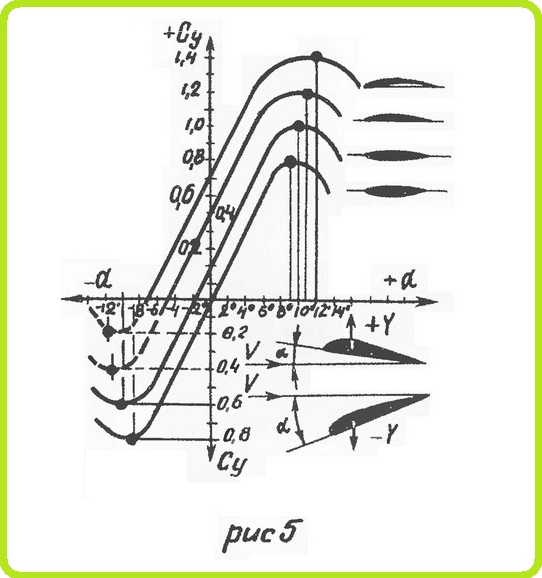
      Точка приложения полной аэродинамической силы называется центром давления. Условились считать, что центр давления лежит на хорде крыла. Если характер обтекания правой и левой половины крыла одинаков, центр давления всего крыла лежит в плоскости симметрии. Нарушение геометрической и аэродинамической симметрии крыла вызовет смещение центра давления.

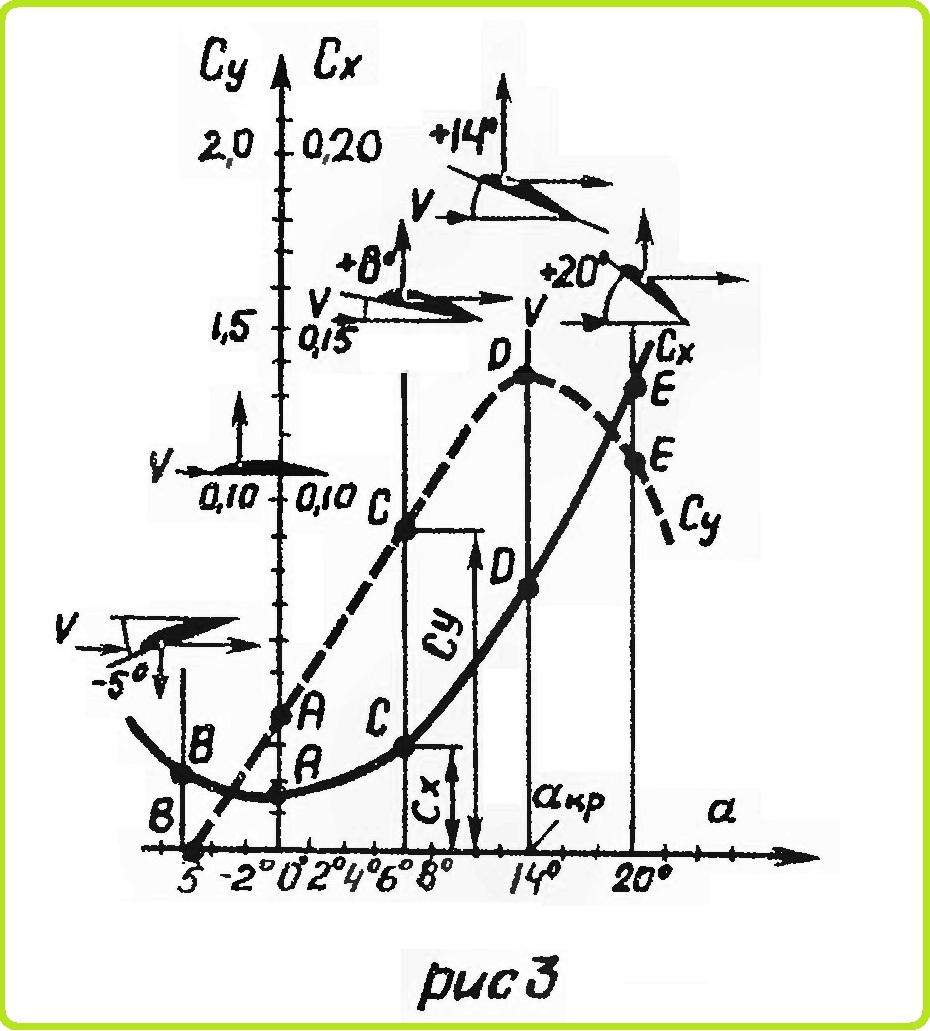
    Положение центра давления на хорде зависит от угла атаки и оказывается различным у профилей разной формы. Характер перемещения центра давления вдоль хорды при изменении угла атаки зависит от формы профиля.

       В этом отношении профили делятся на три категории. У несимметричных 1,2 и вогнуто-выпуклых 3,4 профилей (рис. 4), у которых средняя линия вогнута, центр давления при увеличении угла атаки перемещается вперед и наиболее переднее положение занимает при α, близких к α_кр, В этом случае центр давления находится примерно на расстоянии 25—35% хорды от носика профиля. При уменьшении угла атаки он перемещается назад и при углах атаки, на которых Су становится близким к Су = 0, уходит за пределы крыла.

        У симметричных профилей 4, имеющих прямую среднюю линию, центр давления в пределах значительного диапазона углов атаки занимает постоянное положение и находится примерно на расстоянии 25% длины хорды от носика. При углах атаки больших критического, центр давления у них резко уходит назад.

          У S-образных профилей 6 отогнута вверх задняя кромка. Если хвостик профиля отогнут мало, то перемещение центра давления такое же, как и у профилей первой категории. Бели хвостик отогнут больше, то профиль будет иметь постоянный центр давления. Если же его отогнуть еще больше, то центр давления при увеличении угла атаки отходит назад.

         Перемещение центра давления вызывает изменение момента равнодействующей воздушных сил относительно центра тяжести модели. Для того, чтобы судить об устойчивости крыла данного профиля, необходимо знать, как меняется момент воздушных сил, действующих на крыло, с изменением угла атаки.

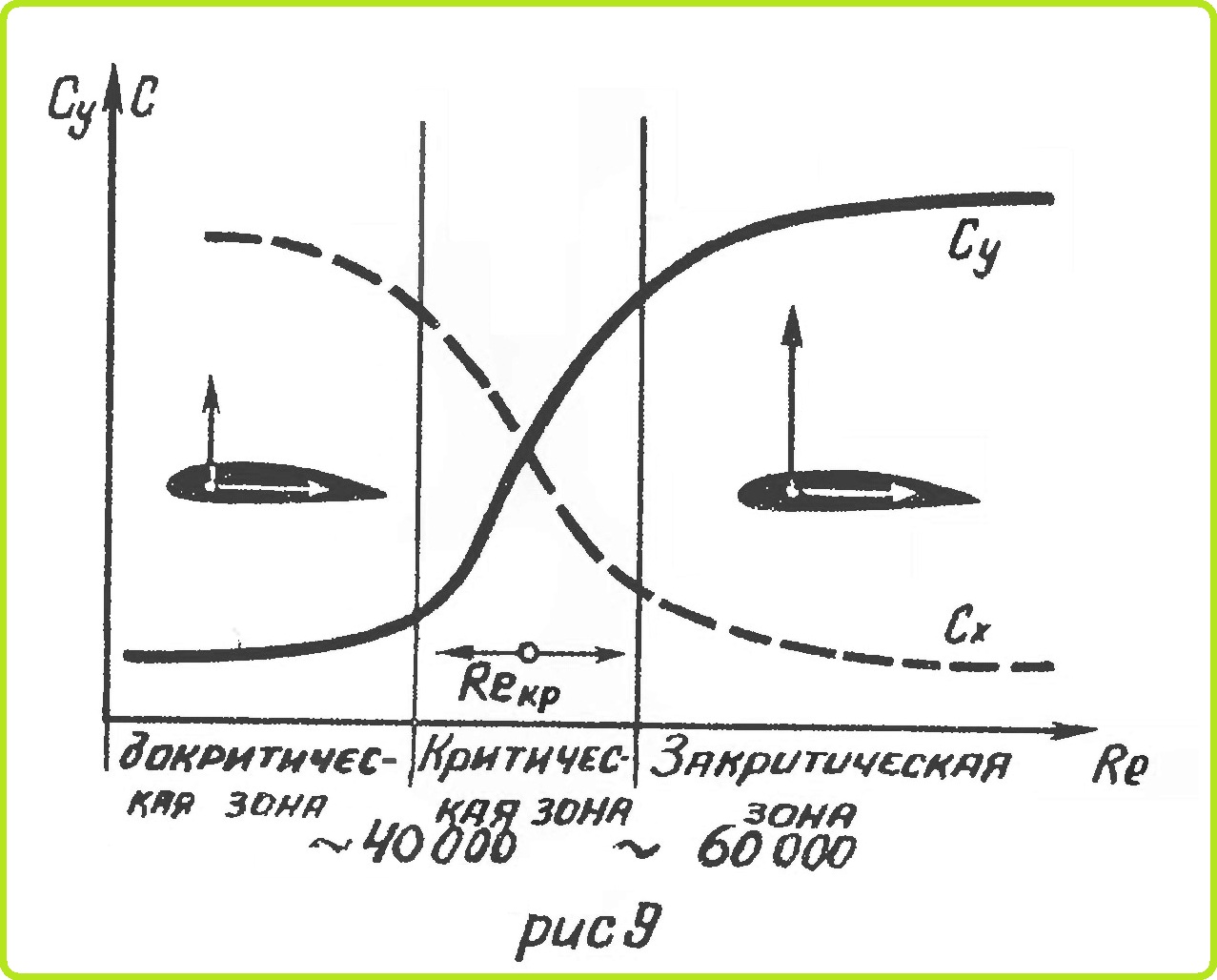
        На рис. 10 изображен профиль крыла модели. Так как при предварительных расчетах конструкция модели еще неизвестна, и, следовательно, неизвестно положение ее центра тяжести, вращение крыла рассматривают не относительно центра тяжести, а относительно точки А, находящейся на носике профиля. Силу R раскладывают не на Y и X, как это делалось раньше, а на силы R_n и R_t.

       Сила R_n мало отличается от Y, поэтому с небольшой ошибкой можно допустить, что R_n = Y. Момент силы R_n относительно точки А равен

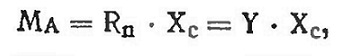
где Х_с— расстояние от центра давления до точки А.

     Так как положение центра давления при разных углах атаки неизвестно, то считают, что крыло вращается силой R_m. приложенной на задней кромке профиля. Для этого необходимо, чтобы

       Это равенство может сохраняться при разных углах атаки, так как изменение Y и Х_с может соответствовать изменению R_m при постоянном плече b. Величину R_m определяют в аэродинамической трубе из условия равновесия относительно опоры весов. При этом замеряют силу R_m при разных углах атаки. Зная момент, нетрудно подсчитать и коэффициент C_mA в формуле

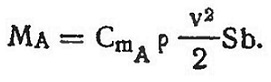
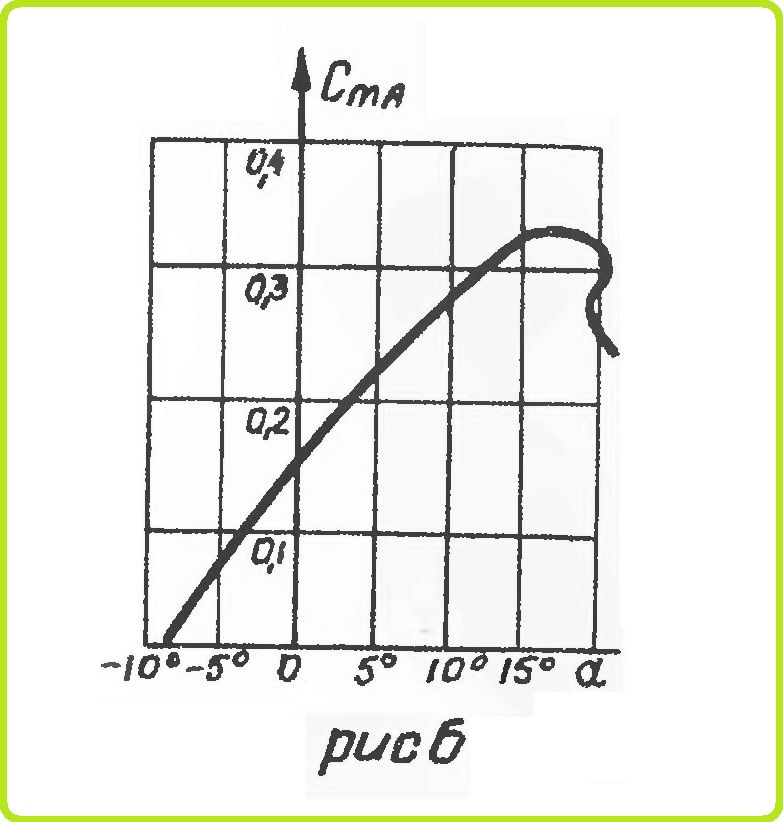
      Зависимость коэффициента C_mA от угла атаки α  представлена на рис. 6.

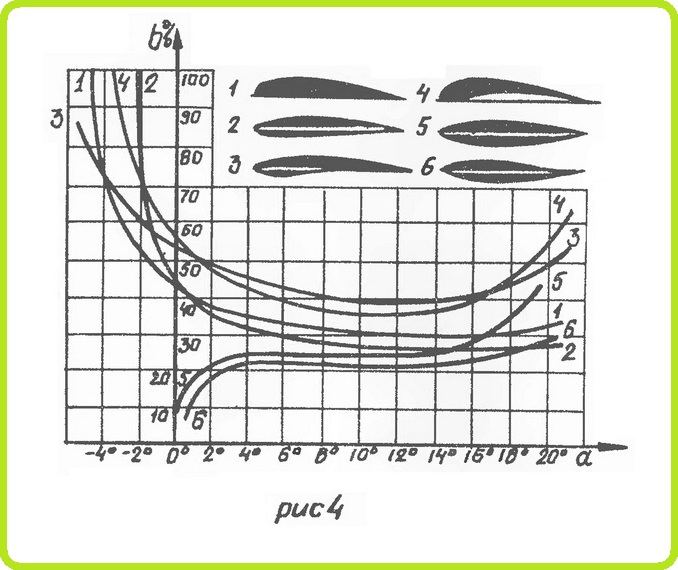
      Значение коэффициентов Сх и Су для различных углов атаки — на рис. 3. Значения коэффициентов Су для различных профилей — на рис. 5. Кривая Су по α для симметричного профиля проходит через начало координат. С увеличением вогнутости профиля кривая зависимости Су по α смещается вверх.

        Объединенный график зависимости Су от Сх при различных α называется полярой (рис. 8). Имея поляру, можно определить ряд величин, которые характеризуют крыло. Если провести касательную к поляре, параллельную оси Сх, то в точке касания получают угол атаки, соответствующий Су _max (рис. 8). Этот угол называется критическим углом атаки «Крит- При увеличении угла атаки сверх критического нарушается обтекание крыла и подъемная сила уменьшается.

Как видно из поляры, при увеличении угла атаки до α _крит , подъемная сила и сопротивление увеличиваются. На больших углах атаки крыло работает в невыгодных условиях вследствие нарушения обтекания.

     Наивыгоднейшим называется такой угол атаки, при котором отношение коэффициента подъемной силы к коэффициенту лобового сопротивления наибольшее. Чтобы найти этот угол, нужно из начала координат провести касательную к поляре.

     Отношение подъемной силы к лобовому сопротивлению называют аэродинамическим качеством крыла.

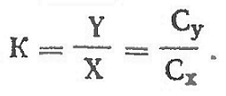
     При полете на угле атаки, имеющем К_max модель проходит наибольшее расстояние. Для того, чтобы модель продержалась наибольшее время в воздухе, необходимо, чтобы угол   атаки был равен экономическому углу.

       Угол атаки нулевой подъемной силы α₀ лежит на пересечении поляры с осью С_х. При этом угле атаки С_у = 0.

         Угол атаки, при котором С_х  имеет наименьшее значение С_{х min} находится в точке касания линии к поляре, проведенной параллельно оси С_у.

     Значения коэффициентов Сх и Су при каком-либо значении угла атаки зависит от числа Re (рис. 9). При Re<Re_кp обтекание профиля ламинарное. Обычно отрыв ламинарного пограничного слоя происходит сразу же за максимально высокой точкой профиля на данном угле атаки, а точнее, за точкой минимума давления, в месте начала повышения давления. С ростом угла атаки точка отрыва ламинарного пограничного слоя перемещается вперед.

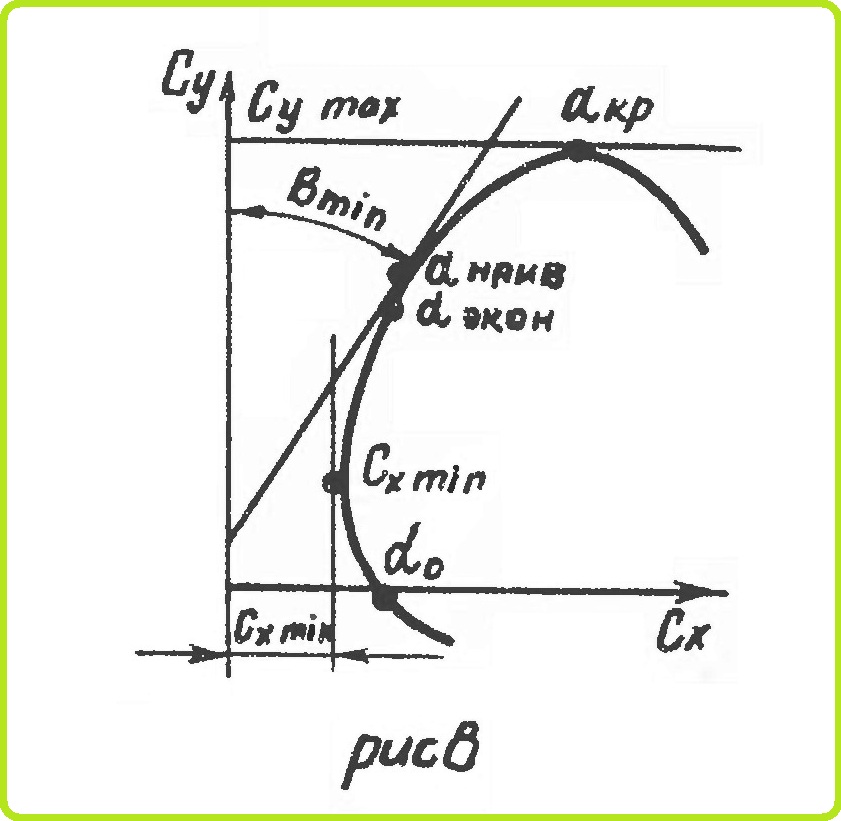
      Застойная зона как бы исключает из работы большую часть верхней поверхности крыла. В результате подъемная сила профиля падает, а перераспределение давлений по верхней поверхности приводит к существенному изменению Су и значительному росту Сх.

При Re>Re_кpит обтекание профиля потоком турбулентное. Благодаря перемешиванию относительная скорость и кинетическая энергия частиц воздуха вблизи профиля более высокая, чем у ламинарного пограничного слоя, и турбулентный пограничный слой может преодолевать повышенное давление на значительном участке задней поверхности профиля. Точка отрыва турбулентного пограничного слоя лежит вблизи задней кромки и тем ближе к ней, чем меньше перепад давления между соседними точками профиля и чем большую скорость имеет внешний поток. Это приводит к росту Су и уменьшению Сх.

---

Н. ЛЯШЕНКО, руководитель заводского клуба юных техников Харьков

Журнал Крылья Родины