Скорость удаления лыжников как найти

Памятка «Учимся решать задач на движение»

В задачах на движение  рассматриваются три взаимосвязанные величины:

S – расстояние (пройденный путь),

t – время движения и

V – скорость – расстояние, пройденное за единицу времени.

Расстояние – это произведение скорости на время движения

S = V ● t

Скорость  – это частное от деления расстояния на время движения

V = S : t

Время – это частное от деления расстояния на скорость движения

t = S : V

Задачи на встречное движение

Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V

 Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?

Схема к задаче:

 

Решение:

S = V ● t

V сближ. = 1V + 2V

1 способ:

1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи

2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи

3) 36 + 42 = 78 (км)

2 способ:

1) 12 + 14 = 26 (км/ч) – скорость сближения

2) 26 • 3 = 78 (км)

Ответ: расстояние между посёлками 78 км.

 Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?

Схема к задаче:

 

Решение:

V сближ. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость сближения

2) 280 : 140 = 2 (ч)

Ответ: машины встретятся через  2 часа.

 Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?

Схема к задаче:

 

Решение:

V = S : t

2V = V сближ. – 1V

1) 340 : 2 = 170 (км/ч) – скорость сближения

2) 170 – 80 = 90 (км/ч)

Ответ: 90 км/ч. скорость второй машины

Задачи на движение в противоположных направлениях

Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. 

V удал. = 1V + 2V

 Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

Схема к задаче:

 Решение:

S = V ● t

1 способ

1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч

2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч

3)36 + 42 = 78 (км) 

2 способ

V удал. = 1V + 2V

S = V ● t

1)12 + 14 = 26 (км/ч) – скорость удаления

2)26 • 3 = 78 (км)

Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.

 Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

Схема к задаче:

 

Решение:

V удал. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч)

Ответ: через 2 часа расстояние между машинами будет 280 км

Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?

Схема к задаче:

  

Решение:

V = S : t

2V = V удал. – 1V

1) 340 : 2 = 170 (км/ч) – скорость удаления машин

2) 170 – 80 = 90 (км/ч)

Ответ: скорость второй машины 90 км/ч.

 

 

 

 

 

 

 

Районный
семинар математиков. 

Тема
“Задачи на движение

в
одном направлении”.

Тип урока
– введение нового знания.

Форма
урока – командная игра.

Класс
4 «А».

Подготовила
и провела

 учитель
начальных классов

 Козакова
Марина Михайловна.

Февраль,
2011/2012 учебный год

МБОУ «СОШ
с. Тамбовки»

Цели урока:

Образовательная. Изучить
способ  решения задач на движение в одном направлении. Обеспечить условия для
усвоения всеми учащимися понятий скорости сближения и скорости удаления.

Развивающая. Развивать
умение сравнивать, анализировать, обобщать. Развивать творчество учащихся и познавательный 
интерес.
Воспитательная. Воспитывать у учащихся чувство уверенности в своих
силах. На примерах задач учить разрешать жизненные вопросы и проблемы. Воспитание
взаимной поддержки во время работы в группах, взаимопомощи.

Уровневые цели для учащихся:

I уровень (базовый)

Понимать
формулировку задачи. Уметь находить расстояние, скорость, время. Понимать
термины «скорость сближения», «скорость удаления». Уметь
решать простейшие задачи на движение в одном направлении и разных направлениях.

II уровень
(конструктивный)

Уметь классифицировать задачи.
Решать более сложные задачи на движение.

III уровень (творческий)

Уметь
решать сложные задачи на движение. Уметь составить задачу по заданной схеме.

Ожидаемый результат:

·      
Каждый
ученик должен проводить классификацию задач по виду движения (в одном
направлении, в разных направлениях)

·      
Уметь
выбирать наиболее рациональный способ решения задачи.

·      
Использовать
изученный материал для решения задач в других темах курса.

Оборудование.

Карточки
с единицами измерения величин, с формулами вычисления скорости, времени,
расстояния; листы бумаги и маркеры для всех учеников; листочки с заданиями для
самостоятельной работы, презентация, интерактивная доска.

План урока:

                 
I.           
Организация
начала занятий.

              
II.           
Актуализация
знаний.

           
III.           
Подготовительный
этап.

           
IV.           
Проблемная
ситуация.

              
V.           
Открытие
нового знания.

           
VI.           
Закрепление
нового материала.

        
VII.           
Усвоение
полученных знаний и способов действий.

     VIII.           
Итог
урок.

           
IX.           
Рефлексия.

              
X.           
Информация
о домашнем задании.

Ход  урока

Этапы урока

Деятельность учителя

Деятельность учащихся

I. Организация начала урока.	Нет человека, который не хотел бы быть здоровым, бодрым, жизнерадостным. А что для этого нужно? -«Жизнь требует движения»,- говорил  Аристотель. А что же такое движение? Как вы понимаете значение этого слова? -Движущимися телами могут быть разнообразные объекты как одушевленного, так и неодушевленного характера. Чаще – это люди … Машины…  Животные… – Что является средой движения? -Я вам предлагаю игру, я назову прилагательные, а вы скажите к какой величине: скорости, времени или расстоянию они подходят? -Быстрее, медленнее? -Длиннее, короче? – Раньше, позже? С данными величинами мы уже знакомы. Решите задачи на смекалку: 1. Шла старушка в Москву, и навстречу ей три старика. Сколько человек шло в Москву? 2. Два одинаковых спутника Земли делают один оборот. Первый за 1ч.40 минут, а второй за 100 минут. Как вы думаете, а какой из спутников вращается быстрее? Почему?	Помогут этому здоровый образ жизни: режим, питание, спорт. Движение – это перемещение, какого-нибудь объекта. Пешеходы, велосипедисты, мотоциклисты, наездники… поезда, теплоходы, катера, лодки… птицы, рыбы, насекомые. Дорога, шоссе, воздушное пространство, водная гладь, космическое пространство. Скорость. Расстояние. Время. Одна – старушка. Оба спутника имеют одинаковое время (1ч.40мин.=100мин.).
II. Актуализация знаний. Устный счёт.	Все вы получаете задания на карточках. После того как каждый из вас запишет  ответ своего примера, вам необходимо расположить их в порядке уменьшения, тогда перевернув карточки, вы прочтёте ключевые слова. В каждой группе будет своё ключевое слово или словосочетание. Итак, внимание,  начали! -Что объединяет все эти виды гонок? –Назовите ключевое слово, в котором соединились лыжная гонка со стрельбой, скорость и меткость! -Что вы знаете об этом виде спорта? (Просмотр 2-3 слайдов презентации). -На уроке мы будем всё время двигаться вперёд, а нашими мишенями станут задания, которые мы выполним.	Задания на карточках: 70∙40   200∙50   300∙30  40∙500 600∙10   500∙90  60∙900  200∙400 83∙1000  70∙80  2000∙7  5∙800 400∙6  90∙40  65∙100  732∙1000 38∙1000  70∙300  800∙40  90∙30 64∙100 530∙100 300∙800 400∙40 40∙500 200∙50 300∙30 70∙40 20000 10000 9000 2800 с пр ин т Ключевые слова: инди-видуаль-ная го-нка с-пр-ин-т па-сь-ю-т ма-сс-с-та-рт э-ста-фет-а сме-шанн-ая эст-афета. -Биатлон! Чтение, слушание.
Подготовительный этап.	Каждая  команда получает задание в виде задачи. Вам необходимо ознакомиться с задачей, решить её и записать ответ. 1. Ветер дует со скоростью 25 м/с. За сколько секунд он утащит воздушный шар на 200 м?  2. Автомобиль ехал 50 км/ч. Какое расстояние он проехал за 5 часов?  3. Рыба-меч за 50 секунд проплывает 1 км 500 м. Какова её скорость? 4. У мамы в кошелке деньги таяли со скоростью 100 рублей в час. За сколько времени там рас-таяло 1000 рублей? 5. Мальчик переплыл на лодке реку за 4 минуты.  С какой скоростью он плыл, если ширина реки 160 метров? 6. Велосипедист за 4 часа проехал 60 км. С какой скоростью он ехал? -Какие знания и умения помогли вам решить эти задачи на движение? На экране формулы и виды задач. Какие виды задач вам известны? Рассмотрим задачу каждого вида.	Работа в группах. От каждой группы выступают по два ученика: 1-читает и анализирует задачу, другой – решение и ответ. 200:25= 8 с. Ветер утащит воздушный шар за 8 секунд. 50 ∙ 5 = 250 км Автомобиль проехал 250 км. 1500:50 = 30 м/с. Рыба-меч развивает скорость 30 м/с 1000:100=10 ч. 1000 рублей растает за 10 часов. 160:4=40 м/мин Скорость мальчика 40 м/мин. 60 : 4 = 15 км/ч Скорость велосипедиста 15 км/ч В задачах на движение рассматриваются три взаимосвязанные величины: S – расстояние (пройденный путь) t – время движения V – скорость формула скорости: V = S : t формула пути: S = V ∙ t Формула времени: t = S : V Существует три вида задач: Задачи на встречное движение; Задачи на противоположное движение; Задачи на движение в одном направлении.
III. Проблемная ситуация.	1) 2 лыжника движутся навстречу друг другу. Скорость одного лыжника 55км/ч, а другого 56 км/ч. Расстояние между ними 150 км. На каком расстоянии лыжники будут друг от друга через 1 час? Рассмотрим рисунок. Эта задача на какое движение? Предлагаются варианты решения. -Как называется скорость передвижения лыжников? -Как её найти? 2) 2 лыжника движутся в противоположных направлениях. Скорость одного лыжника 55км/ч, а другого 56 км/ч. Расстояние между ними 150 км. На каком расстоянии они будут друг от друга через час? Рассмотрим рисунок. Предлагаются варианты решения. О каком движении идёт речь в этой задаче? Как называется скорость передвижения лыжников? -Как её найти? 3) 2 лыжника движутся в одном направлении. Скорость одного лыжника 55км/ч, а другого 56 км/ч. Расстояние между ними 150 км. На каком расстоянии они будут друг от друга через час? Чем эта задача отличается от предыдущих?	На встречное движение. 1.       Найти скорость их сближения: 55+56=111км/ч <=> оба лыжника пройдут 111 км за 1 ч 2.       Узнаём, на каком расстоянии они будут через 1ч.: 150-111=39 км Скорость сближения. Vсближения=V1+V2 1.Находим скорость удаления лыжников: 55+56=111 км/ч<=> оба лыжника пройдут 111 км за 1ч. пути. 2.Чтобы узнать на каком расстоянии они будут через 1ч.: 150+111=261 км Движение в противоположных направлениях. Скорость удаления. Vудаления=V1 +V2 Лыжники двигаются в одном направлении.
IV. Открытие детьми нового знания. V.    Первичное закрепление	-Какие существуют предположения, как решить нашу проблему? -Какое решение будет верное? Почему? -Верно. Составим алгоритм для решения задач на движение в одном направлении с отставанием А на каком расстоянии они будут через 2 часа? 3 часа? -Какой вывод мы сделаем? Какие действия надо выполнить, чтобы найти расстояние, разделяющее объекты?	Обсуждение вариантов решения 1.Группа –Мы  к 55 км + 56 км=111(км)-пройдут оба объекта за 1час. Затем к 111+150=261(км) 2 Группа – От 56-55=1(км)второй объект пройдёт больше первого .К 150+1=151(км) 3Группа- 56-55=1(км/ч)-скорость второго больше.1∙1=1(км)-второй объект пройдёт больше.150+1=151(км) Третье, т.к. чтобы найти расстояние нужно скорость умножить на время, затем прибавить данное расстояние. Алгоритм. 1.     Определи направление движения. 2.     Движение с отставанием? Находим скорость удаления: 56-55=1 км/ч 1∙1=1 км– на 1 км второй лыжник обгонит первого 150+1=151 км – на таком расстоянии они будут через 1ч.  (56-55)x2+150=152(км) (56-55)x3+150=153(км) Чтобы узнать расстояние разделяющее лыжников, необходимо найти скорость удаления, умножить её на время и прибавить к расстоянию.
VI. Коллективное решение с объяснением	Расстояние между биатлонистами  600м. Скорость первого биатлониста  700м/мин, а второго 800м/мин. Нужно узнать, какое расстояние будет между биатлонистами через 8 минут. -В каком направлении двигались биатлонисты? -Движение было с отставанием? Кто отставал? -Знаем время, знаем скорость, можем найти расстояние сразу?	В одном направлении. 1 биатлонист, его  скорость меньше. Нет. Нужно узнать скорость сближения. Затем на какое расстояние 2 биатлонист пробежит больше 1 биатлониста. Решение на доске: 1) Vуд = 800 – 700 = 100 (м/мин.) 2) 100 ∙ 8 + 600 = 1400 (м.)
Закрепление нового материала.	Решение задачи в группах:   Из двух посёлков, расстояние между которыми 27 км, одновременно в одном направлении вышли на прогулку двое ребят на лыжах: Антон и Миша. Скорость Антона 35км/ч, а скорость Миши – 40 км/ч. на каком расстоянии окажутся мальчики через 2 часа?	Работа в группах. 1)Обсуждение в группах. 2)Запись решения задачи. 3)Вычисления. 4)Ответ задачи. 5)Выступление учащихся с объяснением. 6)Оценивание правильности выбранных решений и вычислений. Решение: 1)    40 – 35 = 5 (км/ч) – скорость удаления 2)    5 ∙ 2 = 10 (км) – на 10 км удалится  Миша за 2 часа 3)    10 + 27 = 37 (км)
VIII.Итог урока. IX.Самооценка. Пожелание. Д/з Цветочная церемония.	1. Какие типы задач на движение вы знаете? 2. Что такое скорость? 3. Как найти скорость движения? 3.Чтобы найти расстояние, нужно … 4.Чтобы найти время, нужно … 5. Что такое V сближения? V удаления? -Кто подведёт итог урока? Древние греки говорили: «Если хочешь быть красивым — бегай, если хочешь быть здоровым — бегай, если хочешь быть сильным — бегай». Физические нагрузки нужны всем: больным — чтобы как можно быстрее вернуть здоровье, здоровым — чтобы укрепить мышцы, сердце, сосуды, нервы. Решить старинные задачи. Творческое задание: составить свою задачу на движение в одном направлении.	Учились решать задачи на движение в одном направлении Узнали как найти расстояние на которое удаляется объект. Я работал самостоятельно без ошибок. Получил 5. Я работал с подсказками без ошибок. Получил 4. Я работал с подсказками, допустил ошибки. Получил 3 После каждого этапа урока на доске постепенно открывается рисунок, закрытый геометрическими фигурами. Дети сами оценивают свою работу, раскрашивая аналогичную карточку одним из трех цветов: красным – «Молодец, так держать!»; синим– «Хорошо, но можно лучше!»; зеленым – «Надо подтянуться!»
	Старинная задача. Некий юноша пошел из Москвы к Вологде. Он проходил в день 40 верст. Через день вслед за ним был послан другой юноша, проходивший в день 45 верст. Через сколько дней второй догонит первого? Старинная задача. Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака за 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?

Чтобы быстро решить задачи на движение, в том числе сложные и запутанные, нужно составить к ней схему или таблицу данных.

• Схемы задач на движение помогают представить наглядно условие задачи и найти верное решение.
• Таблица к задачам на движение позволяет структурировать данные, чтобы наглядно видеть исходные данные и неизвестные величины.

Поэтому, чтобы решить сложные задачи на движение, нужно нарисовать схему, а в дополнение к схеме рекомендуется нарисовать таблицу, где в шапке параметры скорости, времени и расстояния. При этом везде применяется основная формула:

Рассмотрим решение следующих типов задач:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решить простые задачи на движение

Для решения простых задач на движение, как правило, схема или таблица не требуется, в них применяется формула нахождения скорости, времени или расстояния. Но иногда, чтобы не запутаться в решении, лучше воспользоваться каким-либо методом. Рассмотрим схему и таблицу, чтобы вы смогли выбрать наиболее удобный для себя способ разобраться в задаче.

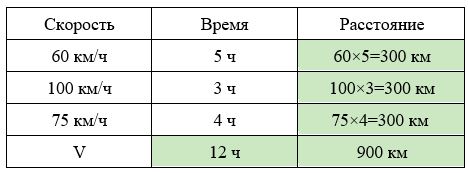
Задача 1. Средняя скорость

Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 

Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь.

• Найдем общее расстояние: 900 км.
• Найдем время в пути: 5 + 3 + 4 = 12 часов.
• Найдем среднюю скорость автомобиля: 900:12 = 75 км/ч.

Задача 2. Движение с остановкой

В 9:00 велосипедист выехал из пункта А в пункт Б. Доехав до пункта Б, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и Б.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности.

• Найдем скорость: 8 : 0,5 = 16 км/ч
• Найдем расстояние: 16×2=32 км.

Задача 3. Уровень ЕГЭ.

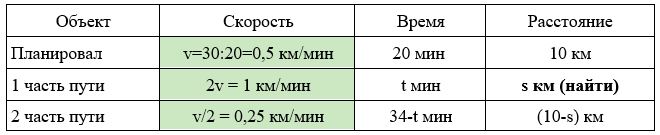
Лыжник планировал проехать 10 км с горы за 20 минут с постоянной скоростью v. Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него 34 минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость, с которой лыжник планировал скатиться: 10 : 20 = 0,5км/мин
• Найдем скорости, с которыми лыжник скатывался: 3км/мин и 0,25км/мин.
• Составим систему уравнений:
  1) 1×t=s  → t=s
  2) 0,25×(34-t)=10-s → 0,25×(34-s)=10-s → s=2 км.

Решить задачи на движение в разных направлениях: сближение и удаление

Задача 4. Скорость удаления

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля  100  км/ч, скорость второго —  70  км/ч. Какое расстояние будет между автомобилями через  4  часа?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) /

Способ 1.
1) 100× 4 = 400 (км)  — проехал первый автомобиль,
2) 70 × 4 = 280 (км)  — проехал второй автомобиль.
3) 400 + 280 = 680 (км).

Способ 2.
1)  (100 + 70),  170  км/ч — это скорость удаления автомобилей.
2) 170× 4 = 680 км.

Задача 5. Скорость сближения

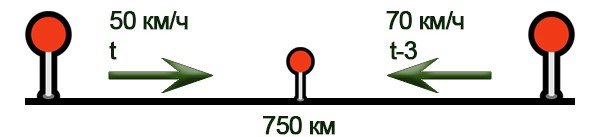
Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

Решение.
Нарисуем схему движения.

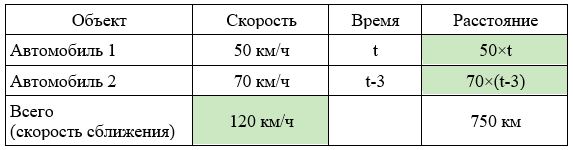
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

Способ 1.

• Составим уравнение: 50×t + 70×(t-3) =750
• Решим уравнение: 120t=960; t=8 часов.
• По условиям задачи нужно найти расстояние от пункта А, то есть расстояние для первого автомобиля: 50×8=400км.

Способ 2.

• За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км.
• Скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля: 600:120=5 часов.
• Таким образом, первый автомобиль всего ехал  8 часов: 50×8=400км.

Задача 6. Скорость сближения

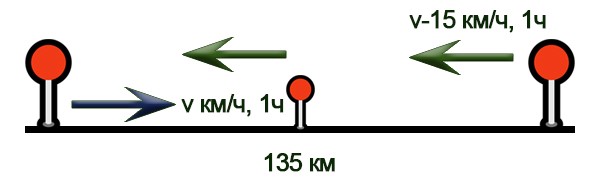
Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?

Решение.
Нарисуем схему движения.

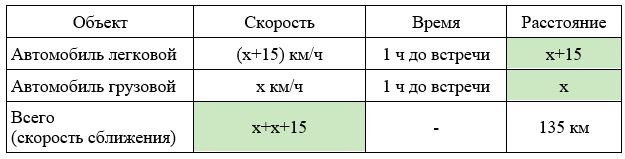
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Пусть x км/ч — скорость грузового автомобиля, тогда (x + 15) км/ч — скорость легкового автомобиля. Получаем уравнение: x+x+15=135; x=60км/ч. 
• Найдем сколько времени грузовой автомобиль затратил на весь путь: 135:60=2,25 часов.
• Найдем сколько времени грузовой автомобиль затратил на путь после встречи: 2,25-1=1,25 часов или 75 минут (1,25*60).
• Ответ: 75 мин.

Задача 7. Уровень ЕГЭ.

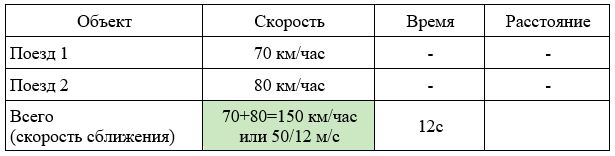
Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость сближения: 70+80=150км/ч.
• Переведем ее в другие единицы измерения: 150 км/ч = 150000/3600 = 50/12 м/с
• Заметим, что фраза “первый поезд прошел мимо пассажира за 12с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12с.
  
• Найдем расстояние 50/12 × 12 =50 метров.

Решить задачи на движение в одном направлении: сближение и удаление

Задача 8. Скорость сближения

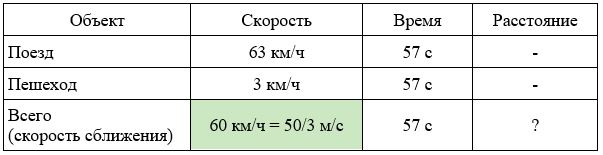
Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость поезда относительно пешехода: 63 − 3 = 60 км/ч
• Переведем скорость сближения в другие единицы измерения: 60 км/ч = 60000/3600=50/3 м/с.
• Найдем длину поезда (расстояние, которое проехал поезд): (50/3)*57=950 м.

Задача 9. Скорость сближения

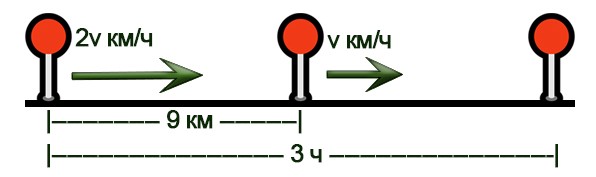
Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость сближения туристов: 9:3=3 км/ч.
• По формуле сближения получаем: 2v-v=3  → v=3 →2v=6 км/ч.
• Ответ: 6

Задача 10. Скорость удаления

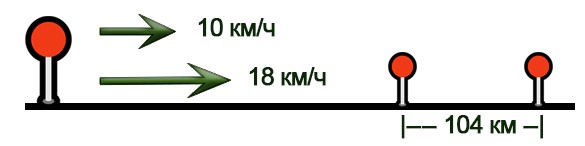
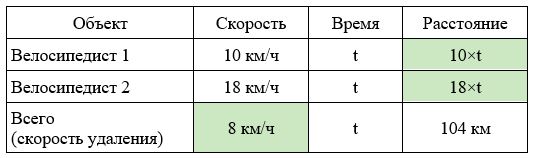
Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость удаления: 18-10=8 км/ч
• Найдем время в пути: 108:8=13 часов.
• Ответ: 13

Задача 11. Скорость удаления

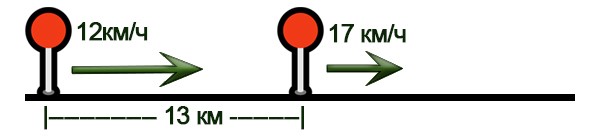
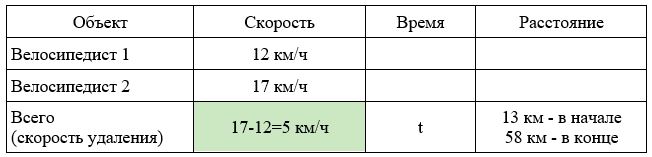
Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость удаления: 17-12=5 км/ч
• Найдем расстояние, на которое они удались друг от друга: 58-13=45 км.
• Найдем время: 45:5=9 часов. 

Задача 12. Уровень ЕГЭ

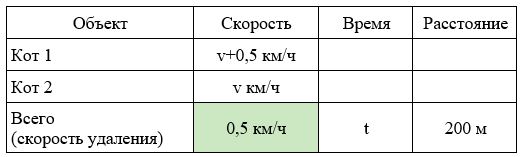
Два кота одновременно выбегают в одном направлении из одного и того же подъезда. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между котами станет равным 200 метрам?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Скорость удаления будет 0,5 км/ч — это скорость, с которой первый кот бежит быстрее второго.
• Найдем время: 0,2 : 0,5 = 0,4 часа
• Переведем время в другие единицы измерения: 0,4 ч = 0,4*60 = 24 мин.

Решить задачи на движение по реке

Задача 13.

Яхта движется по стоячей воде, ее собственная скорость равна 30 км/ч. Встречный ветер каждую минуту сносит яхту на 20 метров. За сколько часов яхта пройдет 259200 метров?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Переведем скорость яхты в другие единицы измерения: 30 км/ч = 500 м/с.
• Найдем скорость удаления: 500-20=480 м/с.
• Найдем время: 259200 :480=540 минут = 9 часов.

Задача 14.

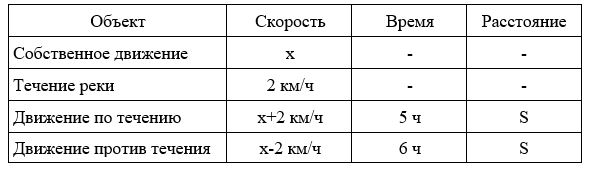
Расстояние от пристани А до пристани Б по течению реки катер прошёл за 5 часов, а на обратный путь он затратил на 1 час больше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 2 км/ч. 

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Пусть скорость катера в неподвижной воде равна x км/ч.
• Составим уравнение: 5×(x+2)=6×(x-2); x=22 км/ч.

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.