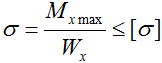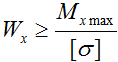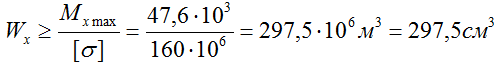Пример решения задачи по расчету минимального момента сопротивления Wx сечения стальной балки, обеспечивающего её прочность.
Задача
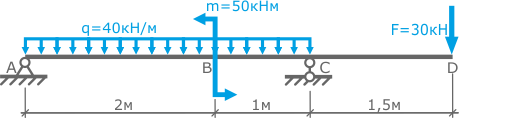
Для заданной стальной балки требуется определить минимальный момент сопротивления сечения Wx для последующего подбора двутавра и расчета размеров других сечений балки по условию прочности.
Допустимые напряжения [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
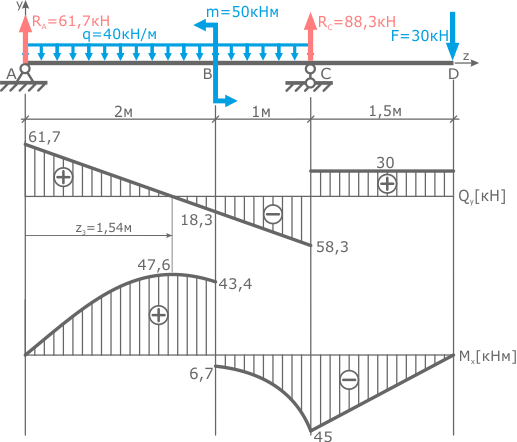
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов.
Прежде чем приступать к расчету размеров сечений балки обеспечивающих ее прочность, определим минимально необходимую величину момента сопротивления сечения Wx.
Момент сопротивления сечений зависит от их формы, размеров и расположения.
Его минимально необходимая величина рассчитывается из условия прочности по нормальным напряжениям при изгибе:
откуда получаем
По построенной эпюре Mx видно, что максимальная величина изгибающего момента составляет 47,6 кНм, поэтому
Таким образом, какую бы форму не имело сечение балки, для обеспечения ее прочности момент сопротивления сечения в данном случае должен иметь величину не менее 297,5 см3.
Теперь можно перейти к определению размеров поперечного сечения балки:
- Расчет диаметра круглого сечения >
- Расчет размеров прямоугольного сечения >
- Подбор номера двутавра >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
В предыдущей статье я рассказывал о моментах инерции, с которыми неразрывно связаны моменты сопротивления. Именно о них сейчас и пойдёт речь. Так что если читатель ещё не читал её — самое время!
А пока нам следует разобраться, что чему сопротивляется. И вообще, является ли организация своего протестного движения моментом сопротивления?
Что такое моменты сопротивления?
В статье про изгиб мы с вами разбирались в том, как найти максимальные напряжения в зоне чистого изгиба
Спойлер:

Где a — максимальное расстояние по интересующей нас оси.
Но чтобы упростить себе расчеты и допускать меньше ошибок, соотношение

Принято называть моментом сопротивления.
Тут может возникнуть вопрос: “Ну так а может не стоило вводить новую величину, а просто оперировать моментами инерции?”
На самом деле так действительно можно сделать, но столкнувшись с большим количеством расчетов читатель и сам наверняка начнет выписывать момент сопротивления. Упрощая алгоритм расчета, мы стремимся исключить возможные ошибки и ускорить сами расчеты. Ведь вместо трехэтажных дробей гораздо удобнее оперировать уже готовым значением.
То есть:
Осевой момент сопротивления – по сути отношение момента инерции к расстоянию до наиболее удаленной от этой оси точки:
По аналогии с полярным моментом инерции для расчетов круглых и близких к ним тел используется полярный момент сопротивления:
Момент сопротивления имеет размерность см3.
Как определить моменты сопротивления простых сечений?
1. Момент сопротивления прямоугольного сечения:
Где Ix:
2. Момент сопротивления квадратного сечения. Частный случай предыдущего пункта:
Где Ix:
3. Момент сопротивления сечения круга:
Где Ix:
4. Момент сопротивления сечения кольцо:
Расчет момента сопротивления сложного сечения
В качестве примера, определим момент инерции и момент сопротивления сечения, изображенного на рисунке ниже:d =20 см, a = 6 см.
1. Определим момент инерции сечения, как разность моментов инерции круга с диаметром d и квадрата со стороной a:
2. Определим момент сопротивления сечения:
3. А теперь давайте попробуем найти разность моментов сопротивления сечения. Будет ли она отличаться от ответа, полученного из двух предыдущих пунктов?
То есть момент сопротивления сечения определяется только через момент инерции! Напрямую складывая/вычитая моменты сопротивления вы получите неправильный ответ!
Подведем небольшой итог:
Момент сопротивления неразрывно связан с моментом инерции.
Моменты сопротивления упрощают расчет нормальных напряжений при изгибе (что особенно важно — максимальных нормальных напряжений), что делает прочностные расчёты при подборе сечения заметно легче и быстрее.
Информация о произведении
Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 845
На этой странице ты можешь найти формулы для расчёта осевых моментов сопротивления простых сечений (фигур).
Формулы для расчёта моментов сопротивления
Моменты сопротивления обозначаются буквой – W.
Моменты сопротивления квадрата


Моменты сопротивления круга


Моменты сопротивления прямоугольника


Моменты сопротивления кольца


На проекте ssopromat.ru, ты также можешь найти другие справочные материалы здесь.
Статические моменты сечения Sx и Sy используются главным образом для определения положения центра площади сечения и центральных осей.
Рассмотрим изменение статических моментов при параллельном переносе осей (рис. 5.1,б). Считая известными F, Sx и Sy в системе координат 0XY определим статические моменты Sx1, Sy1 относительно
новых осей x1, y1.
Учитывая соотношения x1 = x – a, y1 = y – b, получим:
|
Sx1 = ∫ |
y1dF = ∫ ( y − b)dF ; Sy1 = |
∫ |
x1dF = ∫ ( x − a)dF или |
|
F |
F |
F |
F |
|
Sx1 = Sx – bF ; Sy1 = Sy – aF. |
(5.1) |
Оси x1, y1 можно выбрать таким образом, чтобы выполнялись ус-
ловия: Sx1 = 0, Sy1 = 0.
Оси, относительно которых статические моменты сечения равны нулю, называются центральными. Точка пересечения центральных осей называется центром площади сечения.
Принимая Sx1 = 0, Sy1 = 0, из выражений (5.1) координаты центра площади сечения относительно вспомогательных осей x, y определяются по формулам (обозначим xс = а, yc =b):
|
xc = |
S y |
; yc = |
S |
x |
. |
(5.2) |
|
F |
||||||
|
F |
Соответственно, если площадь F и положение центра площади сечения (координаты xс, yc) в системе координат 0ху известны, то статические моменты сечения относительно осей x, y можно определить из выражений (5.2):
|
Sx = F yc ; Sy = F xс. |
(5.3) |
Можно показать, что статистический момент относительно любой оси, проходящей через центр площади сечения, равен нулю.
При определении центра площади сложного сечения применяется следующая процедура:
1) сечение разбивается на n частей, площади (Fi) и положение центров (Ci) площади которых известны;
2)задается вспомогательная система координат, в которой определяются координаты центров площадей (xci, yci) этих частей;
3)вычисляются координаты составного сечения по формулам:
|
∑n Fixci |
∑n Fi yci |
F = ∑n |
||||||||||
|
x |
c |
= |
i= 1 |
; |
y |
c |
= |
i= 1 |
; |
F . |
(5.4) |
|
|
F |
F |
i= |
i |
|||||||||
|
1 |

5.2. Моменты инерции сечения
В табл. 5.2 приведены часто используемые формулы для моментов инерции сечений простой формы, которые получены непосредственно интегрированием (для прямоугольника приведен также и мо-
|
мент инерции при кручении Jk). |
||||
|
Моменты инерции типовых сечений |
Таблица 5.2 |
|||
|
Вид сечения |
Jx |
Jy |
Jp (Jк ) |
|
вh3 |
hв3 |
βhв3 |
||||
|
12 |
12 |
|||||
|
πD4 |
≈ 0,05D4 |
πD4 ≈ |
0,05D4 |
πD4 ≈ |
0,1D4 |
|
|
64 |
64 |
32 |
||||
|
πD4 (1 |
− α 4 ) ≈ |
πD4 |
(1 |
− α 4 ) ≈ |
πD4 (1 |
− α 4 ) ≈ |
|
64 |
64 |
32 |
||||
|
≈ 0,05D4 (1− α 4 ) |
≈ 0,05D4 (1− α 4 ) |
≈ 0,1D4 (1− α 4 ) |
||||
|
вh3 |
_____ |
_____ |
||||
|
36 |

Например, для прямоугольника (рис. 5.2) момент инерции относительно центральной оси х определяется следующим образом :
|
h |
by |
3 |
h |
3 |
|||||||||||||||
|
Jx = ∫ y2dF= |
∫2 |
y2bdy= |
или |
J |
= |
bh |
. |
||||||||||||
|
2 |
x |
||||||||||||||||||
|
3 |
12 |
||||||||||||||||||
|
F |
h |
− |
h |
||||||||||||||||
|
− |
2 |
||||||||||||||||||
|
Рис. 5.2 |
2 |
hb |
3 |
||||||||||||||||
|
Аналогично получим: Jy = |
. |
||||||||||||||||||
|
12 |
Отметим, что для круга и кольца Jx = Jy = 0,5Jp. Это следует из того, что ρ2 = x2 + y2 (см. рис.5.1,а), следовательно, Jp = Jх + Jy.
Рассмотрим изменение моментов инерции сечения при изменении системы координат – при параллельном переносе и повороте осей.
При параллельном переносе осей, например, момент инерции Jх1
изменяется следующим образом (x1 = x – a, y1 = y – b, см. рис. 5.1,б):
|
Jx1 = ∫( y− |
b)2 dF = ∫ y2dF – 2b ∫ ydF + b2 ∫dF = Jх – 2bSx + b2F. |
||
|
F |
F |
F |
F |
Выполнив аналогичные преобразования и для других моментов инерции, получим:
|
Jх1 |
= Jх – 2bSx + b2F; Jy1 = Jy – 2aSy + a2F; |
(5.5) |
|
Jх1y1 = Jхy – aSx – bSy + abF. |
||
|
Если оси x и y – центральные, то Sx = 0, Sy = 0, и тогда формулы |
||
|
(5.5) упрощаются: |
||
|
Jх1 |
= Jх + b2F; Jy1 = Jy + a2F; Jх1y1 = Jхy + abF. |
(5.6) |
Из формул (5.6) следует, что при переходе от центральных осей к нецентральным осевой момент инерции всегда увеличивается.
При повороте осей, учитывая, что x1=xсosα +ysinα , y1=ycosα – xsinα (рис. 5.1,в), моменты инерции изменяются следующим образом:
|
Jx1 = Jx cos2α |
+ Jy sin2α |
– Jxy sin2α ; |
|||
|
Jy1 = Jx sin2α |
+ Jy cos2α |
+ Jxy sin2α ; |
(5.7) |
||
|
Jx1y1 = |
1 |
(Jx – Jy) sin2α |
+ Jxy cos2α . |
||
|
2 |
Вторая формула может быть получена из первой при изменении угла α на 90° . Складывая первые две формулы, находим:
|
Jx1 + Jy1 = Jх + Jy = Jp. |
(5.8) |
Это свойство инвариантности суммы осевых моментов инер-
ции при повороте осей: сумма осевых моментов инерции не изменя-
ется и равна полярному моменту инерции.
Найдем положение осей, относительно которых осевые моменты инерции Jx1 и Jy1 принимают экстремальные значения.
Для этого используем условие dJx1/dα = 0. После преобразований получим:
|
tg2α |
0== |
2Jxy |
. |
(5.9) |
|
|
J y |
− |
Jx |
|||
Такой же результат получается из третьей формулы (5.7) при Jx1y1 = 0.
Оси, относительно которых осевые моменты инерции принимают экстремальные значения (один – max, другой – min), а центробежный момент инерции равен нулю, называются главны-
ми осями инерции (оси x0, y0 на рис. 5.1,г). Соответственно моменты инерции относительно этих осей называются главными моментами инерции (Jmax, Jmin). Иногда главным осям присваивают индексы «1» и «2». Соответственно главные моменты инерции обозначаются J1 и
J2. Обычно считается, что J1 = Jmax, J2 = Jmin. На рис. 5.1,г принято, что Jx0 = Jmax и ось x0 обозначается цифрой 1.
Ось симметрии сечения и любая ей перпендикулярная ось являются главными осями инерции сечения. На рис. 5.1,д показаны знаки Jxy симметричных частей сечения. С учетом этого получается, что центробежный момент инерции всего сечения равен нулю.
Подробнее остановимся на определении главных моментов инерции. Если из формулы (5.9) определен угол α 0, то из первых двух формул (5.7) при α = α 0 находятся значения главных моментов инер-
|
ции: |
|
|
Jx0 = Jx сos2α 0 + Jy sin2α 0 – Jxy sin2α 0 ; |
|
|
Jy0 = Jx sin2α 0 + Jy cos2α 0 + Jxy sin2α 0 . |
(5.10) |
Ясно, что если Jx0 > Jy0 , то Jx0 = Jmax, а Jy0 = Jmin, и наоборот.
Получим формулы для главных моментов инерции, не содержащие тригонометрических функции. Для этого запишем сумму и разность выражений (5.10):
Jx0 + Jy0 = Jx + Jy;
Jx0 – Jy0 = (Jx – Jy) cos2α 0 – 2Jxy sin2α 0 = (Jx – Jy) / cos2α 0 . (5.11)
Во второй формуле использовалась замена 2Jxy = – (Jx-Jy)/tg2α 0 из выражения
(5.9).
Теперь из формул (5.11) получим:
|
Jx0 = |
1 |
(( Jx + Jy)+(Jx – Jy)/cos2α 0 ; |
Jy0 = |
1 |
(( Jx + Jy) – (Jx – Jy)/cos2α 0). |
(5.12) |
||
|
2 |
2 |

Очевидно, что если Jx > Jy, то Jx0 > Jy0. Используя зависимость 1/cos2 0 = ± 1+
tg2 2a0 и формулу (5.9), запишем:
|
1 |
2 |
(Jx − |
2 |
+ |
2 |
||||||
|
= ± 1+ |
4Jxy |
= |
± |
Jy) |
4Jxy |
. |
|||||
|
cos2a0 |
(Jx − |
2 |
(Jx − Jy) |
||||||||
|
Jy) |
В результате получим:
Jx0 = 1(( Jx + Jy) ± ( Jx − Jy )2++ 4Jxy2 );
2
|
Jy0 = |
1 |
(( Jx + Jy) # ( Jx − Jy )2++ 4Jxy2 ). |
(5.13) |
|
|
2 |
||||
|
Верхние знаки берутся при Jx > Jy, а нижние – при Jx < Jy. |
Часто формулы (5.13) объединяют в одну:
|
J1,2 = |
= |
Jx + Jy |
± |
Jx − Jy |
2 |
2 |
||||
|
Jm ax |
( |
) |
+ |
Jxy . |
(5.14) |
|||||
|
m in |
2 |
2 |
||||||||
При этом нужно дополнительно определить соответствие осей x0,
y0 и осей 1, 2.
Если главные моменты инерции известны, то моменты инерции относительно произвольных осей (рис. 5.1,е) могут быть получены из формул (5.7) с учетом того, что Jx0y0 =0:
|
Jx = Jx0 cos2α |
+ Jy0 sin2α |
; |
|
|
Jy = Jx0 sin2α |
+ Jy0 cos2α |
; |
(5.15) |
Jxy = 0,5(Jx0 – Jy0) sin2α .
В частности, из третьей формулы следует, что максимальное значение центробежный момент сечения принимает относительно осей,
повернутых на угол α = 45° к главным осям. При Jx0 = J1 = Jmax, Jy0 = J2 = Jmin получим:
|
Jxymax = |
J1 − J2 |
. |
(5.16) |
2
В расчетных зависимостях для бруса используются характеристики сечений относительно главных центральных осей инерции. Для определения положения этих осей требуется:
1) определить координаты центра площади сечения;
2)определить осевые Jx, Jy и центробежный Jxy моменты инерции относительно центральных осей x, y, параллельных вспомогательным;
3)определить положение главных осей (угол α 0) и главные моменты инерции (Jmax, Jmin) по формулам (5.9), (5.14).

5.3. Радиусы инерции сечения
Моменты инерции сечения относительно осей х и у можно представить как произведения площади F сечения на квадрат некоторой величины, называемой радиусом инерции:
|
Jx = F ix2, Jy = F iy2, |
(5.17) |
где ix , iy – радиусы инерции площади сечения относительно осей х и у.
|
Из выражений (5.17) следует, что: |
|||||||
|
i |
= |
Jx ; |
i |
y |
= |
J y . |
(5.18) |
|
x |
F |
F |
|||||
Главным центральным осям инерции соответствуют главные радиусы инерции сечения:
Соседние файлы в папке Книги и методические указания
- #
04.03.201414.07 Mб253Кочетов Сопротивление материалов.pdf
- #