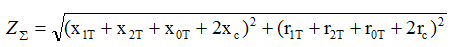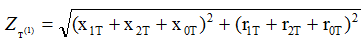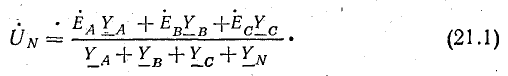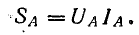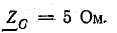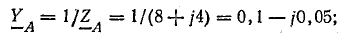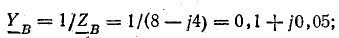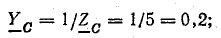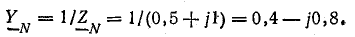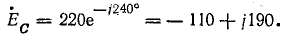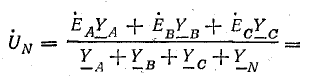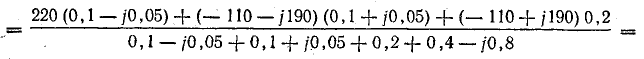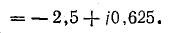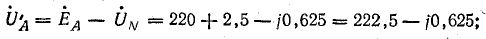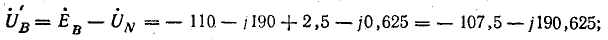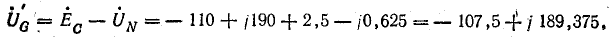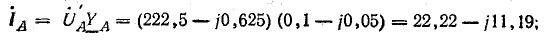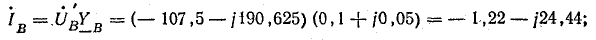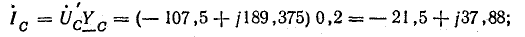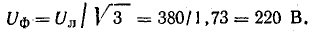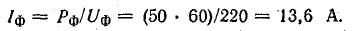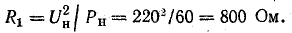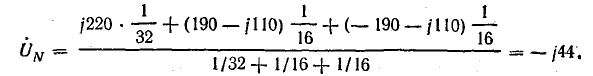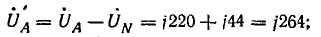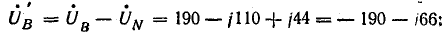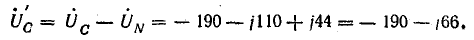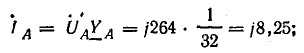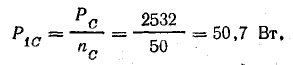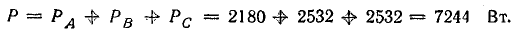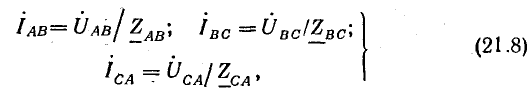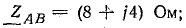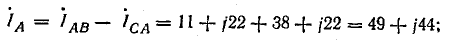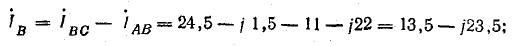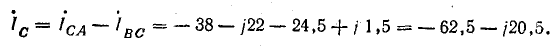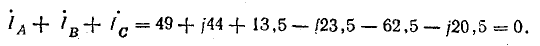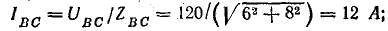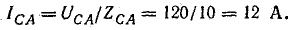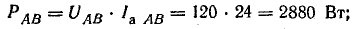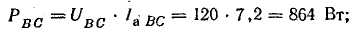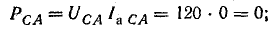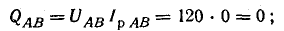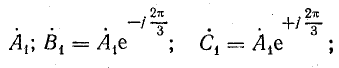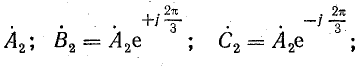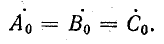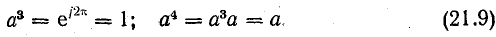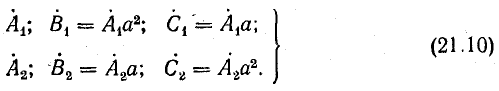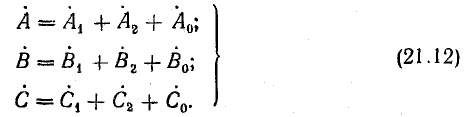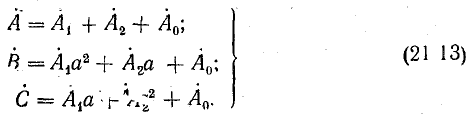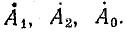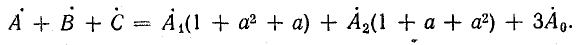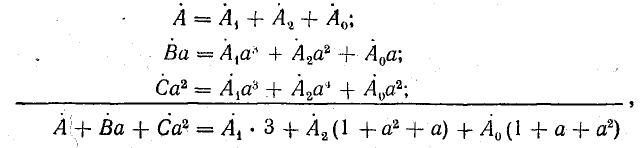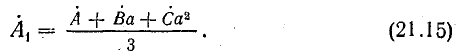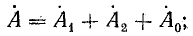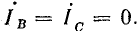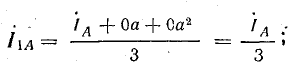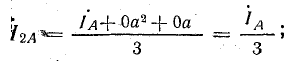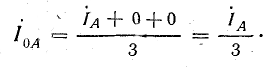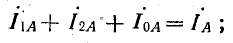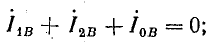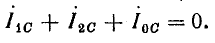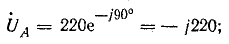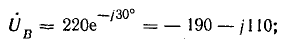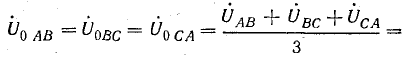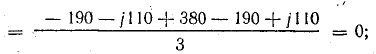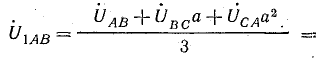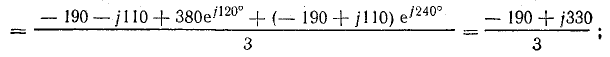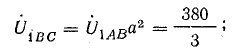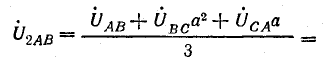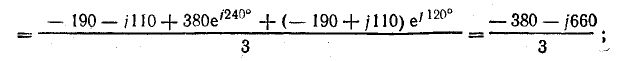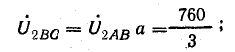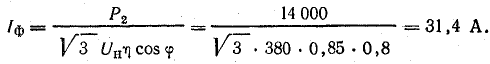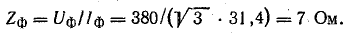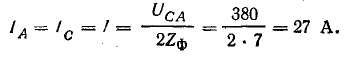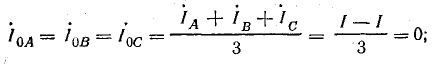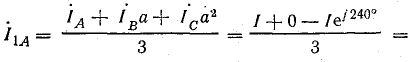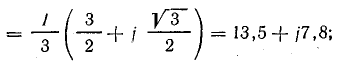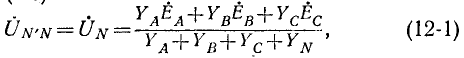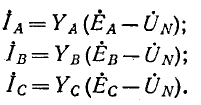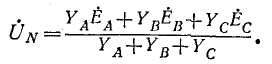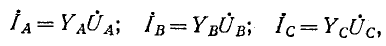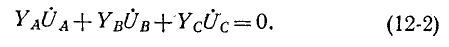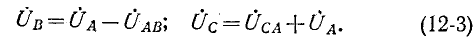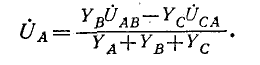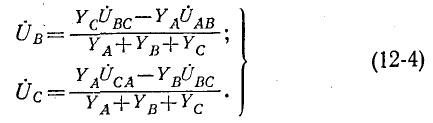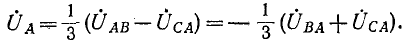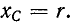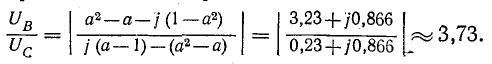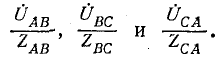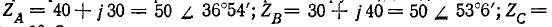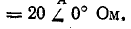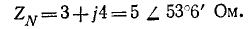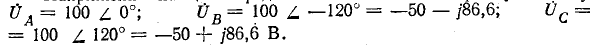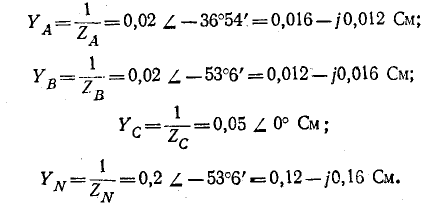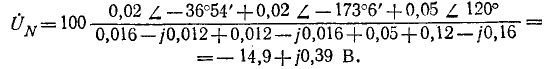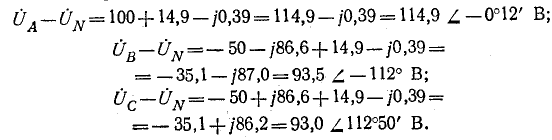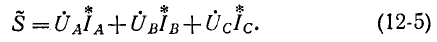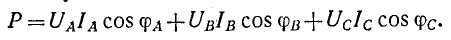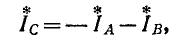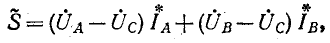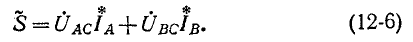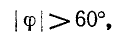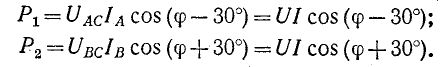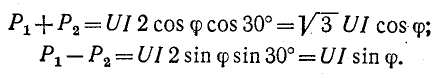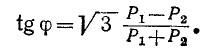Сопротивление нулевого провода как найти

В электрических сетях напряжением до 1000 в с глухим заземлением нейтрали должно быть обеспечено надежное отключение защитным аппаратом однофазового к. з. Это диктуется требованиями техники безопасности.
Расчетными точками для определения величины тока к. з. являются более удаленные (в электрическом смысле) точки сети, так как конкретно этим точкам соответствует меньшее значение тока однофазового к. з.
Величина однофазового тока к. з. может быть определена по приближенной формуле

где U ф — фазное напряжение сети, в;
Z т — полное сопротивление понижающего трансформатора току замыкания на корпус, ом;
Z п — полное сопротивление петли фаза — нуль полосы до более удаленной точки сети, ом.
Расчетные значения полных сопротивлений понижающих трансформаторов при однофазовых замыканиях приведены в табл. 7-1.
Для трансформаторов мощностью более 630 ква при определении тока к. з. можно принять:
Z т =0
Полное сопротивление петли проводов либо жил кабеля полосы определяется по формуле

где R п — активное сопротивление фазного ( R ф ) и нулевого (Ro) проводов, ом;
R п =R ф +R о (7-3 )
Х п — индуктивное сопротивление петли проводов либо жил кабеля, ом.

Активные сопротивления проводов из цветных металлов определяются по табл. 5-1. Средние значения индуктивных сопротивлений петель проводов либо жил кабелей из цветных металлов на 1 км полосы даны в табл. 7-2.
Для железных проводов индуктивное сопротивление петли проводов определяется по формуле

где Х’ п — наружное индуктивное сопротивление петли из прямого и оборотного проводов, равное для воздушной полосы напряжением до 1000 В 0,6 Ом/км; Х» п.п и Х» п.о — внутренние индуктивные сопротивления соответственно прямого и оборотного проводов полосы, Ом/км.
Значения полных сопротивлений петель для проводов и жил кабелей из цветных металлов на 1 км полосы даны в табл. 7-3. В табл. 7-6 указаны сопротивления петли «фаза трехжильного кабеля — железная полоса» для небронированных кабелей.

Таблица 7-1 Расчетные сопротивления трансформаторов при однофазовом к. з. на стороне 400/230 в

Тип	Номинальная мощность, ква	Напряжение обмотки ВН. кв	Схема соединений	Полное сопротивление Zт, ом
ГОСТ401-41
ТМ, ТМА ТМ ТМ ТМ ТМА ТСМА ТСМ ТМ, ТМА ТМ, ТМА ТМ. ТМА ТМ, ТМА ТМ, ТМА ТМ, ТМА ТМ, ТМА ТМ, ТМА ТМ	20 30 50 100 100 100 100 180 180 320 320 560 560 750 1000 1000	6-10 6-10 6-10 6-10 35 6-10 35 6-10 35 6-10 35 6-10 35 6-10 6-10 35	У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун	1,39 0,9 0,54 0,27 0,25 0,26 0,25 0,15 0,14 0,085 0,08 0,048 0,046 0,036 0,027 0,026
ГОСТ12022-66
ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ ТМ	25 40 63 63 100 100 160 160 250 250 400 400 400 630	6-10 6-10 6-10 20 6-10 20-35 6-10 20-35 6-10 20-35 6-10 20-35 6-10 6-10	У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун У/Ун Д/Ун У/Ун	1,04 0,65 0,413 0,38 0,26 0,253 0,162 0,159 0,104 0,102 0,065 0,064 0,022 0,043
ГОСТ11920-66
ТМ ТМ ТМ ТМ	1 000 1 000 1 000 1 000	6-10 20-35 6-10 20-35	У/Ун У/Ун Д/Ун Д/Ун	0,027 0,026 0,009 0,01
—
ТСЗ ТСЗ ТСЗ ТСЗ ТСЗ ТСЗ ТСЗ ТСЗ ТСЗ ТСЗ	160 180 250 320 400 560 630 750 1 000 1 000	6-10 6-10 6-10 6-10 6-10 6-10 6-10 6-10 6-10 6-10	Д/Ун У/Ун Д/Ун У/Ун Д/Ун У/Ун Д/Ун У/Ун Д/Ун У/Ун	0,055 0,15 0,035 0,085 0,022 0,048 0,014 0,036 0,009 0,027

Примечания: Для понижающих трансформаторов с напряжением вторичных обмоток 230/133в значения сопротивлений в 3 раза меньше обозначенных в табл. 7-1.
Условные обозначения схем соединений трансформаторов:
У — звезда; Ун — звезда с выведенной нулевой точкой; Д — треугольник.

Таблица 7-2 Средние значения индуктивных сопротивлений петли прямого и оборотного проводов либо жил кабеля, выполненного из цветных металлов ом/км

Условия прокладки	Индуктивные сопротивления
Кабель до 1 кв либо провода, проложенные в трубах	0,15
Изолированные провода на роликах	0,4
Провода на изоляторах снутри помещений либо по внешним стенкам строения	0,5
Воздушные полосы низкого напряжения	0,6

Таблица 7-3 Полные сопротивления петли прямого и оборотного провода полосы либо жил кабеля, ом/км

Сечение провода, мм.кв	Кабель и провода в трубах	Провода на роликах и изоляторах	Провода воздушных линий
прямого	оборотного	медные	дюралевые	медные	дюралевые	медные	дюралевые
1 1,5 1,5 2,5 2,5 4 4 4 6 6 6 10 10 10 16 16 16 25 25 25 35 35 35 50 50 50 70 70 70 95 95 95 120 120 120 150 150 150	1 1 1,5 1,5 2,5 1,5 2,5 4 2,5 4 6 4 6 10 6 10 16 10 16 25 10 16 35 16 25 50 25 35 70 35 50 95 50 70 120 50 70 150	37,8 31,5 25,2 20,2 15,1 17,3 12,2 9,3 10,6 7,71 6,12 6,50 4,90 3,68 4,26 3,04 2,40 2,58 1,94 1,49 2,38 1,74 1,09 1,60 1,14 0,793 1,03 0,833 0,58 0,755 0,608 0,428 0,568 0,461 0,350 0,535 0,430 0,285	— — — — 25,2 — 20,5 15,8 17,9 13,2 10,5 11,1 8,42 6,32 7,24 5,14 3,96 4,44 3,26 2,56 4,08 2,90 1,84 2,62 1,92 1,29 1,74 1,39 0,932 1,27 0,99 0,797 0,922 0,745 0,561 0,862 0,687 0,446	— — 25,2 20,2 15,1 17,3 12,2 9,3 10,6 7,71 6,14 6,52 4,92 3,71 4,28 3,08 2,45 2,62 1,98 1,55 2,42 1,79 1,16 1,65 1,21 0,890 1,11 0,927 0,706 856 0,712 0,566 — — — — — —	— — — — 25,2 — 20,5 15,8 17,9 13,2 10,5 11,1 8,42 6,32 7,24 5,15 3,99 4,46 3,30 2,60 4,11 2,96 1,90 2,66 1,97 1,36 1,80 1,45 1,03 1,34 1,08 0,815 — — — — — —	— — — — — — — 9,3 — — 6,16 — 4,96 3,75 4,32 3,13 2,52 2,69 2,08 1,68 2,48 1,87 1,29 1,74 1,32 1,05 1,24 1,08 0,896 1,02 0,915 0,772 0,858 0,792 0,732 — — —	— — — — — — — — — — — — — — — — 4,03 4,50 3,34 2,66 4,15 3,00 1,96 2,70 2,03 1,44 1,86 1,53 1,13 1,42 1,18 0,907 1,09 0,945 0,808 1,04 0,808 0,732

Сечение кабеля, мм.кв	Ток и материал жил кабеля	Размеры металлической полосы, мм
20X4	40X4	50X4	50X4	60X4	80X4	100X4, 100X6	100X5, 100X8
Ток срабатывания наибольшего расцепителя автомата, а	150	1400	200	1400	250	1400	300	1400	400	1400	500	1400
Номинальный ток плавкой вставки безынарционного предохранителя, а	60	600	80	600	100	600	120	600	150	600	200	600
Материал жил кабеля:	Полное сопротивление петли, ом/км
3X4

Таблица 7-6 Полные сопротивления петли “фаза 3-х жильного кабеля — железная полоса”, ом/км

Примечание: Сопротивление петли «фаза кабеля -стальная полоса» не остается неизменным для обозначенных в таблице значений тока, так как сопротивление металлической полосы находится в зависимости от тока. Для промежных значений тока величина сопротивления определяется интерполяцией

Надежное отключение защитным аппаратом однофазового к. з. будет обеспечено при условии выполнения соотношения

где К 31 — допустимая кратность малого тока к. з. по отношению к номинальному току плавкой вставки предохранителя либо току срабатывания, либо номинальному току наибольшего расцепителя автомата I 3 ;
I к -наименьшая величина однофазового тока к. з., определяемая по формуле (7-1),а.
Допустимая кратность малого тока к. з. должна быть более 3 по отношению к номинальному току плавкой вставки предохранителя и номинальному току расцепителя автоматического выключателя, имеющего назад зависимую от тока характеристику, и более 1,1 К р по отношению к току срабатывания автоматического выключателя, имеющего только электромагнитный расцепитель (К р — коэффициент, учитывающий разброс черт расцепителя по данным завода).
Для сетей, прокладываемых во взрывоопасных помещениях, допустимые кратности тока к. з. растут до значения 4 по отношению к номинальному току плавкой вставки предохранителя и 6 по отношению к номинальному току расрасцепителя автоматического выключателя с назад зависимой от тока чертой.
Для сетей, защищаемых только от токов к. з., в нужных случаях (к примеру, для отстройки от токов самозапуска движков) допускается завышение токов плавких вставок предохранителей и уставок расцепителей автоматов, но при всем этом кратность тока к. з. обязана иметь значение более 5 по отношению к номинальному току плавкой вставки предохранителя и более 1,5 по отношению к току срабатывания электромагнитного расцепителя автомата.
Значения допустимой кратности тока к. з. для разных критерий прокладки сети приведены в табл. 7-8.

Расчет токов однофазового кз в сети 0,4 кВ

В данной статье пойдет речь об определении величины тока однофазового тока к.з. в сетях 0,4 кВ с глухозаземленной нейтралью.

Данный вопрос очень животрепещущ, так как электрические сети 0,4 кВ, являются более распространёнными.

В текущее время существует два способа расчета однофазового КЗ – четкий и приближенный и оба способа основаны на способе симметричных составляющих.

1. Четкий способ определения тока однофазового КЗ

1.1 Четкий способ определения тока однофазового КЗ, представлен в ГОСТ 28249-93 формула 24, и рассчитывается по формуле:

Используя данный способ можно с большой степенью точности определять токи КЗ при узнаваемых сопротивлениях прямой, оборотной и нулевой последовательности цепи фаза-нуль.

К огорчению, на практике данный способ не всегда может быть применять, из-за отсутствия справочных данных на сопротивления прямой, оборотной и нулевой последовательности для кабелей с дюралевыми и медными жилами с учетом методов прокладки фазных и нулевых проводников.

2. Приближенный способ определения тока однофазового КЗ

2.1 Приближенный способ определения тока однофазового кз при большой мощности питающей энергосистемы (Хс < 0,1Хт), рассчитывается по формуле [Л1, с 4 и Л3, с 39]:

• Uф – фазное напряжение сети, В;
• Zт – полное сопротивление трансформатора току однофазового замыкания на корпус, Ом;
• Zпт – полное сопротивление петли фаза-нуль от трансформатора до точки КЗ, Ом.

2.2 Если же питающая энергосистема имеет ограниченную мощность, то тогда ток однофазового кз определяется по формуле 2-26 [ Л3, с 39]:

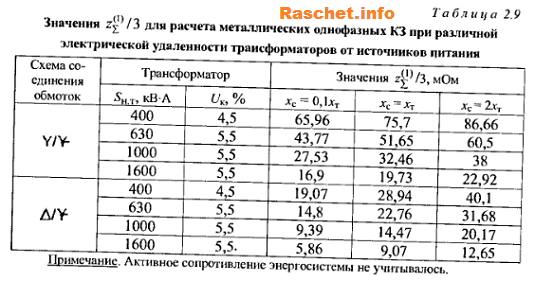
2.3 Значение Z∑ определяется по таблице 2.9 либо можно найти по формуле 2-25 [ Л3, с 39]:

где:
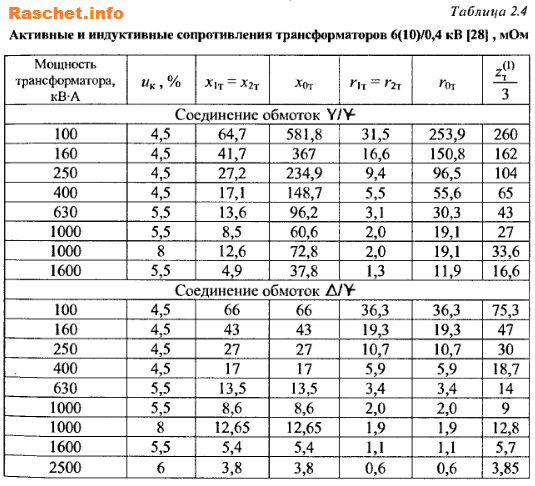
х1т и r1т; х2т и r2т; х0т и r0т — индуктивное и активное сопротивления трансформатора токам прямой, оборотной и нулевой последовательности, мОм. Принимаются по таблице 2.4 [Л3, с 29].

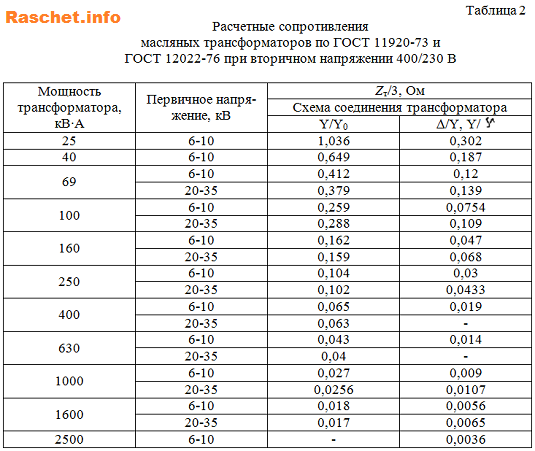
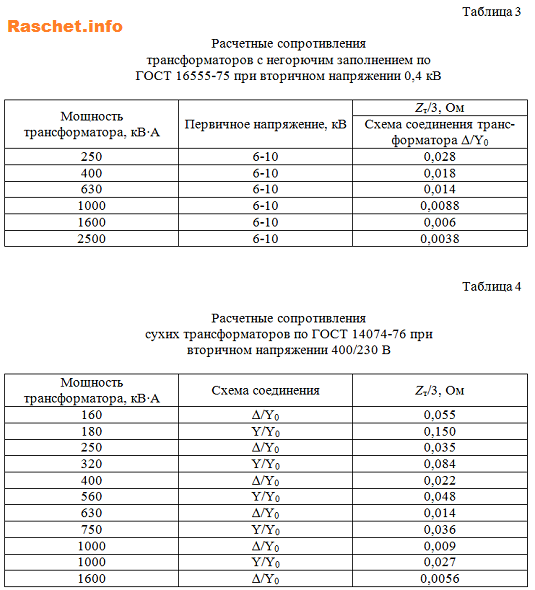
Значение Zт/3 для разных трансформаторов с вторичным напряжением 400/230 В, можно принять по таблицам 2, 3, 4 [Л1, с 6,7].

Сопротивления контактов шин, аппаратов, трансформаторов тока в данном способе не учитываются, так как арифметическая сумма Zт/3 и Zпт делает не который припас.

2.4 Полное сопротивление трансформатора Zт, определяется по формуле 2-24 [Л3, с 39]:

2.5 Полное сопротивление петли фаза-нуль, определяется по формуле 2-27 [Л3, с 40]:

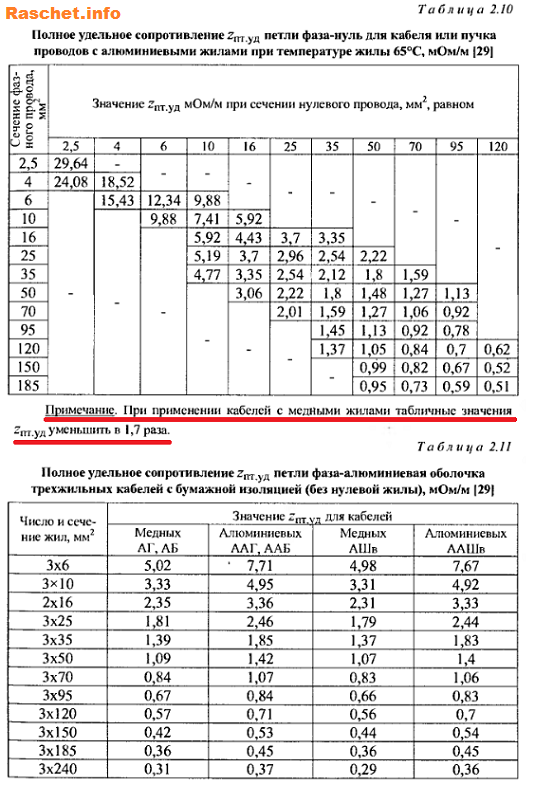
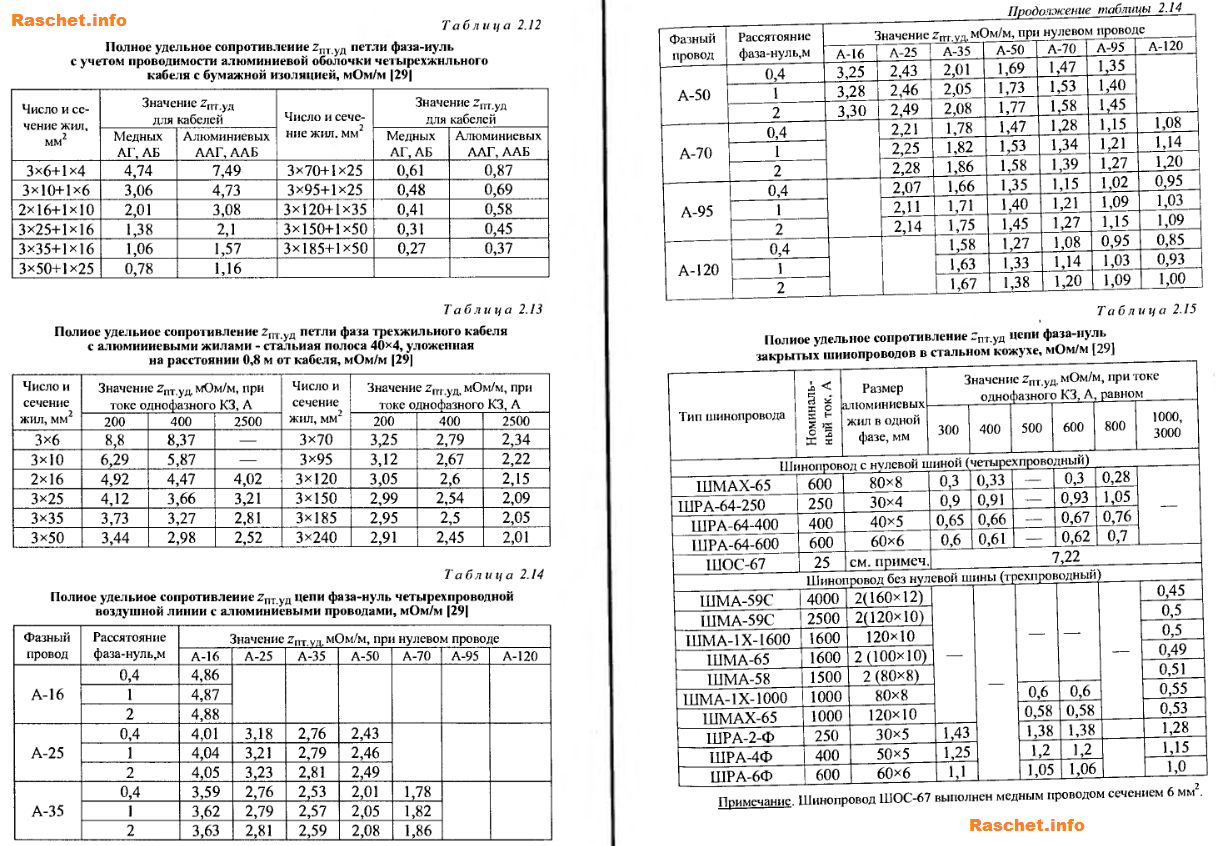
• Zпт.уд. – полное удельное сопротивление петли фаза-нуль для каждого участка от трансформатора до места КЗ определяется по таблицам 2.10 – 2.14 [Л3, с 41,42] либо по таблицам [Л2], мОм/м;
• l – длина участка, м.

Ниже представлены справочные таблицы со значениями удельного сопротивления петли фаза-нуль для разных кабелей и шинопроводов согласно [Л3, с 41,42].

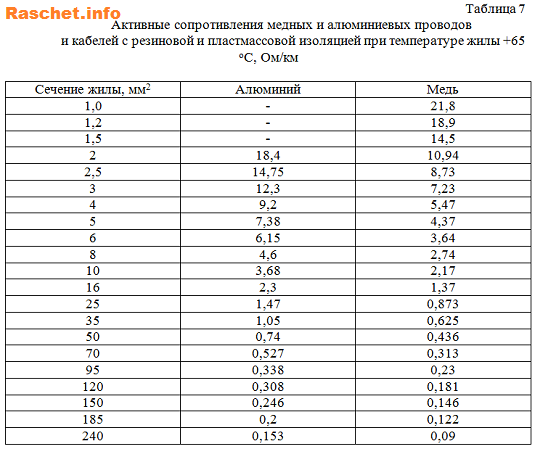
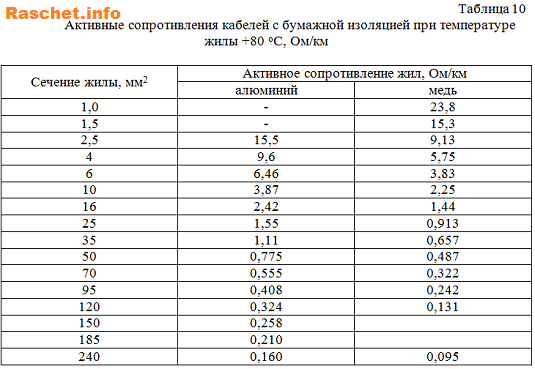
Справочные таблицы 7, 10 со значениями активных сопротивления медных и дюралевых проводов, кабелей [Л1, с 6, 14].

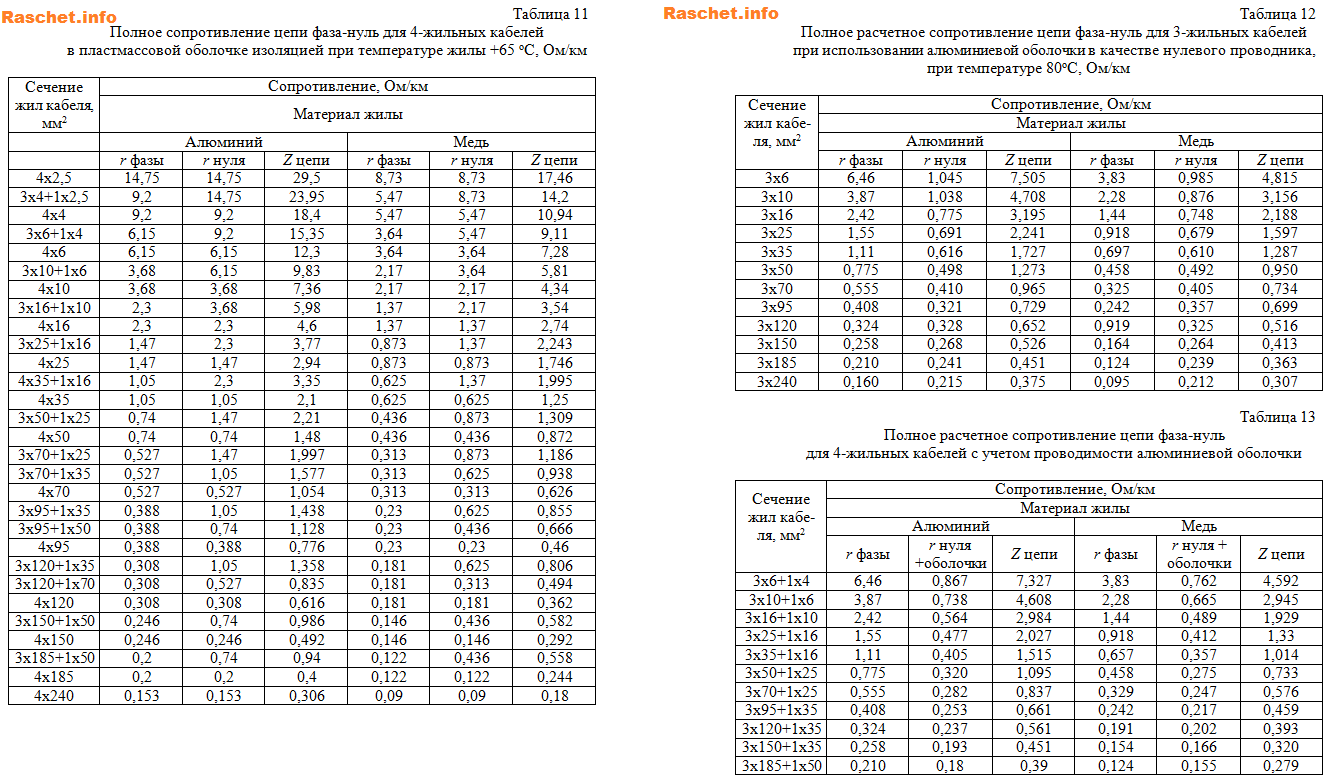
Справочные таблицы 11, 12, 13 со значениями полного расчетного сопротивления цепи фаза-нуль для 3(4) — жильных кабелей с различной изоляций и при температуре жилы +65(+80) С [Л1, с 15, 16].

На практике согласно [Л1, с 5] рекомендуется применять приближенный способ определения тока однофазового КЗ. При таком способе, допустимая погрешность в расчете тока однофазового КЗ при неточных начальных данных в среднем равна – 10% в сторону припаса; 18-20% — при схеме соединения трансформатора Y/Y0, когда преобладает активная нагрузка и для зануления применяется 4-я жила или оболочка кабеля; 10-12% — при использовании железных труб для зануления проводки.

Из выше изложенного, следует, что при использовании данного способа, создаётся не который припас при расчете, который гарантирует срабатывания защитного аппарата, согласно требованиям ПУЭ.

1. Советы по расчету сопротивления цепи «фаза-нуль». Главэлектромонтаж. 1986 г.
2. ГОСТ 28249-93 – Способы расчета в электроустановках переменного тока напряжением до 1 кВ.
3. Беляев А.В. Выбор аппаратуры, защит и кабелей в сети 0,4 кВ. Учебное пособие. 2008 г.

Величина сопротивления нулевой последовательности используется в расчетах однофазного короткого замыкания методом симметричных составляющих. Но, зачастую проблематично найти значение этой величины в справочниках для различного исполнения электрических сетей, и, следовательно, невозможно выполнить расчет. При этом значения сопротивлений фазного и нулевого проводников в справочниках присутствуют. Как же быть?

Можно  использовать следующие формулы расчета сопротивления нулевой последовательности:

где R0л (X0л) – активное (индуктивное) сопротивление нулевой последовательности линии;

Rф (Xф) – активное (индуктивное) сопротивление фазного проводника;

Rн (Xн) – активное (индуктивное) сопротивление нулевого проводника.

 Вывод формул смотри ниже.

Сразу следует подчеркнуть, что этими формулами следует пользоваться, если сопротивление нулевой последовательности неизвестно. Если есть выбор, использовать справочные данные, или выполнить расчет сопротивления нулевой последовательности, то, наверное, следует отдать предпочтение справочным данным.

Итак, основным документом, регламентирующим расчеты токов короткого замыкания до 1000 В, является ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ». В справочном приложении 2 этого ГОСТ, в таблицах №№ 6-14 содержатся данные о сопротивлениях прямой и нулевой последовательностей для различного исполнения кабельных линий. К сожалению, есть варианты исполнения линий, довольно распространенные, для которых нет подходящей таблицы в этом стандарте. Например, нельзя найти параметры 4-жильного кабеля с алюминиевыми жилами в непроводящей оболочке, если сечение жил одинаковое (в табл.11 сечение нулевого провода меньше, чем сечение фазного). Также, отсутствуют аналогичные данные для кабеля с медными жилами (в табл.14 приведены данные для кабеля в стальной оболочке;  да и номенклатура сечений неполная).

В то же время, в справочниках есть данные сопротивлений для любого исполнения линий. Вот только приведены эти данные в виде сопротивлений фазного и нулевого проводников (для применения в расчетах тока однофазного короткого замыкания методом петли «фаза-ноль»), а не сопротивлений прямой, обратной и нулевой последовательностей. Логично предположить, что если результаты расчета по двум разным методам:

• методу петли «фаза-ноль»;
• методу симметричных составляющих,

приравнять, то можно сделать вывод о соотношениях сопротивлений, используемых в этих методах.

Формула расчета тока однофазного КЗ методом петли «фаза-ноль» выглядит следующим образом (см. [2] и [3]):

где U – линейное напряжение сети;

Uф – фазное напряжение сети;

Zпт – полное сопротивление петли фаза-ноль от трансформатора до точки КЗ;

Zс.т. – сопротивление системы и трансформатора току однофазного КЗ

где Х1т, Х2т, Х0т, R1т, R2т, R0т – индуктивные (Х) и активные (R) сопротивления трансформатора токам прямой (1), обратной (2) и нулевой (0) последовательностей;

Хс – индуктивное сопротивление питающей сети;

Rд – сопротивление электрической дуги.

Перепишем формулу (3) в более удобной форме, при этом:

• учтем, что сопротивления прямой и обратной последовательностей равны;
• умножим числитель и знаменатель на 3;
• в знаменателе будем складывать не модули полных сопротивлений, а отдельно их активные и индуктивные составляющие (это сделает расчет более точным).

где Rф (Rн) – активное сопротивление фазного (нулевого) проводника линии;

Xф (Xн) – индуктивное сопротивление фазного (нулевого) проводника линии.

Вот формула расчета тока однофазного КЗ методом симметричных составляющих (см. [1], п.8.2.1, формула 24):

 

где R1сум. (R0сум.) – суммарное активное сопротивление прямой (нулевой) последовательности;

X1сум. (X0сум.) – суммарное индуктивное сопротивление прямой (нулевой) последовательности.

Перепишем формулу (6), подставив в нее значение фазного напряжения, а также расписав более подробно суммарные величины сопротивлений прямой и обратной последовательностей:

где R1л (R0л) – суммарное активное сопротивление прямой (нулевой) последовательности линии;

X1л (X0л) – суммарное индуктивное сопротивление прямой (нулевой) последовательности линии.

После сравнения формул (5) и (7) получим следующие выражения:

Считая, что Rф=R1л, Xф=X1л, выразим из соотношений (8) и (9) величины сопротивлений нулевой последовательности:

 Итак, при отсутствии справочных значений о величине сопротивления нулевой последовательности линии, эти значения можно рассчитать, используя справочные данные сопротивлений фазного и нулевого проводников линии.

Используемая литература

1. ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ».
2. Кужеков С. Л. Практическое пособие по электрическим сетям и электрооборудованию / С.Л. Кужеков, С. В. Гончаров. – Ростов н/Д.: Феникс, 2007.
3. Тульчин И. К., Нудлер Г. И. Электрические сети и электрооборудование жилых и общественных зданий. – 2-е изд., перераб. и доп. – М.: Энерготамиздат, 1990.

Эту статью можно обсудить ниже в комментариях или на форуме.

1. Нулевой провод

Рассмотренные случаи несимметрии в
трехфазных цепях, так или иначе
приводят к изменению напряжений приемника
и сдвига фаз между ними. Изменение
напряжений влечет за собой изменение
токов, т.е. перекос фаз. Перекос фаз в
трехфазной цепи создает неодинаковые
напряжения на фазах приемника, несмотря
на симметрию фазных эдс источника
питания. Это недопустимо, так как
создается аварийный режим работы
трехфазной системы.

Напряжение на нейтральном проводе по
закону Ома

.
(6-114)

Из выражения следует, что напряжение
на нулевом проводе равно нулю при или= 0.

Как известно, ток в нулевом проводе
=+При симметричной нагрузке

В остальных случаях ток в нулевом проводе
имеет отличную от нуля величину и будет
тем больше, чем сильнее отличаются
нагрузки в фазах приемника.

Теоретически сопротивление нулевого
провода никогда не может быть равным
нулю, так как любой провод, соединяющий
точи 0 и 0′, всегда обладает каким-то
сопротивлением. Однако практически,
если сечение нулевого провода составляет
0,3 – 0,5 от сечения линейного провода и
имеет хорошие контакты, то считается,
что = 0. Тогда.

Таким образом, напряжение на
фазах приемника будет равно эдс фаз
генератора и система приемника будет
симметричной, хотя нагрузки на фазах
приемника неодинаковы.

Нулевым является провод,
выравнивающий потенциалы точек 0 и 0′,
поэтому его часто называют уравнительным.
Отсутствие нулевого проводапри несимметричной нагрузке приводит
к перекосу системы. Следовательно,
функция нулевого провода состоит в том,
чтобы при несимметричной нагрузке фаз
приемника сохранить симметричность
системы приемника. Кроме того, наличие
нулевого провода дает возможность
получить от генератора не только
линейное, но и фазное напряжение, что
очень важно при электроснабжении.

1. ТРЕХПРОВОДНАЯ
   СИСТЕМА. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ.

Обмотки трехфазного генератора, а также
трехфазные нагрузки могут быть соединены
еще одним способом: конец первой обмотки
соединяют с началом второй, конец второй
– с началом третьей, конец третьей – с
началом первой, а узлы соединения служат
отводами (рис. 91 а). Такой способ соединения
называют треугольником.

а

б

Рис.91

Кажущегося короткого замыкания в
обмотках генератора не произойдет, так
как в любой момент времени сумма эдс в
его обмотках равна нулю:

=0 (6-115)

и ток при отсутствии внешней нагрузки
в замкнутом треугольнике также равен
нулю.

Это справедливо в том случае, если все
три эдс строго синусоидальны. Но в
работе генератора форма эдс может
отклоняться от синусоидальной, поэтому
соединение треугольником обмоток
генератора, как правило, не применяют.
Однако соединение треугольником широко
используется у трехфазных потребителей,
создающих симметричную нагрузку
(двигатели, печи, осветительные системы
и т.д.).

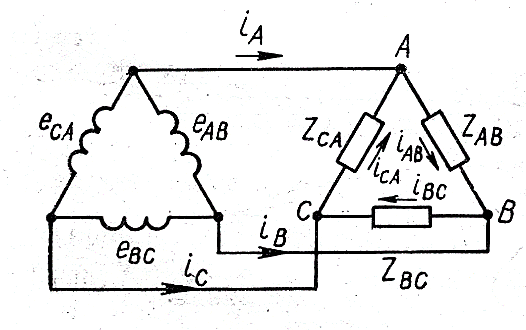
Если включить фазы приемника тока: (рис.91 а)- непосредственно между линейными
проводами трехпроводной системы, то
получим соединение токоприемников
треугольником. При таком соединении
нет различия между фазным и линейным
напряжениями, так как напряжение между
началом и концом каждой фазы приемника
является в то же время линейным
напряжением, т.е.

(6-116)

В общем виде

.
(6-117)

Если различие между фазным и линейным
напряжениями в соединении треугольником
отсутствует, зато появляется различие
между фазными () и линейными (токами приемника.

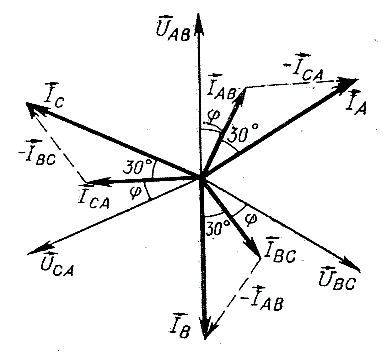
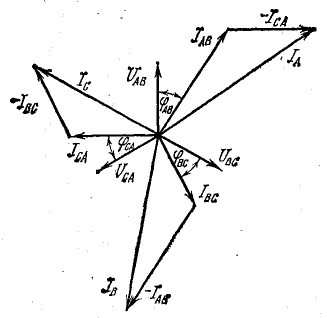
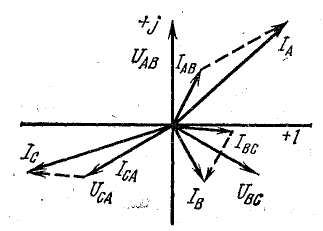
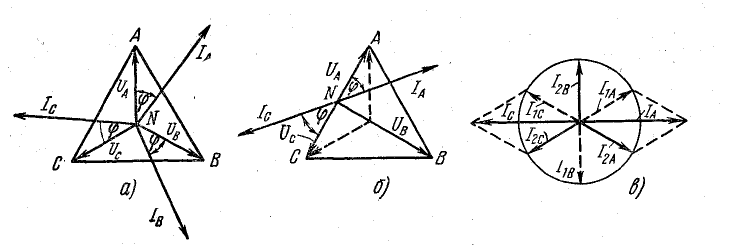
Построим векторные диаграммы токов и
найдем зависимость между их абсолютными
значениями. Условимся положительными
направлениями фазных токов считать
направления от А к В, от В к С и от С к А,
а положительными направлениями линейных
токов – направления от генератора к
приемнику. Тогда по первому закону
Кирхгофа имеем:

(6-118)

откуда

Из последних соотношений видно, что
любой из линейных токов равен геометрической
разности фазных токов.

Также следует, что при любых равных
значениях фазных токов геометрическая
сумма линейных токов равна нулю, т.е.

(6-119)

В случае симметричной нагрузки
(=векторы фазных токов одинаково сдвинуты
по фазе на угол φ относительно
соответствующих векторов напряжений
и создают симметричную трехлучевую
звезду фазных токов (рис.91б).

Для построения на этой же диаграмме
векторов линейных токов воспользуемся
соотношениями ( ), на основании которых
вектор каждого линейного тока представляет
собой разность между двумя соседними
векторами, отсчитанными против часовой
стрелки. Произведя построения, аналогичные
построениям векторов линейных напряжений
(см. рис. ), получим, что векторы линейных
токов образуют трехлучевую звезду,
повернутую относительно звезды фазных
токов на 30⁰. Из полученной диаграммы
видно, что линейные токи представляют
собой основания равнобедренных
треугольников с углами 120⁰при
вершине. Из диаграммы следует, что
соотношение между фазными и линейными
токами равно

(6-120)

Таким образом, два способа
включения потребителей (звездой или
треугольником ) расширяет возможности
использования этих потребителей.
Например, если каждая из трех обмоток
трехфазного электродвигателя рассчитана
на рабочее напряжение 220В, то,
электродвигатель может быть включен
треугольником в сеть 220/127Bили звездой в сеть 380/220В.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Трехфазные несимметричные цепи:

Трехфазная цепь несимметрична, если комплексы сопротивлений ее фаз неодинаковы.

Несимметричной может быть действующая в цепи система э. д. с. (не равны модули э. д. с. или фазовые сдвиги между каждой парой э. д. с.). .
Для расчета несимметричной цепи применяются различные методы в зависимости от ее схемы и вида несимметрии.

Расчет несимметричной трехфазной цепи при соединении источника и приемника звездой

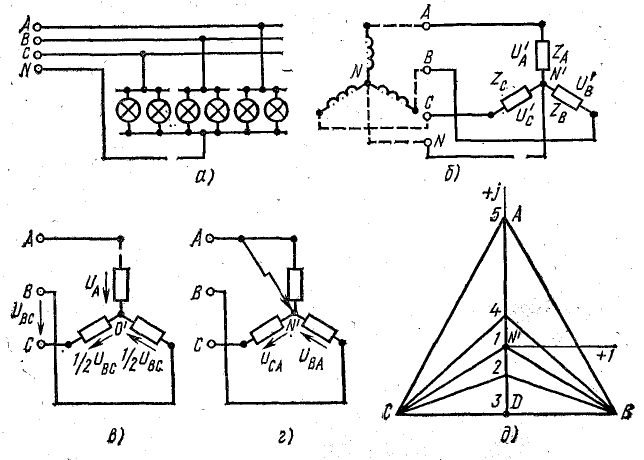
На схеме (см. рис. 20.4) видно, что при соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами — нейтральными точками N и N’. Наиболее удобным методом расчета в данном случае является метод узлового напряжения.

Определение токов

Рассмотрим сначала общий случай расчета цепи с нулевым проводом, сопротивление которого Z_N. При этом сделаем некоторые упрощения: сопротивления линейных проводов и фаз источников будем полагать равными нулю. Если указанные сопротивления нельзя считать равными нулю, их можно отнести к приемнику, прибавив к сопротивлениям последнего по правилам сложения комплексов.
При таком упрощении потенциалы линейных зажимов источника и приемника (например, точек А и А’) можно считать одинаковыми.
Напряжение между нулевыми точками N и N’, или узловое напряжение

Смещение нейтрали

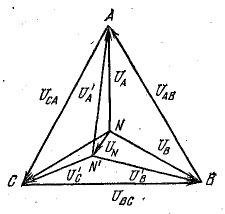
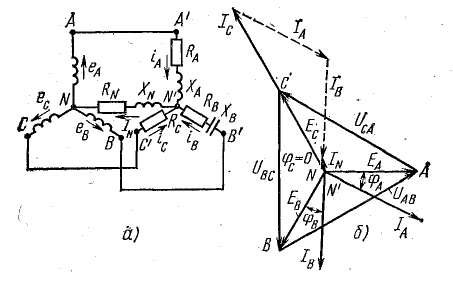
На рис. 21.1 изображена топографическая диаграмма цепи рис. 20.4, а при несимметричной нагрузке.

При наличии сопротивления в нулевом проводе (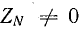) нулевая точка приемника на топографической диаграмме не совпадает с нулевой точкой источника. Поэтому напряжение U_N называют напряжением смещения нейтрали. Вследствие смещения нейтрали напряжения на фазах приемника оказываются неодинаковыми, несмотря на симметрию фазных напряжений источника (см. решение задачи 21.3).

Рис. 21.1. Топографическая диаграмма при несимметричной нагрузке (соединение звездой)

Из формулы (21.1) видно, что симметрия фазных напряжений на нагрузке, когда U_N = 0, достигается в двух частных случаях.
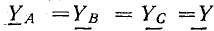
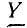
1. При симметричной нагрузке, когда комплексы проводимостей фаз равны: . В этом случае в числителе проводимость  можно вынести за скобку, внутри которой складывается три вектора э. д. с. источника, равных по величине и сдвинутых по фазе на 120°; эта сумма равна нулю (см. рис. 20.8, б) и U_N = 0. Поэтому ток в нулевом проводе равен нулю [см. формулу (21.4)] и необходимость в этом проводе отпадает, а электроснабжение симметричных приемников осуществляется по трехпроводной системе.
2. В четырехпроводной системе, когда сопротивление нулевого провода равно нулю (Y_N = ∞.)

Роль нулевого провода

Нулевой провод является уравнительным. Потенциалы нейтрали источника и приемника с помощью этого провода принудительно уравнены, а поэтому звезда векторов фазных напряжений приемника точно совпадает со звездой фазных напряжений источника.

Четырехпроводная система применяется в электрических сетях с напряжением 380/220 В при электроснабжении от общего источника силовой (электродвигатели) и осветительной (электролампы) нагрузки.
При несимметричной нагрузке обрыв нулевого провода (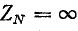) вызывает значительное изменение токов и фазных напряжений, что в большинстве случаев недопустимо. Поэтому в нулевой провод предохранители не устанавливаются.

Определение мощности

При несимметричной нагрузке нужно определить мощность каждой фазы. Например, для фазы А:
    
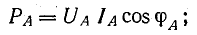
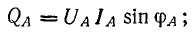
Аналогично определяются мощности других фаз.
Активная мощность всей трехфазной цепи равна сумме мощностей фаз:

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей фаз:

В этой сумме реактивная мощность катушки считается положительной, а реактивная мощность конденсатора — отрицательной.

Задача 21.1.

При соединении звездой с нулевым проводом определить фазные напряжения и токи в приемнике энергии, сопротивления которого заданы комплексами:
    

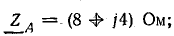
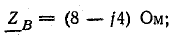
Действующая величина симметричной трехфазной системы э. д. с. 220 В. Сопротивление нулевого провода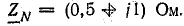  
Построить векторную диаграмму.
Сопротивлениями линейных проводов и внутренними сопротивлениями источника э. д. с. пренебречь.
Решение. Схема, соответствующая условию задачи, показана на рис. 21.2, а.
Проводимости ветвей между узловыми точками NN’:

Рис. 21.2. К задаче 21.1

Комплексы э. д. с. источника:
    
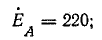
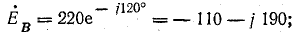
Узловое напряжение



Фазные напряжения приемника:



Токи в фазах и нулевом проводе:




Векторная диаграмма напряжений и токов показана на рис. 21.2, б.
 

Задача 21.3.

Электрические лампы включены звездой в трехфазную сеть с линейным напряжением 380 В. В каждую фазу включены по 50 ламп с номинальной мощностью 60 Вт каждая, номинальным напряжением 220 В. Как изменяются фазные напряжения и токи при изменении нагрузки одной фазы от холостого хода до короткого замыкания при обрыве нулевого провода?
В каждом выбранном случае нагрузки построить векторную диаграмму, определить мощность всей трехфазной цепи.
Решение. Условию задачи соответствует схема рис. 21.3, а, на которой группа ламп в каждой фазе условно показана двумя лампами.
Оставляя постоянным число ламп в фазах В и С, будем менять его в фазе А. Подсчеты по условию задачи выполним для таких нагрузок в фазе А: 50, 25, 100 ламп, короткое замыкание, холостой ход.
1.    При включении в каждую фазу по 50 одинаковых ламп нагрузка симметрична. Поэтому фазные напряжения на нагрузке равны фазным напряжениям в сети:

Напряжение на лампах равно номинальному. В этом случае лампы работают с номинальной мощностью.
Это даёт право определить фазные токи по заданной мощности ламп:

При соединении звездой I_Ф = I_Л, поэтому I_л = 13,6 А. Общая мощность трехфазной цепи
Р = ЗР_Ф = 3 • 60 • 50 = 9000 Вт.
2.    В фазе А включено 25 ламп.
При несимметричной нагрузке напряжения на лампах отличаются от фазных напряжений в сети. Поэтому определить токи по заданной мощности ламп нельзя, так как действительная мощность ламп и фазные напряжения их неизвестны. При решении задачи будем считать, что сопротивление ламп в накаленном состоянии нити практически не меняется при некотором изменении их мощности.
Сопротивление лампы в номинальном режиме

Сопротивление фаз В и С при включении 50 ламп

Сопротивление фазы А

Комплексы фазных напряжений в сети:
   

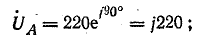
Проводимости ветвей:
   
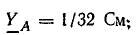
Смещение нейтрали

Напряжения фаз:



Токи в фазах:



Мощность всех ламп в фазах:



Мощность одной лампы:



Общая мощность в трехфазной системе

Векторная диаграмма напряжений для различной нагрузки фазы А показана на рис. 21.3, д.

Положение нулевой точки на диаграмме соответствует такой нагрузке фазы А: 1 — симметричная нагрузка (во всех фазах по 50 ламп); 2 — в фазе А 25 ламп; 3 — фаза А разомкнута (холостой ход); 4 — в фазе А 100 ламп; 5 — в фазе А короткое замыкание.

Выполните расчет трехфазной цепи для случаев нагрузки 3, 4, 5 подобно приведенному расчету для случая нагрузки 2, проверьте соответствие результатов расчета векторной диаграмме рис. 21.3, д.
Как видно, нулевая точка нагрузки при изменении проводимости фазы А перемещается на прямой АD, которая является перпендикуляром, опущенным из точки А к вектору линейного напряжения U_BC. При холостом ходе фазы А (обрыв линейного провода в этой фазе) нулевая точка перемещается в точку D и напряжения на двух других фазах U_B и U_C по величине оказываются равными половине линейного напряжения U_BC (рис. 21.3, б).

Рис. 21.3. К задаче 21.3

То же следует из схемы рис. 21.3, в. В рассматриваемом случае сопротивления фаз В и С оказываются включенными последовательно на линейное напряжение U_BC.

Сопротивления эти равны, поэтому линейное напряжение делится между двумя фазами поровну.

При коротком замыкании фазы А линейный провод этой фазы подводится непосредственно к нулевой точке нагрузки (рис. 21.3, г). Поэтому лампы, включенные в фазы В и С, оказываются под линейным напряжением.

Расчет несимметричной трехфазной цепи при соединении треугольником

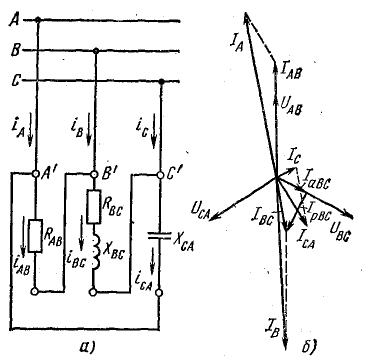
Трехфазная цепь при соединении приемника треугольником и любой схеме соединения фаз источника имеет разветвленную многоконтурную схему (см., например, рис. 20.8, а; 21.5).

Расчет такой цепи выполняется одним из известных методов с учетом состава ее элементов и схемы соединения.

Соединение источника и приемника треугольником

Расчет сложной цепи (см. рис. 20.8, а) значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае напряжения на фазах приемника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.
Если трехфазная система напряжений, приложенных к приемнику, известна, то фазные токи
где 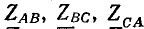— полные сопротивления фаз.
Линейные токи можно определить графически, как показано на рис. 21.4. Если задача решается в комплексной форме, линейные токи находят по формулам (20.7).

Мощность в несимметричной трехфазной цепи при соединении треугольником определяют по тем же формулам, что и при соединении звездой (21.6), (21.7).

Рис. 21.4. Векторная диаграмма токов при несимметричной нагрузке (соединение треугольником)

Рис. 21.5. К вопросу о преобразовании треугольника сопротивлений в эквивалентную звезду в трехфазной цепи

Преобразование звезды и треугольника сопротивлений в трехфазных цепях

Расчет трехфазных цепей при смешанном соединении (звездой и треугольником), с учетом сопротивлений проводов линии представляет значительные трудности.

В этих случаях упрощения достигаются благодаря применению метода взаимного преобразования звезды и треугольника.
На рис. 21.5 приемник энергии соединен треугольником. С учетом сопротивлений проводов линии (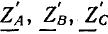) расчет такой цепи удобно выполнить, заменив треугольник сопротивлений эквивалентной звездой. Общее сопротивление фазы определяется сложением сопротивлений проводов линии и эквивалентной звезды приемника.

Если в ходе расчета схемы со смешанным соединением приемников — звездой и треугольником (рис. 21.6) — необходимо определить общее сопротивление фазы, это делается преобразованием звезды в треугольник или треугольника в звезду.
При симметричной нагрузке можно преобразовать треугольник в звезду, а затем две звезды заменить одной. Последняя операция возможна только при симметричной нагрузке, когда фазные напряжения у этих «звезд» одинаковы (смещение нейтрали отсутствует). При несимметричной нагрузке звезду следует преобразовать в эквивалентный треугольник, а затем сложением соответствующих проводимостей определить общую проводимость каждой фазы.

Рис. 21.6. к расчету трехфазной цепи при соединении приемников звездой и треугольником

Если в последнем случае требуется учесть сопротивление проводов, то общий треугольник еще раз приходится преобразовать в звезду и к сопротивлениям звезды прибавить сопротивления проводов линии.

Задача 21.4.

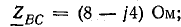
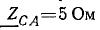
Сопротивления фаз приемника   подключены треугольником к трехфазному генератору, обмотки которого также соединены треугольником. Действующие значения симметричной системы э. д. с. генератора 220 В. Пренебрегая сопротивлениями линейных проводов и обмоток генератора, определить фазные и линейные токи, активную, реактивную и полную мощности каждой фазы и всей цепи. Построить векторную диаграмму.
Решение. Схема рис. 20.8, а соответствует условию задачи. Если сопротивления линейных проводов и обмоток генератора считать равными нулю, то фазные напряжения приемника равны соответствующим э. д. с.:
  
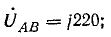
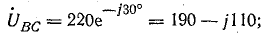
Фазные токи в приемнике:



Линейные токи:



Сумма линейных токов

Равенство нулю суммы линейных токов является общим свойством трехфазных трехпроводных цепей при соединении звездой и треугольником при симметричной и несимметричной нагрузках.

Рис. 21.7. К задаче 21.4

Рис. 21.8. К задаче 21.5

Мощности фаз:



Общая мощность системы:
активная

реактивная

Векторная диаграмма построена на рис. 21.7.
 

Задача 21.5.

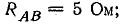
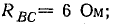
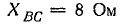
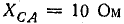
Приемник электрической энергии, соединенный треугольником, включен в сеть с линейным напряжением 120 В. Сопротивления фаз:   (инд.); (емк.).
Начертить схему по условию задачи. Определить фазные и линейные токи, активную, реактивную и полную мощности в каждой фазе и всей цени. Построить векторную диаграмму.
Решение. Схема цепи изображена на рис. 21.8, а.
Решим задачу без применения комплексных чисел. Токи в фазах:



Линейные токи определим графически с помощью векторной диаграммы. Для этого найдем активные и реактивные токи фаз.
В фазе АВ включено активное сопротивление, поэтому
 
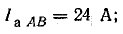
В фазе ВС последовательно соединены R и Х_L, поэтому


В фазе CA включено емкостное сопротивление, следовательно,
 
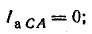
Векторная диаграмма цепи показана на рис. 21.8, б. Для определения линейных токов постройте векторную диаграмму на листе миллиметровой бумаги в масштабах: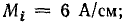  
Линейные токи: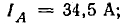   
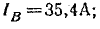
Мощности фаз:
активные

реактивные



полные



Мощность всей цепи:
активная

реактивная

Знак минус указывает на емкостный характер реактивной мощности цепи.

Симметричные составляющие несимметричной трехфазной системы

Несимметричную трехфазную систему токов (напряжений или других синусоидальных величин) можно представить в виде суммы трех симметричных систем.

Разложение несимметричной системы векторов на симметричные составляющие применяется для расчета и анализа несимметричных режимов в трехфазных цепях: при симметричной нагрузке, но несимметричной системе э. д. с., при однофазных и двухфазных коротких замыканиях, при обрыве линейных проводов в цепях с симметричной системой э. д. с.

Комплексы симметричных составляющих

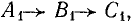
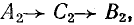
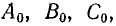
Первая симметричная система имеет прямую последовательность фаз ( рис. 21.9, а), вторая — обратную ( рис. 21.9, б). Третья система, называемая системой нулевой последовательности, состоит из трех равных величин, совпадающих по фазе ( рис. 21.9, в).

Рис. 21.9. Симметричные составляющие несимметричной системы

Система величин:
прямой последовательности

обратной последовательности

нулевой последовательности

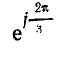
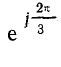
Умножение на  означает поворот вектора на 120″ против движения часовой стрелки. Обозначим через а и будем называть это выражение поворотным множителем.
Поворот вектора против часовой стрелки на 240° можно выразить умножением его на а².
Умножение вектора на а³ не меняет его положения:

С помощью поворотного множителя а системы прямой и обратной последовательности можно записать так:

Сумма синусоидальных величин симметричной системы равна нулю, поэтому

Разложение несимметричной системы на симметричные составляющие

Выразим комплексы несимметричной системы через симметричные составляющие:

Если из этой системы уравнений можно однозначно определить симметричные составляющие через известные величины 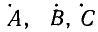несимметричной системы, то этим будет доказана возможность разложения несимметричной системы на три симметричные — прямой, обратной и нулевой последовательности.
Используя выражения (21.10), запишем систему уравнений (21.12) в таком виде:

Решение системы уравнений (21.13) позволяет найти симметричные составляющие
Сложим уравнения:

Учитывая формулу (21.11), найдем

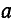
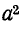
Умножим второе уравнение в системе (21.13) на , а третье — на и сложим все уравнения:

откуда

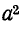
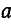
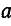
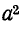
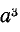
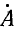
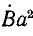
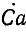
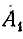
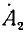
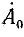
Умножим второе уравнение в системе (21.13) на , а третье на и сложим все уравнения:


 =  +  ₊ 

 +  +  =  (1 +  + ) +  • 3 +  (1 +  + )
откуда
=                                        (21.16)

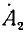
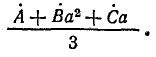
Свойства трехфазных цепей

Отметим некоторые свойства трехфазных цепей  в отношении симметричных составляющих токов и напряжений.

Степень несимметрии линейных напряжений оценивается коэффициентом несимметрии, т.е. отношением составляющей обратной последовательности напряжений к составляющей прямой последовательности.
ε = 100 • U_оп/U_пп.
Отсюда следует, что ток в нулевом проводе можно найти, если утроить величину составляющей тока нулевой последовательности.
В трехпроводной системе сумма линейных токов равна нулю. Из формулы (21.14) следует, что линейные токи в этом случае не содержат составляющей нулевой последовательности. Это справедливо и для линейных напряжений трехфазной системы, сумма которых тоже равна нулю.

Рис. 21.10. Симметричные составляющие токов трехфазной цепи при разомкнутых двух фазах

Отсутствие тока в одной или двух фазах при несимметричном режиме означает, что сумма трех симметричных составляющих токов в этих фазах равна нулю.
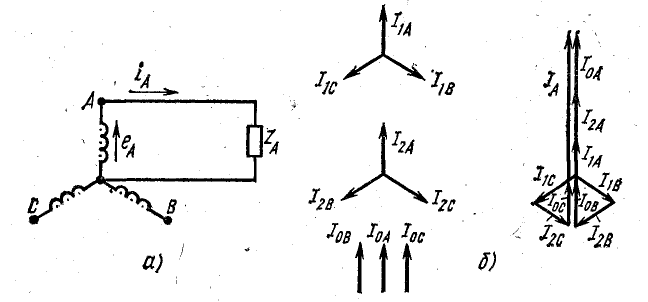
Например, на схеме рис. 21.10, а фазы В и С разомкнуты. Поэтому
Согласно формулам (21.14) — (21.16), симметричные составляющие токов имеют следующие выражения:
прямой последовательности

обратной последовательности

нулевой последовательности

На рис. 21.10, б показаны симметричные составляющие прямой, обратной и нулевой последовательности и их геометрическое сложение; в результате сложения получаем:

Задача 21.8.

В результате неправильной маркировки концов обмоток трехфазного трансформатора (начало фазы А вторичной обмотки помечено как конец) система линейных напряжений несимметрична. Определить симметричные составляющие линейных напряжений при соединении звездой, если фазные напряжения во вторичной обмотке 220 В.
Решение. Запишем комплексы фазных напряжений во вторичной обмотке:



Вектор напряжения 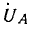 в соответствии с условием задачи повернут на 180°.
Комплексы линейных напряжений:



Составляющие:
нулевой последовательности


прямой последовательности




обратной последовательности

Рис. 21.11. К задаче 21.8

На рис. 21.11, а, б показаны векторы систем прямой и обратной последовательности и их сумма — система трех исходных векторов линейных напряжений.

Задача 21.9.

Трехфазный электродвигатель, включенный в сеть с линейным напряжением 380 В при соединении звездой, имеет мощность на валу Р₂ = 14 кВт; соsφ = 0,8; к. п. д. η = 0,85.
Определить симметричные составляющие токов в обмотке двигателя при обрыве линейного провода в фазе В.
Решение. При нормальной работе ток в фазе двигателя

При симметричной системе напряжений токи в фазах двигателя образуют симметричную систему (рис. 21.12, а). При обрыве линейного провода В векторная диаграмма фазных напряжений и токов показана на рис. 21.12, б.
Ток в фазах В равен нулю (I_B = 0).
Токи в фазах А и С равны по величине, но находятся в противофазе: I_А = I_C.
Для определения величины токов I_А и I_C  найдем расчетное сопротивление фазы двигателя при нормальном режиме, которое будем считать неизменным:

При обрыве линейного провода фазы В обмотки двух других фаз двигателя с одинаковым сопротивлением включены последовательно на линейное напряжение U_CA. Поэтому ток в фазах А и С

Рис. 21.12. к задаче 21.9

Выразим токи в комплексной форме, полагая ток I_A совпадающим с положительным направлением действительной оси:

Токи:
нулевой последовательности

прямой последовательности



обратной последовательности

На рис. 21.12, в изображены симметричные составляющие токов в двигателе при обрыве фазы.

Несимметричный режим работы трехфазной цепи

Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством э. д. с. и т. п.

Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же

методами, которые применяются для расчета однофазных цепей.

Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).

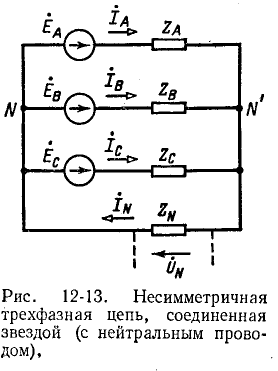
1.    Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 12-13).

Несимметричная трехфазная цепь, показанная на рис. 12-13, может рассматриваться как трехконтурная цепь с тремя э. д. с. Такая цепь может быть рассчитана методами контурных токов, узловых напряжений и другими. Поскольку в схеме имеются только два узла, наиболее целесообразно в данном случае определить узловое напряжение (напряжение смещения) между нейтральными точками N’ и N по формуле,

где 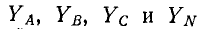— проводимости соответствующих ветвей.

После этого найдем токи:

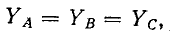
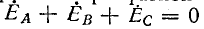
В симметричной трехфазной цепи и поэтому при узловое напряжение равно нулю.

Стучаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода.    j

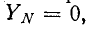
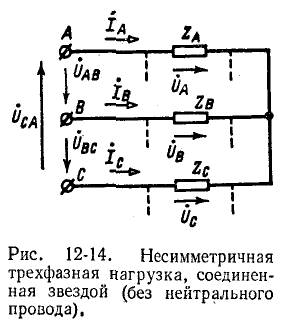
При отсутствии нейтрального провода, полагая в (12-1), имеем:

2.    Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями на выводах (рис. 12-14).

Если заданы линейные напряжения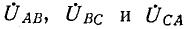на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.

Обозначив фазные напряжения на выводах нагрузки через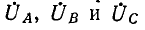(рис. 12-14), получим

где 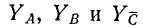— проводимости фаз нагрузки.

Равенство нулю суммы токов трех фаз записывается в виде:

Фазные напряжения могут быть выражены через и заданные линейные напряжения: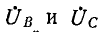

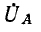
Подстановка (12-3) в (12-2) дает:

Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся:

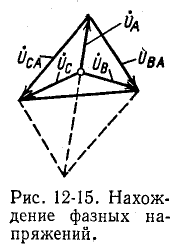
По фазным напряжениям нагрузки находятся фазные токи.

В Случае симметричной нагрузки 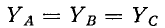вектор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих линейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника.

На рис. 12-15 построение сделано для фазы А по формуле (12-4)1

В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой.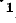

Положим, что конденсатор присоединен к фазе А, лампы — к фазам В и С; емкостное сопротивление конденсатора берется равным по модулю сопротивлению лампы, т. е. 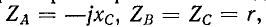причем

Неравенство напряжений на лампах проявится в том, что накал ламп будет разным. 

¹ Для определения чередования фаз на практике обычно пользуются специальным прибором, в котором создается вращающееся магнитное поле, увлекающее за собой диск в ту или другую сторону.

Отношение напряжений согласно выведенным выше выражениям (12-4) равно при симметрии линейных напряжений:

Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоединенная к отстающей фазе, — тускло.

Вместо конденсатора можно применить индуктивную катушку, подобрав ее индуктивное сопротивление приблизительно равным по модулю сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе. Эти соотношения также могут быть получены непосредственно из векторной диаграммы.

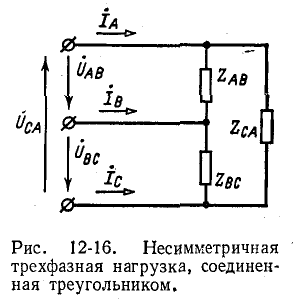
3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на выводах Рис. 12-16. Несимметричная (рис. 12-16).   Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения 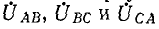(рис. 12-16), то токи в сопротивлениях нагрузки равны:

Токи в линии определяются как разности соответствующих токов нагрузки, например: 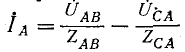и т. д.

Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения 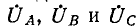источника, соединенного в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмотренному случаю(рис. 12-16).
Пример 12-2. Сопротивления фаз нагрузки, соединенной звездной

Сопротивление нейтрального провода

Напряжения на цепи представляют собой симметричную звезду:

Требуется определить фазные напряжения нагрузки.

Проводимости фаз нагрузки и нейтрального провода

На основании формулы (12-1)

Искомые фазные напряжения нагрузки:

Мощность несимметричной трехфазной цепи

Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:

Действительная часть этого выражения представляет собой активную мощность

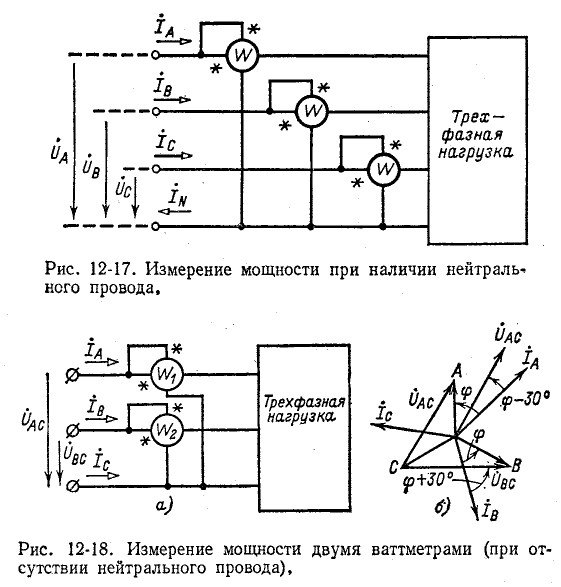
Суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть в соответствии с этим измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения относительно нейтрали и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода (рис. 12-17) или искусственно созданной нейтральной точки.

В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ваттметров

(рис. 12-18). В этом случае выражение (12-5) преобразуется следующим образом: исключая ток 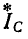с помощью условия
получаем:

или

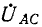
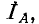
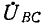
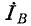
В соответствии с (12-6) при измерении активной мощности двумя ваттметрами к одному из них подводятся напряжение и ток а ко второму — напряжение и ток (рис. 12-18, а). Показания ваттметров складываются алгебраически.

Круговой заменой А, В. и С в выражении (12-6) можно получить выражения для других равноценных вариантов включения двух ваттметров.

Следует иметь в виду’, что если стрелка одного ваттметра отклоняется по шкале в обратную сторону, то, изменив направление напряжения или тока, подводимого к данному ваттметру, записывают полученное показание со знаком минус. При симметричном режиме работы трехфазной цепи такое положение имеет место при

что видно непосредственно из векторной диаграммы (рис. 12-18, б).

При симметричном режиме показания двух ваттметров в схеме рис. 12-18, б будут следующие:

Сумма и разность показаний ваттметров соответственно равны:

Следовательно, при симметричном режиме работы трехфазной цепи тангенс угла сдвига фаз может быть вычислен по формуле