Сопряженные диаметры эллипса как найти

Рассмотрим эллипс, отнесенный к его осям симметрии:

и систему параллельных между собой хорд с угловым коэффициентом (рис. 61).

Рис. 61.

Посмотрим, как располагаются середины этих хорд. Иными словами, выясним, каким условием связаны координаты середин параллельных между собой хорд эллипса. Возьмем любую из хорд и обозначим ее концы через а середину — через М (X, У). Так как точки лежат на эллипсе, то их координаты должны удовлетворять его уравнению (16), т. е.

Выражая угловой коэффициент прямой линии через координаты двух ее точек (гл. III, § 12), будем иметь:

Наконец, заметив, что точка М является серединой отрезка получим:

Исключим из пяти соотношений (17)-(21) четыре вспомогательные величины . С этой целью, вычитая равенство (17) из равенства (18), найдем:

или

Виося в последнее равенство согласно (20) вместо суммы ее значение , а вследствие (21) вместо суммы ее значение и согласно (19) вместо разности ее выражение , мы придадим ему вид:

сокращая на мы получим окончательно;

откуда (при )

Таким образом, координаты середин параллельных между собой хорд эллипса связаны линейной зависимостью. И, значит, середины параллельных хорд располагаются на прямой

В наших рассуждениях мы предполагали, что рассматриваемые хорды имеют угловой коэффициент и, следовательно, не параллельны оси Оу. Середины хорд, параллельных оси Оу, тоже лежат на прямой — на оси Ох (в силу симметрии эллипса относительно осн Ох).

Итак, середины параллельных хорд эллипса лежат на прямой.

Прямая, проходящая через середины параллельных хорд эллипса, называется его диаметром. Все диаметры эллипса проходят через центр. Обозначая угловой коэффициент диаметра эллипса через имеем:

или

Условимся называть диаметр эллипса сопряженным хордам, через середины которых он проходит. Условие (23) или (23) связывает между собой угловые коэффициенты параллельных хорд и сопряженного им диаметра. Так как это

условие симметрично относительно , т. е. не меняется после перестановки , то отсюда заключаем: если диаметр с угловым коэффициентом сопряжен хордам с угловым коэффициентом то и диаметр с угловым коэффициентом сопряжен хордам с угловым коэффициентом кг.

Таким образом, мы получаем пару диаметров, из которых каждый делит пополам хорды, параллельные другому диачетру (рис. 61). Такие два диаметра эллипса называются сопряженными между собой. Их угловые коэффициенты к, и кг связаны условием (23) или (23).

Итак, у эллипса имеется бесчисленное множество пар сопряженных между собой диаметров: каждому диаметру соответствует свой сопряженный диаметр. В частности, оси координат (оси симметрии эллипса) представляют собой пару сопряженных диаметров. Эти два сопряженных между собой диаметра эллипса являются взаимно перпендикулярными. Такие диаметры называют главными диаметрами эллипса.

Из условия (23) следует, что угол между любой другой парой сопряженных между собой диаметров эллипса (b Ф а) отличен от прямого. Если же , т. е. эллипс обращается в окружность, то условие (23) обращается в условие перпендикулярности: Таким образом, сопряженных диаметра окружности перпендикулярны между собой, т. е. всякий диаметр окружности есть главный диаметр (ось симметрии).

Из условия (23) видно, что угловые коэффициенты двух сопряженных диаметров эллипса имеют разные знаки, т. е. диаметры проходят в смежных четвертях.

При увеличении к, угловой коэффициент по абсолютной величине уменьшается, т. е. алгебраически также увеличивается. Это показывает, что при вращении диаметра эллипса против часовой стрелки сопряженный с ним диаметр вращается в ту же сторону.

Пример. Определить длину диаметра эллипса сопряженного диаметру, делящему пополам первый координатный угол (длиной диаметра считают расстояние между точками пересечения его с кривой).

Угловой коэффициент данного диаметра есть 1. Из условия (23) находим угловой коэффициент кг диаметра, ему сопряженного:

Здесь Следовательно, Уравнение этого диаметра будет:

Чтобы найти его длину, нужно определить точки его пересечения с эллипсом, для чего решим совместно уравнения эллипса и диаметра:

Подставляя в первое уравнение выражение у из второго, найдем:

Зная абсциссы точек пересечения, найдем их ординаты:

По формуле расстояния между двумя точками находим длину d искомого диаметра:

откуда

From Wikipedia, the free encyclopedia

In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter. For example, two diameters of a circle are conjugate if and only if they are perpendicular.

Of ellipse[edit]

For an ellipse, two diameters are conjugate if and only if the tangent line to the ellipse at an endpoint of one diameter is parallel to the other diameter. Each pair of conjugate diameters of an ellipse has a corresponding tangent parallelogram, sometimes called a bounding parallelogram (skewed compared to a bounding rectangle). In his manuscript De motu corporum in gyrum, and in the ‘Principia’, Isaac Newton cites as a lemma proved by previous authors that all (bounding) parallelograms for a given ellipse have the same area.

It is possible to reconstruct an ellipse from any pair of conjugate diameters, or from any bounding parallelogram. For example, in proposition 14 of Book VIII of his Collection, Pappus of Alexandria gives a method for constructing the axes of an ellipse from a given pair of conjugate diameters. Another method is using Rytz’s construction, which takes advantage of the Thales’ theorem for finding the directions and lengths of the major and minor axes of an ellipse regardless of its rotation or shearing.

Of hyperbola[edit]

For any φ, the indicated diameters of the circles and hyperbolas are conjugate.

Similar to the elliptic case, diameters of a hyperbola are conjugate when each bisects all chords parallel to the other.^[1] In this case both the hyperbola and its conjugate are sources for the chords and diameters.

In the case of a rectangular hyperbola, its conjugate is the reflection across an asymptote. A diameter of one hyperbola is conjugate to its reflection in the asymptote, which is a diameter of the other hyperbola. As perpendicularity is the relation of conjugate diameters of a circle, so hyperbolic orthogonality is the relation of conjugate diameters of rectangular hyperbolas.

The placement of tie rods reinforcing a square assembly of girders is guided by the relation of conjugate diameters in a book on analytic geometry.^[2]

Conjugate diameters of hyperbolas are also useful for stating the principle of relativity in the modern physics of spacetime. The concept of relativity is first introduced in a plane consisting of a single dimension in space, the second dimension being time. In such a plane, one hyperbola corresponds to events a constant space-like interval from the origin event, the other hyperbola corresponds to events a constant time-like interval from it. The principle of relativity can be formulated “Any pair of conjugate diameters of conjugate hyperbolas can be taken for the axes of space and time”. This interpretation of relativity was enunciated by E. T. Whittaker in 1910.^[3]

In projective geometry[edit]

Every line in projective geometry contains a point at infinity, also called a figurative point. The ellipse, parabola, and hyperbola are viewed as conics in projective geometry, and each conic determines a relation of pole and polar between points and lines. Using these concepts, “two diameters are conjugate when each is the polar of the figurative point of the other.”^[4]

Only one of the conjugate diameters of a hyperbola cuts the curve.

The notion of point-pair separation distinguishes an ellipse from a hyperbola: In the ellipse every pair of conjugate diameters separates every other pair. In a hyperbola, one pair of conjugate diameters never separates another such pair.

References[edit]

Further reading[edit]

• Chasles, Michel (1865). “Diamètres conjugués”. Traité des sections coniques, Ie partie. faisant suite au traité de géométrie supérieure (in French). Paris: Gauthier-Villars. pp. 116–23.

• W. K. Clifford (1878) Elements of Dynamic, page 90, link from HathiTrust.

• Coxeter, HSM (1955). The Real Projective Plane (2nd ed.). Cambridge University Press. pp. 130–5.

• Salmon, George (1900). A Treatise on Conic Sections. London: Longmans, Green & Co. p. 165.

External links[edit]

• “Conjugate Diameters in Ellipse”. cut-the-knot.org.
• Besant, W. H. (1895). “Properties of Conjugate Diameters”. Conic sections treated geometrically. Historical Math Monographs. London; Ithaca, NY: G. Bell; Cornell University. p. 109.

643 Составить уравнение диаметра
эллипса , проходящего через
середину его хорды, отсекаемой на прямой . 644 Составить
уравнение хорды эллипса , проходящей
через точку А(1; -2) и делящейся ею пополам. 645 Составить
уравнения двух взаимно сопряженных диаметров
эллипса , из которых один образует
с осью Ох угол 45⁰. 646 Составить
уравнения двух взаимно двух взаимно сопряженных
диаметров эллипса , из которых один
параллелен прямой . 647 Составить
уравнения двух взаимно сопряженных диаметров
эллипса , из которых один
перпендикулярен к прямой . 648 На чертеже
изображен эллипс. Пользуясь циркулем и линейкой,
построить его центр. 649 Доказать, что оси
эллипса являются единственной парой его главных
диаметров. 650 Пользуясь
свойствами сопряженных диаметров, доказать, что
каждый диаметр окружности является главным.
651 а). В эллипс вписан
равнобедренный треугольник так, что его вершина
совпадает с одной из вершин эллипса. Доказать,
что основание этого треугольника параллельно
одной из осей эллипса; б). Доказать, что стороны
прямоугольника вписанного в эллипс,параллельны
осям этого эллипса; в). На чертеже изображен
эллипс. Пользуясь циркулем и линейкой, построить
его главные диаметры.
652 Доказать, что хорды
эллипса, соединяющие его произвольную
произвольную точку с концами любого диаметра
этого эллипса, праллельны паре его сопряженных
диаметров.
653 а). Доказать, что
сумма квадратов двух сопряженных полудиаметров
эллипса есть величина постоянная (равная сумме
квадратов его полуосей), б). Доказать, что площадь
параллелограмма, построенного на двух
сопряженных полудиаметрах эллипса, есть
величина постоянная (равная площади
прямоугольника, построенного на его полуосях).
654 Составить
уравнение диаметра гиперболы , походящего
через середину ее хорды, отсекаемой на прямой .
655 Дана гипербола . Составить уравнение ее хорды,
которая проходит через точку А(3; -1) и делится
точкой А пополам.
656 Составить
уравнениядвух сопряженных диаметров гиперболы , из которых один проходит через точку
А(8; 1).
657 Составить
уравнения сопряженных диаметров гиперболы , угол между которыми равен 45⁰.
658 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее центр.
659 Доказать, что оси
гиперболы являются единственной парой ее
главных диаметров.
660 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее главные диаметры.
661 Составить
уравнение диаметра параболы , проходящего
через середину ее хорды, отсекаемой на прямой .
662 Дана парабола . Составить уравнение ее хорды,
которая проходит через точку А(2; 5) и делится
точкой А пополам.
663 Доказать, что ось
параболы является единственной ее главным
диаметром.
664 На чертеже
изображена парабола. Пользуясь циркулем и
линейкой, построить ее главный диаметр.

Уравнение эллипса в сопряженных диаметрах

Если провести хорды окружности, параллельные ее диаметру, то середины этих хорд принадлежат перпендикулярному диаметру. Середины хорд, параллельных второму диаметру, принадлежат первому диаметру. При сжатии два перпендикулярных диаметра окружности отображаются в два диаметра эллипса, которые называются сопряженными. Два направления, параллельных направлениям сопряженных диаметров, называются сопряженными.

Если хорды, параллельные одному диаметру эллипса делятся другим диаметром пополам, то и хорды, параллельные другому диаметру эллипса, делятся первым диаметром пополам.

Такие два диаметра являются сопряженными диаметрами эллипса. Каждому диаметру отвечает вполне определенный сопряженный ему диаметр. Главные диаметры (оси) эллипса одновременно являются перпендикулярными и сопряженными диаметрами.

Проведем теперь в окружности два перпендикулярных радиуса OA и OB. В результате сжатия они переходят в два сопряженных полудиаметра OA₁ = a₁ и OB₁ = b₁ эллипса (см. Рис. 21).

где A₀ и B₀ – проекции точек A и B на ось сжатия, а – коэффициент сжатия. Но из равенства треугольников OAA₀ и OBB₀ следут, что OA₀ = BB₀, OB₀ = AA₀. Поэтому

откуда после подстановки значения k находим:

Уравнение эллипса в сопряженных диаметрах

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Если гипербола задана уравнением

, (2)

то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ – угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

Если k и k ’ – угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

05.4. Задачи и размышления

Задачи и размышления

Знакомство со свойствами эллипса, гиперболы и параболы вызывает желание изучить способы построения этих кривых. Рассмотрим некоторые из таких способов.

1. Эллипс можно построить с помощью нити длиной 2а, закрепленной концами в фокусах (рис. 5.20). Очевидно, что длина нити останется неизменной, а фокусы фиксированы. Перемещая нить в натянутом состоянии, получим эллипс.

Рис. 5.20. Построение эллипса с помощью нити,
закрепленной в его фокусах.

Этот способ не всегда может быть удобен на практике. Дадим другой вариант построения эллипса, также вытекающий из его определения.

2. Пусть известно полуфокусное расстояние эллипса C и его большая полуось а.

Располагая фокусы F1 и F2 на расстоянии 2с, проводим дуги окружностей радиусами И поочередно из первого и второго фокусов, выбирая их так, чтобы

Точки пересечения окружностей будут лежать на эллипсе.

При этом допустимые значения и должны удовлетворять условиям:

Откуда следуют эти ограничения?

Меняя и В допустимых границах и строя соответствующие пары окружностей, в их пересечении будем получать точки, принадлежащие искомому эллипсу. Попарные значения и удобно выбрать, используя отрезок длиной 2а (рис. 5.21).

Рис. 5.21. Выбор допустимых значений модулей
фокальных радиусов.

Вершины эллипса, лежащие на малой оси, найдутся при пересечений дуг окружностей c радиусами , проведенных из фокусов и , как из центров.

Рис. 5.22. Построение эллипса по опорным точкам,
получаемым с помощью циркуля.

Для нахождения вершин эллипса, расположенных на большой оси, проводим дуги окружности радиуса a + c из фокусов F1 и F2, как из центров, до пересечения с этой осью.

Докажите, что полученная кривая – эллипс.

3. Рассмотрим еще один способ отыскания точек, принадлежащих эллипсу, с помощью построений, выполняемых линейкой. Построим прямоугольник АBСD, большая сторона которого AD равна 2а – длине большой оси эллипса, а длина меньшей стороны АВ равна 2b – его малой оси (рис. 5.23). Стороны АВ и ВС делим на одинаковое число равных частей. Точки деления соединяем с точками А и D. Выделенные на рисунке точки пересечения лежат на дуге эллипса.

Докажите этот факт.

Рис. 5.23. Построение эллипса по опорным точкам
с помощью линейки.

Подобным способом можно построить параболу (рис. 5.24).

Рис. 5.24. Построение параболы по опорным точкам
с помощью линейки.

Обоснуйте этот способ. Каким будет каноническое уравнение эллипса при известной длине отрезков AB и BC?

4. Рассмотрим один из возможных способов построения гиперболы. Будем считать известными расстояние 2с между фокусами F1 и F2 и разность модулей фокальных радиусов , где 2A – длина ее действительной оси.

Поместим в фокус F1 конец линейки (рис. 5.25), к другому концу которой в точке А прикреплен шнур, длина которого меньше длины линейки на 2а. Другой конец шнура закреплен в фокусе F2.

Рис. 5.25. Построение гиперболы с помощью натянутого шнура и линейки.

При вращении линейки вокруг фокуса F1 натянутый нитью острый конец карандаша (точка М) опишет некоторую кривую.

Для любой точки М на этой кривой будет справедливо:

Что соответствует свойствам гиперболической кривой. Мы получили правую ветвь гиперболы. Аналогично строится ее левая часть.

5. Придумайте новые способы построения эллипса, гиперболы, параболы и обоснуйте их.

Известные понятия диаметра окружности и ее хорды можно обобщить на эллипс, гиперболу и параболу.

Диаметром эллипса (гиперболы) называется любая прямая, проходящая через центр кривой. Диаметром параболы назовем любую прямую, параллельную ее оси, включая и саму ось.

Всякая прямая может пересекать коническое сечение не более чем в двух точках. Если точек пересечения две, то отрезок прямой с концами в точках пересечения называется хордой.

У рассматриваемых кривых обнаруживается одно неожиданное свойство: Середины параллельных хорд конических сечений лежат на их диаметре (рис. 5.26).

Рис. 5.26. Расположение середин параллельных хорд конических сечений.

Для доказательства этого свойства рассмотрим сначала эллипс и гиперболу. Оно очевидно, когда хорды перпендикулярны вертикальной оси симметрии этих кривых. Возможны другие случаи. Пусть семейство параллельных хорд задается уравнением:

Меняя b, мы будем получать параллельные прямые. Уравнения эллипса и гиперболы можно объединить следующей записью:

Координаты концов хорд должны удовлетворять следующей системе уравнений:

Подставляя из второго уравнения этой системы выражение для координаты у в первое, получим:

По теореме Виета легко найти

Полусумма решений и будет являться абсциссой хc середины хорды:

Используя уравнение хорды, находим ординату ее середины:

Таким образом, середины параллельных хорд лежат на прямой

Проходящей через центр эллипса или гиперболы, то есть являющейся диаметром кривой. Угловой коэффициент этого диаметра

Он называется сопряженным по отношению к диаметру , параллельному хордам.

Интересно, что свойство сопряженности диаметров взаимно. Так, угловой коэффициент диаметра, сопряженного диаметру

,

Рассмотрим теперь параллельные хорды параболы

При разных значениях b. Их концы должны удовлетворять системе:

Выполняем очевидные преобразования аналогично предыдущему:

Это означает, что середина хорды имеет ординату

Таким образом, геометрическое место середин хорд параболы – прямая, параллельная оси 0х, то есть диаметр параболы.

6. Дано семейство параллельных прямых,

На которых располагаются параллельные хорды эллипсов:

Всегда ли они будут иметь один и тот же сопряженный диаметр?

7. Дана парабола х = 2у2, ее диаметр и семейство параллельных хорд, образующих с осью 0х угол j= 0,2. Найти длину хорды, пересекающей ось абсцисс в точке х = 2.

8. Хорда эллипса

Наклонена под углом j к оси 0х и имеет длину l. Найдите координаты ее концов. Исследуйте решение.

Вписаны треугольники АВL и СDL так, что стороны АВ=l и СD=m расположены параллельно, а медианы КL и МL лежат на одной прямой. Найти длины медиан. Доказать, что прямая МL пройдет через начало координат. Исследовать решение задачи в зависимости от входящих в него параметров.

10. Дан параллелограмм со сторонами a и b, угол между которыми j. Построить несколько эллипсов, которые могут быть описаны около этого параллелограмма, и найти их уравнения.

11. Доказать, что сумма квадратов двух сопряженных полудиаметров эллипса равна сумме квадратов его полуосей.

12. Доказать, что площадь параллелограмма, построенного на двух сопряженных полудиаметрах эллипса, равна площади прямоугольника, построенного на полуосях эллипса.

13. По изображению эллипса найти с помощью циркуля и линейки его центр.

14. Доказать, что хорды эллипса, соединяющие его произвольную точку с концами любого диаметра, параллельны паре его сопряженных диаметров.

15. Доказать, что отрезки, отсекаемые директрисами на асимптотах, считая от центра гиперболы, равны действительной полуоси. Пользуясь этим свойством, построить директрисы гиперболы.

Рассмотрим параметрические уравнения эллипса. В связи с этим обратимся к задаче.

Пусть точка М делит отрезок АВ на части a и b. Его концы скользят по сторонам прямого угла. Какую траекторию опишет при этом точка М?

Для решения задачи введем прямоугольную декартовую систему координат, расположив ее начало в вершине угла, а оси координат – по направлению сторон прямого угла (рис.5.27). Пусть точка М имеет координаты х и у, а угол , который образован отрезком AB с отрицательной ориентацией оси Ох, равен t радиан.

Рис. 5.27. Вывод параметрических уравнений эллипса

При перемещении концов отрезка А и В по координатным осям (во всех четырех координатных углах) точка М(х, у) опишет кривую, параметрические уравнения которой легко находится:

.

Этой кривой является эллипс, в чем можно убедиться, исключая параметр t. Действительно,

.

16. Найдите параметрические уравнения гиперболы и параболы.

17. Точка М, брошенная под углом к горизонту с начальной скоростью (рис.5.28а), если пренебречь сопротивлением воздуха, движется согласно уравнениям:

Где g – ускорение силы тяжести. На возвышенности, образующей с горизонтом угол , располагается перпендикулярно ей стержень высоты h.

Расстояние от подножья возвышенности до точки М равно l, а до основания стержня – d.

При каких углах точка М сможет перелететь через стержень?

Исследуйте допустимые углы перелета точки М через квадрат, установленный на возвышении вместо стержня (рис.5.28б).

Рис. 5.28. Траектория точки М, преодолевающей препятствия.

18. На рис.5.29 указаны проекции стойки. Ее основание ограничено дугами эллипса. Для крепления стойки к поверхности предполагается просверлить отверстия в тех ее точках, которые соответствуют фокусам эллипса. Используя чертеж детали, опишите аналитически этот эллипс, вычислите его фокусы, укажите на чертеже точки для сверления отверстий и вычислите расстояние от этих точек до наиболее удаленных точек стойки.

19. Верхний слой воды в наклоненном цилиндрическом стакане имеет форму эллипса (рис.5.30). Докажите этот факт и найдите полуоси эллипса, если радиус цилиндра R, а угол наклона .

Рис. 5.30. Верхний слой воды в наклоненном стакане.

20. Найдите траекторию точки, которая во все время движения остается вдвое ближе от заданной прямой, чем от заданной точки.

21. Найдите траекторию точки, для которой во все время движения произведение расстояний до двух данных пересекающихся прямых есть величина постоянная.

На основании первого закона Кеплера Земля движется вокруг Солнца по эллиптической орбите, в одном из фокусов которой расположено наше светило. Найдем скорость Земли в точке наибольшего удаления планеты от Солнца, если эксцентриситет орбиты e=0,0167; большая полуось a=149504000 км; масса Солнца mc=1,97×1030 кг (рис. 5.31).

Рис. 5.31. Орбита вращения Земли вокруг Солнца

Движение Земли в поле гравитации подчиняется закону сохранения энергии, согласно которому во всякой точке орбиты ее полная механическая энергия остается постоянной. Пусть и – радиус-векторы, определяющие, соответственно, наиболее и наименее удаленное положение Земли на орбите вокруг Солнца. Если

,

Есть кинетическая энергия Земли в точках A и B орбиты соответственно, где m3 – ее масса, и равенства

;

Характеризуют ее потенциальную энергию в гравитационном поле Солнца в этих точках, где G=6,67×10-11 м3/кгс2 – гравитационная постоянная, то

.

;

.

.

Это уравнение содержит две неизвестные: и . Чтобы преодолеть возникшую трудность, воспользуемся вторым законом Кеплера, согласно которому, радиус-вектор планеты за одинаковые промежутки времени зачерчивает одинаковые площади. Примем упрощенную гипотезу: за малые промежутки времени траекторию Земли можно считать прямолинейной. Тогда площади соответствующих секторов выразятся приближенно следующим образом:

;

И мы придем к соотношению:

,

Из которого находим связь между скоростями и :

.

Получаем следующее уравнение относительно неизвестной :

,

М/с.

Вот с какой скоростью мчится наша Земля в космическом пространстве. А ведь эта скорость минимальная. В точке В она будет еще выше.

22. Найдите наименьшую и наибольшую скорость Марса на орбите вокруг Солнца, используя соответствующие справочные данные.

Третий закон Кеплера гласит: квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит:

.

23. Используя этот результат, найдите большую полуось орбиты первого искусственного спутника Земли, который был запущен в 1957 году в СССР и имел период обращения 1 час 55 минут по эллиптической орбите, если период обращения Луны вокруг Земли равен 655,2 ч., большая полуось лунной орбиты составляет 382000 км и наименьшее удаление искусственного спутника от центра Земли – 6603 км. Радиус Земли принять равным 6378 км.

Интересно отметить, что скорость, которую необходимо сообщить искусственному спутнику вблизи поверхности Земли в горизонтальном направлении, чтобы он начал двигаться в качестве спутника по круговой орбите радиуса R (рис.5.32), определяется формулой:

.

Принимая g=9,81 м/с2, , получим . Это значение скорости называется первой (1) космической скоростью.

Если скорость V1 будет стремиться к значению

,

Равного для Земли, , то орбита искусственного спутника станет эллиптической и, достигнув, величины V2, второй космической скорости – станет параболической.

При скорости, большей второй космической, спутник будет двигаться по гиперболе.

В последних двух случаях, спутник навсегда покинет Землю и удалится в межпланетное пространство.

Рис. 5.32. Зависимость формы орбиты искусственного спутника Земли от начальной скорости.

24. Между Землей и Луной пролетает космический аппарат так, что расстояния от него до поверхности Земли и до поверхности Луны постоянно остаются равными между собой. Составьте математическую модель, описывающую это движение. В каких условиях она допускает упрощения?

25. На самолетах и кораблях во время второй мировой войны действовала навигационная система, использовавшая разницу времени между моментами приема радиосигналов от двух пар станций, которые испускали их одновременно. Составьте математическую модель этой навигационной системы и оцените ее достоинства и недостатки.

В прожекторах, фарах автомобилей используется параболоид вращения, который получается при вращении параболы вокруг собственной оси: лучи, выходящие из источника света, помещенного в фокус, не рассеиваются, а, отразившись от стенок параболоида, идут параллельно этой оси. Используется и обратный эффект. «Тарелка» – так называется параболическая антенна для спутниковой связи, собирает в одну точку телевизионные сигналы, идущие из космоса. Фокальные свойства кривых второго порядка давали повод для мифотворчества. Очевидно, что в повести «Гиперболоид инженера Гарина» А. Толстой имел в виду все-таки параболоид.

Еще раньше зародилась легенда об Архимеде из Сиракуз, который сжег флот римлян, обороняя свой город с помощью параболических зеркал.

26. Составьте технический проект такой «пушки», которая могла бы поражать противника на расстоянии 50-500 м. Попробуйте оценить ее поражающую мощь.

Вернемся к задаче Паппа, которая была поставлена в начале главы, как к одной из первых решенных Р. Декартом аналитическим методом. Дадим ее общую формулировку.

Даны 2n прямых, лежащих в одной плоскости. Найти геометрическое место точек в этой плоскости, таких, что произведение расстояний от каждой точки этого множества до первых n прямых d1×D2. . ×Dn и произведение расстояний от этих же точек до следующих n прямых dn+1×Dn+1×. ×D2n находились бы для всех точек в одном и том же постоянном отношении L:

Попытка решить ее для n=3 (рис. 5.33) была предпринята нами ранее. Рассмотрим общий случай. Введем систему координат, выбирая ее начало в произвольной точке плоскости и опишем положение заданных прямых соответствующими нормальными уравнениями:

Рис. 5.33. Задача Паппа при n=3.

Пусть – произвольная точка искомого геометрического места точек. Найдем расстояния от нее до данных прямых:

Это и есть уравнение искомой кривой относительно координат x’ и у’ ее точек. Оно будет иметь степень n, в частном случае, например, для четырех прямых 2n=4; n=2 мы получим уравнение второй степени. Такое уравнение, как это уже отмечалось на стр.180, определяет одно из конических сечений. Это весьма неожиданный результат.

27. Каковы возможные обобщения задачи Паппа?

[spoiler title=”источники:”]

http://a-geometry.narod.ru/problems/problems_22.htm

http://matica.org.ua/metodichki-i-knigi-po-matematike/osnovy-vysshei-matematiki/05-4-zadachi-i-razmyshleniia

[/spoiler]

В геометрии сопряженные диаметры – это два диаметра эллипса, которые имеют особое отношение друг к другу.

Здесь диаметр означает хорду, проходящую через центральную точку. Если эллипс – круг, то два диаметра сопряжены тогда и только тогда, когда они ортогональны.

В литературе можно найти следующие эквивалентные определения:

Два диаметра эллипса называются сопряженными, если касательные в конечных точках одного диаметра параллельны другому диаметру.

Два диаметра называются сопряженными, если середины параллельных хорд лежат на них.

• KD3: Если под эллипсом понимать аффинное изображение единичной окружности, то изображения диаметров ортогональных окружностей называются сопряженными .

Доказательство свойств в результатах KD1 и KD2 из того , что любой эллипс является аффинным образом единичной окружности (см Эллипс (Описательный геометрия) ). Поскольку эти два свойства, очевидно, верны для круга, а аффинное отображение отображает центральные точки на центральные точки и поддерживает параллелизм.

В главной оси эллипса всегда сопряжена.

Два сопряженных радиуса эллипса – это два полудиаметра, лежащие на разных сопряженных диаметрах.
Две сопряженные точки эллипса – это две точки эллипса, лежащие на разных сопряженных диаметрах.
Два направления (вектора) называются сопряженными, если существует пара параллельных сопряженных диаметров эллипса.

Сопряженные диаметры играют важную роль в описательной геометрии из Rytz оси конструкции (см эллипса в описательной геометрии ). Главные оси эллипса восстанавливаются из знания двух сопряженных радиусов.

• 

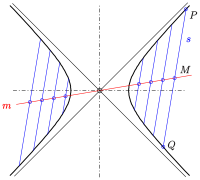
  Гипербола: центры параллельных сухожилий

• 

  Парабола: центры параллельных сухожилий

Комментарий:

1. Центры параллельных хорд гиперболы также лежат на прямой, проходящей через центр. Однако эта прямая линия не обязательно должна быть сухожилием, а именно, когда параллельные сухожилия пересекают обе ветви гиперболы. Поэтому здесь мы говорим только о сопряженных направлениях. Когда сопряженные диаметры упоминаются для гиперболы, диаметр означает диаметр данной гиперболы или сопряженной с ней гиперболы. (Гипербола, сопряженная с гиперболой, имеет уравнение .)
2. Центры параллельных хорд параболы также лежат на прямой. Эта прямая всегда параллельна параболической оси (см. Рисунок). Поскольку парабола не имеет центральной точки, здесь не говорится о сопряженных диаметрах. Иногда диаметр, параллельный параболической оси, называют диаметром.

Расчет сопряженных точек эллипса

Касательная к эллипсу в точке имеет уравнение (см. Эллипс ). Сопрягаемая точка должна лежать на прямой, параллельной касательной, проходящей через нулевую точку (центральную точку). Так это применимо

доволен.

Если , d. ЧАС. эллипс представляет собой окружность, две сопряженные точки принадлежат двум ортогональным радиусам, а последнее уравнение имеет привычный вид (скалярное произведение = 0).

Эллипс через параметрическое представление

учитывая d. ЧАС. как аффинное изображение единичной окружности точки как образы ортогональных радиусов единичной окружности принадлежат сопряженным точкам эллипса. С помощью теорем сложения следует:

Связь с отношениями ортогональности

В предыдущем разделе было показано, что эллипс напрямую связан с симметричной билинейной формой.

• 

Связанный. Эта билинейная форма определяет

• на качестве соотношения ортогональности :

являются ортогональными , если и только если есть, и

• на Метрика :

– длина вектора и

• эллиптическая полярность на прямой . ( Эллиптический здесь означает: полярность не имеет фиксированных точек. Это эквивалентно отсутствию вектора, ортогонального самому себе )

Таким образом, два сопряженных направления ортогональны в определенном здесь смысле, и данный эллипс является «единичной окружностью» по отношению к определенной здесь метрике.

Замечание 1.
Гипербола приводит к симметричной билинейной форме с аналогичными соображениями.

• .

Здесь вы также можете определить отношение ортогональности и метрику. Особенность этого случая заключается в следующем: существуют направления, ортогональные сами себе, а именно направления асимптоты, и есть векторы длины 0, отличные от (0,0)! Эта метрика также называется метрикой Минковского и связанными с ней «кругами» (= гиперболами), кругами Минковского или псевдоевклидовыми кругами . Этот случай играет существенную роль в теории относительности . На дистанционной линии билинейная форма индуцирует гиперболическую полярность . (Здесь гиперболический означает: полярность имеет две неподвижные точки.)

Замечание 2:
Если попытаться провести аналогичные рассуждения для параболы, это приведет к “непригодному” соотношению ортогональности. В этом случае все направления будут ортогональны направлению параболической оси.

Смотри тоже

• Теорема Аполлония

Индивидуальные доказательства

1. ^ Ульрих Граф, Мартин Барнер: начертательная геометрия. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , стр.106 .
2. ↑ К. Леопольд: Геометрические основы архитектурного изображения. Verlag W. Kohlhammer, Штутгарт 2005, ISBN 3-17-018489-X , стр. 61.
3. ↑ Рудольф Фуке, Конрад Кирх, Heinz Nickel: Начертательная геометрия. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4 , стр.183 .