- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №5

авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 1 (учебник)
- Урок 9. Вычитание двузнаных чисел: 40 – 28
ГДЗ учебник по математике 2 класс Петерсон. Урок 9. Вычитание двузнаных чисел: 40 – 28. Номер №5
- Предыдущее
- Следующее
Составь пример на вычитание из круглого числа, реши его графически и записывая в столбик.

reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 9. Вычитание двузнаных чисел: 40 – 28. Номер №5
Решение
40 − 13 = (30 + 10) − (10 + 3) = (30 − 10) + (10 − 3) = 20 + 7 = 27
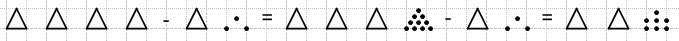
–
40
13
27
- Предыдущее
- Следующее
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Решение уравнений с помощью графиков
Решение линейных уравнений
Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.
Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.
Сейчас же я покажу тебе, как это сделать графическим способом.
Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)
Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:
( displaystyle 2x=2+10)
( displaystyle 2x=12)
Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.
Иными словами, у нас будет:
( displaystyle {{y}_{1}}=2x)
( displaystyle {{y}_{2}}=12)
А теперь строим. Что у тебя получилось?
Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:
Наш ответ: ( displaystyle x=6)
Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!
Вариант 1. Напрямую
Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)
Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:
( displaystyle x=-frac{b}{2a})
( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})
Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.
Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!
Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:
( displaystyle x=frac{-2}{2}=-1)
( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:
Возвращаемся к нашей параболе.
Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?
Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).
При ( displaystyle x=0):
( displaystyle y={{0}^{2}}+0-8=-8)
При ( displaystyle x=2):
( displaystyle y={{2}^{2}}+2cdot 2-8=0)
Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:
Как ты думаешь, что является решением уравнения?
Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).
И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).
Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!
Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.
Что у тебя получилось? То же самое?
Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!
Решение смешанных неравенств
Теперь перейдем к более сложным неравенствам!
Как тебе такое:
( displaystyle 4x<{{x}^{3}})?
Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!
Первое, с чего мы начнем, – это с построения двух графиков:
( displaystyle {{y}_{1}}=4x)
( displaystyle {{y}_{2}}={{x}^{3}})
Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).
Расписал? Теперь строй два графика.
Сравним наши рисунки?
У тебя так же? Отлично!
Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).
Смотри, что получилось в итоге:
А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!
На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).
Это и есть ответ!
Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!
Голосование за лучший ответ
Анастасия ~/~
Мастер
(1062)
11 лет назад
Видимо, нарисовать палочки (кружочки) , а потом необходимое количество зачеркнуть? И считать оставшиеся.. .
А на уроке ничего подобного не рисовали?
Ой, чего только сейчас в школах не придумают..
Mr. Vampir
Мастер
(2126)
11 лет назад
Это значит решить пример с помощью графика, чертежа или какоой-то другой схемы… .
Источник: 2-ой класс…. это тебе не хухры-мухры))))
Ахмадеев Зуфар
Знаток
(365)
5 лет назад
нарисовать то что получается если сложить эти или эные фигуры
Для того чтобы решить уравнение графически,надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Например, дано такое уравнение:
x² – 2x – 1 = 0
Если мы еще не изучали решение квадратных уравнений алгебраическим способом, то можем попробовать сделать это либо разложением на множители, либо графически. Чтобы решить подобное уравнение графически, представим его в таком виде:
x² = 2x + 1
Из такого представления уравнения следует, что требуется найти такие значения x, при которых левая часть будет равна правой.
Как известно, графиком функции y = x² является парабола, а y = 2x + 1 — прямая. Координата x точек координатной плоскости, лежащих как на первом графике, так и на втором (то есть точек пересечения графиков) как раз и являются теми значениями x, при которых левая часть уравнения будет равна правой. Другими словами, координаты x точек пересечения графиков являются корнями уравнения.
Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.
Формирование умения решать задачи является одной из основных целей обучения математике в начальной школе.
При обучении решению текстовых задач необходимо достигнуть двух взаимосвязанных целей — обучить:
1) решению определенных видов задач, что важно потому, что дает необходимый опыт и возможность выделить в решаемой задаче те подзадачи, решение которых известно. Кроме того, при решении каждой новой задачи можно использовать уже знакомые способы и приемы,
2) приемам поиска решения любой задачи, так как на практике приходится встречаться с задачами, при поиске решения которых никакой прежний опыт не помогает и требуется догадка, «открытие».
Можно ли помочь ученику прийти к такой догадке, дать ему некоторое средство, помогающее «открытию» ?
Для того чтобы решить задачу, необходимо построить ее математическую модель, а затем применить известные методы для нахождения числового значения искомых величин.
Условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба называется схематическим чертежом, или схемой.
Текст любой сюжетной задачи можно представить графически. Это и есть переход от словесного моделирования к другим формам моделирования.
Для построения модели любой сюжетной задачи необходимо выделить в задаче цель, данные величины, зафиксировать все отношения, чтобы с опорой на эту модель можно было продолжить анализ, позволяющий составить план и искать оптимальные пути решения.
Опираясь на чертёж, легко можно дать ответ на вопрос задачи. Графический способ даёт возможность более тесно установить связь между арифметическим и геометрическим материалами, развить функциональное мышление детей.
Благодаря применению графического способа в начальной школе можно сократить сроки, в течение которых ученик научится решать различные задачи. В то же время умение графически решать задачу — это важное политехническое умение.
Графический способ даёт иногда возможность ответить на вопрос такой задачи, которую дети ещё не могут решить арифметическим способом.
Графическая информация легче для восприятия, более ёмкая, и, вместе с тем, может быть достаточно условной.
Рисование графической схемы:
во-первых, заставляет ученика внимательно читать текст задачи,
во-вторых, позволяет перенести часть умственных действий в действия практические и закрепить результат в виде материального объекта,
в-третьих, дает возможность искать решение самостоятельно.
Для этого необходимо с первого класса учить детей разбивать текст задачи на смысловые части и моделировать ситуации, отраженные в задаче.
Систематическое использование графического моделирования обеспечит более качественный анализ задачи, осознанный и обоснованный выбор необходимого арифметического действия и предупредит многие ошибки в решении задач учащимися.
Таким образом, чтобы дети лучше представляли себе жизненную ситуацию, отраженную в задаче, легче прослеживали зависимости между величинами, а выбор действия становился для них осознанным и доказательным, необходимо систематически обучать детей моделированию, начиная с полного предметного изображения числового взаимоотношения величин с демонстрацией самого действия задачи.
Затем следует переходить к более обобщенному условно-предметному и графическому моделированию, к краткой записи задачи с использованием создаваемого на глазах у детей и самими детьми чертежа, схемы, после чего можно переходить к более высокой степени абстракции с применением готовых обобщенных опорных схем и таблиц.

Мультимедийный материал помогает иллюстрировать работу над задачей.
Данную презентацию можно использовать в качестве наглядной демонстрации при изучении задач в 1 классе. Анализ условия задачи дополнен анимированным рисунком и схемой, есть запись решения и ответ для самопроверки.
Читаем задачу с доски, анализируем, выбираем главные слова. Щелчок компьютерной мышки подчеркивает главные слова красной линией. Далее последовательно по щелчкам появляется наглядное изображение к задаче – рисунок и схема.
В работе подобраны задачи всех типов, с которыми знакомятся учащиеся 1-х классов. Эти задачи можно использовать в начале 2-го класса на уроках повторения. По аналогии можно составить тексты других задач.
Переход с главного слайда (слайд 2) на слайды с задачами осуществляется кликом мыши по кнопке «карандаш».
Переход с любого слайда на главный слайд с содержанием осуществляется кликом мыши по управляющей кнопке «карандаш».
