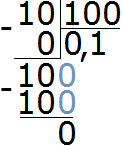Сотая часть от числа как найти

Калькулятор долей

Количество знаков после запятой (0-4):

Как пользоваться калькулятором долей

Чтобы рассчитать долю от числа в процентном либо дробном выражении, введите данные в блоки 1 и 2:

Необходимо определить какую долю от числа 100 составляет число 12? В блоке 1 вводим «12», а в блоке 2 число «100». Результат будет показан в блоке 3.

Чтобы рассчитать долю от числа в абсолютном значении, введите данные в блоки 2 и 3:

Необходимо определить сколько составляет 1/5 от числа 20? В блоке 3 в поле «простая дробь» вводим «1/5», а в блоке 2 число «20». В блоке 1 будет показан результат «20».

Чтобы найти число по известной доле, введите данные в блоки 1 и 3:

Необходимо определить число от которого 30 составляет 20%? В блоке 1 вводим «30», а в блоке 3 в поле «%» число «20». В блоке 2 будет показан результат «150».

212,5

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Равенство двух отношений называют пропорцией.

a : b = c : d или a/b = c/d

• a, d — крайние члены
• b, c — средние члены

Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.

Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем:

Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:

1390 руб. = 100%
x руб. = 14%

Перемножим крест-накрест и найдем x:

x = 1390 × 14 : 100
x = 194,6

Ответ: выгода по скидке составила 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.

Процент	Дробь	Как найти % от числа a
10%	1/10	a : 10
20%	1/5	a : 5
25%	1/4	a : 4
50%	1/2	a : 2
75%	3/4	a : 4 × 3

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем:

значит, нужно заплатить 75% от первоначальной цены.

Используем правило соотношения чисел:

75% — это 3/4 от числа, значит,
8500 : 4 × 3 = 6375 (рублей).

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Онлайн-калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета процента от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть проценты: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

Источник

Проценты

Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.

Что такое процент?

В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% = = 0,01

Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби

Получили 0,1. Теперь 0,1 умножаем на числитель дроби

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

Теперь полученный результат умножаем на 50

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

Ответ: 384 костюмов нового фасона выпустила фабрика.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Нахождения числа по его проценту

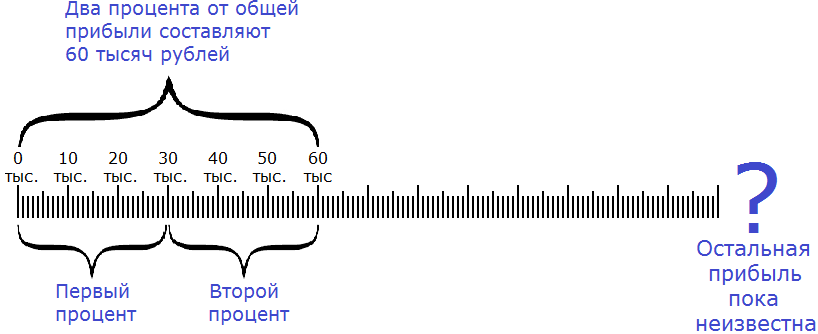
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Источник

Проценты

Процентом от некоторой величины называется одна сотая ее часть и обозначают один процент так: 1%.

Чтобы найти процент от некоторой величины, нужно разделить эту величину на 100.

Пример:

1% от 200 т равен 2 т, так как 200 : 100 = 2.

1% от 5 км равен 50 м, т.к. 1 км = 1 000 м, тогда 5 км = 5 000 м, а 5 000 м : 100 = 50 м.

Величина, от которой вычисляются проценты составляет 100 своих сотых долей, т.е. 100 %.

Например, если говорят, что учащийся выполнил 100% домашнего задания, значит, он выполнил все домашнее задание, которое ему было задано.

Любое число процентов можно записать в виде десятичной дроби или натурального числа.

Для этого нужно число, стоящее перед знаком %, разделить на 100.

Пример:

15% = 15 : 100 = 0,15;

60% = 60 : 100 = 0,60 = 0,6;

700% = 700 : 100 = 7;

23,5% = 23,5 : 100 = 0,235.

Обратите внимание: если у числа на конце справа стоит меньше двух нулей, то деление выполняем по правилу деления десятичных дробей на 100, т.е. перемещая запятую влево на две цифры, учитывая то, что у натурального числа запятую мы подразумеваем на конце справа.

Любую десятичную дробь или любое натуральное можно записать в процентах.

Для этого нужно десятичную дробь или натуральное число умножить на 100 и к результату приписать знак %.

Пример:

3,5 = 3,5100 = 350%;

0,07 = 0,07100 = 7%;

9 = 9100 = 900%.

Обратите внимание: когда мы умножаем десятичную дробь на 100, то перемещаем запятую вправо на две цифры.

Чтобы найти несколько процентов от числа, нужно это число разделить на 100, а затем, полученный результат, умножить на число, стоящее перед знаком %.

Пример:

1) Найти 15% от числа 800.

800 : 100 = 8 — 1% от числа 800.

815 = 120 — 15% от числа 800.

2) Найти 6% от числа 375.

375 : 100 = 3,75 — 1% от числа 375.

3,756 = 22,50 = 22,5 — 6% от числа 375.

×	3	7	5
6
2	2	5	0

Чтобы найти число по его процентам, нужно разделить число, соответствующее известным процентам от числа, на число стоящее перед знаком % и полученный результат умножить на 100 или можно представить проценты в виде десятичной дроби и разделить значение процентов на эту дробь.

Пример:

Найдите число, если 20% этого числа равны 80?

1) 80 : 20 = 4 — 1% от числа.

2) 4100 = 400.

2) 80 : 0,2 = 800 : 2 = 400.

Ответ: 400.

Поделись с друзьями в социальных сетях:

Источник

Слово процент произошло от латинского per cent – на сотню, то есть одна сотая часть. Процент имеет обозначение – %. Для того, чтобы найти 1% от какого-либо числа, следует разделить это число на 100 или умножить на 0,01. Так например, 1% от 500 будет равен 5, а 1% от 50 будет равен 0,5. 1% от 100 всегда равен 1 – и это понятно, потому что 1% – это сотая доля. модератор выбрал этот ответ лучшим Rogne­da [416K] 5 лет назад  Чтобы вычислить 1% от какого-то числа, его величину принимаю за 100%. Соответственно, 1% – это неизвестная величина, в 100 раз меньшая за исходную. Наглядно это видно, если составлю следующую пропорцию, взя за исходное число 349: 349 – 100% х – 1%. Составляя пропорцию, важно не перепутать местами проценты, то есть их пишем друг под другом, или в столбик. Высчитаю данную пропорцию: х = 349 х 1 : 100; х = 3,39. Еще проще высчитать 1% от числа, зная, что это одна сотая от числа, если отделить запятой два знака с конца числа, например: 248 – 2,48; 579 – 5, 79. Ксарф­акс [156K] 6 лет назад  Для того, чтобы найти 1 процент от числа, нужно вспомнить определение процентов. Процент – это одна сотая часть числа. Это понятие произошло от латинского слова “per cent”, которое означает “на сотню”. Таким образом, чтобы рассчитать 1 процент, необходимо заданное число разделить на 100 или умножить его на 0,01. Все эти вычисления легко можно сделать в уме, в крайнем случае можно воспользоваться калькулятором. Примеры 1) Найдём 1 процент от числа 80. Он будет равен: 80 * 0,01 = 0,8. 2) Найдём 1 процент от числа 1500. Он будет равен: 1500 / 100 = 15. 3) Найдём 1 процент от числа 7,8. Он будет равен: 7,8 * 0,01 = 0,078. ovasi­liev [30.8K] 6 лет назад  По определению, один процент – эта одна сотая часть. Но найти его не всегда так тривиально, как могло бы подуматься. Просто его найти в математике от вещественного числа, или в физике, когда вещество чистое и однородное. А вот такая задача: сколько весит один процент воды в одном килограмме десятипроцентного раствора соли в воде? Здесь уже придётся делать два действия: сначала вычислить массу воды – 900 грамм, а потом делить на сто, получая 9 грамм. В экономике с процентами вообще очень много вычислений, потому что денежная выручка сильно структурирована, прежде чем вычислить процент прибыли, нужно “очистить” валовую выручку от налогов, амортизации, сырьевых затрат и прочих статей формирования цены. Autho­r [788K] 6 лет назад  Чтобы найти 1 процент от любого числа нетрудно, если же припомнить смысл этих процентов. Процентом-то и называется доля, соответствующая одной 100-й части от целого. Как, например, необходимо отыскать 1 процент от числа 944. Просто делим, 944/100=9,44. То есть 1 процент от 944 будет равен 9,44 (один процент). Profi­lakti­ka [95.6K] 6 лет назад  Чтобы найти 1 процент от числа, нужно это число разделить на 100. Чтобы разделить число на сто в нашей десятичной системе счисления, нужно всего лишь визуально передвинуть его запятую на два знака влево. Пример: 28881 / 100 = 288.81. Разделите имеющееся у вас число, от которого нужно найти один процент, на сто. Один процент это одна сотая от вводного числа. Пример: 1 процент от 200 равен – 200 : 100=2 1 процент от 12345 равен – 12345 : 100=123,45 Чтобы найти один процент от определенного числа нужно разделить это число на 100%. Так как принято считать число за 100%. То есть от числа 717 один процент будет вычисляться: 717 / 100 = 7,17 7,17 = 1% Серге­й Больш­аков [47.8K] 9 лет назад  Процент – это одна сотая (1/100) часть целого. Например число 70.Сколько будет 1%.Берете 70 и делите на 100= 0,7. Алиса в Стран­е [363K] 6 лет назад  Как приятно вспомнить школу и математику, которая была любимым моим предметом, особенно в старших классах – алгебра, и в институте – высшая математика. Но проценты изучают гораздо раньше. Даже не знаю – в каком сейчас классе. Чтобы вычислить один процент от числа, нужно число поделить на 100, это и будет 1% от числа. Например число 5000. Чтобы узнать сколько будет 1% от 5000: делим 5000 на 100 и получаем 50. Все очень просто. Матве­й628 [90K] 9 лет назад  Найти 1 процент от числа нетрудно, если вспомнить смысл процентов. Процентом называется доля, соответствующая одной сотой части от целого. Поэтому, чтобы найти 1 процент, нужно число разделить на сто частей и взять одну сотую часть от числа. Например, нужно найти 1 процент от 874. 847/100=8,47. То есть 1 процент от 847 равен 8,47. Бекки Шарп [71.2K] 6 лет назад  Один процент – это одна сотая часть числа. То есть делим число на 100 и получаем 1%. Например : Сколько будет один процент от 1000 рублей. 1000 : 100 = 10. Десять рублей – это 1 процент от тысячи. Сколько будет 1 % от 0,001? 0,001 : 100 = 0,00001. Знаете ответ?

Найди сотую часть числа: 200, 500, 700, 800.
Назови сотую часть величины: 5 м, 9 дм, 1 век.