Вероятное (срединное) отклонение случайной величины, распределённой по нормальному закону — половина участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине. Эта характеристика рассеивания, наряду со средним квадратическим отклонением, часто используется в ряде областей применения теории вероятностей, в частности в теории стрельбы для артиллерии и стрелкового оружия[1].
Свойства[править | править код]
Если X — случайная величина, распределённая по нормальному закону, m — её среднее значение, В — вероятное отклонение, σ — среднее квадратическое отклонение и P(a, b) — вероятность попадания величины Х между величинами a и b, то справедливо следующее[2]:
- P(m — 4В, m — 3В) ≈ 0,02
- P(m — 3В, m — 2В) ≈ 0,07
- P(m — 2В, m — В) ≈ 0,16
- P(m — В, m) = 0,25
- P(m, m + В) = 0,25
- P(m + В, m + 2В) ≈ 0,16
- P(m + 2В, m + 3В) ≈ 0,07
- P(m + 3В, m + 4В) ≈ 0,02
- В ≈ 0,674×σ
Пример[править | править код]
В таблицах стрельбы 122-мм гаубицы обр. 1938 г. (М-30) указано, что при ударной стрельбе на максимальную дальность в 11800 м осколочно-фугасной гранатой ОФ-462 на полном заряде при нормальных условиях[3] срединное отклонение по дальности составляет 41 м, срединное боковое отклонение — 10 м.[4] Это означает, что при достаточно большом числе выстрелов с исправлением наводки (чтобы точка прицеливания осталась неизменной) около 50 % точек разрывов попадёт в интервал по дальности 11759—11841 м, а практически все попадания будут лежать в интервале от 11636 до 11964 м. При этом в пределах продольной полосы ±10 м справа и слева от точки прицеливания также будет 50 % точек попаданий. Знание этих величин полезно при оценке требуемого количества боеприпасов для надёжного поражения цели. Например, для указанных выше условий при серии из 100 выстрелов около 25 точек разрывов будет находиться в прямоугольнике с размерами 82×20 м с центром в точке прицеливания, с длинной стороной вдоль направления «орудие—цель». Также срединные отклонения нужны при нахождении безопасной дистанции своих войск до огневого вала. В рассматриваемом случае, с учётом максимального разлёта опасных осколков от разрывов гранат ОФ-462 на расстояние порядка 200 м, своей пехоте для практически безопасного нахождения в обстреливаемой области следует держаться минимум в 4В + 200 ≈ 360 м от точки прицеливания.
Литература[править | править код]
- Вентцель Е. С. Теория вероятностей. — М. Наука, 1964
- ГАУ РККА. Таблицы стрельбы 122-мм гаубицы обр. 1938 г. № 146 и 146/140Д. — М. Воениздат НКО СССР, 1943
Примечания[править | править код]
- ↑ Вентцель Е. С. Теория вероятностей. — М. Наука, 1964, с. 127
- ↑ Вентцель Е. С. Теория вероятностей. — М. Наука, 1964, с. 127, 128
- ↑ То есть цель находится на горизонте орудия, нет наклона оси цапф орудия, атмосферные давление и температура на горизонте орудия равны 750 мм рт. ст. и 15°С соответственно, отсутствие ветра
- ↑ ГАУ РККА. Таблицы стрельбы 122-мм гаубицы обр. 1938 г. № 146 и 146/140Д. — М. Воениздат НКО СССР, 1943, с. 84
Привет, Вы узнаете про вероятное срединное отклонение, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
вероятное срединное отклонение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой 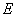 (иногда В).
(иногда В).
Вероятным (срединным) отклонением случайной величины 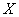 , распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение 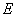 – это половина длины участка оси абсцисс, симметричного относительно точки
– это половина длины участка оси абсцисс, симметричного относительно точки 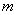 , на который опирается половина площади кривой распределения.
, на который опирается половина площади кривой распределения.
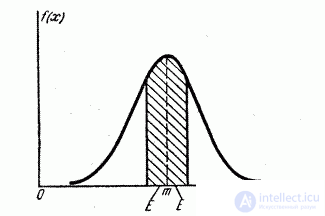
Рис. 6.4.1.
Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».
Рассмотрим случайную величину 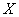 , распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания
, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания 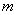 меньше, чем на
меньше, чем на 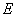 , по определению вероятного отклонения
, по определению вероятного отклонения 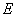 , равна
, равна 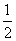 :
:
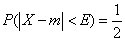 . (6.4.1)
. (6.4.1)
Вероятность того, что она отклонится от 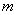 больше, чем на
больше, чем на 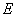 , тоже равна
, тоже равна 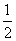 :
:
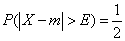 .
.
Таким образом, при большом числе опытов в среднем половина значений случайной величины 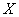 отклонится от
отклонится от 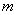 больше, чем на
больше, чем на 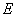 , а половина – меньше . Об этом говорит сайт https://intellect.icu . Отсюда и термин «срединная ошибка», «срединное отклонение».
, а половина – меньше . Об этом говорит сайт https://intellect.icu . Отсюда и термин «срединная ошибка», «срединное отклонение».
Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего квадратического отклонения 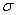 . Вычислим вероятность события
. Вычислим вероятность события 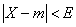 в уравнении (6.4.1) по формуле (6.3.10). Имеем:
в уравнении (6.4.1) по формуле (6.3.10). Имеем:
 .
.
Отсюда
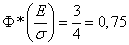 . (6.4.2)
. (6.4.2)
По таблицам функции 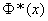 можно найти такое значение аргумента
можно найти такое значение аргумента 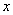 , при котором она равна 0,75. Это значение приближенно равно 0,674; отсюда
, при котором она равна 0,75. Это значение приближенно равно 0,674; отсюда
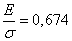 ;
; 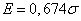 . (6.4.3)
. (6.4.3)
Таким образом, зная значение 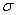 , можно сразу найти пропорциональное ему значение
, можно сразу найти пропорциональное ему значение 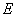 . Часто пользуются еще такой формой записи этой зависимости:
. Часто пользуются еще такой формой записи этой зависимости:
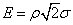 , (6.4.4)
, (6.4.4)
где 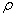 – такое значение аргумента, при котором одна из форм интеграла вероятностей – так называемая функция Лапласа
– такое значение аргумента, при котором одна из форм интеграла вероятностей – так называемая функция Лапласа
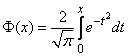
– равна половине. Численное значение величины 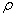 приближенно равно 0,477.
приближенно равно 0,477.
В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой 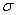 . В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
. В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
Если в качестве характеристики рассеивания принято вероятное отклонение 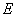 , то плотность нормального распределения записывается в виде:
, то плотность нормального распределения записывается в виде:
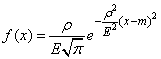 , (6.4.5)
, (6.4.5)
а вероятность попадания на участок от 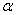 до
до 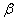 чаще всего записывается в виде:
чаще всего записывается в виде:
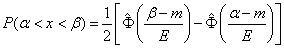 , (6.4.6)
, (6.4.6)
где
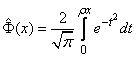 (6.4.7)
(6.4.7)
– так называемая приведенная функция Лапласа.
Сделаем подсчет, аналогичный выполненному в предыдущем n° для среднего квадратического отклонения 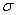 : отложим от центра рассеивания
: отложим от центра рассеивания 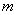 последовательные отрезки длиной в одно вероятное отклонение
последовательные отрезки длиной в одно вероятное отклонение 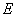 (рис. 6.4.2) и подсчитаем вероятности попадания в эти отрезки с точностью до 0,01. Получим:
(рис. 6.4.2) и подсчитаем вероятности попадания в эти отрезки с точностью до 0,01. Получим:
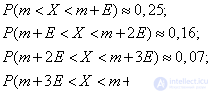
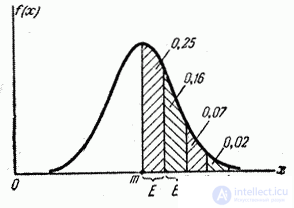
Рис. 6.4.2.
Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке  .
.
Пример. Самолет-штурмовик производит обстрел колонны войск противника, ширина которой равна 8 м. Полет – вдоль колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо по направлению полета. Главные вероятные отклонения: по направлению полета 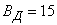 м, в боковом направлении
м, в боковом направлении  м. Не имея в своем распоряжении никаких таблиц интегралов вероятностей, а зная только числа:
м. Не имея в своем распоряжении никаких таблиц интегралов вероятностей, а зная только числа:
25%, 16%, 7%, 2%,
оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.
Решение. Для решения задачи достаточно рассмотреть одну координату точки попадания – абсциссу 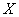 в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания
в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания 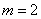 и вероятным отклонением
и вероятным отклонением 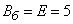 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
(м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
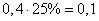 .
.
Влево от центра рассеивания цель занимает участок 6 м. Это – целое вероятное отклонение (5 м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна:
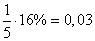 .
.
Таким образом, вероятность попадания в колонну приближенно равна:
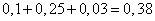 .
.
Вероятность хотя бы одного попадания при трех выстрелах равна:

Надеюсь, эта статья про вероятное срединное отклонение, была вам полезна,счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое вероятное срединное отклонение
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но емко про вероятное срединное отклонение
Макеты страниц
Во многих вопросах прикладной теории вероятностей, в частности в теории стрельбы, а также в теории ошибок, пользуются характеристикой рассеивания, которую называют вероятным, или срединным отклонением. В теории стрельбы ее называют срединной ошибкой.
Определение 1. Вероятным (срединным) отклонением называется такое число Е, что вероятность того, что случайная величина (ошибка, например), подчиненная нормальному закону распределения

попадет в интервал  , равна 1/2 (рис. 437), т. е.
, равна 1/2 (рис. 437), т. е.

Для любой, случайной величины  подчиняющейся нормальному закону распределения с центром рассеивания
подчиняющейся нормальному закону распределения с центром рассеивания  срединное отклонение Е (рис. 438) удовлетворяет соотношению
срединное отклонение Е (рис. 438) удовлетворяет соотношению

Выразим среднеквадратичное отклонение о через срединную ошибку Е.

Рис. 437,

Рис. 438,
Левую часть равенства (1) выразим через функцию  :
:

По формуле (7) § 17 получаем

В равенствах (1) и (4) левые части равны, следовательно, равны и правые:

По таблице значений функции  находим значение аргумента
находим значение аргумента  для которого
для которого  Следовательно,
Следовательно,

Это число 0,4769 принято обозначать через  :
:

Отсюда

Макеты страниц
Во многих вопросах прикладной теории вероятностей, в частности в теории стрельбы, а также в теории ошибок, пользуются характеристикой рассеивания, которую называют вероятным, или срединным отклонением. В теории стрельбы ее называют срединной ошибкой.
Определение 1. Вероятным (срединным) отклонением называется такое число Е, что вероятность того, что случайная величина (ошибка, например), подчиненная нормальному закону распределения

попадет в интервал  , равна 1/2 (рис. 437), т. е.
, равна 1/2 (рис. 437), т. е.

Для любой, случайной величины  подчиняющейся нормальному закону распределения с центром рассеивания
подчиняющейся нормальному закону распределения с центром рассеивания  срединное отклонение Е (рис. 438) удовлетворяет соотношению
срединное отклонение Е (рис. 438) удовлетворяет соотношению

Выразим среднеквадратичное отклонение о через срединную ошибку Е.

Рис. 437,

Рис. 438,
Левую часть равенства (1) выразим через функцию  :
:

По формуле (7) § 17 получаем

В равенствах (1) и (4) левые части равны, следовательно, равны и правые:

По таблице значений функции  находим значение аргумента
находим значение аргумента  для которого
для которого  Следовательно,
Следовательно,

Это число 0,4769 принято обозначать через  :
:

Отсюда

From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
В стрелковой
практике часто приходится сравнивать
разные способы измерения по степени их
точности. Для этого используют какую-то
общую меру точности способов измерения.
Такой мерой является средняя ошибка,
допускаемая при том или ином методе
измерения.
За
среднюю ошибку принимают одну из
следующих мер: или срединную, или
среднюю арифметическую, или среднюю
квадратическую ошибку.
Наиболее
распространенной мерой точности
является срединная
ошибка,
которая обозначается буквой Е.
Срединной
ошибкой называется такая ошибка, которая
по своей
абсолютной величине больше
каждой из ошибок одной половины и меньше
каждой из ошибок другой половины всех
ошибок, расположенных в
ряд в
возрастающем или убывающем порядке.
Исходя
из этого определения, найдем срединную
ошибку из 100 результатов измерений. Для
этого абсолютные величины всех полученных
ошибок расположим в возрастающем порядке
в приводимой ниже таблице.
Таблица № 3.
Результаты измерений
ошибок.
|
№ |
Δ |
№ |
Δ |
№ |
Δ |
№ |
Δ |
№ |
Δ |
|
1 |
2 |
3 4 |
4 5 |
5 6 |
6 8 |
7 9 |
8 |
9 11 |
10 |
|
1 |
+ |
21 |
+ 19 |
41 |
-33 |
61 |
-53 |
81 |
+ 74 |
|
2 |
-2 |
22 |
-20 |
42 |
+ 34 |
62 |
+ 53 |
82 |
+ 75 |
|
3 |
— 5 |
23 |
-20 |
43 |
-35 |
63 |
-56 |
83 |
— 78 |
|
4 |
— 5 |
24 |
-21 |
44 |
+ 36 |
64 |
— 56 |
84 |
— 81
—— |
|
5 |
+ 5 |
25 |
+ 21 |
45 |
-37 |
65 |
+ 57 |
85 |
+ 82 |
|
6 |
— 6 |
26 |
-22 |
46 |
-37 |
66 |
-59 |
86 |
+ 86 |
|
7 |
+ 7 |
27 |
+ 22 |
47 |
+ 38 |
67 |
-61 |
87 |
+ 86 |
|
8 |
— 8 |
28 |
-23 |
48 |
+ 38 |
68 |
+ 62 |
88 |
+ 89 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
9 |
+ 8 |
29 |
-24 |
49 |
+ 39 |
69 |
-63 |
89 |
— 92 |
|
10 |
+8 |
30 |
+24 |
50 |
+39 |
70 |
-63 |
90 |
+98 |
|
11 |
+10 |
31 |
+25 |
51 |
-41 |
71 |
+63 |
91 |
+97 |
|
12 |
-11 |
32 |
-27 |
52 |
-41 |
72 |
+ 64 |
92 |
— 103 |
|
13 |
-12 |
33 |
-27 |
53 |
+ 44 |
73 |
-65 |
93 |
+ 105 |
|
14 |
+ 12 |
34 |
-28 |
54 |
-46 |
74 |
+ 67 |
94 |
-107 |
|
15 |
-13 |
35 |
+ 28 |
55 |
+ 46 |
75 |
-70 |
95 |
-112 |
|
16 |
+ 13 |
36 |
-29 |
56 |
+ 47 |
76 |
+ 70 |
96 |
+ 112 |
|
17 |
-14 |
37 |
+ 29 |
57 |
-49 |
77 |
+ 71 |
97 |
-114 |
|
18 |
-17 |
38 |
-31 |
58 |
+ 49 |
78 |
+ 72 |
98 |
— 117 |
|
19 |
+ 17 |
39 |
-31 |
59 |
-52 |
79 |
-74 |
99 |
— 121 |
|
20 |
+ 18 |
40 |
+ 32 |
60 |
+ 52 |
80 |
+ 74 |
100 |
+ 124 |
Найдем
такую ошибку, которая в ряде всех ошибок
занимает срединное положение. Так как
мы имеем всего 100 измерений, то срединная
ошибка будет занимать место между 50-й
и 51-й ошибками. Абсолютная величина 50-й
ошибки равна 39 м, а 51-й— 41 м. Срединная
ошибка рассматриваемого ряда измерений
равна:
![]()
м.
Действительно,
ошибка величиной 40 м больше каждой
ошибки первой половины ряда всех
ошибок и меньше каждой ошибки второй
половины ряда всех ошибок.
В
приведенной таблице из всех 100 ошибок
50% ошибок по своей
абсолютной величине
меньше найденной нами срединной ошибки.
Посмотрим, сколько в этой половине
положительных и сколько отрицательных
ошибок.
Положительных
ошибок, в пределах 1Е
оказалось 24, т. е., приблизительно, 25%
всех ошибок; отрицательных ошибок в
этих пределах — 26, т. е. также около 25%
всех ошибок.
Найдем
число ошибок в пределах от +1Е
до
+2Е
и
выразим их в %. Ошибок от 41 до 80 м всего
оказалось 33; из них положительных ошибок
— 17, отрицательных — 16, т. е. примерно, по
16%.
Таким
же образом определяется % ошибок в
пределах от ±2Е
до ±3Е
и от ±3 Е
до ±4 Е.
Р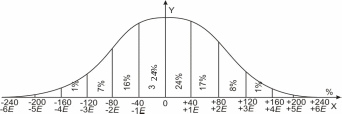
езультаты
подсчетов отразим графиком — шкалой
ошибок (рис. 11),
Рис.
11. Шкала ошибок из опыта.
Если
взять достаточно большое число ошибок,
при котором можно считать, что частота
события равна вероятности его появления,
тогда частота появления ошибок в пределах
одной Е
будет выражена в % на рис. 12. Этот график
представляет собой численное
выражение нормального закона ошибок,
так как он показывает численную
зависимость между величинами ошибок,
выраженными в Е,
и вероятностями получения их в
определенных пределах.
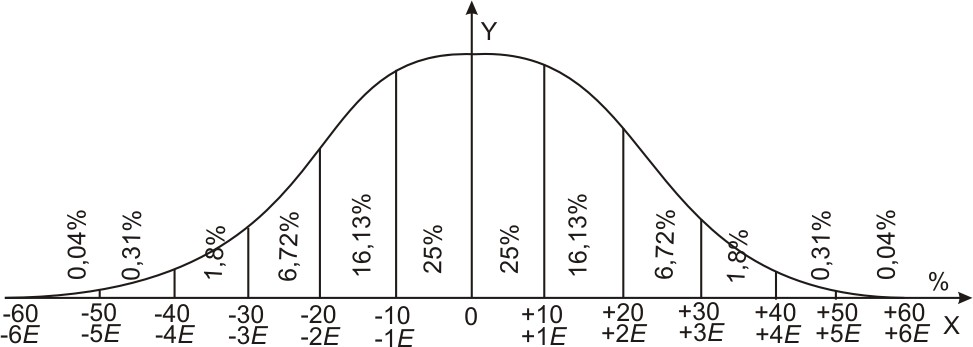
Рис.
12. Численное выражение нормального
закона ошибок.
Так, например, на
основании полученного графика мы можем
сказать, что вероятность получения
ошибки в пределах величин:
-
одной срединной
ошибки равна 25% +25%= 50%; -
двух срединных
ошибок равна 16,13%+25%+25%+16,13% = 82,26%.
На
основании данных рис. 12 можно сказать,
что ошибки измерения по своей величине
могут достигать до ±5Е
и даже до ±6Е.
Но из этого же рисунка видно, что
вероятность получения таких больших
ошибок очень невелика. На самом деле,
вероятность получения ошибки более
4Е
равна 2·(0,31% +0,04%) =0,70%. Это означает, что
из 1000 измерений только в 7 случаях
ошибка может быть больше 4Е.
На
основании этого с целью упрощения
расчетов численное выражение
нормального закона ошибок обычно
округляют, представляя его в виде шкалы
(рис. 13), которую называют шкалой
ошибок.
В этом случае практическим пределом
ошибки для любого способа измерения
принимают предел ± 4Е.
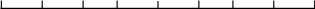
0,02 0,07 0,16
0,25 0,25 0,16 0,07 0,02
-4Е –3Е
–2Е –1Е 0 +1Е +2Е
+3Е +4Е
Рис.
13. Шкала ошибок.
Шкала
ошибок на рис. 13 составлена в целых долях
срединной ошибки Е.
Такую шкалу можно составить с любой
точностью — в любых долях Е.
На рис. 14 дана шкала ошибок, которая
позволяет определить вероятность
получения ошибки в пределах с точностью
до 1/2 Е
и до 1/4 Е.
Так, например, вероятность получить
ошибку в пределах ± 1/2Е
равна 0,13+0,13 =0,26 или 26%; в пределах ±1![]()
Е
равна (0,25+ 0,051)2 =0,602 или 60,2%; в пределах от
– -l![]()
Е
до + 1
Е
равна 0,09 + 0,25 + 0,067 = 0,407 или 40,7%; в пределах
от
+
Е
до+1![]()
Е
равна 0,12 + 0,09 + 0,037 = 0,247 или 24,7%.
|
0,02 |
0,07 |
0,16 |
0,25 |
0,25 |
0,16 |
0,07 |
0,02 |
||||||||||||||||||||||||
|
0,005 |
0,015 |
0,03 |
0,04 |
0,07 |
0,09 |
0,12 |
0,13 |
0,13 |
0,12 |
0,09 |
0,07 |
0,04 |
0,03 |
0,015 |
0,005 |
||||||||||||||||
|
0,002 |
0,004 |
0,005 |
0,008 |
0,011 |
0,014 |
0,019 |
0,024 |
0,031 |
0,037 |
0,044 |
0,051 |
0,056 |
0,064 |
0,066 |
0,067 |
0,067 |
0,066 |
0,064 |
0,056 |
0,051 |
0,044 |
0,037 |
0,031 |
0,024 |
0,019 |
0,014 |
0,011 |
0,008 |
0,005 |
0,004 |
0,002 |
-4Е –3Е
–2Е –1Е 0 +1Е +2Е
+3Е +4Е
Рис.
14. Шкала ошибок с точностью до 1/4 Е.
При
расчетах, требующих большой точности,
пользуются шкалой ошибок, составленной
до 0,01 Е.
Такая шкала имеет вид таблицы, где
вероятность получения ошибки в пределах
от 0 до ± Вдается
как Ф
(В),
т. е. как функция того или иного предела,
выраженного в Е.
Пользование этой
таблицей покажем на примерах.
Положим, что
истинное расстояние до цели равно 800 м.
Наблюдатель, измеряя это расстояние
глазомером, допускает какую-то ошибку.
Срединная ошибка измерения равна 10%
(см. табл. № 4), что в данном случае
составляет 80 м.
Таблица № 4.
Процентный размер
ошибок
|
№ по пор. |
Наименование |
величина |
|
1 2 3 4 5 6 7 |
Ошибка в определении
Ошибка в определении
Ошибка в определении
Ошибка в определении
Ошибка приведения
Ошибка наводки
Ошибка в определении |
10%Д 4%Д 5%Д 1,5м/сек
20% 5°С 0,3 тыс. 0,4 тыс. 0,8 тыс. 2,0 тыс. 0,1 радиана |
1
Определить вероятность получения ошибки
в пределах ±100 м (рис. 15).
Решение
В
=100:80= ±1,25Е.
Вероятность
получения ошибки в заданных пределах
Р
=Ф(В)=Ф(1,25Е)=0,601
или 60,1%.
Рис.
15. Вероятность получения ошибок в
пределах ±1,25Е.
2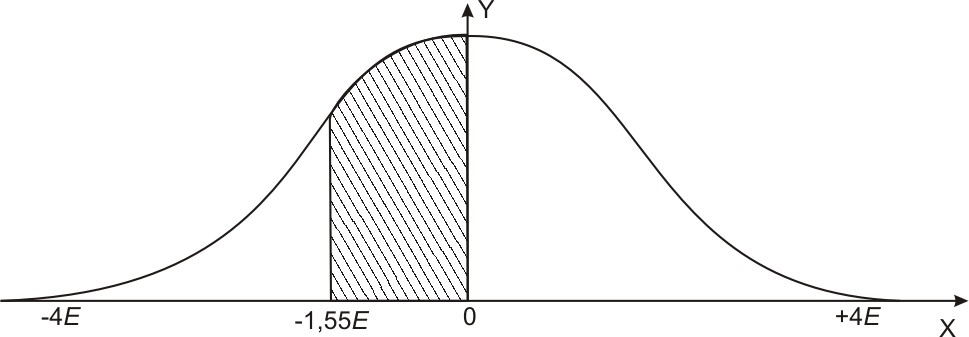
.
Определить вероятность получения
отрицательной ошибки в пределах от
0 до 124 м (рис. 16).
Рис.
16. Вероятность получения ошибок в
пределах от 0 до – 1,55 Е.
Решение
В=
124:80=1,55 Е
и![]()
ли
35,2%.
Повторяя
измерения какой-либо величины одним и
тем же способом, мы получаем разные
результаты с разными по величине и знаку
ошибками. Положим, что мы имеем ряд
измерений и нам требуется определить
ошибку каждого результата измерения.
Для этого надо знать истинное значение
измеряемой величины. Но так как это
невозможно, нужно найти такое значение,
которое можно было бы считать наиболее
подходящим
к истинному значению измеряемой величины.
Данному условию отвечает среднее
арифметическое из всех отдельных
результатов измерений, т. е. средний
результат.
Например, 10 человек
измеряли глазомерным способом расстояние
до одного и того же местного предмета.
При этом были получены следующие
результаты измерений: 930, 1150, 1071, 730, 1050,
955, 760, 1260, 839, 1015 м.
(![]()
Средний
результат 976 м считаем наиболее подходящим
значением измеряемой величины, т. е.
принимаем его за истинное значение.
Теперь можно определить ошибки каждого
результата измерений, как разность
между результатами отдельных измерений
и найденным подходящим значением
измеряемой величины. Мы получим: -46, +
174, +95, -246, +74, -21, -216, +284, -137, +39 м). Определить
средний результат Дср.
Р![]()
асположим
абсолютные значения этих ошибок в
возрастающем (можно в убывающем) порядке:
21, 39, 46, 74, 95,
137,
174, 216, 246, 284 (м). Срединная ошибка этого
ряда будет равна:
Однако
так находить срединную ошибку можно
только при большом количестве измерений.
При малом числе измерений срединную
ошибку определяют одним из следующих
двух способов: или по величине средней
арифметической ошибки, или по величине
средней квадратической ошибки. Для
этого нужно знать, как определяются,
величины названных ошибок и какие
существуют численные зависимости между
этими ошибками и срединной ошибкой.
Средняя
арифметическая ошибка
(E1)
равна
сумме абсолютных значений величин
ошибок, деленной на число ошибок, т. е.
![]()
П![]()
о
условию предыдущего примера, где было
произведено 10 измерений и получено
10 ошибок, средняя арифметическая
ошибка равна:
Между
срединной ошибкой (Е)
и средней арифметической ошибкой (E1)
существует следующая численная
зависимость: срединная ошибка равна
5/6 средней арифметической ошибки Е=5/6Е1
(точнее
Е=0,84535Е1).
На основании этого
можно найти величину срединной ошибки,
если известна величина средней
арифметической ошибки.
По условию нашего
примера срединная ошибка
E=![]()
м.
Средняя
квадратическая ошибка (Е2)
равна квадратному корню из
с![]()
уммы
квадратов абсолютных значений величин
ошибок, деленной на число ошибок без
одной, т. е.
По
условию предыдущего примера из 10
измерений средняя квадратическая
ошибка равна:
М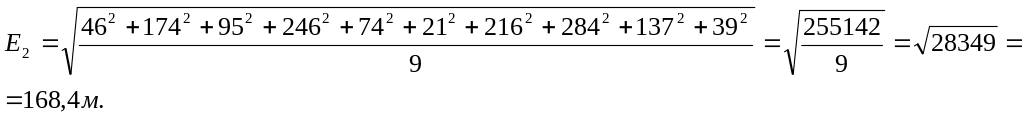
![]()
ежду
срединной ошибкой (Е)
и средней квадратической ошибкой (E2)
установлена следующая зависимость:
срединная ошибка равна 2/3 средней
квадратической ошибки
(точнее,
Е
= 0,67449 Е2).
Н![]()
а
основании этой зависимости найдем
величину срединной ошибки, если известна
величина средней квадратической ошибки
по условию нашего примера:
В
приведенных примерах величина срединной
ошибки Е,
найденная построением ошибок в ряд (116
м), незначительно отличается от величины
срединной ошибки, найденной по средней
арифметической (111 м), и от величины Е,
найденной по средней квадратической
ошибке (112 м). Однако теория стрельбы
установила, что наиболее точно срединная
ошибка может быть определена по средней
квадратической ошибке.
Рассмотрим
пример, на котором покажем, что при
небольшом количестве измерений
срединную ошибку необходимо определять
только через среднюю квадратическую.
Два
офицера при троекратном измерении
расстояния по карте командирской
линейкой допустили следующие ошибки в
миллиметрах: первый измерявший — 1,
3, 5; второй измерявший — 2, 3, 4. Кто из них
работал точнее?
По характеру
допущенных ошибок можно предположить,
что точнее измерял второй.
П![]()
одсчитаем
среднюю ошибку каждого измерявшего,
взяв за нее среднюю арифметическую
величину. Тогда получается, что средняя
арифметическая ошибка первого измерявшего
и![]()
у второго
т.
е. они работали одинаково точно. Однако
сам вид ошибок показывает нам, что точнее
работал второй измерявший. Проверим
это по средней квадратической ошибке,
которая является более высокой мерой
точности при небольшом числе измерений.
Найдем среднюю квадратическую ошибку
первого и второго измерявшего:
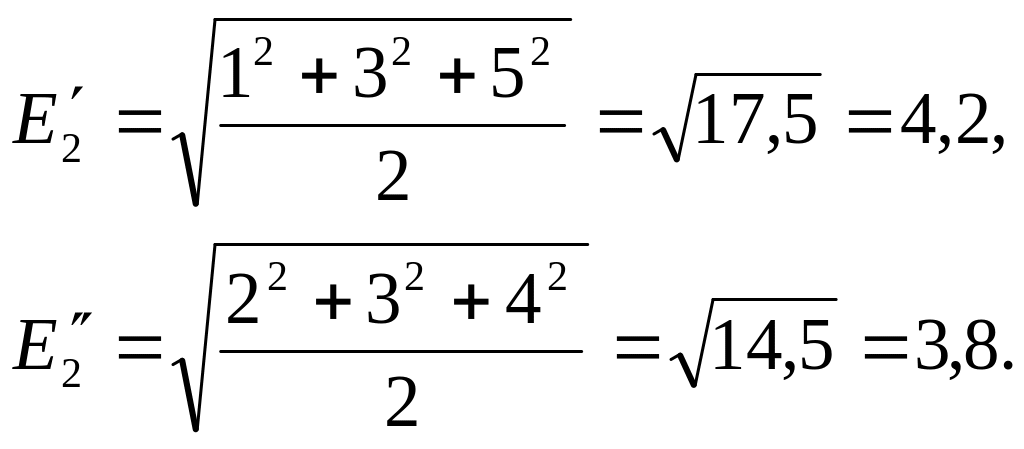
Теперь
мы подтвердили свое предположение о
том, что второй измерявший работал
точнее: у него средняя квадратическая
ошибка меньше, чем у первого. Этот расчет
убеждает нас и в том, что средняя
квадратическая ошибка оказывается
более высокой мерой точности, чем средняя
арифметическая.
Если
же мы в приведенном примере сравним
допущенные измерявшими срединные
ошибки, находя их по положению в ряду,
то мы не придем к правильному решению:
срединные ошибки оказываются равными.
Получается, что точность работы измерявших
одинакова. Это, как мы уже показали,
неверно и произошло потому, что при
малом количестве измерений срединную
ошибку нельзя находить построением
ошибок в ряд.
Итак,
при небольшом числе измерений срединную
ошибку следует находить по средней
квадратической ошибке, зная, что Е =
![]()
Е2.
Тогда в нашем примере
для первого измерявшего Е’=
4,2=2,8,
для второго измерявшего Е»=![]()
·3,8=2,53,
т. е. он работал точнее.
Таким образом, при
малом количестве измерений за подходящее
значение срединной ошибки следует
принимать срединную ошибку, найденную
по средней квадратической.
Вернемся к
рассмотренному ранее примеру с 10-ю
измерениями. Мы нашли ошибку каждого
результата измерения, после чего
определили подходящее значение срединной
ошибки различными способами:
— по месту в ряде
абсолютных значений ошибок срединная
ошибка оказалась равна Е=116
м;
— по средней квадратической ошибке
срединная ошибка равна 112м.
И здесь легко
убедиться в недостаточной точности
первого способа. Действительно, достаточно
добавить к нашему ряду еще одно (11-е)
измерение, как искомая величина Е
резко изменится (вместо 116 м станет 137 м
или 95 м).
Чтобы убедиться в
преимуществе второго способа, применим
к нему те же испытания, что и к первому
способу, т. е. посмотрим, как изменится
искомая величина Е,
если к имеющимся ошибкам 10-ти измерений
добавить ошибку 11-го измерения. Пусть
в одном случае эта ошибка равна 140 м
(больше 137 м), а в другом — 80 м (меньше 95
м).
При 11-ти измерениях
с добавлением ошибки 140 м срединная
ошибка Е,
найденная по средней квадратической,
будет равняться 110м.
При 11-ти измерениях
с добавлением ошибки 80 м срединная
ошибка Е,
найденная по средней квадратической,
будет составлять 108 м.
Как видим, добавочное измерение
незначительно изменяет суждение о
величине срединной ошибки, если ее
определять по средней квадратической
ошибке.
Таким образом,
практически для определения подходящего
значения срединной ошибки следует
применять способ определения срединной
ошибки по средней квадратической,
пользуясь зависимостью
П![]()

ример.
Определить срединную ошибку измерения
дальности до цели, если получены следующие
результаты в м: 360, 400, 450, 390.
Решение:
Статистическое оценивание срединного отклонения
случайной величины
А.В. Тихоненков
Рассмотрена сущность срединного отклонения как характеристики рассеивания случайной величины. Доказана чувствительность этой характеристики к отклонениям закона распределения случайной величины от нормального. Показаны возможные изменения срединного отклонения в статистических расчётах, связанные с недооценкой характеристик выборки.
Ключевые слова: выборка, гипотеза, параметр, распределение, совокупность, функционирование, функция, характеристика, цензурирование
Во многих вопросах прикладной теории вероятностей, в частности в теории стрельбы, а также в теории ошибок для количественной оценки рассеивания используется обычно величина, которую называют вероятным или срединным отклонением (срединной ошибкой) [1].
Вероятным или срединным отклонением (обычно обозначается Ех) называется половина длины интервала, симметричного относительно центра рассеивания, вероятность попадания в который равна 0,5. В интервал длиной 2Ех, симметричный относительно центра рассеивания, попадает в среднем «лучшая» половина значений нормальной случайной величины [2].
Характеристики рассеивания можно определять опытным, опытно-теоретическим и теоретическим методами. Но находят применение только разновидности опытно-теоретического метода с различной степенью участия эксперимента и теории [3].
В основу определения характеристик рассеивания положены опытные значения этих характеристик, полученные для каждой группы испытаний по известной формуле:
где В^ — статистическая оценка вероятного (срединного) отклонения результатов измерений (точек попадания) по координате:
Тихоненков Алексей Викторович — кандидат технических наук, доцент кафедры информатики и математики Международного института экономики и права, докторант Военного учебно-научного центра Сухопутных войск «Общевойсковая академия Вооружённых Сил Российской Федерации». Адрес для корреспонденции: tihonenk@mail.ru
Для цитирования: Вестник МИЭП. 2014. № 1. С. 17-23.
п _ 2
(1)
п
_ I £ £ =
1=1 1
(2)
п
где п — число счетных результатов в данной группе.
Статистическая оценка срединного отклонения В^ по N группам испытаний определяется по формуле:
В = 0,6745
1
N 2
I В^-1) ]=1
N
I п^
н
(3)
Однако уже давно замечена нестабильность исследуемых характеристик при повторных испытаниях, то есть значения В^, вычисляемые по формуле (3), имеют значительный разброс, доходящий до 30-40% и более. Очевидно, нужны методы, позволяющие устранить этот недостаток.
Вероятное отклонение выражается через среднеквадратическое отклонение. Согласно определению,
Г1 ^
Р(
Х-т
X
< Е =
X
2
(4)
Для симметричного (относительно центра рассеивания) интервала известна формула:
г > < 1 = Ф —
Р(
Х-т
X
О
V X У
(5)
Тогда, принимая 1 = Ех, находим:
Ф
Г Е ^
X
О
V X У
0,5.
(6)
По таблице функции Ф(х) получаем значение аргумента х ~ 0,6745, при котором она будет равна 0,5. Следовательно, справедливо соотношение:
Ех/ах = 0,6745.
Отсюда получим:
Ех = 0,6745 ах.
(7)
(8)
Проведенные вычисления доказывают, что исторически в основу определения характеристик рассеивания был положен нормальный закон распределения с исчерпывающими характеристиками — функцией распределения (9) и функцией плотности распределения (10):
Б (X, ц, О)
1
X
1 Г X-Ц
г- Iе
ол/2п -(Ю
2 v о
dx,
(9)
1 -2н2
f (X, ц, о) = —^е о > ■ (10)
ол/ 2п
Однако при малом числе испытаний (для малых выборок) использование нормального закона распределения представляется недостаточно обоснованным. Тем не менее его используют практически во всех областях науки и техники, что приводит к значительному (недопустимому с точки зрения математики) разбросу получаемых опытно-теоретическим путем параметров кучности и значительному их завышению в силу осреднения экспериментальных данных в соответствии с законом нормального распределения.
Предпринимались различные попытки скорректировать случайные отклонения путем учета разброса условий проведения эксперимента (вплоть до атмосферных), однако проблема огрубления характеристик рассеивания этим не снимается.
Ни одна из методик проведения испытаний с целью определения характеристик рассеивания не учитывает также факт получения в результате испытаний цензурированных данных. В многочисленных источниках в качестве основных причин возникновения цензурированных выборок называют:
■ перевод изделий из одного режима применения в другой в процессе испытаний или эксплуатации;
■ использование изделий однократного применения по назначению из режима хранения;
■ объединение данных, полученных при испытаниях по двум и более однотипным планам, либо по планам разных типов [4-8, 9, с. 18].
Очевидно, что данные причины имеют место во всех методиках испытаний для определения срединного отклонения. Исходя из логики проведения таких испытаний, можно утверждать, что исследователь имеет дело с цензурированием интервалом, границами которого являются соответственно минимальное и максимальное отклонение результатов измерения (точек попадания) от номинального значения (точки прицеливания).
В соответствии с определением цензурированной выборки, приведенным в ряде публикаций [10, 11] можно сделать вывод о том, что термины «цензурирование» и «усечение» являются синонимами. Данный вывод подтверждает и В.М. Скрипник: «.термин «цензурирование» удобнее использовать для выборок, а термин «усечение» для законов распределения, усеченных на интервале» [9, с. 15]. Кендалл и Стюарт также предлагают выборки, состоящие из элементов с полными и неполными наработками, называть цен-зурированными, а законы распределения случайных наработок до отказа на интервале [0, Т] — усеченными (урезанными) [12].
Хотя встречаются и иные точки зрения [13, с. 123], усеченными принято называть выборки, в которых отсутствуют значения случайной величины, большие или меньшие некоторого граничного значения, тогда как цензури-
рованными — выборки, в которых часть членов отбрасывается. Тем не менее случайные величины, составляющие как цензурированную, так и усеченную выборку, подчиняются усеченному распределению.
К чему приводит недооценка указанных выше факторов, можно проиллюстрировать на следующем примере. В одной из работ автора доказано, что характеристики функционирования технических систем, являющихся предметом исследования, наилучшим образом согласуются с логарифмически нормальным (логнормальным) законом распределения [14], двусторонне усеченным.
Если случайная величина У распределена нормально, то случайная величина
X = 1пУ (11)
подчинена логарифмически нормальному (или логнормальному) закону распределения с исчерпывающими характеристиками — функцией распределения (12) и функцией плотности распределения (13):
1 (1пх-ц ^ 2
1 х 2 ^ а у
Б (х, ц, а) = —1= е ёх, (12)
а
л/2П
о
1
1 (1пх-цЛ 2
Г (х, ц, а) = —е а ^ . (13)
хал/ 2п
При вычислениях, связанных с логарифмически нормальным распределением, пользуются приемами, используемыми для нормального распределения, заменяя при этом значение случайной величины ее логарифмом [13, с. 35]. Подробный анализ этого распределения дан в работе Эйчисона и Брауна [15].
Для двусторонне усеченного нормального распределения справедливы следующие соотношения для показателей математического ожидания (М(х)) и дисперсии (Б(х)):
М(х)=ц-(^2-^1)ст, (14)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Б(х)=(1+^1-^2-^1)2а2, (15)
где Х2 — величины, рассчитываемые по формулам (16) и (17) соответственно.
^ = , 0б) = ^ , (17)
к 2 Ф(4 2) — ф(^1)
где ф(^1), ф(^2) — плотности вероятностей стандартного нормального распределения; £,2 — величины, рассчитываемые по формулам (18) и (19) соответственно.
^ = (18) о
£ 2 = , (19)
о
где а15 а2 — граничные значения.
При переходе от нормального закона распределения случайной величины к логарифмически нормальному (в силу того, что функция плотности распределения не симметрична относительно математического ожидания (рисунок) возникает необходимость модификации определения для вероятного (срединного) отклонения.
Их
1 г
1 1 *
; *
1 1
• /■Ч
— * * » /
-1 9 •
1 и > ч V
Г 1 ч. 3 —
О г*» Ч1 ■»нсотгм-нтгг-.огоиэспгч тоо^^г^огошспгмт^
N г1 Н моооооо^^^гнгмгмгмгоглог)-^ ^ Т Т 1Л [Л
о о о о о о о о’ о о о о о’ о» о» о» о о о» о» о о» о о» о о» ^ норм.распр, — — усеч. норм.распр. — • логнорм. распр. …….усеч. логнорм,распр.
Функции плотности вероятности
Исходя из приведенных соображений, представляется целесообразным называть вероятным или срединным отклонением половину длины интервала, симметричного относительно центра рассеивания по вероятности, вероятность попадания в который равна 0,5. Результаты соответствующих расчетов приведены в таблице.
Для представленных в таблице исходных данных справедливы следующие утверждения:
■ при использовании зависимостей логнормального закона распределения величина оценки срединного отклонения изменилась на 17,5%;
■ при учете фактора усечения она изменилась на 38,5%;
■ при совместном учете обоих факторов — на 92,9%.
Результаты расчета величины срединного отклонения
Исходные данные и числовые характеристики Законы распределения
нормальный усеченный нормальный логнормальный усеченный логнормальный
x 0,02; 0,05; 0,07; 0,09; 0,12; 0,16; 0,21
lnx -3,912; -2,996; -2,659; -2,408; -2,120; -1,833; -1,561
Ц 0,1028571 0,1028571 -2,49835 -2,49835
о 0,0657557 0,0657557 0,790085 0,790085
$1 -1,260076 -1,78927
$2 1,6294084 1,186837
Ф ($1) 0,180353933 0,080485797
Ф ($2) 0,105776767 0,19726049
А.1 0,213546 0,095185
^2 0,125244 0,233288
M(X) 0,1028571 0,1086635 0,112339 0,077787
D(X) 0,0016361 0,010939 0,000686
ох 0,0657557 0,0404492 0,104591 0,026187
Ex 0,0443522 0,027283 0,036591 0,003144
В данном примере использован один из крайних случаев, однако недооценка отклонения эмпирического закона распределения от нормального и
игнорирование факта цензурирования всегда приводят к значительному искажению характеристик рассеивания.
Литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. — М., 1970. — Т. 2. — С. 495.
2. Журко Д.М. Применение математических методов в военном деле. — М., 1984. — С. 120.
3. Беляева С.Д., Монченко Н.М., Паршин Ж.П. Внешняя баллистика. Ч. II: Устойчивость движения снарядов. — М., 1988. — С. 343.
4. Скрипник В.М., Назин А.Е. Оценка надежности технических систем по цензурированным выборкам / Под ред. А.И. Широкова. — Минск, 1981. -144 с.
5. Gill R.D. Censoring and stochastic integrals // Mathematical center tracts 124. — Amsterdam, 1980. — 172 p.
6. Назин А.Е., Приходько Ю.Г., Скрипник В.М., Явид Ю.Ю. Вопросы обработки статистической информации по цензурированным выборкам. -Минск, 1979. — 86 с.
7. Lagakos S.W. General right censoring and its impact on the analysis of survival data // Biometrics. — 1979. — N 35. — P. 139-156.
8. Беляев Ю.К. Непараметрические методы в задачах обработки результатов испытаний и эксплуатации. — М., 1984. — 60 с.
9. Скрипник В.М., Назин А.Е., Приходько Ю.Г. Анализ надежности технических систем по цензурированным выборкам. — М., 1988.
10. Агзамов С.К., Огульник Ю.М. Определение интервальных оценок и точности показателей долговечности по многократно усеченным выборкам // Надежность и контроль качества. — 1976. — № 9. — С. 49-54.
11. Баталова З.Г., Благовещенский Ю.Н. О точности оценок ресурсов элементов конструкций методом максимума правдоподобия при случайном усечении длительности наблюдений // Надежность и контроль качества. 1979. — № 9. — С. 12-20.
12. Кендалл М.Ж., Стюарт А. Статистические выводы и связь: Пер. с англ. -М., 1973. — 900 с.
13. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М., 2006.
14. Платонов А.А., Тихоненков А.В. и др. Методические основы построения математических моделей и обработки результатов испытаний неуправляемых артиллерийских снарядов. — М., 2010. — 70 с.
15. Aitchison J., Brown J. The lognormal distribution. London, 1951.
Statistical estimation of the median deviation of the random variable Tikhonenkov Aleksey, Candidate of Engineering Sciences, Associate Professor of Computer Science and Mathematics of International Institute of Economics and Law, doctoral Military Training and Research Center of Land Forces «Combined Military Academy of the Armed Forces of the Russian Federation»
The article considers the nature of the median deviation characteristics of dissipation random variable. Sensitivity of these characteristics to the deviation of the distribution law of a random variable from a normalization is proven. The author shows the possible changes of the median deviation in statistics-sky calculations associated with the underestimation of the characteristics of the sample.
Keywords: sampling, hypothesis, argument, distribution, collection, function, planning, function, feature, censoring
Address for correspondence: tihonenk@mail.ru
For citation: Herald of International Institute of Economics and Law. 2014. N 1(14). P. 17-23.
Что такое среднеквадратичное отклонение
Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.
Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.
Определение
Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример
Среднеарифметическое для 3 чисел b1, b2 и b3 определяется как:
(M=frac{b_1+b_2+b_3}3)
Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.
Определение
Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).
А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.
Определение
Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.
Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:
(Da_i=a_i-M)
Также для оценки единичного измерения используется и относительная погрешность, значение которой выражается в процентах. Ее вычисление проводят по формуле:
(sigma=frac{left|triangle a_iright|}Mtimes100%)
Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.
Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).
Определение
Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.
Теперь можно дать определение и «среднеквадратичному отклонению».
Определение
Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».
Оно вычисляется по формуле:
(sigma=sqrt{D_{left|xright|}})
Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.
Как найти среднеквадратическое отклонение
Вычисление среднеквадратичного отклонения на первый взгляд может показаться достаточно сложным и запутанным. Но этот процесс можно облегчить, если воспользоваться следующим алгоритмом действий:
- Найти среднее арифметическое всех членов множества.
- Для каждого элемента вычислить варианту.
- Сложить все полученные на предыдущем этапе значения.
- Разделить число, полученное при выполнении третьего шага, на количество элементов множества.
- Из полученного в предыдущем шаге числа извлечь корень квадратный.
Формула, примеры решения задач
Для четырех измеренных значений величины b формула среднеквадратичного отклонения будет выглядеть следующим образом:
(sigma=sqrt{frac{triangle b_1+triangle b_2+triangle b_3+triangle b_4}4})
где Db1 — Db4 являются абсолютными погрешностями каждой исследуемой величины.
Рассмотрим пример решения конкретной задачи.
Задача
При проведении лабораторной работы по физике школьники несколько раз измерили напряжение электрического тока и получили следующие значения:
(U_1=4.22BU_2=4.30BU_3=4.27BU_4=4.23BU_5=4.20B)
Необходимо рассчитать погрешности (абсолютные и относительные) каждого измерения, дисперсию и среднеквадратическое отклонение.
Решение
Определим среднее арифметическое значение напряжения в данной работе:
(U_c=sqrt{frac{U_1+U_2+U_3+U_4+U_5}5}=frac{4.22+4.30+4.27+4.23+4.20}5=4.244B)
Теперь рассчитаем для каждого полученного измерения абсолютную и относительную погрешности. Так как абсолютная погрешность определяется как разница между средним арифметическим и полученным значением, то
(triangle U_1=0.024triangle U_2=-0.056triangle U_3=-0.026triangle U_4=0.014triangle U_5=0.044)
Находим относительную погрешность:
(sigma_1=frac{left|U_1right|}{U_c}times100%=0.50%sigma_2=frac{left|U_2right|}{U_c}times100%=1.06%sigma_3=frac{left|U_3right|}{U_c}times100%=0.50%sigma_4=frac{left|U_4right|}{U_c}times100%=0.25%sigma_5=frac{left|U_5right|}{U_c}times100%=0.84%)
Зная абсолютные погрешности несложно вычислить дисперсию:
(D=frac{triangle U_1^2+{triangle U_2}^2+{triangle U_3}^2+{triangle U_4}^2+{triangle U_5}^2}5=0.001304)
Теперь можно вычислить среднеквадратичное отклонение:
(sigma=sqrt D=0.0361)
В статистика, то среднеквадратичная ошибка (MSE)[1][2] или среднеквадратическое отклонение (MSD) из оценщик (процедуры оценки ненаблюдаемой величины) измеряет средний квадратов ошибки — то есть средний квадрат разницы между оценочными и фактическими значениями. MSE — это функция риска, соответствующий ожидаемое значение квадрата ошибки потери. Тот факт, что MSE почти всегда строго положительный (а не нулевой), объясняется тем, что случайность или потому что оценщик не учитывает информацию это может дать более точную оценку.[3]
MSE — это мера качества оценки — она всегда неотрицательна, а значения, близкие к нулю, лучше.
МСЭ — второй момент (о происхождении) ошибки и, таким образом, включает в себя как отклонение оценщика (насколько разбросаны оценки от одного образец данных другому) и его предвзятость (насколько далеко среднее оценочное значение от истинного значения). Для объективный оценщик, MSE — это дисперсия оценки. Как и дисперсия, MSE имеет те же единицы измерения, что и квадрат оцениваемой величины. По аналогии с стандартное отклонение, извлечение квадратного корня из MSE дает среднеквадратичную ошибку или среднеквадратичное отклонение (RMSE или RMSD), который имеет те же единицы, что и оцениваемое количество; для несмещенной оценки RMSE — это квадратный корень из отклонение, известный как стандартная ошибка.
Определение и основные свойства
MSE либо оценивает качество предсказатель (т.е. функция, отображающая произвольные входные данные в выборку значений некоторых случайная переменная ) или оценщик (т.е. математическая функция отображение образец данных для оценки параметр из численность населения из которого берутся данные). Определение MSE различается в зависимости от того, описывается ли предсказатель или оценщик.
Предсказатель
Если вектор 


Другими словами, MSE — это иметь в виду 

В матрица обозначение
куда 



MSE также можно вычислить на q точки данных, которые не использовались при оценке модели, либо потому, что они были задержаны для этой цели, либо потому, что эти данные были получены заново. В этом процессе (известном как перекрестная проверка ), MSE часто называют среднеквадратичная ошибка прогноза, и вычисляется как
Оценщик
MSE оценщика 

Это определение зависит от неизвестного параметра, но MSE априори свойство оценщика. MSE может быть функцией неизвестных параметров, и в этом случае любой оценщик MSE на основе оценок этих параметров будет функцией данных (и, следовательно, случайной величиной). Если оценщик 
MSE можно записать как сумму отклонение оценщика и квадрата предвзятость оценщика, обеспечивая полезный способ вычисления MSE и подразумевая, что в случае несмещенных оценок MSE и дисперсия эквивалентны.[4]
Доказательство отношения дисперсии и предвзятости
- В качестве альтернативы у нас есть
Но в реальном случае моделирования MSE можно описать как добавление дисперсии модели, систематической ошибки модели и неснижаемой неопределенности. Согласно соотношению, MSE оценщиков может быть просто использована для эффективность сравнение, которое включает информацию о дисперсии и смещении оценки. Это называется критерием MSE.
В регрессе
В регрессивный анализ, построение графиков — более естественный способ просмотра общей тенденции всех данных. Среднее значение расстояния от каждой точки до прогнозируемой регрессионной модели может быть вычислено и показано как среднеквадратичная ошибка. Возведение в квадрат критически важно для уменьшения сложности с отрицательными знаками. Чтобы свести к минимуму MSE, модель может быть более точной, что означает, что модель ближе к фактическим данным. Одним из примеров линейной регрессии с использованием этого метода является метод наименьших квадратов —Который оценивает соответствие модели линейной регрессии модели двумерный набор данных[5], но чье ограничение связано с известным распределением данных.
Период, термин среднеквадратичная ошибка иногда используется для обозначения объективной оценки дисперсии ошибки: остаточная сумма квадратов делится на количество степени свободы. Это определение известной вычисленной величины отличается от приведенного выше определения вычисленной MSE предиктора тем, что используется другой знаменатель. Знаменатель — это размер выборки, уменьшенный на количество параметров модели, оцененных на основе тех же данных, (н-р) за п регрессоры или (п-п-1) если используется перехват (см. ошибки и остатки в статистике Больше подробностей).[6] Хотя MSE (как определено в этой статье) не является объективной оценкой дисперсии ошибки, она последовательный, учитывая непротиворечивость предсказателя.
В регрессионном анализе «среднеквадратичная ошибка», часто называемая среднеквадратичная ошибка прогноза или «среднеквадратичная ошибка вне выборки», также может относиться к среднему значению квадратичные отклонения прогнозов на основе истинных значений в тестовом пространстве вне выборки, сгенерированных моделью, оцененной в конкретном пространстве выборки. Это также известная вычисляемая величина, которая зависит от образца и тестового пространства вне образца.
Примеры
Иметь в виду
Предположим, у нас есть случайная выборка размера 




ожидаемое значение которого равно истинному среднему значению 
куда 
Для Гауссово распределение, это лучший объективный оценщик (то есть с самой низкой MSE среди всех несмещенных оценок), но не, скажем, для равномерное распределение.
Дисперсия
Обычной оценкой дисперсии является исправлено выборочная дисперсия:
Это объективно (его ожидаемое значение 
куда 

Однако можно использовать другие оценки для 

затем рассчитываем:
Это сводится к минимуму, когда
Для Гауссово распределение, куда 



Далее, хотя исправленная дисперсия выборки является лучший объективный оценщик (минимальная среднеквадратичная ошибка среди несмещенных оценок) дисперсии для гауссовских распределений, если распределение не является гауссовым, то даже среди несмещенных оценок лучшая несмещенная оценка дисперсии может не быть
Гауссово распределение
В следующей таблице приведены несколько оценок истинных параметров популяции, μ и σ.2, для гауссова случая.[8]
| Истинное значение | Оценщик | Среднеквадратичная ошибка |
|---|---|---|
 |
 = несмещенная оценка Средняя численность населения, = несмещенная оценка Средняя численность населения,  |
 |
 |
 = несмещенная оценка дисперсия населения, = несмещенная оценка дисперсия населения,  |
 |
 |
 = смещенная оценка дисперсия населения, = смещенная оценка дисперсия населения,  |
 |
 |
 = смещенная оценка дисперсия населения, = смещенная оценка дисперсия населения,  |
 |
Интерпретация
MSE равна нулю, что означает, что оценщик 

Значения MSE могут использоваться для сравнительных целей. Два и более статистические модели можно сравнить, используя их MSE — как меру того, насколько хорошо они объясняют данный набор наблюдений: несмещенная оценка (рассчитанная на основе статистической модели) с наименьшей дисперсией среди всех несмещенных оценок — это оценка лучший объективный оценщик или MVUE (несмещенная оценка минимальной дисперсии).
Обе линейная регрессия методы, такие как дисперсионный анализ оценить MSE как часть анализа и использовать оценочную MSE для определения Статистическая значимость изучаемых факторов или предикторов. Цель экспериментальная конструкция состоит в том, чтобы построить эксперименты таким образом, чтобы при анализе наблюдений MSE была близка к нулю относительно величины по крайней мере одного из оцененных эффектов лечения.
В односторонний дисперсионный анализ, MSE можно вычислить путем деления суммы квадратов ошибок и степени свободы. Кроме того, значение f — это отношение среднего квадрата обработки и MSE.
MSE также используется в нескольких пошаговая регрессия методы как часть определения того, сколько предикторов из набора кандидатов включить в модель для данного набора наблюдений.
Приложения
- Минимизация MSE является ключевым критерием при выборе оценщиков: см. минимальная среднеквадратичная ошибка. Среди несмещенных оценщиков минимизация MSE эквивалентна минимизации дисперсии, а оценщик, который делает это, является несмещенная оценка минимальной дисперсии. Однако смещенная оценка может иметь более низкую MSE; видеть систематическая ошибка оценки.
- В статистическое моделирование MSE может представлять разницу между фактическими наблюдениями и значениями наблюдений, предсказанными моделью. В этом контексте он используется для определения степени, в которой модель соответствует данным, а также возможности удаления некоторых объясняющих переменных без значительного ущерба для прогнозирующей способности модели.
- В прогнозирование и прогноз, то Оценка Бриера это мера умение прогнозировать на основе MSE.
Функция потерь
Квадратичная потеря ошибок — одна из наиболее широко используемых функции потерь в статистике[нужна цитата ], хотя его широкое использование проистекает больше из математического удобства, чем из соображений реальных потерь в приложениях. Карл Фридрих Гаусс, который ввел использование среднеквадратичной ошибки, сознавал ее произвол и был согласен с возражениями против нее на этих основаниях.[3] Математические преимущества среднеквадратичной ошибки особенно очевидны при ее использовании при анализе производительности линейная регрессия, поскольку он позволяет разделить вариацию в наборе данных на вариации, объясняемые моделью, и вариации, объясняемые случайностью.
Критика
Использование среднеквадратичной ошибки без вопросов подвергалось критике со стороны теоретик решений Джеймс Бергер. Среднеквадратичная ошибка — это отрицательное значение ожидаемого значения одного конкретного вспомогательная функция, квадратичная функция полезности, которая может не подходить для использования в данном наборе обстоятельств. Однако есть некоторые сценарии, в которых среднеквадратичная ошибка может служить хорошим приближением к функции потерь, естественным образом возникающей в приложении.[9]
подобно отклонение, среднеквадратичная ошибка имеет тот недостаток, что выбросы.[10] Это результат возведения в квадрат каждого члена, который фактически дает больший вес большим ошибкам, чем малым. Это свойство, нежелательное для многих приложений, заставило исследователей использовать альтернативы, такие как средняя абсолютная ошибка, или основанные на медиана.
Смотрите также
- Компромисс смещения и дисперсии
- Оценщик Ходжеса
- Оценка Джеймса – Стейна
- Средняя процентная ошибка
- Среднеквадратичная ошибка квантования
- Среднеквадратичное взвешенное отклонение
- Среднеквадратичное смещение
- Среднеквадратичная ошибка прогноза
- Минимальная среднеквадратичная ошибка
- Оценщик минимальной среднеквадратичной ошибки
- Пиковое отношение сигнал / шум
Примечания
- ^ Это может быть доказано Неравенство Дженсена следующим образом. Четвертый центральный момент является верхней границей квадрата дисперсии, так что наименьшее значение для их отношения равно единице, следовательно, наименьшее значение для избыточный эксцесс равно −2, что достигается, например, Бернулли с п=1/2.
Рекомендации
- ^ а б «Список вероятностных и статистических символов». Математическое хранилище. 2020-04-26. Получено 2020-09-12.
- ^ а б «Среднеквадратичная ошибка (MSE)». www.probabilitycourse.com. Получено 2020-09-12.
- ^ а б Lehmann, E. L .; Казелла, Джордж (1998). Теория точечного оценивания (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98502-2. Г-Н 1639875.
- ^ Вакерли, Деннис; Менденхолл, Уильям; Шеаффер, Ричард Л. (2008). Математическая статистика с приложениями (7-е изд.). Белмонт, Калифорния, США: Высшее образование Томсона. ISBN 978-0-495-38508-0.
- ^ Современное введение в вероятность и статистику: понимание, почему и как. Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005 г. ISBN 978-1-85233-896-1. OCLC 262680588.CS1 maint: другие (ссылка на сайт)
- ^ Стил, Р.Г.Д., и Торри, Дж. Х., Принципы и процедуры статистики с особым акцентом на биологические науки., Макгроу Хилл, 1960, стр.288.
- ^ Настроение, А .; Graybill, F .; Боэс, Д. (1974). Введение в теорию статистики (3-е изд.). Макгроу-Хилл. п.229.
- ^ ДеГрут, Моррис Х. (1980). вероятность и статистика (2-е изд.). Эддисон-Уэсли.
- ^ Бергер, Джеймс О. (1985). «2.4.2 Некоторые стандартные функции потерь». Статистическая теория принятия решений и байесовский анализ (2-е изд.). Нью-Йорк: Springer-Verlag. п.60. ISBN 978-0-387-96098-2. Г-Н 0804611.
- ^ Бермехо, Серхио; Кабестани, Джоан (2001). «Ориентированный анализ главных компонентов для классификаторов с большой маржой». Нейронные сети. 14 (10): 1447–1461. Дои:10.1016 / S0893-6080 (01) 00106-X. PMID 11771723.
Привет, Вы узнаете про вероятное срединное отклонение, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
вероятное срединное отклонение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой 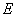 (иногда В).
(иногда В).
Вероятным (срединным) отклонением случайной величины 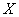 , распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение 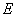 – это половина длины участка оси абсцисс, симметричного относительно точки
– это половина длины участка оси абсцисс, симметричного относительно точки 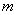 , на который опирается половина площади кривой распределения.
, на который опирается половина площади кривой распределения.

Рис. 6.4.1.
Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».
Рассмотрим случайную величину 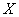 , распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания
, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания 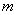 меньше, чем на
меньше, чем на 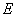 , по определению вероятного отклонения
, по определению вероятного отклонения 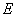 , равна
, равна 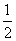 :
:
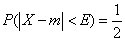 . (6.4.1)
. (6.4.1)
Вероятность того, что она отклонится от 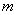 больше, чем на
больше, чем на 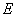 , тоже равна
, тоже равна 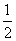 :
:
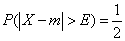 .
.
Таким образом, при большом числе опытов в среднем половина значений случайной величины 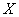 отклонится от
отклонится от 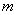 больше, чем на
больше, чем на 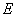 , а половина – меньше . Об этом говорит сайт https://intellect.icu . Отсюда и термин «срединная ошибка», «срединное отклонение».
, а половина – меньше . Об этом говорит сайт https://intellect.icu . Отсюда и термин «срединная ошибка», «срединное отклонение».
Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего квадратического отклонения 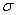 . Вычислим вероятность события
. Вычислим вероятность события 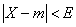 в уравнении (6.4.1) по формуле (6.3.10). Имеем:
в уравнении (6.4.1) по формуле (6.3.10). Имеем:
 .
.
Отсюда
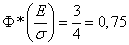 . (6.4.2)
. (6.4.2)
По таблицам функции 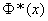 можно найти такое значение аргумента
можно найти такое значение аргумента 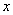 , при котором она равна 0,75. Это значение приближенно равно 0,674; отсюда
, при котором она равна 0,75. Это значение приближенно равно 0,674; отсюда
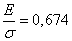 ;
; 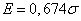 . (6.4.3)
. (6.4.3)
Таким образом, зная значение 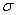 , можно сразу найти пропорциональное ему значение
, можно сразу найти пропорциональное ему значение 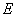 . Часто пользуются еще такой формой записи этой зависимости:
. Часто пользуются еще такой формой записи этой зависимости:
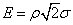 , (6.4.4)
, (6.4.4)
где 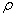 — такое значение аргумента, при котором одна из форм интеграла вероятностей – так называемая функция Лапласа
— такое значение аргумента, при котором одна из форм интеграла вероятностей – так называемая функция Лапласа
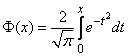
— равна половине. Численное значение величины 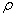 приближенно равно 0,477.
приближенно равно 0,477.
В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой 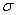 . В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
. В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
Если в качестве характеристики рассеивания принято вероятное отклонение 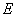 , то плотность нормального распределения записывается в виде:
, то плотность нормального распределения записывается в виде:
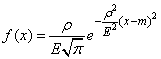 , (6.4.5)
, (6.4.5)
а вероятность попадания на участок от 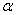 до
до 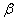 чаще всего записывается в виде:
чаще всего записывается в виде:
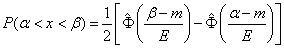 , (6.4.6)
, (6.4.6)
где
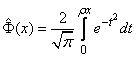 (6.4.7)
(6.4.7)
— так называемая приведенная функция Лапласа.
Сделаем подсчет, аналогичный выполненному в предыдущем n° для среднего квадратического отклонения 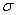 : отложим от центра рассеивания
: отложим от центра рассеивания 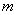 последовательные отрезки длиной в одно вероятное отклонение
последовательные отрезки длиной в одно вероятное отклонение 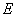 (рис. 6.4.2) и подсчитаем вероятности попадания в эти отрезки с точностью до 0,01. Получим:
(рис. 6.4.2) и подсчитаем вероятности попадания в эти отрезки с точностью до 0,01. Получим:
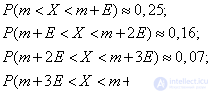

Рис. 6.4.2.
Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке  .
.
Пример. Самолет-штурмовик производит обстрел колонны войск противника, ширина которой равна 8 м. Полет – вдоль колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо по направлению полета. Главные вероятные отклонения: по направлению полета 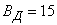 м, в боковом направлении
м, в боковом направлении  м. Не имея в своем распоряжении никаких таблиц интегралов вероятностей, а зная только числа:
м. Не имея в своем распоряжении никаких таблиц интегралов вероятностей, а зная только числа:
25%, 16%, 7%, 2%,
оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.
Решение. Для решения задачи достаточно рассмотреть одну координату точки попадания – абсциссу 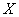 в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания
в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания 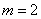 и вероятным отклонением
и вероятным отклонением 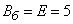 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
(м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
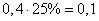 .
.
Влево от центра рассеивания цель занимает участок 6 м. Это – целое вероятное отклонение (5 м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна:
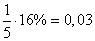 .
.
Таким образом, вероятность попадания в колонну приближенно равна:
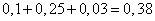 .
.
Вероятность хотя бы одного попадания при трех выстрелах равна:

Надеюсь, эта статья про вероятное срединное отклонение, была вам полезна,счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое вероятное срединное отклонение
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но емко про вероятное срединное отклонение
RMSE
- Среднеквадратичная ошибка, среднеквадратичная ошибка
- Это квадратный корень из отношения суммы квадратов отклонения между значением наблюдения и истинным значением к количеству m наблюдений.
- Он используется для измерения отклонения между наблюдаемым значением и истинным значением.
MAE
- Средняя абсолютная ошибка, средняя абсолютная ошибка
- Среднее значение абсолютных ошибок
- Он может лучше отражать реальную ситуацию с ошибкой предсказанного значения.
Стандартное отклонение
- Стандартное отклонение, стандартное отклонение
- Квадратный корень из дисперсии
- Используется для измерения степени разброса набора чисел

Сравнение RMSE и стандартного отклонения:
Стандартное отклонение используется для измерения степени разброса набора чисел, а среднеквадратичная ошибка используется для измерения отклонения между наблюдаемым значением и истинным значением. Их объекты исследования и исследовательские цели различны, но процесс расчета аналогичен.
Сравнение RMSE и MAE:
RMSE эквивалентно норме L2, а MAE эквивалентно норме L1. Чем больше число раз, тем больше результат вычисления связан с большим значением, в то время как меньшее значение игнорируется, поэтому RMSE более чувствителен к выбросам (то есть, если есть прогнозируемое значение, которое сильно отличается от истинного значения, то RMSE Будет огромно).
Нормальный закон распределения и его параметры:
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.
Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.
Нормальный закон распределения характеризуется плотностью вероятности вида:
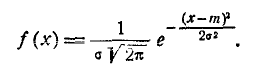 (6.1.1)
(6.1.1)
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная 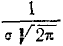 , соответствует точке х = m по мере удаления от точки m плотность распределения падает, и при
, соответствует точке х = m по мере удаления от точки m плотность распределения падает, и при 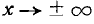 кривая асимптотически приближается к оси абсцисс.
кривая асимптотически приближается к оси абсцисс.
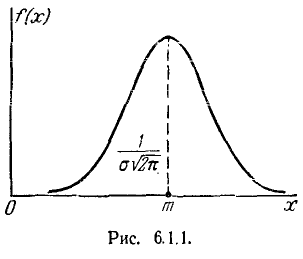
Выясним смысл численных параметров т и о, входящих в выражение нормального закона (5.1.1); докажем, что величина m есть не что иное, как математическое ожидание, а величина  — среднее квадратическое отклонение величины X. Для этого вычислим основные числовые характеристики величины X — математическое ожидание и дисперсию.
— среднее квадратическое отклонение величины X. Для этого вычислим основные числовые характеристики величины X — математическое ожидание и дисперсию.
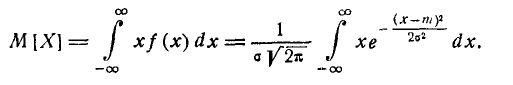
Применяя замену переменной
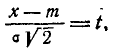
имеем:
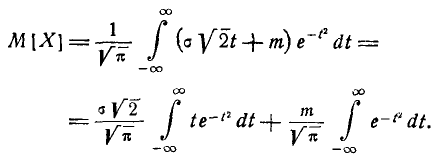 (6.1.2)
(6.1.2)
Нетрудно убедиться, что первый из двух интервалов в формуле (5.1.2) равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:
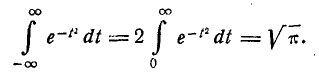 (6.1.3)
(6.1.3)
Следовательно, М[Х] = m
т. е. параметр m представляет собой математическое ожидание вели- величины X. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно — ц. р.). Вычислим дисперсию величины X:
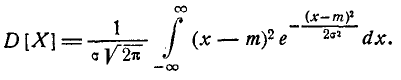
Применив снова замену переменной
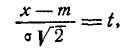
имеем:
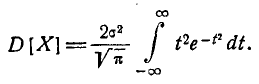
Интегрируя по частям, получим:
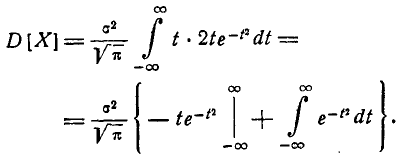
Первое слагаемое в фигурных скобках равно нулю (так как 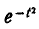 При
При 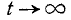 убывает быстрее, чем возрастает любая степень f), второе слагаемое по формуле 5.1.3) равно
убывает быстрее, чем возрастает любая степень f), второе слагаемое по формуле 5.1.3) равно 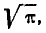 откуда
откуда 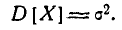
Следовательно, параметр о в формуле 5.1.1) есть не что иное, как среднее квадратическое отклонение величины X.
Выясним смысл параметров m и  нормального распределения. Непосредственно из формулы 5.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (х — m) на обратный выражение 5.1.1) не меняется. Если изменять центр рассеивания т. кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
нормального распределения. Непосредственно из формулы 5.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (х — m) на обратный выражение 5.1.1) не меняется. Если изменять центр рассеивания т. кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
Размерность центра рассеивания—та же, что размерность случайной величины X.
Параметр о характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна  ; при увеличении
; при увеличении  максимальная ордината уменьшается. Так как площадь
максимальная ордината уменьшается. Так как площадь
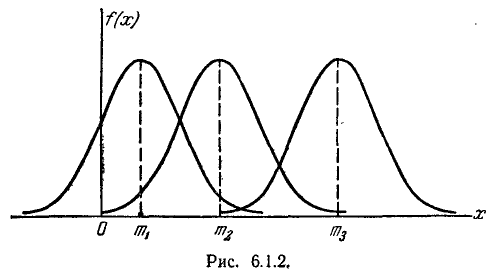
кривой распределения всегда должна оставаться равной единице, то при увеличении о кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении  кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (/, //, ///) при m=0; из них кривая l соответствует
кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (/, //, ///) при m=0; из них кривая l соответствует 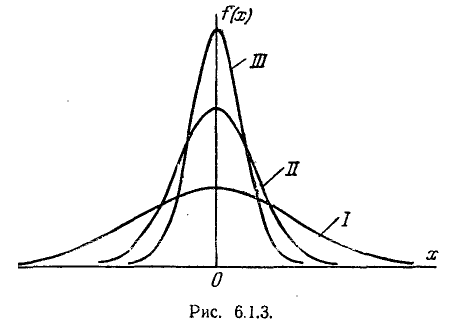
самому большому, а кривая /// — самому малому значению  . Изменение параметра
. Изменение параметра  равносильно изменению масштаба кривой распределения— увеличению масштаба по одной оси и такому же уменьшению по другой.
равносильно изменению масштаба кривой распределения— увеличению масштаба по одной оси и такому же уменьшению по другой.
Размерность параметра  , естественно, совпадает с раpмерноcтью случайной величины X.
, естественно, совпадает с раpмерноcтью случайной величины X.
В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению  :
: 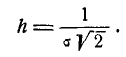
Размерность меры точности обратна размерности случайной величины.
Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности h, можно записать нормальный закон в виде: 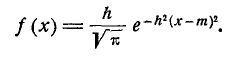

Моменты нормального распределения
Выше мы доказали, что математическое ожидание случайной вели- величины, подчиненной нормальному закону 6.1.1), равно m, а среднее квадратическое отклонение равно  .
.
Выведем общие формулы для центральных моментов любого порядка.
По определению:
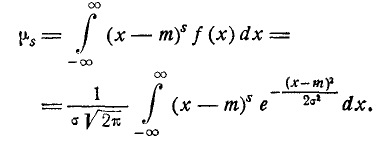
Делая замену переменной
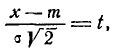
получим:
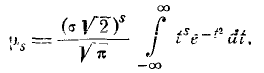 (6.2.1)
(6.2.1)
Применим к выражению (6.2.1) формулу интегрирования по частям: 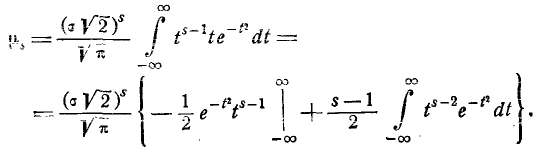
Имея в виду, что первый член внутри скобок равен нулю, получим: 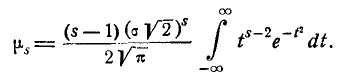 (6.2.2)
(6.2.2)
Из формулы (6.2.1) имеем следующее выражение для 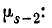
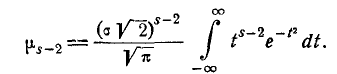 (6.2.3)
(6.2.3)
Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем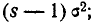 следовательно,
следовательно,
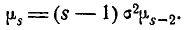 (6.2.4)
(6.2.4)
Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 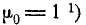 и
и  можно вычислить центральные моменты всех порядков. Так как
можно вычислить центральные моменты всех порядков. Так как  то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.
то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.
Для четных s из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:
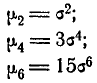
и т. д. Общая формула для момента s-гo порядка при любом четном s имеет вид:
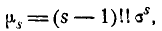
где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s— 1. Так как для нормального закона  то асимметрия его также равна нулю:
то асимметрия его также равна нулю:
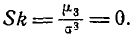
Из выражения четвертого момента
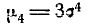
имеем:
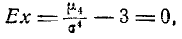
‘) Нулевой момент любой случайной величины равен единице как математическое ожидание нулевой степени этой величины.
т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса — характеризовать сравнительную крутость данного закона по сравнению с нормальным.
Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m,  , на участок от а до
, на участок от а до 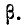 Для вычисления этой вероятности воспользуемся общей формулой
Для вычисления этой вероятности воспользуемся общей формулой
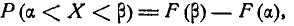 (6.3.1)
(6.3.1)
где F (х)— функция распределения величины X.
Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m,  . Плот- Плотность распределения величины X равна:
. Плот- Плотность распределения величины X равна:
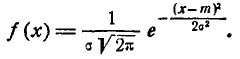 (6.3.2)
(6.3.2)
Отсюда находим функцию распределения
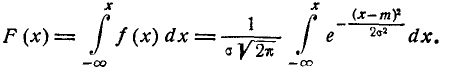 (6.3.3)
(6.3.3)
Сделаем в интеграле (6.3.3) замену переменной
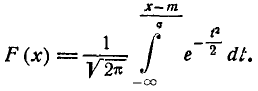 (6.3.4)
(6.3.4)
и приведем его к виду:
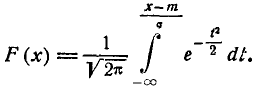 (6.3.4)
(6.3.4)
Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 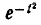 или
или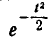 (так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:
(так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:
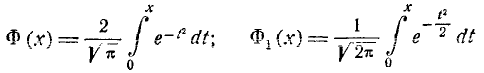
и т. д. Какой из этих функций пользоваться — вопрос вкуса. Мы выберем в качестве такой функции
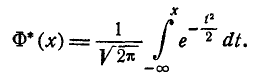 (6.3.5)
(6.3.5)
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами от m = 0,  =1.
=1.
Условимся называть функцию Ф*(х) нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции Ф*(х)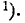
Выразим функцию распределения (6.3.3) величины X с пара- параметрами m и  через нормальную функцию распределения Ф*(х). Очевидно,
через нормальную функцию распределения Ф*(х). Очевидно,
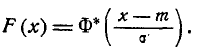 (6.3.6)
(6.3.6)
Теперь найдем вероятность попадания случайной величины X на участок от а до 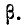 Согласно формуле (6.3.1)
Согласно формуле (6.3.1)
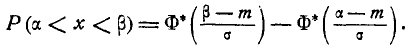 (6.3.7)
(6.3.7)
Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф* (х), соответствующую простейшему нормальному . закону с параметрами 0,1. Заметим, что аргументы функции Ф* в фор- формуле (6.3.7) имеют очень простой смысл: 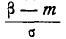 есть расстояние от правого конца участка
есть расстояние от правого конца участка 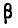 до центра рассеивания, выраженное в средних квадратических отклонениях;
до центра рассеивания, выраженное в средних квадратических отклонениях; 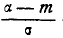 — такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания , и отрицательным, если слева.
— такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания , и отрицательным, если слева.
Как и всякая функция распределения,, функция Ф*(х) обладает свойствами:
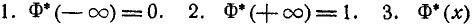 -неубывающая функция
-неубывающая функция
Кроме того, из симметричности нормального распределения с параметрами m = 0,  =1 относительно начала координат следует, что
=1 относительно начала координат следует, что
ф* (— х)=1— Ф* (х). (6.3.8)
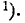 Для облегчения интерполяции в таблицах рядом со значениями функции приведены ее приращения за один шаг таблиц
Для облегчения интерполяции в таблицах рядом со значениями функции приведены ее приращения за один шаг таблиц 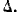
Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения Ф(х) как для положительных, так и для отрицательных аргументов.
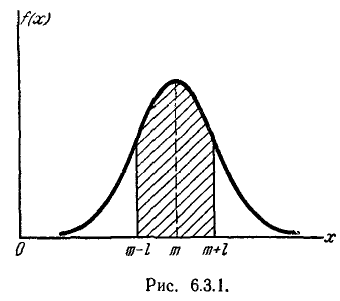
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m. Рассмотрим такой участок длины 2l (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7): 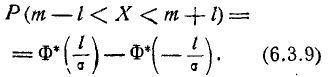
Учитывая свойство (6.3.8) функции Ф*(х) и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:
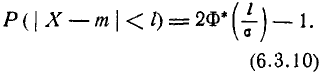
Решим следующую задачу. Отложим от центра рассеивания m последовательные отрезки длиной  (рис. 6.3.2) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.
(рис. 6.3.2) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.
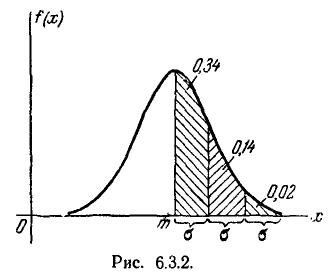
По формуле (6.3.7) находим:
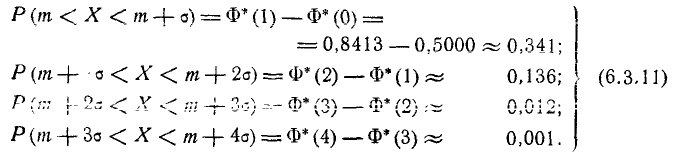
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.
Округляя вероятности попадания в отрезки до 0,01 (до 1%). получим три числа, которые легко запомнить: 0,34; 0,14; 0,02.
Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке m± З .
.
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма«. Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения  .
.
Пример:
Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м) среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).
Решение:
Ошибка измерения есть случайная величина X, подчинен- подчиненная нормальному закону с параметрами m= 1,2 и  = 0,8. Нужно найти вероятность попадания этой величины на участок от а =—1,6 до
= 0,8. Нужно найти вероятность попадания этой величины на участок от а =—1,6 до 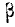 = + 1,6. По формуле (6.3.7) имеем:
= + 1,6. По формуле (6.3.7) имеем:
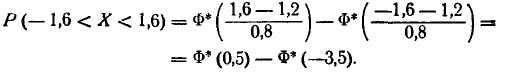
Пользуясь таблицами функции Ф* (х) (приложение, табл. 1), найдем:
Ф* (0,5) = 0,6915; Ф* (—3,5) = 0,0002,
откуда Р (—1,6 < X < 1,6) = 0,6915 — 0,0002 = 0,6913  0,691.
0,691.
Пример:
Найти ту же вероятность, что в предыдущем примере, но при условии, что систематической ошибки нет.
Решение:
По формуле (6.3.10), полагая l=1.6, найдем:
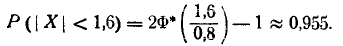
Пример:
По цели, имеющей вид полосы (автострада), ширина которой равна 20 м, ведется стрельба в направлении, перпендикулярном автостраде, прицеливание ведется по средней линии автострады. Среднее квадратическое отклонение в направлении стрельбы равно  = 8 м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.
= 8 м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.
Решение:
Выберем начало координат в любой точке на средней линии автострады (рис. 6.3.3) и направим ось абсцисс перпендикулярно автостраде. Попадание или непопадание снаряда в автостраду определяется значением только одной координаты точки падения X (другая координата Y нам безразлична). Случайная величина X распределена по нормальному закону
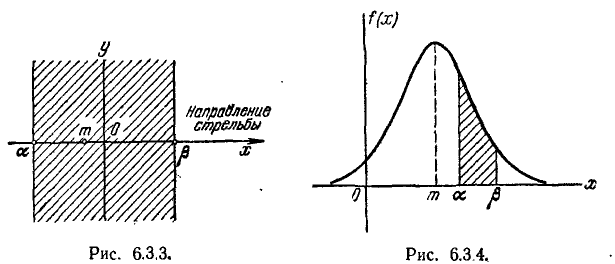
с параметрами m = —3,  = 8. Попадание снаряда в автостраду соответствует попаданию величины X на участок от а = — 10 до
= 8. Попадание снаряда в автостраду соответствует попаданию величины X на участок от а = — 10 до 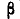 = 4-10. Применяя формулу (6.3.7), имеем:
= 4-10. Применяя формулу (6.3.7), имеем:
Пример:
Имеется случайная величина Х, нормально распределенная, с центром рассеивания m (рис. 6.3.4) и некоторый участок 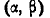 оси абсцисс. Каково должно быть среднее квадратическое отклонение о случайной величины X для того, чтобы вероятность попадания р на участок
оси абсцисс. Каково должно быть среднее квадратическое отклонение о случайной величины X для того, чтобы вероятность попадания р на участок 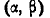 достигала максимума?
достигала максимума?
Решение:
Имеем:
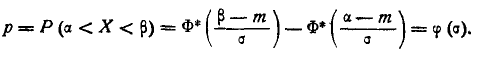
Продифференцируем эту функцию величины  :
:
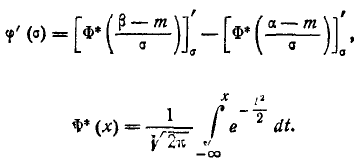
Применяя правило дифференцирования интеграла по переменной, входящей в его предел, получим:
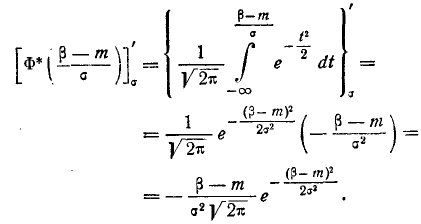
Аналогично
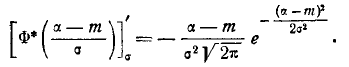
Для нахождения экстремума положим:
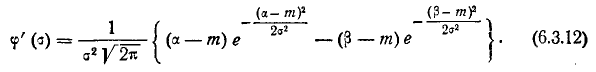
При 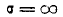 это выражение обращается в нуль и вероятность р достигает минимума. Максимум р получим из условия
это выражение обращается в нуль и вероятность р достигает минимума. Максимум р получим из условия 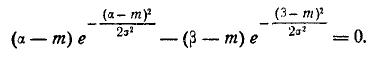 (6.3.13)
(6.3.13)
Уравнение (6.3.13) можно решить численно или графически.
6.4. Вероятное (срединное) отклонение
В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой Е (иногда В).
Вероятным (срединным) отклонением случайной величины X, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение Е — это половина длины участка оси абсцисс, симметричного относительно точки m, на кото- который опирается половина площади кривой распределения.
Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».
Рассмотрим случайную величину X, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания m меньше чем на Е, по определению вероятного отклонения Е, равна 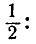
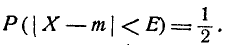 (6.4.1)
(6.4.1)
Вероятность того, что она отклонится от m больше чем на Е, тоже равна 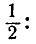
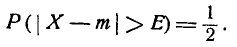
Таким образом, при большом числе опытов в среднем половина значений случайной величины X отклонится от m больше чем на Е, а половина — меньше. Отсюда и термины «срединная ошибка», «срединное отклонение».
Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего rвадратического отклонения  . Установим эту зависимость. Вычислим вероятность события | X — m | < Е в уравнении (6.4.1) по формуле (6.3.10). Имеем:
. Установим эту зависимость. Вычислим вероятность события | X — m | < Е в уравнении (6.4.1) по формуле (6.3.10). Имеем:
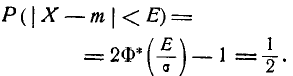
Отсюда
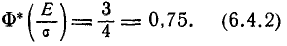
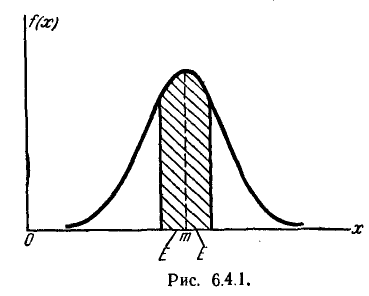
По таблицам функции Ф* (х) можно найти такое значение аргумента х, при котором она равна 0,75. Это значение аргумента приближенно равно 0,674; отсюда
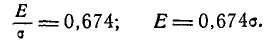 (6.4.3)
(6.4.3)
Таким образом, зная значение  , можно сразу найти пропорциональное ему значение Е. Часто пользуются еще такой формой записи этой зависимости:
, можно сразу найти пропорциональное ему значение Е. Часто пользуются еще такой формой записи этой зависимости:
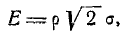 (6.4.4)
(6.4.4)
где р — такое значение аргумента, при котором одна из форм интеграла вероятностей — так называемая функция Лапласа 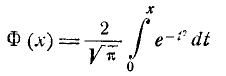
— равна половине. Численное значение величины р приближенно равно 0,477.
В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой  . В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
. В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
Если в качестве характеристики рассеивания принято вероятное отклонение Е, то плотность нормального распределения записывается в виде:
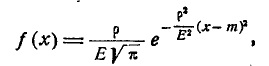 (6.4.5)
(6.4.5)
а вероятность попадания на участок от а до 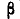 чаще всего записывается в виде:
чаще всего записывается в виде:
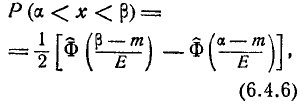
где
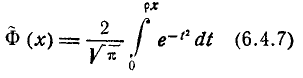 — так называемая приведенная функция Лапласа.
— так называемая приведенная функция Лапласа. 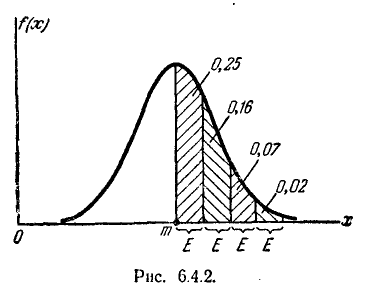
Сделаем подсчет, аналогичный выполненному в предыдущем п° для среднего квадратического отклонения  : отложим от центра рассеивания т. последовательные отрезки длиной в одно вероятное отклонение Е (рис. 6.4.2) и подсчитаем вероятности попа- попадания в эти отрезки с точностью до 0,01. Получим:
: отложим от центра рассеивания т. последовательные отрезки длиной в одно вероятное отклонение Е (рис. 6.4.2) и подсчитаем вероятности попа- попадания в эти отрезки с точностью до 0,01. Получим: 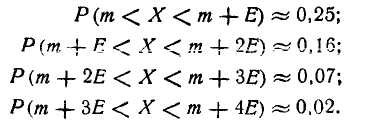
Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке 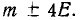
Пример:
Самолет-штурмовик производит обстрел колонны войск противника, ширина которой’ равна 8 м. Полет — вдоль колонны, прицеливание— по средней линии колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо но направлению полета. Главные вероятные отклонения: по направлению полета 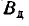 = 15 м, в боковом направлении
= 15 м, в боковом направлении 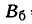 = 5 М. Не имея в своем распоряжении никаких таблиц интеграла вероятностей, а зная только числа:
= 5 М. Не имея в своем распоряжении никаких таблиц интеграла вероятностей, а зная только числа:
25%, 16%, 7%, 2%,
оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.
Решение:
Для решения задачи достаточно рассмотреть одну координату точки попадания — абсциссу X в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания m = 2 и вероятным отклонением 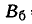 =Е = 5 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
=Е = 5 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
0,4-25% =0,1.
Влево от центра рассеивания цель занимает участок б м. Это — целое вероятное отклонение E м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна: 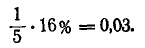
Таким образом, вероятность попадания в колонну приближенно равна:
0,1+0,25 + 0,03 = 0,38.
Вероятность хотя бы одного попадания при трех выстрелах равна: 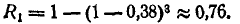
Закон нормального распределения случайных величин

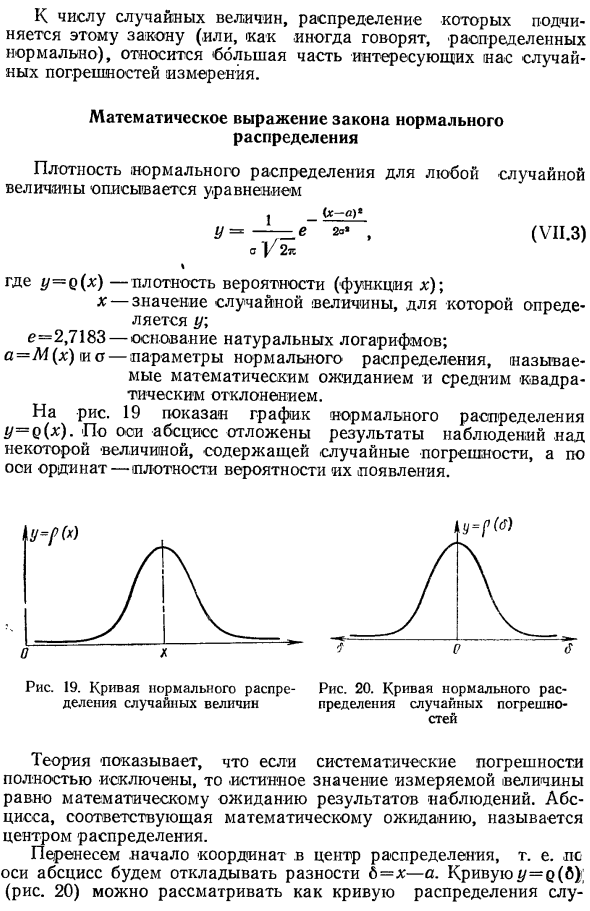


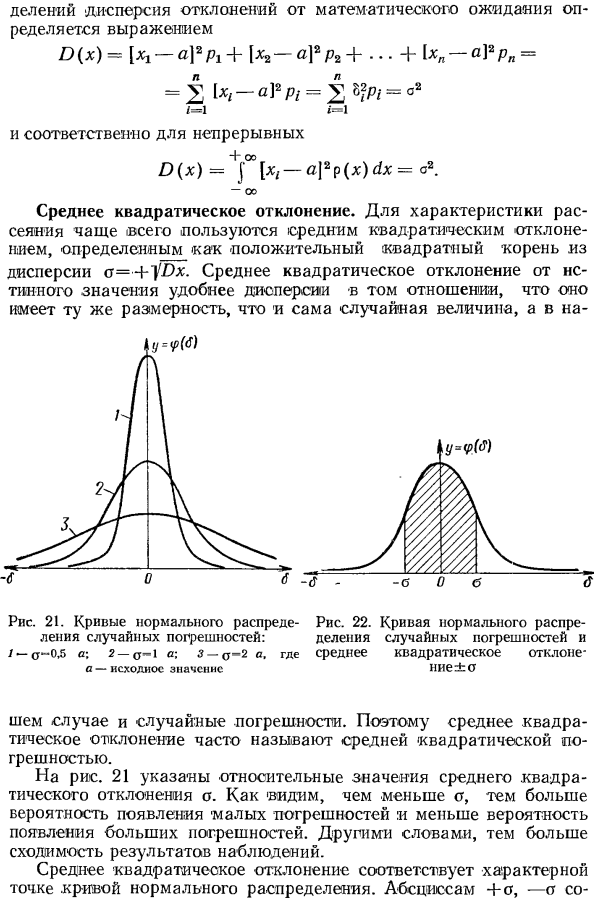

Смотрите также:
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность




![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)






