Статистика как найти долю населения

Что такое доля населения?

17 авг. 2022 г.
читать 2 мин

В статистике доля населения относится к доле людей в популяции с определенной характеристикой.

Например, предположим, что 43,8% жителей определенного города поддерживают новый закон. Значение 0,438 представляет долю населения.

Формула доли населения

Доля населения всегда находится в диапазоне от 0 до 1 (или от 0% до 100% в процентном выражении) и рассчитывается следующим образом:

р = Х/Н

куда:

p: Доля населения
X: количество особей в популяции с определенной характеристикой.
N: Общее количество особей в популяции.

Как оценить долю населения

Поскольку обычно сбор данных для каждого человека в популяции занимает слишком много времени и средств, вместо этого мы часто собираем данные для выборки.

Например, предположим, что мы хотим узнать, какая часть жителей определенного города поддерживает новый закон. Если население состоит из 50 000 жителей, мы можем взять простую случайную выборку из 1000 жителей:

Затем мы рассчитываем долю выборки следующим образом:

р̂ = х / п

куда:

p̂: доля выборки
x: количество лиц в выборке с определенной характеристикой.
n: общее количество лиц в выборке.

Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 367 из 1000 жителей выборки поддержали новый закон, то доля выборки будет рассчитана как 367/1000 = 0,367 .

Таким образом, наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,367 .

Доверительный интервал для доли населения

Хотя пропорция выборки дает нам оценку истинной доли населения, нет никакой гарантии, что пропорция выборки будет точно соответствовать пропорции населения.

По этой причине мы обычно строим доверительный интервал — диапазон значений, которые, вероятно, содержат истинную долю населения с высокой степенью достоверности.

Формула для расчета доверительного интервала для доли населения :

Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n

куда:

p̂: доля выборки
z: выбранное значение z
n: размер выборки

Z-значение, которое вы будете использовать, зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, которое соответствует популярным вариантам выбора уровня достоверности:

| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |

Обратите внимание, что более высокие уровни достоверности соответствуют большим значениям z, что приводит к более широким доверительным интервалам. Это означает, что, например, 95-процентный доверительный интервал будет шире, чем 90-процентный доверительный интервал для того же набора данных.

Пример: доверительный интервал для доли населения

Предположим, мы хотим оценить долю жителей города, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:

Размер выборки n = 100
Доля в пользу закона p̂ = 0,56

Вот как найти различные доверительные интервалы для доли населения:

90% доверительный интервал: 0,56 +/- 1,645 * (√ 0,56 (1-0,56) / 100 ) = [0,478, 0,642]

95% доверительный интервал: 0,56 +/- 1,96 * (√ 0,56 (1-0,56) / 100 ) = [0,463, 0,657]

99% доверительный интервал: 0,56 +/- 2,58 * (√ 0,56 (1-0,56) / 100 ) = [0,432, 0,688]

Примечание. Вы также можете найти эти доверительные интервалы с помощью калькулятора доверительного интервала для пропорции .

Источник

In statistics, a population proportion refers to the fraction of individuals in a population with a certain characteristic.

For example, suppose 43.8% of individuals in a certain city support a new law. The value 0.438 represents a population proportion.

Formula for a Population Proportion

A population proportion always ranges between 0 and 1 (or 0% to 100% in percentage terms) and it is calculated as follows:

p = X / N

where:

p: The population proportion
X: The count of individuals in a population with a certain characteristic.
N: The total number of individuals in a population.

How to Estimate a Population Proportion

Since it is usually too time-consuming and costly to collect data for every individual in a population, we often collect data for a sample instead.

For example, suppose we want to know what proportion of residents in a certain city support a new law. If the population consists of 50,000 total residents, we may take a simple random sample of 1,000 residents:

We would then calculate the sample proportion as follows:

p̂ = x / n

where:

p̂: The sample proportion
x: The count of individuals in the sample with a certain characteristic.
n: The total number of individuals in the sample.

We would then use this sample proportion to estimate the population proportion. For example, if 367 of the 1,000 residents in the sample supported the new law, the sample proportion would be calculated as 367 / 1,000 = 0.367.

Thus, our best estimate for the proportion of residents in the population who supported the law would be 0.367.

Confidence Interval for a Population Proportion

Although the sample proportion provides us with an estimate of the true population proportion, there’s no guarantee that the sample proportion will exactly match the population proportion.

For this reason, we typically construct a confidence interval – a range of values that are likely to contain the true population proportion with a high degree of confidence.

The formula to calculate a confidence interval for a population proportion is:

Confidence Interval = p̂ +/- z*√p̂(1-p̂) / n

where:

p̂: sample proportion
z: the chosen z-value
n: sample size

The z-value that you will use is dependent on the confidence level that you choose. The following table shows the z-value that corresponds to popular confidence level choices:

Confidence Level	z-value
0.90	1.645
0.95	1.96
0.99	2.58

Notice that higher confidence levels correspond to larger z-values, which leads to wider confidence intervals. This means that, for example, a 95% confidence interval will be wider than a 90% confidence interval for the same set of data.

Example: Confidence Interval for a Population Proportion

Suppose we want to estimate the proportion of residents in a city that are in favor of a certain law. We select a random sample of 100 residents and ask them about their stance on the law. Here are the results:

Sample size n = 100
Proportion in favor of law p̂ = 0.56

Here is how to find various confidence intervals for the population proportion:

90% Confidence Interval: 0.56 +/- 1.645*(√.56(1-.56) / 100) = [0.478, 0.642]

95% Confidence Interval: 0.56 +/- 1.96*(√.56(1-.56) / 100) = [0.463, 0.657]

99% Confidence Interval: 0.56 +/- 2.58*(√.56(1-.56) / 100) = [0.432, 0.688]

Note: You can also find these confidence intervals by using the Confidence Interval for Proportion Calculator.

Источник

Содержание

– Как рассчитать долю численности населения?
– Как считается численность населения города?
– Что такое доля городского населения?
– Как рассчитать долю женщин?
– Как вычислить долю в процентах от всего населения?
– Что нужно сделать чтобы найти плотность населения?
– Как рассчитывается миграционный прирост убыль населения?
– Что такое численность?
– Как рассчитать среднегодовую численность населения?
– Где самая высокая доля городского населения?
– Сколько процентов населения мира является сельскими жителями?
– Почему численность городского населения больше чем сельского?
– Как рассчитать общий коэффициент рождаемости?
– Как рассчитать естественный прирост населения?
– Что такое естественный прирост населения и как он рассчитывается?

Как рассчитать долю численности населения?

Доли численности населения отдельных возрастных групп в общей численности населения муниципального образования определены как частное от деления численности каждой возрастной группы на общую численность населения муниципального образования. Результаты приведены в графах 5 – 7 Таблицы 1 (Приложение).

Как считается численность населения города?

Один из определяющих факторов для присвоения населённому пункту статуса города — численность населения. Согласно рекомендациям ООН, для возможности сопоставления урбанизации стран и других целей, предлагается считать городами все поселения, имеющие 20 тысяч жителей и более.

Что такое доля городского населения?

Соотношение между городским населением и сельским населением характеризует степень урбанизированности страны или отдельного региона. По состоянию на 2020 год 56,2 % населения Земли проживало в городах. В 2050 году, по среднему варианту прогноза ООН, в городах будет проживать 68,6 % населения Земли.

Как рассчитать долю женщин?

Рассчитывается путем деления числа родившихся у матерей определенного возраста, состоящих в зарегистрированном браке, на среднее за период число состоящих в браке женщин в этом возрасте и умножения полученного результата на 1000, т. е. в ‰.

Как вычислить долю в процентах от всего населения?

Считаем долю от общего числа

Доля (%) = Число 1/Число 2*100%, где: Число 1 – собственно говоря, наше исходное числовое значение Число 2 – итоговое число, долю в котором мы хотим выяснить

Что нужно сделать чтобы найти плотность населения?

ПЛО́ТНОСТЬ НАСЕЛЕ́НИЯ, степень населённости конкретной территории, численность постоянного населения, приходящаяся на единицу площади (как правило, на 1 км 2). П. н. =P/Q, где P – численность постоянного населения территории; Q – площадь территории без учёта крупных внутр.

Как рассчитывается миграционный прирост убыль населения?

Для расчетов существует формула миграционного прироста: МП = П – В (человек), где МП означает величину миграционного прироста, П – число прибывших, В – число выбывших. Миграционный прирост изображается в виде графиков, диаграмм, таблиц. Рис. 3.

Что такое численность?

Численность — один из демографических показателей. В общем случае — число людей в определённой их совокупности (регион и т. п.). … Численность населения — абсолютная любая моментная величина, отражающая количественные размеры общества, проживающего на определённой территории.

Как рассчитать среднегодовую численность населения?

Среднегодовая численность работников субъектов предпринимательства рассчитывается как сумма количества работников за календарный год, поделенная на двенадцать (с 1 января по 31 декабря).

Где самая высокая доля городского населения?

По абсолютной численности городского населения выделяются Китай (837 миллионов человек в 2018 году) и Индия (461), в них сосредоточена почти треть всего городского населения мира (19,8% и 10,9% соответственно). Доля городских жителей в Китае, по оценке ООН, составляет 59,2%, в Индии – 34,0%.

Сколько процентов населения мира является сельскими жителями?

Прогноз городского и сельского населения мира, 2018

Население мира было преимущественно сельским: в сельских поселениях проживало около 70% населения мира, в городских поселениях – 30% (рис.

Почему численность городского населения больше чем сельского?

Почему численность городского населения больше сельского? Причины: концентрация производственного и жилищного строительства в городах, различия условий жизни в городах и сельской местности. 2.

Как рассчитать общий коэффициент рождаемости?

Общий коэффициент рождаемости рассчитывается как отношение общего числа рождений в стране за год к среднегодовой численности населения, умноженное на 1000‰. Общий коэффициент смертности рассчитывается как отношение общего числа умерших в стране за год к среднегодовой численности населения, умноженное на 1000‰.

Как рассчитать естественный прирост населения?

Естественное движение населения – обобщенное название совокупности рождений и смертей, изменяющих численность населения так называемым естественным путем. Естественный прирост населения – абсолютная величина разности между числами родившихся и умерших за определенный промежуток времени.

Что такое естественный прирост населения и как он рассчитывается?

Естественный прирост населения (ЕП) — превышение рождаемости над смертностью, то есть разница между количеством родившихся и умерших за период времени; основа роста численности населения.

Интересные материалы:

Как найти Недавние места на компьютере?
Как найти недавно открытые документы в ворде?
Как найти неизвестные источники на Xiaomi?
Как найти нераспределенную прибыль?
Как найти номер пенсионного удостоверения?
Как найти номер Снилса?
Как найти норму амортизации?
Как найти новое устройство на компе?
Как найти ножницы в виндовс 10?
Как найти нужную папку на компьютере?

Источник

В статистика, а доля населения, обычно обозначаемый или Греческая буква ,^[1]^[2] это параметр который описывает процентное значение, связанное с численность населения. Например, Перепись населения США 2010 года показали, что 83,7% населения Америки не были латиноамериканцами или латиноамериканцами; значение 0,837 – это доля населения. В целом, доля населения и другие параметры популяции неизвестны. А перепись могут быть проведены для определения фактического значения параметра численности населения, но часто перепись нецелесообразна из-за ее затрат и затрат времени.

Доля населения обычно оценивается через беспристрастный статистика выборки полученный от наблюдательное исследование или же эксперимент. Например, Национальная конференция по технологической грамотности провела национальный опрос 2000 взрослых, чтобы определить процент экономически неграмотных взрослых. Исследование показало, что 72% из 2000 опрошенных взрослых не понимали, что такое валовой внутренний продукт является.^[3] Значение 72% – это примерная пропорция. Доля образца обычно обозначается а в некоторых учебниках .^[1]^[4]^[5]

Математическое определение

А пропорция математически определяется как отношение значений в подмножестве к значениям в наборе .

Таким образом, долю населения можно определить следующим образом:

${ displaystyle P = { frac {X} {N}}}$ (куда Икс – количество успехов в популяции, и это размер населения)

Это математическое определение можно обобщить, чтобы дать определение пропорции образца:

${ displaystyle { hat {p}} = { frac {x} {n}}}$ (куда Икс – количество успехов в выборке, а размер выборки, полученной из совокупности)^[6]^[4]

Оценка

Одно из основных направлений обучения в выведенный статистика определяет “истинное” значение параметра. Как правило, фактическое значение параметра никогда не будет найдено, если только не будет проведена перепись изучаемого населения. Однако существуют статистические методы, которые можно использовать для получения разумной оценки параметра. Эти методы включают доверительные интервалы и проверка гипотезы.

Оценка стоимости доли населения может иметь большое значение в областях сельское хозяйство, бизнес, экономика, образование, инженерное дело, экологические исследования, лекарство, закон, политическая наука, психология, и социология.

Доля населения может быть оценена с помощью доверительного интервала, известного как одна выборка в Z-интервале формула которого приведена ниже:

${ displaystyle { hat {p}} pm z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}$ (куда – доля образца, размер выборки, и $z ^ {*}$ это верхний ${ displaystyle { frac {1-C} {2}}}$ критическое значение стандартное нормальное распределение для уровня уверенности ) ^[7]

Доказательство

Чтобы вывести формулу для одна выборка в Z-интервале, а выборочное распределение пропорций образца необходимо учитывать. Среднее значение выборочного распределения пропорций выборки обычно обозначается как ${ displaystyle mu _ { hat {p}} = P}$ и его стандартное отклонение обозначается как ${ displaystyle sigma _ { hat {p}} = { sqrt { frac {P (1-P)} {n}}}}$ .^[4] Поскольку значение неизвестно, объективная статистика будет использоваться для . Среднее значение и стандартное отклонение переписываются как ${ displaystyle mu _ { hat {p}} = { hat {p}}}$ и ${ displaystyle sigma _ { hat {p}} = { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}$ соответственно. Обращение к Центральная предельная теорема, выборочное распределение пропорций пробы составляет приблизительно нормальный – при условии, что образец достаточно большой и не перекручен.

Предположим, вычисляется следующая вероятность: ${ displaystyle P (-z ^ {*} <{ frac {{ hat {p}} - P} { sqrt { frac {{ hat {p}}) (1 - { hat {p}} )} {n}}}} <z ^ {*}) = C}$ , куда и ${ displaystyle pm z ^ {*}}$ – стандартные критические значения.

Распределение выборки пропорций выборки приблизительно нормально, когда оно удовлетворяет требованиям Центральной предельной теоремы.

В неравенство ${ displaystyle -z ^ {*} <{ frac {{ hat {p}} - P} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}} <z ^ {*}}$ можно алгебраически переписать следующим образом:

${ displaystyle -z ^ {*} <{ frac {{ hat {p}} - P} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}} <z ^ {*} Rightarrow -z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}} } <{ hat {p}} - P <z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} Rightarrow - { hat {p}} - z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} <- P <- { hat {p}} + z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} Rightarrow { hat { p}} - z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} <P <{ hat {p}} + z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}$ Из алгебраической работы, проделанной выше, очевидно с уровня определенности который может оказаться между значениями ${ displaystyle { hat {p}} pm z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}$ .

Условия для вывода

Как правило, формула, используемая для оценки доли населения, требует замены известных числовых значений. Однако эти числовые значения нельзя подставлять в формулу «вслепую», потому что статистические выводы требует, чтобы оценка неизвестного параметра была обоснованной. Чтобы оценка параметра была обоснованной, необходимо проверить три условия:

Данные индивидуального наблюдения должны быть получены из простая случайная выборка интересующего населения.
Отдельные наблюдения данных должны отображать нормальность. Это можно проверить математически с помощью следующего определения:
Отдельные наблюдения данных должны быть независимый друг друга. Это можно проверить математически с помощью следующего определения:

Условия для SRS, нормальности и независимости иногда называют условия для набора инструментов вывода в большинстве статистических учебников.

Пример

Допустим, в условиях демократии проходят президентские выборы. Случайная выборка из 400 имеющих право голоса избирателей из числа избирателей демократического государства показывает, что 272 избирателя поддерживают кандидата B. Политолог хочет определить, какой процент избирателей поддерживает кандидата B.

Чтобы ответить на вопрос политолога, можно построить одновыборочную пропорцию в Z-интервале с уровнем достоверности 95%, чтобы определить долю населения, имеющую право голоса в этой демократии, которая поддерживает кандидата B.

Решение

Из случайной выборки известно, что ${ displaystyle { hat {p}} = { frac {272} {400}} = 0,68}$ с размером выборки . Перед построением доверительного интервала будут проверены условия вывода.

{ Displaystyle (400) (0,68) geq 10 Rightarrow 272 geq 10}

{ Displaystyle (400) (1-0,68) geq 10 Rightarrow 128 geq 10}

Условие нормальности выполнено.

{ Displaystyle N geq 10 (400) Rightarrow N geq 4000}

Численность населения

для этой демократии можно предположить, что избирателей не менее 4000. Следовательно, условие независимости было выполнено.

Когда условия вывода проверены, можно построить доверительный интервал.

Позволять и

Решить для $z ^ {*}$ , то выражение ${ displaystyle { frac {1-C} {2}}}$ используется.

${ displaystyle { frac {1-C} {2}} = { frac {1-0,95} {2}} = { frac {0,05} {2}} = 0,0250}$

Стандартная нормальная кривая с $z ^ {*}$ что дает площадь верхнего хвоста 0,0250 и площадь 0,9750 для ${ Displaystyle Z Leq Z ^ {*}}$ .

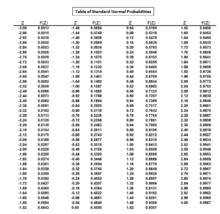
Таблица со стандартными нормальными вероятностями для .

Изучая стандартную нормальную колоколообразную кривую, значение для $z ^ {*}$ может быть определен путем определения того, какой стандартный балл дает стандартной нормальной кривой площадь верхнего хвоста 0,0250 или площадь 1-0,0250 = 0,9750. Значение для $z ^ {*}$ также можно найти с помощью таблицы стандартных нормальных вероятностей.

Из таблицы стандартных нормальных вероятностей значение что дает площадь 0,9750 составляет 1,96. Следовательно, значение для $z ^ {*}$ составляет 1,96.

Значения для , , ${ displaystyle z ^ {*} = 1,96}$ теперь можно подставить в формулу для одной пробы в интервале Z:

${ displaystyle { hat {p}} pm z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} Rightarrow (0,68) pm (1,96) { sqrt { frac {(0,68) (1-0,68)} {(400)}}} Rightarrow 0,68 pm 1,96 { sqrt {0,000544}}}$

Исходя из условий вывода и формулы для доли одной выборки в интервале Z, с уровнем достоверности 95% можно сделать вывод, что процент населения избирателей в этой демократии, поддерживающих кандидата B, составляет от 63,429% до 72,571. %.

Значение параметра в диапазоне доверительного интервала

Часто задаваемый вопрос в выводной статистике – входит ли параметр в доверительный интервал. Единственный способ ответить на этот вопрос – провести перепись. Ссылаясь на приведенный выше пример, вероятность того, что доля населения находится в диапазоне доверительного интервала, равна либо 1, либо 0. То есть, параметр включен в диапазон интервала или нет. Основная цель доверительного интервала – лучше проиллюстрировать, каким может быть идеальное значение параметра.

Распространенные ошибки и неверные интерпретации оценок

Очень распространенная ошибка, возникающая при построении доверительного интервала, – это вера в то, что уровень достоверности, такой как , означает 95% шанс. Это неверно. Уровень уверенности основан на степени достоверности, а не вероятности. Следовательно, значения находятся исключительно между 0 и 1.

Смотрите также

Доверительный интервал биномиальной пропорции
Доверительный интервал
Распространенность
Статистическая проверка гипотез
Статистические выводы
Статистический параметр
Интервал допуска

Доля населения Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Количество успехов: 30 –> Конверсия не требуется
Численность населения: 50 –> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.6 –> Конверсия не требуется

4 Пропорции Калькуляторы

Доля населения формула

Доля населения = Количество успехов/Численность населения

P_Population = N_Success/N_Population

Что такое статистическая пропорция и ее значение?

В статистике некоторые конкретные числовые отношения, которые связывают некоторые важные переменные или параметры, связанные с данными или распределением, называются статистическими пропорциями. Сравнение нескольких данных является основным преимуществом этих пропорций. В статистическом анализе данных различные пропорции имеют широкое применение. Например, во время сравнения двух разных данных, сравнения показателей компании с показателями прошлого года, сравнения качества одного набора продуктов со следующим набором продуктов и т. д., если мы сравниваем фиксированную долю каждой группы данных. , мы можем сделать много полезных выводов.

Источник

Что такое доля населения?

Формула доли населения

Как оценить долю населения

Доверительный интервал для доли населения

Пример: доверительный интервал для доли населения

Formula for a Population Proportion

How to Estimate a Population Proportion

Confidence Interval for a Population Proportion

Example: Confidence Interval for a Population Proportion

Как рассчитать долю численности населения?

Как считается численность населения города?

Что такое доля городского населения?

Как рассчитать долю женщин?

Как вычислить долю в процентах от всего населения?

Что нужно сделать чтобы найти плотность населения?

Как рассчитывается миграционный прирост убыль населения?

Что такое численность?

Как рассчитать среднегодовую численность населения?

Где самая высокая доля городского населения?

Сколько процентов населения мира является сельскими жителями?

Почему численность городского населения больше чем сельского?

Как рассчитать общий коэффициент рождаемости?

Как рассчитать естественный прирост населения?

Что такое естественный прирост населения и как он рассчитывается?

Математическое определение

Оценка

Доказательство

Условия для вывода

Пример

Решение

Значение параметра в диапазоне доверительного интервала

Распространенные ошибки и неверные интерпретации оценок

Смотрите также

Рекомендации

Доля населения Решение

4 Пропорции Калькуляторы

Доля населения формула

Что такое статистическая пропорция и ее значение?

Добавить комментарий Отменить ответ

Что такое доля населения?

Формула доли населения

Как оценить долю населения

Доверительный интервал для доли населения

Пример: доверительный интервал для доли населения

Formula for a Population Proportion

How to Estimate a Population Proportion

Confidence Interval for a Population Proportion

Example: Confidence Interval for a Population Proportion

Как рассчитать долю численности населения?

Как считается численность населения города?

Что такое доля городского населения?

Как рассчитать долю женщин?

Как вычислить долю в процентах от всего населения?

Что нужно сделать чтобы найти плотность населения?

Как рассчитывается миграционный прирост убыль населения?

Что такое численность?

Как рассчитать среднегодовую численность населения?

Где самая высокая доля городского населения?

Сколько процентов населения мира является сельскими жителями?

Почему численность городского населения больше чем сельского?

Как рассчитать общий коэффициент рождаемости?

Как рассчитать естественный прирост населения?

Что такое естественный прирост населения и как он рассчитывается?

Математическое определение

Оценка

Доказательство

Условия для вывода

Пример

Решение

Значение параметра в диапазоне доверительного интервала

Распространенные ошибки и неверные интерпретации оценок

Смотрите также

Рекомендации

Доля населения Решение

4 Пропорции Калькуляторы

Доля населения формула

Что такое статистическая пропорция и ее значение?

Вам также может понравиться

Найти как делают тату

Как найти документ по guid 1c

Как найти парня кате

Добавить комментарий Отменить ответ