Расчет средней величины в интервальных вариационных рядах немного отличается от расчета в рядах дискретных. Как рассчитать среднюю арифметическую и среднюю гармоническую в дискретных рядах можно посмотреть вот ЗДЕСЬ. Такое различие вполне объяснимо – это связано с особенностью интервальных рядов, в которых изучаемый признак приведен в интервале от и до.
Итак, посмотрим особенности расчета на примере.
Пример 1. Имеются данные о дневном заработке рабочих предприятия.
| Дневной заработок рабочего, руб. | Число рабочих, чел. |
| 500-1000 | 15 |
| 1000-1500 | 30 |
| 1500-2000 | 80 |
| 2000-2500 | 60 |
| 2500-3000 | 25 |
| Итого | 210 |
Нам необходимо рассчитать среднедневную заработную плату рабочего.
Начало решения задачи будет аналогичным правилам расчета средней величины, которые можно посмотреть в этой статье.
Начинаем мы с определения варианты и частоты, поскольку ищем мы средний заработок за день, то варианта это первая колонка, а частота вторая. Данные у нас заданы явным количеством, поэтому расчет проведем по формуле средней арифметической взвешенной (так как данные приведены в табличном виде). Но на этом сходства заканчиваются и появляются новые действия.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f |
| 500-1000 | 15 |
| 1000-1500 | 30 |
| 1500-2000 | 80 |
| 2000-2500 | 60 |
| 2500-3000 | 25 |
| Итого | 210 |
Дело в том, что интервальный рад представляет осредняемую величину в виде интервала. 500-1000, 2000-2500 и так далее. Чтобы решить эту проблему необходимо провести промежуточные действия, и только потом подсчитать среднюю величину по основной формуле.
Что же требуется в данном случае сделать. Все достаточно просто, чтобы провести расчет нам нужно, чтобы варианта была представлена одним числом, а не интервалом. Для получения такого значения находят так называемое ЦЕНТРАЛЬНОЕ ЗНАЧЕНИЕ ИНТЕРВАЛА (или середину интервала). Определяется оно путем сложение верхней и нижней границ интервала и делением на два.
Проведем необходимые расчеты и подставим данные в таблицу.

И так далее по всем интервалам рассчитываем центральное значение. В итоге получаем следующие результаты.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f | х’ | |
| 500-1000 | 15 | 750 | |
| 1000-1500 | 30 | 1250 | |
| 1500-2000 | 80 | 1750 | |
| 2000-2500 | 60 | 2250 | |
| 2500-3000 | 25 | 2750 | |
| Итого | 210 | — |
После того как мы рассчитали центральные значения далее проведем расчеты в таблицы и подставим итоговые данные в формулу, аналогично тому как мы уже рассматривали ранее.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f | х’ | x’f |
| 500-1000 | 15 | 750 | 11250 |
| 1000-1500 | 30 | 1250 | 37500 |
| 1500-2000 | 80 | 1750 | 140000 |
| 2000-2500 | 60 | 2250 | 135000 |
| 2500-3000 | 25 | 2750 | 68750 |
| Итого | ∑f = 210 | — | ∑ x’f = 392500 |

В итоге получаем, что среднедневная заработная плата одного рабочего составляет 1869 рублей.

Это пример решения, если интервальный ряд представлен со всеми закрытыми интервалами. Но достаточно часто бывает, когда два интервала открытые, первый и последний. В таких ситуациях прямой расчет центрального значения невозможен, но есть два варианта как это сделать.
Пример 2. Имеются данные о продолжительности производственного стажа персонала предприятия. Рассчитать среднюю продолжительность стада одного сотрудника.
| Длительность производственного стажа, лет | Число сотрудников, человек |
| до 3 | 19 |
| 3-6 | 21 |
| 6-9 | 15 |
| 9-12 | 10 |
| 12 и более | 5 |
| Итого | 70 |
В данном случае принцип решения останется точно таким же. Единственно, что поменялось в этой задаче, так это первый и последний интервалы. До 3 лет и 12 лет и более это и есть те самые открытые интервалы. Именно тут возникнет вопрос, а как же найти центральное значение интервала для таких интервалов.
Поступить в этой ситуации можно двумя способами:
- Предположить какой бы мог быть интервал, учитывая, что нам приведены интервалы равные, то это вполне возможно. Интервал до 3 мог бы выглядеть как 0-3, и тогда его центральное значение будет (0+3)/2 = 1,5 года. Интервал 12 и более мог бы выглядеть как 12-15, и тогда его центральное значение было бы (12+15)/2 = 13,5 года. Все оставшиеся центральные значения интервала рассчитываются аналогично. В результате получаем следующее.
| Длительность производственного стажа, лет х | Число сотрудников, человек f | х’ | x’f |
| до 3 | 19 | 1,5 | 28,5 |
| 3-6 | 21 | 4,5 | 94,5 |
| 6-9 | 15 | 7,5 | 112,5 |
| 9-12 | 10 | 10,5 | 105,0 |
| 12 и более | 5 | 13,5 | 67,5 |
| Итого | ∑f = 70 | — | ∑ x’f = 408,0 |

Средняя продолжительность стажа 5,83 года.
- Принять за центральное значение, то данное которое имеется в интервале, без дополнительных расчетов. В нашем случае в интервале до 3 это будет 3, а в интервале 12 и более это будет 12. Такой способ больше подходит для ситуаций, когда интервалы неравные и предположить какой интервал мог бы быть сложно. Рассчитаем нашу задачу по таким данным далее.
| Длительность производственного стажа, лет х | Число сотрудников, человек f | х’ | x’f |
| до 3 | 19 | 3 | 57,0 |
| 3-6 | 21 | 4,5 | 94,5 |
| 6-9 | 15 | 7,5 | 112,5 |
| 9-12 | 10 | 10,5 | 105,0 |
| 12 и более | 5 | 12 | 60,0 |
| Итого | ∑f = 70 | — | ∑ x’f = 429,0 |

Средняя продолжительность стажа 6,13 года.
Домашнее задание
- Рассчитать средний размер посевной площади на одно фермерское хозяйство по следующим данным.
| Размер посевной площади, га | Количество фермерских хозяйств |
| 0-20 | 64 |
| 20-40 | 58 |
| 40-60 | 32 |
| 60-80 | 21 |
| 80-100 | 12 |
| Итого | 187 |
- Рассчитайте средний возраст работника предприятия по следующим данным
| Возраст персонала, лет | Число сотрудников, человек |
| до 18 | 7 |
| 18-25 | 68 |
| 25-40 | 79 |
| 40-55 | 57 |
| 55 и старше | 31 |
| Итого | 242 |
Теперь Вы умеете рассчитывать среднюю в интервальном вариационном ряду!
Может еще поучимся? Загляни сюда!
Например, средняя арифметическая для интервального ряда
При расчете средней арифметической для
интервального вариационного ряда
сначала определяют среднюю для каждого
интервала, как полусумму верхней и
нижней границ, а затем — среднюю всего
ряда. В случае открытых интервалов
значение нижнего или верхнего интервала
определяется по величине интервалов,
примыкающих к ним.
Пример
3. Определить
средний возраст студентов вечернего
отделения.
|
Возраст |
Число |
Среднее |
Произведение |
|
до |
65 |
(18 + |
1235 |
|
20 — |
125 |
(20 + |
2625 |
|
22 — |
190 |
(22 + |
4560 |
|
26 — |
80 |
(26 + |
2240 |
|
30 и |
40 |
(30 + |
1280 |
|
Итого |
500 |
11940 |
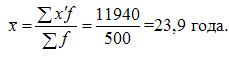
Средние, вычисляемые из интервальных
рядов являются приближенными.
-
Структурные средние величины
Кроме степенных средних в статистике
для относительной характеристики
величины варьирующего признака и
характеристики рядов распределения
пользуются структурными средними: модой
и медианой.
Мода
Мода— это наиболее часто
встречающийся вариант ряда. Мода
применяется, например, при определении
размера одежды, обуви, пользующейся
наибольшим спросом у покупателей.
Модой для дискретного ряда является
варианта, обладающая наибольшей частотой.
При вычислении моды для интервального
вариационного ряда необходимо:
-
сначала определить модальный интервал
(по максимальной частоте), -
затем — значение модальной величины
признака по формуле:
![]()
где:
-
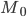 —
—
значение моды -
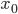 —
—
нижняя граница модального интервала -
i —
величина интервала -
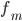 —
—
частота модального интервала -
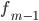 —
—
частота интервала, предшествующего
модальному -
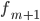 —
—
частота интервала, следующего за
модальным
Определение моды графически:
Мода определяется по гистограмме
распределения. Для этого
правую вершину модального
прямоугольника соединяют с правым
верхним углом предыдущего прямоугольника
, а левую
вершину модального прямоугольника –
с левым верхним углом
последующего прямоугольника. Абсцисса
точки пересечения этих прямых и будет
модой распределения.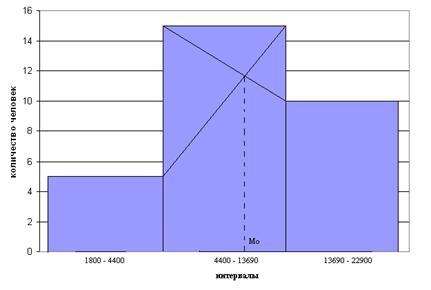
Медиана
Медиана — это значение признака,
который делит вариационный ряд на две
равные по численности части.
Медиана для дискретного ряда.
Для определения медианы в дискретном
рядус нечетнымколичеством
единиц наблюдения сначалапорядковый
номер медианыпо формуле: ![]() ,
,
а затем определяют, какое значение
варианта обладает накопленной частотой,
равной номеру медианы.
Если ряд содержит четное
число элементов, то
медиана будет равна средней из двух
значений признака, находящихся в
середине. Номер первого из этих признаков
определяется по формуле: ![]() ,
,
для второго – ![]() .
.
![]()
= n
(количество элементов в ряду).
Медиана для интервального ряда
При вычислении медианы для
интервального вариационного ряда сначала
определяют медианный интервал, в пределах
которого находится медиана.
Для этого:
-
определяется номер медианы
по формуле: ,
,
полученное значение округляется до
целого большего числа. -
затем по
накопленной частоте определяется
интервал, в который входит элемент с
таким номером, -
затем — значение медианы по формуле:
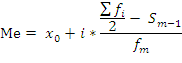
где:
-
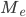 —
—
искомая медиана -
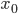 —
—
нижняя граница интервала, который
содержит медиану -
i
— ширина интервала -
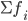 —
—
сумма частот или число членов ряда -
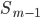 –
–
накопленная частота интервала,
предшествующего медианному -
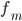 —
—
частота медианного интервала
Пример.
Найти моду и медиану для интервального
ряда.
|
Возрастные |
Число |
Сумма |
|
До 20 |
346 |
346 |
|
20 — 25 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 — 35 |
781 |
3053 |
|
35 — 40 |
212 |
3265 |
|
40 — 45 |
121 |
3386 |
|
45 лет |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определим моду
В
данном примере модальный интервал
находится в пределах возрастной группы
25-30 лет, так как на этот интервал приходится
наибольшая частота (1054).
Рассчитаем
величину моды:
![]()
Это значит, что модальный
возраст студентов равен 27 годам.
-
Определим медиану.
Медианный интервал
находится в возрастной группе 25-30 лет,
так как в пределах этого интервала
расположена варианта, которая делит
совокупность на две равные части (Σfi/2
= 3462/2 = 1731). Далее подставляем в формулу
необходимые числовые данные и получаем
значение медианы:
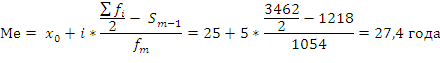
Это значит, что одна половина студентов
имеет возраст до 27,4 года, а другая свыше
27,4 года.
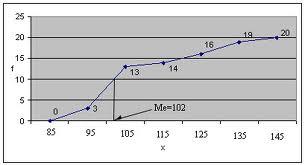
Графически медиана
определяется по кумуляте. Для ее
определения высоту наибольшей ординаты,
которая соответствует сумме всех частот,
делят пополам. Через полученную точку
проводят прямую,
параллельную оси абсцисс,
до
пересечения ее с кумулятой. Абсцисса
точки пересечения является медианой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти середину интервала
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала – «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

Инструкция
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам – это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона – отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.
Источники:
- что такое открытый интервал
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Расчет средней величины в интервальном вариационном ряду

Расчет средней величины в интервальных вариационных рядах немного отличается от расчета в рядах дискретных. Как рассчитать среднюю арифметическую и среднюю гармоническую в дискретных рядах можно посмотреть вот ЗДЕСЬ. Такое различие вполне объяснимо – это связано с особенностью интервальных рядов, в которых изучаемый признак приведен в интервале от и до.
Итак, посмотрим особенности расчета на примере.
Пример 1. Имеются данные о дневном заработке рабочих предприятия.
| Дневной заработок рабочего, руб. | Число рабочих, чел. |
| 500-1000 | 15 |
| 1000-1500 | 30 |
| 1500-2000 | 80 |
| 2000-2500 | 60 |
| 2500-3000 | 25 |
| Итого | 210 |
Нам необходимо рассчитать среднедневную заработную плату рабочего.
Начало решения задачи будет аналогичным правилам расчета средней величины, которые можно посмотреть в этой статье.
Начинаем мы с определения варианты и частоты, поскольку ищем мы средний заработок за день, то варианта это первая колонка, а частота вторая. Данные у нас заданы явным количеством, поэтому расчет проведем по формуле средней арифметической взвешенной (так как данные приведены в табличном виде). Но на этом сходства заканчиваются и появляются новые действия.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f |
| 500-1000 | 15 |
| 1000-1500 | 30 |
| 1500-2000 | 80 |
| 2000-2500 | 60 |
| 2500-3000 | 25 |
| Итого | 210 |
Дело в том, что интервальный рад представляет осредняемую величину в виде интервала. 500-1000, 2000-2500 и так далее. Чтобы решить эту проблему необходимо провести промежуточные действия, и только потом подсчитать среднюю величину по основной формуле.
Что же требуется в данном случае сделать. Все достаточно просто, чтобы провести расчет нам нужно, чтобы варианта была представлена одним числом, а не интервалом. Для получения такого значения находят так называемое ЦЕНТРАЛЬНОЕ ЗНАЧЕНИЕ ИНТЕРВАЛА (или середину интервала). Определяется оно путем сложение верхней и нижней границ интервала и делением на два.
Проведем необходимые расчеты и подставим данные в таблицу.

И так далее по всем интервалам рассчитываем центральное значение. В итоге получаем следующие результаты.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f | х’ |
| 500-1000 | 15 | 750 |
| 1000-1500 | 30 | 1250 |
| 1500-2000 | 80 | 1750 |
| 2000-2500 | 60 | 2250 |
| 2500-3000 | 25 | 2750 |
| Итого | 210 | — |
После того как мы рассчитали центральные значения далее проведем расчеты в таблицы и подставим итоговые данные в формулу, аналогично тому как мы уже рассматривали ранее.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f | х’ | x’f |
| 500-1000 | 15 | 750 | 11250 |
| 1000-1500 | 30 | 1250 | 37500 |
| 1500-2000 | 80 | 1750 | 140000 |
| 2000-2500 | 60 | 2250 | 135000 |
| 2500-3000 | 25 | 2750 | 68750 |
| Итого | ∑f = 210 | — | ∑ x’f = 392500 |

В итоге получаем, что среднедневная заработная плата одного рабочего составляет 1869 рублей.

Это пример решения, если интервальный ряд представлен со всеми закрытыми интервалами. Но достаточно часто бывает, когда два интервала открытые, первый и последний. В таких ситуациях прямой расчет центрального значения невозможен, но есть два варианта как это сделать.
Пример 2. Имеются данные о продолжительности производственного стажа персонала предприятия. Рассчитать среднюю продолжительность стада одного сотрудника.
| Длительность производственного стажа, лет | Число сотрудников, человек |
| до 3 | 19 |
| 3-6 | 21 |
| 6-9 | 15 |
| 9-12 | 10 |
| 12 и более | 5 |
| Итого | 70 |
В данном случае принцип решения останется точно таким же. Единственно, что поменялось в этой задаче, так это первый и последний интервалы. До 3 лет и 12 лет и более это и есть те самые открытые интервалы. Именно тут возникнет вопрос, а как же найти центральное значение интервала для таких интервалов.
Поступить в этой ситуации можно двумя способами:

Средняя продолжительность стажа 5,83 года.

Средняя продолжительность стажа 6,13 года.
Домашнее задание
Теперь Вы умеете рассчитывать среднюю в интервальном вариационном ряду!
Источник
Решение задач по статистике и выводы к ним
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.
Группы компаний по основным производственным фондам, млн. руб. (х)
Середина интервала (Xi) = (начало интервала+конец интервала)/2
Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.
Теперь рассчитаем среднюю арифметическую величину.
 средняя арифметическая =
средняя арифметическая =  = (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
= (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
Далее рассчитаем среднюю взвешенную величину.
 средняя взвешенная =
средняя взвешенная =  = (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
= (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.
Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.
Середина интервала (Xi) = (начало интервала+конец интервала)/2
Источник
Примеры решений задач по статистике
Решение задач по статистике и выводы к ним
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.
|
№ группы |
Группы компаний по основным производственным фондам, млн. руб. (х) |
Число компаний (fi) |
Середина интервала (Xi) = (начало интервала+конец интервала)/2 |
|
1 |
10 – 25 |
2 |
17,5 |
|
2 |
25 – 33 |
8 |
29 |
|
3 |
33 – 42 |
14 |
37,5 |
|
4 |
42 – 49 |
9 |
45,5 |
|
5 |
49 – 62 |
3 |
55,5 |
|
Всего: |
36 |
— |
Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.
Теперь рассчитаем среднюю арифметическую величину.
 средняя арифметическая =
средняя арифметическая =  = (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
= (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
Далее рассчитаем среднюю взвешенную величину.
 средняя взвешенная =
средняя взвешенная =  = (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
= (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.
Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.
|
Число компаний (f) |
Середина интервала (Xi) = (начало интервала+конец интервала)/2 |
Xi*fi |
|
|
|
|
2 |
17,5 |
35 |
-20,5 |
420,25 |
840,5 |
|
8 |
29 |
232 |
-9 |
81 |
648 |
|
14 |
37,5 |
525 |
-0,5 |
0,25 |
3,5 |
|
9 |
45,5 |
409,5 |
7,5 |
56,25 |
506,25 |
|
3 |
55,5 |
166,5 |
17,5 |
306,25 |
918,75 |
|
Итого: 36 |
— |
1368 |
— |
— |
2917 |
Рассчитаем дисперсию.
 =2917/36=81,03. (дисперсия не имеет размерности)
=2917/36=81,03. (дисперсия не имеет размерности)
Среднеквадратическое отклонение рассчитывается как корень квадратный из дисперсии.
 =9 (млн. руб.).
=9 (млн. руб.).
Рассчитаем коэффициент вариации по формуле:
 =(9/38)*100%=23,68%.
=(9/38)*100%=23,68%.
Рассчитаем моду и медиану.
Найдем моду по формуле. 
Модальный интервал находим по наибольшей частоте. Наибольшая частота, т.е. частота модального интервала fМо=14. Модальный интервал от 33 до 42 млн. руб. Значит величина модального интервала i = 42-33=9.
Нижняя граница модального интервала  равна 33.
равна 33.
Частота предмодального интервала  равна 8.
равна 8.
Частота постмодального интервала  равна 9.
равна 9.
Мода будет равна = 33 + 9*((14-8)/(14-8+14-9))=37,9 млн. руб.
Найдем медиану по формуле. 
Медианный интервал находим по накопленной частоте. Суммируются f частоты, пока не достигается значение, превышающее середину совокупности (36/2=18 млн. руб.).
|
Группы компаний по основным производственным фондам, млн. руб. (х) |
Число компаний (f) |
Накопленная частота S |
|
10 – 25 |
2 |
2 |
|
25 – 33 |
8 |
10 |
|
33 – 42 |
14 |
24 |
|
42 – 49 |
9 |
33 |
|
49 – 62 |
3 |
36 |
Таким образом, медианный интервал от 33 до 42 млн. руб. Значит величина медианного интервала i = 42-33=9.
Частота медианного интервала fМе=14.
Нижняя граница медианного интервала  равна 33.
равна 33.
Накопленная частота предмедианного интервала  равна 10.
равна 10.
Медиана будет равна = 33 + 9*((36/2-10)/(14))=38,14 млн. руб.
Расчеты по теме “индексы”
Пример по выборке.
Задача по группировке.
Решение задачи по расчету средней.
Задача по кореляционному анализу
Контрольные и курсовые работы по общей теории статистики и экономической статистике по этим и другим темам представлены в соответствующем разделе сайта.



