Математика,
вопрос задал Dassshhhhaahaha,
5 лет назад
ВладимирБ:
Неравенство , наверное, не строгое
ВладимирБ:
x€(-5;1/2)U(3;4)
ВладимирБ:
Промежутки открытые….
Dassshhhhaahaha:
Сумма будет: -2;4,5?
ВладимирБ:
Верно так x€(-5;-1/2)U(3;4)
ВладимирБ:
Это решение неравенства
ВладимирБ:
Как найти длину интервала, если концы не входят в интервал?
ВладимирБ:
Ответы на вопрос
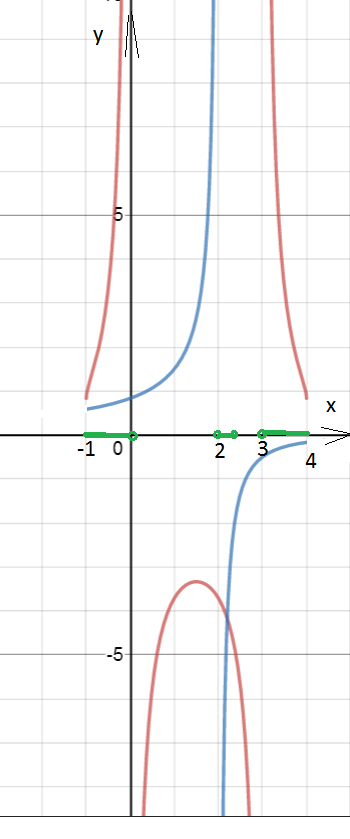
По методу рационализации функция с учетом ОДЗ принимает такие же знаки как
(решение методом интервалов прикрепляю)
Найдем сумму длин интервалов.
Приложения:
Новые вопросы
$begingroup$
I was reading Ivan Niven’s Maxima and Minima without calculus – more precisely the section regarding the Jeep crossing the Desert but that’s not the point.
In that section is given an “almost self-evident lemma” which I understand but I can’t see how I could prove it.
Consider a finite number of closed intervals. possibly
overlapping on a straight line segment AB of length r. If each point of AB belongs to at least s of the intervals. then the sum of the lengths of the intervals is at least rs.
I think the length of AB is of no use (we can scale AB however I want) so the lemma can be rewritten as this :
Consider a finite number of closed intervals. possibly
overlapping on a straight line segment AB of length 1. If each point of AB belongs to at least s of the intervals. then the sum of the lengths of the intervals is at least s.
There’s a figure illustrating the lemma – and I see why it is true, but I wonder how I could prove it (which may be harder than understanding the lemma)
asked Jul 6, 2022 at 9:50
$endgroup$
1
$begingroup$
Here is a proof using, I beg your pardon, (elementary) properties of integration:
Let $I_k$ be the $k$th interval.
Let $chi_k$ be the characteristic function of $I_k$.
($chi(x)=1 iff x in I_k$, $ chi_k(x)=0$ otherwise)
Let
$$f(x):=sum chi_k(x)$$
As, for any $x$, $f(x)ge s$, we have:
$$int_0^r f(x)dx ge s times length([0,r])=sr$$
But
$$int_0^r f(x)dx=sum int_0^r chi_k(x)dx=sum length(I_k)$$
proving the result.
answered Jul 6, 2022 at 10:27
![]()
Jean MarieJean Marie
74.5k7 gold badges43 silver badges105 bronze badges
$endgroup$
2
$begingroup$
Let $L$ be the line segment of length $r$.
Suppose $L$ is covered by finite number of closed intervals be such that each point of $L$ contained in at least $s$ closed intervals .
Then $Lsubset bigcup_{i=1}^{m}bigcap_{j=1}^{nge s} C_{ij}$ where $C_{ij}$ ‘s are closed intervals.
$begin{align}r=ell(L) &le ell(bigcup_{i=1}^{m}bigcap_{j=1}^{nge s} C_{ij}) \&le sum_{i=1}^{m} ell( bigcap_{j=1}^{nge s} C_{ij}) spacequadquad …1\&le frac{1}{n}sum_{i=1}^{m} sum_{j=1}^{nge s} ell(C_{ij})quad … 2end{align}$
Hence $sum_{i=1}^{m} sum_{j=1}^{nge s} ell(C_{ij})ge rnge rs$
$… 1$
$text{finite sub-aditivity of Length function}$
$…2$
$bigcap_{j=1}^{nge s} C_{ij}subset C_{ij}$ forall $j=1, 2,ldots , nge s$
Implies
$ncdotell(bigcap_{j=1}^{nge s} C_{ij}) le sum_{j=1}^{nge s} ell(C_{ij})$
answered Jul 6, 2022 at 12:08
![]()
Sourav GhoshSourav Ghosh
12.5k3 gold badges8 silver badges38 bronze badges
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Ответ:
0.625
Объяснение:
ОДЗ:
1/4-x>0 => x < 1/4, |x+1/2| ≠ 1 => x ≠ -3/2 и x ≠ 1/2
Получаем, что:
x ∈ ( -ထ ; -3/2 )∪( -3/2 ; 1/4 )
После проверки log4 (1/4 – x), равно 1, мы поняли, что это неравенство не будет выполнятся.
Сделаем замену и рассмотрим два случая:
1. log4 (1/4 – x)>0 ⇔ 1/4-x>1 ⇔ x< -3/4
(log|x+1/2| (1/4-x) -1) * log16 (1/4 – x) > log4 1/4-x / |x+1/2| ⇔ 1/2(log|x+1/2|(1/4-x)-1) > log4(1/4-x)/log4(1/4-x) – log4|x+1/2|/log4(1/4-x)⇔1/2(log|x+1/2|(1/4-x)-1) >
>-log1/4-x|x+1/2| ⇔ 1/2(t-1) > 1-1/t ⇔ t^2-3t+2/t > 0 ⇔ (t-1)(t-2)/t > 0
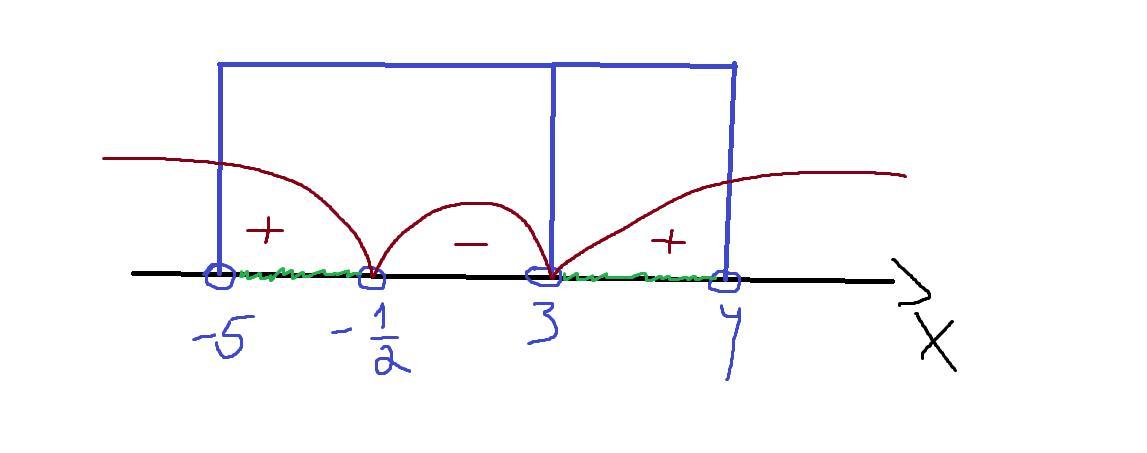
Решим через метод интервалов:
t ∉ (0;1)∪(2;+ထ) => t=log|x+1/2|(1/4-x)>0
Мы знаем, что есть лучи (-ထ;-3/2) и (1/2;ထ)
В ОДЗ входит только (-ထ;-3/2), а это значит что нет такого луча x, что
t ∈ (0;1).
Решим t > 2
log|x+1/2|(1/4-x)>2 ⇔ 1/4-x > x+1/2|^2 ⇔ 1/4-x>x^2+x+1/4 ⇔ x ∈ (-2;0),
x ∈ (-2;0) ⋂ ( -ထ;-3/2 ) => x ∈ (-2;-3/2)
2. log4 (1/4 – x) < 0 ⇔ 1/4-x<1 ⇔ x>-3/4
Относительно t, неравенство = (t-1)(t-2)/t<0 , его решением является множество t ∈ ( -ထ ; 0 ) ∪ (1 : 2), в таком случае, мы будем рассматривать не весь луч, а часть, которая входит в ОДЗ: x ∈ (-3/4;1/4), при всех таких x |x+1/2| < 1 => t ∈ (1;2) => |x+1/2|^2 < 1/4-x < |x+1/2|
Первое неравенство дает условие x ∈ (-2;0), а второе выполняется только при x > -1/8
Получаем решение x ∈ (-1/8;0)
В решение входят 2 интервала (-2;-3/2) и (-1/8;0)
Длина 1-го = 1/2, длина 2-го = -1/8
Получаем сумму 5/8
5/8 = 0.625
Надеюсь, хоть чем-то я тебе помог.
P.s. я только сейчас увидел спец. знаки, переделывать не буду, по старинке, думаю, поймете
Вопросец по неравенству
Мастер
(2384),
закрыт
14 лет назад
Аркадий Редько
Просветленный
(23856)
14 лет назад
1.Найдем область определения выражения:
x+18>0 x>-18; (x-2)(x+2) не равен 0, т. е. х не равен 2 или х не равен -2
2. навйдем ” нули” ,т. е. приравняем числитель к 0. Получим, что корень квадратный из х^2+5=5-x, возведем обе частив квадрат и получим корень х=2 Сделаем проверку, не посторонний ли это корень. Все в порядке.
3. Теперь все эти данные выставим на координатную прямую и получим интервалы
х>-18 x=2 x=-2 от -18 до -2 от -2 до 2 от 2 до плюс бесконечности.
В каждом интервале поставим знаки, которые соответствуют данному выражению.
В первом будет отрицательный, во втором положительный и в третьем положительный. Ваш ответ : ( -18; -2) . Под длиной, видимо, подразумевается разность координат, т. е. – 2 – ( -18)=-2+18 =16
Источник: личные знания
Задача 12267 Найдите сумму длин всех промежутков,…
Условие
![]()
Найдите сумму длин всех промежутков, входящих в решение неравенства 1/(x-2)+5/(6-3sqrt(4+3x-x^2)) > 1/(1+|x-2|)

математика 10-11 класс
2729
Решение
![]()
★
ОДЗ:
{x≠2;
{4+3x-x^2≥0 ⇒ [-1;4]
{6-3sqrt(4+3x-x^2)≠0 ⇒ 3x-x^2)≠0
x∈[-1;0)U(0;2)U(2;3)U(3;4]
Перепишем неравенство в виде
(5/(6-3sqrt(4+3x-x^2))) > (1/(1+|x-2|)-(1/(x-2))
Строим графики
у=(5/(6-3sqrt(4+3x-x^2)))- красного цвета
у=(1/(1+|x-2|)-(1/(x-2))- синего цвета
Условию задачи удовлетворяют те х из области определения, при которых красный график выше чем синий.
Найдем точку пересечения.
Случай х≥2
|x-2|=x-2
5/(6-sqrt(4+3x-x^2))=-1/(x^2-3x+2)
замена
x^2-3x=t
5t+10=-6+3sqrt(4-t)
25t^2+169t+220=0
t=-5 или t=-44/25
x^2-3x+5=0 уравнение не имеет корней D < 0
25x^2-75x+44=0
x=(15+3sqrt(33))/10- корень удовлетворяющий условию х≥2
О т в е т. [-1;0)U(2;(15+3sqrt(33))/10)U(3;4)
Cумма длин 2 целых (3sqrt(33)-5)/10