Сумма первоначального года как найти

Хотите научиться решать задания на простые проценты?

Привет! Меня зовут Александр Георгиевич. Мне $35+$ лет. Я – профессиональный репетитор по математике и информатике. Уже на протяжении $10+$ лет готовлю школьников $9-11$-ых классов к успешной сдаче ЕГЭ по математике/информатике.

На официальном экзамене ЕГЭ по математике вас в обязательном порядке поджидает задача из экономического блока. Есть неплохая вероятность, что попадется задание на простые проценты. В данной статье хочу показать вам решение подобного задания.

Несмотря на то, что вы крайне занятой человек, ценящий собственное время, настоятельно рекомендую вам потратить буквально $2-3$ минуты и познакомиться с отзывами моих учеников. Все они достигли поставленных целей и набрали высокие баллы на  рубежном контроле ЕГЭ.

Для записи ко мне на частную подготовку позвоните по телефону, указанному в шапке данного сайта. Приготовьте любые уточняющие вопросы. Жду вас на первом пробном занятии.

Условие задачи

Вкладчик открыл счет в банке. Процентная ставка по банковским вкладам составляет (8%) в год. Через (3) года на счете вкладчика сформировалась сумма размером (310,000) рублей.

Определить первоначальный банковский вклад (в рублях).

Решение задачи

Если внимательно прочитать условие задачи, то сразу заметно, что нет никаких фраз-маркеров, указывающих на то, что это задание на простые проценты. В общем постановка задачи оставляет желать лучшего! Но, очевидно, что в данном случае нет никакой капитализации процентов, следовательно, применим схему простых процентов.

Давайте введем следующие обозначения:

$V_{старт}$ – размер первоначального вклада	$q$ – ставка банка, выраженная в процентах	$r = frac{q}{100}$ – процентная ставка банка, выраженная в долях
$V_{конец}$ – размер конечного вклада	(n) – общее количество отчетных периодов	(i) – номер текущего отчетного периода

Эти обозначения используются во всех моих заданиях на простые проценты. Это очень удобно, читателю достаточно просто переключаться между различными решениями, не теряя сути математических выкладок.

Из условия вытекает, что:

$V_{конец} = 310 000$, руб.

$q = 8%$

$n = 3$, лет.

$V_{старт} = ?$

Наша цель – определить размер первоначального банковского вклада, выраженный в рублях. Гораздо чаще на экзамене просят выяснить размер конечного вклада! Будьте внимательны при чтении формулировки задания.

В заданиях на простые проценты все упирается в одну единственную формулу. Какую? Ее получение было мною детально описано, когда разрабатывалась математическая модель простых процентов. Не в курсе, что это за модель? Срочно бегите ее изучать, исследовать, зубрить!

$V_{конец} = V_{старт} * (1 + n * r)$ – главная формула схемы простых процентов.

Важно! Когда будете сдавать ЕГЭ по математике, постарайтесь, хотя бы в сокращенной форме, продемонстрировать вывод математической модели простых процентов. Иначе можете не досчитаться баллов, даже, несмотря на то, что получите абсолютно правильный ответ. Будет очень досадно!

Поскольку в формуле фигурирует переменная $r$, а не $q$, то давайте выполним соответствующий перевод: $r = frac{q}{100%} = frac{8%}{100%} = 0.08$.

Кстати, а нам ведь в вышеприведенной зависимости все известно, кроме переменной $V_{старт}$, следовательно, составим и решим следующее незамысловатое линейное уравнение:

$310 000 = V_{старт} * (1 + 3 * 0.08)$

$V_{старт} = frac{310 000}{1.24}$

Чтобы правильно разделить без калькулятора эти неудобные числа, давайте разложим их на некоторые делители и попробуем потом сократить:

$310 000 = 31 * 10 000$ – пока так, хотя это неполное разложение, разумеется.

$1.24 = frac{124}{100} = frac{31 * 4}{4 * 25} = frac{31}{25}$

Собираем все воедино:

$V_{старт} = (31 * 10 000) : frac{31}{25}$

$V_{старт} = frac{31 * 10 000 * 25}{31}$

$V_{старт} = 10 000 * 25$

$V_{старт} = 250 000$, рублей.

Готово! Решили! Это значение и будет выписано в качестве официального ответа. Давайте сейчас проведем верификацию в программе “MS Excel“.

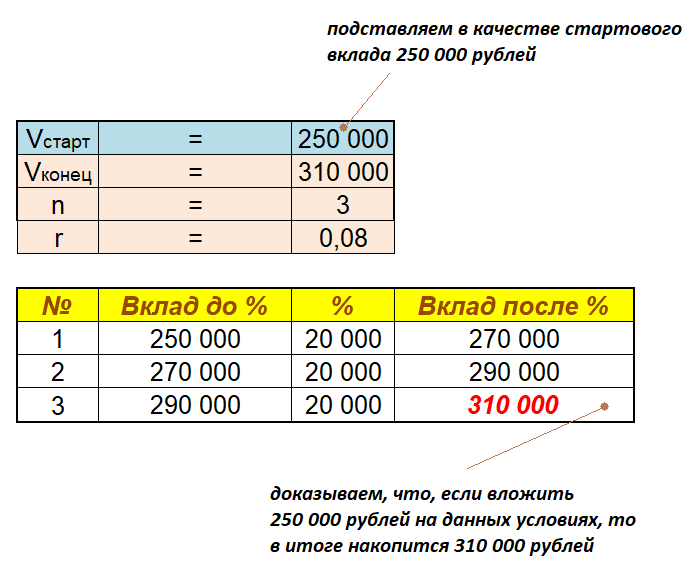
Ответ: $250 000$

Выводы и рекомендации

Задания на простые проценты не покажутся вам сложными, и вы с ними легко справитесь, если:

1. не перепутаете схему простых процентов со схемой сложных процентов;

2. хорошо знаете математическую модель простых процентов.

Это, пожалуй, главные факторы, влияющие на успешность решения подобных заданий!

Примеры условий реальных заданий на простые проценты, встречающихся на ЕГЭ по математике

А сейчас пришло время вам немного поработать самостоятельно. Нужно ведь закрепить пройденный материал. Если что-то не будет получаться – ничего страшного в этом нет. Переходите по ссылке “Перейти к текстовому решению” и внимательно знакомьтесь с моим решением.

Задача №1 Вкладчик поместил сумму размером (80,000) рублей в банк. Процентная ставка банка по вкладам составляет (9%) в год. Схема вложений денег не предполагает капитализацию процентов. Определить, какого размера станет вклад через (6) лет? Перейти к текстовому решению

Задача №2 Вкладчик поместил сумму размером (300,000) рублей в банк. В договоре прописано, что схема начисления процентов на депозит не предполагает их капитализации. Через (9) лет на его балансе образовалось сумма в размере  (516,000) рублей. Определить процентную ставку банка по вкладу. Перейти к текстовому решению

Задача №3 Вкладчик открыл счет в банке. Процентная ставка по банковским вкладам составляет (8%) в год. Через (3) года на счете вкладчика сформировалась сумма размером (310,000) рублей. Определить первоначальный банковский вклад (в рублях). Перейти к текстовому решению

Также вы можете написать мне на почту и задать какие-либо уточняющие вопросы по данным заданиям на простые проценты. Или публикуйте свои вопросы в комментариях к данной статье. Я постараюсь максимально оперативно ответить!

Данный список задач я регулярно обновляю и дополняю, поэтому, рекомендую периодически сюда заглядывать.

Хотите стать профессиональным решателем заданий на простые проценты? Записывайтесь ко мне на индивидуальную подготовку!

Скажу честно, задания из экономического блока ЕГЭ по математике мне импонируют. На своих частных уроках показываю эффективные методики решения всевозможных задач финансовой направленности. Решаем с учеником не только задания на простые проценты, а в том числе и задачи на кредиты, на вклады, про акции, оптимизационного характера, смешанного типа.

Я – репетитор-практик! Это означает, что на частных занятиях мы решаем, решаем и еще раз решаем! Теория без практики мертва на $100%$. Львиную долю урока я посвящаю исключительно практической деятельности. Теоретического материала предостаточно в сети Интернет, да, не всегда полного и адекватного, но, в целом, найти можно, что угодно.

Не забывайте подписываться на мой Youtube-канал, посвященный математике, информатике, программированию, алгоритмам и базам данных. Также регулярно проходят образовательные стримы на twitch-канале. И, пожалуй, подпишитесь на рассылку, чтобы в числе первых узнавать о новых публикуемых материалах.

Ко мне поступает множество заявок на персональное обучение в любое время года, но я физически не могу всем помочь. Поэтому, не откладывайте свое решение в долгий ящик, а действуйте прямо сейчас. Звоните мне по мобильному номеру, задавайте тематические уточняющие вопросы и записывайтесь на первый пробный урок.

Я готов начать решать задания на простые проценты прямо сейчас! А вы готовы начать свой успешный путь?

Процедура
начисления сложных процентов подразумевает,
что в конце каждого интервала начисления
процентная ставка применяется к
наращенной сумме на начало этого
интервала начисления.

где
Р
— первоначальная сумма,

S
—
наращенная сумма,

i
—
годовая процентная ставка (проценты
сложные);

п
—
период начисления процентов (в годах).

Пример
7. Первоначальная сумма Р
=
5000 руб. помещена в банк на п
= 2
года под i
= 15%
годовых (проценты сложные).

Тогда
наращенная сумма после двух лет

Зная
первоначальную сумму Р, наращенную
сумму S, сложную годовую процентную
ставку i

Пример.
Первоначальная сумма Р
=
3000 руб., наращенная сумма S
= 4500
руб., i
= 20%
годовых (проценты сложные).

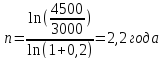
Зная
первоначальную сумму Р, наращенную
сумму S, период начисления п
(в
годах), можно определить сложную годовую
процентную ставку i:

Пример.
Первоначальная сумма P
= 2000
руб., наращенная сумма S
= 3500
руб., период начисления п
= 3
года.

Математическим
дисконтированием называется
операция, когда по наращенной сумме S,
периоду начисления п
и
сложной процентной ставке i
нужно
определить первоначальную сумму Р. Это
делается следующим образом:

Пример
10. Наращенная сумма S
= 7000
руб., период начисления п
= 2 года,
сложная процентная ставка i
= 12%
годовых.

Если
период начисления п
не
является целым числом, то п
= [п] (целая
часть) + {п}
(дробная
часть). Тогда
наращенная сумма

Пример
13. Первоначальная сумма Р
= 6000
руб. помещена в банк на п
= 2,5
года под i
= 20%
годовых (проценты сложные). Найдем
наращенную сумму двумя способами.

Данные
для самостоятельных расчетов – в
приложении
16.

Все
расчеты выполнить в Excel.
Построить графики. Сделать выводы по
полученным результатам.

Приложение
16

Буквенные обозначения величин	Значение величин по вариантам
1	2	3	4	5	6	7	8	9	10
Р	1000	1500	2000	2500	3000	3500	4000	4500	5000	5500
n	2	3	4	5	6	2	3	4	5	6
i	6	8	10	12	14	16	18	20	22	24
S	5000	6000	7000	8000	9000	10000	11000	12000	13000	14000

Практическое занятие 15

При
выработке долгосрочных инвестиционных
решений необходимо знать, какую отдачу
принесут инвестиции, и сопоставить
прибыль от инвестирования в различные
проекты.

Стандартным
подходом можно вложения денег в
безрисковые ценные бумаги (такими
считаются особо надежные государственные
ценные бумаги), которые будут приносить
постоянный доход. Доходность по
инвестициям в такие ценные бумаги
представляет собой альтернативные
издержки по инвестициям, так
как инвестированные в особо надежные
государственные ценные бумаги средства
не могут быть инвестированы еще куда-то.

Альтернативные
издержки по инвестициям также называют
стоимостью
капитала, минимально необходимой нормой
прибыли, ставкой дисконтирования и
процентной
ставкой. Предприятие
должно рассматривать только такие
инвестиционные проекты, прибыль от
которых выше альтернативных издержек
по инвестициям.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

По какой формуле рассчитать изначальную сумму вклада?

Юлия Фомичева

Ученик

(119),
на голосовании

2 месяца назад

Вы открыли депозит в банке под 10% годовых. Через год забрали средства вместе с процентами в сумме 1000 руб. Сколько средств вы вложили в депозит изначально?

Простые задачи по банковскому делу на расчет процентов с решением. Как найти процент?

Определение доходности вклада

1. Задача по банковскому делу с решением

0.3 процента в день сколько будет за год?

Решение задачи

В году 365 дней. Значит 0,3*365=109,5% годовых.

2. 17 процентов годовых от суммы 10000 рублей это сколько денег?

Расчет: 0,17*10000=1700 рублей в год.

3. пример

20000 рублей положены в банк под 18 процентах годовых. Какой доход получит вкладчик через год?

Решение задачи 0,18*20000=3600 рублей в год.

4. Рассчитать доход, если клиент внес в банк 20000 под 7,5 процентов на 4 месяца.

Расчет: 20000*0,075*4/12=500.

5. 27000 сколько составит 10% от этой суммы

Ответ: 0,1*27000=2700.

6. Найти 5 процентов годовых от суммы 145 тысяч рублей.

Решение задачи

0,05*145000=7250 рублей.

7. 600 рублей от 12000 сколько процентов.

Вычисление:

12000 – 100%.

600 – х%.

Х=12000*100%/600=20%.

Ответ:  600 рублей от 12000 составит 20%.

8. Готовая задача

Под какой процент была вложена 2000руб., если через 8 лет сумма наращенного капитала составила 7000 руб.

S=P+I. S=7000. P=2000. Значит I=5000 рублей.

По формуле простых процентов I=P*i*n/100%.

P – первоначальная сумма. i – процентная ставка. n – срок в годах.

S – наращенный капитал.

5000=2000*i*8/100%. Следовательно процентная ставка i = 5000/(2000*100%/8)=20%.

9. Определите наращенную сумму для ссуды 10000 рублей, выданную 5 февраля по 8 июня сего года под 15% годовых.

Если не указана практика расчета процентов, то используется английская (применяемая в России). Значит в году 365 дней. А месяце дней по календарю.

Считаем дни с 5 февраля по 8 июня (5 и 8 не учитываем, в феврале примем 28 дней).

28+31+30+31+7=127.

S=P+I.

P – первоначальная сумма. i – процентная ставка. n – срок в годах.

S – наращенный капитал.

По формуле простых процентов I=P*i*n/100%.

S=10000+10000*0,15*127/365=10523 рублей.

10. Депозит в сумме 180000 руб. положен в банк на 3 года. Сложная процентная ставка 5% годовых. Определите сумму процентов

S=P*(1+i)ⁿ

P – первоначальная сумма. i – процентная ставка. n – срок в годах.

I = S-P. Где I – сумма процентов.

S=18000*(1+0,05)³=20837 рублей.

I = 20837-18000=2837 рублей. – сумма процентов.

11.  Если положить 150000 т.рублей под процент в сбербанк под 8% годовых, сколько можно будет иметь процентов ежемесячно.

Расчет: 150000*0,08=12000 т. рублей в год. Следовательно, 12000/12=1000 рублей процентов месяц.

Задача 1

Определите,
какой из вариантов кредитования (по уровню доходности по ставке простых
процентов) наиболее выгоден для заемщика:

– сумма
первоначального долга 120000 рублей; срок кредитования 250 дней; наращенная
сумма долга 130000 рублей;

– сумма
первоначального долга 120000 рублей; срок кредитования 180 дней; наращенная
сумма долга 128000 рублей;

– сумма
первоначального долга 120000 рублей; срок кредитования 320 дней; наращенная
сумма долга 136000 рублей;

---

Задача 2

Клиент взял
в банке кредит на 180 дней по номинальной ставке 16% и в конце срока вернул всю
сумму долга с процентами, что составило 310 тыс. руб. Определить сумму
выданного кредита.

---

Задача 3

На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?

---

Задача 4

Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.

---

Задача 5

  5 июня клиент взял кредит 200 тыс. руб. При
погашении кредита единым платежом клиент заплатил 230 тыс. руб. Определить срок
операции и дату погашения кредита, если в операции использовалась простая
процентная ставка 18% годовых (точные проценты с фактическим сроком операции).

---

Задача 6

Через 120
дней с момента подписания кредитного договора заемщик должен вернуть банку 750
тыс. руб. Процентная ставка по кредиту равна 18% годовых. Чему равна
первоначальная сумма долга?

---

Задача 7

Банк
принимает депозиты на 3 месяца по ставке 50% годовых, на 6 месяцев по ставке
70% годовых и на год по ставке 90% годовых. Определить суммы, которые может
получить владелец депозита 4500 руб., выбрать наиболее выгодный вариант
размещения вклада.

---

Задача 8

Банк
объявил следующие условия выдачи ссуды на один год: за первый квартал ссудный
процент 50%; за второй квартал – 75%; за третий – 100%; за четвертый квартал –
125%. Определить сумму к возврату в банк, если ссуда составляет 200000 руб.

---

Задача 9

Найдите
простой процент, начисленный за четыре месяца по ставке 1% на сумму 10 тыс.
руб.

---

Задача 10

Ссуда в
размере 50 тыс. руб. была выдана на полгода при условии начисления на нее
простых процентов по ставке 20%. Определите сумму погашения.

---

Задача 11

Банк
начисляет 10 тыс. руб. за использование 800 руб. в течение 60 дней. Найдите
простую процентную ставку, если применяются обыкновенные проценты.

---

Задача 12

Какая
сумма необходима для того, чтобы накопить за пять лет 70 тыс. руб., если на эту
сумму будут начисляться простые проценты по ставке 8%?

---

Задача 13

За
сколько дней сумма 800 тыс. руб. увеличится до 900 тыс. руб., если на исходную
сумму начисляются обыкновенные простые проценты по ставке 9%?

---

Задача 14

Сумма 100
тыс. руб. была получена в долг 20 января с условием начисления на нее точных
простых процентов по ставке 25% и возвращения денег через год в сумме 120 тыс.
руб. Определите дату погашения долга, если год високосный.

---

Задача 15

В один и
тот же день в банк были вложены сумма 20 000 руб. под 4 % годовых и сумма 18
000 руб. под 5 % годовых. Вычислите, через сколько лет оба дохода будут
одинаковыми.

---

Задача 16

Ставка процентов банка по вкладам до
востребования, составлявшая в начале года 10% годовых, через полгода была
снижена до 8% годовых, а еще через 3 месяца до 6% годовых.  Определите общую сумму, полученную клиентом банка
через год, если им был внесен вклад в размере 10 тыс. руб.

---

Задача 17

Банк
предлагает разместить вкладчику 700 000 руб. на срочный депозит в трех
вариантах: а) на 1 день под 6% годовых с последующим реинвестированием
ежедневно в течение месяца; б) на 10 дней под 10% годовых с последующим
реинвестированием каждую декаду в течение месяцев; в) на 1 месяц под 18%
годовых. Определить наиболее выгодный вариант вложения денежных средств.

---

Задача 18

Какая сумма была внесена на счет в
банке, если по истечении 5 лет на счета стало 5200 руб. Начисление процентов
осуществлялось по схеме простых процентов по ставке 10% за каждое полугодие?

---

Задача 19

Ссуда в
размере 10 тыс. руб. выдается по учетной ставке простых процентов 8% годовых.
Определить срок ссуды в годах, если заемщик хочет получить 9,5 тыс. руб.

---

Задача 20

Проценты
по ссуде размером 5 тыс. р., выданной на два месяца, составила 125 р. Какова
процентная ставка?

---

Задача 21

Кредит для покупки товара на сумму
50 тыс. руб. открыт с 12.02 до 02.10 включительно под 18% годовых. Какую сумму
заплатит должник в конце срока при начислении простых процентов?  (временная база – ACT/360)

---

Задача 22

Найти простой процент для 7000 руб.
за пять месяцев при 3% годовых.

---

Задача 23

Какой капитал, будучи отдан в рост
под 7,5%, обратится через год вместе с процентными деньгами в 1343 рубля 75
копеек?

---

Задача 24

Ссуда
800000 руб. выдана на квартал по простой ставке процентов 20% годовых.
Определить наращенную сумму.

---

Задача 25

Какую сумму необходимо положить в
банк на 9 месяцев, чтобы накопить 900 руб., если он принимает вклады на
условиях 30% годовых?

---

Задача 26

Определите размер наращенной суммы
за один год, если первоначальная сумма равна 10 тыс. руб., первые полгода
годовая ставка простых процентов равна 18%, а вторые 21%.

---

Задача 27

Вклад в размере 250 000 руб.
помещен в банк по ставке 15% годовых. Спустя некоторое время получатель снял со
своего вклада 290 000 руб. Необходимо найти срок размещения вклада в
банке.

---

Задача 28

Через сколько лет сумма вклада
утроится, если банк работает по ставке 18% годовых.

---

Задача 29

Банк «Российский кредит» принимает
вклады до востребования по простой ставке 40% годовых. Определить сумму
начисленных процентов и сумму долга с начисленными процентами на вклад 2000 руб.,
размещенный на полгода.

---

Задача 30

Вкладчик положил в банк 3000 руб.,
который выплачивает в год 6% (простых). Какая сумма будет на счету вкладчика
через 170 дней?

---

Задача 31

В банк было положено 150000 руб.
Сколько процентов (простых) выплачивает банк в год? Если через 2 года 9 месяцев
на счету было 270000 руб.

---

Задача 32

Найти
сумму начисленных простых процентов I и конечную сумму S, если
вклад P=1107.08 руб. размещен на t=10 месяцев при годовой
ставке i=70.7%.

---

Задача 33

Сколько
дней t понадобится, чтобы сумма в P=2228.23 рублей
«заработала» I=2.77 рублей, если она инвестируются при ставке i=23.7%
обыкновенного простого процента?

---

Задача 34

В банк положены на срочный
сберегательный счет 10000 руб. на 2 года по простой ставке 9% годовых с
дальнейшей пролонгацией на последующие 3 года по простой ставке 5% годовых:

а) Найдите наращенную сумму по
истечении 5 лет;

б) Найдите наращенную сумму по
истечении 5 лет, если через 2 года вклад изымается и кладется на новый счет на
3 года по простой ставке 5% годовых.

Укажите, какой вариант является
более предпочтительным а) или б)

---

Задача 35

Вами открыт вклад под 21% годовых.
На него начислен процентный платеж в сумме 21 тыс. руб. Найдите величину
вклада, если он был открыт на 21 год.

---

Задача 36

Ссуда в размере 30 000 руб. выдана
на полгода по простой ставке 100% годовых. Определить наращенную сумму.

---

Задача 37

Определите годовую ставку простых
процентов, при которой сумма в 5 тыс. руб. за три квартала возрастет до 6,5
тыс. руб.

---

Задача 38

В банк помещен капитал под 20%
годовых (обыкновенные проценты). По истечении 270 дней его величина составила
575 тыс. руб. Определить величину помещенного в банк капитала и сумму
начисленных процентов.

---

Задача 39

Банк
принимает депозиты на 3 месяца по ставке 15% годовых, на 8 месяцев по ставке
17% годовых и на год по ставке 19% годовых. Определить суммы, которые может
получить владелец депозита 14500 руб. Выбрать наиболее выгодный вариант
размещения вклада.

---

Задача 40

Определить
срок в годах, при начислении простых процентов, по следующим данным:

Процентная
ставка 18%

Вклад –
2000 руб.

Вклад с
процентами – 10200 руб.

---

Задача 41

По
контракту кредитор предоставил в долг 60000 руб. Заемщик должен уплатить 70000
руб. через 90 дней. Определить доходность финансовой операции для кредитора в
виде процентной ставки i простых процентов.

---

Задача 42

Годовая ставка простых процентов в
банке составляет 12%. Через сколько лет вложенная сумма а) удвоится; б)
утроится?

---

Задача 43

В банк
положено 10000 руб., а через 2,5 года на счете было 120000 руб. Определить
ставку процентов банка.

---

Задача 44

За
сколько лет удвоится сумма долга, если применяется простая годовая ставка 17%?

---

Задача 45

При
открытии сберегательного счета при ставке 8% годовых 20 апреля на счет была
положена сумма 1 млн. рублей. Затем 5 июля этого же года было добавлено 500
тыс. руб. 10 сентября сняли сумму 750 тыс. рублей, а 20 ноября того же года
счет был закрыт.

Какую
сумму получил вкладчик при закрытии счета?

---

Задача 46

Какую
сумму надо положить в банк, выплачивающий 4% простых в год, чтобы получить 50
тыс. руб. а) через 4 месяца, б) через 1 год, в) через 2 года 9 месяцев?

---

Задача 47

Договор
предусматривает следующие ставки простых процентов: за первый квартал j₁=20%, за второй квартал j₂=18%, за третий квартал j₃=16%, за четвертый квартал j₄=14%. Определить
коэффициент наращения за год.

---

Задача 48

Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.

---

Задача 49

На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?