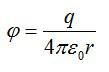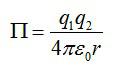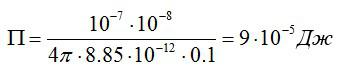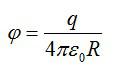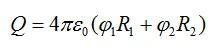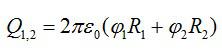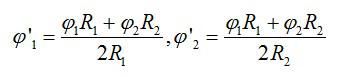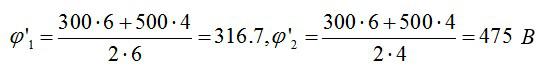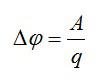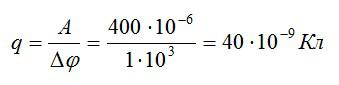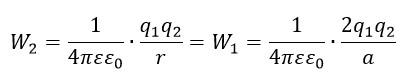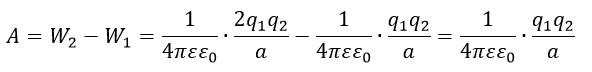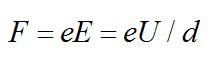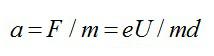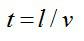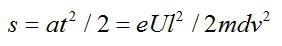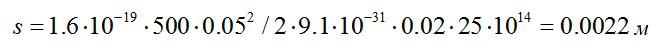Физические задачи по электростатике мало кто любит. Но что поделать, решать их надо. Разберемся, как это делать по-быстрому и с использованием подробных примеров решений задач на разность потенциалов, задач на работу электрического поля и напряженность.
Наш телеграм – полезная информация для абитуриентов и студентов всех специальностей, присоединяйтесь!
Решение задач на разность потенциалов и работу поля: примеры
Задача №1 на потенциальную энергию системы зарядов
Условие
Два точечных заряда величиной 100 нКл и 10 нКл находятся на расстоянии r=10 см друг от друга. Вычислить потенциальную энергию системы этих зарядов.
Решение
Потенциал поля точечного заряда равен:
Так что, потенциальная энергия зарядов будет равна:
Подставим значения из условия и найдем:
Ответ: П=9*10^-5 Дж.
Задача №2 на определение потенциала заряженных шаров
Условие
Шар радиусом R1=6 см заряжен до потенциала 300 В , а шар радиусом R2=4 см – до потенциала 500 В. Найдите потенциал шаров после того, как их соединили металлическим проводом, емкостью которого можно пренебречь.
Решение
Потенциал шара равен:
Суммарный заряд двух шаров будет равен:
После соединения шаров заряд каждого будет равен:
Тогда суммарный потенциал шаров вычислится по формуле:
Подставим значения и найдем:
Ответ: 317 В; 475 В.
Задача №3 на разность потенциалов и работу по перемещению заряда
Условие
Заряд переместился между двумя точками с разностью потенциалов 1 кВ, при этом поле совершило работу, равную 40 мкДж. Найдите величину заряда.
Решение
По определению, разность потенциалов равна работе по перемещению заряда, деленной на величину этого заряда:
Отсюда можно выразить заряд и вычислить ответ:
Ответ: 40 нКл.
Задача №4 на работу электрического поля по перемещению заряда
Условие
Два точечных заряда q1=6 мкКл и q2=2 мкКл, находятся на расстоянии а=60 см друг от друга. Какую работу необходимо свершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?
Решение
Находясь на расстоянии a, точечные заряды обладали потенциальной энергией:
На вдвое меньшем расстоянии энергия зарядов равна:
Работа, затраченная на сближение зарядов:
Подставляем числовые данные и вычисляем:
Ответ: A=0,18 Дж.
Задача №5 на движение заряженной частицы в поле
Условие
Электрон влетает в плоский воздушный конденсатор параллельно его пластинам со скоростью V=5·107 м/с. Расстояние между пластинами d=2 см, разность потенциалов U=500 В. Найти отклонение электрона, вызванное полем конденсатора, если длина его пластины l=5 см.
Решение
При движении в электрическом поле конденсатора на электрон действует сила:
Ускорение электрона, по 2 закону Ньютона, определяется формулой:
Время движения электрона в конденсаторе вычислим, зная длину пластины и скорость частицы:
Отклонение электрона будет равно:
Найдем:
Ответ: 2.2 мм
Вопросы на тему «Работа электрического поля и разность потенциалов»
Вопрос 1. Что такое потенциал электрического поля?
Ответ. Потенциал – скалярная физическая величина, являющаяся энергетической характеристикой электростатического поля.
Потенциал поля равен отношению потенциальной энергии поля (или работы по перемещению заряда из данной точки на нулевой уровень потенциальной энергии) к величине заряда.
Для потенциала применим принцип суперпозиции.
Вопрос 2. Что такое разность потенциалов?
Ответ. Разность потенциалов – это работа по перемещению заряда из одной точки в другую. Разность потенциалов еще называют напряжением, обозначая его как разность потенциалов в начальной и конечной точках траектории заряда.
Вопрос 3. Что происходит с зарядом, когда он попадает в электрическое поле?
Ответ. На заряд со стороны поля действует сила, способная перемещать заряд в поле и совершать работу.
Вопрос 4. Какую природу имеет сила, действующая на заряд? Зависит ли величина работы от траектории заряда в поле?
Ответ. Сила, действующая со стороны поля на заряд, является проявлением электромагнитного взаимодействия. Величина работы поля не зависит от траектории заряда, так как это работа потенциальных (консервативных) сил.
Для наилучшего понимания сути задач на потенциал и работу поля, можно провести параллель между работой по перемещению заряда, потенциальной энергией в механике и работой силы тяжести.
Вопрос 5. Что такое эквипотенциальная поверхность?
Ответ. Это поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значения.
Какие бы задачи вы не решали и где ни учились, профессиональный образовательный сервис для студентов готов оказать помощь с проблемами по учебе любой сложности.
Суммарный потенциал
Cтраница 3
Тогда собственное состояние ку-лоновской задачи с энергией Еа, которая лежит чуть выше максимума суммарного потенциала – кулоновского и штарковского, уже больше не является связанным и ионизуется.
[31]
При невозможности измерения поляризационных потенциалов допускается осуществление катодной поляризации таким образом, чтобы средние значения суммарного потенциала – разности потенциалов ( включающей поляризационную и омическую составляющие) между трубой и электродом сравнения находились в пределах от – 0 9 В до – 2 5 В для трубопроводов с мастичным и ленточным покрытиями, от – 0 9 В до – 3 5 В для трубопроводов с покрытием из экструдированного полиэтилена.
[32]
Приведенные выше величины – 0 85 или – 0 95 в относятся к Де – к суммарному потенциалу при наложенном токе.
[34]
На рис. 12 приведена кривая энергии ионизации ( пунктирная линия) нейтральных атомов при переходе в трехзарядные положительные ионы ( суммарный потенциал отрыва трех электронов), из которой видно постепенное возрастание энергии ионизации и уменьшение восстановительной активности.
[35]
Каждая из сил, FI и FZ, в отдельности будет разрывна в плоскости диска, но суммарная сила F ( и суммарный потенциал Ф) как видно из ( 3), непрерывна при пересечении плоскости двойного слоя.
[37]
Так, если из нефти отбирается два нефтепродукта – бензин и дизельное топливо летнее, – то при изменении соотношения их долей отгона будет изменяться и суммарный потенциал. Связано это с тем, что с уменьшением, например, доли отгона бензина часть его вовлекается в дизельное топливо, и это позволяет расширить его пределы кипения по КК и в сумме получить эти два нефтепродукта в большем количестве, чем в случае увеличения отбора бензина.
[38]
Поэтому в роли коллективного ценового лидера имели возможность выступать и действительно выступали африканские страны – Ливия, Алжир, Нигерия, а также республиканский Иран, хотя фактический суммарный потенциал их нефтяной промышленности заметно меньше саудовского. Тем более не в пользу названной четверки складываются сравнительные финансовые возможности консервации этого потенциала.
[39]
При отсутствии блуждающих токов опасное коррозионное состояние арматуры возникает при концентрации ионов хлора в грунте или в защитном слое бетона более 0 5 мг / л и значениях суммарного потенциала более положительных, чем 0 87 В и более отрицательных, чем 1 2 В.
[40]
Гендерсона-Гессельбаха, полученные для карбоксильного катионита, демонстрируют увеличение кислотности – степени ионизации – при увеличении ионной силы раствора, что соответствует представлениям об экранировании ионов и снижении суммарного потенциала полимера по отношению к проти-воионам.
[42]
Такая ситуация вызвана тем, что потенциалы ( 6, 12) и ( 6, ехр) с указанными выше параметрами приводят к заниженным [3] и завышенным [4] значениям суммарного потенциала.
[43]
В качестве показателей, определяющих природу ионов в растворе, приняты: для ионов главных подгрупп, лантаноидов, а также переходных элементов IV периода – электростатическая характеристика ( величина ионного потенциала pZ / r); для ионов побочных групп с 18-электронной структурой – ковалент-ная характеристика, равная разности между суммарным потенциалом ионизации ( /) и теплотой гидратации иона ( Я): / – Я. Именно эти характеристики наиболее полно отражают свойства ионов в растворах при их взаимодействии с другими ионами и молекулами.
[44]
Страницы:
1
2
3
4
5
Принцип суперпозиции электрических полей

3.9
Средняя оценка: 3.9
Всего получено оценок: 215.
3.9
Средняя оценка: 3.9
Всего получено оценок: 215.
Закон Кулона, описывающий взаимодействие зарядов, относится к двум точечным зарядам. Однако в реальности такая ситуация крайне редка: как правило, реальные заряды точечными не являются, и их количество больше двух. Для определения сил взаимодействия в этом случае необходимо использовать принцип суперпозиции. Кратко рассмотрим принцип суперпозиции электрических полей.
Смысл принципа суперпозиции
Любое тело в природе существует не обособленно, а во взаимодействии с множеством окружающих тел. Поэтому очень часто возникает вопрос о результатах суммы взаимодействий. Например, движение автомобиля — это результат действия сил двигателя, сил трения, сил сопротивления воздуха, сил тяжести, сил реакции опоры и других.
Движение Земли в космическом пространстве — это результат действия сил со стороны не только Солнца, но и окружающих планет. Строго говоря, и ближайшие к Солнцу звезды также вносят свою небольшую лепту в это движение.
Для разных случаев результат совместного действия многих сил должен рассчитываться по-разному. Но наиболее часто употребляемым и наиболее интуитивно понятным является принцип суперпозиции.
Формулировка принципа суперпозиции следующая: результат нескольких величин, действующих одновременно, равен сумме исходных величин.
При этом необходимо помнить два важных момента:
- Сумма должна учитывать характер складываемых величин. Например, для скалярных неотрицательных величин используется обычная арифметическая сумма. Если величины могут быть как положительными, так и отрицательными, сумма должна быть алгебраической. Наконец, для векторных величин необходимо использовать векторные правила сложения.
- Несмотря на свою кажущуюся очевидность, принцип суперпозиции не является универсальным. Он может применяться только в случае линейных и потенциальных взаимодействий. Линейное поле не влияет само на себя, а в потенциальном поле работа силы зависит только от начальной и конечной точки траектории. Например, поле сил трения не является потенциальным, и принцип суперпозиции для сил трения не выполняется.
Принцип суперпозиции в электростатике
Проверим, допустимо ли применять принцип суперпозиции для электрических полей.
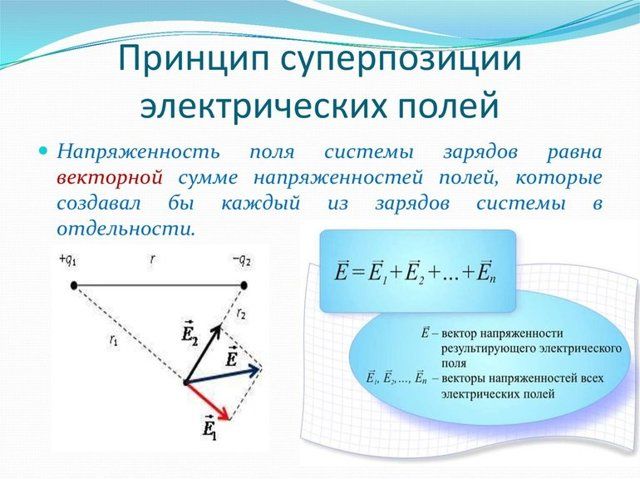
Электрическое поле характеризуется такими параметрами, как напряженность и потенциал. Первая величина — векторная, вторая —скалярная. Следовательно, при суммировании напряженностей необходимо использовать правила векторной арифметики, а при суммировании потенциалов достаточно алгебраического сложения.
Электрическое поле линейно и потенциально. А значит, к нему можно применять принцип суперпозиции. В виде формулы для напряженности электрического поля он выглядит так:
$$overrightarrow E_{общ}= overrightarrow E_1+overrightarrow E_2+…+overrightarrow E_n$$
Для потенциала электрического поля принцип суперпозиции может быть выражен формулой:
$$varphi _{общ}= varphi_1+varphi_2+…+varphi_n$$
Принцип суперпозиции также позволяет определить напряженность или потенциал поля, источником которого является не точечный заряд, а заряд, распределенный по телу.
В этом случае все тело разбивается на множество мелких областей, в каждой из которых заряд считается одинаковым, вычисляется напряженность и потенциал каждой области в рассматриваемой точке, а потом все потенциалы и напряженности складываются. В результате можно получить полную картину электрического поля такого тела с неравномерно распределенным зарядом, построить эквипотенциальные поверхности и линии напряженности.
Что мы узнали?
Если электрическое поле в точке порождается несколькими зарядами, то для определения его напряженности и потенциала необходимо использовать принцип суперпозиции. Суммарная напряженность равна векторной сумме исходных напряженностей. Суммарный потенциал равен алгебраической сумме потенциалов.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 215.
А какая ваша оценка?
Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
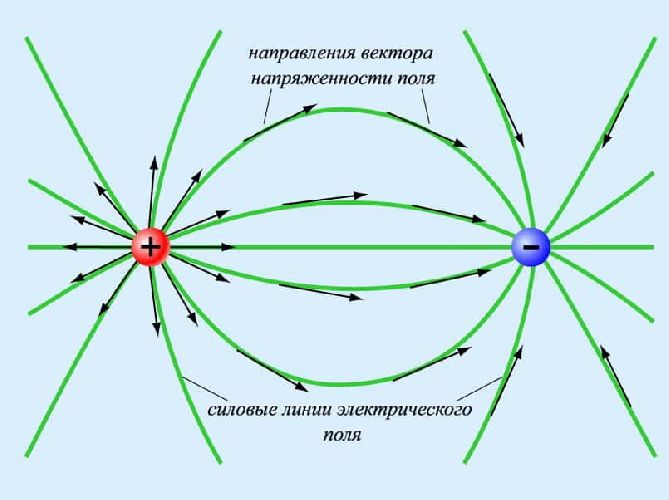
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
Потенциалом электростатического поля называется скалярная характеристика электрического поля.
Напряжённость электрического поля также является характеристикой поля, однако, в случае достаточно большого количества зарядов, поиск напряжённости затруднителен в связи с достаточно трудным сложением векторов. Тогда, для упрощения, вводят понятие потенциала. Данный параметр также описывает насколько сильно или слабо будет действовать поле на помещённый в данную точку заряд.
Потенциал точечного заряда () можно вычислить, исходя из соотношения:
(1)
- где
Принцип суперпозиции потенциала.
В случае нескольких источников, потенциал в точке численно равен сумме потенциалов, образованных от каждого из источников:
(2)
Важно: в соотношении (1) заряд может быть как положительный, так и отрицательный, следовательно, потенциал также может иметь любой знак.